Journal of Electromagnetic Analysis and Applications
Vol.07 No.02(2015), Article ID:54135,11 pages
10.4236/jemaa.2015.72003
Local Electromagnetic Fields Exhibit Temporally Non-Linear, East-West Oriented 1 - 5 nT Diminishments within a Toroid: Empirical Measurement and Quantitative Solutions Indicating a Potential Mechanism for Excess Correlation
Nicolas Rouleau, Michael Persinger*
Behavioural Neuroscience Laboratory, Laurentian University, Sudbury, Canada
Email: *mpersinger@laurentian.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2015; accepted 13 February 2015; published 16 February 2015
ABSTRACT
States of excess correlation have previously been achieved at macroscopic levels by simultaneously exposing two non-local spaces to weak electromagnetic field patterns, generated by toroids, presented in a sequence such that the angular velocity of the field is modulated by changes in frequency over time. Here we systematically investigated effects upon the local space at the center of a single toroid generating the excess correlation sequence. The results indicated that a 1 - 5 nT diminishment in field intensity on the Y- or east-west axis was characteristic of the excess correlation sequence which was not indicated for control conditions. Statistically significant shifts in field intensity approximately 40 to 60 s before the onset of the first field associated with the excess correlation sequence indicated a temporally non-linear effect which converged upon the ratio of g and the rotational velocity of the Earth for the local space where Coriolis-like forces were inferred. Intensity shifts associated with the excess correlation sequence but not controls were quantitatively convergent upon parameters of the hydrogen line (1.42 GHz). Implications for these findings were discussed in relation to Mach’s principle and, in particular, to the electron as a physical unit which was found to relate classical and quantum systems.
Keywords:
Excess Correlation, Toroid, Electromagnetism, Gravity, Coriolis-Like Force, Drift Velocity, Hydrogen Line

1. Introduction
The experimental treatment of two non-local spaces such that they behave as if they were the superimposed and had become the “same space” has theoretical and practical applications. Excess correlations, a frequently employed analogue for “entanglement” [1] , were once exclusively relegated to quantum and subatomic levels. However, demonstrations of excess correlations within gaseous [2] , chemiluminescent reactions [3] , and photon emissions from cells [4] separated by non-traditional distances have indicated that this class of phenomena may exhibit analogues at macrolevels. The most consistent and characteristic of these demonstrations required two loci that were simultaneously exposed to frequency (phase)-modulated magnetic fields displaying changing angular velocities within either a circular array of solenoids or toroids. The excess correlations between the two reactions within the two loci were enhanced when sequences of changing angular velocities were opposite to the increasing or decreasing frequency or phase modulated magnetic fields that were rotated. Our theoretical approach suggests that the rotational features of the Earth and its magnetic field should contribute to conditions that produce these excess correlations. Hence a component of this “excess” correlation would require an alteration of subtle magnetic intensities along the axis of rotation. Here we present experimental support for the contention that very small, approximately 1 to 5 nT steady-state shifts in the east-west component of the local magnetic field precipitated by magnetic fields generated within toroids by the current during creation of the time- varying magnetic fields (whose angular velocities were increased with decreased frequency modulation and then decreased with increased frequency modulation), may reveal a possible mechanism by which excess correlations might be explained.
Based upon the conclusions by Tu et al. [5] that photons may exhibit non-zero rest masses and hence would display a dissociation between group and phase velocities, Dotta et al. [6] exposed pairs of human beings (each pair separated by 10 m) to circumcerebral, complex weak magnetic fields. The rotating magnetic fields were applied through a circular array of 8 solenoids equally spaced around the head at the level of the temporal lobes of each subject. The pattern generated by computer software through the solenoids could be accelerated or decelerated. Dotta and his colleagues [6] found that under optimal conditions when both members of a pair were exposed to the rotating magnetic fields with changing angular velocities, flashing light into the face of one subject sitting within a closed Faraday Cage was associated with the release of photons (~10−11 W・m−2) as measured by photomultiplier tubes from the right hemispheres of the other member of the pair who was sitting in complete darkness in another room. A similar effect was measured for pairs of cell cultures separated by this distance and exposed to the same field parameters simultaneously.
In order to discern if photons, per se, were involved rather than processes associated with living systems, Dotta and Persinger [3] placed small amounts of hypochlorite solutions in two loci separated by 10 m. When the same amount of hydrogen peroxide was injected into each container, the photon emissions were consistent and predictable. If the two areas shared a specific sequence of circularly rotating magnetic fields, simultaneous injection of the same amount of hydrogen peroxide produced twice the response (a doubling of the photon emission duration) as if twice the amount had been injected into the single volume of hypochlorite. The reactions within the two loci under these conditions behaved as if they had been superimposed. This robust phenomenon was clearly observed when the two sites of reactions were separated by 3 km and the magnetic fields were generated by separate sets of equipment.
This “doubling of the photon duration” [3] , as if the reaction had received twice the amount of reactant, only occurred if the two loci containing the hypochlorite were situated in the center of a circular array of solenoids where the angular velocity of the field was first accelerated in conjunction with a decelerating (phase) modulated pattern for a few minutes followed by fields with an accelerating (phase) modulated pattern whose rotational (group) velocity was decreasing. The effect was maintained for about 8 minutes. This conspicuous excess correlation was not measured if the order of the presentations was reversed (decelerating angular velocity, increasing frequency-phase modulation followed by accelerating angular velocity, decreased frequency-phase modulation). If the increasing or decreasing phase-frequency modulated magnetic fields were employed without the changing angular velocity, the effect was not evident as well. To discern if the effect generalized to other fundamental systems, Dotta et al. [7] exposed separate beakers of spring water to the same field parameters for changing angular velocities and magnetic field patterns. When small quantities of protons (a weak acid) were added to one quantity of spring water during this approximately 8-minute window discrete increases in alkalinity were noted in the non-local reaction (the other beaker) within which nothing had been injected.
The circular array of eight-solenoids that produced the discrete bursts of magnetic fields with changing angular velocities was operated by Complex© software and required custom-constructed Digital-to-Analogue Converters (DAC). A more accessible technology was required. After Burke et al. [8] showed statistically significant convergence in LORETA (Low Resolution Electromagnetic Tomography) of cerebral activity between pairs of subjects separated by 400 km wearing toroids operated by Arduino systems, Rouleau et al. [9] employed the same technology to replicate the pH shifts in spring water reported by Dotta et al. [7] . Rouleau et al. [9] found that the Arduino-generated phase and frequency-modulated magnetic fields generated through the same toroids as those employed in the present study resulted in very similar non-local shifts in pH that reflected excess correlations. In that study, the most powerful excess correlation between the two loci involved intensities for the frequency-modulated field that was within the 30 nT range or approaching the background values for power (60 Hz) frequencies. Stronger intensities (300 nT) for the phase modulations displayed less intense excess correlations.
However, in the process of measuring the static components of what is primarily the Earth’s magnetic field by a magnetometer in the three axial planes (X, N-S; Y, E-W, and Z, vertical), we noted an interesting anomaly that was consistent with the magnitude and direction of potential variations in G (ΔG), the gravitational constant, and “geomagnetic” static intensity in the Y-axis. Typical daily fluctuations in G are within the range of ~3 × 10−3 of the average value. Recently Persinger and St-Pierre [10] confirmed the relationship measured by Vladimirsky and Bruns [11] over 25 years ago that approximately 5 nT increases in ambient geomagnetic activity were associated with decreases in ΔG such that an increment of 10−9 T and 10−14 m3・kg−1・s−2 might share the same source of variance. The energy equivalence for the ΔG and this magnitude of magnetic field intensity within 1 L of space converged to be ~3 × 10−14 J [10] . This is effectively the energy equivalent of the rest mass of an electron. We had also shown in other experiments that comparable, small decreases in ambient geomagnetic intensity of about 5 nT were associated with increases in photon emissions from the right hemisphere of human brain during specific cerebral activity [12] . Other experiments demonstrated this inverse effect between geomagnetic changes and photon emissions from cultures of melanoma cells habituating to room temperature after removal from standard incubatory conditions [13] .
2. Methods & Materials
2.1. Equipment
Each toroid core was a plastic ring with a diameter of 25.4 cm (circumference = 79.8 cm). It was wrapped with 225 turns of 16 gauge wire (stereo speaker copper wire). The coil was wrapped in black, vinyl electrical tape. The elevation from the surface upon which the toroid rested and its top (i.e., the diameter of the ring around which the wire was wrapped) was 3.81 cm. An actual picture of the toroid is shown in Figure 1.
A MEDA FVM-400 Vector Magnetometer sensor was placed at the center of the toroid. Fluctuations in background electromagnetic field intensity (nT) were measured. The probe’s X-axis was oriented to magnetic north, positioning the Y-axis within the perpendicular horizontal plane, and the Z-axis within the vertical plane (Figure 2). The entire apparatus was placed on a wooden table positioned 3 m away from and was connected to a Lenovo ThinkPad data logging laptop computer running Windows 7. Raw nT values were collected with an associated sampling frequency of 1 Hz.
The same laptop provided digital-to-analog output to an Arduino Uno R3 microcontroller which carried a patterned current through the toroidal coil. The 5 V output sequence and its associated electromagnetic field has previously demonstrated a capacity to establish states of “excess correlation” between beakers of spring water separated by 1 m [9] as well as brains separated by 300 km [8] such that quantitative fluctuations at point A fluctuated at point B with convergent amplitudes of effect. Leads from the microcontroller to the toroid entered by way of the X-axis of the sensor orientation, parallel to data logging cables. A more specific schematic is shown in Figure 3.
2.2. Measurement Protocol
A 300 s pre-exposure baseline recording was obtained before the initiation of the first field pattern in the sequence.
Figure 1. A picture of the toroid employed in the present study.
Figure 2. The sensor was placed at the center of the toroid, with the X-axis oriented toward Magnetic North. Corresponding Y- and Z-axes are labelled. The sensor cable exited away from Magnetic North in the X-axis and was plugged into a laptop 3 m away from the center of the coil.
Once initiated, the first field―a temporally decelerating pattern―looped continuously for 360 s. A temporally accelerating field was initiated at the 660 s mark, exposing the space within which the sensor was placed for an additional 660 s. The second field pattern was then terminated and 480 s of post-exposure baseline data were collected. This protocol, similar to that employed by Dotta and Persinger [3] and the Rouleau et al. [9] pH shift experiments was called the “Excess Correlation” procedure (Figure 4). The time required for the completion of single pattern sequence during the accelerating phase was 128 ms; for the decelerating field the duration was 203 ms.
Two variants of this protocol were performed as comparators in order to control for non-specific artifacts from the generation of magnetic fields. The first protocol variant (Reverse) involved a reversal of the temporal pattern associated with the first and second field exposure such that the accelerating field preceded the decelerating field. The exposure times of the first and second field remained consistent. The second variant (control) was a control protocol wherein 1800 s of baseline data are collected without the initiation of any field.
All protocols were repeated 6 times for a total of 18 trials. No two trials were completed on the same day.
Figure 3. Schematic of the Arduino-toroid circuit employed in the present experiments.
Figure 4. Two-dimensional representation of the decelerating (top) and accelerating (bottom) field patterns as output from the microcontroller. Note the sequences of 3 ms potentials followed by incrementally longer or shorter intervals of time.
However, all trials were completed between 9 PM-2 AM local time in order to control for diurnal variations in background electromagnetic field intensities. Once collected, raw data were extracted and new variables were computed. First, a 60 s average of field intensity was computed from the center of each exposure phase. For example, the mean and standard deviation for the pre-exposure baseline phase were computed by averaging second-by-second nT values from minute 2.5 of each trial (n = 18) during pre-exposure baseline phase and computing grand averages within each exposure protocol for X-, Y-, and Z-axes. Shifts in intensity (nT) were then computed by subtraction in order to infer net changes in intensity as a function of experimental manipulation. Running 30 s intensity averages were then calculated for all axes and incremental nT shifts were computed in order to infer fine-scale changes.
3. Results
An ANOVA revealed statistically significant differences in nT shifts from the pre-exposure baseline phase to the first field phase along the Y-axis only as a function of exposure protocol [F(2,15) = 7.20, p < 0.01], explaining 53% of the variance. Post-hoc tests revealed the source of variance to be a subtle negative shift (decrease) in field intensity associated with the Excess protocol (M = −2.77, SEM = 0.37) relative to control protocol (M = −0.34, SEM = 0.60), [t(8) = 3.45, p < 0.01, r2 = 0.60]. Similarly negative shifts were observed from pre-expo- sure baseline to the first field exposure in Excess protocol trials relative to Reverse trials (M = 0.35, SEM = 0.72), [t(9) = −3.61, p < 0.01, r2 = 0.59]. There were no significant differences in shifts from pre-exposure baseline to the first field exposure between control and reverse protocols along the Y-axis (p > 0.05). These results are presented in Figure 5. No further differences were noted within X-, Y-, or Z-axes across all shift phases.
In order to discern the temporal characteristics of this shift as a function of exposure protocol, multiple independent t-tests were generated examining incremental shifts from minute 2.5 to 3.0, 2.5 to 3.5, 2.5 to 4.0, etc. The differences between excess and control protocols were first noted when examining the shift from minute 2.5 to 4.0, t(10) = 3.20, p < 0.05. This incremental shift difference between excess and control protocols persisted for 120 s until the shift from minute 2.5 to 6.5, t(10) = 2.03, p > 0.05. There were no significant differences noted for incremental shifts between control and reverse protocols. Differences between excess and reverse protocols were transient, however, and were comparable to those observed for excess and control comparisons. These results are reported in Figure 6.
Correlational analyses were completed to discern any relationship between the aforementioned 30 s-by-30 s serial nT shifts and time. Serial nT shifts along the Y-axis (n = 58) positively correlated with time (r = 0.68, p < 0.001) for the Excess protocol only. These correlations for the Y-axis were not statistically significant for the control or reverse trials (p > 0.05). No further significant relationships were revealed. These results are presented in Figure 7.
Figure 5. Shifts in intensity (nT) as a function of shift phase by exposure protocol. PreFirst refers to shifts from the pre-exposure baseline condition to the first field exposure. FirstSecond refers to shifts from the first field exposure to the second. SecondPost refers to shifts from the second field exposure to the post-exposure baseline.
Figure 6. Incremental shifts in field intensity (nT) across protocol type. Shift increments are indicated in minutes, where 2.5 - 3.0 refers to a nT shift occurring between the beginning to the end of the second half of the second minute. Increments of time with significant differences between conditions are indicated.
Figure 7. A moderate, positive correlation between serial shifts in field intensity (nT) across the Excess protocol for the Y-axis and time.
4. Calculations & Implications
The contribution from the energy from the rotation of the Earth to the east-west magnetic shift measured in our experiments for only the excess correlation procedure should have quantitative consistency. Assuming the mass of the earth to be 5.98 × 1024 kg and the velocity to be 4.63 × 102 m・s−1, the total energy of the system would be 1.27 × 1030 J distributed over a spatial field equivalent to the surface area of the earth (5.1 × 1014 m2), or, about 0.25 × 1016 J・m−2. When applied to the area occupied by an electron as a particle (6.15 × 10−30 m2 per electron), the average energy would be about 1.5 × 10−14 J per electron. This energy is remarkably similar (the same order of magnitude) to the mass equivalent of an electron.
The energy of a system from a magnetic field can be estimated by B2 divided by 2μ when this quotient is multiplied by the volume involved. In this instance μo is magnetic permeability (4π × 10−7 N・A−2) and B is the strength of the field. From Figure 3 the shift (diminishment) of the east-west component of the static field during the “excess correlation” procedure, but not during the reverse or control procedures, was an average of ~1.5 nT. If volume were solved instead:
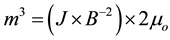 (1)
(1)
the value would be 0.96 × 10−2 m3, or a linear distance of 21 cm. This value is important because it reflects the approximate width of the toroid (25 cm). It is also the approximate wavelength of the most copious standing wave in the universe, the neutral hydrogen line (1.42 GHz). If a procedure were to be developed to capture this condition of excess correlation over non-traditional distances, the hydrogen line would be expected to be involved.
The phenomena may have occurred because of the circumference of the toroid. We had selected these parameters in order to place the toroid over or around the average human head. According to conventional calculations of inductance (L):
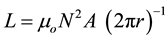 (2)
(2)
where N is the numbers of turns around the toroid, A is the torus’ cross-sectional area and r is the radius of the toroid. For our equipment these values were 225, 3.7 × 10−4 m2, and 1.3 × 10−1 m. The inductance of the toroid would have been 2.9 × 10−5 H.
Application of dimensional analysis for values potentially relevant for a type of universal entanglement suggests that the product of inductance (kg・m2・A−2・s−2), unit charge (A・s), and the square of frequency (s−2), in this case the neutral hydrogen line, would be relevant. Consequently the product of 2.9 × 10−5 H, 1.9 × 10−19 A・s, and (1.42 × 109 Hz)2 results in 9.4 × 10−6 V. In experiments with human brain activity we had considered this an important range because of its congruence with the change of voltage associated with the conduction within a single ion channel in the plasma membrane of a neuron. In the present application the product of this potential difference and the unit charge is associated with a quantity of energy ~ 1.5 × 10−24 J. The value is clearly recognizable because its quantum frequency obtained by dividing it by Planck’s constant (6.626 × 10−34 J・s) is within error of measurement of the 1.42 GHz hydrogen line.
Because the Earth is rotating in an east-west direction and the current within the toroid was rotating as well there would be the potential for Coriolis-like forces to contribute. In the balance of probabilities if they interacted the interface of the process should be manifested by the relationship between the axial drift velocity of the current in the toroid and intrinsic frequency at this latitude as define by the angular velocity of the system and the latitude. Drift velocity is classically defined as:
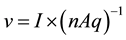 (3)
(3)
where v is velocity, I is the current in the toroid, n is the molar density of the material (in this instance copper), A is the area (of the wire) and q is the unit charge. Both direct measurements of the circuit during the generation of the frequency-modulated magnetic fields during the excess correlation protocol and calculations from the Arduino-toroid circuit indicate that the nominal current was 0.55 mA during the decelerating phase and 0.85 × 10−3 A during the accelerating phase.
Assuming 9.0 gm・cm−3 density for copper, 6.023 × 1023 molecules per mole and 1 electron per atom, this product when divided by copper’s atomic weight (64 gm per mole) shows the numbers of free electrons would be 8.5 × 1028 m−3. When multiplied by the cross-sectional area of the 16 gauge copper wire (1.32 × 10−6 m2) and the unit charge 1.6 × 10−19 A・s for the unit charge, the value is 17.95 × 103 A・(s・m−1)−1. When divided into the 0.55 × 10−3 A (decelerating phase) to 0.85 × 10−3 A (accelerating phase) measured in the circuit, the median drift velocity would between ~3.1 and 4.7 × 10−8 m・s−1. This would occur for a steady current. However our current was oscillating. We assumed that this temporal component could facilitate the drift by the factor f × v, where f is the intrinsic frequency of the oscillations. For the 3 ms intervals employed here, the equivalent f is 3.33 × 102 Hz. For a unit second this results in an enhancement to a “dynamic” drift value between 1.0 to 1.6 × 10−5 m・s−1.
If the forces of interaction between the angular velocity of the system (the Earth) and the internal rotation of the toroid are similar in relation to Coriolis forces, then the radius of the “circular” rotation generated by the toroid can be estimated by:
 (4)
(4)
where v is the drift velocity and f is the Coriolis parameter at the specific latitude (46.39 N) which is determined by the angular velocity of the system. In this instance we assumed the average of the velocity for the decelerating (205 ms) and accelerating (128 ms) cycle completions around the circumference of the toroid, or, 5.1 m・s−1. The value would be 8.6 × 10−5 s−1. When the dynamic drift velocity, v, was divided by the Coriolis parameter, the resulting radius for the “circular motion” or “inertia of the circle” would be between ~11 cm and 18 cm. The diameter for this “circular inertia” would be within the range of the 21 cm hydrogen wavelength. However the nature of the coefficients required for the congruence is not obvious at this time. Higher current intensities and stronger measured magnetic fields within the toroid would solve for different drift velocities and hence different solutions. This may explain the efficacy of the ~30 nT and associated current (mA level) time-varying fields in the excess correlation condition compared to the 300 nT strengths applied in the same manner [9] . The latter required the addition of an amplifier to the circuit.
If the adjustment for time-variation had not been made within the original drift velocity the radius of the inertia of the circle would have been between 3.1 and 4.7 × 10−4 m or a circumference of 1.9 to 3 mm with a corresponding frequency, if electromagnetic, of 1.6 × 1011 Hz to 1 × 1011 Hz. When multiplied by Planck’s constant and divided by the Boltzmann constant of 1.38 × 10−23 J・K−1, the equivalent temperature approaches within a factor of 2 the cosmic background microwave levels. We cannot exclude the possibility at this time that some static component of the current induction, even though it was time varying by the Arduino circuit, occurred. The diminishment of the E-W component of the “geomagnetic” field within the center of toroid was not phasic but constantly persistent for several minutes and occurred only when the excess correlation protocol was applied.
The Coriolis force involved with our parameters for the latitude at which the experiments were conducted according to classic calculations would be 4.32 × 10−4 m・s−2. The energy associated with the mass of an electron (9.11 × 10−31 kg) for this acceleration spread along the circumference of the toroid (0.8 m) would be ~3.15 × 10−34 J. This is remarkably similar to the energy from a unit frequency for Planck’s constant (6.626 × 10−34 J・s), again reiterating the potential significance of the phenomena associated with electrons in this process. It is relevant that the energy equivalence of the mass of an electron multiplied by the square of the fine-structure velocity for a Bohr magneton when multiplied by the time required to complete one orbit is effectively Planck’s constant.
Movement in a circle is uniquely interesting because the process would always be accelerating (m・s−2) and a changing rate of this acceleration (m・s−3) often referenced as a “jerks”, would be a second derivative containing the potential temporal non-continuities that could encourage the conditions we assume may be associated with the observed excess correlations. They could spread over the Minkowski four-dimensional field [14] and appear to violate directional causality. In other words the “effects” of these “jerks” could occur before events and appear to violate causal principles but not necessarily the concept of entanglement. The presence of non-local and advanced correlations for geomagnetic effects had been reported by Korotaev and his colleagues [15] [16] . In the present experiments despite random determination for when a given condition would be initiated, the negative shift in magnetic field intensity in the Y component (east-west) only began to emerge about 40 to 60 s before the initiation of only the excess correlation protocol. The other two (the reversed and control protocol) did not show this “temporal anomaly”.
We suspect that these “jerks” or “sputters” could be coupled to the rotation (angular momentum) of the Earth. Minute but measureable changes in angular momentum or the terrestrial spin have been detected over durations of days or months. Eubanks et al. [17] noted fluctuations with amplitudes in the order of 0.5 ms over periods of 40 to 60 days. They are sometimes coupled to alterations in solar wind velocity and geomagnetic activity. Although there are many potential models to describe the duration of a “unit sputter”, parsimony suggests that it might be a ratio of g to rotational velocity. Hence for the velocity of the earth in Sudbury, Ontario (N 46.69) would be ~420 m・s−1 and when divided by 9.8 m・s−2 would involve a more or less fixed interval of 43 s. This value is within the range of the “retro-occurrence” of the decrease in the east-west component of the static magnetic field inside of the toroid during the excess correlation protocol. The concept of specious present, if valid, would predict that the functional increment of time (Δt) associated with the observation of phenomenon within a relativistic framework could change such that the “future” of one framework could become the “present” of another. When the perceptual Δt is expanded significantly from that of the reference Δt events that appear serial and causal in the smaller temporal window may appear to be simultaneous and superimposed within the wider temporal frame.
We are pursuing the possibility that the excess correlation between two loci at non-traditional distances for photon emissions from chemical reactions, cells, and brain activity when the technology described in this paper has been employed involves a narrow range of energies where geomagnetic activity and gravitational processes interact. According to dimensional analysis the product of G (m3・kg−1・s−2), magnetic field intensity (kg・A−1・s−2) and unit charge (A・s) would be a cubed velocity term. With actual values for ΔG, that is 3 × 10−3 of 6.67 × 10−11 m3・kg−1・s−2, 10−9 T, and 1.6 × 10−19 A・s, the real value is 32 × 10−42 m3・s−3 or 3.16 × 10−14 m・s−1. The frequency associated with the radius of classic electron, 2.82 × 10−15 m, would be ~11 Hz. This is precisely within the range of the second harmonic of Schumann resonance [18] , the standing wave oscillations within the ionosphere-Earth surface cavity, that Minkakov et al. [19] predicted would interface with gravitational waves originating from anywhere in the universe. This convergence does not prove the mathematical solutions of Minkakov’s brilliant insights but supports the supposition that within a narrow range of inverse variations between ΔG and geomagnetic intensity where photons may be manifested [20] , excess correlations could be maximized but only for a limited duration. From a theoretical perspective we expect the duration of excess correlation to be limited. If it were not, then causal connections coupled to locality would ultimately be diluted over time.
Researchers in our laboratory have been designing experiments and testing various configurations of magnetic fields within circular arrays in order to discern potentially the parameters by which excess correlation might occur. We have been pursuing the potential validity of Mach’s principle of “prominence of the universe” [21] which indicates that an event that occurs in one small part of the universe influences the entire universe and vice versa. The presumption is based upon angular momentum. For this to occur within feasible temporal frames Persinger and Koren [22] showed that a term for diffusivity based upon the four-dimensional product of basic circular geometries, particularly 2πr, 4πr2, 4/3πr3 and 2πrf, or 21.3π4r7s−1. By applying dimensional analysis to obtain a similar aggregate based upon universal values they found:
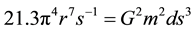 (5),
(5),
where G was the gravitational constant (m3・kg−1・s−2) mass was the estimated mass [23] of the universe (kg), d was the estimated width of the universe, and s was its age. A higher dimensional “diffusivity” term was obtained that produced the resulting velocity of 2.4 × 1023 m・s−1. This velocity, if it reflected “entanglement” latency, should be reflected in the dragging of inertial frames such as those noted in satellite orbits. The predicted temporal value for this drag for the orbit of a satellite was within the same order of magnitude and coefficient (10−16 s) as that measured directly and derived from more complex mathematical models [24] .
The time required for such entanglement to occur around the circumference of the Earth (4 × 107 m) would be that value divided by the entanglement velocity or 2 × 10−16 s. When applied to the diffusion velocity of a charge within the variations of G and 1 nT geomagnetic variation as noted previously, that is 1.7 × 10−14 m・s−1, the distance would be 3.4 × 10−30 m. This value is about 2.1 × 105 more than Planck’s length (1.6 × 10−35 m). The potential significance of this value becomes apparent when the expansion time for an electron is incorporated. Persinger and Koren [25] had calculated that assuming an average (based upon Hubble and Planck telescope data) Hubble’s parameter of 70 km per s per MP arsec (3.1 × 1022 m) or 2.3 × 10−18 s−1, the length (twice the radius, 4.86 × 10−15 m) of an electron would have a velocity of 11.66 × 10−33 m・s−1. When divided into Planck’s length (1.6 × 10−35 m), the time required would be 1.1 ms. There is now experimental evidence that the supports this solution for the electron and the proton [9] .
With this assumption the time required to expand 2.1 × 105 of that value would about 4 to 5 min. A range in this duration would be expected given the significant standard deviation for the actual Hubble parameter which is not a fixed value. The 4 to 5 min duration is within the range of the “entanglement time” noted in our excess correlations for shifts in pH of water when employing the equipment reported in this paper and the displacement of the Y-axis of 1 nT of the magnetic field within the toroid but only during the excess correlation protocol. If this explanation is valid then the “time limited” excess correlations and the anomalous diminishment of intensity of the east-west magnetic component within the toroid during the specific sequence of changing angular velocities (interacting with the earth’s angular momentum at the electron level) would reflect the dynamics of this “expansion time”. We suggest there is a moderate probability that the consistency of quantification could relate Planck-level phenomena to the macrolevel we have measured in the laboratory.
5. Conclusion
The data indicated a temporally non-linear effect within the toroid space which was exclusive to the excess correlation field presentation sequence. Quantitative solutions converged upon the hydrogen line as a standing wave source which might be accessed for practical use in entanglement. Coriolis-like forces present a relativistic approach to excess correlation phenomena, where the local space is affected by planetary rotation. An approximate mechanism is presented which relates physical parameters of the electron to fundamental processes at quantum and universal scales of discourse.
Acknowledgements
The authors would like to thank Trevor Carniello for his insights.
References
- Vedral, V. (2003) Quantum Physics: Entanglement Hits the Big Time. Nature, 425, 28-29. http://dx.doi.org/10.1038/425028a
- Calsamiglia, J., Hartmann, L., Dür, W. and Briegel, H.J. (2005) Spin Gases: Quantum Entanglement Driven by Classical Kinematics. Physical Review Letters, 95, Article ID: 180502. http://dx.doi.org/10.1103/PhysRevLett.95.180502
- Dotta, B.T. and Persinger, M.A. (2012) “Doubling” of Local Photon Emissions When Two Simultaneous, Spatially- Separated, Chemiluminescent Reactions Share the Same Magnetic Field Configurations. Journal of Biophysical Chemistry, 3, 72-80. http://dx.doi.org/10.4236/jbpc.2012.31009
- Dotta, B.T., Buckner, C.A., Lafrenie, R.M. and Persinger, M.A. (2011) Photon Emissions from Human Brain and Cell Culture Exposed to Distally Rotating Magnetic Fields Shared by Separate Light-Stimulated Brains and Cells. Brain Research, 1388, 77-88. http://dx.doi.org/10.1016/j.brainres.2011.03.001
- Tu, L.C., Luo, J. and Gillies, G.T. (2005) The Mass of the Photon. Reports on Progress in Physics, 68, 77-130. http://dx.doi.org/10.1088/0034-4885/68/1/R02
- Dotta, B.T., Mulligan, B.P., Hunter, M.D. and Persinger, M.A. (2009) Evidence of Macroscopic Quantum Entanglement during Double Quantitative Electroencephalographic Measurements of Friends vs Strangers. NeuroQuantology, 7.
- Dotta, B.T., Murugan, N.J., Karbowski, L.M. and Persinger, M.A. (2013) Excessive Correlated Shifts in pH within Distal Solutions Sharing Phase-Uncoupled Angular Accelerating Magnetic Fields: Macro-Entanglement and Information Transfer. International Journal of Physical Sciences, 8, 1783-1787.
- Burke, R.C., Gauthier, M.Y., Rouleau, N. and Persinger, M.A. (2013) Experimental Demonstration of Potential Entanglement of Brain Activity over 300 Km for Pairs of Subjects Sharing the Same Circular Rotating, Angular Accelerating Magnetic Fields: Verification by s_LORETA, QEEG Measurements. Journal of Consciousness Exploration & Research, 4, 35-44.
- Rouleau, N., Carniello, T.N. and Persinger, M.A. (2014) Non-Local pH Shifts and Shared Changing Angular Velocity Magnetic Fields: Discrete Energies and the Importance of Point Durations. Journal of Biophysical Chemistry, 5, 44-53. http://dx.doi.org/10.4236/jbpc.2014.52006
- Persinger, M.A. and St-Pierre, L.S. (2014) Is There a Geomagnetic Component Involved with the Determination of G? International Journal of Geosciences, 5, 450. http://dx.doi.org/10.4236/ijg.2014.54042
- Vladimirsky, B.M. and Bruns, A.V. (1998) Influence of the Sector Structure of the Interplanetary Magnetic Field on the Results of Measurements of the Gravitational Constant. Biophysics, 43, 720-725.
- Persinger, M.A., Dotta, B.T., Saroka, K.S. and Scott, M.A. (2013) Congruence of Energies for Cerebral Photon Emissions, Quantitative EEG Activities and ~5 nT Changes in the Proximal Geomagnetic Field Support Spin-Based Hypothesis of Consciousness. Journal of Consciousness Exploration & Research, 4, 1-24.
- Dotta, B.T., Lafrenie, R.M., Karbowski, L.M. and Persinger, M.A. (2014) Photon Emission from Melanoma Cells during Brief Stimulation by Patterned Magnetic Fields: Is the Source Coupled to Rotational Diffusion within the Membrane? General Physiology and Biophysics, 33, 63-73. http://dx.doi.org/10.4149/gpb_2013066
- Eardley, D.M. and Moncrief, V. (1982) The Global Existence of Yang-Mills-Higgs Fields in 4-Dimensional Minkowski Space. Communications in Mathematical Physics, 83, 171-191. http://dx.doi.org/10.1007/bf01976040
- Korotaev, S.M., Morozov, A.N., Serdyuk, V.O., Gorohov, J.V. and Machinin, V.A. (2005) Experimental Study of Macroscopic Nonlocality of Large-Scale Natural Dissipative Processes. NeuroQuantology, 4, 275-294. http://dx.doi.org/10.14704/nq.2005.3.4.79
- Korotaev, S.M., Serdyuk, V.O., Gorohov, J.V., Pulinets, S.A. and Machinin, V.A. (2004) Forecasting Effect of Macroscopic Nonlocality. Frontier Perspectives, 13, 41-45. http://dx.doi.org/10.14704/nq.2005.3.4.79
- Eubanks, T.M., Steppe, J.A., Dickey, J.O. and Callahan, P.S. (1985) A Spectral Analysis of the Earth’s Angular Momentum Budget. Journal of Geophysical Research, 90, 5385-5404. http://dx.doi.org/10.1029/jb090ib07p05385
- Schumann, W.O. (1952) Uber de strahlundslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionospharenhulle umgeben ist. Zeitschrift für Naturforschung, 7a, 149.
- Minakov, A.A., Nikolaenko, A.P. and Rabinovich, L.M. (1992) Gravitational-to-Electromagnetic Wave Conversion in Electrostatic Field of Earth-Ionosphere Resonator. Radiophysics and Quantum Electronics, 35, 318-323. http://dx.doi.org/10.1007/bf01041780
- Persinger, M.A. (2012) Potential Origins of a Quantitative Equivalence between Gravity and Light. The Open Astronomy Journal, 5, 41-43. http://dx.doi.org/10.2174/1874381101205010041
- Brans, C. and Dicke, R.H. (1961) Mach’s Principle and a Relativistic Theory of Gravitation. Physical Review, 124, 925-935. http://dx.doi.org/10.1103/physrev.124.925
- Persinger, M.A. and Koren, S.A. (2013) Dimensional Analyses of Geometric Products and the Boundary Conditions of the Universe: Implications for a Quantitative Value for the Latency to Display Entanglement. Open Astronomy Journal, 6, 10-13. http://dx.doi.org/10.2174/1874381101306010010
- Whitrow, G.J. (1946) The Mass of the Universe. Nature, 158, 165-166. http://dx.doi.org/10.1038/158165b0
- Ciufolini, I. (2007) Dragging of Inertial Frames. Nature, 449, 41-47. http://dx.doi.org/10.1038/nature06071
- Persinger, M.A. and Koren, S.A. (2007) A Theory of Neurophysics and Quantum Neuroscience: Implications for Brain Function and the Limits of Consciousness. International Journal of Neuroscience, 117, 157-175. http://dx.doi.org/10.1080/00207450500535784
NOTES

*Corresponding author.








