Journal of Electromagnetic Analysis and Applications
Vol.07 No.03(2015), Article ID:54365,7 pages
10.4236/jemaa.2015.73006
New Wavelet Thresholding Algorithm in Dropping Ambient Noise from Underwater Acoustic Signals
Mohammad Monirujjaman Khan, Ratil Hasnat Ashique, Badrun Naher Liya, Md. Mohsin Sajjad, Md. Anisur Rahman, M. T. Hasan Amin
Department of EEE, Primeasia University, Dhaka, Bangladesh
Email: monirkhan.qmul@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 February 2015; accepted 28 February 2015; published 3 March 2015
ABSTRACT
Underwater Wireless Communication, largely dependent on the acoustic communication between the machines, is largely affected by various types of noise in the shallow and deep water. However ambient noise which is due to multiple sources (e.g. shipping, wind) and no one source dominates. Ambient noise masks the acoustic signal to a large extent. Hence today it has drawn the attention of the experts to reduce its effect on the received signal. This paper discusses ambient noise problem and devises a new wavelet thresholding method to reduce its effect. Afterwards a comparative study on statistical parameters is shown to prove the efficiency of the devised method.
Keywords:
Ambient Noise, Wavelet Transform, Thresholding, Signal to Noise Ratio (SNR), Root Mean Square Error (RMSE), Power Spectral Density (PSD), Percentage Root Mean Square Difference (PRD)

1. Introduction
Compared to radio waves, acoustic waves have become the most effective way in underwater wireless communication [1] . It is because radio waves are highly attenuated and spreading occurs due to high frequency. Hence they can propagate only over very short distances. On the other hand if acoustic waves are used, long distance communication can be established. However underwater wireless communication is still challenging due to frequency band limitation and underwater channel disturbances in the form of ambient noise. The disturbance is generated by both natural (seismic, wind marine animals, rain, breaking waves etc.) and manmade sources (shipping, other machineries etc.). We will discuss ambient noise properties in details and reducing algorithm afterwards [2] - [4] .
2. Ambient Noise
Oceans are filled with various types of sound which may be generated by natural or man-made sources. Breaking waves, rain, marine, shrimp, volcanoes, earthquakes can be god examples of natural sources. Ships, military sonars exemplify man made sources.
This background noise present in the ocean is called ambient noise. All types of noise is not present everywhere all the time.
Category by Frequency
Ambient noise sources can be categorized by frequency. The typical frequency range of various types of ambient noise is shown by Wenz in the Wenz curve [5] . In the range of 20 Hz to 500 Hz, the noise is primarily due to distant shipping. In this range frequency content can be detected even after eliminating other types of shipping noise at the receiver. Moreover it is easy to understand that the noise level expressed in terms of signal power level (SPL) will be greater where shipping traffic is heavier. For example, low frequency ambient noise level is lower in the southern hemisphere as shipping traffic is very low. In the frequency range 0.5 KHz to 100 KHz the noise is mainly due to spray and bubbles associated with breaking waves. In this range noise is proportional to wind speed that is noise level increases with increasing wind speed. Above 100 KHz thermal noise dominates which arises due to random motion of water molecules. Thermal noise determines the ultimate minimum level of sound that can be used for communication purpose in a particular time and location [6] .
3. Wavelet Transform
Wavelets are mathematical functions which break up the data into different frequency components and hence each frequency component can be studied at different resolution. Wavelet analysis is superior to Fourier analysis in the sense that Fourier analysis is well suited for frequency analysis but if we require time frequency analysis then Fourier analysis becomes useless. That is wavelet analysis provides us with time frequency data of the signal. That is we can determine through wavelet analysis where and at what frequency noise spikes or discontinuities occur. In fine wavelets are specially designed for non-stationary signals which are transient in behavior [7] [8] .
4. Wavelet Thresholding
For many signals, the low-frequency content is the most important part as because it contains the information. The high-frequency content, on the other hand, imparts flavor or nuance. Considering the human voice, If we remove the high-frequency components, the voice sounds different, but we can still tell what's being said. However, if we remove enough of the low-frequency components, we hear gibberish. In wavelet analysis, we often speak of approximations and details. The approximations are the high-scale, low-frequency components of the signal. The details are the low-scale, high-frequency components. The thresholding process of wavelet coefficients can be divided into two steps.
4.1. Step 1
The first step is the policy choice, i.e. the choice of thresholding function T. Two standard choices are hard and soft thresholding mentioned as
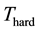 and
and
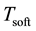 respectively with corresponding transformations are given by,
respectively with corresponding transformations are given by,
 (1)
(1)
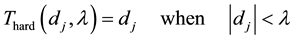 (2)
(2)
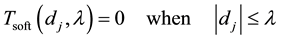 (3)
(3)
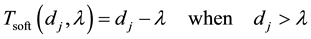 (4)
(4)
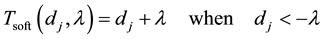 (5)
(5)
The hyperbola function is as stated below,
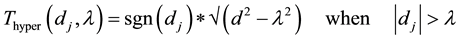 (6)
(6)
 (7)
(7)
The hyperbola function in (6) and (7) is a compromise between soft and hard thresholding functions. The function
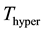 is an almost hard thresholder with the continuity property [9] - [11] .
is an almost hard thresholder with the continuity property [9] - [11] .
4.2. Step 2
The second step is the choice of threshold value [12] [13] . Donho and Johnston (1993) proposed a threshold
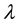 defined as follows:
defined as follows:
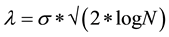 which is called universal threshold by the authors. This threshold is one of the oldest and provides fast and easy thresholding. There are several possibilities for the estimator
which is called universal threshold by the authors. This threshold is one of the oldest and provides fast and easy thresholding. There are several possibilities for the estimator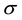 . Some standard estimators are mentioned in (8) and (9):
. Some standard estimators are mentioned in (8) and (9):
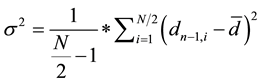 (8)
(8)
 (9)
(9)
where
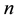 is the highest level of decomposition;
is the highest level of decomposition;



5. Proposed Thresholding Method
The new thresholding method consists of thresholding value estimation and thresholding function design both for detail and approximation coefficients at each level of wavelet decomposition. Detail coefficients carry the original information signal between 8 to 12 KHz range and approximation coefficients carry the noise component. The ambient noise component is dominating in between 1 to 4 KHz range [5] [11] .
As the first step in our proposed thresholding method we offer the new threshold value for detail and approximation coefficients as follows


where,







When data size is large the general thresholding estimation gives under fitted results [7] [8] .
Proposed detail coefficient thresholding function,


Proposed approximation coefficient thresholding function,


where



6. Proposed Noise Reduction Model
In our proposed method we assume a reference signal of 10 KHz frequency. The noise data is provided by MREG, Swansea University, UK. The data was recorded in high tidal current over the board 11/05/2013 at 07.06 am on the West coast of Wales.
The noise reduction algorithm can be described on a step by step basis as follows:
Step1: 10 KHz reference signal is used to produce the noisy signal (noisy signal = Ref. Signal + Noise).
Step 2: A level 8 wavelet Decomposition is performed using discrete wavelet transform (dwt) function.
Step 3: Detail coefficients at level 1 to 8 are modified using proposed thresholding method.
Step 4: Approximation coefficients are at each level are modified using proposed method.
Step 5: Inverse Wavelet Transform is performed to reconstruct the denoised signal.
The algorithm is applied on two sets of noise data to ensure algorithm efficiency.
7. MATLAB® Simulation Results
To proof the efficiency of the proposed thresholding value estimation method and thresholding function, we calculate the SNR, RMSE and PSD of the denoised signal. Table 1 and Table 2 show the result of simulation.
Table 1. Statistical parameter values using various wavelets (noise data set 1).
Table 2. Statistical parameter values using various wavelets (noise data set 2).
Figure 1. Noise PSD for data set 1.
In Table 1 and Table 2 we calculate SNR, RMSE and PSD respectively for wavelet filter types “db2”, “Haar”, “coif1” and “sym4” using hard, soft and proposed thresholding function. For each type of function we have calculated the statistical parameter values using universal and proposed threshold estimation method.
Figure 2. Noise PSD for data set 2.
Figure 3. Noise signal (reference signal + noise) PSD using data set 1#.
8. Conclusion
From the above data it is clear that the devised method has produced improved SNR, PSD and lower RMSE for all noise data sets compared with global soft or hard thresholding methods. The PSD of noise signal being almost similar in frequency contents is showing that the noise spectrum have a peak in the lower frequency region as expected with the information signal at higher frequency region showed in Figures 1-5. The soft thresholding function with proposed estimation method has produced improved SNR with lower RMSE especially when noise signal strength is strong. The devised method seems to be efficient for all wavelet filter types applied to this experiment.
Figure 4. Noisy signal (reference signal + noise) PSD using data set 2.
Figure 5. PSD of denoised signal using proposed method.
Acknowledgements
The authors would like to thank Mr Merin Broudic, Research Assistant Marine Renewables, Low Carbon Research Institute (LCRI Marine), School of Engineering, Swansea University, UK, for his perpetual support.
References
- Teng, D., Chen, H. and Zhu, N. (2010) Computer Simulation of Sound Field Formed around Transducer Source Used in Underwater Acoustic Communication. 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), Chengdu, 20-22 August 2010, V1-144-V1-148.
- Kinsler, L.E., Frey, A.R., Coppens, A.B. and Sanders, J.V. (1982) Fundamentals of Acoustics. 3rd Edition, John Wiley & Sons, New York.
- Dahl, P.H., Miller, J.H., Kato, D.H. and Andrew, R.K. (2007) Underwater Ambient Noise. Acoustics Today.
- Veni, K.S., Murugan, S.S. and Natarajan, V. (2011) Modified LMS Adaptive Algorithm for Detection of Underwater Acoustic Signals Against Ambient Noise in Shallow Water of Indian Sea. IEEE International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, 3-5 June 2011, 901-905.
- Raj, K.M., Murugan, S.S., Natarajan, V. and Radha, S. (2011) Denoising Algorithm using Wavelet for Underwater Signal Affected by Wind Driven Ambient Noise. IEEE-International Conference on Recent Trends in Information Technology (ICRTIT), Chennai, 3-5 June 2011, 943-946.
- Stojanovic, M. (2006) Underwater Wireless Communications: Current Achievements and Research Challenges. IEEE Newsletter.
- Bassett, C. (2010) Underwater Ambient Noise at a Proposed Tidal Energy Site in Puget Sound. M.S Thesis, Department of Mechanical Engineering, University of Washington, WA.
- Chang, S.G., Yu, B. and Vetterli, M. (2000) Adaptive Wavelet Thresholding for Image Denoisingand Compression. IEEE Transactions on Image Processing, 9, 1532-1546.
- Cohen, R. (2012) Signal Denoising Using Wavelets. Project Report, Department of Electrical Engineering Technion, Israel Institute of Technology, Haifa.
- Antoniadis, A., Leporini, D. and Pesquet, J.-C. (2002) Wavelet Thresholding for Some Classes of Non-Gaussian Noise. Statistica Neerlandica, 56, 434-453.
- Discovery of Sound of the Sea. University of Rhode Island. www.dosits.org
- Daubechies, I. (1992) Ten Lectures on Wavelets. SLAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970104
- Stojanovic, M. (2014) Underwater Wireless Communications. Wiley-Blackwell, an Imprint of John Wiley & Sons Ltd.







