Received 2 September 2014; revised 29 September 2014; accepted 21 October 2014

ABSTRACT

Following a previously introduced entropy approach and reviewing experimental measurements, we find a similarity option between photoelectric effects, photovoltaic effects and thermoelectric effects. The photovoltaic effect and the thermoelectric effect are proved in this study to be driven by a Seebeck effect which depends mainly on the thermal potential of the incident radiation and the interacting materials. Hence, we apply such exciting conclusion to derive an advanced efficiency limit of the developed and multijunction solar cells that exceed the previously derived limit by Shockley and Queisser.

Keywords:

Electromagnetic Waves, Entropy, Thermoelectric Effect, Seebeck Effect, Photoelectric Effect, Photovoltaic Effect

1. Introduction

According to the similarity and analogy of laws that govern the flow of heat and electric current and reviewing their common features as a flow of energy and entropy [1] , it was possible to prove that the electric current is a flow of electromagnetic waves that have an electric potential [2] . However, the heat is expressed in terms of the thermal potential times the flow of thermal entropy [2] . By the reviewed analogy, the flow of electric charge can be expressed also in terms of the electric potential times the flow of electrical entropy [3] . Such approach was expressed into an introduced fundamental equation of thermodynamic that adopts such consideration [2] . The definition of electric current as a flow of electromagnetic waves that have an electric potential was confirmed in previous studies [3] - [5] . The speed of flow of electric current at a velocity that approaches the velocity of light, the transformation of electric power through space during Tesla experiment and many experimental results prove the truth of such postulated definition [6] - [8] .

The thermoelectric effect is defined in literature as conversion of thermal energy into electrical energy due to replacing thermal potential of the flowing energy by electric potential or vice-versa [9] . Such definition of the thermoelectric effect states the only difference between electric current and heat flow, or flow of electromagnetic waves, is replacing the thermal potential by an electric potential due to a thermoelectric effect. This definition of the thermoelectric effect states also the reversibility of the conversion process from thermal flow to electricity flow and vice-versa by exchanging the potentials of the energy. It means the heat flow and the electric flow should have a common nature as introduced by the followed entropy approach as a flow of electromagnetic waves.

The presented study will consider such postulated definition of electric current as a base to prove the similarity of the Seebeck effect, the photoelectric effect and the photovoltaic effect. In the second section of the presented study the postulated definition of electric current will be considered to introduce a modified definition of the Seebeck effect. In the third section, experimental results of measurements of Planck’s constant by a photocell will be reviewed to show an option of similarity between the photoelectric effect and the defined Seebeck effect. Accordingly, experimental measurements of the performance of photovoltaic cells will be analyzed in the fourth and fifth sections to prove the similarity between the photovoltaic effect and the defined Seebeck effect. In the sixth section, the found conclusion of the photovoltaic effect as a thermoelectric effect will be applied to derive through an entropy approach a practical limit of the efficiency of the photovoltaic cells. The found limit adopts the measured efficiency of the recently produced photovoltaic cells that exceed the previously found limit by Shockley and Queisser.

2. The Seebeck Effect

Seebeck effect, as a thermoelectric effect, is defined in literature as production of an electromotive force, or potential difference, and consequently an electric current in a loop of materials consisting of at least two dissimilar conductors when its two junctions are maintained at different temperatures [10] .

Accordingly, when the junctions of such loop have a temperature difference “ΔT”, it is generated an electricpotential difference “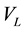” which can be found according to the following equation:

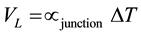(1)

In Equation (1), the term “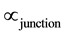” represents the Seebeck coefficient of the junction [11] . According to this relation, Seebeck coefficient represents the increase of the electrical potential in the loop per unit rise in the temperature difference between the two junctions; such coefficient is found in the range of 40 - 60 μV/K for metal thermocouples and in the range of 100 - 200 μV/K for semiconductor thermocouples. Thermocouples and advanced thermoelectric generators depend on the Seebeck effect for temperature measurements and electric power generation successively [12] . According to the postulated definition of electric current and the definition of the thermoelectric effects; it possible to define the Seebeck effect as converting the flow of electromagnetic waves of thermal potential into a flow of electromagnetic waves of electric potential.

3. The Photoelectric Effect

Figure 1 shows a photocell’s circuit in which light of a known frequency is shone upon a potassium cathode in an evacuated tube [13] . According to literature; the incident light causes negative charges to be emitted from the cathode to the anode or the collector to produce flow of electric current through the anode’s circuit [14] . In these experiments which were done to measure Planck’s constant, the potential of the collector, or the cell’s anode, was made negative with respect to the cathode to stop the flow of charges from the cathode [15] . In these experiments; the flow of current was found to be stopped at different voltages that increased by the decrease of the wavelengths of the emitted radiation.

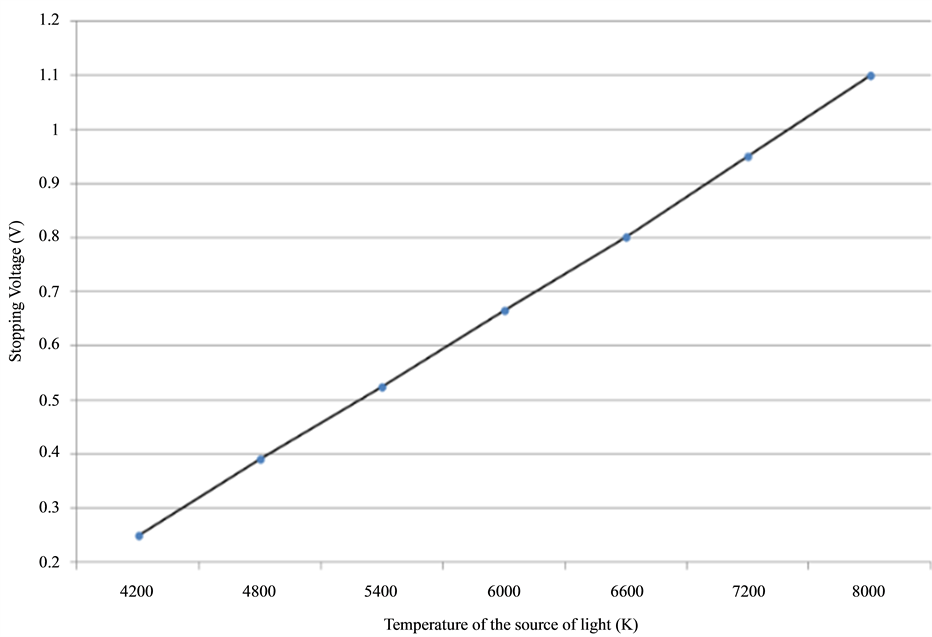
Figure 2 shows the results of these experiments where the wavelength of the incident electromagnetic radiation, as found in literature, is replaced here by the temperature of the source of such radiation by using Wien’s law of radiation [16] . The stopping voltage was found independent on the metal of the cathode or intensity of radiation [17] [18] . According to the measurement data in Figure 2, the dependence of the stopping voltage on the temperature of the source of radiation is found to be linear and the slope of such linear dependence is found in the order of 160 μV/K. Comparing such value of the measured electrical potential rise per unit thermal potential

rise of the incident radiation in the photocell measurements, or the measured slope of the found dependence, to the definition and the values of the Seebeck coefficient of metals and semiconductors, they have the same definition and are in the same order of magnitudes. Such results mean the conversion of the incident radiation into electrical potential in photocells may be due to a similar thermoelectric effect as the Seebeck effect that converts the heat flow into electric current. According to the postulated definition of electric current, it is possible to explain the incident heat waves from a high source temperature will gain upon reflection on a low temperature cathode an electric potential which is proportional to the thermal potential of the incident radiation by a similar effect as the Seebeck effect. Accordingly; it is possible to define the thermoelectric effect as conversion of the incident radiation into electric current in photocells due to replacing the thermal potential of the incident heat by electric potential by a similar Seebeck effect as in thermocouples [19] . Such definition proves that the flow of electric current from the cathode has actually an electric potential that is balanced by the anode’s potential when it is stopped. According to the traditional definitions of the photoelectric effect as a flow of emitted electrons from the cathode plate that haven’t any specific potential, it is hard to explain how such electrons are stopped and the trials of many authors to explain such process were inconvenient [20] . So, the results of this experiment represents a proof of the truth of the postulated definition of electric current as electromagnetic waves and find a plausible explanation for defining the photoelectric effect as a Seebeck effect.

4. The Photovoltaic Effect

According to the found similarity between the photoelectric effect and the defined Seebeck effect; it is expected to find a similarity option between the photovoltaic effect and Seebeck effect as both the photoelectric effect and the photovoltaic effect are explained as emission of electrons by bouncing photons. So, the measured performance of a typical silicon solar photovoltaic cell, Figure 3, is analyzed. The output potential of such cell depends mainly on the frequency or the thermal potential of the incident radiation while it is independent on the intensity of solar radiation [21] . Figure 3 shows the measured open circuit voltage for such cell “” is in the range 0.6 - 0.7 Volts while the temperature difference between the source of radiation or the sun’s temperature and the junction's temperature “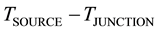” is about 5800 K. Such measurement data determine the potential rise per unit thermal potential of the incident radiation in the range 120 - 150 μV/K. Such units and values are also similar to the units and range of Seebeck coefficients of metal and semiconductor thermocouples as previously determined. So, if the Seebeck coefficient of the Silicon photovoltaic junction is “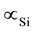”, the induced potential in photovoltaic cells is related to the difference in temperature between the source of radiation “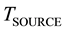” and the photovoltaic junction “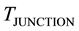” by the following relation that is also applied to find the electromotive force “E” in thermocouples [19] .

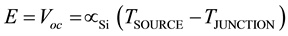(2)

The value of Seebeck coefficient in Equation (2) as defined according to Equation (1) is identical to tabulated values of the Seebeck coefficient of Silicon [22] . Such result proves that the photovoltaic effect is also driven by a thermoelectric effect as Seebeck effect. According to the postulated definition of electric current, it is possible to define the photovoltaic effect as conversion of the incident thermal radiation from a high source temperature “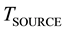” on a cell’s junction at a low temperature “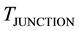” into electric current by replacing its thermal potential by electrical potential due to a Seebeck effect.

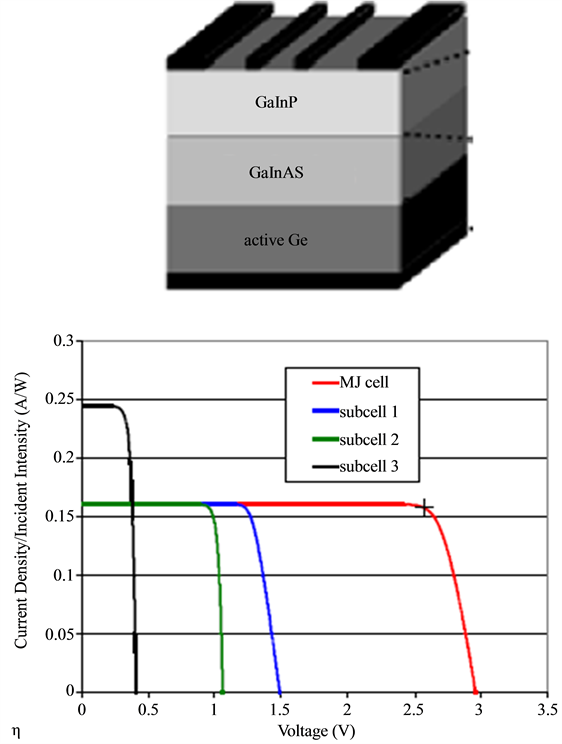
5. Multijunction Photovoltaic Cell

The application of the same multijunction technique for magnifying the electrical potential difference in multijunction solar cells and in thermopiles, or multijunction thermocouples, represents also a proof of a similarity option between the photovoltaic effect and the Seebeck effect [23] [24] . According to literature, multi-junction solar cells are considered like homo-junction cells in series, so, their open circuit voltage is the sum of the voltages of the sub-cells, while their short circuit current is that of the sub-cell with the smallest current [25] . However, the state-of-the-art device of a multijunction solar cell is a lattice-matched triple-junction solar cell consisting from GaInP, GaInAs and Ge stacked on top of each other, Figure 4 [26] [27] . The measured open circuit potential “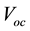” for the inserted subcells, when each is operated separately, is found in literature as seen in Figure 4: 1.22 V for the

GaInP subcell, 1.04 V for the GaInAs subcell and 0.25 V for the Ge subcell and a total open circuit potential of 2.5 Volt [28] . Such multijunction solar cell has reached a measured conversion efficiencies of 41.6% at concentrations of 364 suns [29] . Yet, detailed balance model calculations showed that the bandgap combination of the lattice-matched design is not optimally adjusted to the solar spectrum and failed to predict such high efficiency [30] .

A rather modified analysis for prediction of such multijunction solar cells that considers the previously attained conclusions will be tried in this study. So, the potential rises through the considered multijunction solar cell will be estimated as the sum of the potential rises in the involved subcells by applying Equation (2) for each subcell. Then, it is possible to consider the multijunction as a thermopile formed of three junctions and to apply a similar relation as that applied on thermopiles to find the electromotive force or potential “ ” [27] [28] :

. (3)

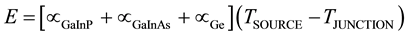
In Equation (3), the flowing radiation gains a potential rise when crossing each PV junction by the Seebeck coeffi- cient of the corresponding junction times the same thermal potential of the flowing radiation “”, as the incident radiation on the three junctions belongs to the same source temperature “” and the three junctions have the same temperature “”. According to the mentioned measured data “” of each subcell, the Seebeck coefficient of these subcells can be calculated according to Equation (2) as follows:, , and. Accordingly, the total potential rise can be calculated according to (2) as follows:

(4)

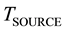
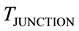
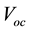
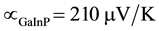
Such value is identical to the measured “” of the whole multijunction cell [29] [30] . However, such result is expected according to the course of calculations, but Equation (3) may be useful for prediction of the performance of different multijunction solar cells according to the selections of grouping such photocells.

6. Thermodynamic Analysis of Efficiencies of Photovoltaic Cells

Regarding the previous conclusions of sections 2, 3 and 4, it is possible to consider the photovoltaic cell as a thermoelectrical generator driven by Seebeck effect. Hence, the efficiency of a photovoltaic cell can be expressed as a thermoelectric generator as follows [31] :

(5)

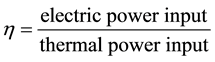
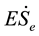
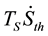
According to literature, the charges transport in conductors is characterized by energy and entropy transport [1] . So, the magnitude of output electric power can be expressed as the product of the electric potential times the rate of the flowing entropy, “”, similar to the definition of heat flow as the product of thermal potential times the rate of entropy flow, “” [3] . Introducing such expressions into Equation (5), the efficiency of the cell can be expressed as follows:

(6)

In (6), represents a scale constant for conversion the temperature from the Kelvin scale into volts [32] . The difference between the thermal entropy flow “” and the electric entropy flow “” can be determined in terms of irreversible entropy production as a measure of the possible irreversibilities in such process. According to the previous analysis and the definition of the thermoelectric effect; the conversion of thermal energy into electric energy by replacing the thermal potential by electric potential is a reversible process. 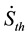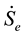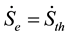So, it is possible to assume the absence of any irreversibility and to insert the following equality of the flow of electric and thermal entropy flows [33] :

. (7)

Substituting the electric potential in “E” in Equation (6) in terms of the temperature difference “” according to Equation (2) and considering the equality in Equation (7); the efficiency of the cell can be expressed as follows:

(8)

So, the cell’s efficiency may attain the Carnot cycle efficiency by increasing the Seebeck coefficient of the junction. Accordingly, the introduced multijunction technology that accumulates the resultant Seebeck coefficient of many subcells, as found in Equation (3), may lead to reach the Carnot cycle efficiency if the resultant Seebeck coefficient reaches the value of the conversion constant which is theoretically possible [34] . However, comparing such approach to the detailed balance model as introduced by Shockley and Queisser [35] , their approach had the same reasoning that considers the photovoltaic effect is influenced by the thermal potentials of the incident radiation and the photocell, but their analysis considers the source of irreversibility belongs to interactions between the incident light, as waves, and the output electric current, as traditionally considered, as electrons. In the present study, such irreversibility is absent as the incident energy and the flowing current belong to the same nature, as waves, but each have a potential that may be mutually replaced. So, the process can be considered as reversible and the efficiency may equal to the efficiency of a reversible engine operating between the assigned source and sink temperatures [34] .

7. Conclusion

Starting from a previously postulated definition of electric current as a flow of electromagnetic waves that have a specified, positive or negative, potential, it was possible to prove that the classical definition of thermoelectric effect as conversion of thermal energy into electrical energy implies the truth of such postulated definition of electric current. So, it was possible also to prove that the photoelectric and the photovoltaic effects are driven by a similar effect as the Seebeck effect which depends mainly on the thermal potential of the incident radiation and the interacting materials. We use such conclusion to deal with the photovoltaic cells as a thermoelectric power generator and to find a new limit of the efficiency of advanced and the multijunction solar cells that exceed the broken limit of Shockley and Queisser. The found limit proves the conversion of the incident thermal radiation into electric current by the photovoltaic effect is a reversible process whose efficiency equals the efficiency of a Carnot cycle operating between the temperatures of the source of radiation and of the photovoltaic junctions.

References