Received 16 July 2014; revised 12 August 2014; accepted 7 September 2014

ABSTRACT

The generation of different waves in the atmosphere and ionosphere caused by seismic and volcano activities has changed the transparency for cosmic radio waves. It is possible to analyze two cases: the first case caused by the atmospheric acoustic wave, which creates a periodic structure of the electron density in the ionosphere. It is shown that the resonant passing of the radio waves takes place, when the length of the acoustic wave is equal to one or a few lengths of the radio wave. The second case produces the electron density decrease in the F-layer of the ionosphere resulting in an increase in the transparency of the ionosphere for cosmic radio waves. The review of these phenomena is provided in this work and both cases have been confirmed experimentally.

Keywords:

Transparency, Plasma, Radio Waves

1. Introduction

The problem of the generation of different waves caused by the seismic activity and other phenomena are in the base of the lithosphere-atmosphere and ionosphere coupling [1] . It is possible to give a basic classification of different phenomena that confirm this coupling. At present it is clear that this coupling takes place mainly through three basic channels: electromagnetic [2] -[4] , acoustic [5] -[7] and chemical [1] ones. The electromagnetic channel is known in principle: variable electric currents, which appear in the lithosphere during and before earthquakes in accordance with Maxwell’s equations excite electromagnetic fields that penetrate almost instantaneously into the ionosphere, creating in it an electromagnetic response.

The acoustic channel of the lithosphere and the ionosphere has been established very reliably due to ground and space observations [8] [9] . During earthquakes, or strong explosions, acoustic waves are excited at the Earth’s surface and launch acoustic pressure waves, propagating almost vertically upwards, into the atmosphere. The vertical component of the displacement of an acoustic wave perturbs the profile of electron density of E- and F-layers of the ionosphere up and down with the frequency of the acoustic wave. Electromagnetic plasma waves in the ionosphere are also excited. These phenomena appear in the ionosphere some minutes after an earthquake or a strong explosion [10] . In terms of the connection between the atmosphere and the lithosphere, a very important property of atmospheric acoustic waves is that their amplitudes increase exponentially with the altitude, so that displacements of the order of millimetres on the Earth’s surface grow into displacements of the order of kilometers at ionosphere heights.

The chemical channel causes other phenomena: anomalies of the propagation of radio waves above the volcano and the epicenter of strong seismic active sites; perturbations of the sporadic Es-layer emission in the ionosphere; geochemical and biological processes in the seas and oceans etc. The same appears before the volcanic activity takes place. Before volcano explosion some big particles and chemical compounds, visually observed, consist with gases H₂O, CO₂, S, SO₂, radon release [9] .

The acoustic-electromagnetic phenomenon consists in the transformation of the atmospheric acoustic waves caused by the oscillations of Earth’s surface into plasma waves in the ionosphere, in the excitation of magnetic fields there. Also such a phenomenon leads to an appearance of a periodical structure of the ionosphere electronic concentration, and to a transparency and displacement of the E- and F-layers of the ionosphere due to acoustic atmospheric waves. These effects become very effective because of the property of the atmospheric acoustic waves to increase their amplitudes when propagating in the vertical direction.

In this review it is interesting to compare two effects of increase of transparency for cosmic radio waves. One effect is caused by formation of a periodic structure by acoustic waves. Another effect results in the decrease of the electron density of F-layer of the ionosphere caused by acoustic waves.

2. Periodic Structure

A very important factor is the unique property of the atmospheric acoustic waves. Their amplitude increases exponentially with the altitude 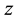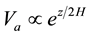, where 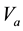is the amplitude of the velocity of the acoustic wave, , 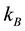is the Boltzmann’s constant and 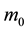is the mass of neutral molecules. So, the wave with a certain amplitude at the ground surface of some millimeters a second will be converted into the wave on the ionosphere altitude, with an amplitude about the speed of the sound. It is necessary to take into account the law of the dispersion for vertically spreading atmospheric acoustic waves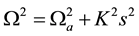, where is the cut-off frequency, 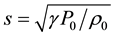is the speed of the sound [11] . This dispersion is obtained from the hydrodynamic and adiabatic equations in an one dimensional case for the velocity, the density of gas, and the pressure (, , respectively) in a linear approximation. It is possible obtain the acoustic waves

velocity described as. It would be noted that the energy flow. The

fact that damping of the acoustic waves caused by the viscosity increases with the frequency as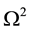, shows that the increase of the atmospheric acoustic waves will be essential at the very low frequencies. The observations confirm this conclusion. One of the difficulties for the experimental investigation of the increase of the transparency is the losses of the acoustic waves [10] . Only a very low frequency acoustic wave can propagate through the atmosphere into the ionosphere. For the generation of very low frequency acoustic wave in the ionosphere, the following technique can be used. We consider the interaction of two powerful acoustic waves with frequencies, and wave vectors generated with two acoustic generators located at the earth’s surface. Due to the nonlinear interaction in the atmosphere a low frequency acoustic wave, the frequency is equal can be obtained. The analysis of the nonlinear interaction of two acoustic waves is done by using a nonlinear approach for the velocity of the acoustic atmospheric wave, where, , , are the linear and nonlinear parts of the velocity of acoustic atmospheric wave. The modulation of the ionosphere plasma density is determined by the nonlinear part of the velocity, where is the modulation caused by the nonlinear low frequency wave. Under the presence of the low frequency atmosphere acoustic wave, the wave vector and wave equation for the electromagnetic wave changes to where is the modulation amplitude determined of the refraction index, which depends on the specific form of the radio waves. The wave transmitted into the plasma is analyzed by the wave equation. Temporal dependence taken in the form) :

(1)

This is the Schrodinger equation for a particle in a periodical potential field. In case of this equation determines the transmitted wave in the plasma. At the condition the resonance is obtained. The resonance condition can also be written in the form, where is the acoustic wave length. Thus, the condition of resonance indicates the length of the acoustic wave must be equal to the whole number of the radio wave lengths. Now we may write down the equations for the

Umov-Pointing vector of the transmitted wave as, where the value,

where is the flow density of the initial wave, and. This formula is

obtained with the conditions, ,. As it is seen from this formula the value of may be comparable and larger than. It should be noted that for the cosmic radio waves with frequencies, (,are the Langmuir and cyclotron frequencies) the ionosphere plasma is the media with the refraction index. By this condition the transparency coefficient for a cosmic radio wave, in the absence of acoustic atmospheric wave, is very small. So our result is not contrary to the energy conservation low.

Mechanism of transparency for cosmic radio waves caused by low frequency sound wave is very strong. As example here the generators and nonlinear interaction of waves are used. But really in nature the ultralow frequency sound wave is produced by strong seismic and volcano activity. So, this process is produced the big changing of transparency for radio waves. It is possible to observe the stars more clearly.

3. Modulation Ionosphere Plasma Caused Ulf Sound Waves

The seismic and volcano activity caused ultra low frequency acoustic waves (ULF) at frequencies 0.05 - 0.5 s⁻¹ which may reach heights z = 60 - 200 km, where the maximum values of the ionosphere plasma occur. In this case it is necessary analyzed the modulation caused by density decrease in the F-layer. In analysis it possible to take into account is the nonlinear propagation of the acoustic pulse in the atmosphere which is described by classic hydrodynamic equations. To consider the propagation of sound waves in the atmosphere and the ionosphere, it is necessary to consider the dependencies of temperature, molar mass, and effective atmosphere height on the coordinate. Generally, the effective atmosphere height is not a constant. The dependencies of the density, sound velocity, and viscosity on height are [1] :

(2)

Here the following function is used:

(3)

is the Sutherland constant. Note that dependencies of, , possess a characteristic scale about 60 km, so that it is possible to neglect the derivatives with respect to. In Figure 1, the dependencies, , , and are presented.

or the maximum value of the modulation is estimated as

(4)

Our simulations have shown that in the case of the acoustic sources of natural origin, the density modulation of the F-layer is quite small:, but if the ULF is excited by a powerful antenna this modulation may be strong:. It is possible that there is a corresponding modulation of transparency of the F-layer with respect to the transmission of radio frequency waves (at frequencies 15 - 25 MHz) from space objects. In this case it is necessary to make analysis of acoustic wave passage.

Below, the coordinate frame where OZ axis is directed vertically upwards is used. The ionosphere data for

plasma in geomagnetic field which used in the simulations of nonlinear passage of acoustic wave are given in Figure 2 [12] . The electron cyclotron frequency at height z = 100 - 200 km is taken as. The angle between the vertical axis OZ and the direction of the geomagnetic field is chosen as 30˚, also the angle between the plane, which includes the OZ axis and the geomagnetic field, and OX axis is 30˚.

In the case of one-dimensional non-uniformity along the vertical coordinate, for oblique incidence of plane electromagnetic wave with the components,.

Generally, the set of Equation (2), with boundary conditions at magnetosphere heights more as 200 km and at Earth’s surface, should be used. In our analysis, for the sake of simplicity it is analyzed a case when the perturbation scale is considerably larger than the wavelength of EMW, i.e. when the geometric optic approximation is valid:

(5)

Note that there are two proper solutions of this equation.

Therefore, the transmission coefficient of radio waves through the ionosphere for each kind of wave is:

(6)

A transmission coefficient of the electromagnetic radio wave (EMW) has been estimated within the geometric optics approximation. The initial density of the ionosphere has been modified in accordance with the formula:

(7)

In attitude the modulation has the beginning and the distance approximately equal. Note that under a propagation of ULF acoustic pulses both compression and rarefaction of density may occur.

The main result is as follows (see Figure 3). Due to the modulation of plasma density within the F-layer, it is possible to obtain changes of transparency of 2 to 5 times, if the frequency of the radio wave is near the cut-off. Moreover, it is possible to obtain an increase of transparency when the decrease of the plasma density at heights z more as 200 km takes place.

4. Conclusion

In this work two cases were exposed that showed an increase of transparency for cosmic radio waves. The first one is a period structure and the second one causes decrease of plasma density in the F-layer, based on our simulation and experimental results [12] [13] . The simulation has demonstrated the following result. At the altitude of about 160 km, the effect of a decrease of plasma density is observed. In case of higher altitude, there is effective inflation of periodic structure. The observation time and altitude lead to the accumulation of the two effects. Each effect has the same intensity. For resolving these two effects, it is necessary to provide new experiments with different altitudes between 60 km and 200 km.

References