Journal of Electromagnetic Analysis and Applications
Vol.06 No.10(2014), Article ID:49655,15 pages
10.4236/jemaa.2014.610026
Asymmetric Electrostatic Force
Katsuo Sakai
Electrostatic Generator Research Laboratory, Yokohama, Japan
Email: gy7a-ski@asahi-net.or.jp
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 July 2014; revised 1 August 2014; accepted 26 August 2014
ABSTRACT
Asymmetric electrostatic forces are a very interesting and new phenomenon. The magnitude of an electrostatic force that acts on a point charge does not change when the direction of the electric field is reversed. On the contrary, the magnitude of the electrostatic force that acts on a charged asymmetric shaped conductor does change when the direction of the electric field is reversed. 5 years ago, this phenomenon was reported by a simple experiment and a simulation and named as an Asymmetric electrostatic force unofficially by the author. After that, several simulations confirmed this phenomenon. However, several experiments did not yet confirm it clearly. The difference between the simulations and the experiments depends upon differences of their conditions. The simulations had been done under ideal (perfect) conditions; the experiments, on the contrary, had been done under actual (not perfect) conditions. In the new experiment, its conditions were improved to near ideal (perfect) conditions. As a result the existence of the Asymmetric electrostatic force was more clearly confirmed.
Keywords:
Asymmetric Electrostatic Force, Asymmetric Conductor, Charged Conductor, Charge Decay Rate, Axis Symmetry Finite Difference Method

1. Introduction
Historically, the main application of electrostatics has been Xerography and powder coating. The main materials used in these technologies are charged powders. The electrostatic force that acts on this powder has been calculated using the following Coulomb equation:
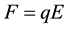 (1)
(1)
where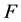 : Electrostatic force [N];
: Electrostatic force [N];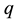 : Charge quantity [C];
: Charge quantity [C];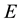 : Strength of electric field [V/m].
: Strength of electric field [V/m].
This equation can be applied to a point charge [1] , and a charged powder can be treated as a point charge. It is apparent from this equation that the magnitude of the electrostatic force that acts on the charged powder does not change when the direction of the electric field is reversed.
On the contrary, the magnitude of the electrostatic force that acts on a asymmetric charged conductor changes largely when the direction of the electric field is reversed. It was found by simple simulation and experiment on 2009 [2] . And this phenomenon was named as Asymmetric electrostatic force unofficially.
The existence of this phenomenon has been confirmed by a few simulations [3] -[6] . But it has not yet been confirmed clearly by experiments [3] [4] [6] . For example, Figure 1 shows the latest result of this phenomenon study.
In this figure, the electrostatic force in forward electric field is larger than that in backward electric field. However, the difference between those two forces is very large in simulation, but it is very small in experiment. Therefore, this experiment result can not confirm the existence of this phenomenon clearly.
This study has been done with using a cylinder-disk shape conductor and a small experimental instrument. Figure 2 and Figure 3 show the asymmetric conductor and the instrument respectively.
Figure 1. Electrostatic forces that acts on the charged asymmetric conductor in forward or backward electric field. They were measured by the experiment, and simulated by the axis symmetry finite difference method (previous work).
Figure 2. The front and side view of the asymmetric shaped conductor (previous and new work).
Figure 3. Schematic layout of the experimental instrument used to measure the shifted distance of the asymmetric conductor by a electrostatic force (previous work).
The difference between the simulation result and the experiment result must be depending on their different conditions. There are three important differences between the simulation and the experiment. First of all, electrostatic force acts on the surface of the asymmetric conductor perpendicularly in the simulation, but it acts on obliquely in the experiment as shown in Figure 4.
The reason is that the asymmetric conductor was made by thin aluminium plate and the surface became thin Al2O3 layer naturally.
Secondarily, the cylinder surface of the asymmetric conductor is always parallel to the direction of the electric field and the disk surface is always perpendicular to the direction of the electric field in the simulation, but the surfaces are not parallel or perpendicular to the direction of the electric field as shown in Figure 5 actually.
Thirdly, the distance between the asymmetric conductor and the electrode is kept 50 mm in simulation. But it was shorten to 20 mm in experiment as shown in Figure 5 actually. As a result, image force between the asymmetric conductor and the electrode became large.
Therefore, if those three differences between the simulation and the experiment are reduced, the experimental result will be closer to the simulation result and the existence of Asymmetric electrostatic force will be confirmed more clearly.
2. Experiment
Figure 2 shows the front and side views of the asymmetric shaped conductor used in this experiment. They are axis symmetrical shaped conductors. Because the latter mentioned simulation method can only simulate axis- symmetrical shaped conductors.
Figure 4. Electric line of force acting on the Al layer perpendicularly and electric line of force acting on the Al2O3 layer covering the Al layer obliquely.
Figure 5. Maximum angle of the surface of the asymmetric conductor is about 13 degree to the electric field (previous work).
The asymmetric conductor consists of a disk and a hollow cylinder, as shown in Figure 2. The diameters of the disk and cylinder are 30.0 mm and 20.0 mm, respectively. The width of the cylinder is 10.0 mm. They were made from thin gilding aluminium plates. As a result, the electrostatic force always acts on the gold surface perpendicularly. The thicknesses of the disk and the cylinder are 0.2 mm and 0.3 mm respectively. Because the asymmetric conductor was made by hand, the cylinder surface of the asymmetric conductor is not perfectly parallel to the direction of the electric field and the disk surface is not perfectly perpendicular to the direction of the electric field.
Figure 6 shows the schematic layout of the improved experimental instrument that was used to measure the distance that the asymmetric conductor was shifted by an electrostatic force.
The instrument consisted of two parallel electrodes and a parallel ruler. The distance between the electrodes was enlarged from previous 100 mm to 200 mm. As a result, the minimum distance between the asymmetric conductor and the electrode was enlarged from previous 20 mm to 70 mm. Then the maximum image force between the asymmetric conductor and the electrode was reduced to less than 1/10.
One electrode was connected to a high-voltage power supply, and the other was grounded. As a result, a strong electric field was created between them. The electric field had two directions, to which I refer as the forward and backward direction electric fields.
The asymmetric conductor were hung with four raw silk threads at the center of the two electrodes. The length of the threads was enlarged from previous 170 mm to 460 mm. As a result, maximum angle of the surface of the asymmetric conductor to the direction of the electric field is reduced from about 13 degree to about 3 degree.
Those threads served as insulators. The position of the asymmetric conductor was measured by the eye using the ruler. Matsusada Precision HAR-50P6 was used as a high voltage power supply. The amount of charge on the asymmetric conductor was measured using a coulomb meter (Type NK-1001 KASUGA DENKI, INC. Japan).
Figure 7 shows an explanatory drawing of the experimental procedure.
The experiment was performed using the following procedure:
1) The left and right electrodes were grounded, and the asymmetric conductor was put in contact with the narrow grounded aluminium tape to discharge.
2) The non-charged conductor was centered between the electrodes, and the position of the conductor was measured using the ruler. This position was the start position.
3) The right electrode was charged to +22 kV, and the left electrode was grounded to create the electric field.
4) The conductor was contacted with the narrow grounded aluminum tape for induction charging. The tape was then kept away from the conductor so that the negative charge was maintained on the conductor.
Figure 6. Schematic layout of the improved experimental instrument used to measure the shifted distance of the asymmetric conductor by a electrostatic force (new work).
Figure 7. A schematic of the experimental procedure.
5) The right electrode was grounded again. After that, the charged conductor continued to vibrate. It eventually came to rest at or near the starting position.
6) The right electrode was charged up to +10 kV, and as a result, the negatively charged conductor was shifted to the right by the electrostatic force that acted on this conductor. This electric field was the forward direction electric field. The shifted position of the conductor was measured with the ruler. The voltage of the right electrode was subsequently changed from +10 kV to +12 kV, and a new position was measured. Furthermore, the voltage was changed to +14 kV, +16 kV, +18 kV and +20 kV, and each position were measured. The difference between the shifted position and the start position was the shifted distance
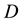 of the asymmetric conductor.
of the asymmetric conductor.
7) The right electrode was grounded, and the left electrode was connected to a high-voltage power supply to create a backward direction electric field between them.
8) The same procedure as 6) was repeated.
This experiment was repeated 6 times. Figure 8 shows the measured shifted distance of the asymmetric conductor.
This experiment was performed in a low temperature (15˚C) and low humidity (10% RH) room. It is expected that the induced charge on the asymmetric conductor will not diminish for a considerable amount of time. For confirming this expectation, the amount of charge on the asymmetric conductor was measured using the Coulomb meter. It was measured at 20, 40, 60, 120, 180, 300 and 600 sec after the induction charging. The measurement was repeated two times. Figure 9 shows those results.
It is apparent from Figure 9 that the induced charge on the conductor is not constant and reduces as a function of time. The above-mentioned experimental procedure needed approximately 310 sec from the charge induction to the final measurement. Therefore, the charge quantity on the asymmetric conductor is not treated as constant. However, the rate of change is not large due to the low temperature and low humidity environment. The decay rate can be presented as the following equation:
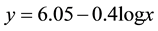 (2)
(2)
where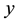 : Quantity of charge (nC);
: Quantity of charge (nC); : time after charge induction (sec).
: time after charge induction (sec).
Therefore, the measured shifted distances with a slightly decayed charge were corrected to the shifted distance with the same charge quantity of the first measurement by using Equation (2). Because, the electrostatic force is proportional to the quantity of the charge and the shifted distance is proportional to the electric force.
Figure 10 shows the corrected measured shifted distances of the asymmetric conductor.
In Figure 10, the shifted distances in the forward electric field are almost larger than the shifted distances in the backward electric field. But, some shifted distances in the forward electric field are equivalent or lower than the shifted distances in the backward electric field. If it happens at the same charge quantity, the existence of Asymmetric electrostatic force will be refused.
Figure 8. The shifted distance of the asymmetric conductor that was measured six times with six different strength electric field (original data).
Figure 9. Quantity of charge on the asymmetric conductor in low temperature (15˚C) and low humidity (10% RH) condition as function of time.
Figure 10. The shifted distance of the asymmetric conductor that was measured six times with six different strength electric field (charge quantity correction data).
Therefore, the both shifted distances in the same experiment, that means the same charge quantity, are compared. Figure 11 shows that result.
In Figure 11, all shifted distances in the forward electric field are larger than that in the backward electric field. The differences of the shifted distances between the six experiments depend on the induced charge quantity difference
Next, those measured shifted distances were converted into electrostatic forces that acted on the asymmetric conductor with the following procedure.
Figure 11. The shifted distance of the asymmetric conductor when the applied voltage was 20 kV. That was measured repeatedly six times (Exp.1 - Exp.6).
The shifted distance



The ratio of the lengths









where


The electrostatic force that acted on the negatively charged asymmetric conductor in different electric fields were calculated from the corrected shifted distances that were presented in Figure 10 using Equation (3).
Figure 13 show the results.
It is apparent from Figure 13 that the magnitude of the electrostatic force that acts on the charged asymmetric conductor in the forward electric field is larger than the magnitude of the electrostatic force that acts on the charged asymmetric conductor in backward electric field.
Therefore, the existence of Asymmetric electrostatic force is more clearly confirmed with the improved experimental instrument than the previous work.
3. Theory
The first reason of Asymmetric electrostatic force is the transfer of the charge (electron) in the asymmetric conductor. Namely, many of the induced charge (electron) concentrate into the disk at the forward electric field. But at the backward electric field, many electrons transfer to the cylinder. The concentrate rate of the electron to the disk is not constant. It changes depend on not only shape of the conductor, but also quantity of charge (electron) and the strength of the electric field.
For an example, Figure 14 shows a simulated charge distribution of the disk-cylinder shape conductor.
It has seven different surface areas as shown at Figure 14 left half. Figure 14 right half shows the charge quantity on the seven different areas at the forward and backward electric field. It is apparent from this graph that many charges (electrons) transfer from the front surface of the disk to the cylinder when the direction of the electric field is reversed.
This is a simulation result. Therefore, trial experiment to confirm this charge (electron) transfer had been performed. The charged asymmetric conductor was separated in the high electric field. And quantity of the charge on the disk and quantity of the charge on the cylinder were measured separately. This separating was performed by hand. As a result, many times it failed. Only a few times it succeeded. Figure 15 shows the succeeded result.
It is apparent from this graph that many charges (electrons) actually gather to the disk of the charge carrier at the forward electric field and many charges (electrons) actually gather to the cylinder of the charge carrier at the backward electric field.
The second reason of Asymmetric electrostatic force is the well-known nature of a charged conductor. Namely, the electrostatic force that acts on the surface of the conductor is always perpendicular to the surface.
The disk-cylinder shape conductor has seven different surface areas as shown at Figure 16 left half.
The seven electrostatic forces (F1 - F7) that act on the seven different surface areas are all perpendicular to each surface. Therefore, three electrostatic forces (F2, F3, and F6) that act on peripheral surfaces of the disk and cylinder become zero. Because, they cancel each other at an interval of 180 degrees.
Figure 16 right half shows the seven electrostatic forces that act on the seven different areas at the forward and backward electric field. It is apparent from this figure that the electrostatic force, toward right F7 is larger than the electrostatic forces toward left F1 + F4 + F5 at the forward electric field, on the contrary, F1 + F4 + F5 is not so larger than F7 at the backward electric field. (Caution: three electrostatic forces (F2, F3, and F6) that act on peripheral surfaces of the disk and cylinder are totaly zero.)
This is the main concept of Asymmetric electrostatic force.
Figure 17 shows the ideal condition of Asymmetric electrostatic force.
Namely, all charges (electrons) gather on the front surface of the disk that is perpendicular to the electric field at the forward electric field, and all charges (electrons) transfer to the peripheral surface of the cylinder that is parallel to the electric field at the backward electric field. As a result, strong electrostatic force to right direction generates at the forward electric field, and any electrostatic force to left direction does not generate at the backward electric field.
Figure 12. Schematic diagram of the electrostatic force, the gravity force and the tensile force that acts on the charged asymmetric shaped conductor in a electric field.
Figure 13. The electrostatic force that acts on the charged asymmetric conductor. It was measured six times with six different strength electric field.
Figure 14. The simulated charge quantity on the seven different areas of the disk-cylinder shape conductor at the forward and backward electric field.
Figure 15. Quantity of the charge on the disk and quantity of the charge on the cylinder. They were measured separately after the charged disk-cylinder shape conductor was separated in the high electric field.
Figure 16. The seven electrostatic forces that act on the seven different areas of the disk-cylinder shape charged conductor at the forward and backward electric field.
From this point, this design of the charge carrier shown in Figure 2 is not perfect. Because, some charges (electrons) remain on the back surface of the disk at the forward electric field, and some charges (electrons) remain on the front surface of the disk at the backward electric field as shown in Figure 14. The best design of the charge carrier for Asymmetric electrostatic force has been researching today.
Figure 17. The ideal condition of Asymmetric electrostatic force.
Finally, if the shape of the conductor is special, the conductor that has negative charge can progress toward negatively high potential place like as the yacht that progress toward the wind [4] .
4. Consideration
The existence of Asymmetric electrostatic force has been more clearly confirmed by the improved experimental instrument. The previous experimental instrument had some differences from the ideal condition (Simulation condition). Those differences were improved and the improved experimental condition was close to the ideal condition (Simulation condition). Therefore, the experimental result must be close to the simulation result. Then, a simulation was performed by the axis symmetry finite difference method using the same conditions with the experiment. The detail of the simulation and the reliability of the simulation program are described in Appendix.
Figure 18 shows the simulation result and the experiment result that is average of the six experiments.
It is apparent from Figure 1 (previous work) and Figure 18 (new work) that the experimental result of the new work is closer to the simulation result than the experimental result of the previous work. However, the new work result is not equal to the simulation (ideal) result.
This is because the inclination of the cylinder of the asymmetric charge carrier to the direction of the electric field has not been improved perfectly. If the surface of the cylinder part is parallel to the electric field as shown in Figure 19 left half.
The electrostatic force Fa that acts on the edge A of the cylinder is the same of the electrostatic force Fb that acts on the edge B of the cylinder. On the contrary, if the surface of the cylinder part is incline to the electric field as shown in Figure 19 right half, electrostatic force Fa becomes strong and electrostatic force Fb becomes weak. This is because density of electron and strength of electric field at A become more large and density of electron and strength of electric field at B become more little. As a result, parallel component of the electrostatic force Fa becomes larger than parallel component of the electrostatic force Fb. Therefore, the backward electrostatic force becomes more strong.
Unfortunately, this is not a simulation result. the axis symmetry finite difference method can not treat this inclined condition. Therefore, this is an expectation on my experience.
If the more improved experimental instrument will be used, the experimental result will be equal to the simulation (ideal) result and the existence of Asymmetric electrostatic force will be perfectly confirmed.
For that purpose, a new experimental method that keep always the surface of the cylinder part parallel to the electric field must be selected. Figure 20 shows the possible method.
A spring balance is hanging a symmetric charged conductor between the upper electrode and the lower electrode. When high voltage is applied to the lower electrode, the asymmetric conductor will be pulled by an electrostatic force. The strength of the electrostatic force can be calculated by the shifted distance. In this design, it is expected that the surface of the cylinder part is always parallel to the electric field.
And the asymmetric conductor and the experimental instrument must be made by a mechanical method in place of a handmade method.
Figure 18. Electrostatic forces that acts on the charged asymmetric conductor in forward or backward electric field. They were measured by the experiment, and simulated by the axis symmetry finite difference method.
Figure 19. The cylinder of the disk-cylinder shape conductor (left) is parallel to the direction of the electric field, and the cylinder (right) is not parallel to the direction of the electric field.
Figure 20. A new experimental method that keep always the surface of the cylinder part parallel to the electric field. A spring balance is hanging a disk-cy- linder shape charged conductor between the upper electrode and the lower electrode.
5. Conclusion
The existence of Asymmetric electrostatic force has been confirmed more clearly than the previous experiment by the improved asymmetric conductor and experimental instrument. However, the experimental result is not yet equal to the simulation (ideal) result. Therefore, a new experimental method and a precise manufacture of the asymmetric conductor and the experimental instrument must be needed. Then the same experimental result with the simulation result will be achieved. As a result, the existence of Asymmetric electrostatic force will be confirmed perfectly.
Acknowledgements
The author is thankful to KASUGA DENKI, INC. Japan that allowed me to use the Coulomb meter for free.
References
- Halliday, D., Resnick, R. and Walker, J. (2002) Fundamentals of Physics. 6th Edition Japanese Version Chapter “Electric Charge” Question 1, Wiley & Sons. Inc., Hoboken.
- Sakai, K. (2009) The Electrostatic Force That Acts on the Charged Asymmetric Conductor in A High Electric Field. Proceedings of 2009 ESA annual Conference (2009) P2.07.
- Sakai, K., et al. (2010) Electrostatics: Theory and Applications. 1st Edition, Nova Science Publish, New York (Chapter 1).
- Sakai, K. (2010) Asymmetric Electrostatic Forces and a New Electrostatic Generator. 1st Edition, Nova Science Publish, New York.
- Sakai, K. (2010) Electrostatic Force That Acts on Non-Sphere Shape Charged Conductors. Proceedings of 2010 ESA annual Conference (2010) G4.
- Sakai, K. (2011) A Simple Experiment Result That Confirmed Asymmetric Electrostatic Force. Proceedings of 2011 ESA annual Conference (2011) B4.
- Matsubara, Y. (1992) Improved Finite Difference Expression for Laplace’s and Poisson’s Equations on the Surface of Dielectrics. Journal of the Institute of Electrostatics Japan, 16, 440-442.
- Matsubara, Y. (1992) A Guide to the Calculation of Electric Field Part Ⅲ Application of the Finite Difference Method to Electric field in an Oil Tank. Journal of the Institute of Electrostatics Japan, 16, 530-538.
- Matsubara, Y. (1994) A Method to Calculate the Potential of Ungrounded Conductors. Journal of the Institute of Electrostatics Japan, 181-184.
- (1998) Handbook of Electrostatic, Japan, 1013-1014.
Appendix
Reliability of the Used Simulation Program
Usually, the results of the two-dimensional simulation sometimes disagree with the experimental results. Therefore, simulations must be performed using a three-dimensional method. Unfortunately, I do not have the three- dimensional program. I learned the finite difference method from Dr. Matsubara's papers [7] - [9] and wrote a two-dimensional program by myself. Fortunately, the axis symmetry finite difference method can simulate the three-dimensional world. This is mathematically a two-dimensional program, but this is physically a three-di- mensional program. Of course, this program is limited for simulating an axis-symmetric material. However, disk- and cylinder-shaped materials can be simulated.
Before simulating the above-mentioned experiment, the reliability of the handmade simulation program must be confirmed. For this purpose, the following problem was selected because this problem can be solved analytically.
Figure 21 shows the selected problem [10] .
There are two parallel electrodes. The distance between them is “







where
When





Next, the induced charge


The quasi-sphere consists of two disks and 18 conical disks. The thickness of those 20 disks was 0.1 mm. The diameter of the 2 disks was 1.0 mm. The upper and lower diameters of the 2 conical disks were 0.9 mm and 1.0 mm, respectively. The other 16 conical disks had different diameters, as shown in Figure 22.
The induced charge


It is apparent from Figure 23 that the simulation does not agree with the calculated results. Nevertheless, this finding does not mean that the handmade simulation program was wrong. It instead means that the quasi-sphere was not the same as the perfect sphere. It is apparent from Figure 22 that the volume of the quasi-sphere is less than that of the perfect sphere. Both volumes must be the same. The diameter of the perfect sphere that has the same volume as the quasi-sphere was determined to be 0.866 mm.
Figure 24 shows the new calculation result that used the 0.866-mm diameter.
It is apparent from Figure 24 that the simulation results are in agreement with the calculation results. This finding means that this handmade simulation program is accurate.
The Simulation Method and Its Result
The above-mentioned experiment was performed between the right and left square electrodes, as shown in Fig- ure 6. The height and width of those electrodes were both 100 mm. The distance between the electrodes was 200 mm.
This axis symmetry program cannot use square-shaped material. The square electrodes were replaced with circular electrodes, as shown in Figure 25.
Figure 21. The selected problem that confirm the reliability of the handmade axis symmetric finite difference program. A conductive sphere is contacting with the under electrode. How much charge will be induced into the sphere?
Figure 22. The layout of the quasi-sphere and the upper and lower electrodes.
Figure 23. The simulation and calculation results of the induced charge Q and the electrostatic force F. The simulation used the quasi-sphere, on the contrary, the calculation used the perfect sphere.
Each electrode had a radius of 53.7 mm. The distance between the electrodes was 200 mm. The asymmetric conductor consisting of a disk and a hollow cylinder (Figure 2) was placed at the center of both electrodes. The right electrode, the asymmetric conductor and the left electrode were lined up on the Z-axis, as shown in Figure 25.
The simulation target space between the electrodes was divided into small cells. The space was divided into 40 cells in the R direction and 61 cells on the Z-axis. Figure 26 shows the cells that are around the hollow cylinder and part of the disk.
In Figure 26, broad lines show the surface of the cylinder and the disk of the asymmetric conductor. The simulation accuracy can be improved by minimizing cell, size, this tend to require longer simulation times, however. Therefore, a cell size of 0.1 mm was limited to the cells around the conductor. The sizes of the cells were varied depending on the distance from the conductor: 0.1 mm near the conductor, followed by 0.4 mm, 1.6 mm and 6.4 mm near the electrodes.
Figure 24. The simulation and calculation results of the induced charge Q and the electrostatic force F. The simulation used the quasi-sphere, and, the calculation used the perfect sphere that has the same volume as the quasi-sphere.
Figure 25. The layout of the two electrodes and the asymmetric conductor that were used in the axis symmetry finite difference simulation.
Figure 26. The cell layout that are around the hollow cylinder and a part of the disk.
The potential at a particular cell point was calculated using the potential of the 4 neighboring cells point (i.e., right, left, upper and under). The potential of all 2440 cell points was calculated by solving multiple simultaneous equations, starting from points whose potentials were already known. For example, the potential at the points of the two electrodes were known. The potentials of those points were +20 kV or 0 V. The strength E of the electric field on the surface of the conductor was calculated using the potentials of the four corner points of the surface cells that neighbored the conductor. There were 70 surface cells.
The surface charge density




where

Figure 27. The electrostatic force that acts on the charged asymmetric conductor in forward or backward electric field as a function of strength of electric field.
The charge




The electrostatic force


The electrostatic force acting on the 7 areas of the conductor was calculated by summing the electrostatic forces acting on each cell of the same area. Figure 16 shows the 7 areas and the 7 electrostatic forces that acted on these areas when the right electrode was set to +20kV (the forward electric field).
In the left half of Figure 16, F1, F2, F3, F4, F5, F6, F7 indicate the 7 electrostatic forces that act on the edge of the hollow cylinder, outer peripheral area of the hollow cylinder, inner peripheral area of the hollow cylinder, outside of the back area of the disk, inside of the back area of the disk, edge of the disk and the front side of the disk, respectively.
The right half of Figure 16 shows the magnitude of the simulated 7 electrostatic forces. This simulation was conducted under the following conditions:
The voltage of the right electrode was 20 kV, the voltage of the left electrode was 0 V and the charge on the asymmetric conductor was

The total electrostatic force Fe that acts on the charged asymmetric conductor was calculated using the following Equation (9):

The forces F2 and F3, which act on the outer and inner peripheral surface of the hollow cylinder, and F6, which acts on the edge of the disk, were not included in Equation (9) because they cancel each other at an interval of 180 degrees and ultimately become zero.
For example, in Figure 16,





The total electrostatic force that acts on the asymmetric conductors under different conditions was calculated using the same method. Figures 27 show the results.
It is apparent from Figure 27 that if the shape of conductor is asymmetric in the direction of electric field, then the magnitude of the electrostatic force that acts on the conductor changes dramatically when the direction of the electric field is reversed.
Therefore, the existence of the Asymmetric electrostatic force has been clearly confirmed again such as the previous simulation by the physical three-dimensional simulation.






























