Journal of Electromagnetic Analysis and Applications
Vol. 5 No. 2 (2013) , Article ID: 28498 , 9 pages DOI:10.4236/jemaa.2013.52008
Analysis of the Performance of Optical Code-Division Multiple-Access System (OCDMA), Operating with Gold Codes under Nonlinear Effects
![]()
1Laboratório de Telecomunicações e Ciência e Engenharia dos Materiais (LOCEM), Departamento de Física, Universidade Federal do Ceará (UFC), Fortaleza, Brazil; 2Laboratório Especializado em Sistema de Telecomunicações e Ensino (LESTE), Departamento de Telemática, Instituto Federal do Ceará (IFCE) Campus Fortaleza, Fortaleza, Brazil; 3Grupo de Física Aplicada e Docência (GFAD), Instituto Federal do Ceará (IFCE) Campus Sobral, Sobral, Brazil; 4Departamento de Engenharia de Teleinformática (DETI), Centro de Tecnologia, Universidade Federal do Ceará (UFC), Fortaleza, Brazil; 5Departamento de Engenharia de Energias, Universidade da Integração Internacional da Lusofonia Afro-Brasileira (UNILAB), Redenção, Brazil.
Email: *sombra@ufc.br
Received November 23rd, 2012; revised December 22nd, 2012; accepted January 5th, 2013
Keywords: Fiber Bragg Grating; Gold Code; OCDMA; All-Optical Digital Processing of Signals
ABSTRACT
A numerical simulation study of the performance of encoding and decoding of short optical pulse in OCDMA (Optical Code Division Multiple Access) systems under non-linear optical effects is presented. The performance of encoding and decoding short pulses is obtained through use of device FBG (fiber Bragg grating) where the codes are inserted through discrete jumps in the optical phase (±π). The multiuser interference is also the object of the present study, where a figure of merit (interference figure) is used to quantify the interference in multiuser auto and cross correlation. We evaluate the dependence of the multiuser interference for the coupling constant of FBG. Finally, the interference inserted in the autocorrelation due to nonlinear effects generated in the nonlinear switching of the coded pulse in a dual core nonlinear directional coupler is examined, where temporal broadening of pulses decoded is observed.
1. Introduction
The increasing demand for traffic information is leading to an increase of the capacity and functionality of communication systems. In this context, characteristics such as bandwidth, security of transmitted information and the data rate transmission, are critical to the evolution of systems. In this sense, access and multiplexing techniques allow the simultaneous existence of multiple users on the network sharing the same optical domain. The most popular techniques are TDMA (Time Division Multiple Access), FDMA (Frequency Division Multiple Access) and CDMA (Code Division Multiple Access). The main advantages of CDMA over other techniques include the capacity for higher connectivity, more flexible bandwidth usage, higher granularity and scalability within optical networks, improved crosstalk performance, asynchronous access, and potential for improved system security, as each user on the network has a specific address code [1, 2].
Depending on the coding approach, the optical CDMA can be divided into the following categories: temporal encoding, spectral amplitude encoding, spectral phase encoding and spatial encoding [1]. A hybrid encoding can be achieved through the use of two of the encodings listed above. Initially, the OCDMA technology uses the temporal encoding employing a delay line network. In this method, an ultrashort optical pulse is converted into a pulse train with low intensity, so each replica pulse occupies a temporal position according to the delay line, resulting in the coded pulse. For decoding, a second delay line network having a complementary delay response was used so that the pulses in the train are despread into the same time slot [3].
The coding in the spectral amplitude, in turn, is realized with the inclusion of a broadband signal in spatial filters with amplitude masks. The pattern of filtered frequencies signal is encoded, so each code is represented by a sequence of different arrangements of masks amplitude [4]. As the spectral amplitude encoding, spectral phase encoding considers a ultrashort pulse (broadband) initially dispersed by a diffraction grating. The spectral phase encoding uses the spectral content of the signal being encoded, that is, different displacements are applied to different frequency components [5].
The spatial encoding, in turn, uses various fibers or including multi-core fibers [6]. Used to propagate images in optical fibers, this type of coding has received attention in hybrid coding schemes, which are used two simultaneous encoding schemes, such as coding space-time coding or wavelength-time [7].
FBG has shown excellent performance for the results of autocorrelation and cross correlation in OCDMA systems [2]. A form of code using FBG optical signals is to arrange the grating in a specific sequence, using the center frequency of the grating reflection. In this encoding scheme, the position of the grating and the wavelength of reflection are the key points to coded spectral and temporal information. In [2] a scheme using FBG encoding and decoding was presented, where grating is a pure amplitude-modulated grating containing various discrete sections of grating (spatial chips), which exhibit either full or zero refractive index modulation [2]. The encoding using the optical phase of light as a parameter, is obtained with the inclusion of discrete jumps in phase (±π) in the fiber Bragg grating. The inserted sequences of phases are defined by the used code.
To achieve good and high-contrast code recognition, one needs to restrict the use of codes within the system to those that have both distinct autocorrelation features with a single dominant, well-defined autocorrelation peak and low peak-level mutual cross-correlation functions. The used chip patterns are usually the well known M-sequences, or are based on combinations of M-sequences such as Gold codes, Kassami codes, or Walsh-Hadamard codes, which are known to have such properties [4]. Such codes are also applicable to OCDMA. The quality of the code recognition and the number of orthogonal codes supported by a given code length is a strong function of the code length and degree of polarity (i.e., the number of possible coding levels) of the implementation. Both of these properties improve significantly with the use of longer codes and increasing degrees of polarity.
2. Theoretical Procedure
2.1. Fiber Bragg Grating
A FBG consists of a periodic perturbation of the refractive index in the longitudinal direction of the core of an optical fiber. The perturbation of the refractive index of the core of an optic fiber is a periodic structure that acts as a band-reject filter. Thus, a narrow spectral band of an incident optic field through a fiber is reflected by successive and coherent scatterings, caused for the variations of the index. The coupling is more intense between modes occurs in the wavelength of Bragg, λB, this condition can be thought of as a phase-matching condition, presented Equation (1) below [8-10],
 , (1)
, (1)
where Λ is the grating period, neff is the effective index and N is the order of Bragg [9-13].
The coupled-mode theory [11-13] has been used to describe the dynamics of fiber Bragg grating. Wave propagation in a linear periodic medium has been studied extensively using coupled-mode theory. For optical fibers is necessary to include both the nonlinear changes and the periodic variation of the refractive index by using Equation (2)
 , (2)
, (2)
where n2 is the nonlinear parameter and δng(z) accounts for periodic index variations inside the grating [13].
Using Maxwell equations, considering the refractive index given for Equation (2), Af and Ab vary slowly with z and keeping only the nearly phase-matched terms, the equations in coupled mode can be written in time domain as:
 (3)
(3)
 , (4)
, (4)
where Af and Ab are forward and backward amplitude, respectively [13]. The measurement of the grating detuning d and the coupling coefficient k are given, respectively:
 , (5)
, (5)
 . (6)
. (6)
For a transversally uniform grating, we can write  . The Equations (3) and (4) include the nonlinearity SPM (Self-Phase Modulation) and XPM (CrossPhase Modulation), that multiply the nonlinear parameter give
. The Equations (3) and (4) include the nonlinearity SPM (Self-Phase Modulation) and XPM (CrossPhase Modulation), that multiply the nonlinear parameter give . The terms b1 and b2 are the relative inverse of the group velocity and dispersion of the group velocity (GVD-Group Velocity Dispersion). The α/2 term, in these equations, is relative to the inserted losses for the system. In the present study the loss and nonlinearities will be neglected (α = 0 and γ = 0), which is associated to the small length of the device [10,13].
. The terms b1 and b2 are the relative inverse of the group velocity and dispersion of the group velocity (GVD-Group Velocity Dispersion). The α/2 term, in these equations, is relative to the inserted losses for the system. In the present study the loss and nonlinearities will be neglected (α = 0 and γ = 0), which is associated to the small length of the device [10,13].
2.2. Analytical Generation of Gold Codes
Gold sequences considers the bit-by-bit (modulo-2) sum of two pseudorandom sequences of the same length but generated by two distinct primitive polynomials. If one sequence is shifted and the second sequence is kept fixed bit-by-bit,  different sequences can be generated, one for each different shift. Considering the two original PN sequences, altogether
different sequences can be generated, one for each different shift. Considering the two original PN sequences, altogether  of Gold different sequences of length N can be generated with one pair of primitive polynomials [14-16].
of Gold different sequences of length N can be generated with one pair of primitive polynomials [14-16].
From two distinct primitive polynomials  we obtain six Gold sequences. The four additional codes were obtained considering the Equation (7)
we obtain six Gold sequences. The four additional codes were obtained considering the Equation (7)
 (7)
(7)
Below we present two of the codes (primitive polynomials) used in this work. Other codes had been generated from Equation (7),
 (8.1)
(8.1)
 . (8.2)
. (8.2)
2.3. Nonlinear Optical Fiber Couplers
All-optical data processing devices are fundamentals components for future integrated photonic circuits. Fiber couplers, also known as directional couplers, constitute an essential component of lightwave technology. They are used routinely for a multitude of fiber-optic devices that require splitting of an optical field into two coherent but physically separated parts.
The basic nonlinear coherent coupler, introduced by Jensen [15], consists of two similar waveguides made of a material with third-order susceptibilities, embedded in a host with purely linear susceptibility. When the guides are placed parallel to each other and in close proximity over a given distance, the guide fields overlap to some extent and power can be transferred between the two.
When all the power is initially launched into one of the guides, the nonlinear susceptibility can give rise to selftrapping of power in the original guide. The output power in the original guide, for a device length equal to a coupling length, can be made to switch from essentially zero percent at low power levels, to one hundred percent for input power levels exceeding a characteristic threshold [16].
The light proceeding from ones of the input gates (I1 or I2) will be guided for one of the output gates (O1 or O2), and depend, in linear regime, on the coupling length (Lc). Thus, in the linear regime, the behavior of the coupler is associated to the Lc parameter as [15-32]:
 . (9)
. (9)
Jensen [15] showed that varying the input light in the nonlinear coupler could lead to pulse switching between the cores. He therefore foresaw the possible use of a nonlinear directional coupler as an optical switch. The nonlinear Schrödinger equations describe of the nonlinear coupler and such equation is expressed by:
 , (10)
, (10)
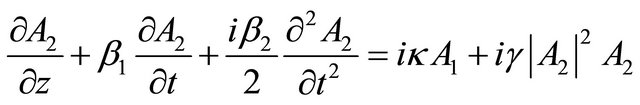 , (11)
, (11)
where A1 and A2 are input amplitude, respectively. The Equations (10) and (11) take in consideration only the effect of self-phase SPM, and neglect the XPM (crossphase modulation) effect, which is considered to be small [12-16]. In our simulation we study the behavior of switching process of coded optical pulses in the nonlinear coupler.
3. Results
3.1. Coding and Decoding of Optical Pulses
In this Section, the coding and decoding of short pulses with full width at half maximum of 2.5 ps will be presented. For coding we used the hyperbolic-secant pulse given by Equation (12), where Af is the pulse amplitude, A0 is the initial amplitude and T0 is the temporal width of the pulse. The used codes, for this study are presented in Section 2.2. We conducted this study based in the spectral phase encoding, through discrete jumps in the optical phase (±π) along the length of FBG,
 . (12)
. (12)
In our simulations, we have used the coupled-mode Equations (3) and (4), described in Section 2.1, which neglects the effects of nonlinearity, dispersion and losses. The characteristics of the FBG used in our simulations were: effective refractive index of neff = 1.452, coupling constant κ = 24.05 m−1 and length of 41.58 mm, with each chip of 0.66 mm length. In the coding process, the full width at half maximum of pulses takes the value of 402.5 ps in accordance with the Equation (13) (see Figure 1),
 , (13)
, (13)
where L is length of the fiber and c is velocity of light.
Figure 2(a) presents the autocorrelation and cross-correlation considering the sequences 1 and 2 presented in Section 2.2. The autocorrelation is achieved using the sequence 1 for both FBG encoder and decoder, in which one can observe that the results show good autocorrelation characteristic, in view of the low interference presented in the decoded pulse. Like the encoded and decoded pulse is obtained by reflection of the grating, and only part of the input power is reflected, the decoded pulse obtained after two reflections (encoding and decoding) is in time larger than the input pulse. For the frequency band of the reflected pulse is less than the input pulse. The decoded pulse presents full width at half maximum time of 5.7 ps, which is 3.2 ps larger than the input pulse, as presented in Figure 2(b). In the same figure is presented cross-correlation between the sequence coding 1 and sequence decoding 2. We can see, from the figure, that the cross-correlation presents values close to zero except for a peak in the autocorrelation (0.13 a.u.) around 350 ps, making this method very attractive for CDMA communications.

Figure 1. Setup of short optical pulse encoded and decoded.

Figure 2. (a) Autocorrelation (code 1/code 1) and cross-correlation (code 1/code 2); (b) Autocorrelation—TFWHM = 5.7 ps and input pulse—TFWHM = 2.5 ps.
3.2. Multi-Users Interference
To study the multiuser interference (MAI), we consider the interference of 1 to 6 different users (sequences 1 - 6) simultaneously. The design for the study of multiuser interference is shown in Figure 3, in which we can observe that the encoded signal is inserted in the decoding grating with the sequence 1. Additional users are added simultaneously to the user 1 (sequence 1), and autocorrelation is achieved. The Figure 4 presents the autocorrelation for the code sequence 1, considering 1 to 5 additional extra codes. As additional channels are inserted, the profile of the output pulse presents higher interfereence peaks due to overlapping of the results of autocorrelation (code 1) and cross correlation (codes 2 - 6). Another observed effect is the temporal broadening of pulses, increasing to about 16 ps for 6 simultaneous users.
To quantify the multiuser interference, we calculated a figure of merit (Interference Figure—IF), expressed in Equation (14). In this equation, SIR1 represents the signal to interference ratio, considering only one user present in the process of encoding and decoding, and SIRi, the signal to interference ratio for i users sending information simultaneously. Figure 5 shows the result for the evolution of the figure of merit given by Equation (14),
 . (14)
. (14)
One can notice that one has an increase in the interference figure as a function of the increase in the number of users sending information simultaneously.
The figure also presents the result of the figure of merit for several values of the coupling constant (the band of reflection of the FBG, which is proportional with the κ value), where one observe a nonlinear dependence of the IF with the coupling constant. We observe an increase in the IF with the increases the band of the FBG from k = 24.11 m−1 with a maximum of 13.45 dB in k = 120.54 m−1, from this value the IF decreases until a minimum value in k = 241.08 m−1 (approximately 2 dB for 6 users). The increase in interference with the coupling constant, between the values k = 24.11 m−1 to k =

Figure 3. Setup of the decoding process.

Figure 4. Decoding of the code 1 as a function of the presence of others users (we add 1 to 5 canals).

Figure 5. Interference figure as a function of the number of users (codes).
120.54 m−1, is due to the increase in the cross-correlation energy of additional users. After this value, the decrease in the interference level could be explained by the superposition of the cross-correlation energy in the region of the decoded pulse.
To confirm the accuracy of the previously obtained results, we performed a comparative analysis between the energies of the interference generated by the additional channels on the autocorrelation and cross-correlation energy. In the autocorrelation, the energy of interference obtained for autocorrelation is achieved by calculating the area of interference in figure intensity of decoded pulses shown in Figure 4. The calculation of the energy of interference, for the cross-correlation, was performed through the total energy of the obtained response, considering the situations where we have the codes: 2; 2 and 3; 2, 3 and 4; 2, 3, 4, 5; 2, 3, 4, 5 and 6 simultaneously, decoding with 1 (sequence 1) in the grating decoding. Figure 6 reveals the high degree of agreement of both methods to obtain the cross correlation energy.
3.3. OCDMA Operating with Gold Codes under Nonlinear Effects
In this study we consider the effect of nonlinearities in the coded OCDMA pulses. The codified pulse is inserted in an optical nonlinear coupler and its decoding occurs later, after the switching. During the switching in the coupler, the pulses are under the effect of the nonlinear index of refraction and dispersion. The simulated configuration is presented in Figure 7 where we present the outputs a and b where we have the decoding of the coded pulse. The nonlinear optical coupler is projected in such a way that for input powers below the critical power (1.32 W) the input pulse is completely switched for output 4. A gain factor (0, 10, 20 and 30 dB) was introduced before the nonlinear optical coupler to perform the study of the nonlinearities effect in the switched optical pulses and in the decoding process. In the gates (a) and (b) we will obtain the decoded pulses. Figures 8(a)-(d) present

Figure 6. Comparison of the figure of merit obtained through autocorrelation and cross-correlation, for k (24.11 m−1; 72.32 m−1; 120.54 m−1; 192.86 m−1; 241.08 m−1) as a function of the number of users.
the coded signals in output 3 and 4, for the 0, 10, 20 and 30 dB of gain, using the code1 signal (see Equation (8.1)). One observe that for the gain of 0 (Figure 8(a)) and 10 dB (Figure 8(b)) the energy is almost entirely switched to output 4, it occurs because the input power is below the critical power. For 20 dB (Figure 8(c)) of gain the codified signal its partially switched to output 4, where one can observe strong distortions in the output pulses in channel 3 and 4. For 30 dB (Figure 8(d)) of gain the energy is present totally in output 3, because the input power is above critical power, and one can observe strong fluctuations in the switched pulse in channel 3.
After the coded signals interact through the nonlinear optical fiber coupler, one has the decoding process through

Figure 7. Schematic of switching of the encoded pulses in a nonlinear optical coupler and the subsequent decoding process.
the FBG/decoder (see Figure 7).
The outputs “a” and “b” are the output for the decoded pulses (see Figure 7). For the decoding presented in Figures 9(a) and (b) and 10(a) and (b) one can observe the effect of the nonlinearity in the decoded pulses. The pulses are switched using an optical circulator after the decoding in the FBG. The decoded pulses suffers the effect due to the nonlinearity described in Equations (10) and (11). Figures 9 and 10 present the decoded pulses for several gains (0, 10, 20 and 30 dB). The same behavior observed in Figures 9(a) and (b) for the decoding pulse for gains of 0 and 10 dB, where almost all energy is switched to channel 4, that is expected for characteristics the Figure 8. We observe in Figure 10, that the input energy is divided in channel 3 and 4, where distortions in pulse of channel 3 is observed. For 30 dB of gain we observe strong distortions in channel 3 (Figure 10(b)). Comparing the decoded pulses (code 1) in Figures 9 and 10, we observe that the time duration of these pulses are strongly dependent of the nonlinear effects like nonlinear index of refraction and dispersion of the fiber coupler. The time duration is changing from approximately 5.7 ps (0 dB) to 12.5 ps (30 dB). The switching in the nonlinear coupler introduced a temporal increase in the width of the decoded pulses. Comparing the decoded pulse without the nonlinear effects, presented in Figure 2 (TFWHM = 5.7 ps), the increase in time duration due to nonlinear effects
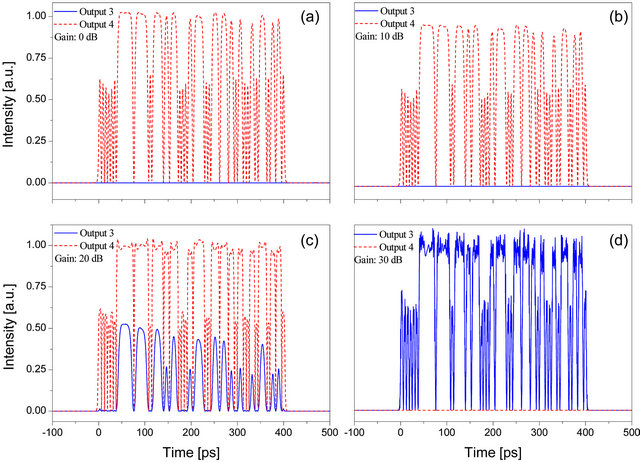
Figure 8. Encoded signal switched out from the nonlinear directional coupler for 0 (a), 10 (b), 20 (c) and 30 dB (d) of gain.

Figure 9. Decoding signal output 3 and 4, for gain (a) 0 dB; (b) 10 dB.

Figure 10. Decoding signal output 3 and 4, for gain (a) 20 dB; (b) 30 dB.
were up to 10 ps for 30 dB.
Figure 11 presents SNR in output “b” (see Figure 7). One can notice a decrease in the SIR with the increase of the gain. The increase of the gain is leading to higher nonlinear effects (described in Equations (10) and (11)) which is responsible to an increase of the SIR. In the same figure one has the SIR value for the decoded signal without the interaction with the coupler (4.3 dB), which is 0.1 dB above the value when comparing with the SNR with 0 dB gain (4.2 dB). The SIR value was calculated based in Section 3.2. We observe in Figure 11 that for the 30 dB of gain, the SIR is negative because the remainder energy is higher than the energy of the decoded signal.
4. Conclusion
In this work, a performance study of encoding and decoding of short optical pulse in OCDMA (Optical Code Division Multiple Access) systems is presented. The performance of encoding and decoding of short optical pulses is obtained using fiber Bragg gratings (FBG), in

Figure 11. Signal to Interference Ratio as a function of the gain factor.
which the Gold codes are inserted through discrete jumps in the optical phase (±π). The process of encoding and decoding of short pulses, using spectral phase coding, was studied in the context of multiuser interference and interference associated to nonlinearities in a dual core optical coupler. A dependence of the autocorrelation as a function of the number of users on the network was observed. A study of the multiuser interference as a function of the reflection band of Bragg grating was performed. A figure of merit (Interference Figure) was obtained to quantify the multiuser interference in autocorrelation and cross correlation, which was obtained in a maximum of 13.45 dB for interference with six users. The process of autocorrelation and cross correlation present a non-linear dependence with the coupling constant. Autocorrelation and cross-correlation were obtained after switching in a nonlinear dual core directional optical coupler. The switching of the coded pulses in the nonlinear optical coupler, interfere in the decoding process. Distortions and fluctuations in the coding pulses, in the output channel was observed. Decoded pulses, after the nonlinear coupler (output a) is presenting a broadening in the time duration associated to the nonlinear effects. We evaluated how the nonlinear switching is leading to a decrease of the SNR. Time broadening of the decoded pulse switched from the dual core nonlinear optical coupler is observed. Considering that the input pulse has a time duration of 2.5 ps, an increase to 5.7 ps, was observed as a result of the coding and decoding process. The time duration is changing from approximately 5.7 ps (0 dB) to 12.5 ps (30 dB) after the switching in the nonlinear coupler. The signal to Interference ratio (SNR) showed an increase in the interference level of 7 dB considering the increase of the amplification level (0 to 30 dB gain) which is leading to the increase of the nonlinearity.
5. Acknowledgements
We thank CNPq, FUNCAP, CAPES, FINEP for the financial support.
REFERENCES
- P. R. Prucnal, “Optical Code Division Multiple Acess— Fundamentals and Applications,” CRC Press Taylor & Francis, 2006.
- P. C. Teh, P. Petropoulos, M. Ibsen and D. J. Richardson, “A Comparative Study of the Performance of Sevenand 63-Chip Optical Code-Division Multiple-Access Encoders and Decoders Based on Superstructured Fiber Bragg Gratings,” Journal of Lightwave Technology, Vol. 19, No. 9, 2001, pp. 1352-1365. doi:10.1109/50.948283
- P. R. Prucnal, M. A. Santoro and T. R. Fan, “Spread Spectrum Fiber-Optic Local Área Network Using Optical Processing,” IEEE/OSA Journal of Lightwave Technology, Vol. 4, No. 5, 1986, pp. 547-554. doi:10.1109/JLT.1986.1074754.
- V. Jyoti and R. S. Kaler, “Design and Implementation of 2-Dimensional Wavelength/Time Codes for OCDMA,” International Journal for Light and Electron Optics, Vol. 122, No. 10, 2011, pp. 851-857. doi:10.1016/j.ijleo.2010.05.025.
- A. M. Weiner, J. P. Heritage and J. A. Salehi, “Encoding and Decoding of Femtosecond Pulses,” Optics Letters, Vol. 13, No. 4, 1988, pp. 300-302. doi:10.1364/OL.13.000300
- K. Kitayama, “Novel Spatial Spread Spectrum Based Fiber Optic CDMA Networks for Image Transmission,” IEEE Journal on Selected Areas in Communications, Vol. 12, No. 4, 1994, pp. 762-772. doi:10.1109/49.286683
- E. Park, A. J. Mendez and E. M. Garmire, “Temporal/ Spatial Optical CDMA Networks-Design, Demonstration, and Comparison with Temporal Networks,” IEEE Photonics Technology Letters, Vol. 4, No. 10, 1992, pp. 1160- 1162. doi:10.1109/68.163765
- A. Grunnet-Jepsen, A. E. Johnson, E. S. Maniloff, T. W. Mossberg, M. J. Munroe and J. N. Sweetser, “Demonstration of All-Fiber Sparse Lightwave CDMA Based on Temporal Phase Encoding,” IEEE Photonics Technology Letters, Vol. 11, No. 10, 1999, pp. 1283-1285. doi:10.1109/68.789718
- R. Kashyap, “A New Class of Fibre Grating Based BandPass Filters: The Asymmetric Interferometer,” Optics Communications, Vol. 153 No. 1-3, 1998, pp. 14-18. doi:10.1016/S0030-4018(98)00211-9
- R. Kashyap, “Fibre Bragg Gratings,” Academic Press, London, 1999.
- Y Murakami, “Characteristics of a Grating-Folded Optical Directional Coupler,” Fiber and Integrated Optics, Vol. 24, No. 5, 2005, pp. 445-456. doi:10.1080/01468030590966553.
- L. R. Chen, S. D. Benjamin, P. W. E. Smith and J. E. Sipe, “Ultrashort Pulse Reflection from Fiber Gratings: A Numerical Investigation,” Journal of Lightwave Technology, Vol. 15, No. 8, 1997, pp. 1503-1512. doi:10.1109/50.618383
- G. P. Agrawal, “Applications of Nonlinear Fiber Optics,” Academic Press, London, 2009.
- J. S. Lee and L. E Miller, “CDMA Systems Engineering Handbook,” Artech House, London, 1998.
- S. M. Jensen, “The Nonlinear Coherent Coupler,” IEEE Journal of Quantum Electronics, Vol. 18, No.10, 1982, pp. 1580-1583. doi:10.1109/JQE.1982.1071438
- W. D. Deering and M. I. Molina, “Power Switching in Hybrid Coherent Couplers,” IEEE Journal of Quantum Electronics, Vol. 33, No. 3, 1997, pp. 336-340. doi:10.1109/3.556001
- J. M. Soto-Crespo and E. M. Wright, “All-Optical Switching of Solitons in Twoand Three-Core Nonlinear Fiber Couplers,” Journal of Applied Physics, Vol. 70, No. 12, 1991, pp. 7240-7243. doi:10.1063/1.349768
- M. G. Da Silva and A. S. B. Sombra, “All-Optical Soliton Switching in Three-Core Nonlinear Fiber Couplers,” Optics Communications, Vol. 145, No. 1-6, 1998, pp. 281- 290. doi:10.1016/S0030-4018(97)00503-8
- M. G. Da Silva, A. F. Teles and A. S. B. Sombra, “Soliton Switching in Three-Core Nonlinear Directional Fiber Couplers,” Journal of Applied Physics, Vol. 84, No. 4, 1998, pp.1834-1842. doi:10.1063/1.368615
- N. Sugimoto, T. Nagashima, T. Hasegawa, S. Ohara, K. Taira and K. Kikuchi, “Bismuth-Based Optical Fiber with Nonlinear Coefficient of 1360 W-1 km-1,” Optical Fiber Communication Conference, Los Angeles, 23-27 February 2004. doi:10.1109/OFC.2004.1362296.
- J. W. M. Menezes, W. B. Fraga, G. F. Guimarães, A. C. Ferreira, H. H. B. Rocha, M. G. Silva and A. S. B. Sombra, “Optical Switches and All-Fiber Logical Devices Based on Triangular and Planar Three-Core Nonlinear Optical Fiber Couplers,” Optics Communications, Vol. 276, No. 1, 2007, pp. 107-115. doi:10.1016/j.optcom.2007.03.071
- A. F. G. F. Filho, J. R. R. Sousa, A. F. M. Neto, J. W. M. Menezes and A. S. B. Sombra, “Periodic Modulation of Nonlinearity in a Fiber Bragg Grating: A Numerical Investigation,” Journal of Electromagnetic Analysis and Applications, Vol. 4, No. 2, 2012, pp. 53-59. doi:10.4236/jemaa.2012.42007
- K. D. A. Sabóia, A. S. B. Queiroz, F. T. Lima, C. S. Sobrinho, J. W. M. Menezes and A. S. B. Sombra, “Optical Bistability in an Acousto-Optic Tunable Filter (AOTF) Operating With Short Optical Pulses,” Journal of Electromagnetic Analysis and Applications, Vol. 4, No. 3, 2012, pp. 112-117. doi:10.4236/jemaa.2012.43015
- A. C. Ferreira, M. B. C. Costa, A. G. Coêlho Jr., C. S. Sobrinho, J. L. S. Lima, J. W. M. Menezes, M. L. Lyra and A. S. B. Sombra, “Analysis of the Nonlinear Optical Switching in a Sagnac Interferometer with Non-Instantaneous Kerr Effect,” Optics Communications, Vol. 285, No. 6, 2012, pp. 1408-1417. doi:10.1016/j.optcom.2011.10.026
- J. W. M. Menezes, J. R. R. Sousa, M. B. C. Costa, A. C. Ferreira, F. T. Lima, C. S. Sobrinho, M. L. Lyra and A. S. B. Sombra, “Numerical Analysis of the Instantaneous and Relaxed Kerr Model for Generation of the All-Optical Logic Gates with Triangular Fiber Coupler (TFC),” Journal of Nonlinear Optical Physics & Materials, Vol. 21, No. 3, 2012, Article ID: 1250037. doi:10.1142/S0218863512500373
- A. C. Ferreira, C. S. Sobrinho, J. W. M. Menezes, W. B. Fraga, H. H. B. Rocha, A. Wirth Jr., K. D. A. Sabóia, G. F. Guimarães, J. M. S. Filho and A. S. B. Sombra, “A Performance Study of an All-Optical Logic Gate Based in PAM-ASK,” Journal of Modern Optics, Vol. 56, No. 8, 2009, pp. 1004-1013. doi:10.1080/09500340902871371
- J. W. M. Menezes, W. B. Fraga, A. C. Ferreira, G. F. Guimarães, A. F. G. F. Filho, C. S. Sobrinho and A. S. B. Sombra, “All-Optical Half Adder Using All-Optical XOR and AND Gates for Optical Generation of “SUM” and “CARRY,” Fiber and Integrated Optics, Vol. 29, No. 4, 2010, pp. 254-271. doi:10.1080/01468030.2010.485290
- A. W. Lima Jr., M. G. da Silva, A. C. Ferreira and A. S. B. Sombra, “All-Optical Nonlinear Switching Cell Made of Photonic Crystal,” Journal of the Optical Society of America A, Vol. 26, No. 7, 2009, pp. 1661-1667. doi:10.1364/JOSAA.26.001661
- J. W. M. Menezes, W. B. Fraga, F. T. Lima, G. F. Guimarães, A. C. Ferreira, M. L. Lyra and A. S. B. Sombra, “Study of the Performance of an All-Optical Half Adder Based on Three-Core Nonlinear Directional Fiber Coupler under Delayed and Instantaneous Nonlinear Kerr Response,” Fiber and Integrated Optics, Vol. 30, No. 3, 2011, pp. 201-230. doi:10.1080/01468030.2011.568669
- C. S. Sobrinho, A. C. Ferreira, J. W. M. Menezes, G. F. Guimarães, W. B. Fraga, A. F. G. F. Filho, H. H. B. Rocha, S. P. Marciano, K. D. A. Sabóia and A. S. B. Sombra, “Analysys of an Optical Logic Gate Using a Symmetric Coupler Operating With Pulse Position Modulation (PPM),” Optics Communications, Vol. 281, No. 5, 2008, pp. 1056-1064. doi:10.1016/j.optcom.2007.10.046
- K. D. A. Sabóia, A. C. Ferreira, C. S. Sobrinho, W. B. Fraga, J. W. M. Menezes, M. L. Lyra and A. S. B. Sombra, “Optical Cryptography under PPM-PAM Modulation Based in Short Optical Pulses in an Acoustic-Optic Tunable Filter (AOTF),” Optical and Quantum Electronics, Vol. 41, No. 14-15, 2009, pp. 963-980. doi:10.1007/s11082-010-9409-8
- J. W. M. Menezes, W. B. Fraga, A. C. Ferreira, K. D. A. Sabóia, A. F. G. F. Filho, G. F. Guimarães, J. R. R. Sousa, H. H. B. Rocha and A. S. B. Sombra, “Logic Gates Based in Two and Three-Modes Nonlinear Optical Fiber Couplers,” Optical and Quantum Electronics, Vol. 39, No. 14, 2007, pp. 1191-1206. doi:10.1007/s11082-008-9186-9
NOTES
*Corresponding author.

