Journal of Electromagnetic Analysis and Applications
Vol.4 No.7(2012), Article ID:21261,4 pages DOI:10.4236/jemaa.2012.47038
Effect of Helix Pitch Angle on the Modal Dispersion Characteristic of Step-Index Optical Fiber
![]()
1Department of Applied Physics, Institute of Technology, Banaras Hindu University, Varanasi, India; 2Faculty of Engineering, Multimedia University, Cyberjaya, Malaysia.
Email: *onkar_akm@yahoo.co.in
Received April 12th, 2012; revised May 17th, 2012; accepted May 29th, 2012
Keywords: Modal Dispersion; Pitch Angle; Modal Cut-Off
ABSTRACT
The general characteristic equation is derived for the helically cladded step-index optical fiber. The dispersion curves are drawn for the different pitch angles Ψ and mode order ν = 1. The effect of helix pitch angle on the dispersion characteristics and also on the modal cut-off condition is examined. Except for the lowest order mode, all the modes appear in pairs. The lowest order mode displays the negative dispersion for the some value of normalized frequency V and depends on the helix pitch angle Ψ.
1. Introduction
Optical waveguides have been investigated extensively since past few decades considering the different crosssectional geometry and different refractive index profiles [1-10]. The basic difference between a metallic and a dielectric waveguide lies in the way of confinement and guidance of electromagnetic waves—the waves are guided by the reflection from a conducting boundary in the former case while in the later case, the wave guidance is achieved by the total internal reflection phenomenon (TIR). The media with higher refractive index surrounded by a media of comparatively lower refractive index hinders the light from spreading out. Bandwidth and loss considerations are the two important concerns in the modern communication technology on which special attention is to be paid for the optimum use of optical fibers. An optical fiber is a special kind of optical waveguide which have the filamental cross-sectional dimension and guides the EM energy as a result of total internal reflection. Many researchers have studied the propagation characteristics of optical fibers with more emphasis on dispersion characteristics and modal analysis [4,5, 9,10]. E. Snitzer [11] studied about the characteristics of cylindrical dielectric waveguide modes near cut-off and far from cut-off and suggested a method for the designation of modes. Subsequently, a concise method for the designation of modes, which is valid for the waveguides of arbitrary refractive index profile, arbitrary number of modes supported and arbitrary cross-sectional dimension was presented by Snyder et al. [12] and discussed it in the cases when 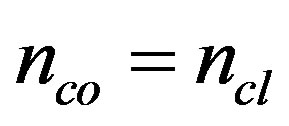 and when
and when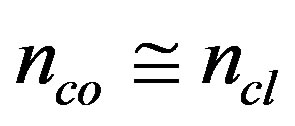 . The condition when
. The condition when 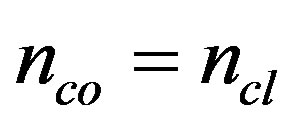 is unrealistic, since the wave will not encounter any discontinuity in the refractive index and for the normalized frequency V to be arbitrary, the wavelength of the illuminating source must be zero, which is unphysical. Modal study gives us a deep insight about the polarization properties of EM waves propagating down the fiber. Conducting helices are of promising importance in the field of travelling wave tubes and these were dealt in detail by considering the different type of helicity [6-8,13-15]. Almost, a new kind of optical fiber was proposed and analyzed by Singh et al. [4] in which the circular dielectric core of the fiber was wounded with conducting helical wires which serves the purpose of cladding. Though the introduction of helix over the core displays a complex structure of the optical fiber, still it has the technological importance in the field of travelling wave tubes (TWTs).
is unrealistic, since the wave will not encounter any discontinuity in the refractive index and for the normalized frequency V to be arbitrary, the wavelength of the illuminating source must be zero, which is unphysical. Modal study gives us a deep insight about the polarization properties of EM waves propagating down the fiber. Conducting helices are of promising importance in the field of travelling wave tubes and these were dealt in detail by considering the different type of helicity [6-8,13-15]. Almost, a new kind of optical fiber was proposed and analyzed by Singh et al. [4] in which the circular dielectric core of the fiber was wounded with conducting helical wires which serves the purpose of cladding. Though the introduction of helix over the core displays a complex structure of the optical fiber, still it has the technological importance in the field of travelling wave tubes (TWTs).
In the present work, the comprehensive and elaborative study of the dispersion characteristic of helically cladded step-index optical fiber is presented assuming the winding spacing to be uniform (i.e. the number of turns per unit length of the fiber) throughout for all the pitch angles (0˚ - 90˚). The general characteristic equation, which is valid for any mode order ν and helix pitch angle ψ, is derived by employing the helical boundary condition. The effect of helix pitch angle ψ on the modal dispersion characteristics and modal cut-offs of the proposed optical fiber for the higher mode order is investigated. The introduction of helical cladding over the core facilitates as an additional controlling parameter to control the modal dispersion. The central idea behind the study of such a complex waveguide germinates from the fact that it will find great technological importance in the field of optical communication.
2. Theoretical Analysis
Assuming a harmonic variation of fields in time, phase, and frequency, the longitudinal field components in the core and cladding regions are
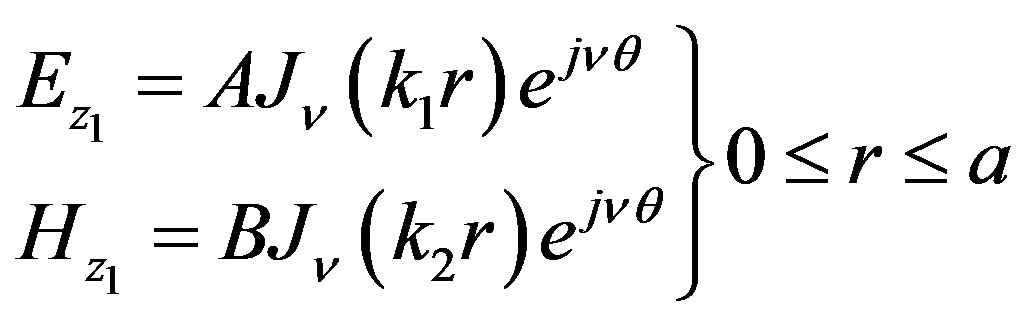
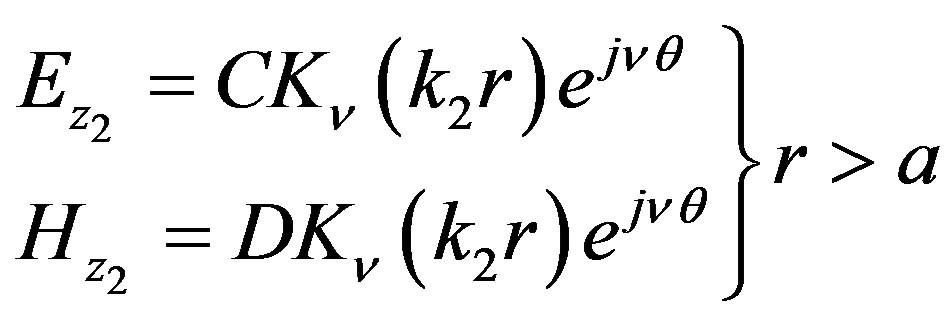
where A, B, C, and D are the field constants to be determined with the help of boundary conditions and the parameters
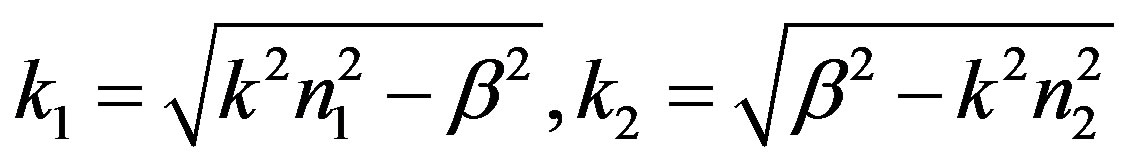
Other field components can be retrieved by using the Maxwell’s equations. Matching the field components at the core cladding interface  we get a
we get a  matrix whose determinant leads to the eigen-value equation. The general characteristic equation for the helically cladded step-index fiber is
matrix whose determinant leads to the eigen-value equation. The general characteristic equation for the helically cladded step-index fiber is
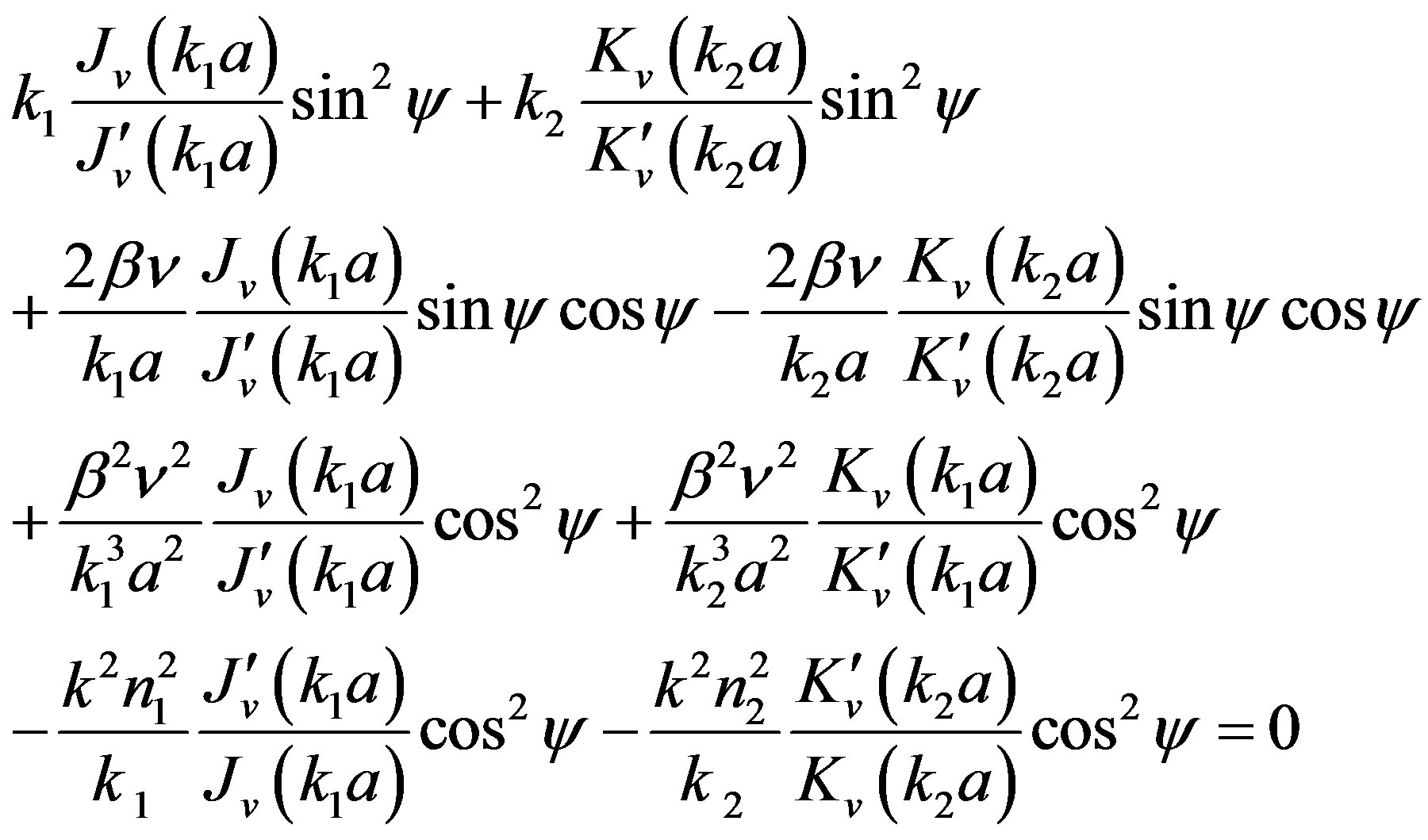
3. Results and Discussion
To study the dispersion characteristics of helically cladded step-index optical fiber, we plot the dispersion curves between the normalized propagation constant b and normalized frequency V for various helix pitch angles ψ where the dispersion parameters b and V are defined as 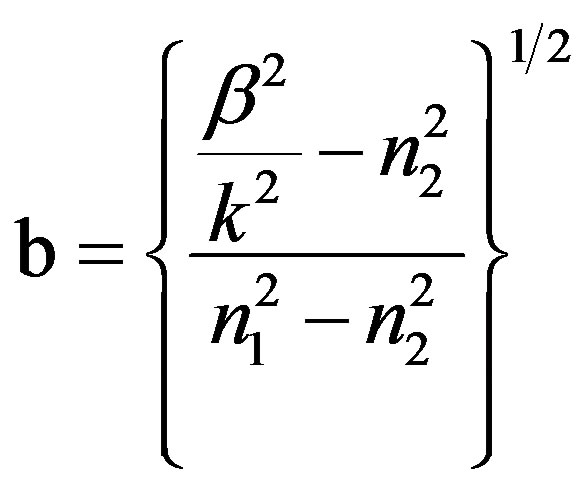 and
and 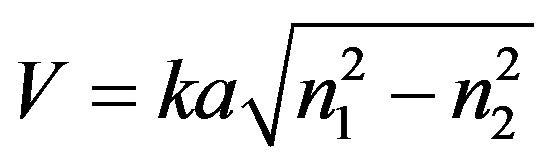 . From Figures 1-8 it is clear that the dispersion curves show the normal expected nature except for the lower order mode which displays abnormal behavior i.e. by increasing the normalized frequency V, the normalized propagation constant b starts decreasing and reaches to certain minimum value and after that it again starts increasing and saturates as it happens in the case of standard step-index optical fibers. As it is inferred from the dispersion curves that this decrease in the value of normalized propagation constant b is somewhat different for the different helix pitch angles for the same value of normalized frequency V. This abnormal behavior occurs due to the periodicity encountered by the wave in the z-direction. Thus, as a concluding remark, we may say that the periodicity in helical winding renders the lowering of propagation constant up to the certain limit. By further increasing the pitch angle beyond
. From Figures 1-8 it is clear that the dispersion curves show the normal expected nature except for the lower order mode which displays abnormal behavior i.e. by increasing the normalized frequency V, the normalized propagation constant b starts decreasing and reaches to certain minimum value and after that it again starts increasing and saturates as it happens in the case of standard step-index optical fibers. As it is inferred from the dispersion curves that this decrease in the value of normalized propagation constant b is somewhat different for the different helix pitch angles for the same value of normalized frequency V. This abnormal behavior occurs due to the periodicity encountered by the wave in the z-direction. Thus, as a concluding remark, we may say that the periodicity in helical winding renders the lowering of propagation constant up to the certain limit. By further increasing the pitch angle beyond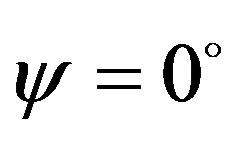 , the nearly degenerate modes are getting farther apart. Thus, the effect
, the nearly degenerate modes are getting farther apart. Thus, the effect
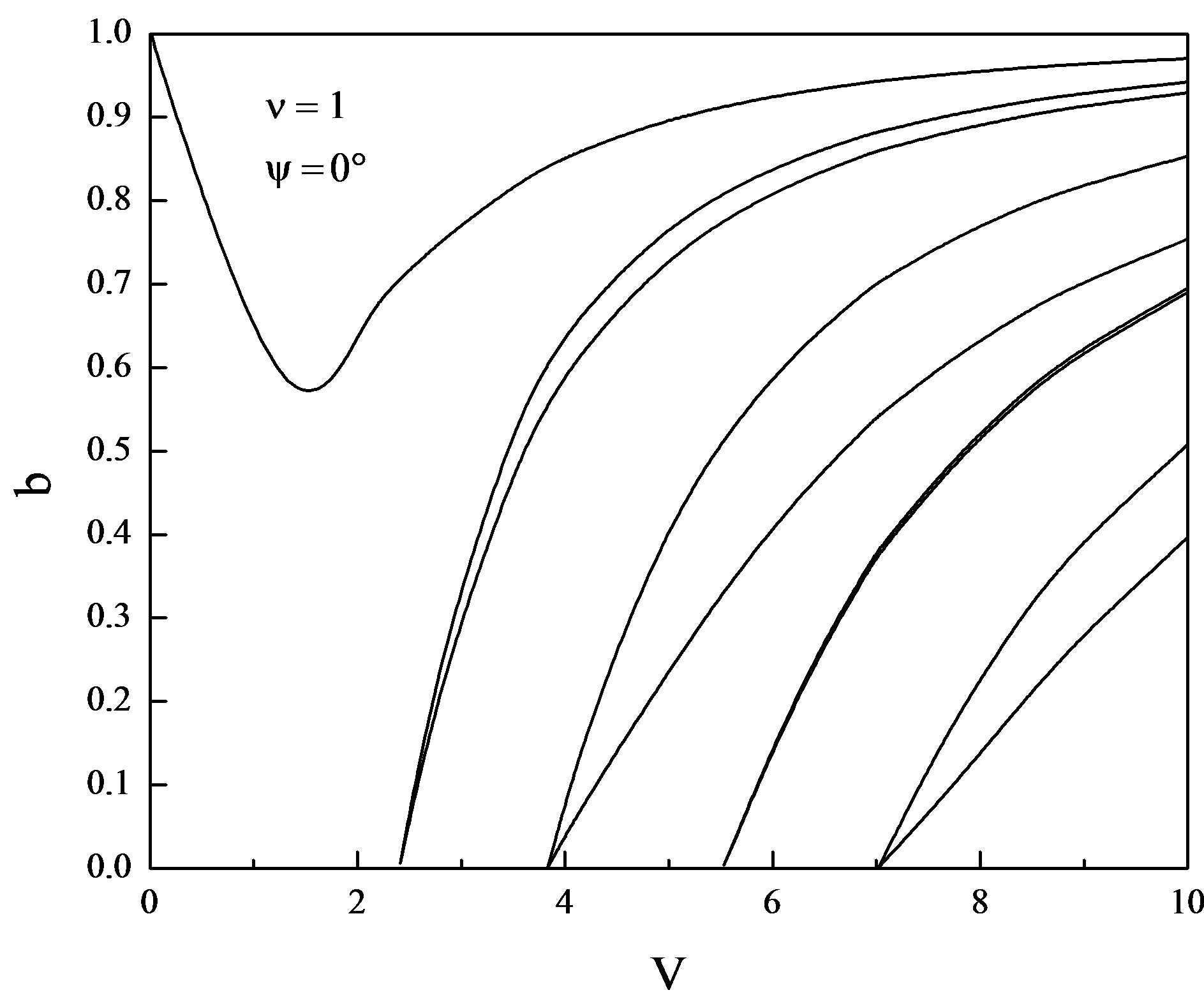
Figure 1. Normalized frequency V vs. b for ψ = 0˚ and ν = 1.
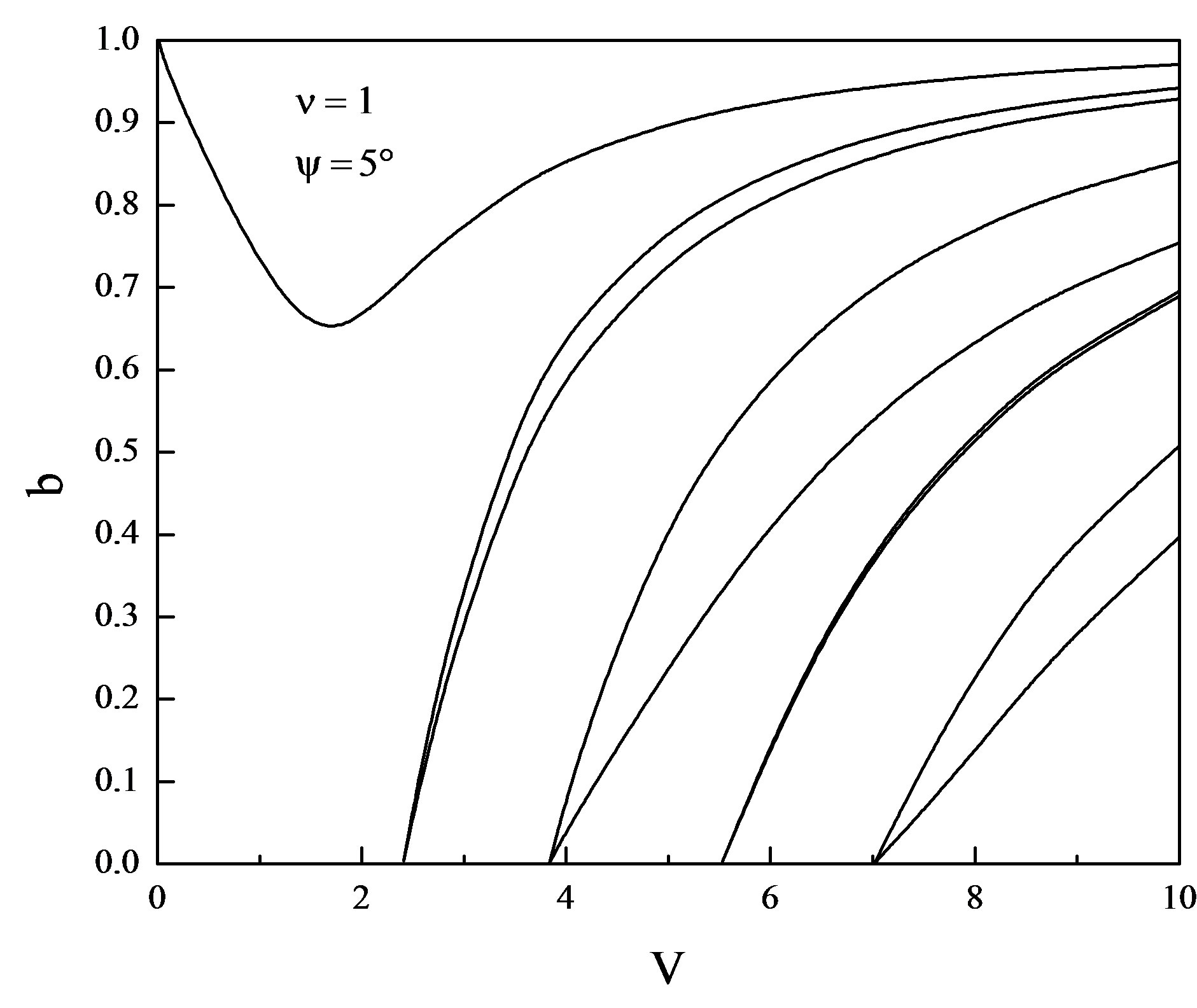
Figure 2. Normalized frequency V vs. b for ψ = 5˚ and ν = 1.

Figure 3. Normalized frequency V vs. b for ψ = 15˚ and ν = 1.
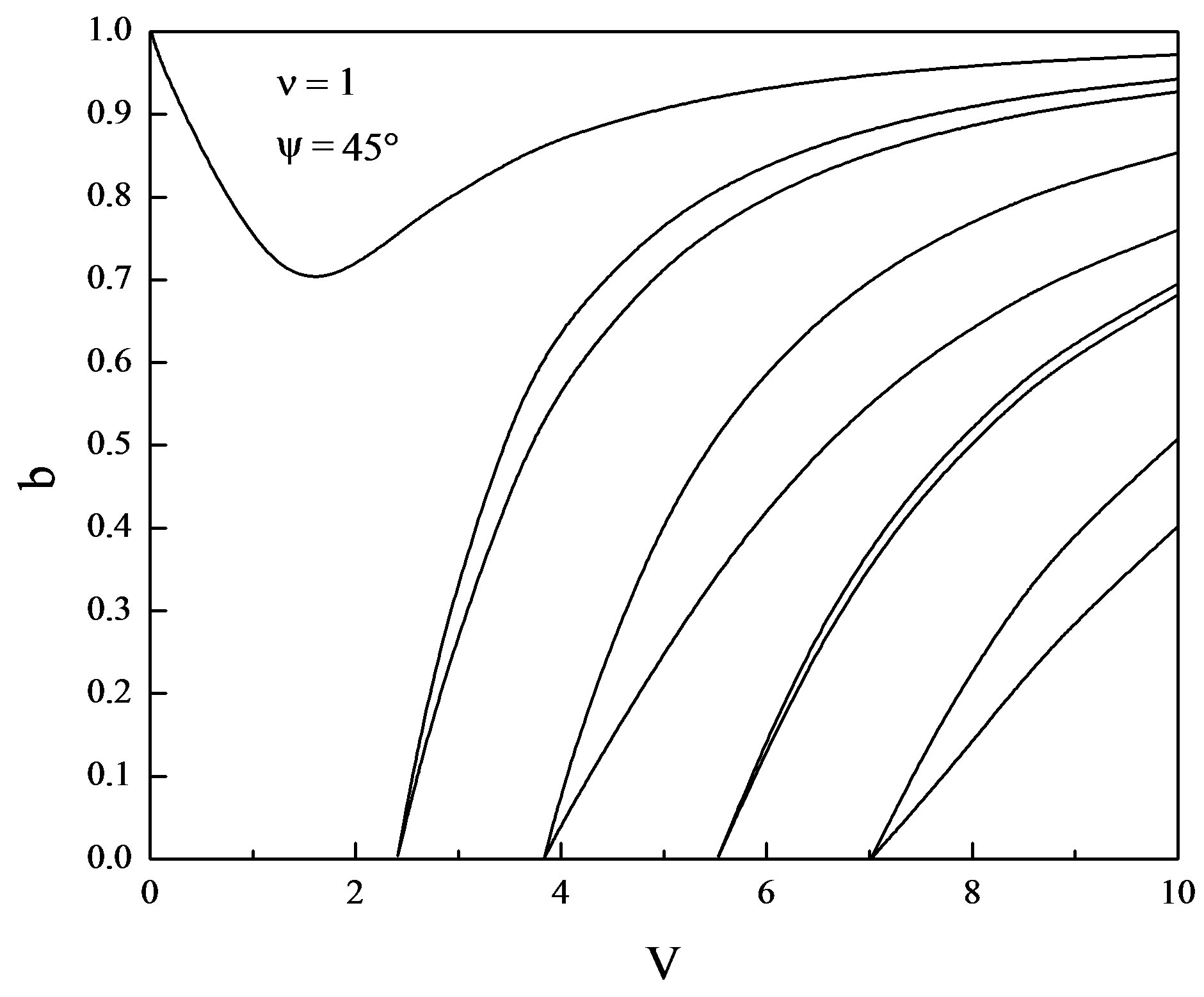
Figure 4. Normalized frequency V vs. b for ψ = 45˚ and ν = 1.
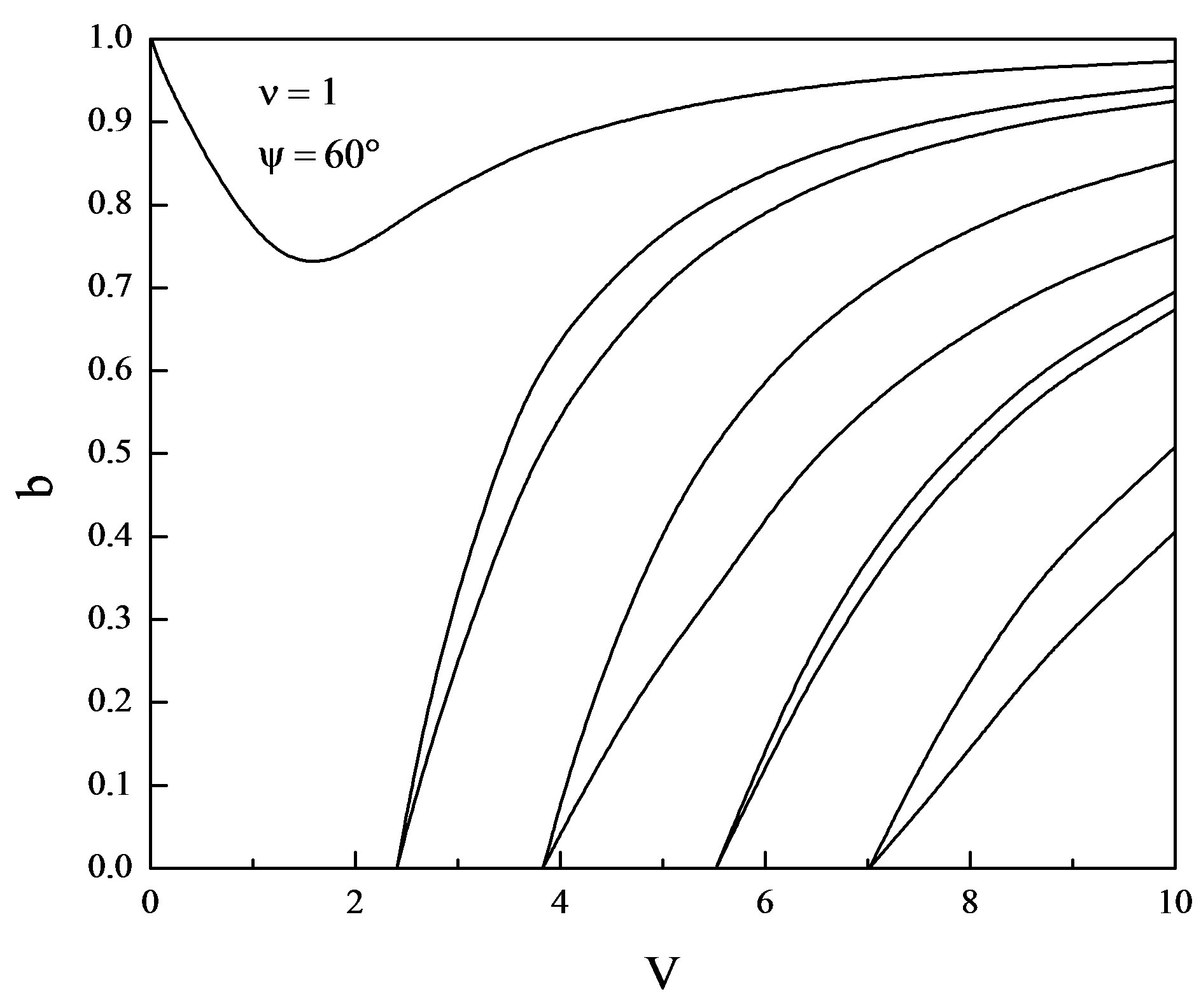
Figure 5. Normalized frequency V vs. b for ψ =60˚ and ν = 1.
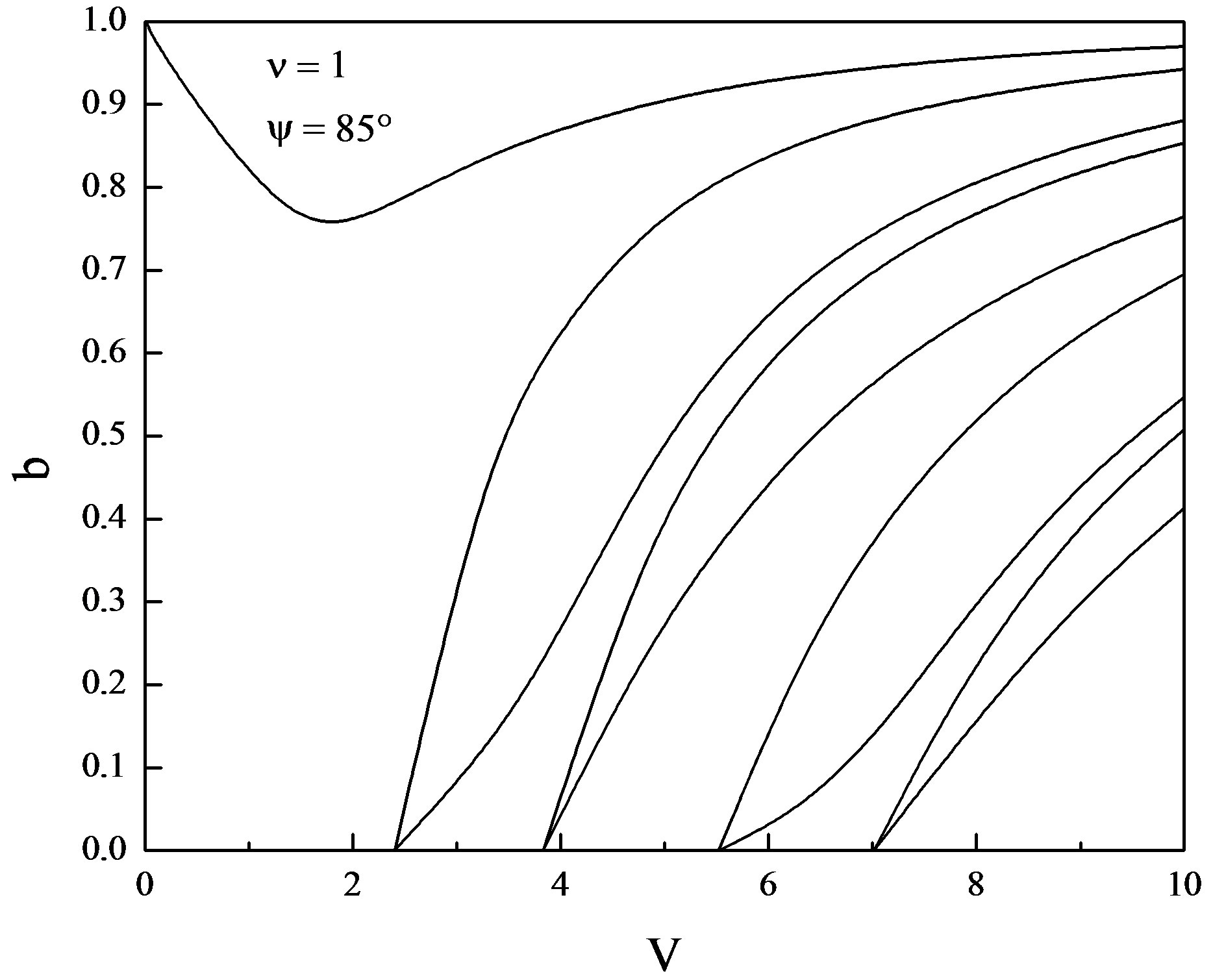
Figure 6. Normalized frequency V vs. b for ψ = 85˚ and ν = 1.
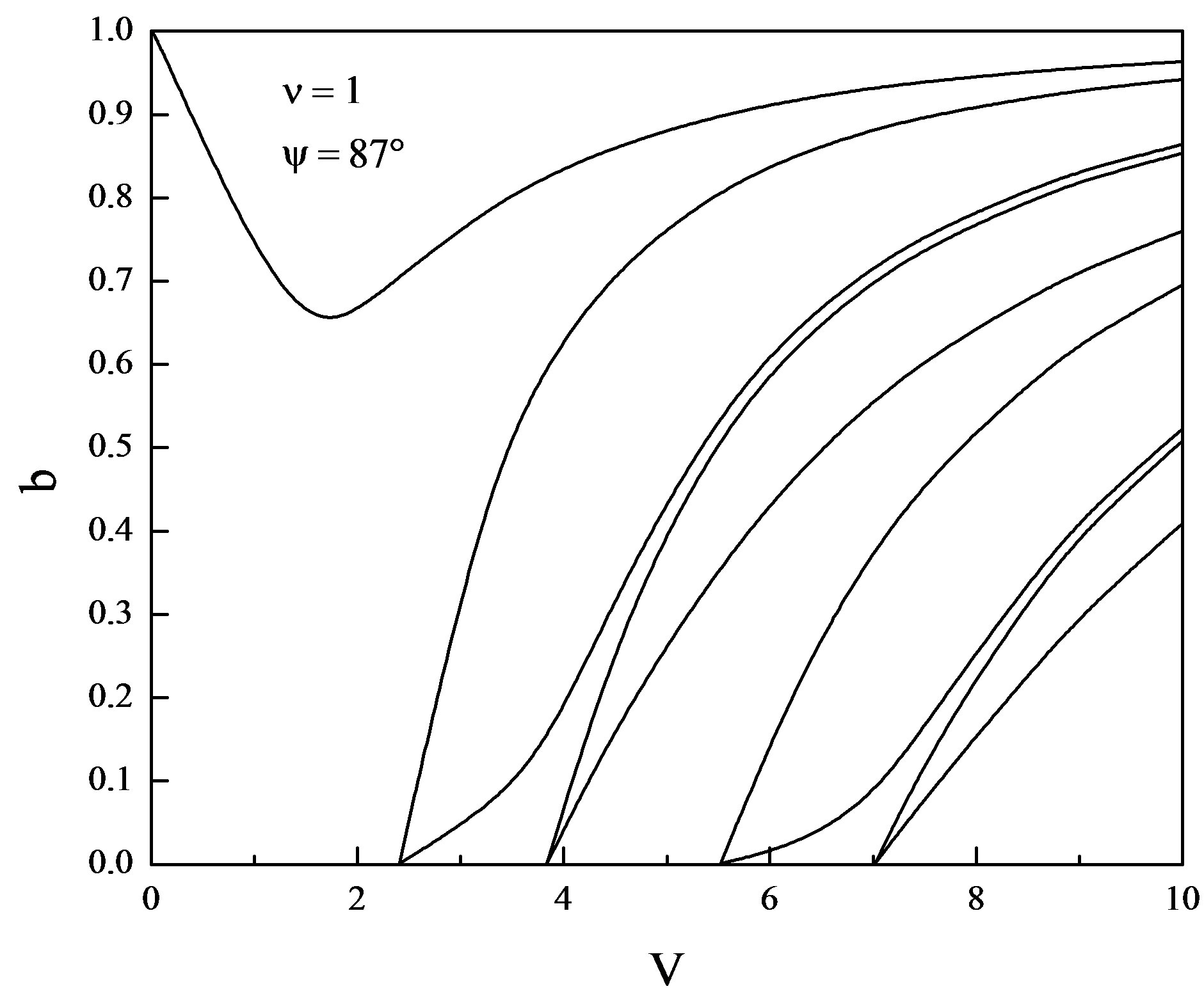
Figure 7. Normalized frequency V vs. b for ψ = 87˚ and ν = 1.
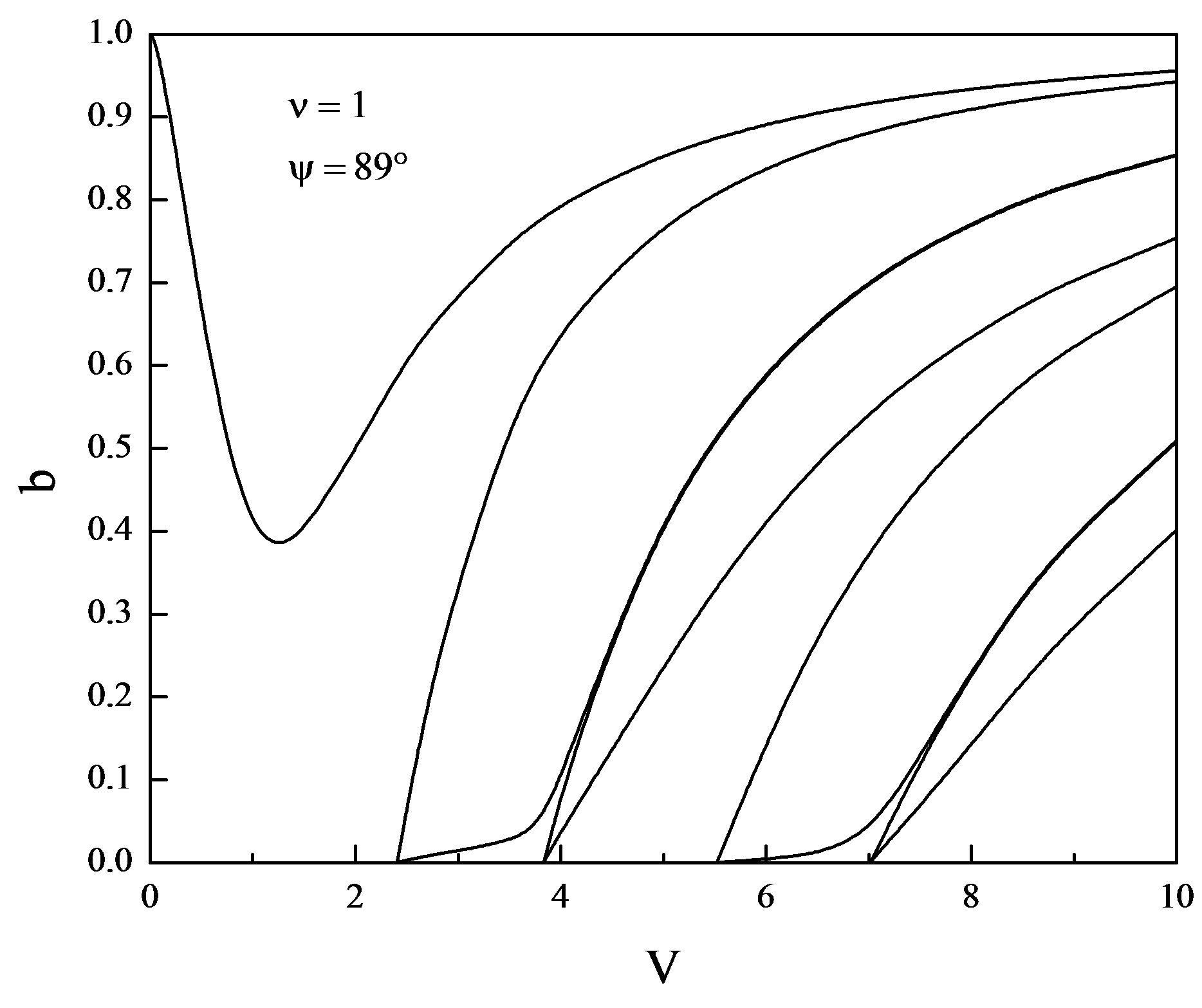
Figure 8. Normalized frequency V vs. b for ψ = 89˚ and ν = 1.
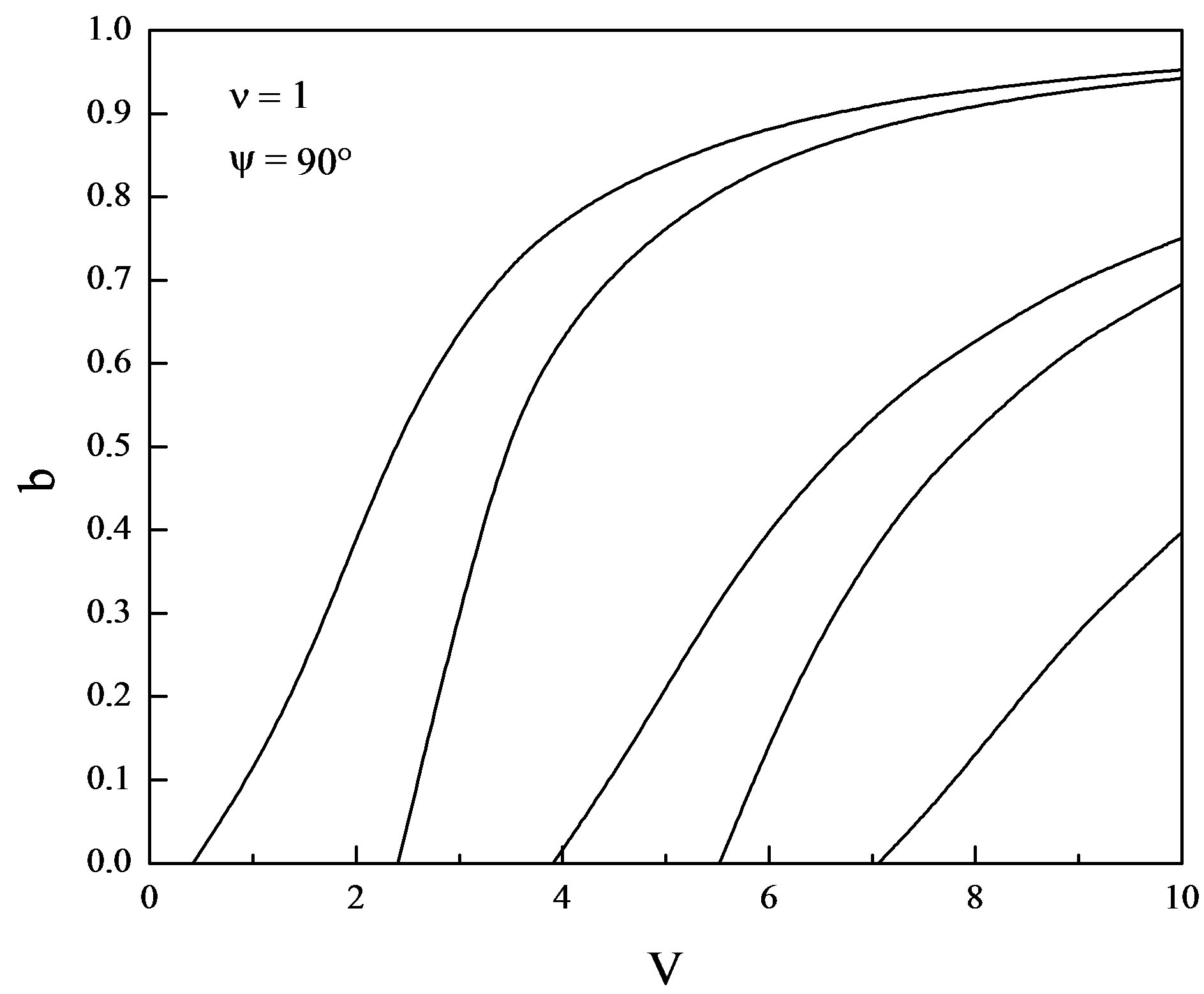
Figure 9. Normalized frequency V vs. b for ψ = 90˚ and ν = 1.
of helical winding is to split the nearly degenerate modes. The merger of modes starts significantly when the pitch angle is increased from 85˚ and is most persistent for the pitch angle 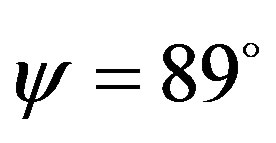 (Figure 8). It is also worth notable that deep in the principal mode start increasing when the pitch angle is increased beyond the 85˚ and is maximum for the pitch angle 89˚. When the pitch angle assumes the value
(Figure 8). It is also worth notable that deep in the principal mode start increasing when the pitch angle is increased beyond the 85˚ and is maximum for the pitch angle 89˚. When the pitch angle assumes the value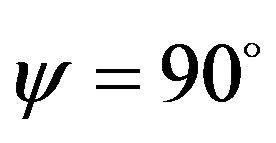 , the number of guided modes is reduced. This is attributed due to the fact that the complete elimination of periodicity in the z-direction occurs. From all these dispersion curves (Figures 1-9) it is evident that the modal cut-offs remain invariant though we have varied the value of pitch angle from 0˚ to 89˚. Thus, as a concluding remark, we may say that the helix pitch angle does not affect the modal cut-offs. The case when the pitch angle
, the number of guided modes is reduced. This is attributed due to the fact that the complete elimination of periodicity in the z-direction occurs. From all these dispersion curves (Figures 1-9) it is evident that the modal cut-offs remain invariant though we have varied the value of pitch angle from 0˚ to 89˚. Thus, as a concluding remark, we may say that the helix pitch angle does not affect the modal cut-offs. The case when the pitch angle 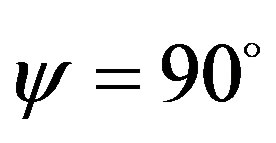 is quite different from those for the other angles (0˚ - 89˚). At this pitch angle, the helical windings are just parallel to the fiber axis, thus eliminating altogether the periodicity in z-direction.
is quite different from those for the other angles (0˚ - 89˚). At this pitch angle, the helical windings are just parallel to the fiber axis, thus eliminating altogether the periodicity in z-direction.
4. Conclusion
The general characteristic equation which is valid for any mode order and pitch angle is derived employing the helix boundary condition. The dispersion curves reflect the negative dispersion characteristic for the principal mode only. All other modes appear in pairs and show the normal expected nature. The magnitude of minima of the principal mode varies on helix pitch angle. The abnormal dispersion and degeneracy of modes disappear when the pitch angle reaches to 90˚.
REFERENCES
- A. W. Snyder and J. D. Love, “Optical Waveguide Theory,” Chapman and Hall, London, 1983.
- C. R. Pollock, “Fundamentals of Optoelectronics,” Tom Casson, Chicago, 1995.
- D. A. Watkins, “Topics in Electromagnetic Theory,” John Wiley & Sons, New York, 1958.
- U. N. Singh, O. N. Singh II, P. Khastgir and K. K. Dey, “Dispersion Characteristics of a Helically Cladded StepIndex Optical Fiber: An Analytical Study,” Journal of Optical Society of America, Vol. 12, No. 7, 1995, pp. 1273-1278.
- D. Kumar and O. N. Singh II, “Modal Characteristic Equation and Dispersion Curves for an Elliptical Step-Index Optical Fiber with a Conducting Helical Winding on the Core-Cladding Boundary—An Analytical Study,” Journal of Lightwave Technology, Vol. 20, No. 8, 2002, pp. 1416-1424. doi:10.1109/JLT.2002.800799
- J. R. Pierce, “Travelling Wave Tubes,” D. Van Nostrand Co., Princeton, 1950.
- S. Sensiper, “Electromagnetic Wave Propagation on Helical Conductor,” Proceedings of IRE, Vol. 43, No. 2, February 1955, pp. 149-161. doi:10.1109/JRPROC.1955.278072
- H. G. Unger, “Winding Tolerances in Helix Waveguide,” Bell System Technical Journal, Vol. 39, 1960, pp. 627- 643.
- N. S. Kapany and J. J. Burke, “Fiber Optics. IX. Waveguide Effects,” Journal of Optical Society of America, Vol. 51, No. 10, 1961, pp. 1067-1078. doi:10.1364/JOSA.51.001067
- P. J. B. Clarricoats and K. B. Chan, “Propagation Behavior of Cylindrical-Dielectric-Rod Waveguides,” Proceedings of IEEE, Vol. 120, 1973, pp. 1371-1378.
- E. Snitzer, “Cylindrical Dielectric Waveguide Modes,” Journal of Optical Society of America, Vol. 51, No. 5, 1961, pp. 491-498. doi:10.1364/JOSA.51.000491
- A. W. Snyder and W. R. Young, “Modes of Optical Waveguides,” Journal of Optical Society of America, Vol. 68, No. 3, 1978, pp. 297-309. doi:10.1364/JOSA.68.000297
- S. K. Datta, L. Kumar and B. N. Basu, “Analysis of Dielectric Loss in a Helix Slow-Wave Structure,” Defence Science Journal, Vol. 59, No. 5, 2009, pp. 549-552.
- S. Ahn and A. K. Ganguly, “Analysis of Helical Waveguide,” IEEE Transactions on Electron Devices, Vol. 33, No. 9, 1986, pp. 1348-1355. doi:10.1109/T-ED.1986.22669
- J. B. Kyle and R. W. Grow, “The Helically Wrapped Circular Waveguide,” IEEE Transactions on Electron Devices, Vol. 34. No. 8, 1987, pp. 1873-1884.
NOTES
*Corresponding author.

