Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 2 (2011) , Article ID: 4120 , 6 pages DOI:10.4236/jemaa.2011.32006
Influence of Nonlocality on Amplification of Space Charge Waves in n-GaN Films
![]()
Autonomous University of State Morelos (UAEM), Cuernavaca, Mexico.
Email: svetlana@uaem.mx, v_grim@yahoo.com
Received December 22nd, 2010; revised January 17th, 2011; accepted January 20th, 2011
Keywords: gallium nitride, films, negative differential conductivity, space charge waves, amplification, nonlocality
ABSTRACT
It is investigated theoretically the amplification of space charge waves (SCWs) due to the negative differential conductivity (NDC) in n-GaN films of submicron thicknesses placed onto a semi-infinite substrate. The influence of the nonlocal dependence of the average electron velocity on the electron energy is considered. The simplest nonlocal model is used where the total electron concentration is taken into account. The relaxation momentum and energy frequencies have been calculated. The influence of the nonlocality on NDC results in the decrease of the absolute value of its real part and appearance of the imaginary part. The calculation of the diffusion coefficient leads to essential errors. The simulations of spatial increments of the amplification of SCWs demonstrate that the nonlocality is essential at the frequencies f ≥ 150 GHz, and the amplification is possible up till the frequencies f ≤ 400 ∙∙∙ 500 GHz.
1. Introduction
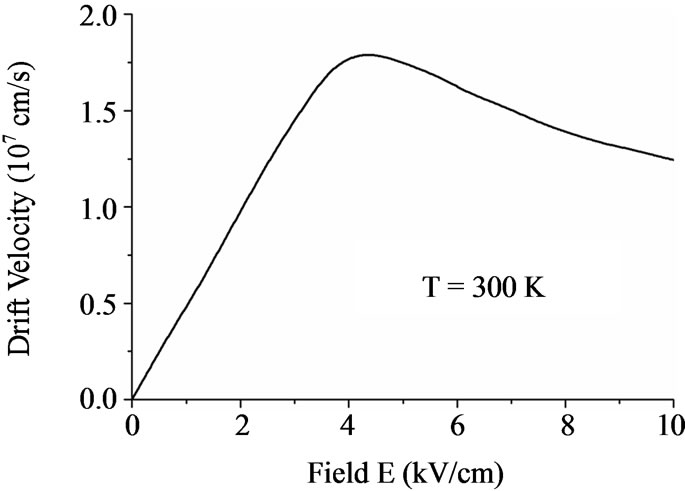
The amplification of traveling space charge waves (SCWs) of the microwave range in n-GaAs films has been under investigations for many years [1-6]. When propagating in bias electric fields higher than the critical value for observing negative differential conductivity (NDC), SCWs are subject to amplification. However, the critical value of the bias electric field in GaAs is Ec = 3.5 kV/cm, which limits the maximum values of the microwave electric field of SCWs. In addition, the frequency range of amplification of SCWs in GaAs films is f < 50 GHz, see Figure 1. At the frequencies f > 50 GHz, it is better to use new materials possessing NDC at higher frequencies f = 100 ∙∙∙ 500 GHz, like gallium nitride GaN [7-23]. The attracting properties of GaN are: a high critical bias field Ec ~ 100 kV/cm; the extended frequency range for observing NDC f ≤ 500 GHz; high temperature stability; NDC at high doping levels n0 ~ 1017 ∙∙∙ 1018 cm-3. Some comparative data on GaAs and GaN are given in Figures 2 and 3.
A comparison of GaAs and GaN shows that NDC occurs in GaAs when the occupancy of higher valleys (L, X ones) is 30% and more, see Figure 2(b). In GaN the occupancy of higher valleys is essentially lower, of about 10%, see Figure 3(c). Therefore, in GaAs it is impossible to describe the amplification of SCWs by means of the simplest nonlocal hydrodynamic model, where the unified electron concentration, average electron velocity, and energy are considered, instead of more detailed characteristics for lower and higher valleys [6]. For GaN, it is possible to check the adequacy of the simplest nonlocal model. Moreover, there are evidences that in the zinc blende n-GaN the mechanism of NDC is different from the intervalley transfer, but is due to the inflection of the electron dispersion [23].
In the present paper the spatial increments of amplification of SCWs due to NDC have been calculated. The influence of the nonlocal dependence of the drift velocity
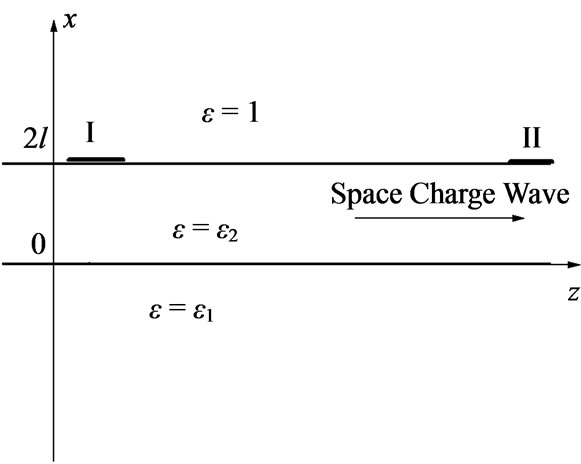
Figure 1. Geometry of the problem. The n-GaN film occupies the region 0 < x < 2l, x > 2l is vacuum, x < 0 is a semiinfinite substrate. I is an input antenna, II is output one.
on the average electron energy is investigated. The momentum and energy relaxation frequencies are computed. It is shown that the nonlocality is essential at the frequencies f ≥ 200 GHz and leads to decrease of the spatial increment of amplification. The amplification of SCWs is possible up till the frequencies f ~ 500 GHz. It is demonstrated that for the calculation of the diffusion coefficient it is necessary to apply a more exact theory, because the simplest nonlocal theory leads to essential errors.
 (a)
(a)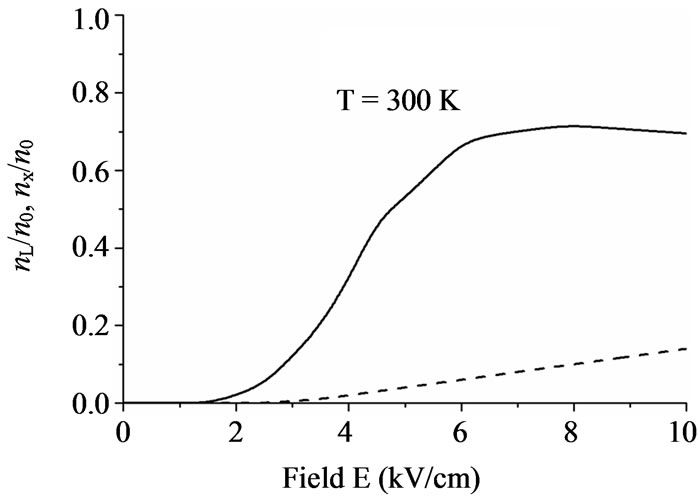 (b)
(b) (c)
(c)
Figure 2. The data on GaAs. Part (a) is the dependencies of drift velocity on electric field at different temperatures; part (b) is dependencies of occupancies of upper (L, X) valleys on electric field; part (c) is dependence of real and imaginary part of differential conductivity on frequency [24-26].
 (a)
(a)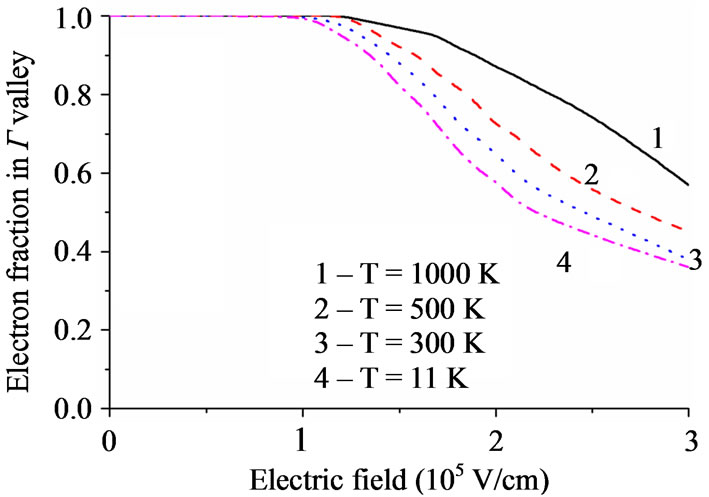 (b)
(b)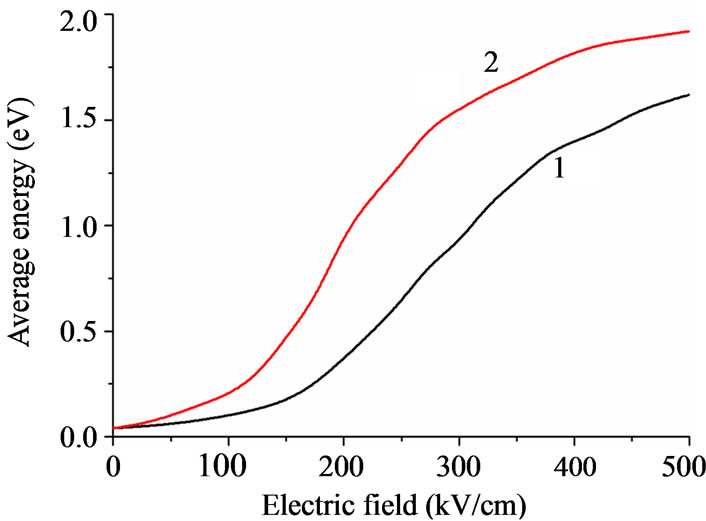 (c)
(c)
Figure 3. The data on GaN. Part (a) dependencies of drift velocity on electric field for wurtzite (1) and zinc blende (2) phases; part (b) is dependencies of occupancy of lower (G) valley on electric field for wurtzite GaN at different temperatures; part (c) is dependence of average electron mass on electric field for wurtzite (1) and zinc blende (2) phases [10,11].
2. Nonlocal Hydrodynamic Equations and Relaxation Frequencies
In the simplest nonlocal electron hydrodynamics, the electron fluid is described by the total electron concentration n for all valleys jointly, the average electron velocity v, and average electron energy w. The equations of balance of the number of particles, the momentum, and the energy are [1,2,6]:
 (1)
(1)
Here n, v, and w are the electron concentration, the average velocity, and the average electron energy;np, nw are the momentum and energy relaxation frequencies; m* is the effective mass, T is the electron temperature in energetic units, k is the thermoconductivity coefficient; w00 = 0.039 eV is the electron energy at 300 K. It is assumed that np, nw, m* are functions of the average electron energy w. The estimations have demonstrated that the thermoconductivity is not essential for the dynamics of SCWs up till the frequencies 2.3 THz. In addition, the electron kinetic energy is one order smaller than the average electron energy, thus, the electron temperature is T » (2/3) w.
From the stationary dependencies of the drift velocity v = v(E) and the electron energy w = w(E), it is possible to obtain the relations E = E(w), v=v(w), m = v(w)/E(w) º m(w), then the relaxation frequencies can be calculated as:
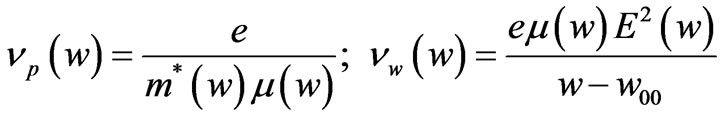 (2)
(2)
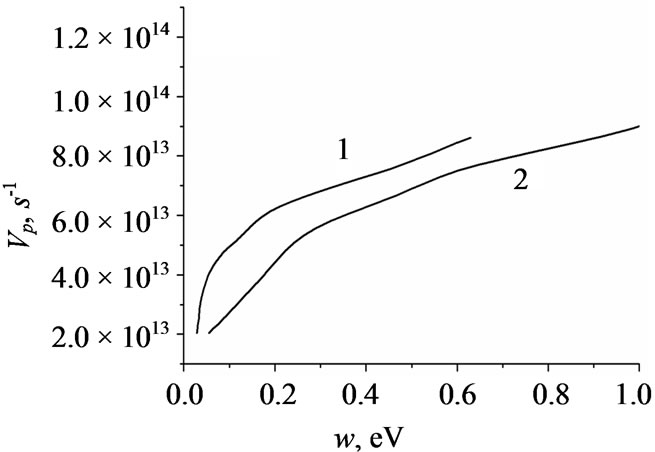
The calculated dependencies are given in Figure 4. One can see that the momentum relaxation frequency is np  nw, therefore, for the frequencies of SCW f < 1 THz it is possible to neglect by the inertia of electrons:
nw, therefore, for the frequencies of SCW f < 1 THz it is possible to neglect by the inertia of electrons:
 (3)
(3)
Here m, D are mobility and diffusion of electrons:
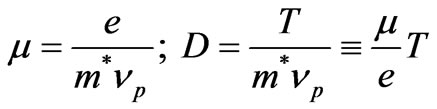 (4)
(4)
After substitution of (3) into the equations for n and w, one can get the following equations:
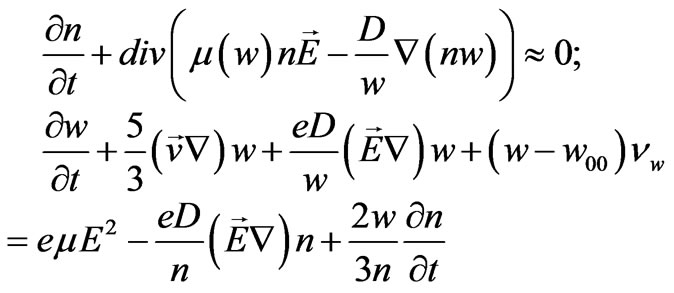 (5)
(5)
 (a)
(a)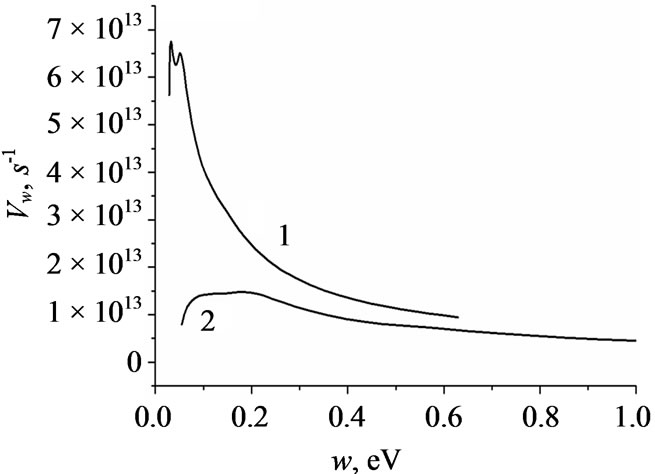 (b)
(b)
Figure 4. The calculated relaxation frequencies np(w), nw(w) for GaN. Curve 1 is for wurtzite structure, curve 2 is for zinc blende one.
Below we investigate the linear amplification of SCW in GaN films on the dielectric substrate. The case of zinc blende n-GaN is considered. The following representation is used:
 (6)
(6)
Here w0, n0, v0, E0 are steady state values of the average electron energy, concentration, the drift velocity, and the bias electric field;  are high frequency parts. Note that w0 º w(E0) > w00. The equations for the high frequency parts are:
are high frequency parts. Note that w0 º w(E0) > w00. The equations for the high frequency parts are:
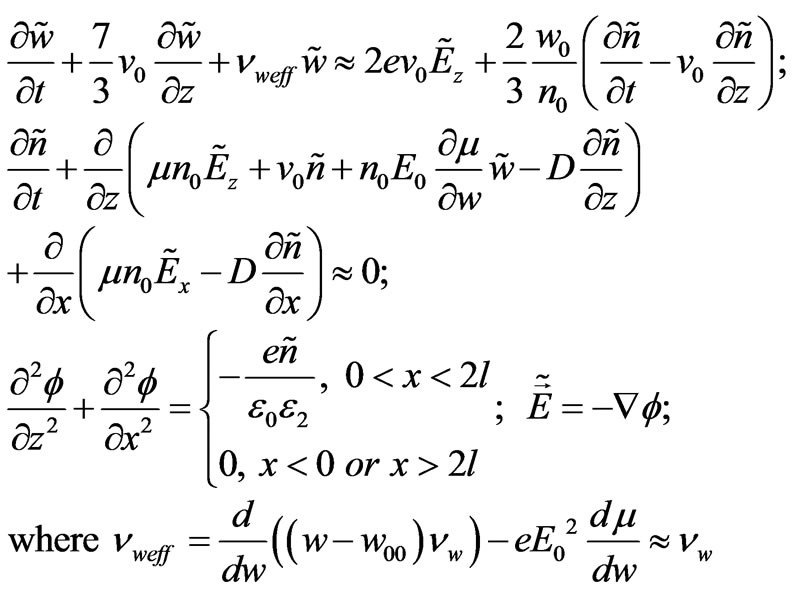 (7)
(7)
Jointly with the equations for the electron fluid, the Poisson equation for the electric field is used. Equation (7) should be added by boundary conditions of continuity of the electric potential j, x-component of the electric induction -e(x)¶j/¶x, and absence of the surface charge at the boundaries of the film:

3. Amplification of Space Charge Waves
The solutions of Equation (7) as traveling waves are considered:
 (8)
(8)
If at some frequencies the imaginary part of the longitudinal wave number is k” > 0, then the spatial amplification of SCW takes place.
It is possible to get the expression for through
through 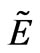 and
and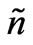 :
:
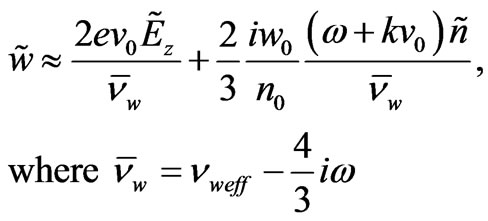 (9)
(9)
In Equation (9) the first term with  corresponds to modification of the drift terms in the equation for electron concentration, whereas the second term with
corresponds to modification of the drift terms in the equation for electron concentration, whereas the second term with 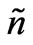 results in a modification of the diffusion coefficient. One can see that at higher frequencies the effective relaxation frequency
results in a modification of the diffusion coefficient. One can see that at higher frequencies the effective relaxation frequency 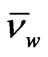 becomes complex, its imaginary part is proportional to the signal frequency. This decreases the amplification of SCWs at higher frequencies After the substitution of (9), one can get the following equation for
becomes complex, its imaginary part is proportional to the signal frequency. This decreases the amplification of SCWs at higher frequencies After the substitution of (9), one can get the following equation for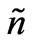 :
:
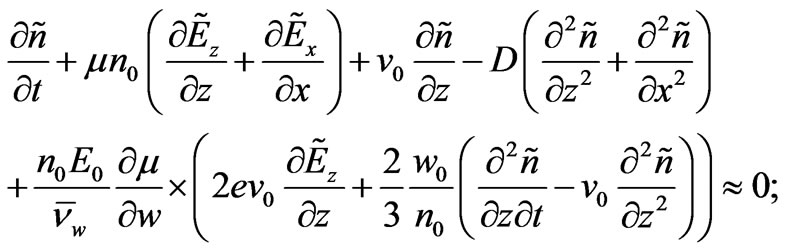 (10)
(10)
Or, in the equivalent form,
 (11)
(11)
At lower frequencies f £ 150 GHz, where the local dependence of the drift velocity on electric field v = v(E) can be used, the amplification is determined by the derivative dv/dE º d(mE)/dE < 0. An analysis of Equation (11) yields that at higher frequencies this derivative should be substituted by the following complex expression:
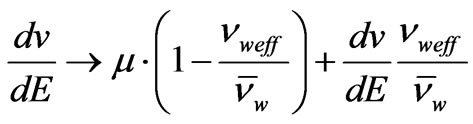 (12)
(12)
One can see that at higher frequencies the differential conductivity becomes complex, and, moreover, above some frequency f » 600 GHz NDC disappears. Therefore, it is possible to use the simplest nonlocal model for estimations of the frequency range of amplification of SCW. Because nw » 2 ´ 1013 s-1, the amplification of SCW in n-GaN can be observed at the frequencies f º w/2p < 0.5 nw/2p.
There is a problem of estimating the diffusion coefficient. The simplest nonlocal model leads to the modification of the longitudinal diffusion coefficient Dz:
 (13)
(13)
Because dm/dw < 0, on the first view the nonlocal model results in the decrease of Dz. Nevertheless, one can see that at lower frequencies, where 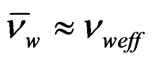 and the local diffusion-drift equations are valid, the second term in (13) does not depend on frequency. At higher frequencies, the second term in (13) becomes complex and the absolute real part decays slightly. Moreover, the estimations give that
and the local diffusion-drift equations are valid, the second term in (13) does not depend on frequency. At higher frequencies, the second term in (13) becomes complex and the absolute real part decays slightly. Moreover, the estimations give that
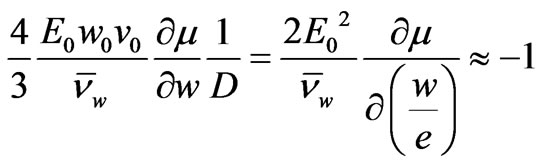 (14)
(14)
Thus, from the simplest nonlocal model it seems impossible to estimate the diffusion coefficient correctly even at lower frequencies. The situation is not crucial for n-GaN as for n-GaAs, where an application of the simplest nonlocal model leads to perfectly incorrect results (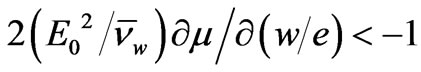 there, and the longitudinal diffusion coefficient becomes negative).
there, and the longitudinal diffusion coefficient becomes negative).
For simulations of the spatial increment of the amplification of SCW we have used the value of the diffusion coefficient obtained within the framework of the local model. In Figure 5 the results of simulations of the spatial increment are given. An influence of the nonlocality is essential at the frequencies f ³ 150 ∙∙∙ 200 GHz. It is possible to obtain the amplification at the frequencies f £ 500 GHz in GaN films of submicron thicknesses.
4. Conclusions
The simplest variant of nonlocal hydrodynamics gives a possibility of estimating the decay in amplification of space charge waves in n-GaN films at higher frequencies,
 (a)
(a)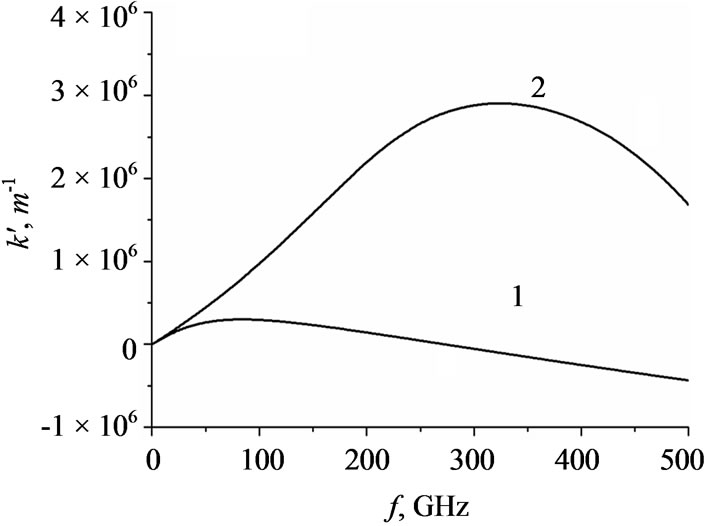 (b)
(b)
Figure 5. Spatial increments of amplification of SCWs in n-GaN films. The bias field is E0 = 150 kV/cm, the thickness of the film is 2l = 0.5 mm. Part a) is for n0 = 1 ´ 1017 cm-3, Part b) is for n0 = 5 ´ 1017 cm-3. The curve 1 is within the nonlocal model, curve 2 is in the local approximation.
due to decrease of the absolute value of the negative differential conductivity. Nevertheless, to obtain the correct value of diffusion coefficient, it is necessary to use the more adequate model, based on the detailed balance equations for each valley. The estimations have given that it is possible to obtain the amplification of space charge waves in n-GaN films of submicron thicknesses up till the frequencies 400…500 GHz.
5. Acknowledgment
Authors thank Dr. Alex Vertiy for his useful discussing and advices, which improve the understanding of the obtaining results.
REFERENCES
- A. Barybin, “Waves in Thin-Film Semiconductor Structures with Hot Electrons (in Russian),” Izdatel'stvo Nauka, Moscow, 1986.
- M. S. Shur, “GaAs Devices and Circuits,” Plenum Press, New York, 1987.
- D. G. Sannikov and D. I. Sementsov, “Waveguide Interaction between Light and an Amplified Space-Charge Wave,” Physics of the Solid State, Vol. 49, No. 3, March 2007, pp. 488-492. doi:10.1134/S1063783407030171
- V. Grimalsky, E. Gutierrez-D., A. Garcia-B. and S. Koshevaya, “Resonant Excitation of Microwave Acoustic Modes in n-GaAs Film,” Microelectronics Journal, Vol. 37, No. 5, March 2006, pp. 395-403. doi:10.1016/j.mejo. 2005.06.003
- G. E. Chaika, V. N. Malnev and M. I. Panfilov, “Interaction of Light with Space Charge Waves,” Proceedings of SPIE, Vol. 2795, 1996, pp. 279-286. doi:10.1117/12.2392 20
- A. Garcia-B., V. Grimalsky, E. Gutierrez-D. and S. Koshevaya, “Dispersion Relation for Two-Valley QuasiHydrodynamic Models in SCWs Propagation in n-GaAs Thin Films,” 25th International Conference on Microelectronics (MIEL 2006), Belgrade, Serbia and Montenegro, 14-17 May 2006.
- S. J. Pearton, J. C. Zolper, R. J. Shul and F. Ren, “GaN: Processing, Defects, and Devices,” Journal of Applied Physics, Vol. 86, No. 1, July 1999, pp. 1-79. doi:10.1063/1.371145
- S. Jain, M. Willander, J. Narayan, and R. Van Overstraeten, “III-Nitrides: Growth, Characterization, and Properties,” Journal of Applied Physics, Vol. 87, No. 3, February 2000, pp. 965-1006. doi:10.1063/1.371971
- V. Gruzhinskis, P. Shiktorov, E. Starikov and J. H. Zhao, “Comparative Study of 200-300 GHz Microwave Power Generation in GaN TEDs by the Monte Carlo Technique,” Semiconductor Science and Technology, Vol. 16, No. 8, August 2001, pp. 798-805. doi:10.1088/0268-1242/16/9/311
- M. Levinshtein, S. Rumyantsev, and M. Shur, “Properties of Advanced Semiconductor Materials: GaN, AlN, InN,” Wiley, New York, 2001.
- S. O. Kasap, P. Capper, Eds., “Springer Handbook of Electronic and Photonic Materials, Chapter 32, Group III Nitrides,” Springer, New York, 2007, pp. 753-804.
- V. V. Grimalsky, S. V. Koshevaya, L. M. Gaggero-S. and F. Diaz-A., ‘‘Excitation of Hypersound Due to Coupling with Space Charge Waves in GaN Films,’’ Progress in Electromagnetics Research International Symposium PIERS-2007, Beijing, March 26-30, pp. 244-248.
- B. E. Foutz, L. F. Eastman, U. V. Bhapkar and M. S. Shur, “Comparison of High Field Electron Transport in GaN and GaAs,” Applied Physics Letters, Vol. 70, No. 21, May 1997, pp. 2849-2851. doi:10.1063/1.119021
- B. Aslan, L. F. Eastman and Q. Diduck, “Simulation and Experimental Results on GaN Based Ultra-Short Planar Negative Differential Conductivity Diodes for THz Power Generation,” International Journal of High Speed Electronics and Systems (IJHSES), Vol. 19, No. 1, March 2009, pp. 1-6. doi:10.1142/S0129156409006035
- G. Simin, M. S. Shur and R. Gaska, “5-Terminal THz GaN Based Transistor with Fieldand Space-Charge Control Electrodes,” International Journal of High Speed Electronics and Systems (IJHSES), Vol. 19, No. 1, March 2009, pp. 7-14. doi:10.1142/S0129156409006047
- M. Mukherjee, S. Banerjee and J. P. Banerjee, “Dynamic Characteristics of III-V and IV-IV Semiconductor Based Transit Time Devices in the Terahertz Regime: A Comparative Analysis,” Terahertz Science and Technology, Vol. 3, No. 3, September 2010, pp. 97-109.
- V. N. Sokolov, K. W. Kim, V. A. Kochelap and D. L. Woolard, “Terahertz Generation in Submicron GaN Diodes within the Limited Space-Charge Accumulation Regime,” Journal of Applied Physics, Vol. 98, No. 6, September 2005, pp. 064507-0645013. doi:10.1063/1.2060956
- A. Castro-R., A. García-B. and F. Trejo-M., “Nonlinear Interaction of Space Charge Waves in GaN Films,” Proceedings of 2010 7th IEEE International Conference on Electrical Engineering Computing Science and Automatic Control (CCE), Mexico, 8-10 September 2010, pp. 604- 607. doi:10.1109/ICEEE.2010.5608615
- V. V. Grimalsky, S. V. Koshevaya, L. M. Gaggero-S. and F. Diaz-A., “Excitation of Hypersound Due to Coupling with Space Charge Waves of Millimeter Wave Range in GaN Films,” Journal of Infrared, Millimeter and Terahertz Waves, Vol. 30, No. 3, March 2009, pp. 233-242. doi:10.1007/s10762-008-9440-z
- S. Banerjee, M. Mukherjee and J. P. Banerjee, “Bias Current Optimization of Wurtzite-GaN DDR IMPATT Diode for High Power Operation at THz Frequencies,” International Journal of Advanced Science and Technology, Vol. 16, No. 3, March 2010, pp. 11-20.
- P. R. Tripathy, A. K. Panda and S. P. Pati, “Prospects of Wide Band Gap Material ZB-GaN over Low Band Gap GaAs-Based IMPATT Devices,” International 4th IEEE Conference on Computers and Devices for Communication (CODEC-2009), Institute of Radio Physics & Electronics University of Calcuta, 14-16 December 2009, Kolkata, pp. 1-4.
- S. Hauguth, V. Lebedev, Ch. Mauder, F. Niebelschütz, H.-J. Büchner, G. Jäger and O. Ambacher, “Novel III-Nitride Based Transparent Photodetectors for Standing Wave Interferometry,” Physica Status Solidi (a), Vol. 205, No. 8, August 2008, pp. 2080-2084. doi:10.1002/pssa.200778888
- J. T. Lü and J. C. Cao, “Terahertz Generation and Chaotic Dynamics in GaN NDR Diode,” Semiconductor Science and Technology, Vol. 19, No. 4, April 2004, pp. 451-456.
- M. Levinstein, S. Rumyantsev and M. Shur, “Handbook Series on Semiconductor Parameters,” World Scientific, London, 1996.
- J. Pozhela and A. Reklaitis, “Electron Transport Properties in GaAs at High Electric Fields,” Solid-State Electronics, Vol. 23, No. 9, September 1980, pp. 927-933. doi:10.1016/0038-1101(80)90057-X
- H. D. Rees, “Hot Electron Effects at Microwave Frequencies in GaAs,” Solid State Communications, Vol. 7, No. 2, February 1969, pp. 267-269. doi:10.1016/0038-1098(69) 90396-2

