Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 7 (2011) , Article ID: 5905 , 6 pages DOI:10.4236/jemaa.2011.37041
Enhancement of Phase Matching Ability in One-Dimensional Photonic Crystal through Plasma Material
![]()
Department of Physics, Faculty of Science, Banaras Hindu University, Varanasi, India.
Email: viveks@bhu.ac.in
Received April 15th, 2011; revised May 17th, 2011; accepted June 1st, 2011.
Keywords: One dimensional photonic crystal, plasma photonic crystal, transfer matrix method, Dispersion relation, Phase matching
ABSTRACT
We have theoretically studied the modal dispersion equation and effective refractive index of one-dimensional plasma photonic crystals (1-D PPCs) having different materials in one unit cell. The dispersion relations related for such structure is derived by solving Maxwell’s equation using the transfer matrix method. It is found that the presence of plasma in a unit cell enhanced the phase matching ability and provides additional degree of freedom to control phase matching condition compared to the conventional one-dimensional photonic crystals (1-D PCs).
1. Introduction
In the recent years, the Photonic Crystals (PCs) which is also called Photonic Band Gap Materials (PBGMs) have received much attention and the large number of new type of PCs have been studied and fabricated [1-5]. The ability to confine and control the light has a wide range of applications in the area of optics and laser physics. The interactions of electromagnetic wave with plasma have ability to control the light because plasma in microwave devices have modified the dispersion properties and enhances the efficiency of plasma lens [6], plasma antennas [7] and plasma stealth aircraft [8]. Firstly, Kuo and Fatith [9] studied the propagation of electromagnetic wave in rapid created time varying periodic plasma. Hojo et al. [10] have studied the dispersion relation of electromagnetic wave propagation in 1-D binary PPCs and they found that the band gap can be controlled by the plasma density and plasma width. Prasad et al. [11] have theoretically studied the modal dispersion characteristics, group velocity, and effective group as well as phase index of refraction of 1-D ternary PPCs structure having periodic multilayers of three different materials in one unit cell. They also found that such structure provide additional degree of freedom to control dispersion characteristic, group velocity and effective index of refraction compared to 1-D ternary PCs. The PPCs can be tailored to produce unique and useful modal characteristics such as: single-mode operation at a wide wavelength range [12], ultra short pulses and to control their parameters [13,14], highly tunable dispersion [13-15], to slow down light pulses in a controllable manner [15], to match phase and group velocities in non-linear optics and to perform many optical functions such as optical switching, etc. Tarasishin et al. [16] have illustrated the idea of phase and group-velocity matching of short pulses involved in second-harmonic generation in a one-dimensional PBG structure. Naumov et al. [17] show the enhancement of phase matching abilities through 1-D ternary PCs. They also gave the possible application of this property for synthesizing trains of subfemtosecond and attosecond pulses.
The objective of this work is to study the phase matching abilities of one-dimensional PPCs because these periodic plasma structures, which are controllable by external parameters, can create more new possibilities in PCs. The paper is organized as follow: in Section 2 the dispersion relation of the proposed structure is given. The phase matching condition used in this paper is also presented. Section 3 is devoted to result and discussion. A conclusion is drawn in section 4.
2. Theoretical Modeling
2.1. Dispersion Relations for PPCs
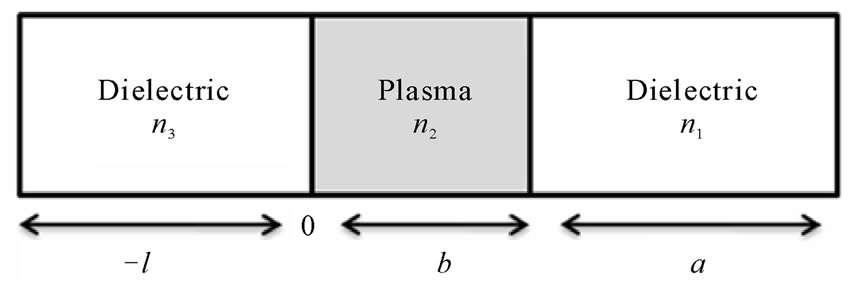
The schematic diagram of 1-D ternary PPCs is represented in Figure 1(a). The unit cell of proposed 1-D ternary PPC has a plasma material with refractive index n2 sandwiched between two different dielectric materials having indices n1 and n3. Refractive index n(z) shows periodicity with lattice constant, d = a + b + l, where a, b, l are the width of consecutive layers having refractive index n1, n2 and n3 respectively. It means that 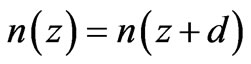 . Hence the index profile for 1-D ternary PPC is written as
. Hence the index profile for 1-D ternary PPC is written as
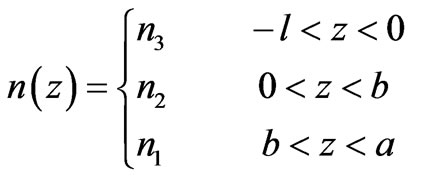 (1)
(1)
where 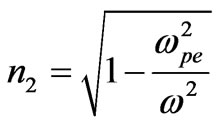 and
and  is the electron plasma frequency and np is density of plasma. To derive the dispersion relations and phase matching conditions for electromagnetic wave propagation in an infinite photonic band gap structures, the Maxwell’s equation is solved by using the transfer matrix method [18]. One dimensional Maxwell’s wave equation for electromagnetic (EM) waves propagating in z-direction normal to the layers in the photonic crystal is written as
is the electron plasma frequency and np is density of plasma. To derive the dispersion relations and phase matching conditions for electromagnetic wave propagation in an infinite photonic band gap structures, the Maxwell’s equation is solved by using the transfer matrix method [18]. One dimensional Maxwell’s wave equation for electromagnetic (EM) waves propagating in z-direction normal to the layers in the photonic crystal is written as
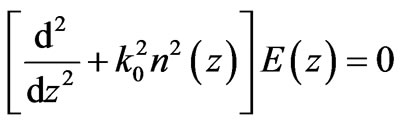 (2)
(2)
where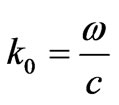 ,
, 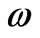 is the frequency of electromagnetic waves propagating in the crystals and c is the velocity of light in free space. Its solutions for three alternate layers can be written as:
is the frequency of electromagnetic waves propagating in the crystals and c is the velocity of light in free space. Its solutions for three alternate layers can be written as:
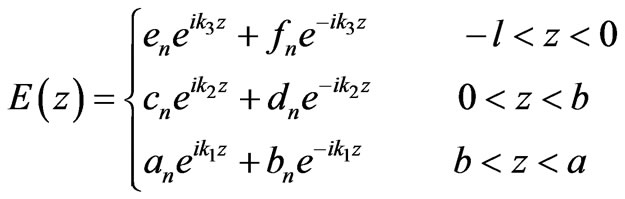 (3)
(3)
where an, bn, cn, dn, en and fn are unknown coefficients and k1, k2 and k3 are wave-vectors in three regions and can be expressed as:
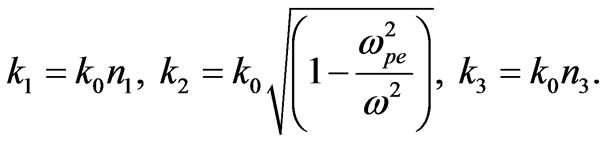
Imposing the continuity of electric field 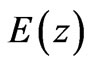 and its derivatives
and its derivatives 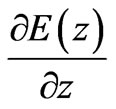 at interfaces and arranging coefficients
at interfaces and arranging coefficients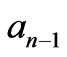 ,
, 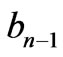 ,
,  and
and  by transfer matrix method
by transfer matrix method
 (a)
(a) (b)
(b)
Figure 1. (a) Schematic representation of the unit cell of 1-D ternary PPC; (b) Schematic representation of the unit cell of 1-D binary PPC.
[18], we obtained the following matrix relation:
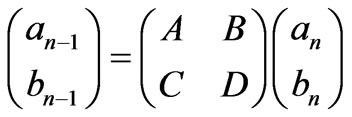 (4)
(4)
where A, B, C and D are the matrix elements for unit cell translation matrix that relates the complex amplitude of the incident wave an−1 and the reflected plane wave bn−1 in one layer of a unit cell to those of the equivalent layer in the next unit cell. Using Bloch’s theorem  where Bloch function
where Bloch function 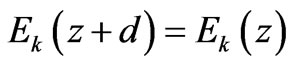 and after simplification, with w > wpe the dispersion relation for 1-D ternary PPC may be written as:
and after simplification, with w > wpe the dispersion relation for 1-D ternary PPC may be written as:
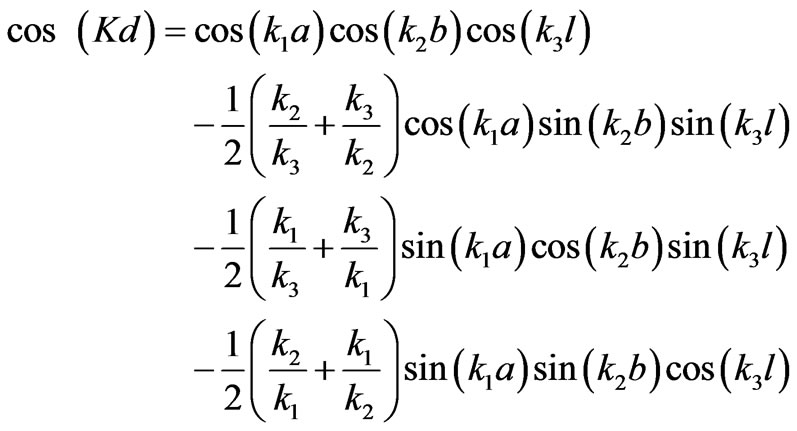 (5)
(5)
where K is the Bloch wavenumber.
The schematic diagram of 1-D binary PPCs is represented in Figure 1(b). The similar dispersion equation for 1-D binary PPC [10,19] is written as
 (6)
(6)
where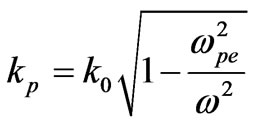 ,
, 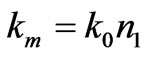 , d = a + b, a and b are the width of dielectric and plasma region respectively.
, d = a + b, a and b are the width of dielectric and plasma region respectively.
2.2. Dispersion Relations for PCs
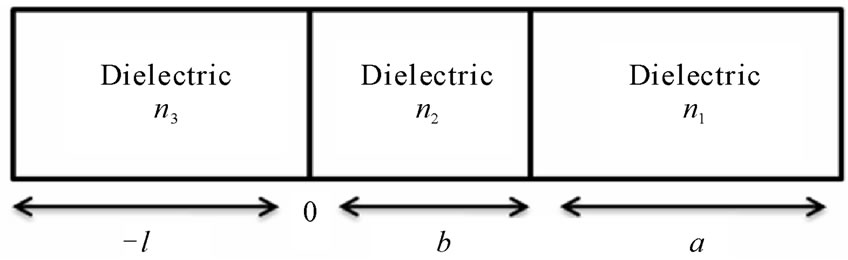
The schematic diagrams of 1-D ternary and binary PCs are represented in Figures 2(a) and (b) respectively. The dispersion relation for 1-D ternary PC is given as [17]
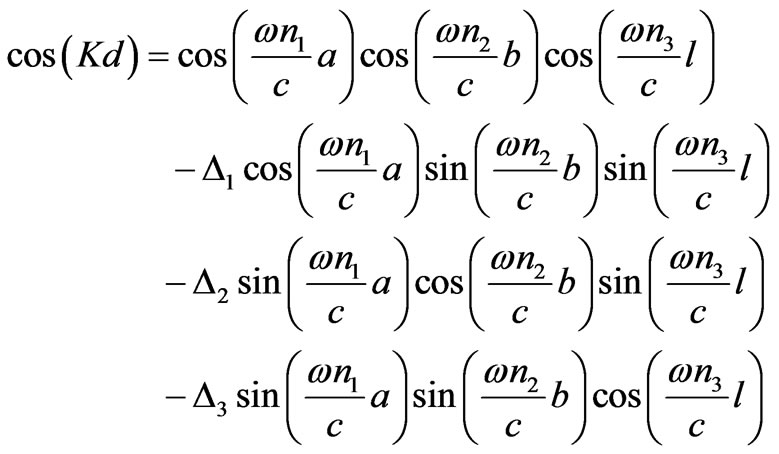 (7)
(7)
where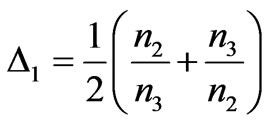 ,
, 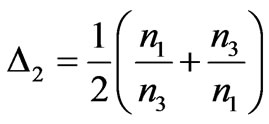 ,
,
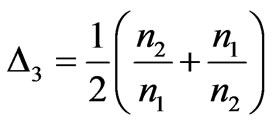 , d = a + b + l, a, b and l is the width of respective dielectric media.
, d = a + b + l, a, b and l is the width of respective dielectric media.
The dispersion relation for 1-D binary PC is written as
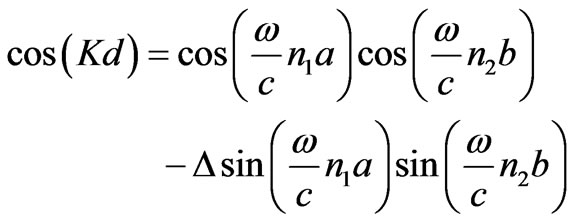 (8)
(8)
where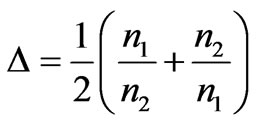 , d = a + b, a and b is the width
, d = a + b, a and b is the width
 (a)
(a)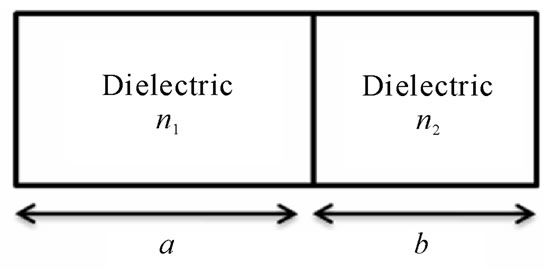 (b)
(b)
Figure 2. (a) Schematic representation of the unit cell of 1-D ternary PC; (b) Schematic representation of the unit cell of 1-D binary PC.
of respective dielectric media.
We can also define the effective refractive index as the ratio between the speed of light in vacuum and the effective phase velocity of the wave in the medium [17,20]. Hence we have
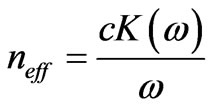 (9)
(9)
3. Results and Discussion
In this section we estimate the phase matching abilities for the four different PC structures. These structures are shown in Figures 1 and 2. Figure 3 shows the dispersion relation for 1-D ternary PPC at n1 = 3.46, n2 = 3.36, p = 1, a/d = 0.3, b/d = 0.5, c/d = 0.2 and n1 = 3.46, n2 = 3.36, p = 0.6, a/d = 0.5, b/d = 0.1, c/d = 0.4. It is clear from the Figure 3 that the allowed and forbidden bands gap are strongly depend on the plasma frequency, plasma density and plasma width. Therefore by choosing suitable value of these parameters we can control the allowed and forbidden bands of the PPCs.
Since we are interested in phase matching conditions, we focus our attention on the real part of the effective index. By using equations (5)-(8), we have computed the effective refractive index 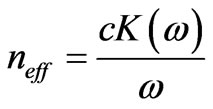 as a function of frequency ω normalized to the c/d for different PC structures.
as a function of frequency ω normalized to the c/d for different PC structures. 
Figure 4 shows the real part of effective refractive index of 1-D ternary PPC with a = 0.5, b = 0.1, l = 0.4n1 = 3.46, n3 = 3.36, normalized plasma frequency
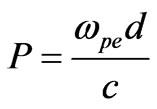 = 0.60 as a function of normalized frequency.
= 0.60 as a function of normalized frequency.
It is clear from Figure 4 that the ternary 1-D PPC pro-
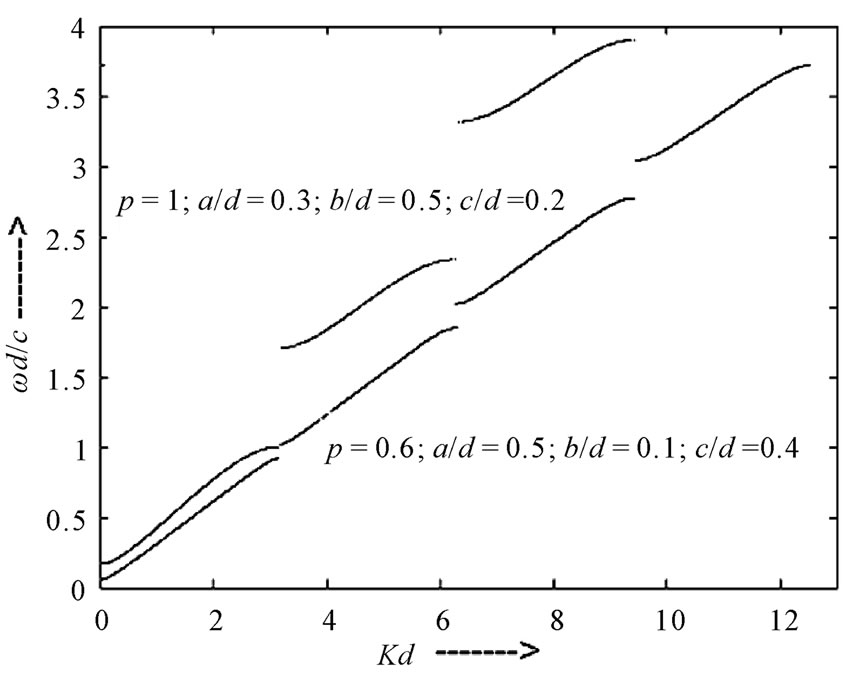
Figure 3. Dispersion curves for 1-D ternary PPC at various values of selection parameters.
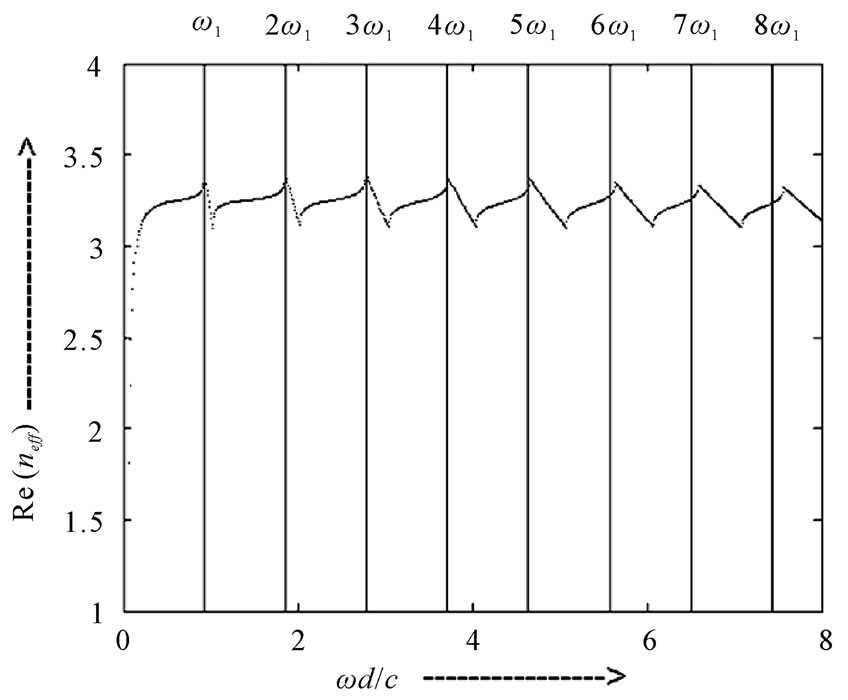
Figure 4. The variation of real part of effective refractive index for 1-D ternary PPC with normalized frequency.
vide anomalous dispersion for equidistance set of frequencies ω1, 2ω1, 3ω1, 4ω1, 5ω1, 6ω1, and 7ω1. This dispersion of the structure can be used to compensate for the material dispersion. Thus the material dispersion can be compensated for this set of spectral component. Here the phase velocities of radiation with frequency ω1, can be phased matched with its second to seven harmonics in the 1-D ternary PPC. Figure 5 shows the real part of effective refractive index of 1-D binary PPC with a/d = 0.82, b/d = 0.18, n1 = 3.46, and p = 0.60 as a function of normalized frequency. The 1-D binary PPC provide anomalous dispersion for four equidistance frequencies ω1, 2ω1, 3ω1, 4ω1. Thus the material dispersion can be compensated for these four equidistant frequencies. By comparing the Figure 4 with Figure 5 we observe that in 1-D ternary PPC allows a larger number of optical fields with different frequencies to be simultaneously phase matched.
Figure 6 shows the real part of effective refractive index of conventional 1-D ternary PC with a/d = 0.35, b/d = 0.35, l/d = 0.30, n1 = 3.46, n2 = 1.8, n3 = 3.36 as a function of normalized frequency. It is clear from Figure 6 that the ternary 1-D PC provide anomalous dispersion for two equidistance frequencies ω1, and 2ω1, therefore it equalize the phase velocities of radiation on these two frequencies. Figure 7 shows the real part of effective refractive index of conventional 1-D binary PC with a/d = 0.60, b/d = 0.40, n1 = 3.46, and n2 = 2 as a function of normalized frequency. This structure provides anomalous dispersion for one frequency ω1. Hence for this structure, the material dispersion can be compensated for the spectral component ω1.
By comparing the Figure 6 with Figure 7 we observe that in 1-D ternary PC allows a larger number of optical
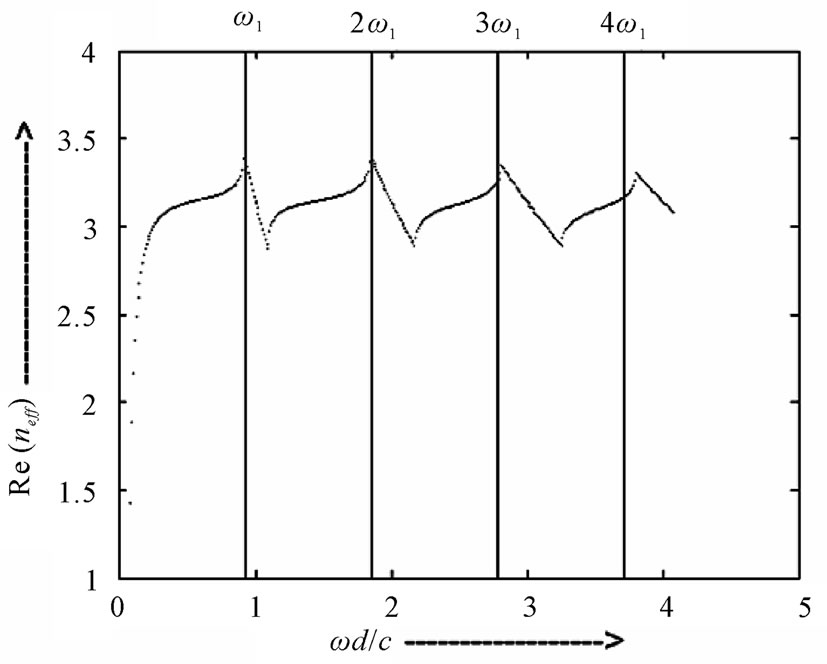
Figure 5. The variation of real part of effective refractive index for 1-D binary PPC with normalized frequency.
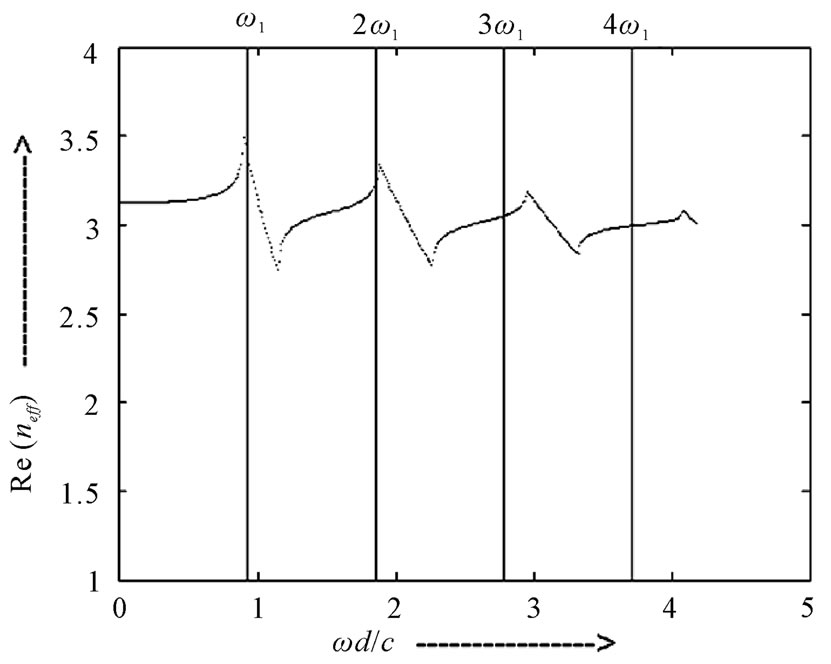
Figure 6. The variation of real part of effective refractive index for 1-D ternary PC with normalized frequency.

Figure 7. The variation of real part of effective refractive index for 1-D binary PC with normalized frequency.
fields with different frequencies to be simultaneously phase matched. From above discussion we conclude that increase in the number of material in a unit cell can increase the phase matching ability of the PCs. But if we compare Figure 5 with Figure 6 then in 1D binary PPC the phase velocities of radiation can be phased matched with its second to four harmonics simultaneously while in conventional 1-D ternary PC it is second to three harmonics. Therefore, 1D binary PPC will give better result than the conventional 1-D ternary PC. In the same way 1-D ternary PPC offers the equalization of the phase velocity of radiation from second to seven harmonics simultaneously. This is much larger than those shown in Figure 6 for 1-D ternary PC or shown by Naumov et al. [17]. It is clear from above discussion that plasma in 1-D PC enhances the phase matching ability and provides an additional degree of freedom to control the dispersion relation.
4. Conclusions
We have theoretically investigated the phase matching abilities of 1D photonic crystal through the effective index approach. The dependence of band gap on plasma frequency, plasma density and plasma width are observed in 1-D PPC. We have also compared the phase matching abilities of 1-D PC with 1-D PPC for both binary and ternary cases. Our analysis shows that the introduction of thin plasma layers in PCs enhanced the phase matching ability considerably.
5. Acknowledgements
The authors are grateful to Dr. B. Prasad and Dr. R. D. S. Yadava for their continuous encouragement and supports in many ways.
REFERENCES
- J. D. Giannopoulos, P. Villeneuve and S. Fan, “Photonic Crystals: Putting a New Twist on Light,” Nature, Vol. 386, No. 143, 1997, pp. 143-149. doi:10.1038/386143a0
- L.-G. Wang, H. Chen and S. Y. Zhu, “Omnidirectional Gap and Defect Mode of One-Dimensional Photonic Crystals with Single Negative Materials,” Physical Review B, Vol. 70, No. 24, 2004, pp. 1-6.
- V. Kuzmiak and A. Muradudin, “Photonic Band Gap in One and Two Dimensional Periodic Systems with Metallic Components in the Presence of Dissipation,” Physical Review B, Vol. 55, No. 12, 1997, pp. 7427-7444. doi:10.1103/PhysRevB.55.7427
- C. J. Wu, “Transmission and Reflection in a Periodic Superconductor/Dielectric Film Multilayer Structure,” Journal of Electromagnetic Waves and Applications, Vol. 19, No. 15, 2006, pp. 1991-1996. doi:10.1163/156939305775570468
- J. C. McCalmont, M. M. Sigalas, G. Tuttle, K. M. Ho and C. M. Soukoulis, “A Layer-by-Layer Metallic Photonic Band Gap Structure,” Applied Physics Letters, Vol. 68, No. 19, 1996, pp. 2759-2761. doi:10.1063/1.115589
- A. A. Goncharov, A. V. Zatuagan and I. M. Protsenko, “Focusing and Control of Multiaperture Ion Beam of Plasma Lense,” IEEE Transactions of Plasma Science, Vol. 21, No. 5, 1993, pp. 578-581. doi:10.1109/27.249646
- B. Chaudhury and S. Chaturvedi, “Three-Dimensional Computation of Reduction in Radar Cross Section Using Plasma Shielding,” IEEE Transactions of Plasma Science, Vol. 33, No. 6, 2005, pp. 2027-2034. doi:10.1109/TPS.2005.860122
- T. Dwyer, J. Greig, D. Murphy, et al., “On the Feasibility of Using an Atmospheric Discharge Plasma as an RF Antenna,” IEEE Transactions on Antenna and Propagation, Vol. 32, No. 2, 1984, pp. 141-146. doi:10.1109/TAP.1984.1143275
- S. P. Kuo and J. Fatith, “Interaction of an Electromagnetic Wave with a Rapidly Created Spatially Periodic Plasma,” Physical Review E, Vol. 56, No. 2, 1997, pp. 2143-2150. doi:10.1103/PhysRevE.56.2143
- H. Hoja and A. Mase, “Dispersion Relation of EM Waves in One Dimensional Plasma Photonic Crystal,” Journal of Plasma Fusion Research, Vol. 80, No. 2, 2004, pp. 89-90. doi:10.1585/jspf.80.89
- S. Prasad, V. Singh and A. K. Singh, “Modal Propagation Characteristics of EM Waves in Ternary One-Dimensional Plasma Photonic Crystals,” Optik, Vol. 121, No. 16, 2010, pp. 1520-1528. doi:10.1016/j.ijleo.2009.02.024
- S. K. Srivastava and S. P. Ojha, “Omnidirectional Reflection Bands in One-Dimensional Photonic Crystal Structure Using Fullerene Films,” Progress in Electromagnetics Research, Vol. 74, 2007, pp. 181-194. doi:10.2528/PIER07050202
- P. Yeh, A. Yuriv and S. S. Hony, “Electromagnetic Propagation in Periodic Stratified Media,” Journal of the Optical Society of America A, Vol. 67, No. 4, 1977, pp. 423- 438. doi:10.1364/JOSA.67.000423
- G. Cerullo, M. Nisoli, S. Stagira, S. de Silvestri, G. Tempea, F. Krausz and F. Krausz, “Mirror Dispersion Controlled Sub-10-Fs Optical Parametric Amplifier in the Visible,” Optics Letters, Vol. 24, No. 21, 1999, pp. 1529- 1531. doi:10.1364/OL.24.001529
- N. I. Koroteev, S. A. Magnitskii, A. V. Tarasishin and A. M. Zheltikov, “Compression of Ultrashort Light Pulses in Photonic Crystals: When Envelopes Cease to be Slow,” Optics Communications, Vol. 159, No. 1-3, 1999, pp. 191-202. doi:10.1016/S0030-4018(98)00571-9
- V. Tarasishin, S. A. Magnitskii and A. M. Zheltikov, “Matching Phase and Group Velocities in Second-Harmonic Generation in Finite One-Dimensional Photonic Band-Gap Structures,” Laser Physics, Vol. 11, No. 1, 2001, pp. 31- 38.
- A. N. Naumov and A. M. Zheltikov, “Ternary One-Dimentional Photonic Band Gap Structures: Dispersion Relation, Extended Phase Matching Abilities, and Attosecond Outlook,” Laser Physics, Vol. 11, No. 7, 2001, pp. 879-884.
- P. Yeh, “Optical Waves in Layered Media,” John Wiley and Sons, New York, 1988.
- B. Guo, “Transfer Matrix for Obliquely Incident Electromagnetic Waves Propagating in One Dimension Plasma Photonic Crystals,” Plasma Science and Technology, Vol. 11, No. 1, 2009, pp. 18-22. doi:10.1088/1009-0630/11/1/04
- M. Centini, C. Sibilia, M. Scalora, G. D’Aguanno, M. Bertolotti, M. J. Bloemer, C. M. Bowden and I. Nefedov, “Dispersive Properties of Finite, One-Dimensional Photonic Band Gap Structures: Applications to Nonlinear Quadratic Interactions,” Physical Review E, Vol. 60, No. 4, 1999, pp. 4891-4898. doi:10.1103/PhysRevE.60.4891

