Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 7 (2010) , Article ID: 2329 , 8 pages DOI:10.4236/jemaa.2010.27052
Analysis of Double and Single Sided Induction Heating Systems by Layer Theory Approach
![]()
General & Theoretical Electrical Engineering Department, University of Duisburg-Essen, Duisburg, Germany.
Email: layth.qaseer@uni-duisburg-essen.de
Received February 11th, 2010; revised April 8th, 2010; accepted April 15th, 2010.
Keywords: Eddy currents, electromagnetic analysis, energy conversion, induction heating
ABSTRACT
The iterative layer theory approach is applied to the analysis of double sided and single sided induction heating systems for continuous heating of thin metal strips. The excitation is transverse to the direction of strip motion and can be three phase or single phase. Nonmagnetic as well as ferromagnetic strips are employed. The important system parameters, namely, strip resistance, reactance, induced power and electromagnetic force are introduced. Accuracy of the method is verified with measurement of practical induction heating system together with comparison to numerical and analytical methods.
1. Introduction
THREE phase induction heating systems such as transverse flux induction heating (TFIH) systems and traveling wave induction heating (TWIH) systems have been extensively studied in recent years. While numerical techniques are more popular and particularly useful for investigating the induced current and power distributions taking into account longitudinal and transverse edge effects, analytical methods are more convenient for the integral parameters determination and analysis.
3-D finite element method (FEM) has been employed in the analysis of TFIH systems [1-8] while 2-D and 3-D FEM have been employed in the analysis of TWIH systems [9-13]. Few papers relating to analytical methods for the analysis of single phase and traveling wave but cylindrical induction heating systems have been published [14-17].
Only a few researchers pay attention to this area in the world.
The TWIH is not fully appreciated with respect to their main advantages and possible industrial applications [18].
A. Ali, V. Bukanin from St. Petersburg Electrotechnical University in Russia and F. Dughiero, M. Frozen, S. Lupi, P. Siega, V. Nemkov from University of Padua in Italy have obtained significant achievements in this area. In the very recent years, Takamitsu Sekine, Hideo Tomita, Shuji Obata and Yokio Saito from Tokyo Denki University in Japan have designed an excellent traveling wave induction heating system and carried out experiment [19].
An analytical method based on the decomposition of the main magnetic flux imposed by means of an excitation coil into partial magnetic fluxes along different regions that comprise the assembly. The basic circuit parameters that feature the electric performance in induction heating devices having an excitation axial winding as found in induction motors for generating rotary magnetic fields are mathematically modeled [20].
Modern analytical approaches using transmission line terminology [21-23] are confined to lossless or low conductivity (dielectric) media where displacement currents are prominent at microwave frequencies in the order of hundreds of gigahertz, which is not the case as in this approach where induced power is the major objective of induction heating, moreover these methods are primarily applied to isotropic media while the layer theory is applied to both isotropic and anisotropic media, also it is not mentioned in these references whether these approaches may be used in the case of three phase (traveling wave) excitation.
The layer theory approach has been mainly used for the analysis of linear, tubular linear and helical motion induction motors as given in [24-26].
TWIH systems widely common in literature are of the double sided induction heating (DSIH) system type as it employs upper and lower excitation inductors with respect to the long and thin continuously moving strip. Single sided induction heating (SSIH) systems are TWIH systems that employ one inductor for exciting the metal strip while single phase induction heating systems are commonly known as longitudinal flux induction heating (LFIH) systems.
The primary object of this paper is to propose a general mathematical model for the induction heating system using the actual topology for single phase and three phase excitations with any number of poles for SSIH and DSIH systems. As a second object, the paper employs the multi-layer approach with the appropriate current sheet to calculate the flux density components, induced power in the strip, terminal impedance and the magnetic force acting on the strip in the direction of field travel in the case of TWIH systems.
2. Mathematical Model
2.1 Three – Phase Excitation
A general multi-region problem is analyzed. Figure 1 shows a cross-section of the N-region model used in the theory. The model is taken to be a set of planar regions. The current sheet lies between regions r and r + 1.
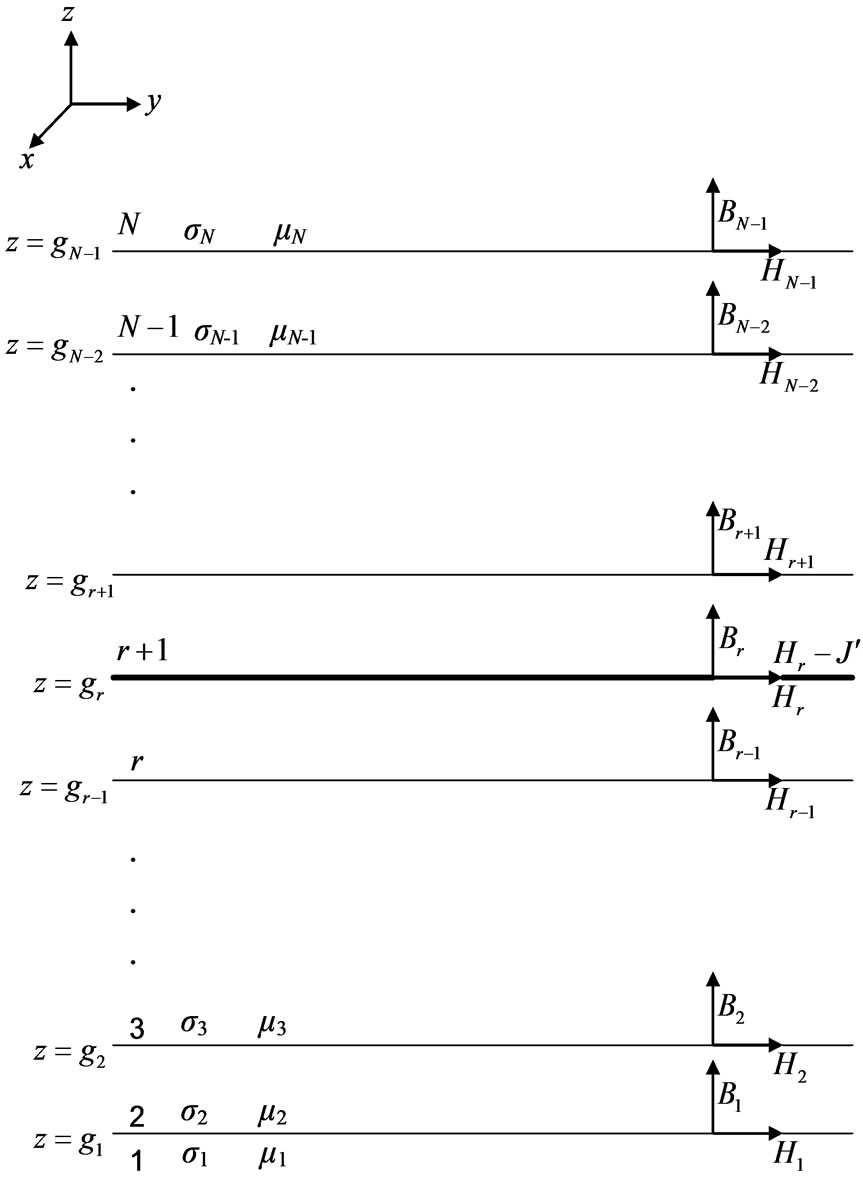
Figure 1. General model with current sheet at boundary 
The current sheet varies sinusoidally in the y-direction and with time. It is of infinite extent in the x-direction and infinitesimally thin in the z-direction.
Regions 1-N are layers of materials where the general region n has a conductivity σn and anisotropic relative permeability µn. The anisotropy is an approximation made in order to deal with slotted regions. The regions are traveling at velocity  relative to a stationary reference frame where λ is the wavelength of applied field, f is the frequency and sn is the slip in region n defined as
relative to a stationary reference frame where λ is the wavelength of applied field, f is the frequency and sn is the slip in region n defined as

where fn is frequency of the field experienced by region n. In this frame the traveling field has a velocity .
.
It is assumed that displacement current is negligible and magnetic saturation is neglected. Maxwell’s equations for any region in the model are
 (1)
(1)
 (2)
(2)
 (3)
(3)
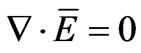 (4)
(4)
 (5)
(5)
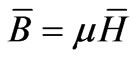 (6)
(6)
The boundary conditions may be summarized as follows
1) The normal component of the magnetic flux density Bz is continuous across a boundary.
2) All field components vanish at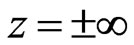 .
.
3) The tangential component of magnetic field strength Hy is continuous across a boundary, but allowance must be made for the current sheet in the manner explained in Section 3.
2.1.1 Excitation Current Density
It is assumed that the winding produces perfect sinusoidal traveling wave. The line current density may be represented as
 (7)
(7)
where  and k are the line current density, angular frequency and wave length factor respectively. The line current density is given by
and k are the line current density, angular frequency and wave length factor respectively. The line current density is given by

where I, p, τ and Neff are the r.m.s. value of the phase current, number of poles, pole pitch and effective number of series turns per phase respectively. The wave length factor is defined as
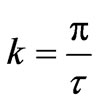 (8)
(8)
2.1.2 Field Equation of a General Region
As a first step in the analysis the field components of a general region are derived, assuming that all fields vary as exp[ j(ωt – ky)], and omitting this factor for simplicity reasons from all the field expressions that follow. Taking only the xcomponent from both sides of (2) yields

From (3) we have

which leads to
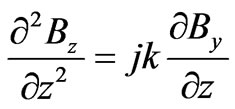 (9)
(9)
Taking the zcomponent from both sides of (2) yields
 (10)
(10)
Taking only the x-component from both sides of (1) yields
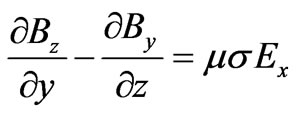 (11)
(11)
Therefore, using (9) and (10) into (11) yields
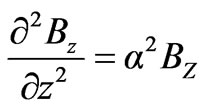 (12)
(12)
where
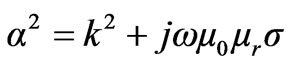
The solution is given by
 (13)
(13)
where A and C are arbitrary constants to be determined from the boundary conditions.
From (3) we get
 (14)
(14)
2.1.3 Field Calculations at the Region Boundaries
Figure 2 shows a general region n of thickness Sn the normal component of magnetic flux density on the lower boundary is Bn-1 and the tangential component of magnetic field strength is Hn-1. The corresponding values on the upper boundary are  and
and . From (13) and (14)
. From (13) and (14)
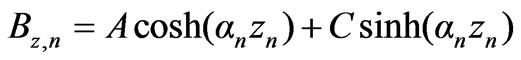 (15)
(15)

Figure 2. General region n
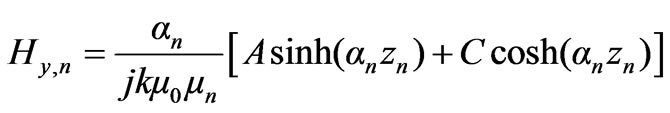 (16)
(16)
Equivalent expressions for Bz,n-1 and Hz,n-1 can be found by replacing zn by zn-1. Now for the regions where 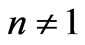 or N
or N
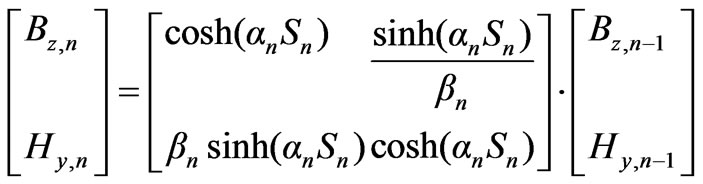 (17)
(17)
or
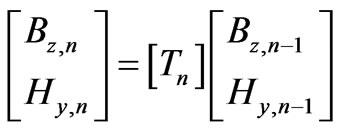 (18)
(18)
where
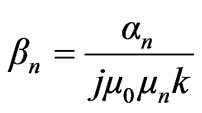 (19)
(19)
Hence given the values of Bz and Hy at the lower boundary of a region, the values of Bz and Hy at the upper boundary are immediately obtainable from this simple transfer matrix relation. At the boundaries where no excitation current sheet exists, Bz and Hy are continuous; thus for example, if two regions are considered with no current sheet at the common boundary, knowing Bz and Hy at the lower boundary of the first region, Bz and Hy at the upper boundary of the second region can be calculated by successive use of the underlying two transfer matrices. Considering the current sheet to be at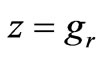 , then
, then
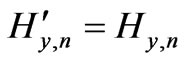 ,
, 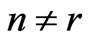 (20)
(20)
and
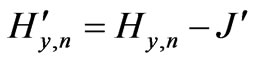 ,
,  (21)
(21)
where 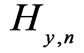 is the tangential magnetic field strength in close lower proximity to the boundary and
is the tangential magnetic field strength in close lower proximity to the boundary and 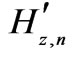 is the tangential magnetic field strength in close upper proximity to the boundary.
is the tangential magnetic field strength in close upper proximity to the boundary.
Given the current sheet excitation at 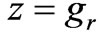 the overall structure divides into an upper part, which is modeled according to
the overall structure divides into an upper part, which is modeled according to
 …
…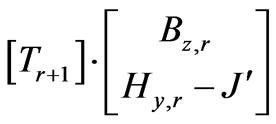 (22)
(22)
and an inner part which supports the following relation
 …
…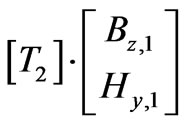 (23)
(23)
If the top region is now considered, then as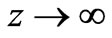 ,
,  and all field quantities tend to zero, hence on the boundary
and all field quantities tend to zero, hence on the boundary 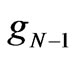 the field quantities are related by
the field quantities are related by
 (24)
(24)
Therefore at any z within region N the field quantities become

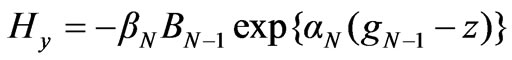
Considering the bottom region where n = 1, the field quantities are related by
 (25)
(25)
and at any z within region 1
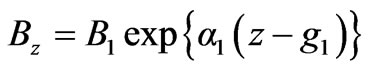
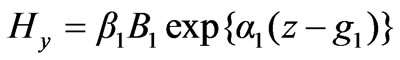
2.1.4 Surface Impedance Calculations
The surface impedance looking outwards at a boundary of 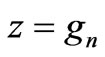 is defined as
is defined as
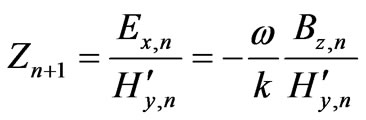 (26)
(26)
and the surface impedance looking inwards is defined as
 (27)
(27)
Using the method obtained in [17] with the values of Bz,N-1, Hy,N-1, Bz,1, Hy,1 and [Tn] as derived in the previous section then
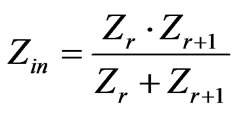 (28)
(28)
where Zin is the input surface impedance at the current sheet and Zr+1 and Zr are the surface impedances looking outwards and inwards at the current sheet. Substituting for Zr and Zr+1 using (26) and (27) respectively, and rearranging the terms yields
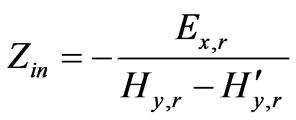 (29)
(29)
Substituting (21) into (29) yields
 (30)
(30)
Thus the input surface impedance at the current sheet has been determined. This means that all field components can be found by making use of this and (27), (22), (23).
2.1.5 Terminal Impedance, Power and Tangential Force
The terminal impedance per phase per metre of axial length can be derived [17] in terms of Zin as
 (31)
(31)
Having found Ex, Bz and Hy at all boundaries, it is then a simple matter to calculate the power entering a region through the concept of Poynting vector. The time average power density passing through a surface is given by
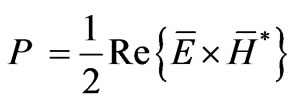 W/m2
W/m2
Hence the time average power density flowing upwards from the current sheet at 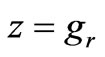 is given by
is given by
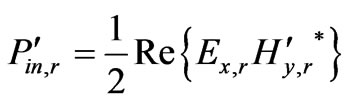
and the time average power density flowing downwards from the current sheet at 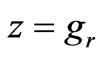 is given by
is given by

The net power density in a region is the difference between the power in and power out
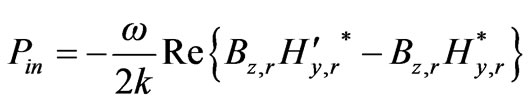 (32)
(32)
It follows that the tangential force density Fy acting on the strip is the net power density induced divided by traveling wave velocity 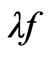
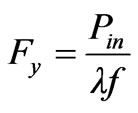 N/m2 (33)
N/m2 (33)
2.1.5.1 Single Phase Excitation This is a simpler problem than the three phase one and only regions below or above the current sheet (depending where the strip is located) need be considered. Other regions do not in any way affect the field distribution. The excitation is provided by a single coil of N1 turns per metre of axial length carrying alternating current in the transverse direction. The line current density takes the form
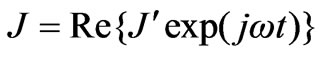 (34)
(34)
with

In this case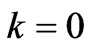 , all field relations, Maxwell’s equations and boundary conditions hold. The solution is given by
, all field relations, Maxwell’s equations and boundary conditions hold. The solution is given by
 (35)
(35)
where
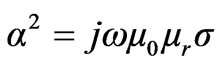 (36)
(36)
If the plane 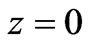 passes through the central axis of the strip then
passes through the central axis of the strip then

where b is the thickness of the strip and 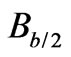 is the axial (tangential) component of magnetic flux density at the upper surface of the strip. The axial component of magnetic flux density at the lower surface of the strip is given by
is the axial (tangential) component of magnetic flux density at the upper surface of the strip. The axial component of magnetic flux density at the lower surface of the strip is given by

Hence we can write
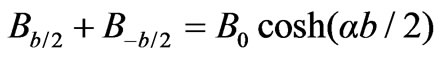 (37)
(37)
where B0 is the axial component of magnetic flux density at the centre of the strip.
The input surface impedance at the current sheet becomes
 (38)
(38)
where Zr is obtained using (27).
The net power density induced in the strip is obtained using the concept of Poynting vector and therefore the net power density in the strip is
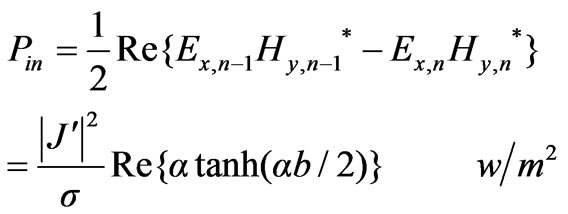 (39)
(39)
The terminal impedance is given by the relationship
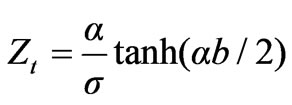 (40)
(40)
3. Numerical Results
The solution procedure that has been described in the previous sections is used to analyze two examples to check validity and accuracy. One example is a single phase practical induction heating system with ferromagnetic strip [27]. The importance of this example is that measurement is available in addition to calculation. The other example is based on FEM solution for DSIH system [9].
For comparison reasons, FEM computation is adopted in our analysis which is widely used as a numerical technique for this kind of applications.
In our implementation, the field domain is divided into a number of regions, each being defined by its coordinates, permeability and conductivity. Each region is descritized using first order triangular elements [28]. The induced power in the strip is obtained through the solution of governing differential equation for each nodal magnetic vector potential. Three values of power are computed: the power integrated over the coil, the air gap power and the power integrated over the strip.
The solution is assumed to be convergent when these three values do not differ by more than 1% which is termed as the power mismatch or power imbalance.
3.1 Practical Single Phase Induction Heating System
Problem data are given in table 1. Results obtained using the layer theory approach and FEM are in good agreement with measurement as shown in table 2. This agreement is attributed to the fact that strip thickness is very small compared to strip length and width which coincides with the assumptions made in the mathematical model.

Table 1. Problem data for practical induction heating system (based on [27], Ex. 13)
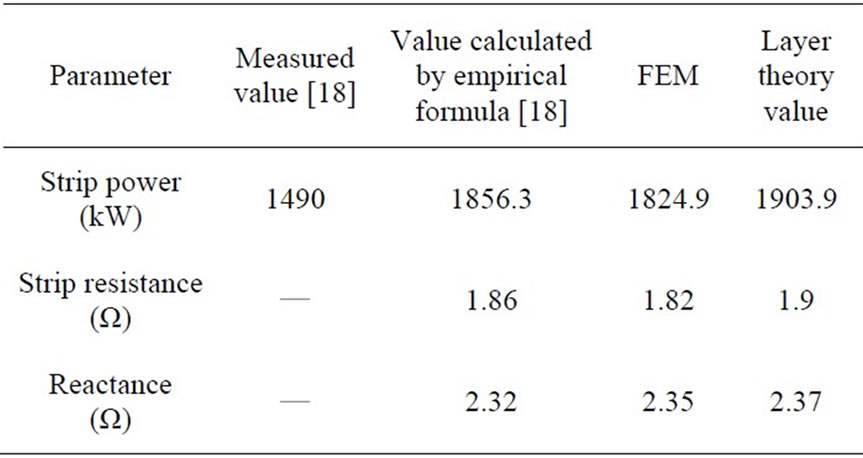
Table 2. Computed parameters of the practical single phase induction heating system
Figure 3 shows the variation of the axial component of magnetic flux density along strip depth at mid coil axial length for single phase model using FEM analysis and the layer theory approach. The agreement between the results of both methods may be considered good with a maximum relative deviation of 4.9%. It is shown in this figure that the axial component of magnetic flux density decreases rapidly (exponentially) from the surface of the strip for both sides due to skin effect. Obviously there is no normal component for single phase induction heating system and this can be derived directly from Maxwell’s equations.
3.2 Single Sided and Double Sided Traveling Wave Induction Heating Systems
Reference [9] employed a double sided induction heating system whose data are given in table 3.

Figure 3. Variation of axial flux density component with strip depth for single phase induction heating model
Table 3. Problem data for traveling wave DSIH and SSIH systems (based on Reference [9])
For the sake of comparison, the same model is adopted as a single sided induction heating system using the same line current density by removing one of the inductors along with its backing iron. Table 4 shows the computed parameters for both systems using FEM and the layer theory approach. Again the results correlate well as discussed in Subsection 3.1.
Figure 4 and Figure 5 show respectively the variation of normal and tangential (axial) flux density components along magnetic gap length. The maximum deviation between the results of both methods is found to be 5.2%.
Figure 6 and Figure 7 show the variation of normal and tangential (axial) flux density components along distance normal to the strip. Again both methods correlate well within 4%. In both systems the axial flux density component in the air gap is greater than the normal component, this may be attributed to the fact that the pole pitch is much greater than the air gap length in both systems and in this case these systems are considered as axial flux machines. It is clear from these figures that the axial component of magnetic flux density is decreased within the strip due to skin effect which is not effectively pronounced in the normal component to the strip.

Table 4. Computed parameters for traveling wave induction heating systems

Figure 4. Variation of normal flux density component along normal distance to strip for double sided induction heating system
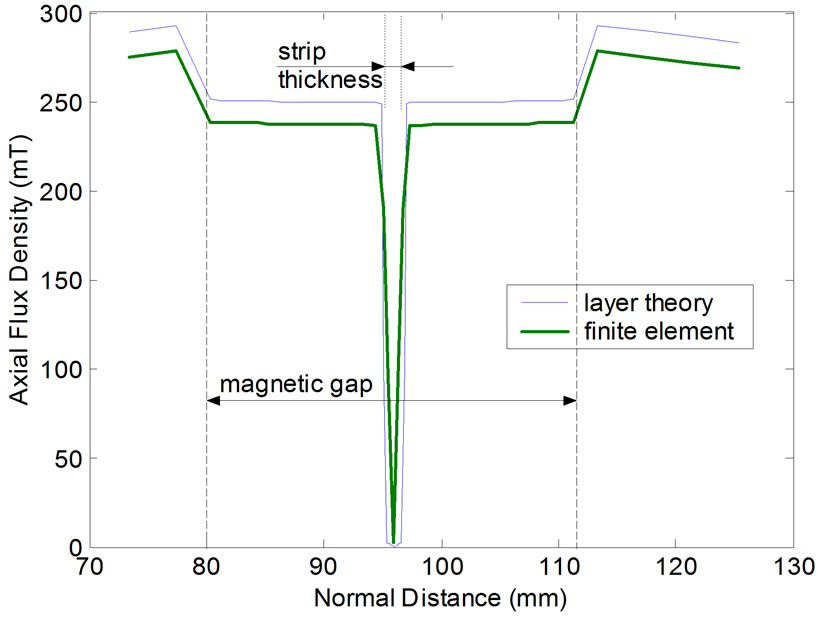
Figure 5. Variation of axial flux density component along normal distance to strip for double sided induction heating system
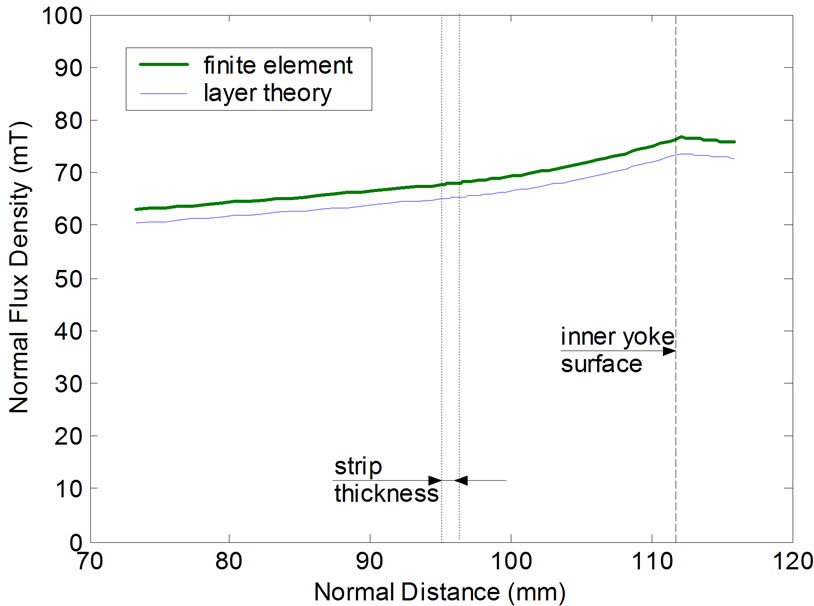
Figure 6. Variation of normal flux density component along normal distance to strip for single sided induction heating system

Figure 7. Variation of axial flux density component along normal distance to strip for single sided induction heating system
4. Conclusions
The layer theory approach has been used for the analysis of single sided, double sided traveling wave and single phase induction heating systems. This method has been applied to compute electrical parameters of various induction heating systems with ferromagnetic and nonmagnetic thin strips.
The results show clearly that the theoretical results correlate well with finite element method results in addition to experimental one. This may be considered as fair justification to the analysis method proposed in this paper.
5. Acknowledgements
The author is deeply indebted to Professor Daniel Erni, his host and co-worker at the University of Duisburg-Essen for advice and encouragement.
REFERENCES
- F. Dughiero, M. Forzan and S. Lupi, “3-D Solution of Electromagnetic and Thermal Coupled Field Problems in the Continuous Transverse Flux Heating of Metal Strips,” IEEE Transactions on Magnetics, vol. 33, no. 2, 1997, pp. 2147-2150.
- V. Bukanin, F. Dughiero, S. Lupi, V. Nemkov and P. Siega, “3D-FEM Simulation of Transverse-Flux Induction Heaters,” IEEE Transactions on Magnetics, vol. 31, no. 3, 1995, pp. 2174-2177.
- F. Dughiero, M. Forzan, S. Lupi and M. Tasca, “Numerical and Experimental Analysis of an Electro-Thermal Coupled Problem for Transverse Flux Induction Heating Equipment,” IEEE Transactions on Magnetics, vol. 34, no. 5, 1998, pp. 3106-3109.
- N. Bianchi and F. Dughiero, “Optimal Design Techniques Applied to Transverse-Flux Induction Heating Systems,” IEEE Transactions on Magnetics, vol. 31, no. 3, 1995, pp. 1992-1995.
- Z. Wang, X. Yang, Y. Wang, and W. Yan, “Eddy Current and Temperature Field Computation in Transverse Flux Induction Heating Equipment for Galvanizing Line,” IEEE Transactions on Magnetics, vol. 37, no. 5, 2001, pp. 3437-3439.
- Z. Wang, W. Huang, W. Jia, Q. Zhao, Y. Wang and W. Yan, “3-D Multifields FEM Computations of Transverse Flux Induction Heating for Moving Strips,” IEEE Transactions on Magnetics, vol. 35, no. 3, 1999, pp. 1642- 1645.
- D. Schulze and Z. Wang, “Developing an Universal TFIH Equipment Using 3D Eddy Current Field Computation,” IEEE Transactions on Magnetics, vol. 32, no. 3, 1996, pp. 1609-1612.
- S. Galunin, M. Zlobina and K. Blinov, “Numerical Model Approaches for In-Line Strip Induction Heating,” Proceedings of 2009 IEEE EUROCON Conference, SaintPetersburg, 18-23 May 2009, pp. 1607-1610.
- F. Dughiero, S. Lupi, V. Nemkov and P. Siega, “Travelling Wave Inductors for the Continuous Induction Heating of Metal Strips,” Proceedings of 7th Mediterranean Electrotechnical Conference, Antalya, 12-14 April 1994, pp. 1154-1157.
- L. L. Pang, Y. H. Wang and T. G. Chen, “Analysis of Eddy Current Density Distribution in Slotless Traveling Wave Inductor,” Proceedings of 2008 International Conference on Electrical Machines and Systems, Wuhan, 17- 20 October 2008, pp. 472-474.
- S. Lupi, M. Forzan, F. Dughiero and A. Zenkov, “Comparison of Edge-Effects of Transverse Flux and Traveling Wave Induction Heating Inductors,” IEEE Transactions on Magnetics, vol. 35, no. 5, 1999, pp. 3556-3558.
- Y. Wang and J. Wang, “The Study of Two Novel Induction Heating Technology,” Proceedings of 2008 International Conference on Electrical Machines and Systems, Wuhan, 17-20 October 2008, pp. 572-574.
- S. Ho, J. Wang, W. Fu and Y. Wang, “A Novel Crossed Traveling Wave Induction Heating System and Finite Element Analysis of Eddy Current and Temperature Distributions,” IEEE Transactions on Magnetics, vol. 45, no. 10, 2009, pp. 4777-4780.
- F. Dughiero, S. Lupi and P. Siega, “Analytical Calculation of Traveling Wave Induction Heating Systems,” Proceedings of 1993 International Symposium on Electromagnetic Fields in Electrical Engineering, Warsaw, 1993, pp. 207-210.
- V. Vadher and I. Smith, “Traveling Wave Induction Heaters with Compensating Windings,” Proceedings of 1993 International Symposium on Electromagnetic Fields in Electrical Engineering, Warsaw, 1993, pp. 211-214.
- A. Ali, V. Bukanin, F. Dughiero, S. Lupi, V. Nemkov and P. Siega, “Simulation of Multiphase Induction Heating Systems,” Proceedings of 2nd International Conference on Computation in Electromagnetics, Nottingham, 12-14 April 1994, pp. 211-214.
- L. Bunni and K. Altaii, “The Layer Theory Approach Applied to Induction Heating Systems with Rotational Symmetry,” Proceedings of 2007 IEEE Southeast Conference, Richmond, 22-25 March 2007, pp. 413-420.
- L. L. Pang, Y. H. Wang and T. G. Chen, “New Development of Traveling Wave Induction Heating,” IEEE Transactions on Applied Superconductivity, vol. 20, no. 3, 2010, pp. 1013-1016.
- T. Sekine, H. Tomita, S. Obata and Y. Saito, “An Induction Heating Method with Traveling Magnetic Field for Long Structure Metal,” Electrical Engineering in Japan, vol. 168, no. 4, 2009, pp. 32-39.
- E. Carrillo, M. Barron and J. Gonzalez, “Modeling of the Circuit Parameters of an Induction Device for Heating of a Non-Magnetic Conducting Cylinder by Means of a Traveling Wave as an Excitation Source,” in Proceedings of 2nd International Conference on Electrical & Electronics Engineering, Mexico City, 7-9 September 2005, pp. 258-261.
- X. M. Yang, T. J. Cui and Q. Cheng, “Circuit Representation of Isotropic Chiral Media,” IEEE Transactions on Antennas & Propagation, vol. 55, no. 10, 2007, pp. 2754- 2760.
- A. C. Boucouvalas, “Wave Propagation in Biaxial Planar Waveguides Using Equivalent Circuit in Laplace Space,” Proceedings of 1995 UK Performance Engineering of Computer & Telecommunication Systems, Liverpool, 5-6 September 1995, pp. 258-266.
- H. Oraizi and M. Afsahi, “Analysis of Planar Dielectric Multilayers as FSS by Transmission Line Transfer Matrix Method (TLTMM),” Progress in Electromagnetics Research, Vol. 74, 2007, pp. 217-240.
- E. M. Freeman, “Traveling Waves in Induction Machines: Input Impedance and Equivalent Circuits,” IEE Proceedings, vol. 115, no. 12, 1968, pp. 1772-1776.
- E. M. Freeman and B. E. Smith, “Surface Impedance Method Applied to Multilayer Cylindrical Induction Devices with Circumferential Exciting Currents,” IEE Proceedings, vol. 117, no. 10, 1970, pp. 2012-2013.
- J. H. Alwash, A. D. Mohssen and A. S. Abdi, “Helical Motion Tubular Induction Motor,” IEEE Transactions on Energy Conversion, vol. 18, no. 3, 2003, pp. 362-396.
- N. R. Stansel, “Induction Heating,” McGraw-Hill, New York, 1949.
- S. J. Salon, “Finite Element Analysis of Electrical Machines,” Kluwer Academic Publishers, Boston, 1995.

