Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 4 (2010) , Article ID: 1672 , 10 pages DOI:10.4236/jemaa.2010.24028
Radiation Characteristics of Antennas on the Reactive Impedance Surface of a Circular Cylinder Providing Reduced Coupling
![]()
1Department of Electrical Engineering, University of Douala (Ecole Normale Supérieure d`Enseignement Technique) Douala, Cameroon; 2Center for Computational Nanosciences, Department of Physics and Astronomy, Ball State University, Muncie, USA.
Email: jessibencm@yahoo.fr, erhedin@bsu.edu, ysjoe@bsu.edu
Received December 16th, 2009; revised January 18th, 2010; accepted January 22nd, 2010.
Keywords: Decoupling, Radiation, Reactive Impedance Structure
ABSTRACT
The radiation characteristics of waveguide antennas located on the surface of a circular cylinder are investigated theoretically and numerically. A reactive impedance structure is used to provide reduced coupling between two antennas on the surface of a cylinder. Using the moment method, a solution to the problem of the radiation of a single and two parallel-plate waveguides located on the surface of a reactive impedance cylinder is derived. The influence of the reactive impedance structure on the coefficient of standing waves, the radiation patterns, and the decoupling between antennas is studied.
1. Introduction
In radio engineering, a group of near-omnidirectional antenna radiators having a common flange, such as an open end of the waveguide (or aperture), are widely used. In practice it is often required to limit the coupling between the receiving and transmitting antennas located on the same surface at a small distance from each other.
The known methods of decreasing interaction between antennas utilize the alteration of amplitude and phase distribution on some surfaces. Among accepted measures to decrease coupling between antennas are mutual shielding of antennas and deposition of additional screens (or shields) across the line of connection. In the case with near-omnidirectional antennas, two groups of additional measures are applied: radio-absorbing materials and surface decoupling devices.
As the review of a number of articles [1-8] shows, the most widespread and successful way of solving the problem of coupling antenna devices is the use of reactive impedance structures, specifically corrugated structures. The most widespread type of decoupling structure is a metallic structure with a rectangular cut of corrugations. It has been shown that the value of decoupling generally depends on electrical and geometrical parameters of the reactive impedance structures [9-12]. However, solving the problem of optimum placement of the decoupling device using this approach is impossible [9]. In [9,11], the authors used corrugated structures with different depths of corrugations. The waveguide antennas discussed in [9] are on the surface of a cylinder, and in [11] they are located on a plane. For each case, it has been shown that the coupling coefficient was reduced in the presence of a corrugated structure. The planar structure, however, more seriously influences the radiation pattern of the antenna which is near to the structure. [10] reviews different structures for reducing the coupling between antennas. Through the method of integral equations it is shown that the decoupling properties of the structure are determined only by the structure’s length and in fact do not depend on the periodicity of the structure. In addition, it is shown that the weakening of coupling between antennas in a wide range of frequencies can be obtained to a larger extent on convex surfaces than on flat ones [10]. The change of the coupling value is sufficiently influenced by areas located near the antennas and by the degree of the decoupling, which is defined by the maximum rate of change of surface reactive impedance [11]. The authors of [12] consider engineering techniques of evaluating reduced coupling between near-omnidirectional slot antennas located on the surface of a model object, which consists of a circular cylinder and a rectangular plate. The calculations showed an effective means of obtaining the required reduction in spatial coupling is the correct choice of mutual placement and orientation of the antennas, which should be taken into account when designing the system.
This paper explores in detail the problem of mutual coupling between two antennas located on the surface of a circular cylinder separated by a corrugated structure with constant depth of corrugation. We will present a strict solution to the problem of the analysis of the radiation characteristics of a single antenna in the shape of the open end of a parallel-plate waveguide. Unique to our work is that we solve the problem in the presence of a second waveguide antenna. First, we study the radiation pattern and the dependence of the coefficients of standing waves on the value of the constant reactive impedance of a single waveguide located on the surface of a circular cylinder. We also present the decoupling coefficient in the presence and in the absence of the reactive surface impedance. These are novel contributions of this study. Second, we consider reduced coupling between two waveguide antennas where the presence of two antennas leads to distortion of their radiation patterns. In this system, we show that the presence of capacitive impedance almost completely eliminates distortions in their radiation patterns made by the receiving antenna. Hence, the radiation pattern of both antennas coincides with that of a single antenna with a reactive impedance flange. The presentation of radiation patterns for single and double antennas with and without impedance flanges for the cylindrical configuration with a corrugated decoupling structure is original to our work. We show that the presence of capacitive impedance nearly eliminates distortions caused by the proximity of the receiving antenna. While independent verification of the validity of our specific numerical results is not available, as this is original work, references cited earlier show similar results for similar waveguide systems which support our conclusions.
The paper is organized as follows: In Section 2, a solution to the problem of the radiation of a parallel-plate waveguide located on the surface of a reactive impedance cylinder is derived. Next, Section 3 considers a solution to the problem of the reduction in coupling between two waveguide antennas located on the surface of a reactive impedance cylinder and presents the formula of some key parameters of antennas. In Section 4, the numerical results for the decoupling coefficients and radiation patterns for both single and double waveguide antennas on the surface of a circular cylinder are presented. Finally, Section 5 is devoted to conclusions.
2. Radiation of a Cylindrical Waveguide
2.1 Statement of the Problem
First of all, we try to find a solution to the twodimensional problem of electromagnetic field (EMF) radiation from the open end of a parallel-plate waveguide located on the surface of a reactive impedance cylinder (r=R) shown in Figure 1. The waveguide has width, a, and spans between angles 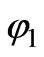 and
and  on the curved surface of the conductor. We will calculate the EMF as a function of radius, r, and azimuthal angle,
on the curved surface of the conductor. We will calculate the EMF as a function of radius, r, and azimuthal angle, . To solve for the EMF in the waveguide, its aperture, and in the free space outside of the cylindrical surface, we assume a certain excitation wave within the waveguide, and impedance boundary conditions on the surface of the cylinder between the openings of the transmitting and receiving waveguides. Then we make use of the Lorentz lemma and assume subsidiary field sources in each space. We then obtain integral correlations for the fields in each space. A system of integral equations results, which can be transformed into a system of linear algebraic equations that are solved for the field components by advanced numerical techniques, as explained in detail below.
. To solve for the EMF in the waveguide, its aperture, and in the free space outside of the cylindrical surface, we assume a certain excitation wave within the waveguide, and impedance boundary conditions on the surface of the cylinder between the openings of the transmitting and receiving waveguides. Then we make use of the Lorentz lemma and assume subsidiary field sources in each space. We then obtain integral correlations for the fields in each space. A system of integral equations results, which can be transformed into a system of linear algebraic equations that are solved for the field components by advanced numerical techniques, as explained in detail below.
Let the parallel-plate waveguide be excited by a wave characterized by  and
and :
:
 and
and 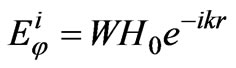
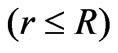 (1)
(1)
where 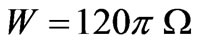 is the characteristic resistance of free space,
is the characteristic resistance of free space, 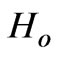 is the amplitude of the incident wave,
is the amplitude of the incident wave,

Figure 1. The open end of a single waveguide antenna located on the surface of a circular cylinder
and 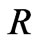 is the radius of the cylinder. On the surface
is the radius of the cylinder. On the surface 
 the following reactive impedance boundary conditions are fulfilled:
the following reactive impedance boundary conditions are fulfilled:
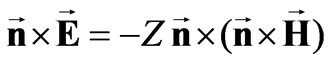 and
and (2)
(2)
where 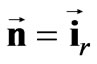 is the unit normal to the surface of the cylinder (
is the unit normal to the surface of the cylinder (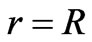 ),
), is the surface reactive impedance, and
is the surface reactive impedance, and 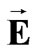 and
and are the electric and magnetic fields, respectively.
are the electric and magnetic fields, respectively.
Next, we determine the EMF in the regions both outside of the cylinder (space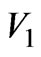 ) and inside the radiating waveguide (space
) and inside the radiating waveguide (space ). Then, we calculate the coefficient of standing waves (CSW) of the transmitting antenna and the radiation pattern of such an antenna (see Section 3).
). Then, we calculate the coefficient of standing waves (CSW) of the transmitting antenna and the radiation pattern of such an antenna (see Section 3).
2.2 Solution of the Problem
In order to solve for the EMF’s, it is necessary to use the Lorentz lemma in integral form [13], where constant pre-factors are omitted:
 (3)
(3)
where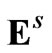 and
and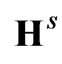 are vectors of the intensity of the electric and magnetic fields of subsidiary sources in volumes;
are vectors of the intensity of the electric and magnetic fields of subsidiary sources in volumes; 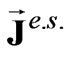 and
and 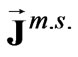 are complex amplitudes of current densities of the subsidiary electric and magnetic sources in volumes;
are complex amplitudes of current densities of the subsidiary electric and magnetic sources in volumes;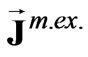 and
and are amplitudes of linear current densities of adjacent source threads. In accordance with the stated polarization of the radiated field, Equation (2), as subsidiary sources in spaces V1 and V2, we choose a current thread in phase with the magnetic current parallel to the z-axis:
are amplitudes of linear current densities of adjacent source threads. In accordance with the stated polarization of the radiated field, Equation (2), as subsidiary sources in spaces V1 and V2, we choose a current thread in phase with the magnetic current parallel to the z-axis:
 and
and 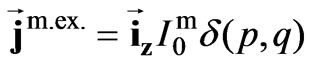 (4)
(4)
where 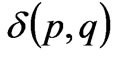 is a two-dimensional delta-function, p is the point of observation, q is the point of integration, and
is a two-dimensional delta-function, p is the point of observation, q is the point of integration, and  is the current amplitude. To simplify the solution of the problem in the integral correlation, we impose boundary conditions on the subsidiary fields which arise from the subsidiary sources:
is the current amplitude. To simplify the solution of the problem in the integral correlation, we impose boundary conditions on the subsidiary fields which arise from the subsidiary sources:
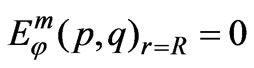 (5)
(5)
This standard boundary condition states that the tangential component of the subsidiary electric field on the curved cylindrical surface is zero.
2.3 Integral Correlations for Space V1
We now consider integral correlations for each of the spaces shown in Figure 1. By placing a subsidiary source at the point 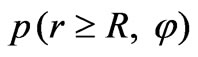 and taking into account boundary conditions in the Lorentz lemma of Equation (3), we obtain
and taking into account boundary conditions in the Lorentz lemma of Equation (3), we obtain
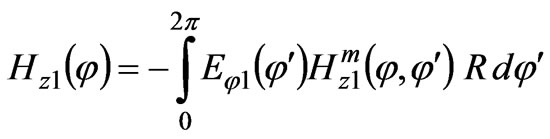 (6)
(6)
where 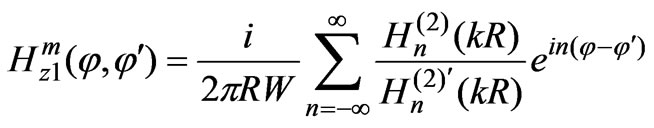 is the subsidiary magnetic field on the surface of an ideal conducting cylinder. Here,
is the subsidiary magnetic field on the surface of an ideal conducting cylinder. Here,  is the imaginary operator,
is the imaginary operator, 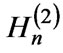 is the
is the  -order Hankel function of the second kind, and
-order Hankel function of the second kind, and 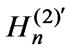 is its derivative. In Equation (6), there are two unknown values: Eφ1 and Hz1 are the fields of the threads of the electric and magnetic currents in free space, respectively. In order to eventually solve for them, two more equations are required. These come from the Lorentz lemma in the space V2 and the subsequent coupling between the waveguides (Section 3).
is its derivative. In Equation (6), there are two unknown values: Eφ1 and Hz1 are the fields of the threads of the electric and magnetic currents in free space, respectively. In order to eventually solve for them, two more equations are required. These come from the Lorentz lemma in the space V2 and the subsequent coupling between the waveguides (Section 3).
2.4 Lorentz Lemma for Space V2
The subsidiary magnetic field in the space V2 that is produced on an aperture of a cylindrical waveguide is obtained from the Lorentz lemma of Equation (3). By imposing boundary conditions on the tangential component of the subsidiary electric field vector at the walls of the parallel-plate waveguide and on its aperture , we obtain an integral correlation for the EMF inside the waveguide V2:
, we obtain an integral correlation for the EMF inside the waveguide V2:
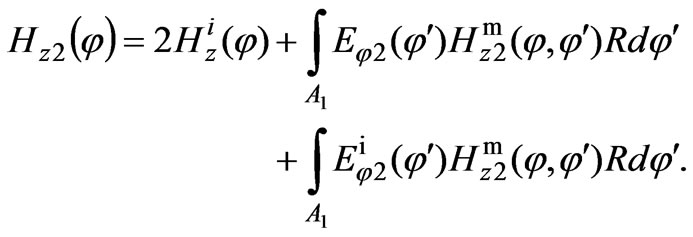 (7)
(7)
The field in the aperture of the waveguide is then written as the following correlation:
 (8)
(8)
where the field of the subsidiary source can be written as
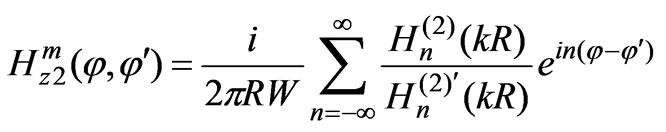 (9)
(9)
3. Reduced Coupling of Two Cylindrical Waveguides
Let us now consider the problem of reducing the coupling between two parallel-plate waveguide antennas located on the surface of the reactive impedance cylinder. In Figure 2, we show two aperture antennas with opening sizes of a and b which are located on the surface of a reactive impedance cylinder (r = R). These two antennas (transmitting and receiving ones), which have the shape of the open end of parallel-plate waveguides, are separated by distance L from each other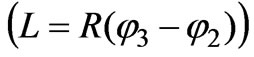 . The boundary conditions, stated in Equation (2), exist on the surface
. The boundary conditions, stated in Equation (2), exist on the surface 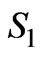 (
(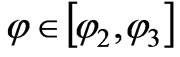 and
and ) which separates two antennas. Because another waveguide with an opening of size b is added, one more equation (relative to the field in the opening of the receiving waveguide) is included in the system of integral equations. In addition, we need to determine the field in the receiving waveguide (space V3), the radiation patterns, and the decoupling coefficient.
) which separates two antennas. Because another waveguide with an opening of size b is added, one more equation (relative to the field in the opening of the receiving waveguide) is included in the system of integral equations. In addition, we need to determine the field in the receiving waveguide (space V3), the radiation patterns, and the decoupling coefficient.
3.1 Integral Correlations for Space V3
To solve this problem, we use the same integral form of the Lorentz lemma. In this space, V3, the lemma is different from Equation (8) only in the absence of additional sources and by the size of the opening of V3:
 (10)
(10)
where 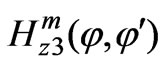 is the subsidiary magnetic field in the space V3.
is the subsidiary magnetic field in the space V3.
3.2 System of Integral Equations
By taking into account the boundary conditions of Equation
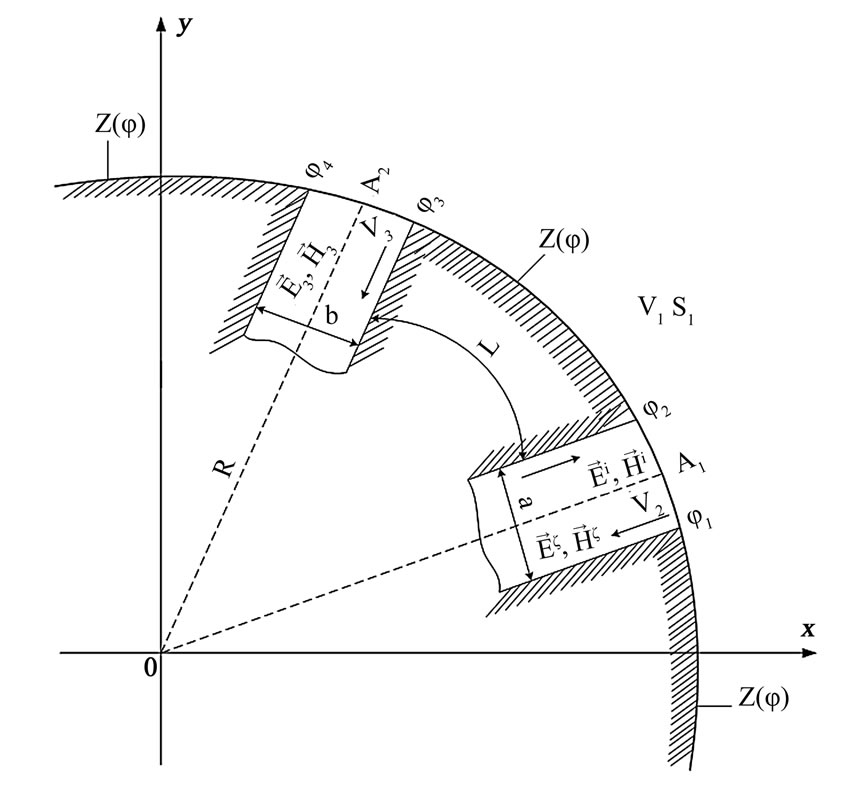
Figure 2. Geometry of the structure with two parallel-plate waveguide antennas located on the surface of the reactive impedance cylinder
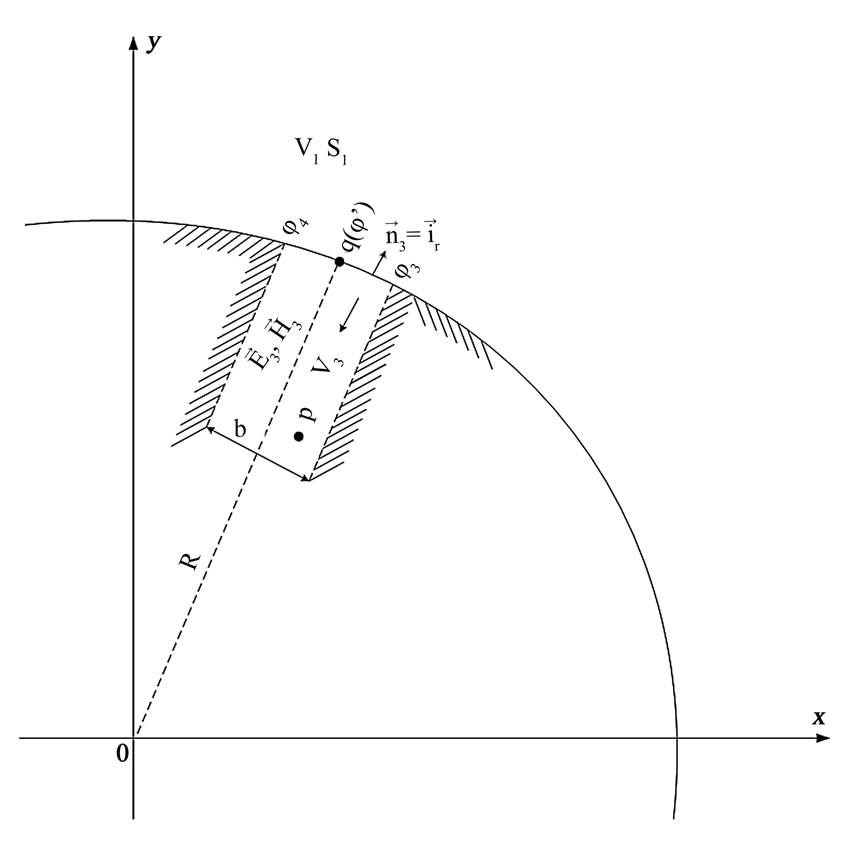
Figure 3. the open end of a waveguide located on the surface of a circular cylinder for space V3
(2) on the surface of the reactive impedance flange and the equality of the tangential components of the EMF in the openings of the waveguides (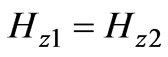 ,
,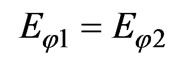 when
when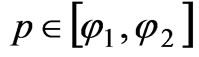 and
and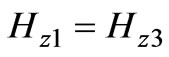 ,
,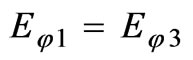 when
when ), we obtain a system of integral equations relative to the unknown tangential component of the electric field
), we obtain a system of integral equations relative to the unknown tangential component of the electric field  on the surface of the cylinder
on the surface of the cylinder 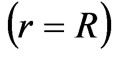 (see Figure 3):
(see Figure 3):
 (11)
(11)
where the subsidiary magnetic fields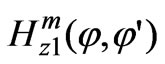 ,
, 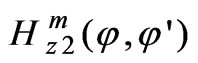 and
and 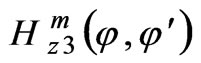 are solutions to the non-uniform Helmholtz equations for the complex amplitudes of the field vectors for regions V1, V2, and V3, respectively.
are solutions to the non-uniform Helmholtz equations for the complex amplitudes of the field vectors for regions V1, V2, and V3, respectively.
In calculating the subsidiary fields in the spaces V2 and V3, it is assumed that they have a rectangular shape, short-circuited in the openings of the ideally flat conducting wall. The apertures of the antennas coincide with these walls. In this case, the subsidiary fields in Equation (11) are defined by the following correlations:
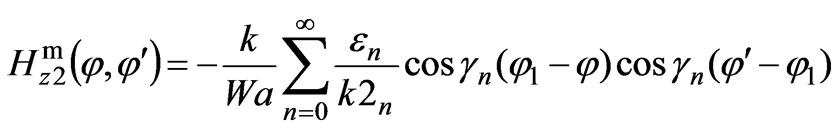
 (12)
(12)
where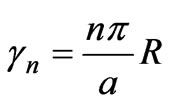 ,
,  ,
, 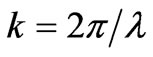 is the wave number, and λ is the wavelength. Also,
is the wave number, and λ is the wavelength. Also,
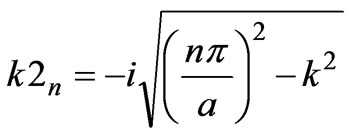 ,
,  , and the dielectric permittivity of the
, and the dielectric permittivity of the  layer is given by
layer is given by
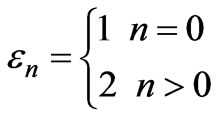 .
.
The required solution has a specific feature at the edges of the structure 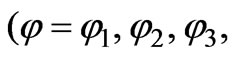 and
and . It is taken into account by inserting a new unknown weighting parameter,
. It is taken into account by inserting a new unknown weighting parameter, 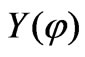 , which has the same specific feature as the function required in the system of integral equations in Equation (11):
, which has the same specific feature as the function required in the system of integral equations in Equation (11):
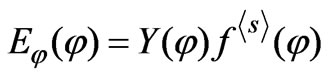 (13)
(13)
where
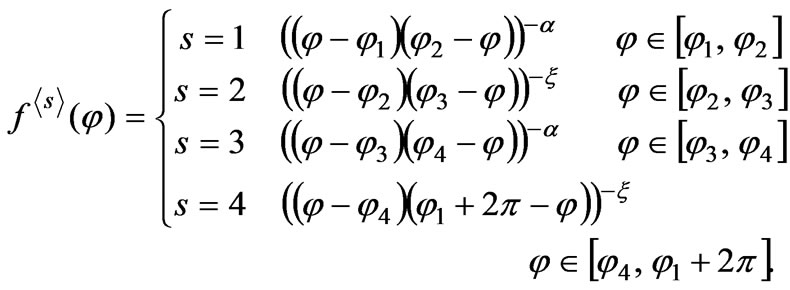 (14)
(14)
By solving the integral equations using the KrylovBogolyubov method [14] and calculating the coefficients of the matrix in a system of linear algebraic equations, the subsidiary field given in Equation (9) can be rewritten as (see Appendix A)
 (15)
(15)
where we take into account the decomposition of the Hankel function into the Bessel series (addition theorem of cylindrical functions). Here, Jn is the Bessel function of order n and 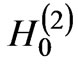 is the second kind of the zero-order Hankel function. Therefore, the fields in the opening of antennas and on the reactive impedance part of the flange are found. In the following section, formulas for key parameters of the antennas are given in terms integral correlations involving the field components which have all been obtained.
is the second kind of the zero-order Hankel function. Therefore, the fields in the opening of antennas and on the reactive impedance part of the flange are found. In the following section, formulas for key parameters of the antennas are given in terms integral correlations involving the field components which have all been obtained.
3.3 Key Parameters of Antennas
The expressions for the coefficient of standing waves in the transmitting antenna, the EMF power directed into the receiving antenna, and the coefficient of coupling 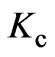 between antennas are defined by the same correlations as in [15] with only a substitution of the components of the Cartesian coordinate system for those of the cylindrical coordinate system.
between antennas are defined by the same correlations as in [15] with only a substitution of the components of the Cartesian coordinate system for those of the cylindrical coordinate system.
• The amplitude of the reflected wave of main type 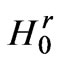 in the active waveguide
in the active waveguide 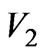 is defined by the following correlation:
is defined by the following correlation:
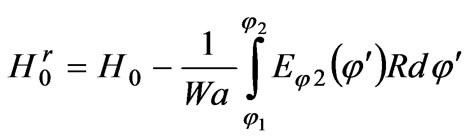 (16)
(16)
• The expression for the coefficient of standing waves is
 (17)
(17)
where 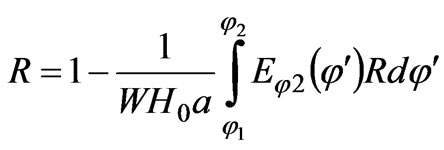 is the coefficient of reflection.
is the coefficient of reflection.
• The power of the field acquired by the antenna 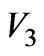 is
is  (18)
(18)
• The coefficient of coupling between antennas is defined by
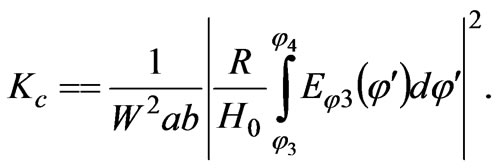 (19)
(19)
The decoupling coefficient K, which is the inverse value of , is defined as
, is defined as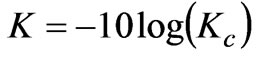 .
.
• The radiation pattern of antenna 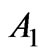 can be found from the integral correlation of Equation (6), where
can be found from the integral correlation of Equation (6), where  is already obtained from the solution of SLAE in Equation (A-1). In this process, it is required to move the point of observation P to infinity and to use the asymptote of the Hankel function with a significant argument [
is already obtained from the solution of SLAE in Equation (A-1). In this process, it is required to move the point of observation P to infinity and to use the asymptote of the Hankel function with a significant argument [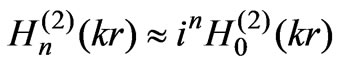 ]. As a result, we obtain
]. As a result, we obtain
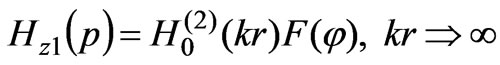 (20)
(20)
where 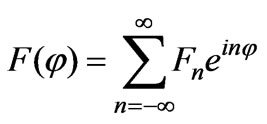 is the radiation pattern of antenna
is the radiation pattern of antenna ,and
,and
 are the coefficients of the decomposition of the radiation pattern into a complex Fourier series. We notice here that the radiation patterns of both antennas can be calculated at once in the mode of reception by solving the problem of cylinder excitation by a flat wave.
are the coefficients of the decomposition of the radiation pattern into a complex Fourier series. We notice here that the radiation patterns of both antennas can be calculated at once in the mode of reception by solving the problem of cylinder excitation by a flat wave.
4. Numerical Results and Discussion
4.1 Radiation of a Single Parallel-Plate Waveguide
The surface impedance 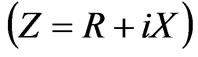 has an inductive character when
has an inductive character when 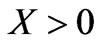 and a capacitive character when
and a capacitive character when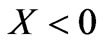 . For the systems of interest, the reactive impedance is purely reactive
. For the systems of interest, the reactive impedance is purely reactive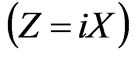 . Figure 4 shows the dependences of the CSW on the value of the constant reactive impedance
. Figure 4 shows the dependences of the CSW on the value of the constant reactive impedance  of the waveguide located on the surface of a circular cylinder with radius
of the waveguide located on the surface of a circular cylinder with radius 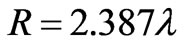
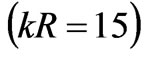 . The sizes of the openings of waveguides are (a)
. The sizes of the openings of waveguides are (a) 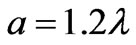 and (b)
and (b)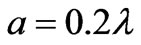 , respectively. When the size of opening decreases, the magnitude of CSW increases by a factor of 4.5 (from Figure 4(b) to Figure 4(a)). The least value of CSW for all sizes of antennas on cylinders is found with purely reactive impedance of inductive character
, respectively. When the size of opening decreases, the magnitude of CSW increases by a factor of 4.5 (from Figure 4(b) to Figure 4(a)). The least value of CSW for all sizes of antennas on cylinders is found with purely reactive impedance of inductive character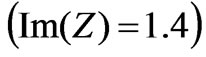 . We notice that use of the reactive impedance distribution on the surface of a cylinder (on a curved flange) leads to a significant increase of CSW. Furthermore, in the case of a cylinder with all circumstances equal, the influence of reactive impedance turns out to be less than in the plane case.
. We notice that use of the reactive impedance distribution on the surface of a cylinder (on a curved flange) leads to a significant increase of CSW. Furthermore, in the case of a cylinder with all circumstances equal, the influence of reactive impedance turns out to be less than in the plane case.
We present the radiation pattern of a single waveguide antenna on a circular cylinder of radius 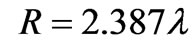 with ideal conducting flange (Z=0: dotted line) and capacitive flange (
with ideal conducting flange (Z=0: dotted line) and capacitive flange (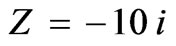 : solid line) in Figure 5. The size of the aperture is
: solid line) in Figure 5. The size of the aperture is 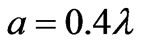 (
(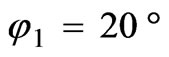 and
and ). The dash-dotted line shows the impact of the reactive impedance part of the flange on the radiation pattern. As we can see, the capacitive impedance really distorts (or wrings out) the wave, increasing the directivity of the antenna. The dashed line represents the geome-
). The dash-dotted line shows the impact of the reactive impedance part of the flange on the radiation pattern. As we can see, the capacitive impedance really distorts (or wrings out) the wave, increasing the directivity of the antenna. The dashed line represents the geome-
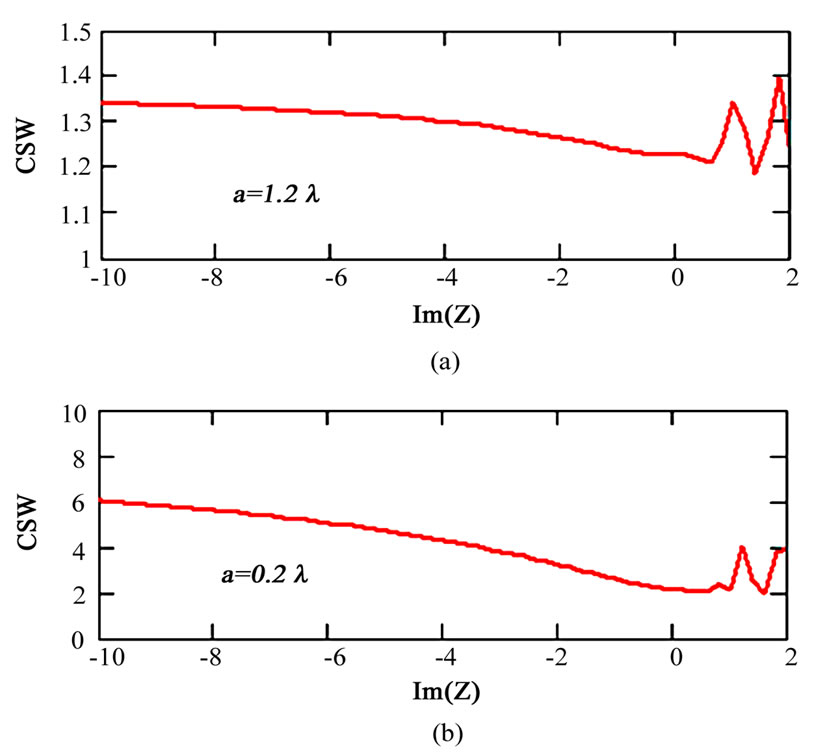
Figure 4. (Color online) The CSW as a function of the constant reactive impedance  of the waveguide located on the surface of a circular cylinder with radius
of the waveguide located on the surface of a circular cylinder with radius 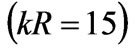
 for (a)
for (a) 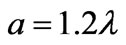 and (b)
and (b) . An increase in the size of opening leads to a decrease of CSW.
. An increase in the size of opening leads to a decrease of CSW.

Figure 5. (Color online) Radiation pattern of a single waveguide antenna on a circular cylinder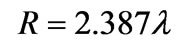 with an ideal conducting flange (
with an ideal conducting flange ( : dotted line) and capacitive flange (
: dotted line) and capacitive flange (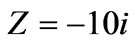 : solid line), where the size of the aperture is equal to
: solid line), where the size of the aperture is equal to 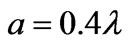 (
(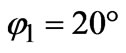 and
and ). The dash-dotted line shows the impact of the reactive impedance part of the flange on the radiation pattern. The dashed line represents the geometry of the problem
). The dash-dotted line shows the impact of the reactive impedance part of the flange on the radiation pattern. The dashed line represents the geometry of the problem
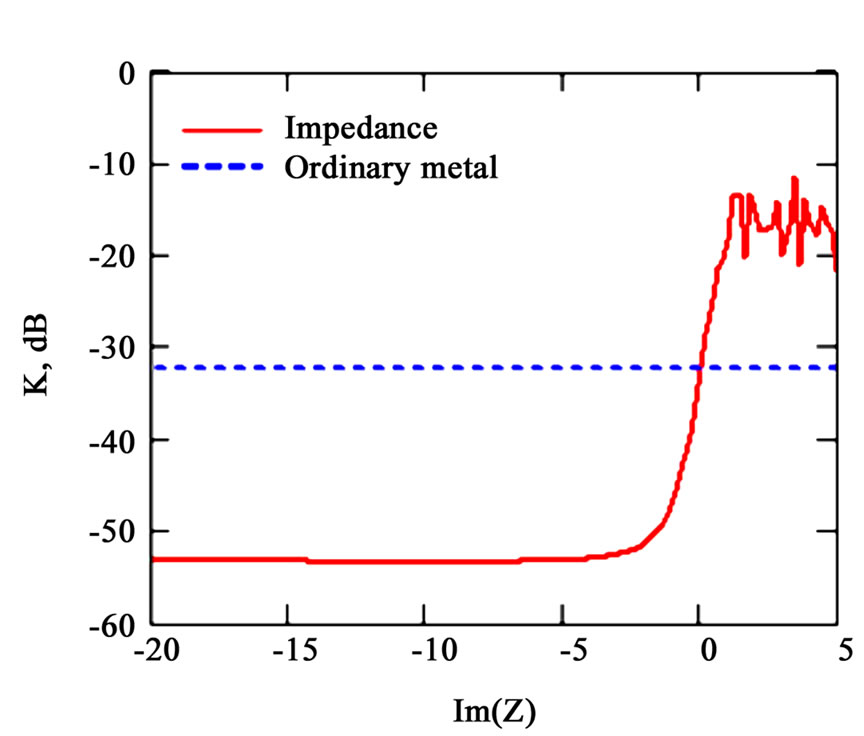
Figure 6. (Color online) Decoupling coefficient 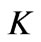 as a function of reactivity,
as a function of reactivity, 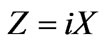 (solid line) with parameters
(solid line) with parameters , and
, and . The dashed line corresponds to the decoupling of the antennas on the surface of an ideal conducting cylinder
. The dashed line corresponds to the decoupling of the antennas on the surface of an ideal conducting cylinder
try of the problem (location and relative sizes of the opening of the radiating antenna).
4.2 Radiation of Two Waveguide Antennas
Now, we study the decoupling coefficients and radiation patterns in the two waveguide antennas on the surface of a circular cylinder. Figure 6 shows the dependence of the decoupling coefficient K on the value of the reactivity of the normalized reactive impedance of the cylindrical flange 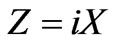 (solid line) with parameters
(solid line) with parameters 
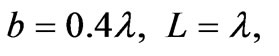 and
and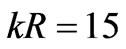 . The dashed line corresponds to the decoupling of antennas on the surface of an ideal conducting cylinder. Numerical studies show that the behavior of the decoupling coefficient for the cylindrical construction is almost the same as the plane case (see Figure 8 in [15]). The only exception is that for the cylindrical medium the decoupling of the antennas is higher by 10 dB because of additional screening by the convex surface. In addition, the maximum value (
. The dashed line corresponds to the decoupling of antennas on the surface of an ideal conducting cylinder. Numerical studies show that the behavior of the decoupling coefficient for the cylindrical construction is almost the same as the plane case (see Figure 8 in [15]). The only exception is that for the cylindrical medium the decoupling of the antennas is higher by 10 dB because of additional screening by the convex surface. In addition, the maximum value (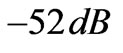 ) of the decoupling level is reached with a large value of capacitive impedance (
) of the decoupling level is reached with a large value of capacitive impedance (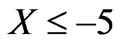 ).
).
In order to examine the variation of the decoupling level, we consider a corrugated structure in vacuum with a constant depth of corrugation d on the cylindrical surface shown in the inset of Figure 7. The decoupling coefficient K as a function of the normalized depth 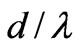 in this structure is plotted in Figure 7 as a solid line. The maximum level of decoupling (
in this structure is plotted in Figure 7 as a solid line. The maximum level of decoupling (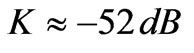 when
when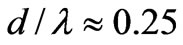 ) is increased by 10 dB more in comparison with the plane case [15]. The reason is that with the cy-
) is increased by 10 dB more in comparison with the plane case [15]. The reason is that with the cy-
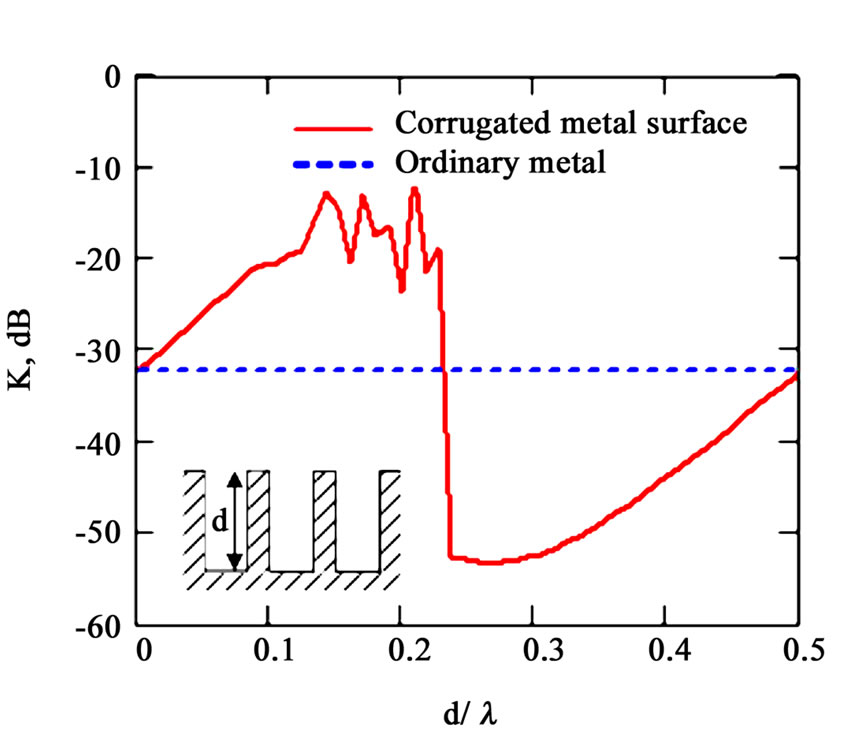
Figure 7. (Color online) Decoupling coefficient  versus the normalized depth
versus the normalized depth  for a corrugated structure in vacuum (solid line). The dotted line corresponds to the decoupling of antennas on the surface of an ideal conducting cylinder
for a corrugated structure in vacuum (solid line). The dotted line corresponds to the decoupling of antennas on the surface of an ideal conducting cylinder
lindrical surface, increasing the distance between the antennas also increases the screening by means of a surface shadowing. The constant decoupling level K for an ideal conducting cylindrical surface is shown as a dotted line.
Next, we investigate a modulation of the separation between two antennas on the surface of a circular cylinder in order to see how the decoupling level of antennas changes. In Figure 8, we show the dependence of the decoupling coefficient K on the surface reactive impedance 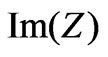 for the same antennas as in Figures 6 and 7 (
for the same antennas as in Figures 6 and 7 (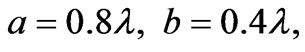 and
and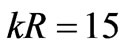 ), but located at the two different distances of (a)
), but located at the two different distances of (a) 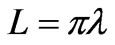 and (b)
and (b)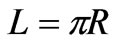 . When the distance between two antennas is
. When the distance between two antennas is , which corresponds to an angular distance of
, which corresponds to an angular distance of  between the centers of their openings, constant reactance causes an additional increase of the decoupling up to -84 dB (solid line) in Figure 8(a). The decoupling of antennas on the surface of an ideal conducting cylinder (dotted line) is also large (K= -46 dB) in comparison with the plane case. It is evident from Figure 8(b) that the maximum decoupling corresponds with a diametrical arrangement of antennas at
between the centers of their openings, constant reactance causes an additional increase of the decoupling up to -84 dB (solid line) in Figure 8(a). The decoupling of antennas on the surface of an ideal conducting cylinder (dotted line) is also large (K= -46 dB) in comparison with the plane case. It is evident from Figure 8(b) that the maximum decoupling corresponds with a diametrical arrangement of antennas at  (i.e., the angle between the centers of their openings is approximately equal to 180o). It is noteworthy to mention that independent of the location of antennas, negative reactance leads to an increase of decoupling. In addition, the greater the distance between antennas, the higher the decoupling level. As for the cylinder, due to the finite nature of this distance (diametrically placed antennas are located at the maximum distance), the decoupling level is always limited.
(i.e., the angle between the centers of their openings is approximately equal to 180o). It is noteworthy to mention that independent of the location of antennas, negative reactance leads to an increase of decoupling. In addition, the greater the distance between antennas, the higher the decoupling level. As for the cylinder, due to the finite nature of this distance (diametrically placed antennas are located at the maximum distance), the decoupling level is always limited.
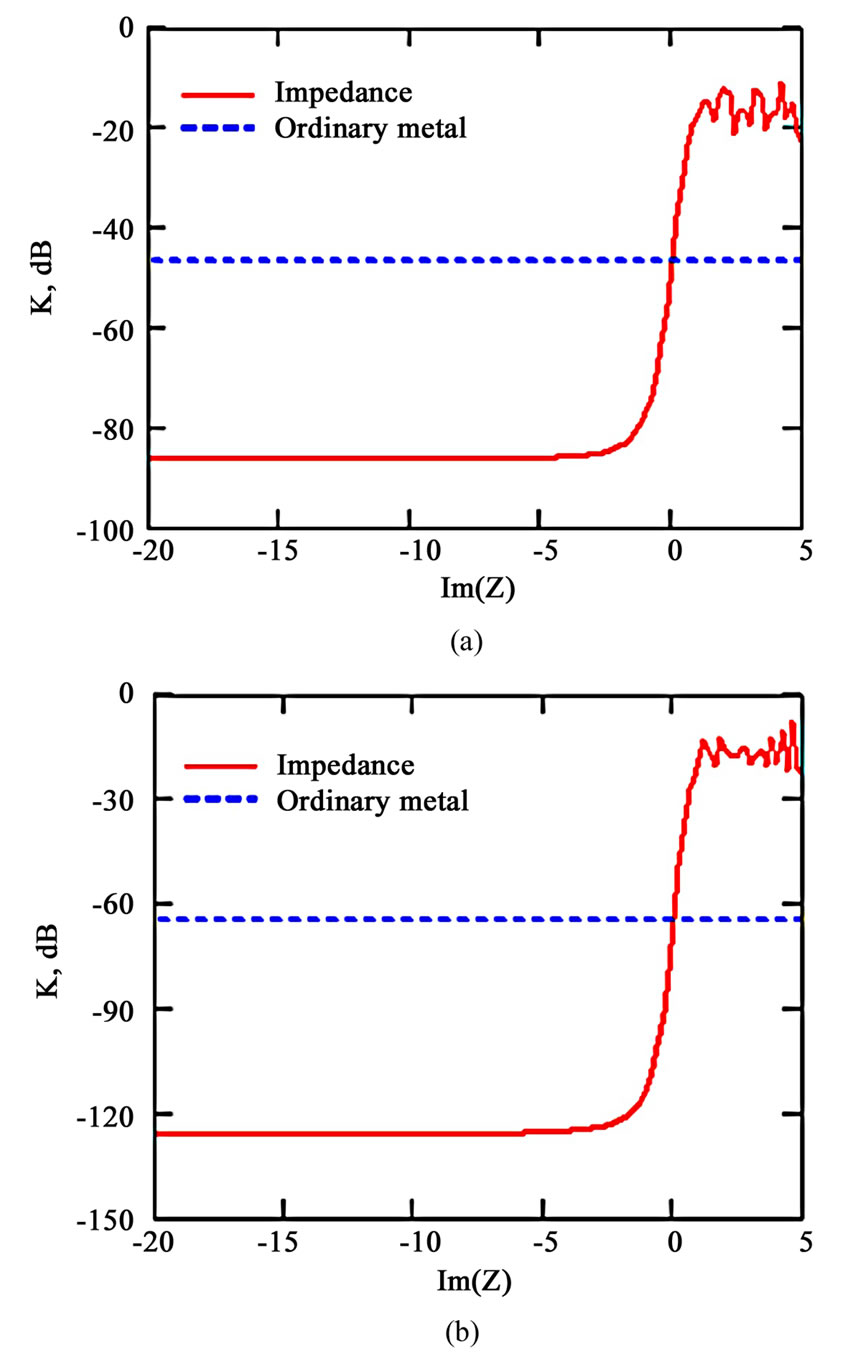
Figure 8. (Color online) (a) Decoupling coefficient 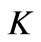 as a function of the surface reactive impedance
as a function of the surface reactive impedance  for the same antennas as in Figures 6 and 7, but located at the two different distances of (a)
for the same antennas as in Figures 6 and 7, but located at the two different distances of (a) 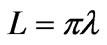 (an angular distance of
(an angular distance of 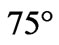 between the centers of their openings) and (b)
between the centers of their openings) and (b) 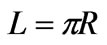 (the angle between the centers of their openings is approximately equal to
(the angle between the centers of their openings is approximately equal to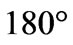 ). The decoupling of antennas on the surface of an ideal conducting cylinder is shown as a dotted line
). The decoupling of antennas on the surface of an ideal conducting cylinder is shown as a dotted line
The radiation patterns of a system which has both the transmitting antenna A1 and the receiving antenna A2 are presented in Figure 9, where the parameters of the system are defined as ,
, 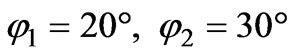 for
for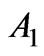 ,
,  ,
, 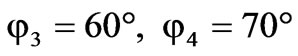 for
for , the radius of a circular cylinder is
, the radius of a circular cylinder is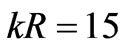 ,, and the distance between the antennas is
,, and the distance between the antennas is . The geometry of the structure is depicted as a dashed line. It is clearly seen in Figure 9 that the radiation pattern for an ideal conducting cylinder (dotted line) is distorted due to the presence of an additional antenna. (Compare to the dotted line in Figure 5). On the other hand, the radiation pattern for the capacitive impedance (solid line) is not affected by the
. The geometry of the structure is depicted as a dashed line. It is clearly seen in Figure 9 that the radiation pattern for an ideal conducting cylinder (dotted line) is distorted due to the presence of an additional antenna. (Compare to the dotted line in Figure 5). On the other hand, the radiation pattern for the capacitive impedance (solid line) is not affected by the
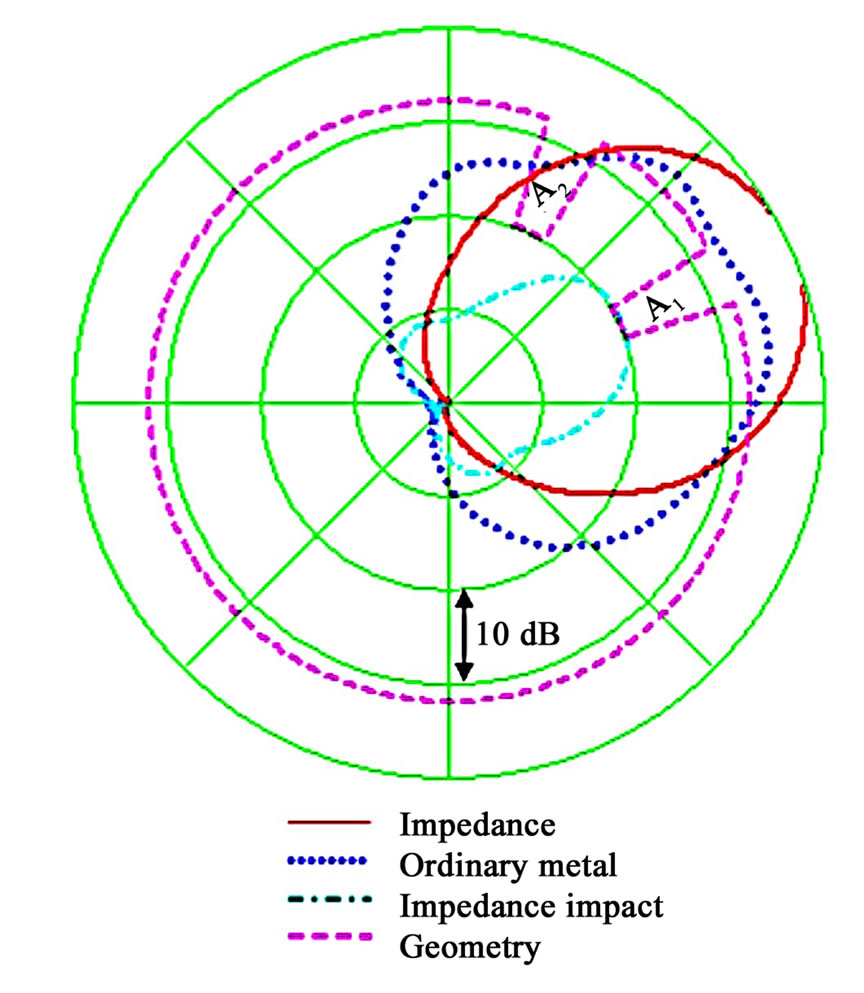
Figure 9. (Color online) Radiation patterns of the structure with the transmitting antenna  (
(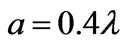 ,
,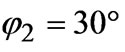
 ) and the receiving antenna
) and the receiving antenna  (
( ,
,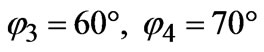 ) located on an ideal conducting cylinder (dotted line) and on the reactive impedance
) located on an ideal conducting cylinder (dotted line) and on the reactive impedance 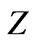 cylinder (solid line), where the radius is
cylinder (solid line), where the radius is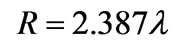 (
(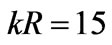 ) and the distance between the antennas is
) and the distance between the antennas is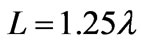 . The dashed line represents the geometry of the system
. The dashed line represents the geometry of the system
presence of a receiving antenna. Hence, the radiation pattern of both antennas coincides with that of a single antenna with a reactive impedance flange. We note that the obtained result here is in the case of frequencyindependent impedance. The undistorted radiation pattern will be modified when frequency-dependent surface impedance is used. The impact of the reactive impedance part of the flange on the radiation patterns is indicated as the dash-dotted line.
5. Conclusions
On the basis of the theoretical and numerical research conducted in this paper, we obtained several significant results. First, we calculated a strict solution to the problem of the analysis of the radiation characteristics of a single antenna in the shape of the open end of a parallel-plate waveguide located on the surface of a circular cylinder. Included in this configuration were a reactive impedance flange and a receiving antenna of the same construction; specific boundary conditions of an electric field on the edge were taken into account. Additionally, correlations for the key parameters of the antennas (CSW, radiation patterns of antennas, and the decoupling coefficient) were obtained.
We have also studied the influence of a constant, purely reactive impedance (as a mathematical model of corrugated structures) on the radiation pattern, CSW, and the decoupling level of antennas. These results were obtained with the help of numerical modeling, and coincide well with standard results [16]. A comparative evaluation of the decoupling level on a plane and on the surface of a circular cylinder was performed. A specific difference between a cylindrical surface and a flat one is that for the cylindrical case, increasing the distance between the antennas also increases their screening by means of a surface shadowing.
A study of the radiation pattern for an ideal conducting cylinder showed that the presence of two antennas leads to distortion of their radiation patterns. However, the presence of capacitive impedance almost completely eliminates distortions made by the receiving antenna. The radiation pattern of both antennas coincides with that of a single antenna with a reactive impedance flange.
In conclusion, to reach the required levels of decoupling between antennas, it is necessary to use structures with a complicated reactive impedance corrugation on the flange of the antennas, just as in the case of a plane. For this purpose, in future work we need to study further how to set up and solve the problem of the synthesis of such structures.
6. Acknowledgment
One of the authors (J.-F. D. Essiben) wishes to thank Prof. Yu. V. Yukhanov from Taganrog Institute of Technology at the Southern Federal University in Russia for helpful discussions.
REFERENCES
- N. C. Karmakar and M. N. Mollah, “Potential Applications of PBG Engineered Structures in Microwave Engineering,” Microwave Journal, Horizon House Publications, Inc, London, Vol. 47, 2004, pp. 22-44.
- A. Harvey, “Periodic and Guiding Structures at Microwave Frequencies,” IRE Transactions on Microwave Theory and Techniques, Vol. 8, June 1959, pp. 30-61.
- T. C. Rao, “Plane Wave Scattering by a Corrugated Conducting Cylinder at Oblique Incidence,” IEEE Transactions on Antennas and Propagation, Vol. 36, August 1988, pp. 1184-1188.
- G. Manara, G. Pelosi, A. Monorchio and R. Coccioli, “Plane-Wave Scattering from Cylinders with Transverse Corrugations,” Electronic Letters, Vol. 31, No. 6, March 1995, pp. 437-438.
- A. Freni, “Scattering from a Dielectric Cylinder Axially Loaded with Periodic Metallic Rings,” Proceedings on Institution of Electric and Engineering-Microwave Antennas Propagation, Vol. 143, No. 3, June 1996, pp. 233-237.
- A. Freni, C. Mias and R. L. Ferrari, “Hybrid Finite-Element Analysis of Electromagnetic Plane Wave Scattering from Axially Periodic Cylindrical Structures,” IEEE Transactions on Antennas and Propagation, Vol. 46, No. 12, December 1998, pp. 1859-1866.
- P. S. Kildal, A. A. Kishk and A. Tengs, “Reduction of forward Sscattering from Cylindrical Objects Using Hard Surfaces,” IEEE Transactions on Antennas and Propagation, Vol. 38, No. 10, October 1990, pp. 1537-1544.
- I. Short and K. M. Chen, “Backscattering from an Impedance Loaded Slotted Cylinder,” IEEE Transactions on Antennas and Propagation, Vol. 17, No. 3, May 1969, pp. 315-323.
- A. G. Kurkchan and M. K. Zimnov, “Coupling between Antennas on a Cylinder in the Presence of Corrugated Structures,” Radiotechnics and Electronics, Vol. 12, No. 9, 1985, pp. 2308-2315.
- S. Benenson and A. I. Kurkchan, “Decoupling of Antennas by Means of Periodic Structures,” Radiotechnics and Electronics, Vol. 37, No. 12, 1995, pp. 77-89.
- A. G. Kurkchan, “Coupling between Antennas in the Presence of Corrugated Structures,” Radiotechnics and Electronics, Vol. 22, No. 7, 1977, pp. 1362-1373.
- K. K. Belostotskaya, M. A. Vasilyev and V. M. Legkov, “Spatial Decouplings between Antennas on Big Size Solids,” Radiotechnics, No. 10, pp. 77-79, 1986.
- V. G. Koshkidko, B. M. Petrov and Y. V. Yukhanov, “Equivalent Surface Impedance of Passive Impedance Loads on the Basis of a Hole in the Screen, Loaded with a 2D Cavity,” Radiotechnics and Electronics, Vol. 42, No. 6, pp. 652-661, 1997.
- O. N. Tereshin, V. M. Sedov and A. F. Chaplin, “Synthesis of Antennas on Decelerating Structures,” Communication Press, Moscow, 1980.
- Y. S. Joe, J.-F. D. Essiben and E. M. Cooney, “Radiation Characteristics of Waveguides Antennas Located on the Same Impedance Plane,” Journal of Physics D: Applied Physics, Vol. 41, 2008.
- L. D. Bakhrakh and E. G. Zeikin, “Reference Book on Antenna Engineering,” Vol. 1, Moscow, 1997.
APPENDIX A: Calculation of Subsidiary Fields Using Integral Equation
The solution of the integral equations in Equation (11) can numerically be solved by the Krylov-Bogolyubov method [14]. As a result, the integral equation is reduced to a system of linear algebraic equations (SLAE) relative to:
 :
:
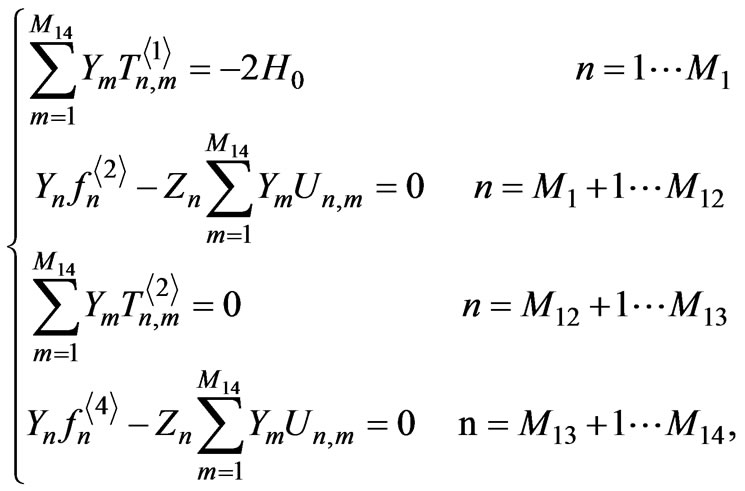 (A-1)
(A-1)
where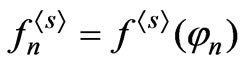 ,
,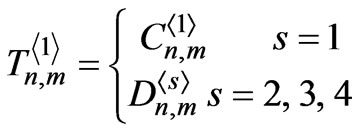 ,
,
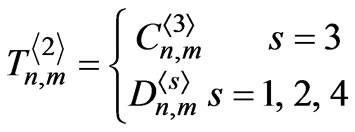 ,
, .
.
Here, 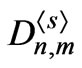 ,
,  , and
, and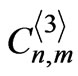 are defined respectively as follows:
are defined respectively as follows:
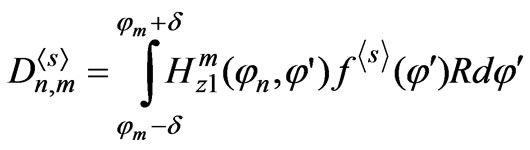 ,
,
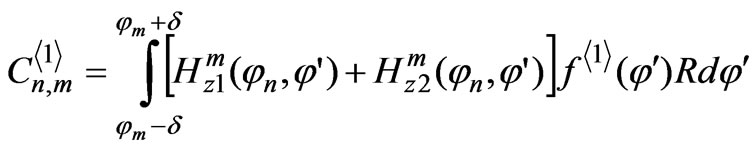 ,
,
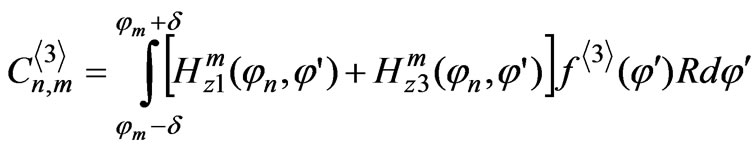 .
.
Finally, 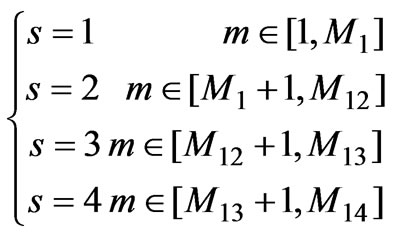
 , where
, where ,
,  ,
,  ,
, 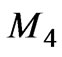 are the numbers of points of collocation on the parts
are the numbers of points of collocation on the parts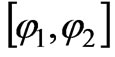 ,
, 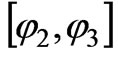 ,
,  ,
,  , and
, and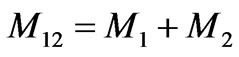 ,
, 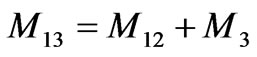 ,
,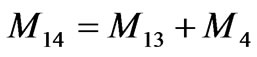 .
.
When calculating the solutions of the integral expressions and the coefficients of the matrix of SLAE in Equation (A-1), we have to consider the difficulty of their calculation near the coincidence of the points of integration and collocation , where the subsidiary fields of Equations (9) and (12) have logarithmic singularities. We observe an opportunity for improving the conformity of the rows in Equations (9) and (12). Different points (
, where the subsidiary fields of Equations (9) and (12) have logarithmic singularities. We observe an opportunity for improving the conformity of the rows in Equations (9) and (12). Different points ( ) in a row in Equation (9), which is shown below as Equation (A-2),
) in a row in Equation (9), which is shown below as Equation (A-2),
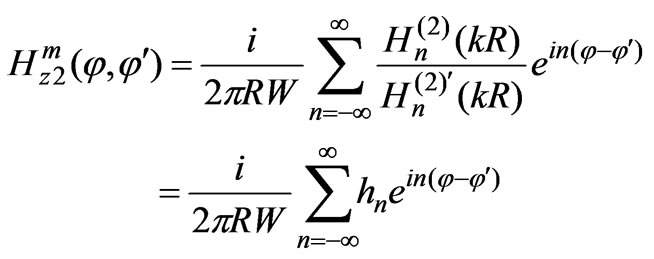 (A-2)
(A-2)
conform in an unsuitable way, because the coefficients have an asymptote
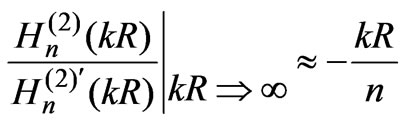 (A-3)
(A-3)
In order to improve the conformity of the row in Equation (9), we multiply the Hankel functions in Equation (9) by the Bessel function. Then, we can get asymptotes as a closed form:
 (A-4)
(A-4)
which is different from Equation (A-3) by the constant.

