International Journal of Communications, Network and System Sciences
Vol.11 No.09(2018), Article ID:87776,12 pages
10.4236/ijcns.2018.119011
On the Performance Analysis of One Tap Equalizers in Oversampled OFDM Systems
Hassan Ali1, Fahad Khan2
1School of Electrical Engineering and Computing, The University of Newcastle, Callaghan, Australia
2Department of Electrical and Computer Engineering, COMSATS University Islamabad, Abbottabad Campus, Abbottabad, Pakistan

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 18, 2018; Accepted: September 25, 2018; Published: September 28, 2018
ABSTRACT
Oversampling is commonly encountered in orthogonal frequency division multiplexing (OFDM) systems to ease various performance characteristics. In this paper, we investigate the performance and complexity of one tap zero-forcing (ZF) and minimum mean-square error (MMSE) equalizers in oversampled OFDM systems. Theoretical analysis and simulation results show that oversampling not only reduces the noise at equalizer output but also helps mitigate ill effects of spectral nulls. One tap equalizers therefore yield improved symbol-error-rate (SER) performance with the increase in oversampling rate, but at the expense of increased system bandwidth and modest complexity requirements.
Keywords:
One Tap Equalization, Oversampling, Orthogonal Frequency Division Multiplexing, Inverse Fast Fourier Transform

1. Introduction
Orthogonal frequency division multiplexing (OFDM) is an attractive multicarrier modulation technique for high data rate transmission systems [1], [2], due to high spectral efficiency, immunity to impulse noise, robustness in multipath fading environments to combat inter-symbol interference (ISI) and more importantly due to its simple one tap equalization. This modulation technique has been successfully adopted in many contemporary as well as advanced broadband communication applications [3]- [8].
Oversampling of the OFDM signal (or oversampled inverse fast Fourier transform (IFFT)) is adopted in many practical OFDM systems to enhance various performance characteristics. Oversampling is used in [9][10], to reduce the jitter noise. In [11], oversampling of the OFDM signal is suggested to approximate more accurately the peak-to-average power ratio (PAR) and therefore several PAR reduction approaches and corresponding PAR distribution studies based on oversampled OFDM signals have appeared in the literature [12][13][14]. Oversampling is also commonly practiced in OFDM systems to reduce the steepness requirements of the analogue anti-aliasing low pass filter (LPF) at the digital-to-analogue converter (DAC) [15], [16]and thus simplify the analogue filter implementation complexity. Oversampling can be implemented by using a higher length IFFT and padding zeros at the unused subcarrier positions. For example, in European DAB and in DVB-Terrestrial (DVB-T) system (EN300401 2001a; EN300744 2001b), an IFFT of length 2048 is used and the number of modulated carriers is of the order of ≈1500 and ≈1700, respectively, while the rest of the data at the remaining carriers is set to zero. Since oversampling increases the total number of carriers due to increased IFFT length, sidelobes of OFDM spectrum therefore show a steeper decay and closer to the rectangular shape. Therefore, another purpose of oversampling in OFDM is to achieve spectral compactness [17]. While above applications of oversampling seem to ignore its effect at the receiver side, several recent papers have also shown that it is a powerful tool to improve the receiver performance. For example, in [18], Hamid et al. proposed a method to reconstruct the clipped OFDM signals based on other samples in oversampled OFDM. Enhanced iterative methods are proposed in [19][20]that exploit oversampling to reconstruct clipped and filtered OFDM signals. An optimized iterative clipping and filtering method is proposed in [21]. In [22], frequency domain oversampling (FDO) is examined in multipath channels to improve the error performance of a minimum mean-square error (MMSE) single carrier frequency domain equalizer (SC-FDE).
In wireless systems, OFDM has the ability to convert a frequency selective fading channel into parallel frequency flat fading sub-channels which are equalized using one tap zero-forcing (ZF) and MMSE equalizers. Unfortunately, no attention is given to the performance analysis and complexity of one tap equalizers in oversampled OFDM systems. The objective of this paper is therefore to fill this gap. To facilitate our analysis, we put symbol rate sampled and oversampled OFDM system models, independent of any PAR reduction technique under a common denominator as they form the basis of developing the efficient low complexity equalizers. In this study, our major point of concern is the degradation in the one tap equalizer output signal-to-noise ratio (SNR) (or equivalently decision point SNR) affecting the probability of symbol error. Based on our theoretical analysis and simulation results, we conclude that oversampling is more profitable than thought as it not only improves the per-symbol equalization performance of ZF and MMSE OFDM receivers but also makes them more resilient to channel nulls. The cost to achieve this improved performance is the increased system bandwidth and modest increase in the receiver complexity.
This paper is organized as follows: Section 2 presents the matrix data models of the oversampled and symbol based OFDM. In Section 3, corresponding one tap equalizers, probability-of-error expressions, corresponding performance analysis and complexity issues are considered. In Section 4, illustrating simulations are carried out while conclusions are drawn in Section 5.
Notation: We use boldface capital (lower case) letters to denote the matrices (column vectors), sometimes with subscripts to stress on their sizes. An identity matrix is denoted as and an all-zero matrix of size is denoted as . is used to denote expectation operation, Euclidean norm, for trace of a matrix , for Hermitian transpose, and for complex conjugate. Argument i is used to denote ith block of symbols. The meaning of other variables will be clear from the context.
2. Received Data Model
2.1. Oversampled OFDM
We consider an oversampled OFDM data transmission system, shown in Figure 1. A high speed incoming bit stream, after complex modulation (mapping), is converted into complex data symbols of length N which is transformed into an OFDM signal via N-point IFFT. The resulting continuous time complex baseband OFDM signal can be written as
(1)
where , denotes modulo N, represents the size N complex input data symbol/bock, represents the complex modulated symbol of the kth subcarrier, N is the number of subcarriers, and is the symbol period of the OFDM signal.
An oversampled version of the OFDM waveform (1) can be written as
(2)
where , and is the oversampling factor.
Figure 1. Oversampled OFDM system.
Let the samples associated with the ith OFDM signal be denoted as . With this notation, we can now express the ith oversampled OFDM signal (2) arranged in a vector of length M as . The vector can be obtained by using a length-M IFFT on the extended data vector obtained by inserting zeros in the middle of the information symbol vector . Several different oversampling strategies can be defined. The approach above is our choice here as it results in trigonometric interpolation of the OFDM time domain signal [23].
To describe how the zeros are inserted in , we define the precoding matrix
(3)
Pre-multiplying the data vector by yields the extended data vector . The relationship between and , and thus the associated matrix data model can be expressed as:
(4)
where is the FFT matrix with entry , and the power loss factor is used here to retain the same power before and after the oversampling.
The OFDM signals based on the system model (4) are cyclically extended, digital-t-analogue (D/A) conversion and transmit filtering are performed, the signal is modulated to some carrier frequency, power amplified and then transmitted through the channel. At the receiving end, the reverse action takes place. After frequency down-conversion, receive filtering and analogue-to-digital (A/D) conversion, the cyclic prefix (CP) parts of the subsequent OFDM symbols are removed. We represent the overall combined effect of the spectral shaping pulse, the continuous time channel, the receive filter and the sampling through a discrete time causal, length finite impulse response (FIR) filter, with impulse response . To avoid inter-block-interference (IBI) between successive OFDM data blocks, the CP must be larger than or equal to the channel order. Assuming perfect synchronization and carrier recovery, the time domain received baseband data vector can then be expressed as:
(5)
where the FIR channel vector is represented by the circular channel matrix with first row and is the additive white Gaussian noise (AWGN) vector with covariance .
After demodulation with the M-point FFT matrix, the data model (5) becomes
(6)
where and is a diagonal matrix with entries denoting the kth subcarrier channel frequency response.
Notice that the middle elements of are zeros, hence, the corresponding elements of are nothing but corresponding samples of the noise data vector. These redundant noise samples do not play any role in symbol recovery due to independence of subcarriers. We therefore discard middle zeros from . To do this, we define the receive matrix . Pre-multiplying the received vector by , the data model (6) thus simply reduces to
(7)
where equals the matrix with all rows removed for which the corresponding entries of are zero, denoting the vector on the diagonal of and equals the AWGN vector with all entries removed from which corresponding entries of are zero.
2.2. Nyquist Rate Sampled OFDM
The OFDM system with is known as the Nyquist rate (or critical) sampling based OFDM, therefore: 1) no zeros are appended in the transmission; 2) an N size IFFT is used and 3) we set . As a result of this, at the transmitter side, data model (4) becomes
(8)
Notice that the transmission power in oversampled and Nyquist rate based OFDM is maintained at
i.e., the transmission power in both cases is equal and is given by the power used to transmit data. It is important to mention here that the total transmit power is the sum of power used to transmit data and the power used to transmit the CP. However, the CP power being typically small is normally ignored [24].
At the receiver side, the N-point FFT demodulated ith observed block is then
(9)
where is an circulant matrix with first row , , with denoting the kth subcarrier channel frequency response.
3. Equalization Performance Analysis and Complexity
For the data model (7) above, and matrix can be used to describe a linear equalizer that yields . ZF and MMSE equalizers can be written respectively, as
(10)
Based on the data model (9), a matrix can be used as a linear equalizer to yield . Its ZF and MMSE versions can be written as
(11)
From a unifying input-output perspective, in both the received data models (7) and (9) the kth transmitted symbol at the kth subcarrier equals the transmitted symbol scaled by the complex kth sub-channel gain that is corrupted by AWGN. The corresponding equalizers in Equations (10) and (11) are diagonal matrices, thus implying per-subcarrier/one tap equalization simplicity.
3.1. Probability of Error Analysis
The oversampled OFDM, one tap ZF and MMSE equalization outputs can be written respectively as
(12)
(13)
An important measure of performance of one tap equalizers is the SNR at the output of the equalizer. In both the cases, SNR at the kth symbol output can be written as
(14)
Now if: 1) M-ary QAM symbols are used, 2) and 3)
, then the average probability of symbol error can be approximated as [25], [26]:
(15)
where denotes the probability of the kth symbol received incorrectly and the Q-function .
If the ZF and MMSE equalizers are used on the Nyquist rate data model, then the overall probability expression (15) is valid with the SNR at the kth output given by
(16)
Notice that . As a consequence the symbol errors on the kth subcarrier decrease as increases. Consequently, average probability of error will become low due to high average SNR at the equalizer output. In the following, we therefore focus on the Equations (14) and (16) to analyze the average probability of error performance of one tap equalizers. The equations differ in the following aspects.
1) In Equations (14) and (16), ignoring the channel fading effect, we observe that noise powers (the numerator terms) are not equal. Due to the scaling factor , the has lower noise power as compared with the noise power in . The noise power can be minimized and thus can be improved further as the scaling factor is decreased by increasing J.
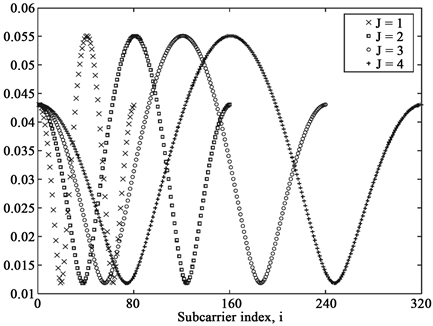
2) Frequency response of a channel with tap coefficients [−0.0156 − 0.0102i, 0.0051 + 0.0033i, −0.0257 − 0.0164i]with increasing value of J is shown in Figure 2. For the frequency response can be seen with two severe nulls, however, for increasing values of J, the spectrum gets spreaded. Due to which the response as seen by the equalizer (i.e., ) in Figure 3 suffers from a single
Figure 2. Nyquist sampled (J = 1) and oversampled frequency response (J = 1, 2, 3 and 4).
Figure 3. Frequency response as received by symbol based and oversampled OFDM equalizers.
moderate null which finally disappears with increasing J. By comparing the frequency responses and , in both the cases it can be observed that the elements of i.e., are relatively large in magnitude than the elements of (i.e. ). This improvement in channel gains due to oversampling obviously causes high signal power in as compared with .
3) The disadvantage associated with the oversampled OFDM one tap equalizers is the loss of symbol detectability. If the transfer function happens to have null on (or close to) the corresponding subcarrier (i.e., if is zero or close to zero), the corresponding symbol carried by that frequency will be impossible to detect due to significant drop in . Similar discussion holds for symbol based one tap equalizers. However, notice that the frequency response vector is different from and as evident from Figure 1 due to spectral spreading it is less likely that will have null on or close to the carrier frequency. This is an important point as the effect of the deep fading channels is normally mitigated by the so-called coded OFDM [27]at the cost of reduced bandwidth efficiency and complex equalization.
The above properties show that oversampling not only improves SNR but helps in avoidance of losing data due to channel nulls at the price of increased FFT complexity and bandwidth loss. Also, SNR can be improved, and equalizers can be made more resilient to channel nulls by increasing the oversampling rate. The elements of data vector can thus be estimated more reliably (this lowers the probability of error) and will give oversampled OFDM one tap equalizers an edge in performance relative to symbol based OFDM one tap equalizers. We underscore here that the oversampled OFDM can be considered as a special case of precoded OFDM systems which involves data rate expansion due to insertion of zeros at the transmitter and have been devised to counteract channel effects [28].
3.2. Equalization Complexity
computations are needed to calculate equalizers in and . Also, computations are required to detect the symbol estimates using . If we account the computations needed for FFT, only computations are needed per symbol. On the other hand, similar discussion holds for and , except that computations needed for FFT. So, the complexity per symbol of conventional equalizer is . Due to the increased FFT size, the per-symbol equalization complexity of the oversampled equalizers is obviously slightly higher than the Nyquist sampled equalizers.
4. Simulations
In order to verify the performance edge of the oversampled OFDM one tap equalizers, we consider a baseband OFDM system with the number of subcarriers N = 80, and J = 1, 2, 3, 4. The randomly generated input data were modulated by 4-ary Quadrature Amplitude Modulation (4-QAM) and the quasi-static Rayleigh fading channel was assumed to have taps (3-ray channel).The carrier frequency was set at 900 MHz and the Doppler frequency was fixed at MHz. This means that the vehicle was moving at a speed of 80 Km/h. In Figure 4, the frequency response of the channel shows deep amplitude fades of up to −40 dB. We assumed that channel sate information (CSI) was perfectly known to the receiver and the SER performance was averaged over 1000 independent runs for OFDM symbols.
Figure 5(a) and Figure 5(b) compare the SER v/s SNR performance of the one tap ZF and MMSE equalization schemes, respectively, with the varying J. We can see that presence of channel nulls in the Rayleigh faded channel severely degrades the SER performance of the Nyquist rate based OFDM one tap equalizers. In case of oversampled OFDM, performance plots of one tap equalizers
Figure 4. Amplitude plot of the Rayleigh fading channel.
Figure 5. SER v/s SNR comparison of one tap equalizers for the Rayleigh fading channel with Lc = 3, N = 80, and varying J: (a) ZF, and (b) MMSE.
improve as the oversampling factor is increased. Also, observe that performance plots in case of ZF and MMSE equalization do not differ. This is obviously since SNR in both the cases does not change .
5. Conclusion
The widespread application of OFDM is mainly motivated by simple one tap equalization that it affords. In this paper, oversampling was studied from the one tap equalization performance and complexity perspective. With the theoretical analysis and simulations, we justified that oversampling not only improves equalizer output SNR but also helps in avoidance of losing data due to channel nulls. Increased oversampling thus lowers the probability of error but of course at the price of increased bandwidth and FFT size. In our simulations, we limited J to at most 4 times as in most of the practical OFDM systems it varies between 2 and 4 to achieve the desired system performance [16]. Also, for the ease of analysis, we did not consider any PAR reduction technique while modelling oversampled and Nyquist based OFDM systems and corresponding equalizers. However, our results (with some performance degradation) can be easily extended to include PAR reduction techniques allowing one tap equalization. For example, see [29][30][31].
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Ali, H. and Khan, F. (2018) On the Performance Analysis of One Tap Equalizers in Oversampled OFDM Systems. Int. J. Communications, Network and System Sciences, 11, 187-198. https://doi.org/10.4236/ijcns.2018.119011
References
- 1. van Nee, R. and Prasad, R. (2000) OFDM for Wireless Multimedia Communications. Artech House.
- 2. Rohling, H., Ed. (2011) OFDM: Concepts for Future Communication Systems. 1st Edition, Springer-Verlag Berlin Heidelberg. https://doi.org/10.1007/978-3-642-17496-4
- 3. (2000) Digital Video Broadcasting (DVB): Framing Structure, Channel Coding and Modulation for Digital Terrestrial Television. 1st Edition, ETSI, EN 300 744.
- 4. (2000) Radio Broadcasting Systems: Digital Audio Broadcasting (DAB) to Mobile, Portable and Fixed Receivers. 1st Edition, ETSI, EN 300 401.
- 5. (1997) Asymmetric Digital Subscriber Line (ADSL) Metallic Interface. ANSI, ANSI/TEI/9J-007.
- 6. Lin, H. (2015) Flexible Configured OFDM for 5G Air Interface. IEEE Access, 3, 1861-1870. https://doi.org/10.1109/ACCESS.2015.2480749
- 7. (2012) 950 MHz-Band Telemeter, Tele Control and Data Transmission Radio Equipment for Specified Low Power Radio Station, ARIB std-t108 ver. 1.0 ed. Association of Radio Industries and Business.
- 8. Park, M. (2013) IEEE 802.11ah Specification Framework Document, Version 14, DCN IEEE 802.11-13/0014r0.
- 9. Yang, L. and Armstrong, J. (2010) Oversampling to Reduce the Effect of Timing Jitter on High Speed OFDM Systems. IEEE Communications Letters, 14, 196-198. https://doi.org/10.1109/LCOMM.2010.03.091963
- 10. Umar, S., Priya, N., Gayathri, P, Subba Reddy, T. and Abdul, A.M. (2018) Design of Jitter Spectral Shaping as Robust with Various Oversampling Techniques in OFDM. In: Satapathy, S., Bhateja, V. and Das, S. Eds., Smart Computing and Informatics, Smart Innovation, Systems and Technologies, Springer, Singapore, 77.
- 11. van Nee, R., and de Wild, A. (1998) Reducing the Peak-to-Average Power Ratio of OFDM. Proc. 48th IEEE Vehicular Technology Conference. Pathway to Global Wireless Revolution (Cat. No.98CH36151), Ottawa, Ont., 2072-2076.
- 12. Dinis, R. and Gusmao, A. (1999) On the Performance Evaluation of OFDM Transmission Using Clipping Techniques. Proceedings of IEEE VTS 50th Vehicular Technology Conference (VTC), 2923-2928.
- 13. Jayalath, A.D.S. and Athaudage, C.R.N. (2004) On the PAR Reduction of OFDM Signals Using Multiple Signal Representation. IEEE Communications Letters, 8, 425-427. https://doi.org/10.1109/LCOMM.2004.832767
- 14. Ochiai, H. and Imai, H. (2001) On the Distribution of the Peak-to-Average Power Ratio in OFDM Signals. IEEE Transactions on Communications, 49, 282-289. https://doi.org/10.1109/26.905885
- 15. Schulze, H. and Lüders, C. (2005) Theory and Applications of OFDM and CDMA Wideband Wireless Communications. John Wiley Sons Ltd., England. https://doi.org/10.1002/0470017406
- 16. Saul, A. and Auer, G. (2005) Improving the Performance of Clipping Techniques for OFDM Systems by Guard Bands. Proceedings of 10th International OFDM Workshop 2005 (InOWo), Hamburg, Germany, 31 August-1 September 2005.
- 17. Chung, C.-D. (2006) Spectrally Precoded OFDM. IEEE Transactions on Communications, 54, 2173-2185. https://doi.org/10.1109/TCOMM.2006.884850
- 18. Saedi, H., Sharif, M. and Marvasti, F. (2002) Clipping Noise Cancelation in OFDM Systems Using Oversampled Signal Reconstruction. IEEE Communications Letters, 6, 73-75. https://doi.org/10.1109/4234.984699
- 19. Ali-Hemmati, R., Azmi, P., Seyfe, B. and Shikh-Bahaei, K. (2008) Iterative Cancellation of Clipping Noise in Multilevel Quadrature Amplitude Modulation Multi-Carrier CDMA System. IET Communications, 2, 300-305. https://doi.org/10.1049/iet-com:20070033
- 20. Yang, L., Song, K. and Siu, Y.M. (2017) Iterative Clipping Noise Recovery of OFDM Signals Based on Compressed Sensing. IEEE Transactions on Broadcasting, 63, 706-713. https://doi.org/10.1109/TBC.2017.2669641
- 21. Wang, Y.-C. and Luo, Z.-Q. (2011) Optimized Iterative Clipping and Filtering for PAPR Reduction of OFDM Signals. IEEE Transactions on Communications, 59, 33-37. https://doi.org/10.1109/TCOMM.2010.102910.090040
- 22. Balevi, E. and Ylmaz, A. (2016) Analysis of Frequency Domain Oversampled MMSE SC-FDE. IEEE Communications Letters, 20, 232-235. https://doi.org/10.1109/LCOMM.2015.2504927
- 23. Fraser, D. (1989) Interpolation by FFT Revisited—An Experimental Investigation. IEEE Transactions on Acoustics, Speech, and Signal Processing, 37, 665-675.
- 24. Wang, Z. and Giannakis, G.B. (2000) Wireless Multicarrier Communications. IEEE Signal Processing Magazine, 17, 29-48. https://doi.org/10.1109/79.841722
- 25. Mark, J.W. and Zhuang, W. (2003) Wireless Communications and Networking. 4th Edition, Prentice Hall, Upper Saddle River, NJ.
- 26. Proakis, J.G. (2004) Digital Communications. 4th Edition, McGraw Hill International Editions, New York, NY.
- 27. Zou, W. and Wu, Y. (1995) COFDM: An Overview. IEEE Transactions on Broadcasting, 41, 1-8. https://doi.org/10.1109/11.372015
- 28. Xia, X. (2001) Precoded and Vector OFDM Robust to Channel Spectral Nulls and with Reduced Cyclic Prefix Length in Single Transmit Antenna Systems. IEEE Transactions on Communications, 49, 1363-1374. https://doi.org/10.1109/26.939855
- 29. Ochiai, H. and Imai, H. (2002) Performance Analysis of Deliberately Clipped OFDM Signals. IEEE Transactions on Communications, 50, 89-101. https://doi.org/10.1109/26.975762
- 30. Bauml, R.W., Fischer, R.F.H. and Huber, J.B. (1996) Reducing the Peak-to-Average Power Ratio of Multicarrier Modulation by Selected Mapping. Electronics Letters, 32, 2056-2057. https://doi.org/10.1049/el:19961384
- 31. Lu, Q., Gui, L. and Fang, X.-Z. (2006) A New Scheme to Mitigate OFDM High PAR Problem by Minimizing the Signal’s Nonlinear Distortion Caused by HPA. IEEE Transactions on Broadcasting, 52, 576-578. https://doi.org/10.1109/TBC.2006.884733