International Journal of Communications, Network and System Sciences
Vol.07 No.01(2014), Article ID:41670,8 pages
10.4236/ijcns.2014.71001
Performance Enhancement of Discrete Multi-Tone Systems with a Trigonometric Transform
Samir Abd Elghafar1,2, Salaheldin M. Diab1, Bassiouny M. Sallam1, Moawad I. Dessouky1, El-Sayed M. El-Rabaie1, Fathi E. Abd El-Samie1
1Department of Electronics and Electrical Communications, Faculty of Electronic Engineering, Menoufia University, Menouf, Egypt
2Department of Electrical Engineering, Jazan University, Jazan, KSA
Email: samir.ghaffer@yahoo.com, dr_salah_diab@yahoo.com, b_m_salam@hotmail.com, dr_moawad@yahoo.com, srabie1@yahoo.com, fathi_sayed@yahoo.com
Copyright © 2014 Samir Abd Elghafar et al. This is an open access article distributed under the Creative Commons Attribution Li- cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intel- lectual property Samir Abd Elghafar et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
The sine transform can be used as a tool to conquer the problems of discrete multi-tone (DMT) systems to in- crease the bit rate. In the proposed discrete sine transform based discrete multi-tone (DST-DMT) system, we make use of the energy compaction property of the DST to reduce the channel effects on the transmitted signals. The mathematical model of the proposed DST system is presented in the paper. Simulation experiments have been carried out to test the effect of the proposed DST-DMT system. The results of these experiments show that the performance of the DST-DMT system is better than that of the traditional FFT-DMT system. The results also show that employing the proposed TEQ in the DST-DMT system can increase the bit rate by about 2.57 Mbps.
Keywords
DMT System; Discretesine Transform; Discrete Fourier Transform; Time Domain Equalizer
1. Introduction
One of the major problems in DMT systems is the inter- ference problem, whether it is inter-symbol interference (ISI) or intercarrier interference (ICI). The data are trans- mitted in DMT systems in the form of symbols. Attach- ing a guard period of v samples to each DMT symbol eradicates the ISI, when v ≥ L − 1, where L is the length of the channel impulse response (CIR) [1]. When the guard period is a cyclic prefix (CP), i.e. a copy of the last v samples of a DMT symbol, the ICI is reduced [2]. The guard period decreases the channel throughput by a fac- tor of N/(N + v), where N is both the symbol length and the FFT length. When v becomes large relative to N, this factor reduces so that the performance loss may be un- reasonable. Hence, v is chosen to be relatively small compared to N. The asymmetric digital subscriber line (ADSL) and the very high-bit-rate digital subscriber line (VDSL) standards set v to N/16. In the field, however, ADSL and VDSL channel impulse responses can exceed N/16 samples [3].
A solution to this problem is the channel shortening equalizer, commonly known as the TEQ. This equalizer is required to shorten the length of the effective channel. The TEQ is a finite impulse response (FIR) filter. The equalized channel, which is the cascade of the channel and the TEQ, can be modeled as a delay by Δ samples followed by an FIR filter, whose impulse response is the target impulse response (TIR) of v + 1 samples. The TIR would fit into a target window of v + 1 samples starting at sample index ∆ + 1 in the shortened impulse response (SIR). The rest of the SIR would ideally be zero [4].
Different TEQ design methods optimize the FIR coef- ficients based on training data under different criteria. The minimum mean square error (MMSE) design mini- mizes the mean square error between the output of the physical path consisting of the channel and FIR filter and the output of a virtual path consisting of a transmission delay ∆ and a TIR [1,5-7]. The maximum shortening
SNR (MSSNR) method attempts to minimize the ISI in the time domain [3]. This method maximizes the ratio of the energy of the effective channel impulse response in- side a target window of ν + 1 samples to that outside the target window. The minimum-ISI (Min-ISI) method ge- neralizes the MSSNR method by weighting the ISI in the frequency domain to place the ISI in unused and more noisy sub-channels [4]. The traditional TEQ-frequency domain equalizer (FEQ) structure equalizes all sub-chan- nels in a combined fashion, which may limit the bit rate performance. Alternative receiver architecture was pro- posed in [8], in which the authors suggested the transfer of the TEQ operations to the frequency domain by mov- ing the TEQ into the FEQ. The combined TEQ-FEQ would yield a multi-tap FEQ structure, in which each sub-channel (tone) is separately equalized. Another al- ternative structure was proposed in [9], in which the au- thors proposed the transfer of the FEQ into the TEQ to yield complex-valued time-domain equalizer filter banks. Combined equalization approaches yield higher data rates than decoupled approaches for the downstream ADSL case [10].
Multi-carrier modulation (MCM) techniques including the DMT and the orthogonal frequency division multip- lexing (OFDM) have been used, extensively, in many wireless networks standards, such as IEEE 802.1la, IEEE 802.16a, and wire-line digital communication systems, such as the ADSL [11-13]. All of these systems employ the complex exponential functions as orthogonal bases. Particularly, in the DMT systems, modulation by the IFFT and demodulation by the FFT create orthogonal sub-channels [14]. However, the complex exponential functions are not the only orthogonal bases that can be used to construct baseband multicarrier signals. A single set of sinusoidal functions can be used as orthogonal bases to implement the MCM scheme, and this scheme can be synthesized using the DST [12].
It is known that the DST has an excellent energy com- paction property. It uses only real arithmetics. This reduces the signal processing complexity, especially, for real pulse-amplitude modulation signaling, where the DFT based processing still uses complex arithmetics and suffers from the in-phase/in-quadrature imbalance prob- lems, which may cause appreciable performance degra- dations [15]. A number of researchers have recently pro- posed the use of the DST in MCM systems, particularly, OFDM [11-13].
In this paper, we propose the DST-DMT systems to allow high bit rate transmission. The performance of the DST-DMT system with the proposed TEQ is tested and compared with the performance of the FFT-DMT system with the TEQ given in [16] over the eight CSA. In [16], a different FIR TEQ is designed for each tone, and the FFT becomes a bank of Goertzel filters, and a single tap FEQ is also used. The rest of the paper is organized as follows. The DFT-DMT system is presented in Section 2. The proposed DST-DMT system is discussed in Section 3. The TEQ design algorithm is presented in Section 4. The simulation parameters are given in Section 5. In Section 6, the simulation results are presented and discussed. In the last section, the general conclusions are given.
2. The DFT-DMT System
Let  be the
be the 
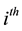 sample DMT symbol to be transmitted. The preceding and the following symbols are the
sample DMT symbol to be transmitted. The preceding and the following symbols are the  and
and 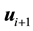 symbols, respectively. The transmitted signal variance is
symbols, respectively. The transmitted signal variance is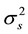 . Let v be the length of
. Let v be the length of
the CP and 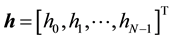 is the
is the 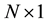 channel impulse response. Let
channel impulse response. Let  be the
be the
Received October 10, 2013; revised November 10, 2013; accepted November 17, 2013
 TEQ. In this paper, we assume that the TEQ sub-channel filters are of equal size
TEQ. In this paper, we assume that the TEQ sub-channel filters are of equal size  for simplicity.
for simplicity.
Let Δ be the transmission delay of the signal between the transmitter and the receiver and let
 (1)
(1)
be the convolutional matrix of the DMT symbols ,
, 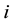 and
and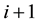 . Define the
. Define the  matrix
matrix
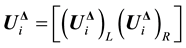 , where
, where 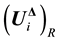 and
and 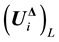 are,
are,
respectively, given by:
 (2)
(2)

Matrices 




Let 


For the conventional DFT-DMT system, the channel input sequence 

So, we can define the vector

such that the inner product of 

Let the near end crosstalk (NEXT) or additive white
Figure 1. DFT-DMT system model. xCP means remove the CP.
Gaussian noise (AWGN) vector be:

Then the (N + M ‒ 1) × M AWGN or NEXT convolu- tion matrices with the TEQ, GAWGN or GNEXT is:


The received data contains the noise due to the ISI, ICI, AWGN, NEXT, and suffers from the effects of the channel. Now, we see the dependence of the received signal on the TEQ. The ideal received signal has no noise and is formatted to fit the demodulation scheme. In DMT modulation, this means that the received symbol has mi- nimal noise due to AWGN, NEXT, and ISI. We can de- sign the TEQ to process the received samples to achieve this target.
Next, we will express the desired signal as a function of the TEQ taps. The desired circular convolution of the 

and the 


So, the received data 

We then write 

where E[・] is the statistical expectation operator and

the ratio of the desired data, which excludes the effects of the noise including the ISI and ICI, to the difference be- tween the received data and the desired data.
Derive 

where 


and


Similarly, derive 

where 






pendent of 



where 










The 

Using the SNR model, the number of bits per symbol that can be supported is:

where 



Maximizing the number of bits allocated to a single channel, 

This is the well-known generalized eigenvalue prob- lem [16] and the solution is the generalized eigenvector 


Hence,
where 

Bits/symbol.
3. The proposed DST-DMT System
For the proposed DST-DMT system with TEQ filter bank, the channel input sequence 

where

and 
So, the defined vector in Equation (8) will be:

such that the inner product of 
that in the above equation 


Depending on the defined vector in Equation (29) and
using the above algorithm, we can derive a new
corresponding to the largest generalized eigenvalue

Figure 2. The proposed DST-DMT system model. xCP means remove the CP.

Hence,

where 
Bits/symbol (32).
4. TEQ Design Algorithm
The first derivative of (23) is:

where

Notice that
sing 


Let

where
Set iteration counter




1)
2)
3) Compute
4)
5) If 


6) If 


7)
8)
9) Go back to Step 1 and repeat.
5. Simulation Parameters
We use the eight CSA loops as our test channels [4]. All channel impulse responses consist of 512 samples sam- pled at a rate of 2.208 MHz. We add a fifth-order Che- byshevhighpass filter with cutoff frequency of 5.4 kHz and passband ripples of 0.5 dB to each CSA loop to take into account the effect of the splitter at the transmitter. The DC channel (channel 0), channels 1 - 5, and the Ny- quist channel are not used. We model the channel noise as −140 dBm AWGN distributed over the bandwidth of 1.104 MHz plus near-end-cross-talk (NEXT) noise. The NEXT noise consists of 8 ADSL disturbers as described in the ANSI T1.413 - 1995 standard [4]. The input signal power is 23 dBm distributed equally over all used sub- channels and both the FFT size, and the DST size are set to N = 512. M = 17 and v = 32. The coefficients of the FIR filters are obtained from the MATLAB Discrete Multitone Time-Domain Equalizer (DMTTEQ) Toolbox that was implemented by the Embedded Signal Proces- sing Lab at the University of Texas [19].
Bandwidth optimization is applied by shutting down (not assigning any transmit power to) sub-channels with initial SNR lower than the required SNR to transmit two bits with a given SNR gap of 9.8 + 6 − 4.2 = 11.6 dB. This corresponds to a system margin of 6 dB and a coding gain of 4.2 dB. We are not using any bit loading algorithm, so all bit rate results are calculated from the SNR distribution after the TEQ filter bank is placed into the system. We assume that the power allocation is constant over all used sub-channels and that it is not changed after the TEQ filter bank is placed in the system.
6. Simulation Results
We present simulation results to analyze and compare the performance of the proposed DST-DMT system with TEQ filter bank with the conventional DFT-DMT system with a TEQ. Figure 3 compares the SNR achieved with the proposed DST-DMT system and the conventional DFT-DMT system for CSA loop 1 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL disturbers. The figure gives insight into why the performance of the proposed DST-DMT system with a TEQ filter bank out- performs the conventional DFT-DMT system with a TEQ filter bank. The proposed system has a flat magni- tude response over most of the spectrum except at the positions of the highest ISI, while for the conventional system, the SNR decreases as the frequency increases, as displayed in Figures 3-5 for CSA loops 1, 4 and 8, re- spectively.
Figure 6 shows the bit allocation to each sub-chan- nelfor the conventional DFT-DMT system with a TEQ filter bank as compared to that of the proposed DST- DMT system with a TEQ filter bank for CSA loop 1 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL disturbers. The proposed system achieves a higher bit allocation for each sub-channel over most of the spec- trum except at the positions of the highest ISI, because each sub-channel carries different numbers of bits de- pending on its SNR. The number of bits assigned to each sub-channel in the case of the conventional system de-


Figure 3. SNR achieved using the proposed system and the conventional system for CSA loop 1 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT is modeled as 8 ADSL disturbers. (a) The con- ventional DFT-DMT system with TEQ filter bank; (b) The proposed DST-DMT system with TEQ filter bank.

Figure 4. SNR achieved using the proposed system and the conventional system for CSA loop 4 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL disturbers. (a) Conventional DFT- DMT system with TEQ filter bank; (b) The proposed DST-DMT system with a TEQ filter bank.

Figure 5. SNR achieved using the proposed system and the conventional system for CSA loop 8 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL disturbers. (a) Conventional DFT- DMT system with a TEQ filter bank; (b) the proposed DST-DMT with a TEQ filter bank.
creases as the frequency increases, as displayed in Fig- ures 6-8 for CSA loops 1, 4 and 8, respectively.
Table 1 lists the data rates achieved with the proposed DST-DMT system with TEQ filter bank for the CIR in- cluding CSA loops 1-8, as well as that of the convention- al DFT-DMT system. The proposed DST-DMT system achieves higher data rates for each CIR than the conven- tional DFT-DMT system in the range of (2.899 ? 5.369) Mbps.
7. Conclusions
In this paper, we proposed a new TEQ filter bank along with the use of the DST in order to achieve higher bit rates in DMT systems. Simulations experiments have
shown that the proposed DST-DMT system with TEQ filter bank provides a better performance than the con- ventional DFT-DMT system. The results indicate that the proposed DST-DMT system achieves a higher SNR in each sub-channel (over most of the spectrum except at the positions of the highest ISI) than the conventional DFT-DMT system over the eight CSA loops. It was also concluded that the proposed DST-DMT system with TEQ filter bank achieves higher bit rates than the con- ventional DFT-DMT system. We can say that the major advantage of the DST-DMT system with TEQ filter bank is in the energy compaction property of the DST. This property leaves most of the samples at the end of each symbol close to zero, which reduces the ISI, dramatical-

Figure 6. Bit allocation to each sub-channel using the proposed system and the conventional system for CSA loop 1 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL disturbers. (a) Conventional DFT-DMT system with a TEQ filter bank; (b) The proposed DST-DMT system with a TEQ filter bank.

Figure 7. Bit allocation to each sub-channel achieved using the proposed system and the conventional system for CSA loop 4 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL distur- bers. (a) Conventional DFT-DMT system with a TEQ filter bank. (b) The proposed DST-DMT system with a TEQ filter bank.

Figure 8. Bit allocation to each sub-channel achieved using the proposed system and the conventional system for CSA loop 4 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT modeled as 8 ADSL distur- bers. (a) Conventional DFT-DMT system with a TEQ filter bank; (b) The proposed DST-DMT system with a TEQ filter bank.
Table 1. The achievable bit rates in Mbps for the proposed DST-DMT system with TEQ filter bank and the conven- tional DFT-DMT system for the CIR involving standard CSA loops 1-8 with M = 17, N = 512, v = 32, input power = 23 dBm, AWGN power = −140 dBm/Hz, and NEXT mod- eled as 8 ADSL disturbers.
ly, leading to a great performance enhancement.
REFERENCES
[1] I. Lee, J. S. Chow and J. M. Cioffi, “Performance Evaluation of a Fast Computation Algorithm for the DMT in High-Speed Subscriber Loop,” IEEE Journal on Selected Areas in Communications, Vol. 13, No. 9, 1995, pp. 1564-1570. http://dx.doi.org/10.1109/49.475530
[2] K. Vanble, M. Moonen and G. Leus, “Linear and Deci- sion-Feedback Per Tone Equalization for DMT-Based Transmission Over IIR Channels,” IEEE Transactions Signal Processing, Vol. 54, No. 1, 2006, pp. 258-273.
[3] G. Arslan, B. Lu, L. D. Clark and B. L. Evans, “Iterative Refinement Methods for Time-Domain Equalizer Design,” EURASIP Journal on Applied Signal Processing, Vol. 2006, 2005, pp. 1-12. http://dx.doi.org/10.1155/ASP/2006/43154
[4] G. Arslan, B. L. Evans and S. Kiaei, “Equalization for Discrete Multitone Transceivers to Maximize Bit Rate,” IEEE Transactions Signal Processing, Vol. 49, No. 12, 2001, pp. 3123-3135. http://dx.doi.org/10.1109/78.969519
[5] J. S. Chow and J. M. Cioffi, “A Cost-Effective Maximum Likelihood Receiver for Multicarrier Systems,” Proceed- ings of the IEEE International Conference on Communi- cations, Chicago, 1992, pp. 948-952.
[6] J. S. Chow, J. M. Cioffi and J. A. Bingham, “Equalizer Training Algorithms for Multicarrier Modulation Sys- tems,” Proceedings of the IEEE International Conference on Communications, Geneva, May 1993, pp. 761-765.
[7] N. Al-Dhahir and J. M. Cioffi, “Efficiently Computed Re- duced-Parameter Input-Aided MMSE Equalizers for ML Detection: A Unified Approach,” IEEE Transactions on Information Theory, Vol. 42, No. 3, 1996, pp. 903-915.
[8] K. Van Acker, G. Leus, M. Moonen, O. van de Wiel and T. Pollet, “Per Tone Equalization for DMT-Based Sys- tems,” IEEE Transactions on Communications, Vol. 49, No. 1, 2001, pp. 109-119. http://dx.doi.org/10.1109/26.898255
[9] M. Ding, Z. Shen and B. L. Evans, “An Achievable Per- formance Upper Bound for Discrete Multi Tone Equali- zation,” Proceedings of IEEE Global Telecommunica- tions Conference, Dallas, November-December 2004, pp. 2297-2301.
[10] R. K. Martin, K. Vanbleu, M. Ding, et al., “Unification and Evaluation of Equalization Structures and Design Algorithms for Discrete Multi-Tone Modulation Systems,” IEEE Transactions Signal Processing, Vol. 53, No. 10, 2005, pp. 3880-3894.
[11] A. Rushdi and J. Tuqan, “PAPR Reduction in Trigono- metric-Based OFDM Systems,” IEEE Signals, Systems and Computers, Conference Record of the 41th Asilomar Conference, 4-7 November 2007, Pacific Grove, pp. 1747-1751.
[12] P. Tan, and N. C. Beaulieu, “A Comparison of DCT- Based OFDM and DFT-Based OFDM in Frequency Off- set and Fading Channels,” IEEE Transactions on Com- munications, Vol. 54, No. 11, 2006, pp. 2113-2125. http://dx.doi.org/10.1109/TCOMM.2006.884852
[13] P. Tan and N. C. Beaulieu, “An Improved DCT-Based OFDM Data Transmission Scheme,” IEEE 16th Interna- tional Symposium on Personal, Indoor and Mobile Radio Communications, 11-14 September 2005, pp. 745-749.
[14] E. Khan and C. Heneghan, “Iterative Refinement Me- thods for Time-Domain Equalizer Design,” EURASIP Journal on Applied Signal Processing, Vol. 2006, pp. 1-12, Article ID: 43154.
[15] P. Tan and N. C. Beaulieu, “A Comparison of DCT- Based OFDM and DFT-Based OFDM in Frequency Off- set and Fading Channels,” IEEE Transactions on Com- munications, Vol. 54, No. 11, 2006, pp. 2113-2125. http://dx.doi.org/10.1109/TCOMM.2006.884852
[16] M. Milosevic, L. F. C. Pessoa, B. L. Evans and R. Bal- dick, “DMT Bit Rate Maximization with Optimal Time Domain Equalizer Filter Bank Architecture,” Proceedings of the IEEE Asilomar Conference on Signals, Systems, and Computers, November 2002, Vol. 1, pp. 377-382.
[17] A.-Y. Wu and T.-S. Chan, “Cost-Efficient Parallel Lattice VLSI Architecture for the IFFT/FFT in DMT Transceiver Technology,” Proceedings of the 1998 IEEE Internation- al Conference on Acoustics, Speech and Signal Process- ing, 1998, Vol. 6, pp. 3517-3520.
[18] A. B. Watson, “Image Compression Using the Discrete Cosine Transform,” Mathematica Journal, Vol. 4, No. 1, 1994, pp. 81-88.
[19] “MATLAB Discrete Multitone Time-Domain Equalizer (DMTTEQ) Toolbox,” University of Texas, Austin. http://www.ece.utexas.edu/~bevans/projects/adsl/dmtteq/dmtteq.html


















