Journal of Computer and Communications
Vol. 1 No. 3 (2013) , Article ID: 36353 , 7 pages DOI:10.4236/jcc.2013.13001
New Approach for Relay and Transceiver Design for Interference Alignment in MIMO Interference Channels
![]()
Department of Electrical Engineering, Iran University of Science and Technology, Narmak, Iran.
Email: hossein vaezy@elec.iust.ac.ir, Vakili@iust.ac.ir
Copyright © 2013 Hossein Vaezy, Vahid Tabataba Vakili. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 5th, 2013; revised July 8th, 2013; accepted July 15th, 2013
Keywords: Interference Alignment; Degree of Freedom; Multiple Input Multiple Output (MIMO); Amplify and Forward (AF)
ABSTRACT
Wireless relaying has been known to provide the improvements in link reliability, spectral efficiency, and coverage extension. In this paper, we use full duplex relays for Interference Alignment (IA) in K-users Interference Channel (IC) and show K Degrees of Freedom (DOF) is achievable. In first hop, relays receive signals from transmitters and forward them to receivers in second hop. Two iteratively algorithms are proposed for computing relays function, precoder, and decoder matrices. First algorithm minimizes leakage interference at receivers that has appropriate performance at high Signal to Noise Ratio (SNR) region. Furthermore, the second algorithm has better performance at low-mediate SNR. The performance of proposed algorithms are compared with other schemes and validated with simulation in terms of achieved sum rate.
1. Introduction
One of the main problems in the studying of Interference Channels (ICs) is how to decrease the undesired effects of multiuser interference. In practice several schemes exist for interference mitigation. In the first scheme, interference can be treated as noise and just focus on extracting the desired signals [1-3]. However, in practice this scheme has widespread use due to implementation simplicity but does not increase the data rate. Another conventional scheme is channel orthogonalization that transmitted signals are chosen to be non-overlapping in time, frequency or space [4]. Consequently, lead to Time Division Multiple Access (TDMA), Frequency Division Multiple Access (FDMA) or Space Division Multiple Access (SDMA), respectively. However, this scheme extensively reduces the interference it causes non-effective use of communication resources and divides them between users. In other words, an IC with M transmitter-receiver pairs can use only 1/M of resources for each of users. Other scheme that recently has attracted much attention is Interference Alignment (IA). IA is a radical idea that finds out of analysis of interference networks capacity. Since capacity calculation of wireless networks in general is an open problem, an increased interest exists for approximated capacity characteristics. Number of Degrees of Freedom (DOF) that has been known as multiplexing gains, provide approximate capacity for IC with K users and M antennas for each user. This can be expressed as
 (1)
(1)
where 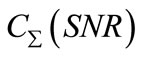 is sum capacity as a function of Signal to Noise Ratio (SNR). Also,
is sum capacity as a function of Signal to Noise Ratio (SNR). Also, 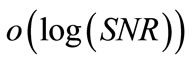 is approximation error. At high SNR regime, the second term becomes negligible in comparison to first term. The main result implies that at high SNR regime, each user in wireless channels is able to achieve one half of capacity regardless of user number in the absence of interference. IA approach in wireless channels refers to idea that constructed signals in a way that interference signals overlapped in one half of the space and the other half was free from interference [5,6]. This result is much interesting, since sum of the used resources for the whole network can become much larger than available resources. Accordingly, it is necessary to fit the undesired signals from different users into a small space.
is approximation error. At high SNR regime, the second term becomes negligible in comparison to first term. The main result implies that at high SNR regime, each user in wireless channels is able to achieve one half of capacity regardless of user number in the absence of interference. IA approach in wireless channels refers to idea that constructed signals in a way that interference signals overlapped in one half of the space and the other half was free from interference [5,6]. This result is much interesting, since sum of the used resources for the whole network can become much larger than available resources. Accordingly, it is necessary to fit the undesired signals from different users into a small space.
In [5], authors utilize channel variation properties to perform IA by extending the signals over multiple time intervals. By using time extension, the authors show that a DOF of M/2 is possible for M-user IC. In the other side, a distributed algorithm for achieving IA with multiple antenna nodes is presented in [7] that utilize reciprocity property of wireless channels. They observed that IA without symbols extension is infeasible in special cases and showed that IA without symbols extension can be achieved by using relay. Feasibility conditions for IA were analyzed in [8], it considers IA as multivariate polynomial system and proved that due to the number of equations are larger than number of variables, without symbols extension the wireless interference network is unable to achieve IA. Ref [9] shows that half duplex Amplify and Forward (AF) relays are unable to increase DOF of interference networks but can help to do IA with limited symbols extension. It indicates that if number of relays is sufficiently large DOF of interference channel can reach DOF of X channel [10]. Relay aided IA is considered for quasi static X channel [11]. Interference channel with K users compeer to K layers of half duplex AF relays are considered in [12]. It is shown that K DOF is achieved when the number of relays is almost K (K − 1). Theory of irrational independence of numbers rather than linear independence of rational vectors is introduced in [13] and showed that maximum DOF of interference channels is achievable. Realizing this theory in realistic scenarios is still an open problem because nodes need to know channel state Information (CSI) completely and determine that channel gains are rational or irrational. K users IC with half duplex AF relays is analysed in [14]. It considers direct link from source to destination and suppose that each relay allot to a receiver. In [15] K users IC with half Duplex AF relays is considered and for IA attempts to fix precoders and decoders in order to design relays so interferences from direct links are negated with interferences from relays.
In this paper, K users IC compeer to full duplex AF relays are considered that each of nodes equipped with multiple antennas and the direct links from sources to destinations are ignored. Two iteratively new algorithms are proposed for computing relays function, precoder, and decoder matrices. Leakage interferences at receivers are minimized in first algorithms. This algorithm diminishes interference at receivers but do not attempt to improve power of desired signals in receiver. In the second algorithm, Signal to Interference plus Noise Ratio (SINR) is maximized by designing precoders and decoders matrix and interferences are diminished by relays. This algorithm has better performance at low to mediate SNR regime. Simulation results are validated in terms of average sum rate and show that two algorithms have same performance at high SNR regime.
The rest of this paper is organized as follows: Section II provides an introduction to the system model of the MIMO interference channel based on interference alignment. In Section III, we discuss the precoder, decoder, and relay function design for system. Section IV presents the simulation results. Finally, concluding remarks are given in Section V.
Notation: for a matrix ,
, 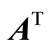 , and
, and  indicates the transpose and hermitian transpose of
indicates the transpose and hermitian transpose of , respectively and
, respectively and  is the column vector consisting of all the columns of
is the column vector consisting of all the columns of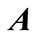 . Also
. Also 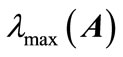 shows maximum eigenvalue of matrix
shows maximum eigenvalue of matrix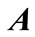 . For matrices
. For matrices 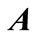 and
and ,
, 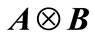 indicates the kronecker product of two matrices.
indicates the kronecker product of two matrices. 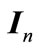 denotes identity matrix of size
denotes identity matrix of size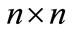 . The notation of
. The notation of 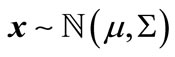 means that
means that 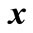 is complex Gaussian distribution with mean vector
is complex Gaussian distribution with mean vector 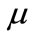 and covariance matrix
and covariance matrix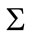 .
.
2. System Model
In this paper, a Multiple Input Multiple Output (MIMO) interference channel with relays is considered as is shown in Figure 1. We indicate each of the mth transmitters, nth receivers and lth relay nodes with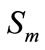 ,
, 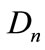 , and
, and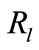 , respectively.
, respectively.
The K source-destination node pairs and R full duplex AF relays are considered that each of the source, destination and relay nodes are equipped with ,
,  , and
, and  antennas, respectively. There are K independent sequences for each of the users. All the relays are full duplex and they receive signals from source nodes and forward them to destination nodes. Direct link from source to destination node is not considered. All the source, destination, and relay nodes are supposed to have the perfect channel knowledge of the whole system. We show the channel coefficients between mth source and lth relay node, lth relay and nth destination node with
antennas, respectively. There are K independent sequences for each of the users. All the relays are full duplex and they receive signals from source nodes and forward them to destination nodes. Direct link from source to destination node is not considered. All the source, destination, and relay nodes are supposed to have the perfect channel knowledge of the whole system. We show the channel coefficients between mth source and lth relay node, lth relay and nth destination node with 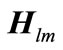 and
and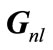 , respectively. Then the received signals at relays and destination nodes are given by:
, respectively. Then the received signals at relays and destination nodes are given by:
 (2)
(2)
where 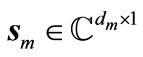 are dm independent coded data streams transmitted from
are dm independent coded data streams transmitted from  and normalized in the form of
and normalized in the form of .
. 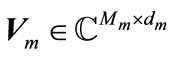 indicates linear precoder in
indicates linear precoder in  and
and  denotes circularly symmetric complex additive Gaussian noise in relay with zero mean and unit variance.
denotes circularly symmetric complex additive Gaussian noise in relay with zero mean and unit variance.
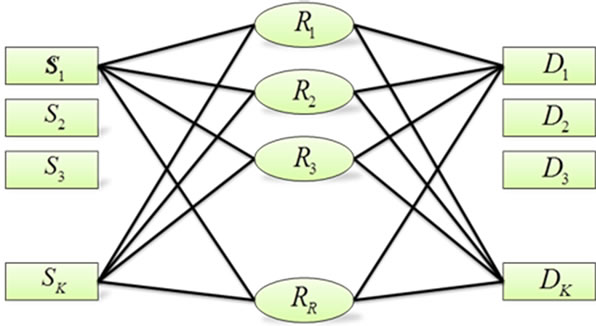
Figure 1. Network model.
In the second hop, the relays amplify received signals and forward them to destination nodes. The lth relay function is indicated by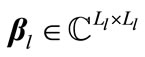 . Therefore, the received signals in destination nodes are given by:
. Therefore, the received signals in destination nodes are given by:
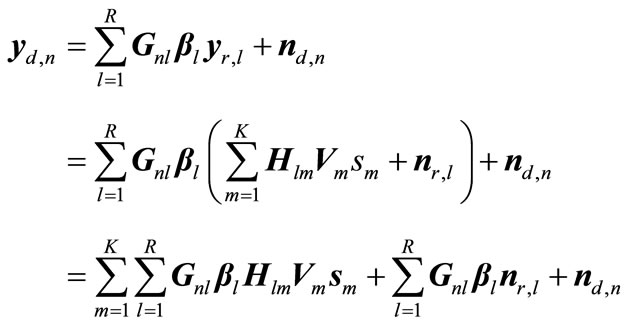 (3)
(3)
where 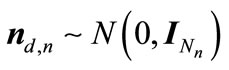 denotes circularly symmetric complex additive Gaussian noise in destination with zero mean and unit variance.
denotes circularly symmetric complex additive Gaussian noise in destination with zero mean and unit variance.
For simplicity we define 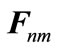 as equivalent channel between nth transmitter, and mth receiver is given by:
as equivalent channel between nth transmitter, and mth receiver is given by:
 (4)
(4)
Therefore, the received signals at nth destination node are given by:
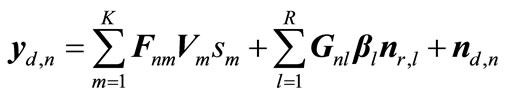 (5)
(5)
 (6)
(6)
If all channel coefficients are generic and obtains from independent continues distribution, then necessary conditions for interference alignment are given by:
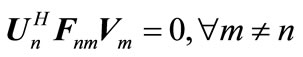 (7)
(7)
 (8)
(8)
where 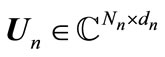 shows suppression vectors in destination nodes
shows suppression vectors in destination nodes . The condition (7) guarantees that interferences are aligned and can be omitted with suppression vector in nth destination. The condition (8) guarantees that nth receiver can decode
. The condition (7) guarantees that interferences are aligned and can be omitted with suppression vector in nth destination. The condition (8) guarantees that nth receiver can decode  data streams successfully. Then, interference alignment is feasible for a given tuple DOF
data streams successfully. Then, interference alignment is feasible for a given tuple DOF .
.
In the next section, we propose two new algorithms for interference alignment with relay. Simulation results show advantage of each algorithm.
3. Iterative Algorithms for Precoder, Decoder, and Relay Design
In this section we present iterative algorithms for IA for given tuple DOF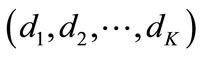 .
.
3.1. Proposed MINimum Leakage Algorithm (PMINL)
The goal in this algorithm is to diminish leakage interference that exists in receiver after interference suppression. To this end, we need to reduce power of leakage interference in destination [7]. Leakage interference in nth receiver is expressed as:
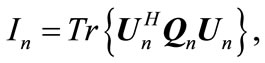 (9)
(9)
where 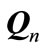 is covariance matrix of interference in nth receiver and is given by:
is covariance matrix of interference in nth receiver and is given by:
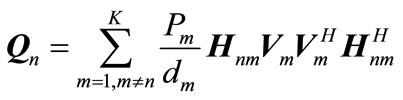 (10)
(10)
We need to design  for a given tuple
for a given tuple 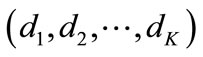 so that condition (7) is satisfied. Also, leakage interference converges to zero at the receiver. In this algorithm, it is assumed that the given tuple
so that condition (7) is satisfied. Also, leakage interference converges to zero at the receiver. In this algorithm, it is assumed that the given tuple 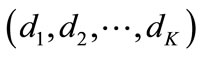 is achievable. Hence, we describe the above problem as an optimization problem:
is achievable. Hence, we describe the above problem as an optimization problem:
 (11)
(11)
In this section we present an iterative solution for above optimization problem. So, we optimize problem in three steps, in each step we fix two parameters and design third parameter and continue process when the algorithm converges to constant parameters.
Step 1: design decoder matrix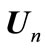 , with fixed
, with fixed  and
and 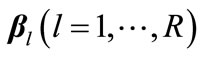 as below optimization problem:
as below optimization problem:
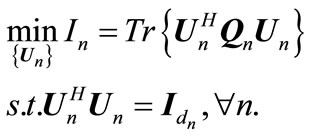 (12)
(12)
So that 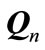 is equal to covariance matrix of interference at nth receiver. It can easily be seen that
is equal to covariance matrix of interference at nth receiver. It can easily be seen that 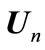 is equal to
is equal to 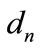 eigenvectors equivalent by minimum eigenvalues of
eigenvectors equivalent by minimum eigenvalues of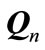 . The minimum value of leakage interference at nth receiver is equal to summation of
. The minimum value of leakage interference at nth receiver is equal to summation of 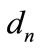 minimum eigenvalues of
minimum eigenvalues of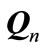 .
.
Step 2: design precoder matrix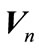 , with fixed
, with fixed  and
and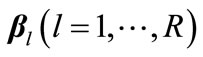 .
.
The Property that is used here is the reciprocity of original and reciprocal channel [7]. Alignment conditions for original channel and reciprocal channel are equal. If the tuple DOF of users be achievable for original channel then the same tuple DOF is achievable for reciprocal channel. In other words, in reciprocal channel each user design its interference suppression matrix that is precoder matrix for other user in original channel and this make the problem to be altruistic. Therefore, each user in the network attempts to minimize interference for other users and thereby enhance the throughput of total network. We design precoder matrix by solving following optimization problem that minimize leakage interference in reciprocal network.
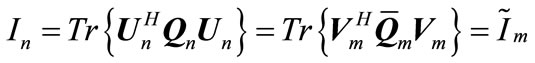 (13)
(13)
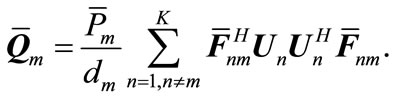 (14)
(14)
where 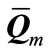 is covariance matrix of interference and
is covariance matrix of interference and 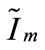 is leakage interference in mth receiver in reciprocal network. It can easily be demonstrated that precoder matrix
is leakage interference in mth receiver in reciprocal network. It can easily be demonstrated that precoder matrix  is equal to eigenvectors equivalent by
is equal to eigenvectors equivalent by 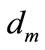 minimum eigenvalues of
minimum eigenvalues of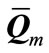 .
.
Step 3: design relay function with fixed precoder and decoder matrices:
In this step, precoder and decoder matrices  are fixed. Then, design relay function
are fixed. Then, design relay function  in order to minimize total leakage interference at receivers. The objective function is defined as the total leakage interfereence. Leakage interference is calculated as follows:
in order to minimize total leakage interference at receivers. The objective function is defined as the total leakage interfereence. Leakage interference is calculated as follows:
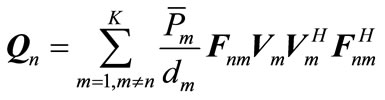 (15)
(15)
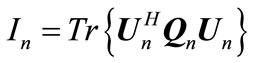 (16)
(16)
 (17)
(17)
By utilizing property of kroncker product and vectorize operation, we can summarize total leakage interfereence as follows:
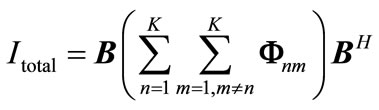 (18)
(18)
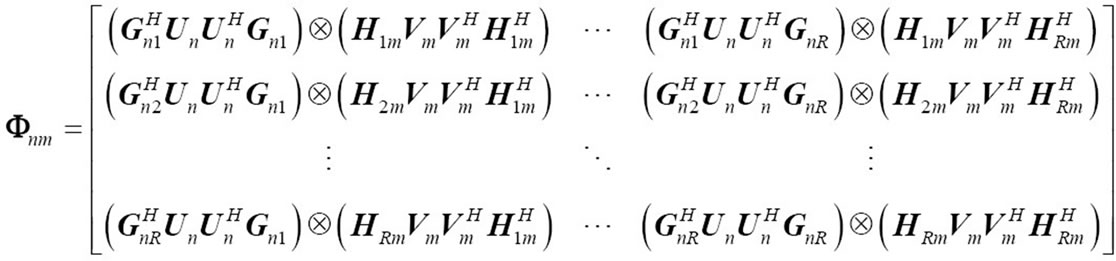 (19)
(19)
where vector 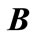 and matrix
and matrix 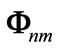 are defined as belows, respectively:
are defined as belows, respectively:
 (20)
(20)
Then, the optimization problem can be expressed as follows:
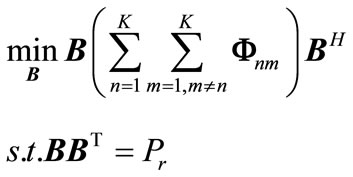 (21)
(21)
where 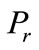 is summation of power of each relay. It can be easily seen that vector
is summation of power of each relay. It can be easily seen that vector  is equal to eigenvector equialent to minimum eigenvalues of
is equal to eigenvector equialent to minimum eigenvalues of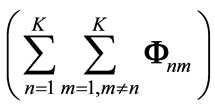 and minimum value of total leakage interference at receiver is the same as minimum eigenvalue of
and minimum value of total leakage interference at receiver is the same as minimum eigenvalue of
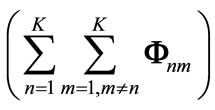 .
.
Here new algorithm that minimizes leakage interfereence at receivers is proposed. In the next section we utilize another algorithm that have better performance at low SNR and is the same as PMINL algorithm, at high SNR regime.

Algorithm 1: PMINL algorithm
3.2. Proposed MAXimum Signal to Interference plus Noise Ratio (PMAXSINR)
In the PMINL algorithm leakage interference at receivers is minimized to improve throughput of total system. But we do not consider power of desired signal at each receiver. In other words, we do not guarantee any power level for desired signals. This is because we do not consider direct channel 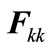 in the process of precoder, decoder, and relay matrix design. Therefore, new optimization problem is introduced so the objective functions are SINR at receivers [7]. Hereby, we can obtain desired signals at receivers by maximizing desired signal power and minimizing leakage interference. So, relays are designed for minimizing leakage interference and precoderdecoder matrices for maximizing desired signal power. Hence, by using relay we can weaken interferences and amplify the desired signals.
in the process of precoder, decoder, and relay matrix design. Therefore, new optimization problem is introduced so the objective functions are SINR at receivers [7]. Hereby, we can obtain desired signals at receivers by maximizing desired signal power and minimizing leakage interference. So, relays are designed for minimizing leakage interference and precoderdecoder matrices for maximizing desired signal power. Hence, by using relay we can weaken interferences and amplify the desired signals.
SINR at nth receiver duo to lth symbol is defined as below:
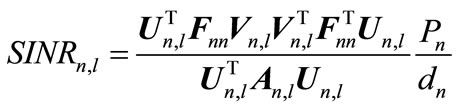 (22)
(22)
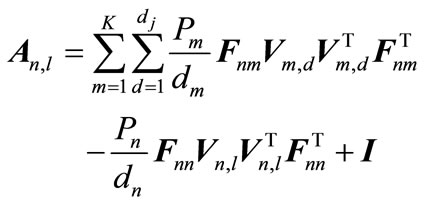 (23)
(23)
where  is the covariance matrix of interference and noise at nth receiver due to the lth transmitted symbol. Similar to the previous algorithm, PMAXSINR algorithm is performed in three steps.
is the covariance matrix of interference and noise at nth receiver due to the lth transmitted symbol. Similar to the previous algorithm, PMAXSINR algorithm is performed in three steps.
Step 1: In this step, precoder and relay matrices are fixed. Then, design decoder matrix that maximize SINR at receivers. So the objective function can be described as follows:
 (24)
(24)
Lemma1: Consider positive definite matrix 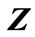 and hermitian matrix
and hermitian matrix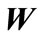 , both of size
, both of size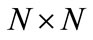 . Then based on the generalized eigenvalue problem [16], for any
. Then based on the generalized eigenvalue problem [16], for any 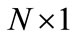 column vector
column vector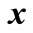 :
:
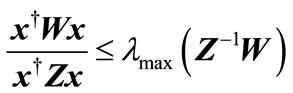 (25)
(25)
where 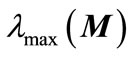 denotes maximum eigenvalue of matrix
denotes maximum eigenvalue of matrix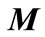 . The inequality is satisfied when
. The inequality is satisfied when 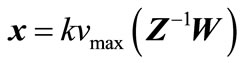 where
where 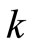 is any nonzero constant and
is any nonzero constant and  denotes eigenvector equivalent by the maximum eigenvalue of
denotes eigenvector equivalent by the maximum eigenvalue of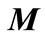 . For the special case of W = ww† that
. For the special case of W = ww† that 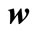 is column vector:
is column vector:
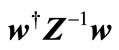
 (26)
(26)
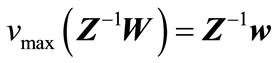 (27)
(27)
Based on lemma1, it can be seen that solution of above problem is eigenvector equivalent to maximum eigenvalue of 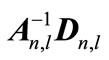 where,
where,
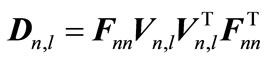 (28)
(28)
Based on lemma1, solution of above problem can be describe as follows:
 (29)
(29)
Step 2: In this step, decoder and relay matrices are fixed. Then, precoder matrices are designed.
Note that in this step we use reciprocity property of the channel and repeat step1 for reciprocal channel so decoder matrices in reciprocal channels are precoder matrices in original channels. Based on the lemma1, simply be seen that:
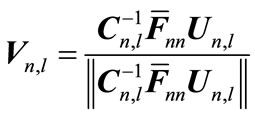 (30)
(30)
While 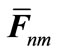 is pseudoinverse of channel matrix between mth transmitter and nth receiver in reciprocal channel and variable
is pseudoinverse of channel matrix between mth transmitter and nth receiver in reciprocal channel and variable  is defined as follows:
is defined as follows:
 (31)
(31)
Step 3: In this step, precoder and decoder matrices are fixed. Then, design relays function so diminish adverse effect of interference at receivers. Firstly, we must obtain covariance matrix of interference at each receiver then design relays function so that minimize total interference at receivers. Similar to previous algorithm (PMINL), total leakage interference are described as:
 (32)
(32)
where matrix 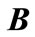 and
and 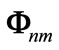 are defined as previous algorithm. Then,
are defined as previous algorithm. Then, 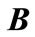 is:
is:
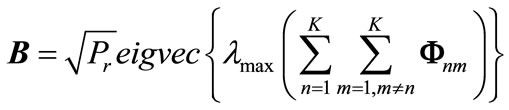 (33)
(33)

Algorithm 2: PMAXSINR algorithm
4. Simulation Results
In this section, the performance of proposed algorithms is evaluated and achieved average sum-rate is taken as a measure of the system performance. For numerical anaysis, we assume that each channel coefficient of MIMO channel matrices is supposed to follow independent and identically distributed (i.i.d) complex Gaussian distribution with zero mean and unit variance. The channels in two hop are quasi static and fix during one transmitted symbols. In Figure 2 we show appropriate performance of PMINL algorithm for two cases of with and without relays in which number of users and relays are equal to 3, number of antennas at each node are 4 and 2 data symbols are sent from each transmitter.
Figure 3 indicates increasing performance of PMINL algorithm for different number of relays. This figure implies that by increasing number of relays, average sum rate of network can be improved. Performance of proposed algorithm (PMAXSINR) is showed in Figure 4 for the both mentioned cases.
Figure 5 indicates performance of PMAXSINR algorithm for several relays number. For comparison average sum rate of PMINL and PMAXSINR algorithms are sketched in Figure 6. Better performance of PMAXSINR algorithm is observed at low SNR regime.
Note that at high SNR two algorithms have equal performance.
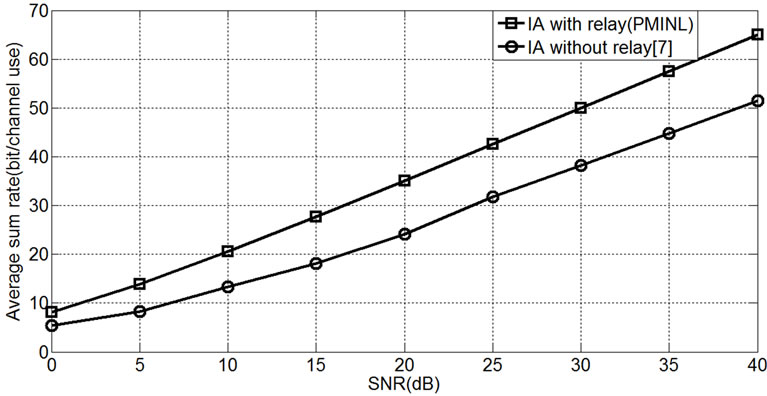
Figure 2. PMINL algorithm for M = N = L = 4, K = R = 3, d = 2.
Figure 3. PMINL algorithm for M = N = 4, L = 5, K = 3, d = 4.
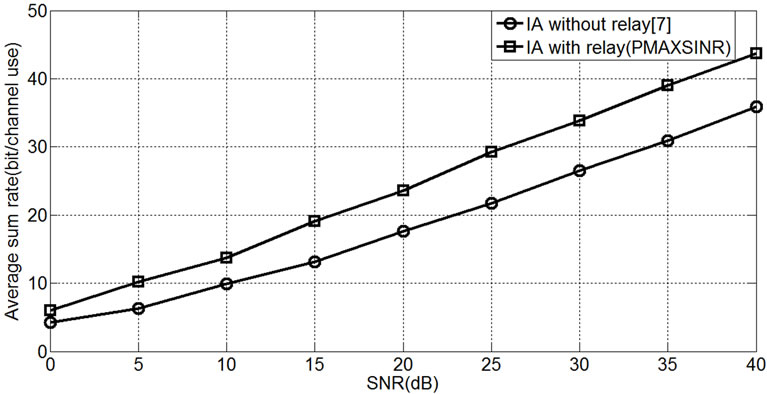
Figure 4. PMAXSINR algorithm for M = N = L = 4, K = R = 3, d = 2.
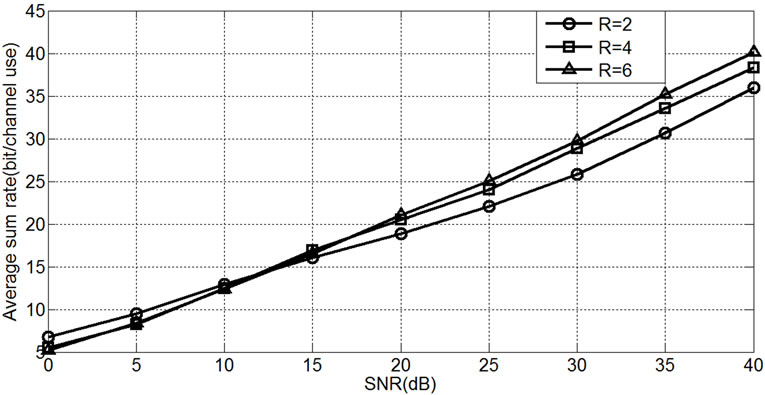
Figure 5. PMAXSINR algorithm for M = N = 4, L = 5, K = 3, d = 4.
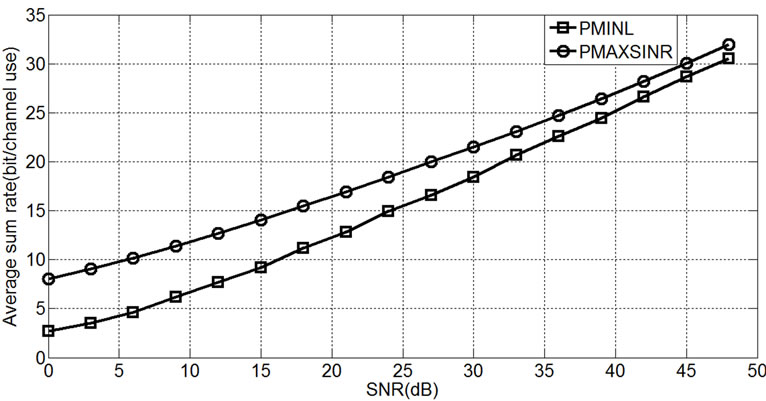
Figure 6. Comparison between PMINL and PMAXSINR algorithm for M = N = L = 4, K = 2, R = 3, d = 4.
5. Conclusion
In this paper, full duplex AF relays are used for IA in interference channels and are showed that with relays can reach to K DOF of IC. Here an iterative numerical approach for Interference Alignment is developed in K user interference channels. Then, two altruistic algorithms for IA are proposed that both of them employ reciprocity property of channels. Unlike selfish approaches where each transmitter tries to maximize his own rate by trans mitting along those signaling dimensions where his desired receiver sees the least interference, we follow an unselfish approach where each transmitter primarily tries to minimize the interference to unintended receivers. In the first algorithm (PMINL) precoder, decoder matrices and relay functions are designed only for minimizing leakage interference at receivers. So, we must use an algorithm that does not diminish power of desired signals at receivers. Hence, PMAXSINR algorithm is proposed. In this algorithm we design precoder and decoder for maximizing power of desired signal. Then, relays function are designed for minimizing leakage interference at receivers.
REFERENCES
- R. Etkin, D. Tse and H. Wang, “Gaussian Interference Channel Capacity to within One Bit,” IEEE Transaction on Information Theory, Vol. 54, No. 12, 2007, pp. 5534- 5562. doi:10.1109/TIT.2008.2009807
- A. Motahari and A. K. Khandani, “Capacity Bounds for the Gaussian Interference Channel,” IEEE Transaction on Information Theory, Vol. 55, No. 2, 2009, pp. 620-643.
- X. Shang, G. Kramer and B. Chen, “A New Outer Bound and the Noisy-Interference Sum-Rate Capacity for Gaussian Interference Channels,” IEEE Transaction on Information Theory, Vol. 55, No. 2, 2009, pp. 689-699. doi:10.1109/TIT.2008.2009793
- A. Host-Madsen and A. Nosratinia, “The Multiplexing Gain of Wireless Networks,” IEEE International Symposium on Information Theory, Adelaide, 4-9 September 2005, pp. 2065-2069.
- V. Cadambe and S. Jafar, “Interference Alignment and the Degrees of Freedom of the k User Interference Channel,” IEEE Transaction on Information Theory, Vol. 54, No. 8, 2008, pp. 3425-344. doi:10.1109/TIT.2008.926344
- M. A. Maddah-Ali, A. S. Motahari and A. K. Khandani, “Communication over MIMO X Channels: Interference Alignment, Decomposition, and Performance Analysis,” IEEE Transactions on Information Theory, Vol. 54, No. 8, 2008, pp. 3457-3470. doi:10.1109/TIT.2008.926460
- K. Gomadam, V. R. Cadambe and S. A. Jafar, “A Distributed Numerical Approach to Interference Alignment and Applications to Wireless Interference Networks,” IEEE Transaction on Information Theory, Vol. 57, No. 6, 2011, pp. 3309-3322. doi:10.1109/TIT.2011.2142270
- C. M. Yetis, T. Gou, S. A. Jafar and A. H. Kayran, “On Feasibility of Interference Alignment in MIMO Interference Networks,” IEEE Transactions on Signal Processing, Vol. 58, No. 9, 2010, pp. 4771-4782.
- V. R. Cadambe and S. A. Jafar, “Can Feedback, Cooperation, Relays and Full Duplex Operation Increase the Degrees of Freedom of Wireless Networks?” IEEE International Symposium on Information Theory, Toronto, 6-11 July 2008, pp. 1263-1267.
- V. R. Cadambe and S. A. Jafar, “Interference Alignment and the Degrees of Freedom of Wireless X Networks,” IEEE Transactions on Information Theory, Vol. 55, No. 9, 2009, pp. 3893-3908.
- B. Nourani, S. A. Motahari and A. K. Khandani, “Relay-Aided Interference Alignment for the Quasi-Static X Channel,” IEEE International Symposium on Information Theory, Seoul, 28 June 2009-3 July 2009, pp. 1764-1768.
- S. W. Jeon, S. Y. Chung and S. A. Jafar, “Degrees of Freedom of Multi-Source Relay Networks,” 47th Annual Allerton Conference on Communication, Control, and Computing, 30 September-2 October 2009, pp. 388-393.
- A. S. Motahari, S. Oveis Gharan, M. A. Maddah-Ali and A. K. Khandani, “Real Interference Alignment: Exploiting the Potential of Single Antenna Systems” IEEE Transactions on Information Theory, 2009. http://arxiv.org/abs/0908.2282
- H. Ning, C. Ling and K. K. Leung, “Relay-Aided Interference Alignment: Feasibility Conditions and Algorithm,” IEEE International Symposium on Information Theory, Austin, 13-18 June 2010, pp. 390-394.
- H. Al-Shatri and T. Weber, “Interference Alignment Aided by Non-Regenerative Relays for Multi-User Wireless Networks,” Proceeding of 8th International Symposium on Wireless Communication Systems, Aachen, 6-9 November 2011, pp. 271-275.
- K. V. Mardia, J. T. Kent and J. M. Bibby, “Multivariate Analysis,” Academic, San Diego, 1979.

