Int'l J. of Communications, Network and System Sciences
Vol.6 No.3(2013), Article ID:28905,9 pages DOI:10.4236/ijcns.2013.63014
Linear and Nonlinear Time Domain Block Equalizers on MIMO Frequency Selective Channels
Department of Computer Science and Engineering, Graduate School of Engineering, Nagoya Institute of Technology, Nagoya, Japan
Email: chx17515@stn.nitech.ac.jp, iwanami@nitech.ac.jp
Received January 24, 2013; revised February 13, 2013; accepted February 21, 2013
Keywords: MIMO Frequency Selective Fading Channel; ISI; IAI; Time Domain Block Equalizer; BLE; BNLE
ABSTRACT
Single-Carrier (SC) transmission with the same bandwidth as Multi-Carrier (MC) transmission (such as OFDM) may have far shorter symbol duration and is considered to be more robust against time selective fading. In this paper, we proposed the novel equalization and signal separation schemes in time domain for short block length transmission, i.e., Block Linear Equalization (BLE) and Block Nonlinear Equalization (BNLE) on MIMO frequency selective fading channels. The proposed BLE uses the MMSE based inverse matrix in time domain and the BNLE utilizes the QRD-M (QR Decomposition with M algorithm) with appropriate receiver complexity. We compared the computational complexity among the conventional SC-FDE (Frequency Domain Equalization) scheme and the proposed equalizers. We also used the Low-Density Parity Check (LDPC) decoder concatenated to the proposed BLE and BNLE.
1. Introduction
For high speed mobile communications with wide transmission bandwidth, Inter-Symbol Interference (ISI) due to multipath propagation must be compensated. For the ISI compensation, the channel equalization such as FDE with Guard Interval (GI) in OFDM can effectively equalize the frequency selective fading [1,2]. However, with increasing number of subcarriers in OFDM, the symbol duration becomes large and the long symbol duration causes the problem of durability against time selective fading. Although it is considered that OFDM can cope with time selective fading with some compensation technique such as V-BLAST detection for each subcarrier [3], the long symbol duration in OFDM is essentially difficult to adapt the receiver for rapid time selective fading. On the other hand, SC transmission with the same transmission bandwidth as OFDM is able to have much shorter symbol duration than OFDM and the short time block transmission with small number of symbols is strong against time selective fading. In [4], Turbo encoded MIMO SC transmission scheme is introduced. The authors used the FDE to cancel the ISI and IAI by decomposing the frequency selective channel to the flat Rayleigh fading channel accommodated at each frequency index. The receiver processes the received signal between the FDE and Turbo decoder iteratively. However, in compensating the ISI for SC block transmission with small number of symbols, the FDE is not efficient, because the FDE with small number of FFT points cannot effectively equalize the channel frequency selectivity. Accordingly, instead of FDE, the time domain equalization is effective for the short block length with small number of symbols and has been considered in [5-11]. In [5], the soft canceller with MMSE filter compensates the ISI and IAI in time domain, however, it needs soft replicas provided by the turbo decoder and the error correction encoding at the transmitter is required. In [6,7] the author proposed the method using Maximum Likelihood Detection (MLD) with successive cancellation, where the simulated results are all based on 2-tapped delay line model. However, as the number of multipath is larger than 2 actually, the amount of computation will dramatically increase when the number of multipath becomes large. In order to solve this problem, the authors introduced the oversampling technique, but this leads to extremely high synchronization requirements for the whole system.
In [8-10], the authors developed the time domain signal separation and equalization schemes for both cases when the Channel State Information (CSI) is available at the transmitter and only available at the receiver on MIMO frequency selective channels. Those papers are preliminaries for this paper. In [11], the author proposed the sequential processing receiver in time domain for eliminating the ISI and IAI and compared it with MIMO Maximum Likelihood Sequence Estimation (MLSE) equalizer. However, those receivers can basically work as the sequential receiver.
In this paper, we propose the novel linear and nonlinear block equalization schemes in time domain for the SC transmission with short block length, where the CSI is only available at the receiver. We firstly defined the extended MIMO channel matrix H over the space and time domain for MIMO frequency selective channels. By carefully designing the transmit signals, we proposed several novel signal separation and equalization receiver structures using block processing in time domain with small number of transmit symbols. From the simulation results, the proposed receivers showed the excellent BER characteristics compared with the conventional SC FDE receiver, especially when the block size is small. In addition, we compare the computational complexity among SC-FDE, BLE, BNLE QRD-M and MLD, where we employ the similar steps in the case of BNLE [QRD-M] [12]. In order to demonstrate or prove the feasibility of error correction encoding for the proposed schemes, we also applied the Low Density Parity Check (LDPC) code, which was originally proposed by Gallager [13] and has attracted much attention recently [14].
This paper is organized as follows. In Section 2, we introduce the system model on SISO and MIMO frequency selective channels. The proposed block equalization schemes will be described in Section 3, where we proposed and compared the several linear and nonlinear block equalization receivers. In Section 4, the simulation results are shown. In Section 5, the conclusions are given.
Throughout the paper, we illustrate some of the notations as follows; vectors and matrixes are expressed by the bold italic letters. 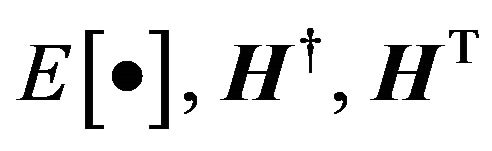 and
and 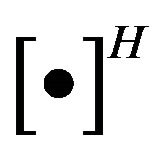 denote the expectation, pseudo-inverse, transpose and conjugate transpose of matrices, respectively.
denote the expectation, pseudo-inverse, transpose and conjugate transpose of matrices, respectively.
2. System Description
We first introduce the SISO channel model on the frequency selective fading channel. The receive signal 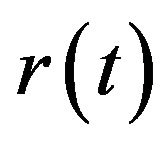 can be written as
can be written as
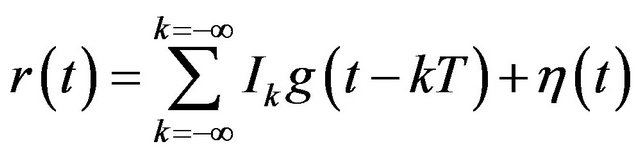 (1)
(1)
where 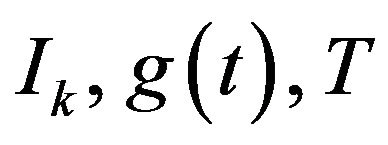 and
and 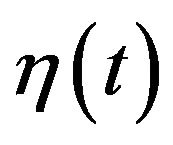 are the transmit signal point at time k, overall channel impulse response including pulse shaping and transmit filters, the symbol duration and the AWGN noise, respectively. The matched filter
are the transmit signal point at time k, overall channel impulse response including pulse shaping and transmit filters, the symbol duration and the AWGN noise, respectively. The matched filter  is employed for the receive signal
is employed for the receive signal 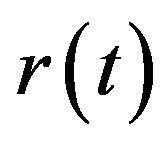 and the symbol time sampling is made. The sampled signal is then passed through the noise whitening filter to get the receive signal point
and the symbol time sampling is made. The sampled signal is then passed through the noise whitening filter to get the receive signal point 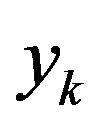 at time k
at time k
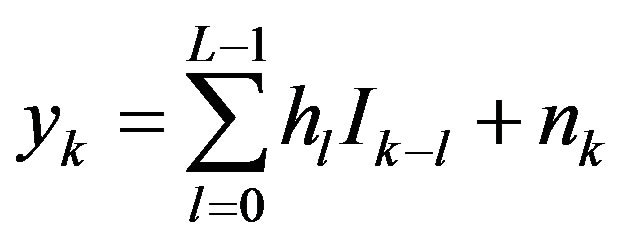 (2)
(2)
where 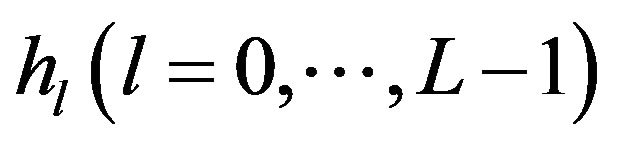 is the tap coefficient and
is the tap coefficient and 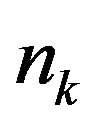 is the independent complex Gaussian noise variable. Equation (2) is referred to as the tapped delay line model [15].
is the independent complex Gaussian noise variable. Equation (2) is referred to as the tapped delay line model [15].
Figure 1 shows the delay profile of SISO multipath channel in the tapped delay line model, where we assume that the tap coefficients 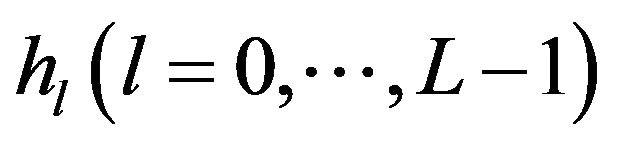 have i.i.d. Rayleigh amplitude distributions.
have i.i.d. Rayleigh amplitude distributions.
We consider the spatial multiplexing system with 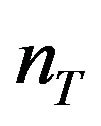 transmit and
transmit and 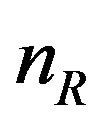 receive antennas. We define the spacetime extended matrix to apply the block processing for the multipath channel model.
receive antennas. We define the spacetime extended matrix to apply the block processing for the multipath channel model.
The extended matrix H with the size 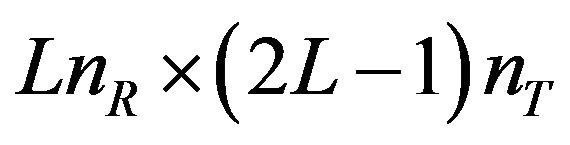 can be written as follows.
can be written as follows.
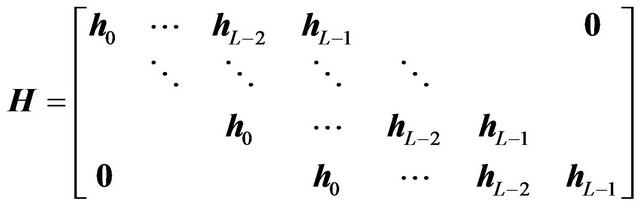 (3)
(3)
where L is the number of multipath and 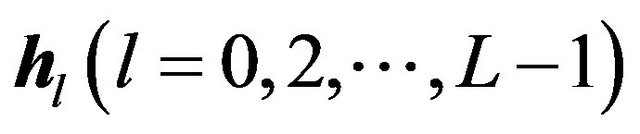 is the element matrix, which follows the quasi-static flat fading with the size of
is the element matrix, which follows the quasi-static flat fading with the size of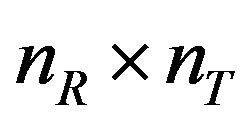 , i.e.,
, i.e.,
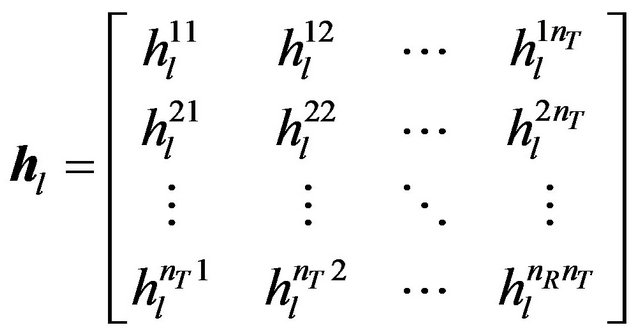 (4)
(4)
where 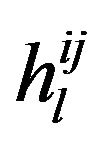 is the l-th delay path gain from the j-th transmit antenna to the i-th receive antenna, and
is the l-th delay path gain from the j-th transmit antenna to the i-th receive antenna, and 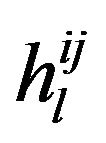 follows the i.i.d. Rayleigh amplitude distribution. It is also assumed
follows the i.i.d. Rayleigh amplitude distribution. It is also assumed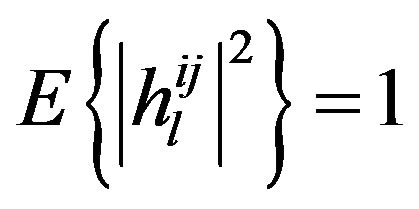 , i.e., the average channel gain is normalized to one. The channel is assumed quasi-static, i.e., the channel gains are static within a block length, but change independently from block to block.
, i.e., the average channel gain is normalized to one. The channel is assumed quasi-static, i.e., the channel gains are static within a block length, but change independently from block to block.
In this paper, we assumed that the extended channel matrix H is known at the receiver, i.e., the receiver has the perfect Channel State Information (CSI) by sending training sequences just before the data block.
Using H, we obtain the extended input and output re-
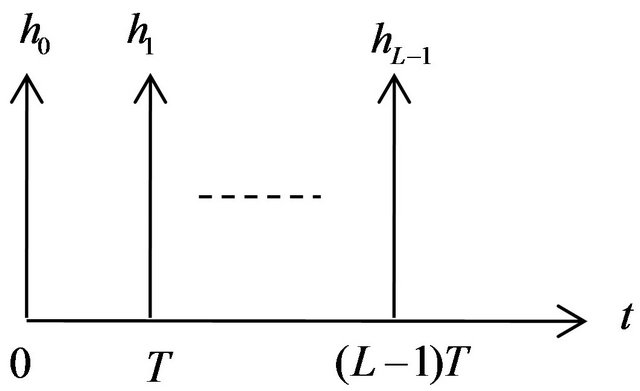
Figure 1. Delay profile of L path channel.
lationship given by
 . (5)
. (5)
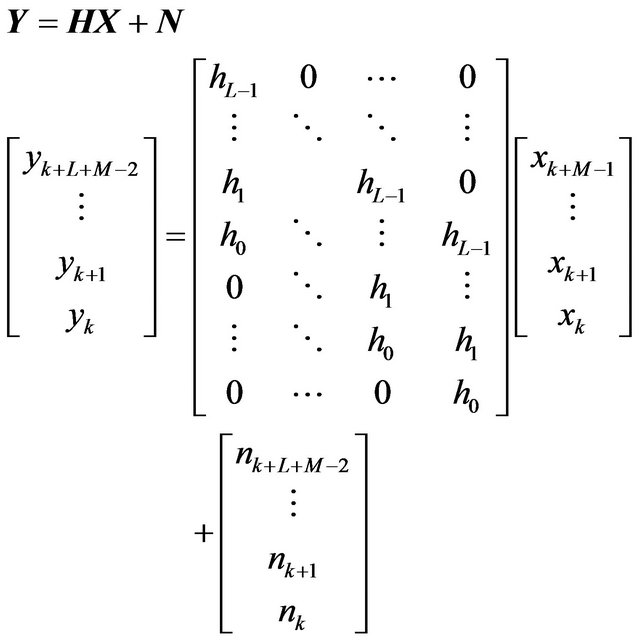
where Y is the extended receive vector expressed as
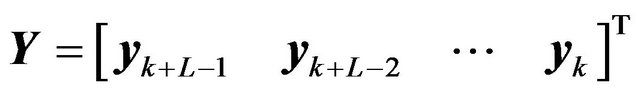 (6)
(6)
and  is the element receive signal vector at time k. X is the extended transmit signal vector expressed as
is the element receive signal vector at time k. X is the extended transmit signal vector expressed as
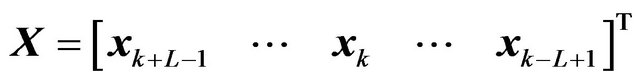 (7)
(7)
and 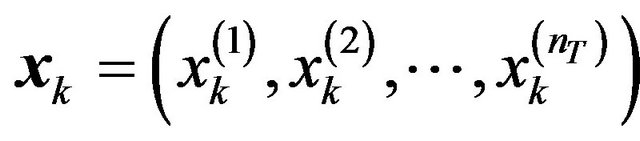 is the element transmit signal vector at time k. N is the extended receive noise vector expressed as
is the element transmit signal vector at time k. N is the extended receive noise vector expressed as
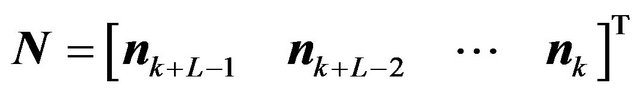 (8)
(8)
where 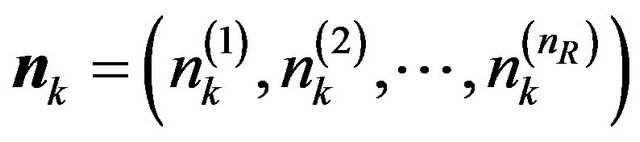 is the element additive white Gaussian noise vector at time k. It also holds the following equations
is the element additive white Gaussian noise vector at time k. It also holds the following equations 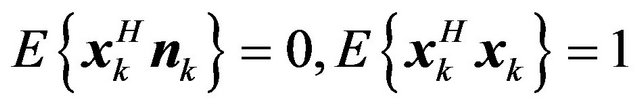 and
and .
.
3. Block Linear and Nonlinear Equalizers for MIMO Quasi-Static Frequency Selective Fading Channels
This paper focuses on the signal separation and equalization of MIMO SC transmission schemes. In order to illustrate the BER performances of proposed schemes clearly, it is necessary to give a brief introduction of MIMO SC-FDE as the reference scheme.
3.1. MIMO SC-FDE
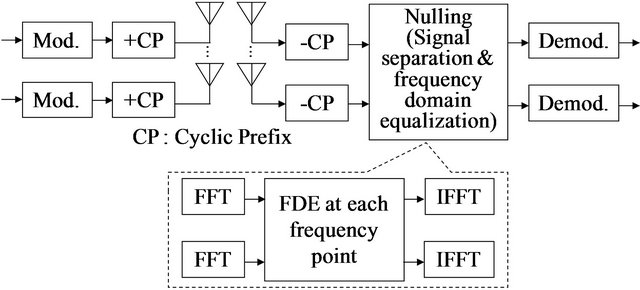
In Figure 2, the equivalent baseband model of transmitter and receiver in MIMO SC-FDE on the MIMO quasistatic frequency selective channels is depicted. Figures 2(a) and (b) show the MIMO SC-FDE with CP (Cyclic Prefix) and the one with ZP (Zero Padding) named as MIMO SC-FDE-CP and MIMO SC-FDE-ZP, respectively. At each transmit antenna, the data bit stream is grouped into the block. After periodically inserting the CP or ZP, all the blocks are transmitted simultaneously from the multiple transmit antennas over the frequency selective channels using the same carrier frequency. At the receiver, the CP is removed and the ZP is processed by the matrix conversion. Then the received data are converted into frequency domain by using Fast Fourier Transform (FFT). Frequency Domain equalization (FDE) are then performed. Finally, the Inverse Fast Fourier Transform (IFFT) is used to convert the frequency domain signal to the time domain for demodulation.
3.1.1. MIMO SC-FDE-CP
The MIMO SC-FDE-CP scheme is illustrated in Figure 2(a). The transmit and receive vector representations with the channel expression of  from transmit antenna j to receive antenna i in the FFT frame is denoted as
from transmit antenna j to receive antenna i in the FFT frame is denoted as
 (9)
(9)
where 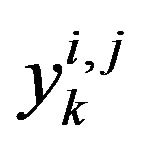 is the receive signal at time k from the transmit antenna j to the receive antenna i,
is the receive signal at time k from the transmit antenna j to the receive antenna i, 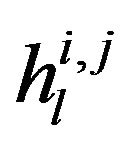 is the complex channel gain of the l-th delay path,
is the complex channel gain of the l-th delay path, 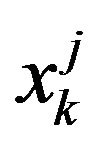 is the transmit symbol at time k from the transmit antenna j and
is the transmit symbol at time k from the transmit antenna j and 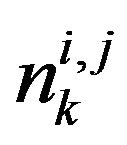 is the complex Gaussian noise at time k. We have set the block length to N symbols. The channel matrix
is the complex Gaussian noise at time k. We have set the block length to N symbols. The channel matrix  in (9) becomes the circulate convolution matrix and the FDE can be done using FFT.
in (9) becomes the circulate convolution matrix and the FDE can be done using FFT.
3.1.2. MIMO SC-FDE-ZP
The MIMO SC-FDE-ZP scheme is illustrated in Figure 2(b). The transmit and receive vector representation with the channel expression of 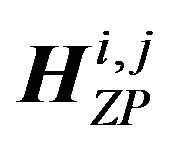 from the transmit antenna j to the receive antenna
from the transmit antenna j to the receive antenna 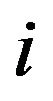 is given by
is given by
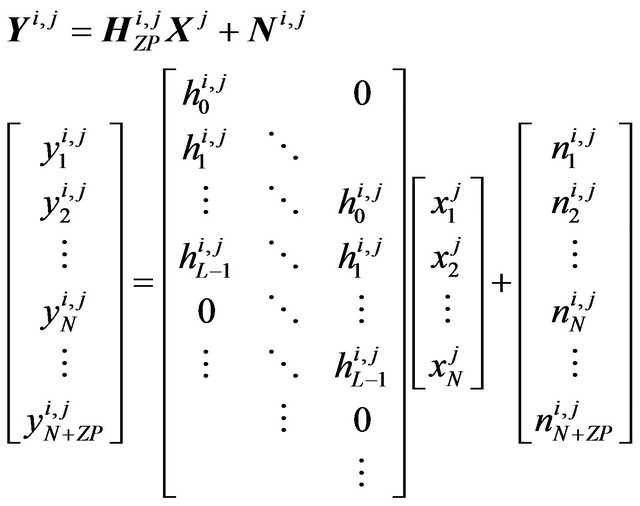 (10)
(10)
where each element in (10) is almost the same as in (9), but as shown in (10) the channel matrix 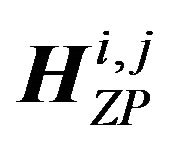 now becomes the linear convolutional matrix. Also the size of receive vector
now becomes the linear convolutional matrix. Also the size of receive vector 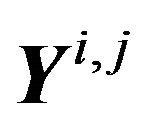 is extended to
is extended to 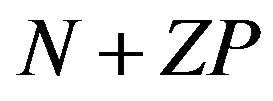 due to the zero padding.
due to the zero padding.
3.2. Block Equalizer in Time-Domain
For the transmit signal vector in (7), we can expand its size arbitrary, i.e.
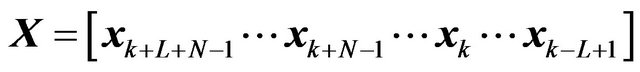 (11)
(11)
where N is again the number of symbols in a block. Accordingly, the sizes of extended transmit vector, channel matrix, receive vector and noise vector are expressed as 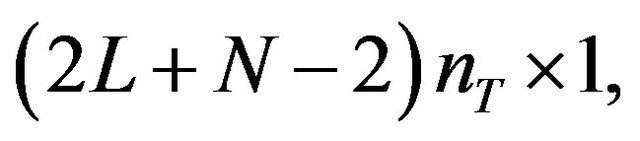
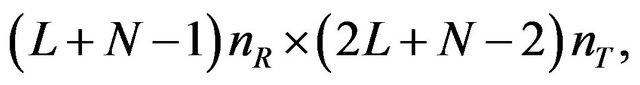
 , and
, and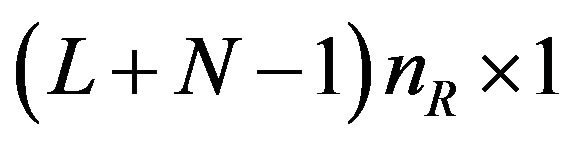 , respectively. The receive vector can be written as
, respectively. The receive vector can be written as
 (a)
(a) (b)
(b)
Figure 2. Transmitter and receiver model of MIMO-SCFDE. (a) SC-FDE-CP; (b) SC-FDE-ZP.
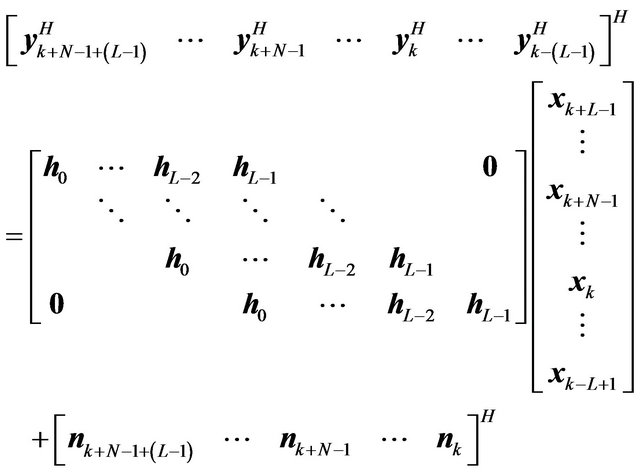 (12)
(12)
In order to avoid the Inter-Block Interference (IBI) at the receiver, the transmit vector is processed by using Zero-Padding as shown in the Figure 3.
We insert 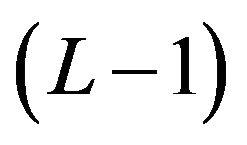 zero symbols before and after the signal vector separately. The receive vector in (12) can be written as
zero symbols before and after the signal vector separately. The receive vector in (12) can be written as
 (13)
(13)
where  is the extended channel matrix with
is the extended channel matrix with  .
.
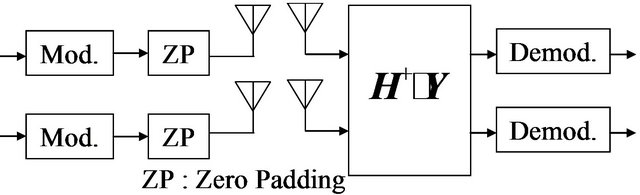
The transmit and receive models of the proposed time domain block equalizers are shown in Figure 4.
3.2.1. BLE (Block Linear Equalizer)
When the channel matrix is given as in (13), we can compensate the ISI and the IAI simultaneously by using Moore Penrose inverse matrix in the analogy of nulling operation as in MIMO flat fading channels.
The inverse matrix based on Zero Forcing (ZF) criterion is given by (14)
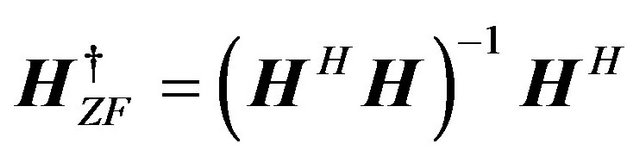 (14)
(14)
where  denotes the pseudo-inverse matrix of H. The pseudo-inverse matrix exists when the number of columns is less than or equal to the number of rows. The estimates of X, which is denoted as
denotes the pseudo-inverse matrix of H. The pseudo-inverse matrix exists when the number of columns is less than or equal to the number of rows. The estimates of X, which is denoted as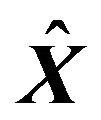 , is given by
, is given by
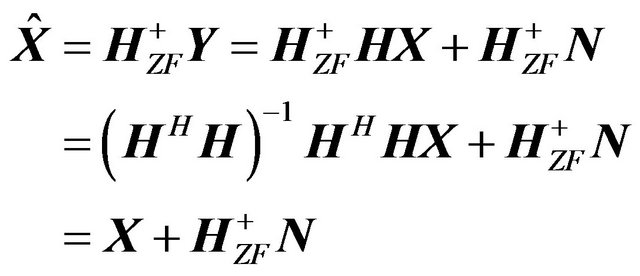 (15)
(15)
Equation (15) means that the ISI and IAI due to the channel are completely equalized. However, the disadvantage of ZF is that it suffers from the noise enhancement.
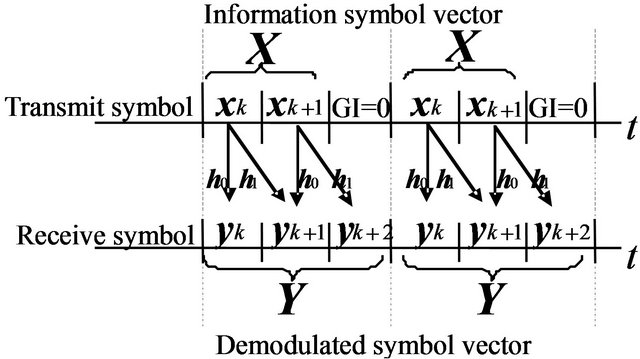
Figure 3. Illustration of zero-padding to prevent IBI at receiver on MIMO multipath channel (L = 2, N = 2).
 (a)
(a)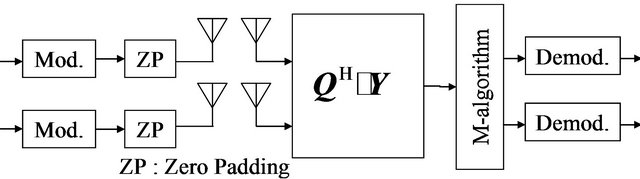 (b)
(b)
Figure 4. Transmitter and receiver models of proposed time domain block equalizers. (a) BLE; (b) QRD-M.
In order to circumvent the noise enhancement, the inverse matrix solution with the MMSE (Minimum Mean Square Error) criterion is obtained as
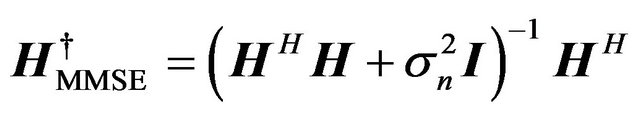 (16)
(16)
By multiplying  by Y from the left hand side of (13), the estimates of
by Y from the left hand side of (13), the estimates of 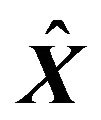 based on MMSE criterion can be obtained. The MMSE solution in (16) trades off the signal separation quality for the noise enhancement reduction through the small term of
based on MMSE criterion can be obtained. The MMSE solution in (16) trades off the signal separation quality for the noise enhancement reduction through the small term of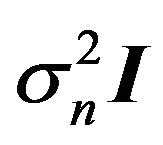 .
.
Next we simply discuss the BLE in SISO and SIMO cases. In SISO case, the channel input and output equation is given by
 (17)
(17)
where each element in (17) becomes scalar value and this corresponds to 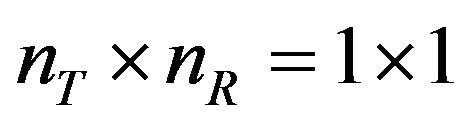 for the element
for the element 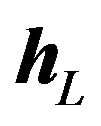 in (4).
in (4).
In SIMO case, the proposed BLE can also be applied, where the element in (13) becomes the vector with 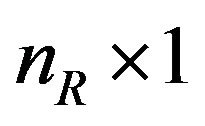 and the channel input and output expression is given by
and the channel input and output expression is given by
 (18)
(18)
It is necessary to discuss a special case in SIMO with the block size of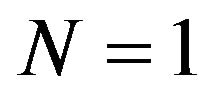 . When the block size equals 1, Equation (13) can be written as
. When the block size equals 1, Equation (13) can be written as
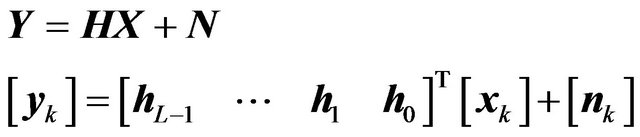 (19)
(19)
where the elements in (19) are represented as
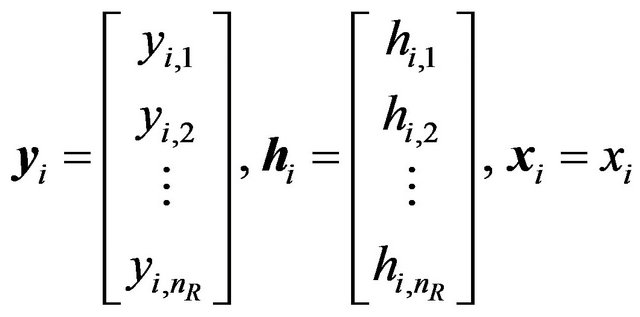 (20)
(20)
From (19) and (20), the Maximum Radio Combining (MRC) is available and the weight vector is written as
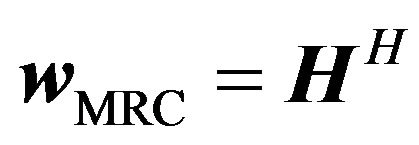 (21)
(21)
The received signal after the MRC is expressed as
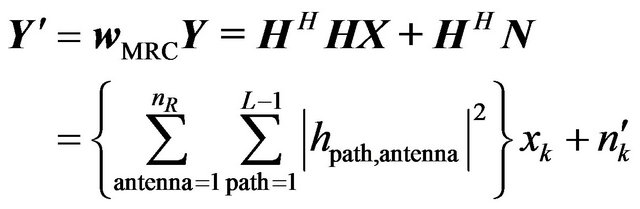 (22)
(22)
It is observed that the term 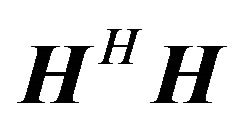 achieves the sum of all the squared channel gains over all the receive antennas, and the full diversity with the order
achieves the sum of all the squared channel gains over all the receive antennas, and the full diversity with the order 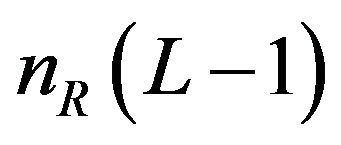 is obtained in this case.
is obtained in this case.
3.2.2. BNLE (Block NonLinear Equalizer)
In [6,7], the author proposed the idea of imaginary transmit antenna and employed the layered MLD detection to avoid the ISI. However, the computational complexity greatly increases when the number of receive antennas is large. Here we propose the QR decomposition with an M-algorithm (QRD-M). It is expected that the great reduction in computational complexity can be achieved without degrading the performance when compared with full MLD.
The QR-decomposition of channel matrix H is obtained as
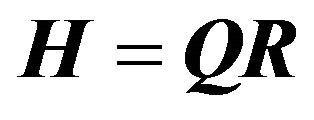 (23)
(23)
where Q is the 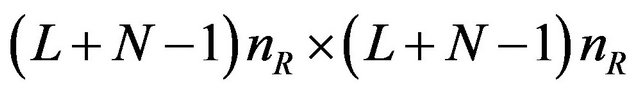 unitary matrix, R is the
unitary matrix, R is the  upper triangular matrix and
upper triangular matrix and . After multiplying
. After multiplying 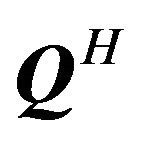 by the received signal Y from the left hand side, we get
by the received signal Y from the left hand side, we get
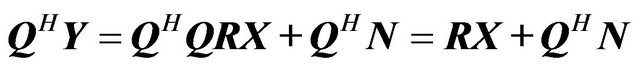 (24)
(24)
and the estimate 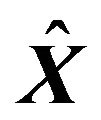 is given by
is given by
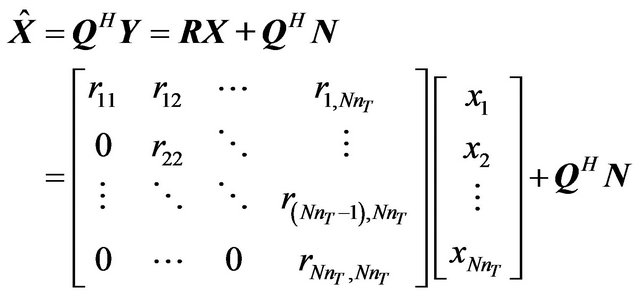 (25)
(25)
From Equation (25), it is observed that by applying the tree search with the decoding order from 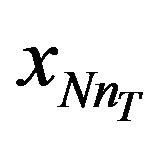 to
to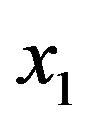 , we can calculate the Euclidian distance based branch metric and path metric of (26) and (27) respectively, for all the possible values of
, we can calculate the Euclidian distance based branch metric and path metric of (26) and (27) respectively, for all the possible values of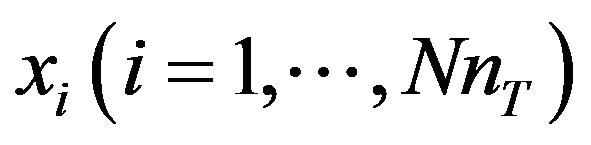 .
.
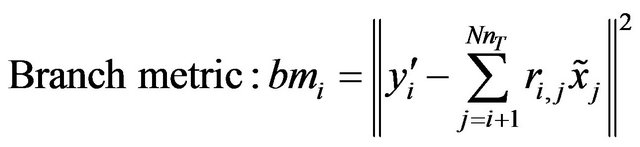 (26)
(26)
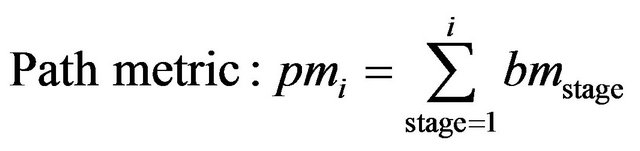 (27)
(27)
The accumulated path metrics are then ordered. Only M nodes with the smallest accumulated path metrics are retained and the rest is deleted. The same procedure is applied to the nodes in the next layer and this process continues up to the first layer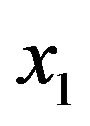 . In QRD-M algorithm, the parameter M is used as the number of limit to the maximum survived branches in the breadth-first tree algorithm. By setting M equal to different values, it can provide different tradeoff solutions between the system performance and the complexity. The larger M value, the better performance is obtained, however the larger complexity is required.
. In QRD-M algorithm, the parameter M is used as the number of limit to the maximum survived branches in the breadth-first tree algorithm. By setting M equal to different values, it can provide different tradeoff solutions between the system performance and the complexity. The larger M value, the better performance is obtained, however the larger complexity is required.
4. Computer Simulation
4.1. BLE and BNLE
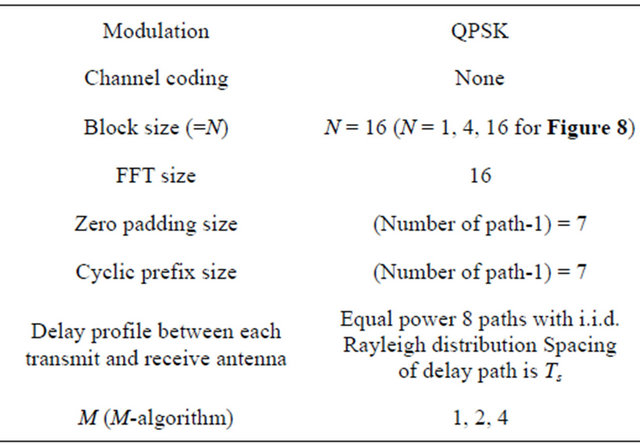
In this section, we show the BER performance of the proposed schemes in MIMO, SIMO, and SISO quasistatic frequency selective channels. First we have compared the BER characteristics of BLE with the existing SC-FDE. The simulation conditions are shown in Table 1.
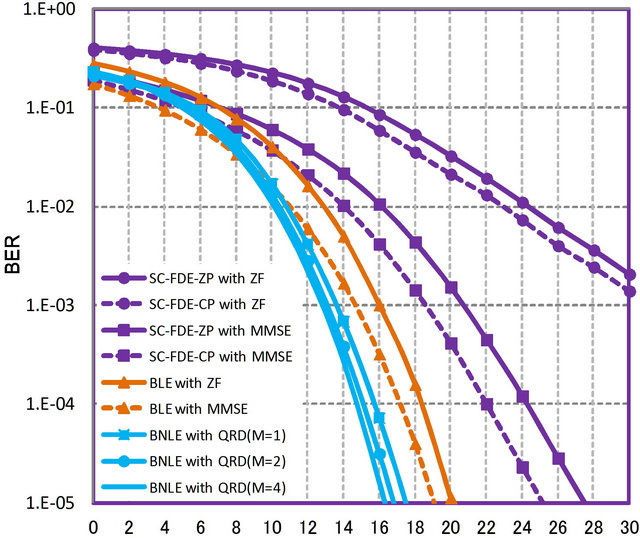
As shown in Figure 1, the multipath channel between each transmit and receive antenna is modeled as the tapped delay line with L taps spaced by symbol duration Ts and each tap gain follows the independent complex Gaussian random variable with equal power, i.e., the quasi-static multipath Rayleigh fading channel with equal delay path power has been assumed. Under the same simulation condition, we have made the comparison among the MIMO, SIMO, and SISO channels. Figure 5 shows the BER performance with nT = nR = 4, L = 8 and we set the transmit block length to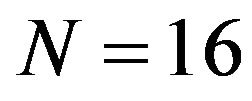 . In order to fairly compare the SC-FDE with the proposed schemes, we assume that the size of zero padding is 7 and the length of CP is
. In order to fairly compare the SC-FDE with the proposed schemes, we assume that the size of zero padding is 7 and the length of CP is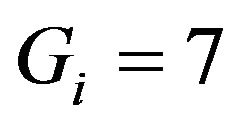 , and by the Section 3.2, we insert
, and by the Section 3.2, we insert 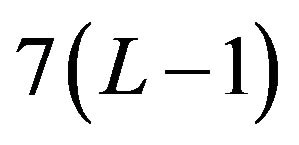 zero symbols before and after the transmit signal vector. Since ZF-FDE with CP scheme can completely eliminate the inter block interferences, it performs better than ZF-FDE with ZP, the latter suffers from noisy prefix copy and sometime leads to a loss in frequency diversity [16]. Using the inverse matrix, the proposed time domain QRD-M and BLE schemes get the
zero symbols before and after the transmit signal vector. Since ZF-FDE with CP scheme can completely eliminate the inter block interferences, it performs better than ZF-FDE with ZP, the latter suffers from noisy prefix copy and sometime leads to a loss in frequency diversity [16]. Using the inverse matrix, the proposed time domain QRD-M and BLE schemes get the
Table 1. Computer simulation conditions for Figures 5-8.
Average Eb/N0 [dB]/receive antenna
Figure 5. BER comparison of proposed time domain block equalizers on MIMO quasi-static frequency selective channels (4 × 4 antennas).
full multipath diversity (the SISO case in equation (17) well supports this characteristic) and obtain the better BER performance by 5 - 8 dB at BER = 10−5 than the SC-FDE based on MMSE criterion. We can say, for the short block length like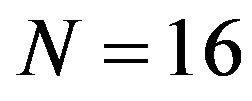 , BLE and QRD-M show the excellent performances among the compared schemes. In the case of BNLE with QRD-M with M = 1, we can obtain the better BER performance than BLE with MMSE by about 1 dB. From the complexity aspects of QRD-M algorithm, we only consider the case of M = 1 in the followings.
, BLE and QRD-M show the excellent performances among the compared schemes. In the case of BNLE with QRD-M with M = 1, we can obtain the better BER performance than BLE with MMSE by about 1 dB. From the complexity aspects of QRD-M algorithm, we only consider the case of M = 1 in the followings.
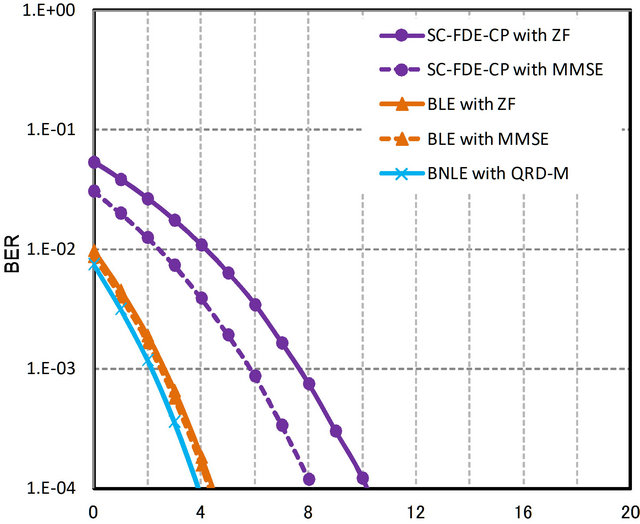
In Figure 6, the simulation results for SIMO channel are shown. The proposed scheme can improve the average  by 4 dB at BER = 10−5.
by 4 dB at BER = 10−5.
In Figure 7, we give the simulation results for SISO channel. Comparing the SC-FDE with MMSE with the BLE with MMSE, the proposed BLE with MMSE exhibits the better BER by 2 dB - 6 dB at BER = 10−5. How-
Average Eb/N0 [dB]/receive antenna
Figure 6. BER comparison of proposed time domain block equalizers on SIMO quasi-static frequency selective channels (1 × 4 antennas).

Average Eb/N0 [dB]/receive antenna
Figure 7. BER comparison of proposed time domain block equalizers on SISO quasi-static frequency selective channels (1 × 1 antenna).
ever, these improvements are mainly brought by the effect of MRC, which is only usable for the size of N = 1. On the other hand, the SC-FDE with CP or ZP only uses the nulling operation, thus the receive powers from multiple receive antennas are not fully combined for the signal separation and equalization.
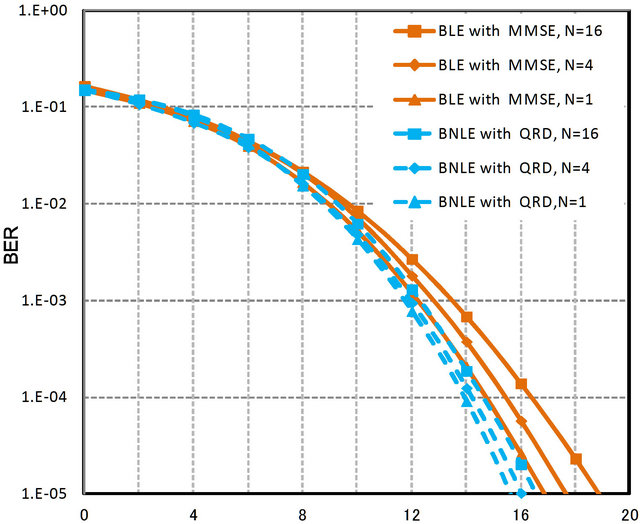
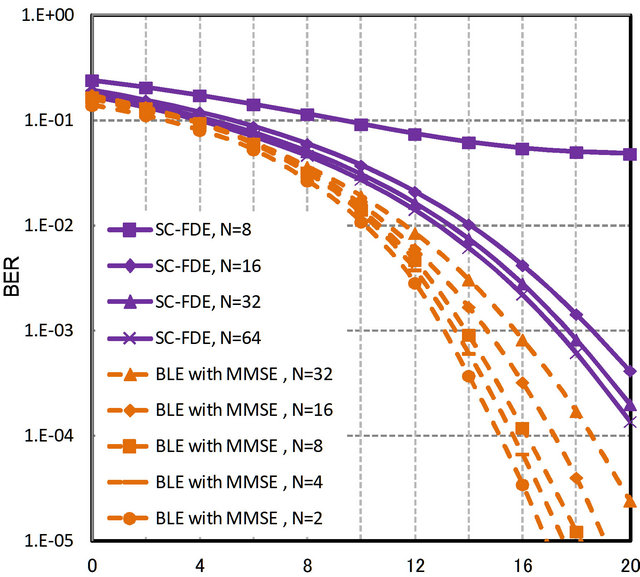
Figures 8 and 9 shows the BER performance for different blocks length of N on SISO and MIMO quasistatic frequency selective channels. The simulation result shows that the shorter block length can get more diversity gain in BLE and BNLE receivers. BLE suffers from the problem of exponential growth of computational complexity for calculating the inverse matrix when the
Average Eb/N0 [dB]/receive antenna
Figure 8. BER comparison between BLE with MMSE and BNLE with QRD-M for the different block length of N on SISO quasi-static frequency selective channels (1 × 1 antenna).
Average Eb/N0 [dB]/receive antenna
Figure 9. BER comparison between BLE and SC-FDE with MMSE for the different block length of N on MIMO quasistatic frequency selective channels (4 × 4 antennas).
block size N becomes large. However, this problem does not exist for SC-FDE because of the FFT processing in frequency domain. Accordingly the merit that the shorter block length exhibits the better BER in BLE seems beneficial to the short time block transmission under the fading channel with time selectivity, because the short time block transmission is not very much influenced by the rapid time variation of the channel.
4.2. Analysis of Computational Complexity
We compare the computational complexity among the proposed schemes. The total numbers of real products and additions required for detecting one transmit symbol are derived as follows:
MIMO SC-FDE:
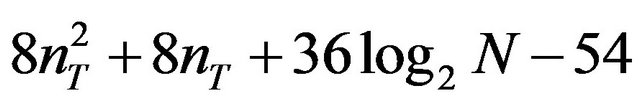 (28)
(28)
MIMO BLE with ZF:
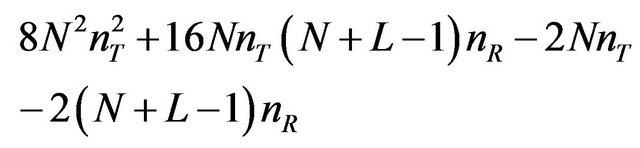 (29)
(29)
MIMO BLE with MMSE:
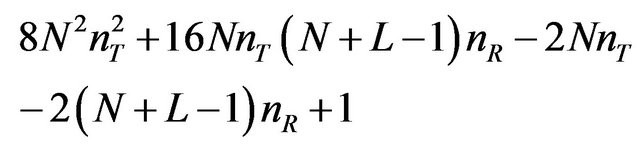 (30)
(30)
MIMO BNLE with QRD-M:
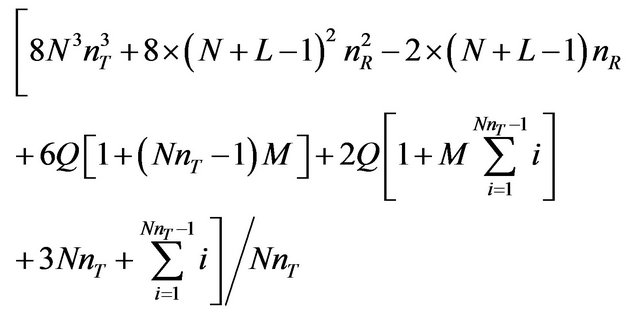 (31)
(31)
MIMO BNLE with full MLD:
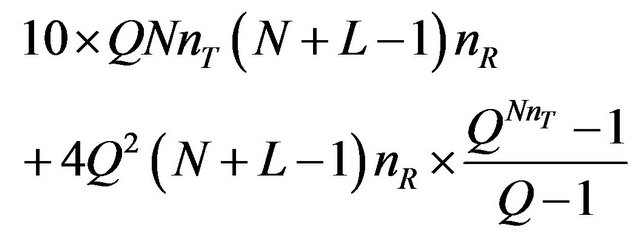 (32)
(32)
where N is the block length in BLE or BNLE and also is the number of sample point in one block of MIMO SC-FDE. Q is the number of modulation levels and in this paper we set Q = 4 (QPSK) and M = 1. The computational complexities under different parameters are shown as in Table 2.
From Table 2 we can say that the computational complexity increases with the order of SC-FDE < QRD-M < BLE ZF < BLE MMSE < full MLD. Especially, we found that SC-FDE has the least computational complexity in those four schemes. If enough memories to store the products and additions are available, the QRD-M scheme will show the best performance. In addition, in the case of short block length, BNLE with QRD-M needs less amount of computation comparing to SC-FDE.
4.3. LDPC Coded BLE and BNLE
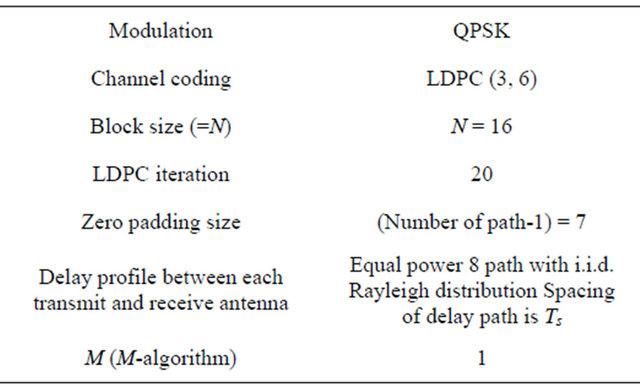
In this section, we employed the LDPC encoding process in the transmitter to verify the feasibility of applying LDPC codes for BLE and BNLE. The sum-product algorithm is used to decode the LDPC code at the receiver. The simulation conditions are shown in Table 3. Figure 10 shows the BER performance of proposed LDPC coded
Table 2. Computational complexity/symbol.
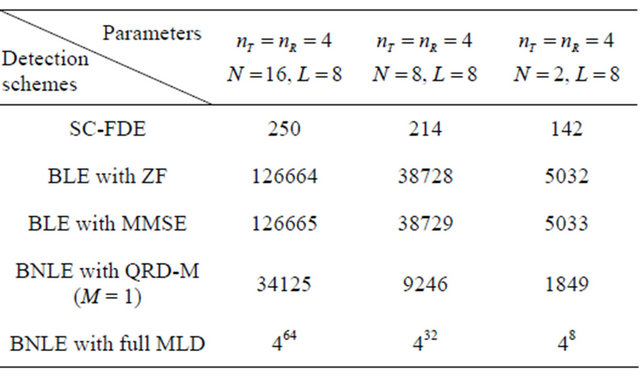
Table 3. Computer simulation conditions for Figure 10.

Average Eb/N0 [dB]/receive antenna
Figure 10. BER performances of proposed LDPC coded time domain block equalizers on MIMO quasi-static frequency selective channels (4 × 4 antennas).
schemes with nT = nR = 4 for MIMO quasi-static frequency selective fading. The simulation results demonstrate that the proposed LDPC coded equalization schemes can obtain the great improvements in BER characteristics. As shown in Figure 10, the LDPC coded BLE and BNLE with QRD-M schemes obtain the better BER performances by about 8 dB at BER = 10−5 compared with the corresponding uncoded schemes.
5. Conclusion
In this paper, we have proposed the time domain block linear and nonlinear equalizers for the signal separation and equalization of single carrier transmission on quasistatic frequency selective MIMO, SIMO, and SISO channels. We have compared the BER characteristics of the proposed time domain equalizers with the conventional frequency domain SC-FDE. As a result, the proposed time domain block equalizers which utilize the zero symbol insertion and short block length transmission exhibit the better BER characteristics than the conventional SC-FDE. The proposed block nonlinear equalizer using QRD-M exhibits the best BER performance. From the computational complexity analysis, we have found that the proposed BNLE with QRD-M can greatly reduce the computational burden at the receiver compared with the one using full MLD. We also applied the LDPC code to the proposed block equalization schemes and the large coding gains were observed. The single carrier transmission used in the proposed scheme is superior to the multicarrier transmission like OFDM in PAPR and the signal separation and equalization in time domain for the proposed schemes is especially suited to the short block length transmission. As the single carrier transmission is robust against the non-linear amplifiers due to the low PAPR and the short block length transmission is not very much affected by the rapid channel variation, the proposed time domain equalizers is supposed to be useful for the high speed uplink transmissions under rapidly time varying frequency selective channels.
6. Acknowledgements
This study has been supported by the Scientific Research Grant-in-aid of Japan No. 24560454.
REFERENCES
- D. Falconer, S. L. Ariyavisitakul, A. Benyamin-Seeyar and B. Eidson, “Frequency Domain Equalization for SingleCarrier Broadband Wireless Systems,” IEEE Communications Society Magazine, Vol. 40, No. 4, 2002, pp. 58-66. doi:10.1109/35.995852
- N. Le Khoa, H. Ishikami, Y. Iwanami and E. Okamoto, “A Consideration on the Improvement of LDPC Coded MIMO OFDM with Sphere Decoding through Outside Iterative Data Feedback,” IEICE Transactions on Communications B, Vol. 91, No. 1, 2008, pp. 112-117.
- G. L. Stuber, J. R. Barry, S. W. McLaughlin, Y. Li, M. A. Ingram and T. G. Pratt, “Broadband MIMO-OFDM Wireless Communications,” Proceedings of the IEEE, Vol. 92, No. 2, 2004, pp. 271-294. doi:10.1109/JPROC.2003.821912
- J. Karjalainen, N. Veselinovic, K. Kansanen and T. Matsumoto, “Iterative Frequency Domain Joint-over-Antenna Detection in Multiuser MIMO,” IEEE Transactions on Wireless Communications, Vol. 6, No. 10, 2007, pp. 3620- 3631. doi:10.1109/TWC.2007.060037
- T. Abe and T. Matsumoto, “Space-Time Turbo Equalization in Frequency-Selective MIMO Channels,” IEEE Vehicular Technology Society, Vol. 52, No. 3, 2003, pp. 469-475. doi:10.1109/TVT.2003.813227
- D. K. C. So and R. S. Cheng, “Layered Maximum Likelihood Detection for V-BLAST in Frequency Selective Fading Channels,” IEEE 55th Vehicular Technology Conference, VTC Spring, Birmingham, 6-9 May 2002, pp. 135-139. doi:10.1109/VTC.2002.1002679
- D. K. C. So and R. S. Cheng, “Layered Maximum Likelihood Detection for MIMO Systems in Frequency Selective Fading Channels,” IEEE Transactions on Wireless Communications, Vol. 5, No. 4, 2006, pp. 752-762. doi:10.1109/TWC.2006.1618924
- Y. Goto, Y. Iwanami and E. Okamoto, “Improvement of BER Characteristics with Eigen-Mode Transmission in MIMO Frequency Selective Channels,” IEICE Transactions on Communications, Vol. 90, No. 10, 2007, pp. 1045-1049.
- Y. Takahashi, Y. Iwanami and E. Okamoto, “A Comparison of Time Domain Equalizers by Block Processing in SISO Single Carrier Transmission,” IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC’07), Athens, 3-7 September 2007.
- Y. Takahashi, Y. Iwanami and E. Okamoto, “A Time Domain Block Equalization Scheme on SIMO Frequency Selective Channels,” IEEE Region 10 Conference (TENCON’07), Taipei, 30 October-2 November 2007.
- S. Nakanobu, Y. Iwanami and E. Okamoto, “A Comparative Study on Time Domain Sequential Equalizer with MLD and MLSE Equalizer on MIMO Frequency Selective Channels,” IEICE Transactions on Communications, Vol. E-93B, No. 11, 2010, pp. 3197-3202.
- C.-J. Ahn, “Parallel Detection Algorithm Using Multiple QR Decompositions with Permuted Channel Matrix for SDM/OFDM,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 4, 2008, pp. 2578-2582. doi:10.1109/TVT.2007.913179
- R. Gallager, “Low Density Parity Check Codes,” IRE Transactions on Information Theory, Vol. 8, No. 1, 1962, pp. 21-28. doi:10.1109/TIT.1962.1057683
- D. J. C. Mackay and R. M. Neal, “Near Shannon Limit Performance of Low Density Parity Check Codes,” Electronics Letters, Vol. 33, No. 6, 1999, pp. 457-458. doi:10.1049/el:19970362
- J. G. Proakis, “Digtial Communications,” 4th Edition, McGraw-Hill Inc, New York, 2001.
- Z. D. Wang, G. B. Giannakis and M. De Courville, “Cyclic Prefixing or Zero Padding for Wireless Multicarrier Transmissions,” IEEE Transactions on Communications, Vol. 50, No. 12, 2002, pp. 2136-2148. doi:10.1109/TCOMM.2002.806518

