Int'l J. of Communications, Network and System Sciences
Vol.4 No.2(2011), Article ID:4021,5 pages DOI:10.4236/ijcns.2011.42009
Scheme for Secure Communication via Information Hiding Based on Key Exchange and Decomposition Protocols
Computer Science Department, New Jersey Institute of Technology, University Heights, Newark, USA
E-mail: verb@njit.edu
Received January 26, 2011; revised February 8, 2011; accepted February 9, 2011
Keywords: Complex Modulus, Cryptanalytic Protection, Decomposition, Gaussian Modular Arithmetic, Information Hiding, Key Exchange, Modular Elliptic Curve, Secure Communication
Abstract
This paper considers a decomposition framework as a mechanism for information hiding for secure communication via open network channels. Two varieties of this framework are provided: one is based on Gaussian arithmetic with complex modulus and another on an elliptic curve modular equation. The proposed algorithm is illustrated in a numerical example.
1. Introduction and Problem Definition
In this paper it is demonstrated how to use various Diffie-Hellman key establishment (DHKE) protocols in order to design a computationally efficient cryptographic schemes for secure communication between two parties {called Alice and Bob}. One of these key establishment protocols is based on modular elliptic curves (ECDHKE) [1]. Another DHKE protocol is based on arithmetic of complex integers with complex modulus [2].
DHKE protocol based on complex integers: In this scheme both parties agree to select a Gaussian integer L = (g, h) := g + ih called generator and a complex modulus (l, p) := l + ip with real integer components l and p. Alice and Bob independently select secret real integers alpha and beta respectively. Alice and Bob respectively compute their public keys:
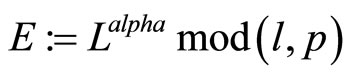 ; (1)
; (1)
and
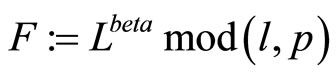 . (2)
. (2)
Then Alice and Bob compute respectively
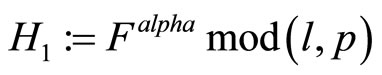 (3)
(3)
and
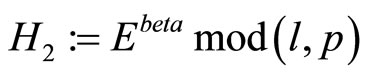 . (4)
. (4)
As a result,
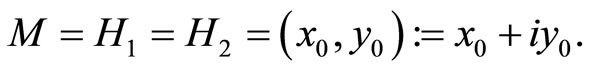 (5)
(5)
Therefore a pair of real integers 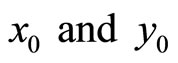 can be used by Alice and Bob to design a cryptographic protocol.
can be used by Alice and Bob to design a cryptographic protocol.
DHKE based on elliptic curves: Consider a modular elliptic curve (EC)
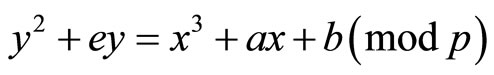 (6)
(6)
where a, b, e and p are integer parameters of the EC, and modulus p is an odd real prime [3]. If (6) is used for ECDHKE between Alice and Bob, then both parties create a mutual secret key 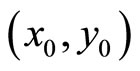 that is a point on (6). The scheme is analogous to (1)-(5): Alice and Bob select a point Q with high order on (6) and real integers alpha (Alice’s secret key) and beta (Bob’s secret key). Then they respectively compute their public keys:
that is a point on (6). The scheme is analogous to (1)-(5): Alice and Bob select a point Q with high order on (6) and real integers alpha (Alice’s secret key) and beta (Bob’s secret key). Then they respectively compute their public keys:
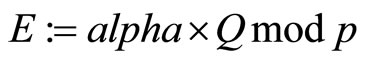 ; (7)
; (7)
and
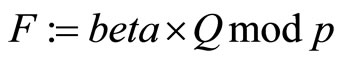 . (8)
. (8)
Here both E and F are points on (6).
Then Alice and Bob compute respectively
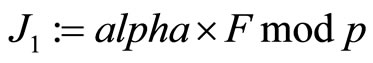 ; (9)
; (9)
and
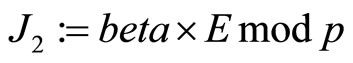 . (10)
. (10)
As a result,
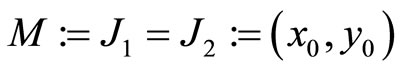 . (11)
. (11)
2. Decomposition
Consider randomly selected non-zero integers 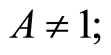
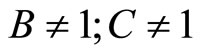 that are co-prime with p. Consider positive integers k, q and r that satisfy
that are co-prime with p. Consider positive integers k, q and r that satisfy
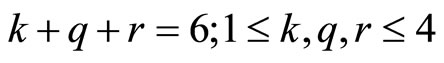 . (12)
. (12)
Compute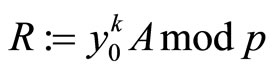 ;
;
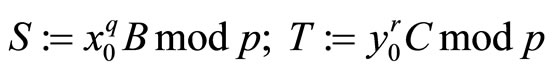 (13)
(13)
or 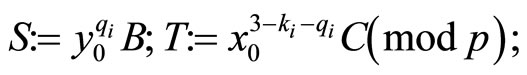
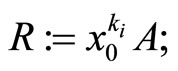
{for details see Step5 below};
Select integers u, v and w that satisfy
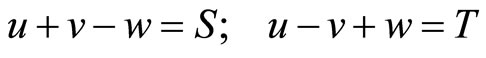
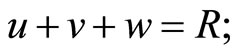 . (14)
. (14)
Then (14) implies that
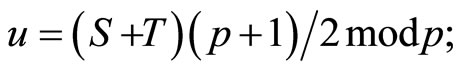 (15)
(15)
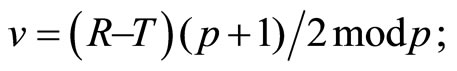 (16)
(16)
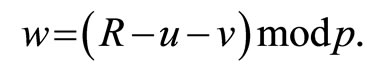 (17)
(17)
Here k and q are secret keys that satisfy
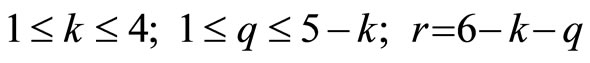 ; (18)
; (18)
where k and q are periodically updated.
There are ten combinations of positive integers satisfying (12); these combinations are listed in lexicographically increasing order in Table 1.
3. Numeric Illustration
Let p=99991; consider an elliptic curve
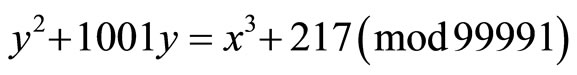 . (19)
. (19)
Suppose Alice and Bob have established a secret key for communication as point 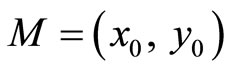 = (86275, 81549); it is easy to verify that P indeed satisfies (19). Juxtapose
= (86275, 81549); it is easy to verify that P indeed satisfies (19). Juxtapose 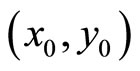 and let G := 8627581549.
and let G := 8627581549.
4. Information Hiding Protocol—{k, q}
Step1: Communicating parties (Alice and Bob) establish a key M = 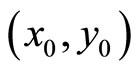 using one of schemes listed in section 1;
using one of schemes listed in section 1;
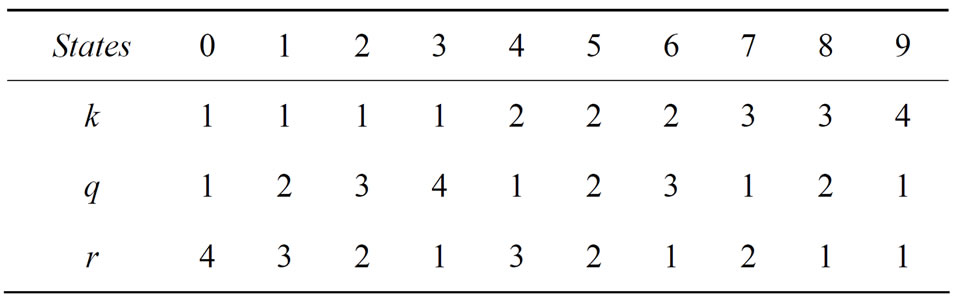
Table 1. All combinations of exponents.
Step2: Juxtapose coordinates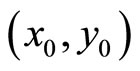 ;
;
let
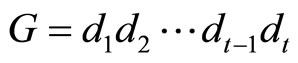 , (20)
, (20)
where 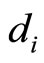 are its decimal digits.
are its decimal digits.
Here
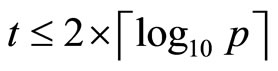 ;
;
Step3: Suppose Alice wants to transmit a plaintext array
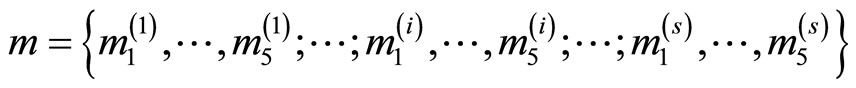
where
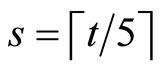 . (21)
. (21)
Encryption of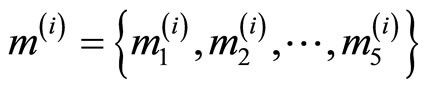 :
:
Step4: Using  select corresponding
select corresponding 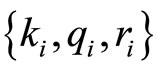 from Table 1;
from Table 1;
Step5: if 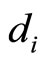 is even, then compute
is even, then compute 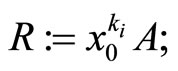
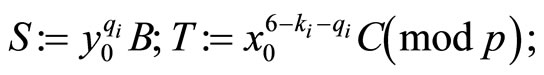
else
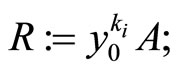
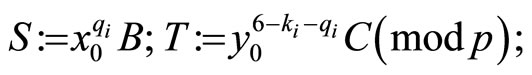 (22)
(22)
Step6: Compute the information hiding keys (15)-(17): {u, v, w};
Step7: {enhancement of crypto-immunity}:
for 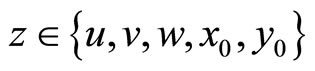 do if
do if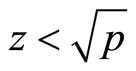 , then
, then 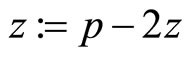 else z := 2z;
else z := 2z;
Step8: compute
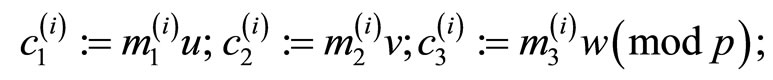 (23)
(23)
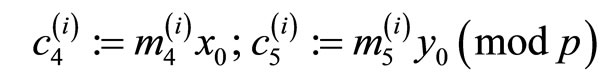 . (24)
. (24)
Decryption is performed in reverse.
Remark2: After t cycles Alice and Bob must use a DHKE to establish a new mutual secret key G.
Choice of A, B and C: one way to choose A and B is to assign even digits of G to A and odd digits of it to B. Then select C that is a multiplicative inverse of AB modulo p:
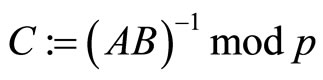 [4]. (25)
[4]. (25)
Remark3: The ideas of decomposition can be applied to any secret key; where splitting is completely independent of how this key is established.
5. Plaintext Pre-conditioning
If there is a pair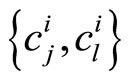 , where both components are smaller than p, then with high probability holds that
, where both components are smaller than p, then with high probability holds that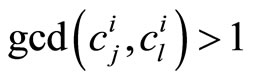 . Therefore either
. Therefore either
 or
or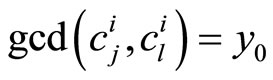 . (26)
. (26)
To preclude this possibility consider the following protocol of plaintext pre-conditioning: subdivide plaintext m into arrays of blocks in such a way that for every block 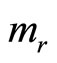 holds
holds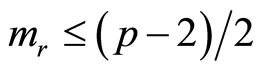 ; if
; if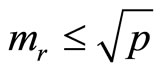 , then assign
, then assign
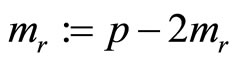 (27)
(27)
Remark4: Notice that the right-most binary digit of 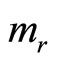 equals 1.
equals 1.
6. Numeric Illustration Continued
Assign all even digits of G := 8627581549 to A and all odd digits of G to B.
Then A = 67859, {in Table 2 they are shown in bold font}, B = 82514, and 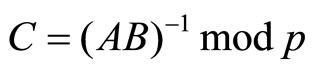 = 87964 [3].
= 87964 [3].
Indeed: (21508*87964) mod99991 = 1.
Since G does not have digits 0 and 3, then only eight of ten combinations of {k, q, r} that are listed in Table 1 are used to compute the information hiders u, v, w:
Computation of encryptors u, v, w
For 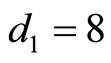 {see the 1st column in Table 2} compute
{see the 1st column in Table 2} compute
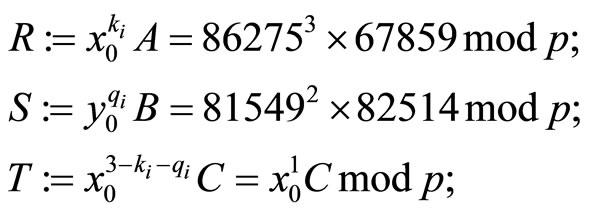
and then compute encryptors u, v and w (15)-(17).
For 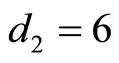 {see the 2nd column in Table 2} compute
{see the 2nd column in Table 2} compute
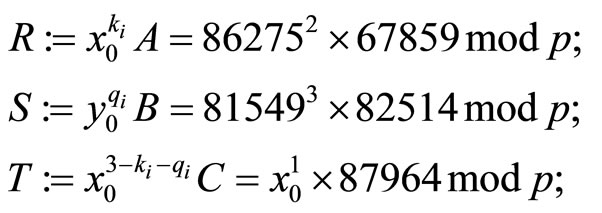
and then compute encryptors u, v and w.
See Table 3 of all encryptors for i = 1,2, t.
t.
Plaintext pre-conditioning
Let 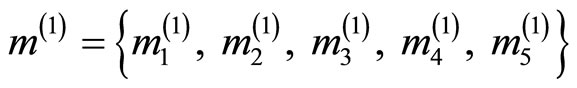 = {266, 45769, 37585, 36488, 46572}.
= {266, 45769, 37585, 36488, 46572}.
Remark5: Notice that each component in m is smaller
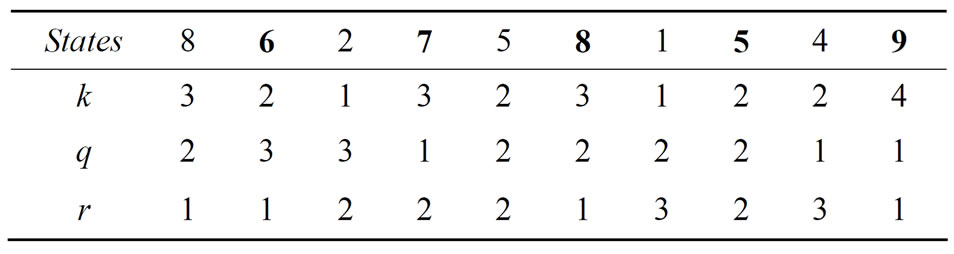
Table 2. Sequence of exponents k, q and r based on secret key .
.
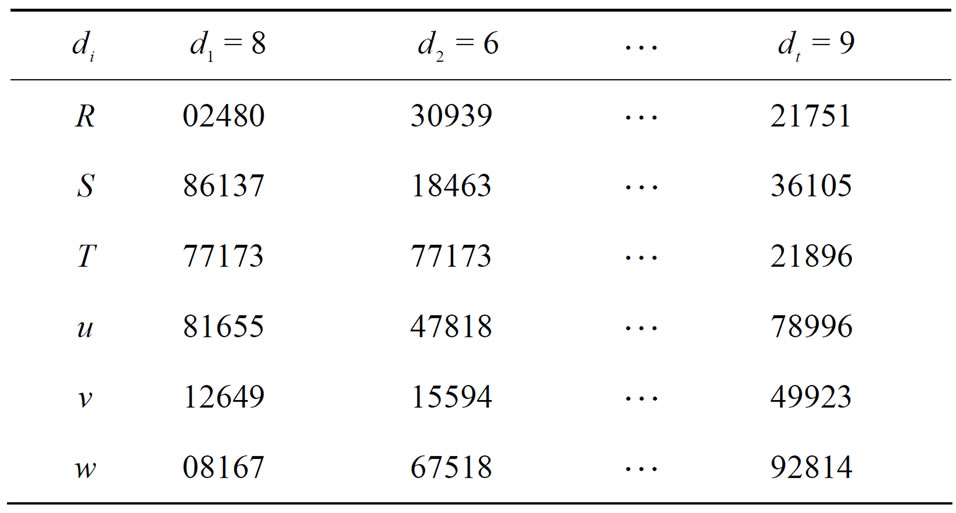
Table 3. Encryption stage: information hiders u, v, w and ciphertexts.
than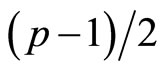 .
.
Because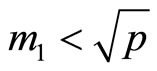 , reassign
, reassign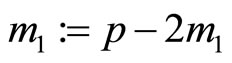 ; {odd integer}.
; {odd integer}.
Since all other blocks in plaintext m are greater than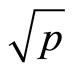 , therefore reassign
, therefore reassign
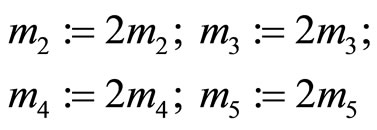
{all four are even integers}.
Encryption {see Step7}:
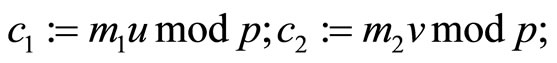
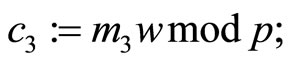
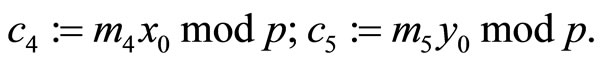
Alice sends ciphertext  to Bob via open communication channels. See Table 3 with encryptors R, S, T, u, v and w; Table 4 with plaintext arrays
to Bob via open communication channels. See Table 3 with encryptors R, S, T, u, v and w; Table 4 with plaintext arrays 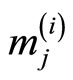 and Table 5 of corresponding ciphertext arrays.
and Table 5 of corresponding ciphertext arrays.
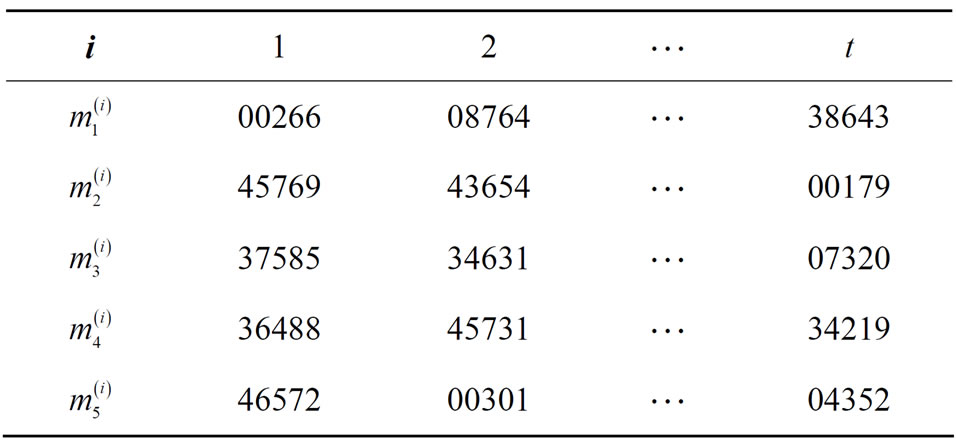
Table 4. Plaintext arrays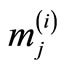 ; i = 1,2,
; i = 1,2, ,t.
,t.
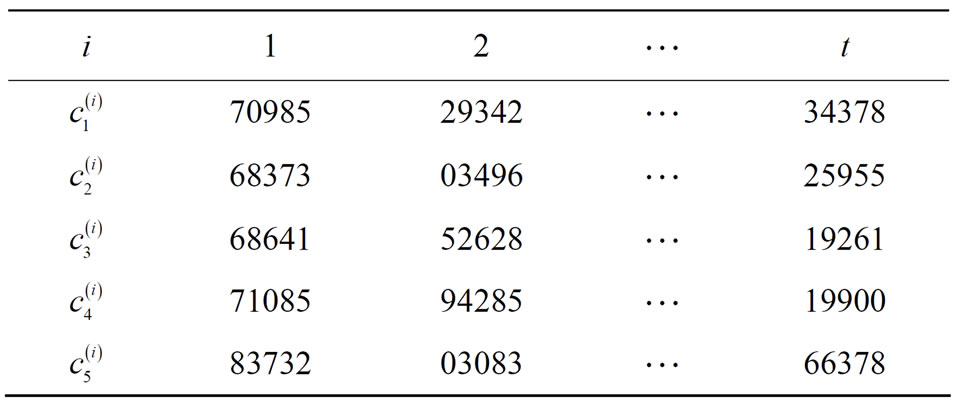
Table 5. Ciphertext arrays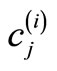 ; i = 1,2,
; i = 1,2, ,t.
,t.
Decryption is performed in reverse: since Bob knows the mutual secret key M =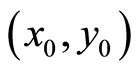 , he finds A, B, k, q and r; then computes C, R, S, T; and the multiplicative inverse values of u, v and w.
, he finds A, B, k, q and r; then computes C, R, S, T; and the multiplicative inverse values of u, v and w.
7. Key Establishment Based on Gaussian Modulus
Consider (l, p) = (1000, 3001); and a generator L = (2269, –2204). All corresponding steps and actions by Alice and Bob are provided in Table 6.
Therefore, M = (–0502, 1853) is the mutual secret key established between Alice and Bob. Notice that components in M can be positive and negative. If a component is negative, post digit “2” in front of its left-most digit; if the component is positive, post digit “9” in front of its left-most digit. Therefore M := (20502, 91853). For large l and p in modulus (l, p), the probability is negligibly small that either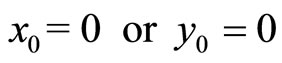 .
.
8. Computational Complexity
For every digit in juxtaposed G it is possible to encrypt one plaintext array.
With high probability each component in 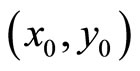 has the same number of digits t as modulus p. Therefore in G there are about 2t digits. For each digit we select an appropriate combination of keys {k, q, r} from Table 1 and encrypt five blocks of the plaintext. Therefore for every G we can encrypt
has the same number of digits t as modulus p. Therefore in G there are about 2t digits. For each digit we select an appropriate combination of keys {k, q, r} from Table 1 and encrypt five blocks of the plaintext. Therefore for every G we can encrypt 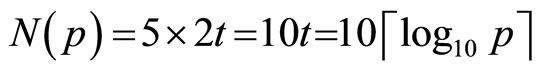 blocks.
blocks.
In application, to assure strong crypto-immunity,
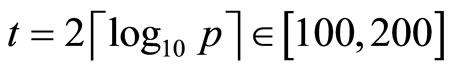 .
.
Thus, if p is a 50-digit long integer, then 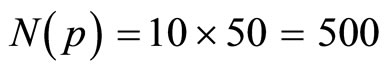 blocks of plaintext.
blocks of plaintext.
9. Reduction of Complexity
To reduce computational complexity of encryption for every G, we pre-compute and store for every 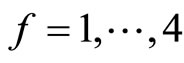
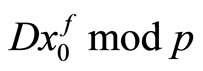 and
and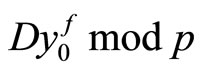 , where
, where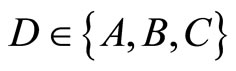 .
.
Another way to reduce complexity is to avoid computation of multiplicative inverse C (24). Instead we can partition G onto about equal number of digits. For instance, if G = 2718281828459045, we can either assign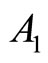 := 27182;
:= 27182;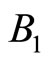 := 818284 and
:= 818284 and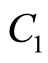 := 59045 or to substitute di
:= 59045 or to substitute di

Table 6. Key establishment (1)-(5).
gits 1,2, ,9,1,2,
,9,1,2, into G:
into G:
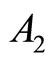 := 1728384858657085;
:= 1728384858657085;
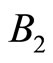 := 2112231425469748;
:= 2112231425469748;
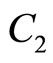 := 2718283848556075.
:= 2718283848556075.
10. Conclusion
In the proposed cryptocol it is shown that for every pair of integers in secret key 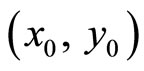 there are numerous ways to compute integers {u, v, w} that hide information on the encryption stage.
there are numerous ways to compute integers {u, v, w} that hide information on the encryption stage.
11. Acknowledgements
I express my appreciation to NJIT students A. Koripella and M. Sikorski for their assistance and suggestions that improved style of this paper, to D. Kanevsky for his participation in discussion, and to C. Pomerance and H. Cohen for their advices about complex modulus reduction.
12. References
[1] W. Diffie and M. Hellman, “New Directions in Cryptography,” IEEE Transactions on Information Theory, Vol. IT-22, No. 6, 1976, pp. 644-654. doi:10.1109/TIT.1976. 1055638
[2] S. G. Krantz, “Modulus of a Complex Number,” Handbook of Complex Variables, Birkhäuser Publishing Ltd., Boston, 1999, pp. 2-3.
[3] J. Hoffstein, J. Pipher and J. Silverman, “An Introduction to Mathematical Cryptography,” Springer, New York, 2008.
[4] B. Verkhovsky, “Enhanced Euclid Algorithm for Modular Multiplicative Inverse and Its Application in Cryptographic Protocols,” International Journal of Communications, Network and System Sciences, Vol. 3, No.12, 2010, pp. 901-906. doi:10.4236/ijcns.2010.312123
Appendix
A1. Generalization
Step1A: Establish a secret key M between communicating parties and juxtapose it.
Remark6: Either Gaussian arithmetic with complex modulus or other mechanisms for DHKE can be used to establish M.
Step2A: Using M, the parties select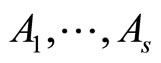 , where s is an integer parameter of encryption protocol;
, where s is an integer parameter of encryption protocol;
Step3A: for i=1, ,t
,t
for j=1, ,s do
,s do
if 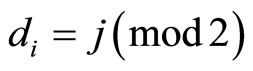 (A1)
(A1)
then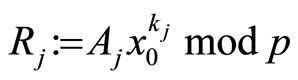 , (A2)
, (A2)
else 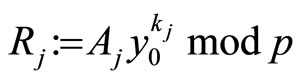 ; (A3)
; (A3)
Step4A: Compute for j=2, 3, ,s
,s
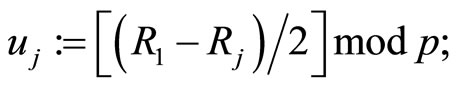 (A4)
(A4)
and 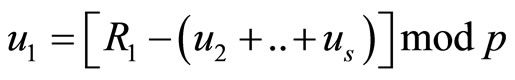 (A5)
(A5)
Step5A {encryption}: for i from 1 to s
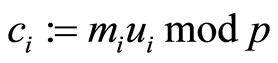 . (A6)
. (A6)
A2. Selection of Table for 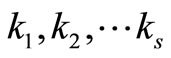
If s > 3, the number of possible combinations for secret keys 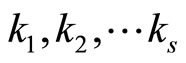 grows exponentially if s is increasing.
grows exponentially if s is increasing.
This is an additional potential for randomization. If a protocol designer of encryption/decryption scheme represents G in a numeric form with base n, then it is possible to select n combinations of secret exponents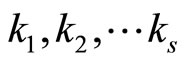 , where each combination corresponds to every digit of G. Therefore the parties must exchange between themselves a
, where each combination corresponds to every digit of G. Therefore the parties must exchange between themselves a 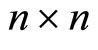 square matrix:
square matrix:
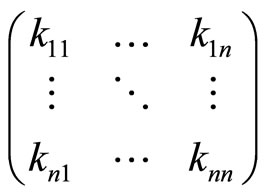 (A7)
(A7)
For example, if s = 4 and n = 16, then we need to specify sixteen combinations of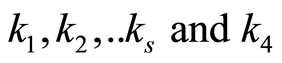 .
.
If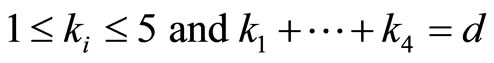 , then the number of possible combinations of k’s is 35 for d = 8.
, then the number of possible combinations of k’s is 35 for d = 8.

