Int'l J. of Communications, Network and System Sciences
Vol.2 No.4(2009), Article ID:536,9 pages DOI:10.4236/ijcns.2009.24027
Self-Encoded Multiple Access Multiuser Convolutional Codes in Uplink and Downlink Cellular Systems
University of Nebraska-Lincoln, Omaha, NE, USA
Email: jjung@mail.unomaha.edu, {wjang1, lnguyen1}@unl.edu
Received March 9, 2009; revised May 5, 2009; accepted June 20, 2009
Keywords: Spread Spectrum, Self-Encoded Multiple Access, Multiuser Convolutional Coding,Multiuser Detection
ABSTRACT
Self-encoded spread spectrum eliminates the need for traditional pseudo noise (PN) code generators. In a self-encoded multiple access (SEMA) system, the number of users is not limited by the number of available sequences, unlike code division multiple access (CDMA) systems that employ PN codes such as m-, Gold or Kassami sequences. SEMA provides a convenient way of supporting multi-rate, multi-level grades of service in multimedia communications and prioritized heterogeneous networking systems. In this paper, we propose multiuser convolutional channel coding in SEMA that provides fewer cross-correlations among users and thereby reducing multiple access interference (MAI). We analyze SEMA multiuser convolutional coding in additive white Gaussian noise (AWGN) channels as well as fading channels. Our analysis includes downlink synchronous system as well as asynchronous system such as uplink mobile-to-base station communication.
1. Introduction
In CDMA communications, each user is assigned a unique PN spreading sequence that has a low cross-correlation with other users' sequences. This prevents code collisions between the users and controls MAI. PN code generators are typically linear feedback shift register circuits that generate maximal-length or related sequences. These deterministic sequences provide low cross-correlations that are critical for achieving good system performance. Although random codes have often been employed for analysis purposes [1], they present a practical implementation problem because data recovery by the intended receiver requires a prior knowledge of the codes for signal despreading. As a result, the random codes in these studies would remain fixed once they have been generated. In previous work, we have proposed a novel spread spectrum technique that does not use PN codes [2]. The new technique is unique in that traditional transmit and receive PN code generators are not needed.
Our approach abandons the use of PN codes in SEMA that can reduce MAI, and provide a multi-rate and multi-level grade of service for multimedia communications and prioritized networks [3–6]. A realization of the self-encoding principle for a direct sequence spread spectrum systems is illustrated in Figure 1. As the term implies, the spreading code is obtained from the random digital information source itself. At the transmitter, the delay registers are constantly updated from 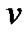 -tap, serial delay of the data, where
-tap, serial delay of the data, where 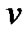 is the code length. The delay registers generate the code chips that switch at
is the code length. The delay registers generate the code chips that switch at 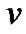 times the data rate for signal spreading. The random nature of the digital information source means that binary symbols can be modeled as independent and identically distributed Bernoulli random variables. Symbol values of +1 and -1 occur equally likely with a probability of 0.5. As a result, the spreading sequences are not only randomly generated and independent of the current symbol, but also dynamically changing from one symbol to the next. This smoothes out the spectrum of the signals and eliminates the spectral lines associated with PN sequences. The self-encoding operation at the transmitter is reversed at the receiver. The recovered data are fed back to the
times the data rate for signal spreading. The random nature of the digital information source means that binary symbols can be modeled as independent and identically distributed Bernoulli random variables. Symbol values of +1 and -1 occur equally likely with a probability of 0.5. As a result, the spreading sequences are not only randomly generated and independent of the current symbol, but also dynamically changing from one symbol to the next. This smoothes out the spectrum of the signals and eliminates the spectral lines associated with PN sequences. The self-encoding operation at the transmitter is reversed at the receiver. The recovered data are fed back to the 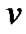 -tap delay registers, which provide an estimation of the
-tap delay registers, which provide an estimation of the
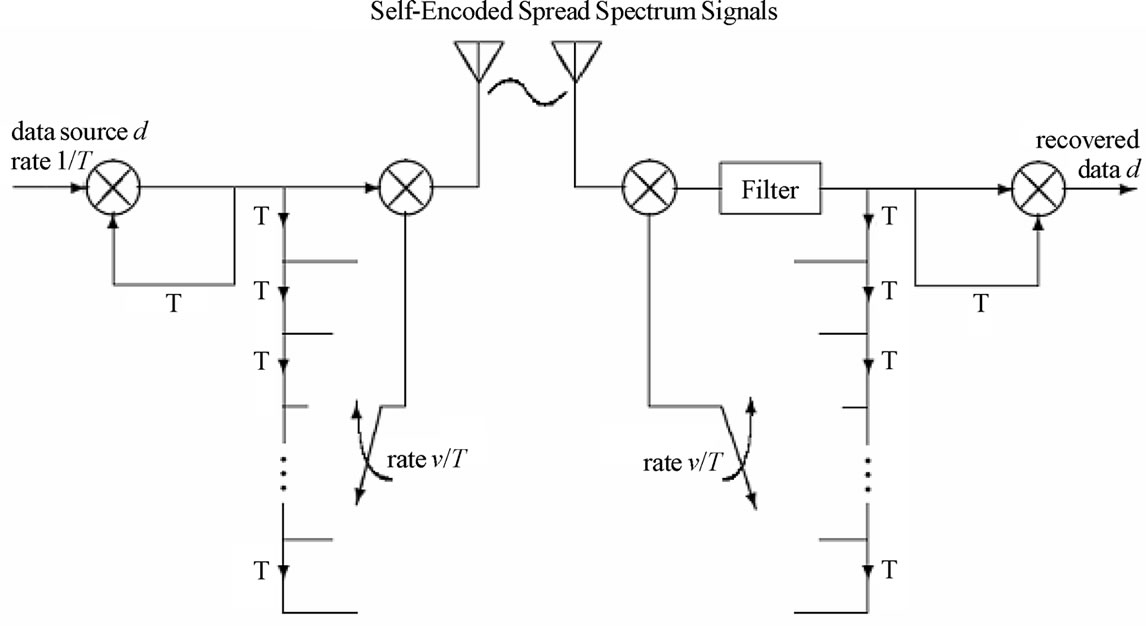
Figure 1. Self-encoded, direct-sequence spread spectrum.
Transmitte’s spreading codes required for signal despreading. Data recovery is by means of a correlation detector. Notice that the contents of the delay registers in the transmitter and receiver should be identical at the start of the transmission. This is accomplished as part of the initial synchronization procedure. In the following, we develop SEMA multiuser convolutional coding, and investigate the performance with and without precoding or multiuser detection. Convolutional codes with Viterbi decoding have been studied for decades and applied in practical communication systems such as wide area networks (IS-95, CDMA2000) and local area networks (IEEE 802.11a and b). In order to improve the performance, we present the shift generator matrix concept that provides lower cross-correlations among users and reduces the MAI in the system. We present the performance analysis and simulation both in uplink asynchronous and downlink synchronous channels.
2. System Model
2.1. SEMA System and Multiuser ConvolutionalCoding
Figure 2 shows the block diagram of SEMA with multiuser detection and channel coding. The SEMA spread block is as illustrated in Figure 1. Notice that the detection errors may accumulate in the delay registers and are the source of self-interference (SI) in the receiver.
Acquisition and tracking of self-encoded sequences can be performed in a similar manner to PN sequences with the proviso that the chip updates are enabled once data transmission has commenced following code acquisition. At the chip rate, the self-encoded chips are latched at the output register by shifting the registers serially, with the output being fed back to the input register. The input feedback is switched to the data during the last chip period of the current symbol for a new chip input. This resembles a simple linear feedback register circuit of length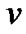 , with zero valued taps except for the input and output taps, where the input register is updated periodically by the data and the output register provides the spreading sequence.
, with zero valued taps except for the input and output taps, where the input register is updated periodically by the data and the output register provides the spreading sequence.
The conventional convolutional codes in Figure 2 applied to single user self-encoded spread spectrum significantly reduce SI due to detection errors in the despreading registers at the receiver. However, under SEMA these codes generate the same code words for different users and may lead to code collisions. We propose to mitigate this problem with shift generator matrix for SEMA multiuser convolutional coding. For example, if the first user employs the generator matrix given in octal form, G1=[5 7 7], the second and the third user can use G2=[7 5 7] and G3=[7 7 5], respectively. The property of G2 and G3 is identical to G1 in that they have the same weight transfer function and maximum free distance,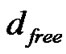 . This method guarantees the maximum free distance per single user and provides lower cross-correlations among the users. Figure 3 compares the crosscorrelation of code words from generator matrix G1 and its shift generator matrices, G1 and G2, in two user systems. The plots show that cross-correlations of the codes using the shift generator matrices are smaller than those with the same matrix [4].
. This method guarantees the maximum free distance per single user and provides lower cross-correlations among the users. Figure 3 compares the crosscorrelation of code words from generator matrix G1 and its shift generator matrices, G1 and G2, in two user systems. The plots show that cross-correlations of the codes using the shift generator matrices are smaller than those with the same matrix [4].
2.2. Matched Filter Receiver
For a multiuser system with K +1 users (K interferers), the received signal at the matched filter is
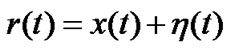 (1)
(1)
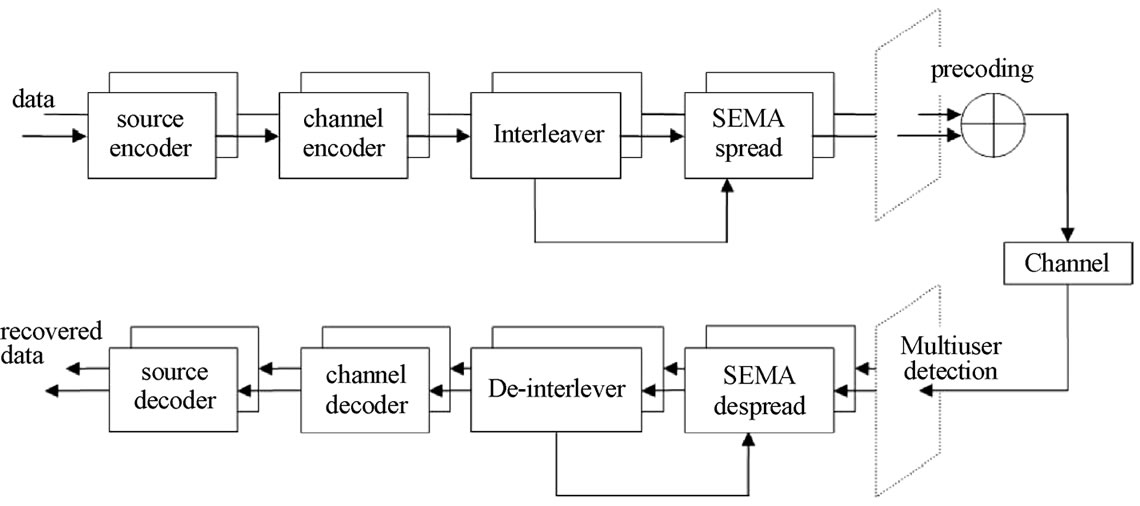
Figure 2. Self-encoded multiple access (SEMA) with channel coding.
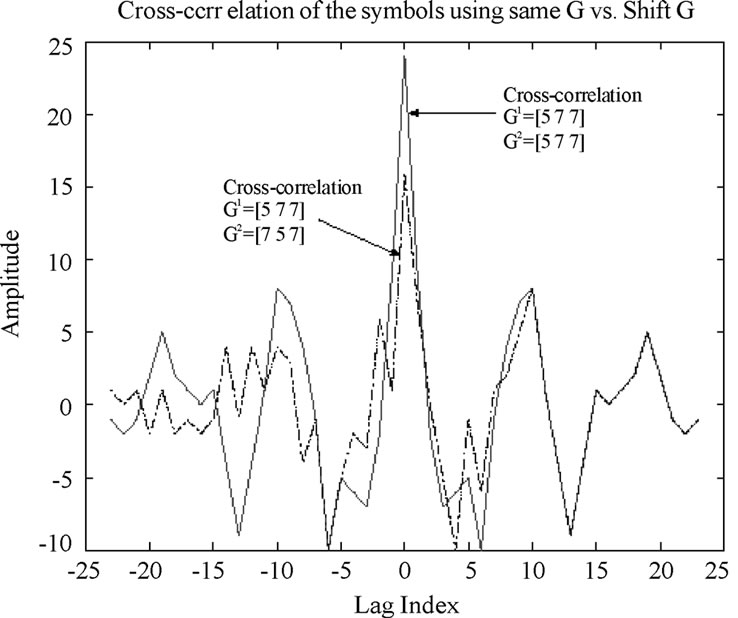
Figure 3. Cross-correlations of the same generator matrix and shifted generator matrices in SEMA.
where x(t) is the transmitted signal, and 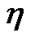 (t) is AWGN noise with a two-sided power spectral density of
(t) is AWGN noise with a two-sided power spectral density of 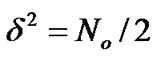 . The transmitted signal in Equation (1) is given by
. The transmitted signal in Equation (1) is given by
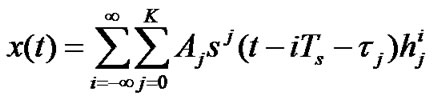 (2)
(2)
where 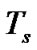 is the symbol duration and
is the symbol duration and 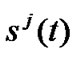 is a spreading sequence during
is a spreading sequence during 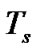 for the
for the 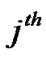 user.
user. 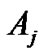 is the amplitudes of the
is the amplitudes of the 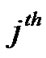 user,
user, 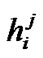 is the encoded symbol of the
is the encoded symbol of the 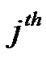 user during the
user during the 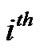 symbol interval, and
symbol interval, and 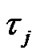 is the time delay of
is the time delay of 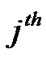 user signal, with 0≤
user signal, with 0≤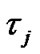 ≤
≤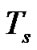
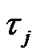 is zero for synchronous systems. For simplicity we do not consider carrier offset in uplink asynchronous systems. The output of the convolutional encoder
is zero for synchronous systems. For simplicity we do not consider carrier offset in uplink asynchronous systems. The output of the convolutional encoder 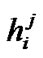 for
for 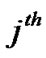 user and
user and 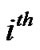 symbol is given by [7]
symbol is given by [7]
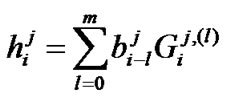 (3)
(3)
where 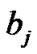 and
and 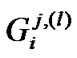 are the set of the
are the set of the 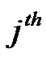 user data sequences and the indices denoting the
user data sequences and the indices denoting the 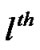 column and
column and 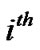 row in the generator matrix, respectively. The generator matrix is
row in the generator matrix, respectively. The generator matrix is
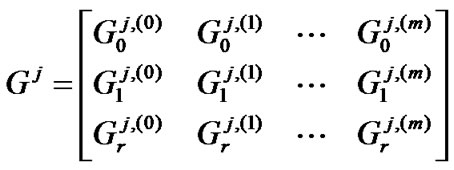 (4)
(4)
where m is the memory size in the encoder, and r is the code rate.
Assuming that the signature waveforms have unit energy, the output of the matched filters of the 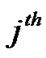 user signature waveform during the
user signature waveform during the 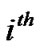 symbol interval is
symbol interval is
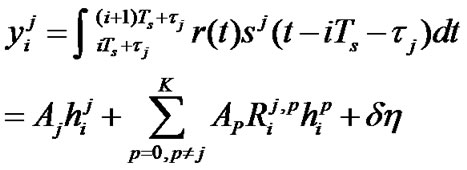 (5)
(5)
Equation (5) consists of the signal 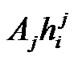 , Gaussian noise
, Gaussian noise 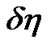 , and the multiple access interference
, and the multiple access interference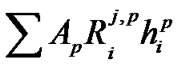 .
. 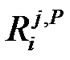 is the cross-correlation of the spreading sequences of the
is the cross-correlation of the spreading sequences of the 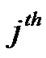 user and
user and 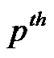 user during the
user during the 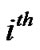 symbol interval. In our analysis, the MAI is modeled as noise [8].
symbol interval. In our analysis, the MAI is modeled as noise [8].
At the receiver, the despreading codes are updated by the detected data. If the data are incorrectly recovered, the incoming signals are correlated with an erroneous sequence set. This may lead to additional errors at the receiver and cause SI, which can be serious at a low signal-to-noise ratio (SNR). To combat self-interference, a longer spreading sequence is desired [3]. We will show that powerful error correcting code can also reduce SI.
2.3. Precoding and Multiuser Detection
Precoding: Decorrelating and precoding techniques have been developed for multiuser detections [6,8,9]. Decorrelating detector is used for multiuser detection at the receiver, whereas precoding is employed at the transmitter to eliminate or reduce MAI. To reduce MAI, we examine the precoding system with interleaver. From Equations (1) and (2), we consider a synchronous system and rewrite (2) as
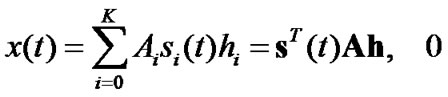 ≤t≤Tb (6)
≤t≤Tb (6)
where 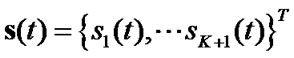 is the signature waveforms vector, and
is the signature waveforms vector, and 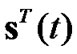 is the transpose of
is the transpose of 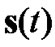 . Then, the output of the matched filters can be expressed as
. Then, the output of the matched filters can be expressed as
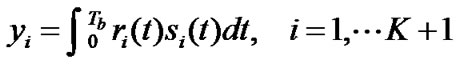 (7)
(7)
Equation (7) can be rewritten in a vector form, with 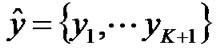 as follows
as follows
 (8)
(8)
A is the diagonal matrix of amplitudes, R is the crosscorrelation matrix, and h is the vector of the data symbols of K+1 users. The basic concept of precoding is to eliminate MAI at the receiver before transmitting signals. In other words, the transmit signals in Equation (2) become
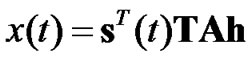 (9)
(9)
where the precode matrix T is chosen as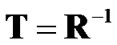 . Then, the output of the bank of matched filters at the receiver will be
. Then, the output of the bank of matched filters at the receiver will be
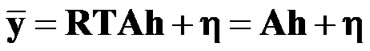 (10)
(10)
In order to maintain the average power with precoding the same as without precoding, we modify the precode transformation matrix as [6,8,10]
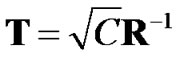 (11)
(11)
such that
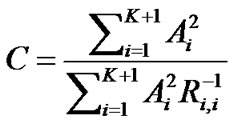 (12)
(12)
Multiuser Detection: Decorrelation detection is a suboptimal multiuser detection with comparatively low complexity. Receiver-based decorrelator can be found in [11]:
 (13)
(13)
3. Performance Analysis
3.1. Self-Interference in SEMA
Due to detection errors, the despreading sequence may not be identical to the spreading sequence at the transmitter. Since the recovered symbols are used to despread the signals, a chip error will remain in the shift registers and affect the following symbol decision until it is shifted out of the registers. This results in error propagation and causes SI: the bit error rate (BER) of SEMA is a dynamic quantity that depends on the signal-to-noise ratio (SNR), spreading factor, the number of users and transmitted symbols. The effect of SI is reduced as the spreading factor or the SNR increases.
The average bit error probability, 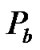 , can be described by a Bernoulli distribution in terms of v and l, where l is the number of chip errors in the despreading registers and v is the spreading length. When v is large, the BER of SEMA can be well approximated by [12,13]
, can be described by a Bernoulli distribution in terms of v and l, where l is the number of chip errors in the despreading registers and v is the spreading length. When v is large, the BER of SEMA can be well approximated by [12,13]
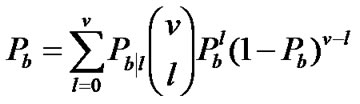 (14)
(14)
where the conditional bit error probability is
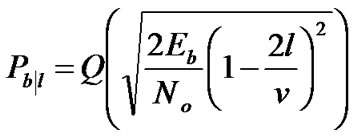 (15)
(15)
To ameliorate the effect of error propagation, differential encoding as shown in Figure 1 was proposed and analyzed in [13]. Figure 4 shows the performance with and without differential encoding for a spreading length of 8. The effect of error propagation was analyzed by averaging 100 simulation runs of 10,000 bits, followed by 100, 000 bits. The results demonstrate that differential encoding eliminates the effect of error propagation on the BERs. Figure 5 shows the BER performance with differential encoding for various values of spreading length. We can see that the effect of SI is negligible for ≥2dB for the spreading length larger than 4. Since l is equal to the number of bit errors in a v bit se-
≥2dB for the spreading length larger than 4. Since l is equal to the number of bit errors in a v bit se-
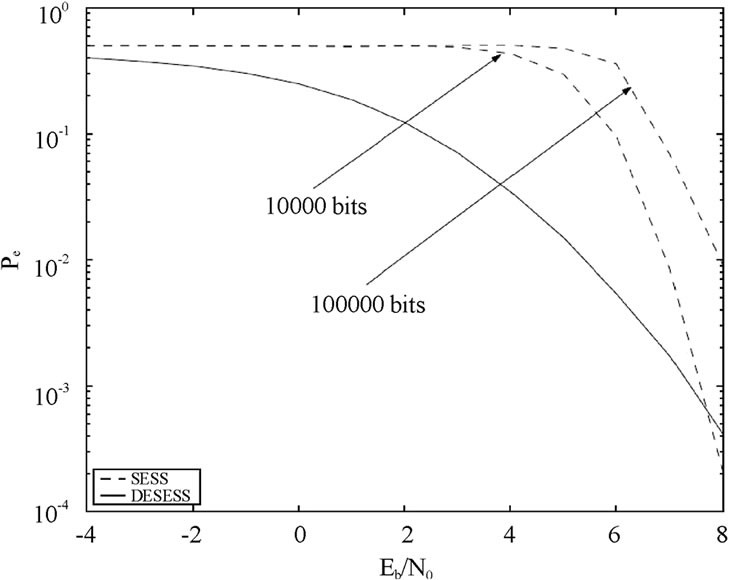
Figure 4. Comparison of BER of Self-encoded spread spectrum (SESS) and differentially encoded SESS (DESESS), reproduced from [13].
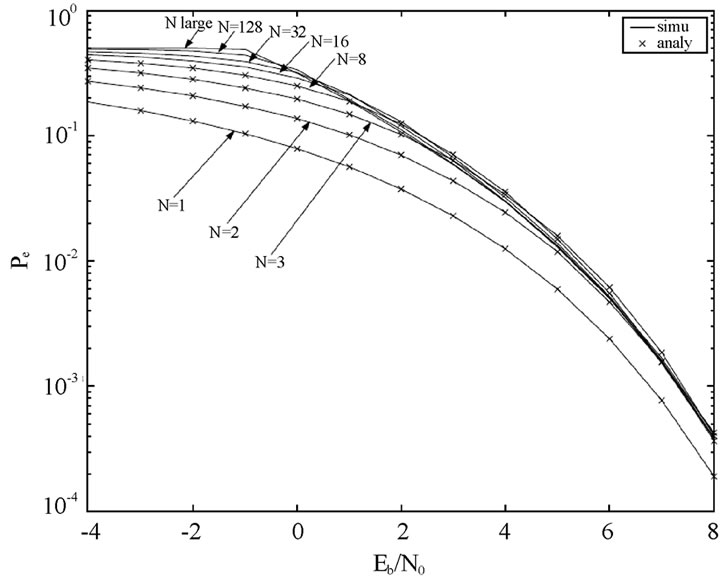
Figure 5. BER of SESS with differential encoding where N is the spreading length, reproduced from [13].
quence, as v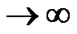 we have
we have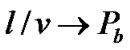 . Therefore, with differential encoding, the BER for large spreading length approaches the following
. Therefore, with differential encoding, the BER for large spreading length approaches the following
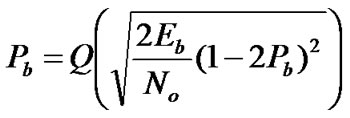 (16)
(16)
3.2. SEMA in AWGN Channels
The downlink cellular system can be described as a synchronous system. The delay in synchronous transmission is zero for all users (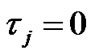 ). With the assumptions that the information sequences are independent and identically distributed, the probability density function (pdf) of MAI and noise is [9]
). With the assumptions that the information sequences are independent and identically distributed, the probability density function (pdf) of MAI and noise is [9]
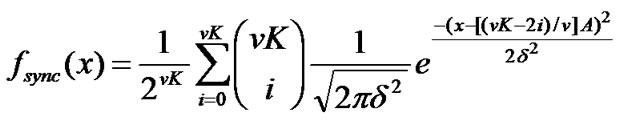 (17)
(17)
with variance [9]
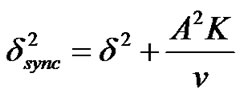 (18)
(18)
The probability of a bit error in synchronous channels is [9]
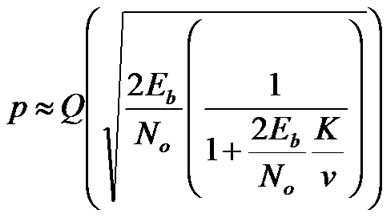 (19)
(19)
where 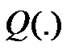 is
is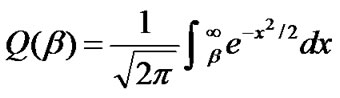 .
. 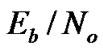 is the bit energy-to-noise ratio.
is the bit energy-to-noise ratio.
Signals in asynchronous systems arrive with different delays for all users as in uplink cellular systems. Thus, when the delay factor for user j is 0≤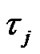 ≤
≤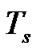 , the pdf of the MAI and noise is shown to be [14]:
, the pdf of the MAI and noise is shown to be [14]:
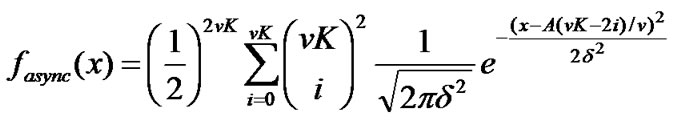
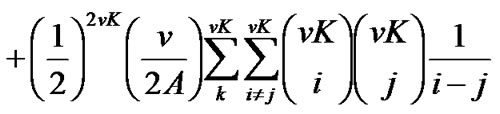
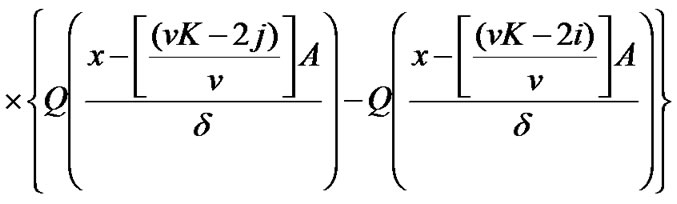
In asynchronous systems, the carriers of users are not synchronized. Therefore an additional term, 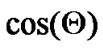 , 0≤
, 0≤ ≤
≤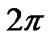 , should be included in MAI. However, we do not include the term in our discussion for simple presentation. In fact, incorporating the carrier mismatch will reduce MAI and improve the system performance a little. As a result, our analysis is somewhat conservative.
, should be included in MAI. However, we do not include the term in our discussion for simple presentation. In fact, incorporating the carrier mismatch will reduce MAI and improve the system performance a little. As a result, our analysis is somewhat conservative.
The variance of MAI and noise in the asynchronous channels is
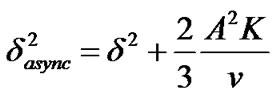 (21)
(21)
and the probability of a bit error in asynchronous channels is given as
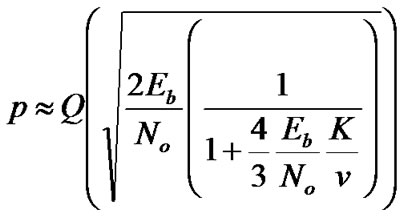 (22)
(22)
Notice that from Equations (18) and (21), the variance of asynchronous systems is less than that of synchronous systems, by a factor of 2/3.
3.3. SEMA Multiuser Convolutional Coding
Figure 6 shows the state diagram for r = 1/3, constraint length L = 3 convolutional code with the generator matrix G = [5 7 7]. The state diagram does not change when the generator matrix is shifted, i.e., G = [7 7 5] or [7 5 7]. Figure 7 illustrates the two trellis diagrams of one state to the next with the shift generator matrices. These matrices result in the same state diagram as in Figure 6. In Figure 6, the letters a, b, c, d, and e represent state 00, 01, 10, 11, and returning state 00. On each branch between any two states, the power of D represents the symbol weight of the transition while the
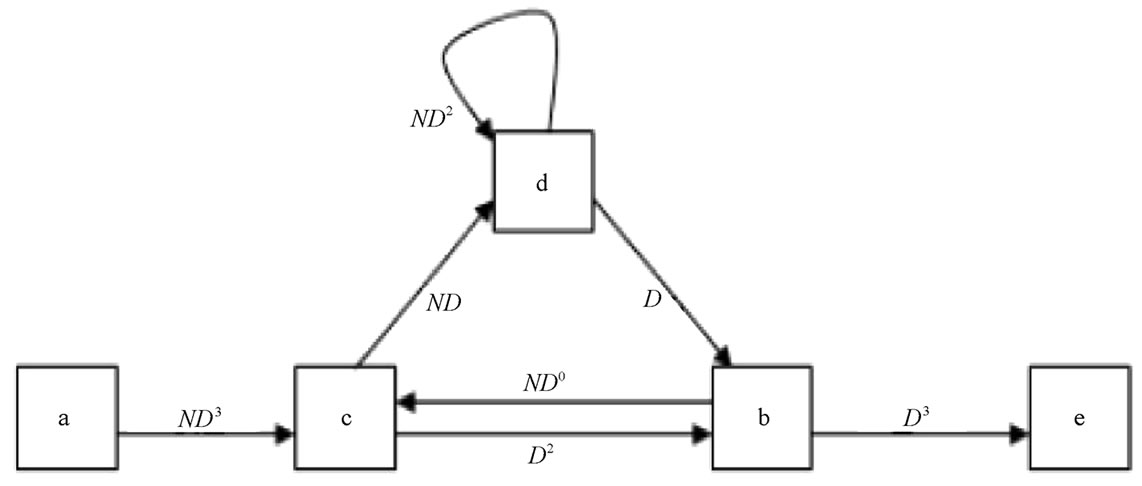
Figure 6. State diagram of R=1/3, L = 3 convolutional code.
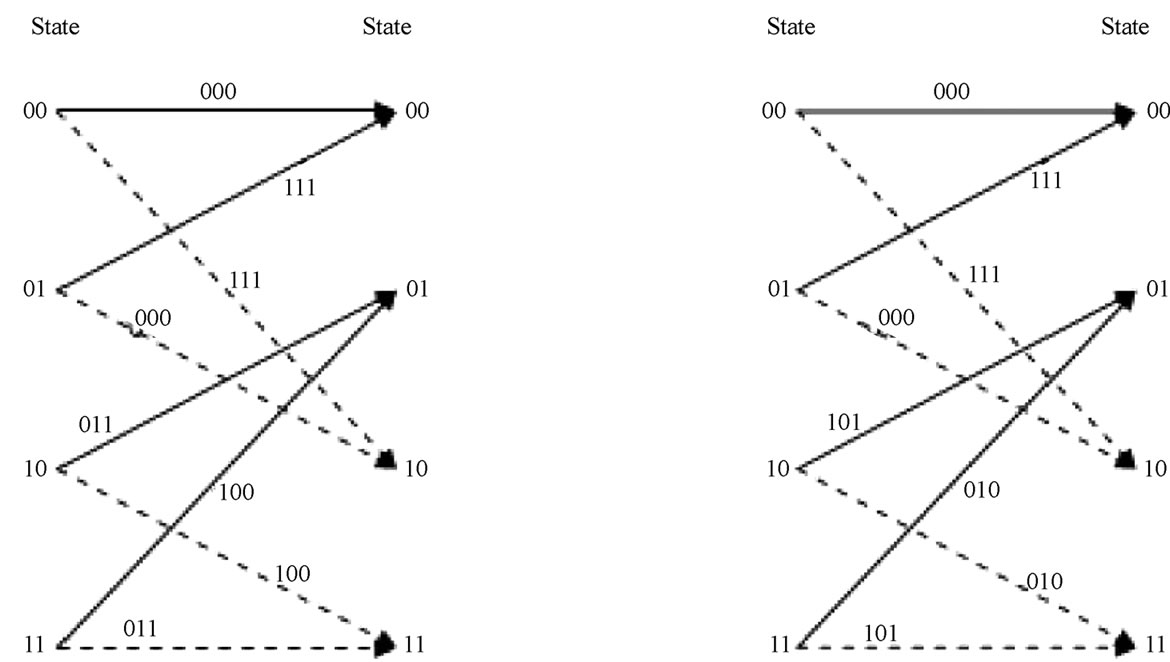 (a) (b)
(a) (b)
Figure 7. Trellis diagram of R =1/3, L = 3 convolutional code (a) G1 = [5 7 7] and (b) G2 = [7 5 7].
power of N tells us the weight of the information bit weight. From this diagram, we derive the transfer function using Mason’ formula [15]:
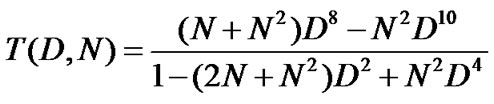 (23)
(23)
It can be shown from Equation (23) that dfree of this system is 8. For the hard-decision maximum likelihood decoder, Viterbi decoding algorithm for the binary symmetric channel (BSC) is used. We apply the transfer function upper bounds derived from the union bound computation for analytical comparison to the simulation results. From [15,16], we obtain the first-event error probability and the bit error probability:
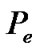 <
<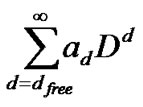 <
<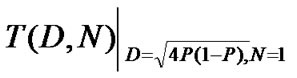
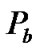 <
<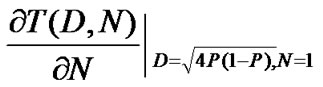 (24)
(24)
where 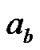 is the coefficient of the transfer function, and p is the probability of a bit error for BSC. The BER can be calculated from Equation (24) by replacing p with (19) and (22) (using symbol energy-to-noise ratio Es/No instead of Eb/No) for synchronous and asynchronous systems, respectively. For moderate and high signal-to-noise ratios, it is well known that dfree in the union bound for the BER dominates the bound [17]. Thus, we limit the first term in Equation (24) to find the asymptotic BER of our simulations.
is the coefficient of the transfer function, and p is the probability of a bit error for BSC. The BER can be calculated from Equation (24) by replacing p with (19) and (22) (using symbol energy-to-noise ratio Es/No instead of Eb/No) for synchronous and asynchronous systems, respectively. For moderate and high signal-to-noise ratios, it is well known that dfree in the union bound for the BER dominates the bound [17]. Thus, we limit the first term in Equation (24) to find the asymptotic BER of our simulations.
3.4. SEMA and Multiuser Detection in FadingChannels
From Equations (11), (12) and (13), the bit error probability for precoding and decorrelating detector, respectively, is given by [10]
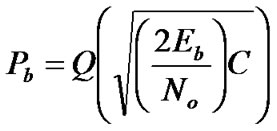 (25)
(25)
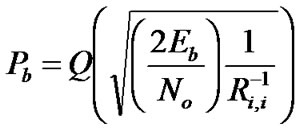 (26)
(26)
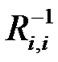 denotes the
denotes the 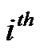 row and
row and 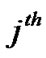 column of
column of 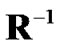 . The performance of SEMA with precoding/multiuser detection and convolutional coding in AWGN channels can be derived from equations (19) and (22) as [8]
. The performance of SEMA with precoding/multiuser detection and convolutional coding in AWGN channels can be derived from equations (19) and (22) as [8]
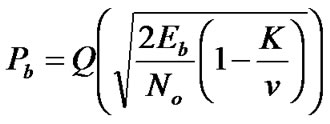 (27)
(27)
which replaces p in Equation (24) to find the BER. The BER of SEMA with precoding/multiuser detection in Rayleigh fading channel can be obtained as
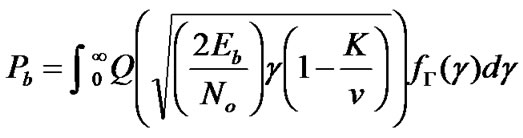
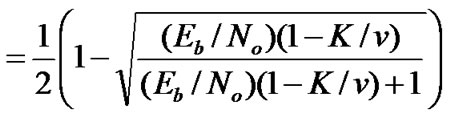 (28)
(28)
where 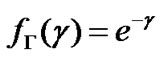 for Rayleigh fading channels. Equation (28) (using
for Rayleigh fading channels. Equation (28) (using 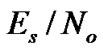 instead of
instead of 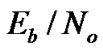 ) replaces p in Equation (25) to find the BER in fading channels.
) replaces p in Equation (25) to find the BER in fading channels.
4. Simulation Results
In Subsection 3.1, we observed that SI is dominant at low SNR regions with small spreading length. The differential encoding was employed to mitigate the effect of error propagation. In fact, SI becomes negligible under high SNR and with a sufficiently large spreading length. The BER performance then approaches random spread spectrum (RASS). Figure 8 shows the example performance of SEMA with Turbo coding [6]. The plots show that the BER
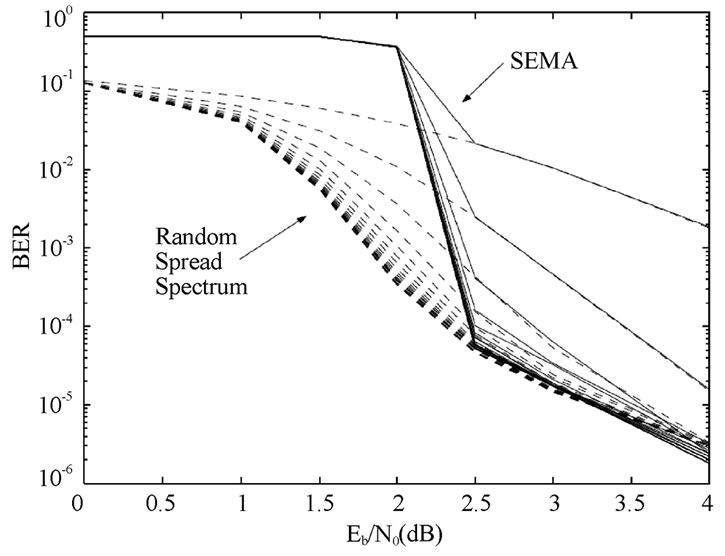
Figure 8. SEMA and random spread spectrum, Turbo coding, two users, v= 16 chips/symbol, AWGN, reproduced from [6].
approaches RASS not only asymptotically but also iteratively for ≥2.5 dB. The results indicate that we can ignore SI in examining the asymptotic behavior of the system.
≥2.5 dB. The results indicate that we can ignore SI in examining the asymptotic behavior of the system.
Figure 9 plots the BER of SEMA without interleaving. The performance is clearly unacceptable due to code collisions. The performance of RASS without SI is also shown for comparison: SEMA does not approach RASS even at high SNRs. The performance with interleaving is plotted in Figure 10. The results clearly demonstrate that interleaving is essential in SEMA. Figure 11 compares the performance of SEMA with and without shift generator matrix. At about 10-4 BER, the performance with G1 = [5 7 7] applying to both users is approximately 2dB worse than that with shifted matrices G1 = [5 7 7] for user 1 and G2 = [7 5 7] for user 2. Figure 12 shows the BER with the example convolutional code of rate 1/3 and constraint length 4. A larger constraint length is needed for a larger number of users. The BER performance de-
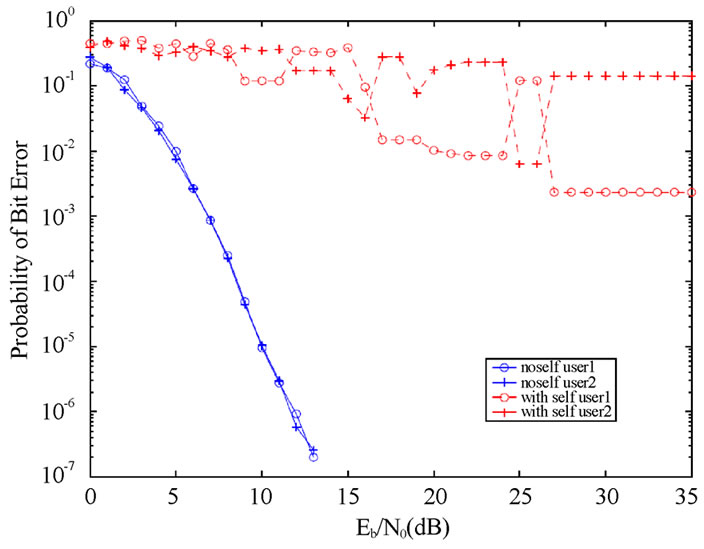
Figure 9. SEMA with and without SI, multiuser convolutional code, G=[5 7 7], R = 1/3, L = 3, v =16 chips/bit, two users, AWGN, no Interleaver.
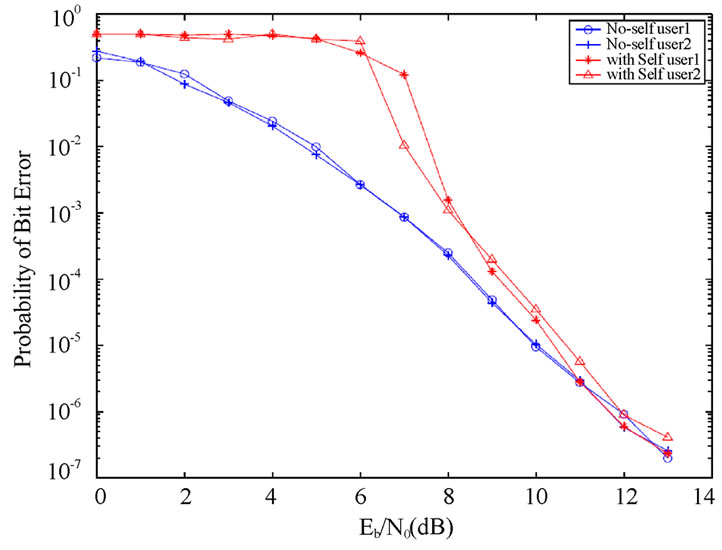
Figure 10. SEMA with and without SI, multiuser convolutional code, G=[5 7 7], R = 1/3, L = 3, v = 16 chips/bit, two users, AWGN, interleaver.
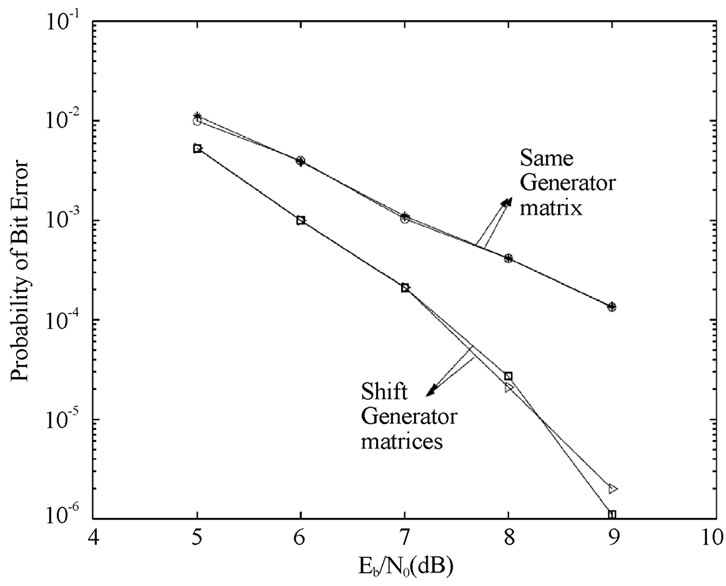
Figure 11. SEMA without SI, multiuser convolutional code, G=[5 7 7], R =1/3, L=3, v =128 chips/symbol, two users, synchronous, AWGN.
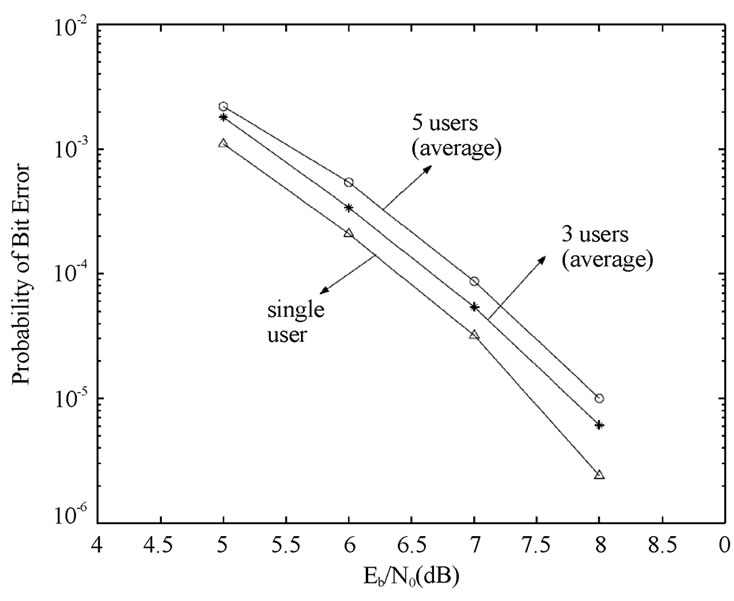
Figure 12. SEMA without SI, multiuser convolutional code, G=[13 15 17], R = 1/3, L = 4, v = 128 chips/symbol, one, three, five users, synchronous, AWGN.
grades by about 0.5dB, indicating that MAI is still manageable for five users with shifted generator matrices.
The plots in Figure 13 indicate that asynchronous system performs better than the synchronous system. About 1 dB difference is observed between the theoretical upper bound and simulations in the synchronous system as well as the asynchronous system. The performance of SEMA in Rayleigh fading channels is shown in Figure 14. The BER of precoding and decorrelating receiver decreases linearly with SNR for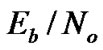 ≥8 dB, while the performance of the matched filter receiver starts to saturate at
≥8 dB, while the performance of the matched filter receiver starts to saturate at 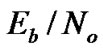 =12 dB. The results show that precoding and multiuser detection can improve SEMA system performance with additional complexity. Figure 15 compares the analytical calculations to the simulation results of SEMA in Rayleigh fading channels. The per-
=12 dB. The results show that precoding and multiuser detection can improve SEMA system performance with additional complexity. Figure 15 compares the analytical calculations to the simulation results of SEMA in Rayleigh fading channels. The per-
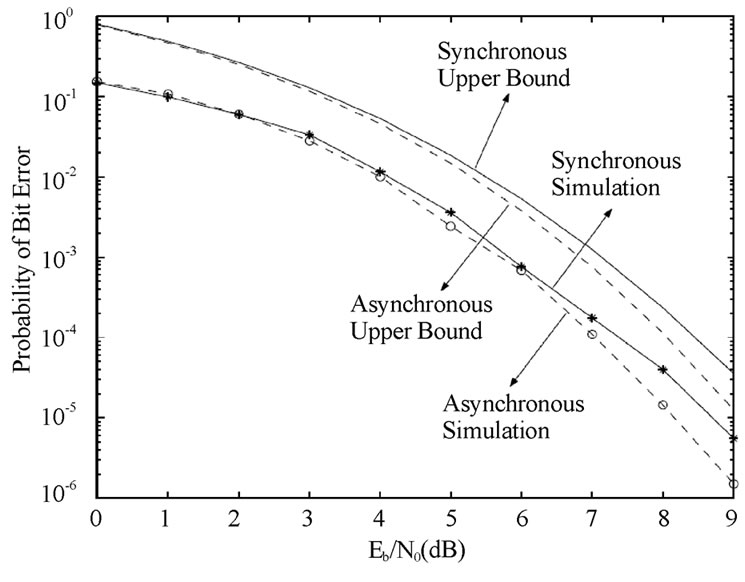
Figure 13. SEMA without SI, multiuser convolutional code, G=[13 15 17], R = 1/3, L =4, v =128 chips/symbol, five users, synchronous and asynchronous, AWGN.
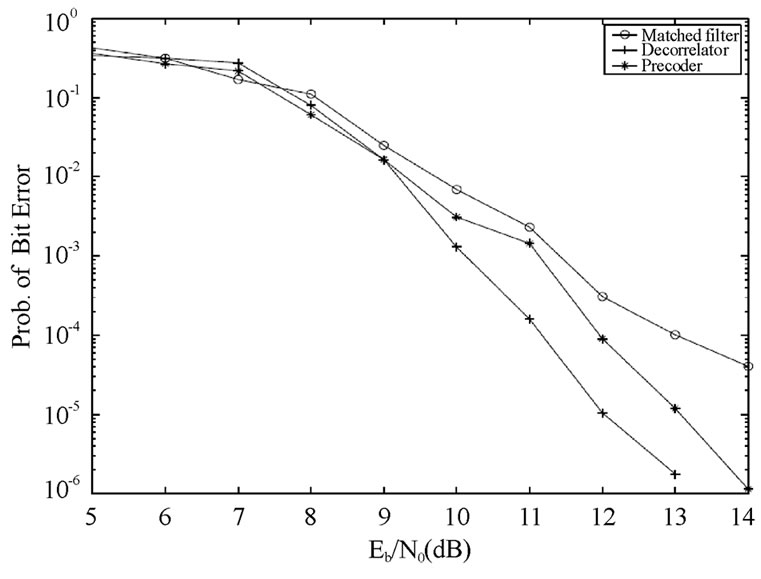
Figure 14. SEMA, multiuser convolutional code, G=[13 15 17], R = 1/3, L = 8, v = 64 chips/symbol, precoding and multiuser detection, two users, Rayleigh fading.
formance of precoding and multiuser detection is comparable to each other and is within 2dB of the theoretical results.
5. Conclusions
SEMA provides a feasible implementation of multi-rate transmissions and multi-level grades of service. These are desirable features in multimedia communications and prioritized heterogeneous networking systems. In this paper, we developed multiuser convolutional coding directly applicable to SEMA in synchronous downlink as well as asynchronous uplink cellular systems. We show that SEMA multiuser convolutional coding can improve performance over conventional convolutional coding. The performance analysis shows that the performance of SEMA in the uplink channel is better than the downlink
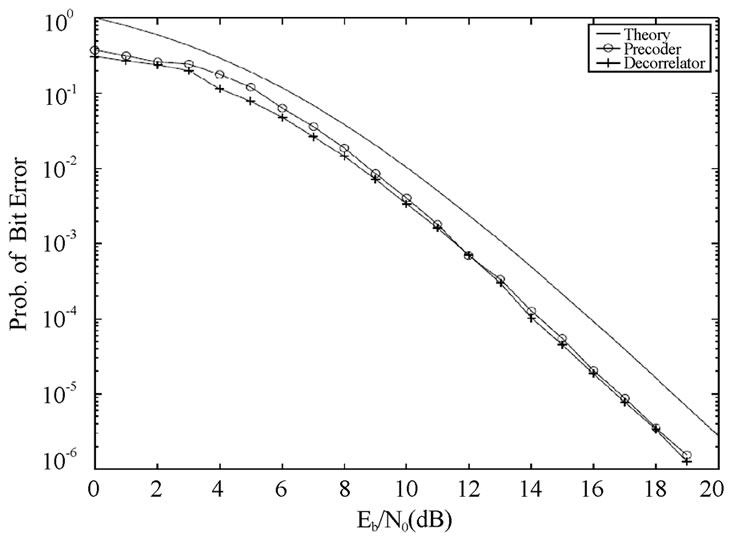
Figure 15. SEMA without SI, multiuser convolutional code, G=[5 7 7], R = 1/3, L = 3, v = 32 chips/symbol, precoding and multiuser detection, three users, Rayleigh fading.
channel. There is a critical SNR at which the self-interference introduced by SEMA becomes negligible and BER improves rapidly. It is important that the operating point of SEMA to be beyond the critical SNR, which depends on channel characteristics and system parameters such as spreading length and the number of users. Beyond the critical SNR, the performance of SEMA is equivalent to the random spread spectrum. The performance of SEMA can be significantly improved by multiuser detection or precoding, as well as channel coding such as multiuser convolutional coding introduced in this paper.
6. Acknowledgements
This work was supported in part by the contract award FA9550-08-1-0393 from the U. S. Air Force Office of Scientific Research. Thanks are due to Dr. J. A. Sjogren whose support has allowed the authors to investigate the field of self-encoded multiple access multiuser convolutional codes.
7. References
[1] T. F. Wong, T. M. Lok, and J. S. Lehnert, “Asynchronous multiple-access interference suppression and chip waveform selection with aperiodic random sequences,” IEEE Transactions on Communications, Vol. 47, No. 1, pp. 103-114, January 1999.
[2] J. S. Lehnert and M. B. Pursley, “Error probability for binary direct sequence spread-spectrum communications with random signature sequences,” IEEE Transactions on Communications, Vol. COM-35, No. 1, pp. 87-98, January 1987.
[3] L. Nguyen, “Self-encoded spread spectrum and multiple access communications,” Proceedings of the IEEE 6th International Conference on Spread Spectrum Technology & Applications, NJIT, NJ, September 2000.
[4] J. Jung, W. M. Jang and L. Nguyen, “Convolutional codes with shift generator matrices in synchronous and asynchronous self-encoded spread spectrum multiple access,” Conference on Information Sciences and Systems (CISS’03), The Johns Hopkins University, MD, March, 2003.
[5] J. Jung, W. M. Jang, and L. Nguyen, “Implementation of self-encoded spread spectrum multiple access with convolutional coding,” IASTED International Conference WOC, pp. 250-254, July 2002.
[6] W. M. Jang, L. Nguyen, and M. Hempel, “Self-encoded spread spectrum and Turbo coding,” Journal of Communications and Networks, Vol. 6, No. 1, pp. 9-18, March 2004.
[7] W. M. Jang and W. Wu, “Distributed and centralized multiuser detection with antenna arrays,” IEEE Transactions on Wireless Communications, Vol. 4, No. 3, pp. 855-860, May 2005.
[8] W. M. Jang, L. Nguyen, and M. Hempel, “Precoded random spreading multiple access in AWGN channels,” IEEE Transactions on Wireless Communications, Vol. 3, No. 5, pp. 1477-1480, September 2004.
[9] W. M. Jang, L. Nguyen and P. Bidarkar, “MAI and ICI of Synchronous Downlink MC-CDMA with Frequency Offset,” IEEE Transactions on Wireless Communications, Vol. 5, No. 3, pp. 693-703, March 2006.
[10] B. Vojcic and W. M. Jang, “Transmitter precoding in synchronous multiuser communications,” IEEE Trans. on Commun., Vol. 46, No. 10, October 1998.
[11] S. Verdu, Multiuser Detection, Cambridge Univ. Press, New York, pp. 72, 104-119, 1998.
[12] Y. Kong, L. Nguyen and W. Jang, “On the BER of self-encoded spread spectrum communication system,” Proceedings of the IASTED International Conference, Wireless and Optical Communications, Banff, Canada, pp. 202-206, June 27-29, 2001.
[13] Y. Kong, L. Nguyen and W. M. Jang, “Self-encoded spread spectrum modulation with differential encoding,” IEEE International Symposium on Spread Spectrum Techniques and Applications, pp. 471-474, September 2-5, 2002.
[14] W. M. Jang, L. Nguyen, and M. W. Lee, “MAI and ICI of asynchronous uplink MC-CDMA with frequency offset,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 4, pp. 2164-2179, July 2008.
[15] S. B. Wicker, “Error control systems for digital communication and storage,” Prentice Hall, New Jersey, pp. 264-330, 1995.
[16] J. G. Proakis, “Digital communications, 4th Edition, McGrawHill, New York, pp. 471-541, 2001.
[17] S. Lin and D. J. Costello, Jr., “Error control coding: fundamentals and applications,” Prentice Hall, New Jersey, pp. 287-346, 1983.

