Int'l J. of Communications, Network and System Sciences
Vol.2 No.6(2009), Article ID:688,8 pages DOI:10.4236/ijcns.2009.26050
Performance of Block Space-Time Code in Wireless Channel Dynamics
1The Peter Kiewit Institute of Information Science, Technology & Engineering, Omaha, USA
2Department of Computer and Electronics EngineeringUniversity of Nebraska–Lincoln, Omaha, USA
Email: wjang@unlnotes.unl.edu, jjung@mail.unomaha.edu
Received March 9, 2009; revised May 8, 2009; accepted July 15, 2009
Keywords: Space-Time Codes, Diversity, Multiple Transmit Antennas, Self-Encoded Spread Spectrum.
ABSTRACT
In this work, we observe the behavior of block space-time code in wireless channel dynamics. The block space-time code is optimally constructed in slow fading. The block code in quasi-static fading channels provides affordable complexity in design and construction. Our results show that the performance of the block space-time code may not be as good as conventionally convolutional coding with serial transmission for some channel features. As channel approaches fast fading, a coded single antenna scheme can collect as much diversity as desired by correctly choosing the free distance of code. The results also point to the need for robust space-time code in dynamic wireless fading channels. We expect that self-encoded spread spectrum with block space-time code will provide a robust performance in dynamic wireless fading channels.
1. Introduction
Space-time codes introduce temporal and spatial correlation into signals transmitted from different antennas in order to provide diversity at the receiver as well as coding gain without sacrificing bandwidth [1,2]. Most optimal space-time codes have been developed in block code in slow fading channels [1,3–7]. The block code in quasi-static fading channels provides affordable complexity in design and construction. It has been shown that in a system with t transmit and r receive antennas, and a slow fading channel, the average channel capacity with perfect channel state information (CSI) at the receiver is about min{t,r} times larger than that of a single antenna system [8]. Tight exponential upper bound is obtained on the decoding error probability of block codes transmitted over fully interleaved fading channels with perfect CSI at the receiver [10]. These bounds do not require integration in their final version, and they are reasonably tight in a certain portion of the data region that exceeds the cutoff rate of the channel. If channel-state information is also available to the transmitter, very high capacity is achievable without the need for time diversity [9]. However, mobile communication channels are dynamic and undergo slow fading to fast fading rather quickly as mobile speeds and surrounding structures change. Some space-time codes have been developed for fast fading channels under the assumption of low data rates and low signal-to-noise ratios [1]. Nevertheless, as wireless Internet services are incorporated into mobile communications, space-time codes that are optimal for fast fading channels, high data rate and low bit error rate (BER) are required.
In this work, we consider the performance of current space-time code that is optimally constructed for slow fading channels (hereafter we called it the block space-time code). We raise the question whether the performance of the block space-time code would be at least as good as conventional serial code when channel characteristics change dynamically. In this paper, we analyze and compare two different transmitter structures: the parallel transmitter that employs the block spacetime code and the serial signal transmitter. Conventional channel code, such as convolutional code with a single transmit antenna, is used in the serial signal transmitter. We compare the BER of the two systems under the same bandwidth, average transmit power, data rate and a similar encoder processing complexity. The results suggest that the performance of the block space-time code can be degraded below the conventional code for some channel features.

Figure 1. Trellis diagram of block space-time code and convolutional code.
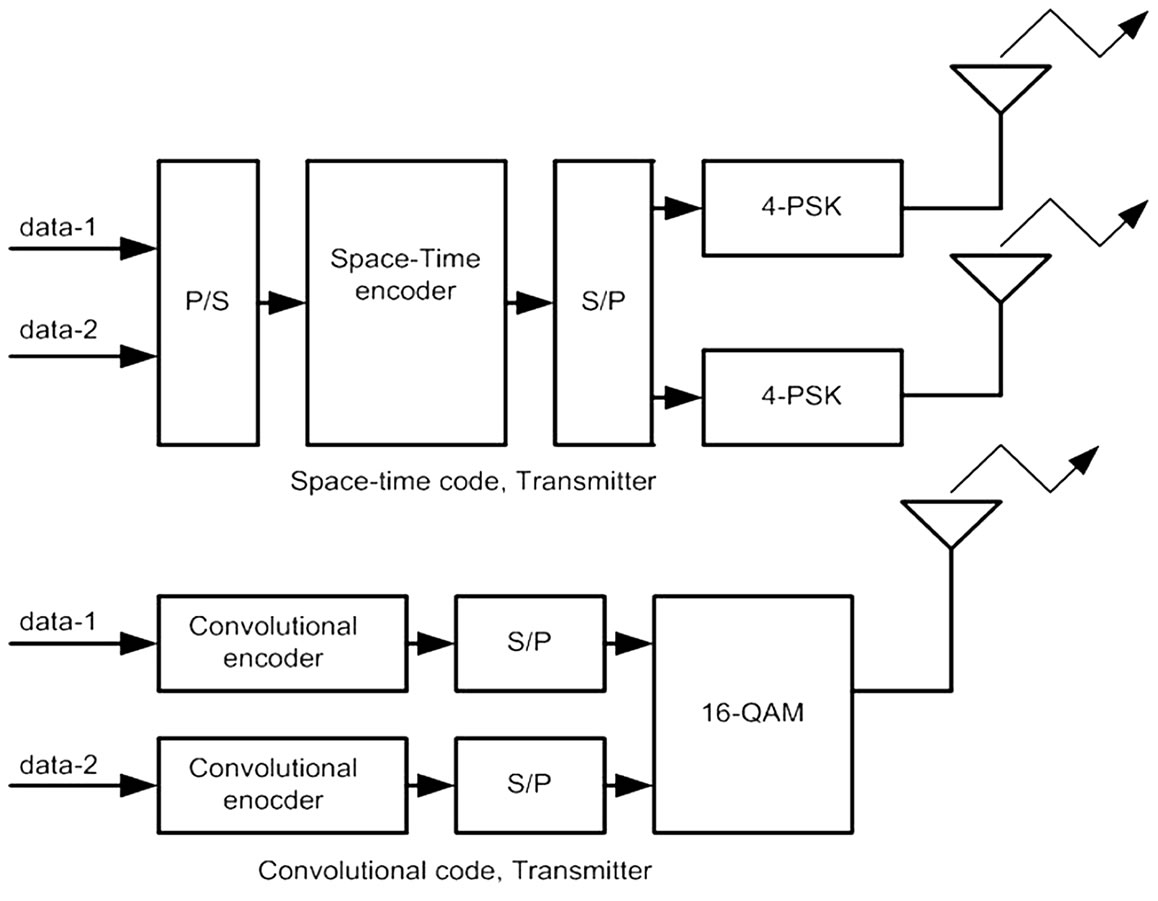
Figure 2. Transmitter structures.
Self-encoded spread spectrum (SESS) introduced in [11] eliminates the need for traditional pseudo noise (PN) code generators. As the term implies, the spreading code is obtained from the random digital information source itself. Multiuser convolutional code directly applicable to SEMA in cellular system is developed in [12]. A chip interleaving and iterative detection scheme for SEMA improve system performance significantly in fading channels [13]. The cooperative SESS performance is shown to be superior to other conventional cooperative systems [14]. We currently conduct the research on SESS with multiple-input multiple-output (MIMO). Our future work is to develop SESS block space-time code. Due to the inherent time diversity in SESS, we expect SESS block space-time code to maintain a robust performance in dynamic wireless fading channels.
2. System Model
2.1. Block Space-Time Code
We consider a base station to a mobile communication where the base-station equipped with n antennas and the mobile is equipped with r antennas. Data are encoded by the channel encoder, and the encoded data go through a serial-to-parallel converter and are split into n streams of data. Each stream of data is the input to a pulse shaper. Then, the output of each shaper is modulated. We consider the 8-state trellis code [1] shown in Figure 1. We use the 8-state 4-PSK trellis space-time code to obtain numerical results for comparison, although our analysis can be generalized to other space time-codes. The space-time code and 4-PSK modulation using two transmitter antennas is shown in Figure 2. The two streams of incoming data, data-1, d1, and data-2, d2, are encoded, pulse-shaped, modulated and transmitted in parallel over the two transmit antennas. Alternatively, the two data streams can be considered divided from a common data source. The signal constellation employed here is 4-PSK and the signal points are labeled by the elements of Z4, the ring of integers modulo 4. The edge level c1c2 in Figure 1 shows that signal c1 is transmitted over the first antenna and that signal c2 is transmitted over the second antenna. This code can be described in terms of a sequence (d1,d2) of binary inputs. The output signal pair  at time t is given by [1]
at time t is given by [1]
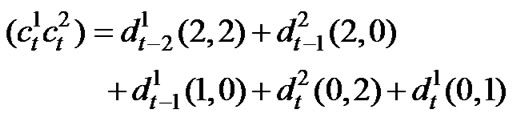 (1)
(1)
At each time slot t, the output of modulator-i is a signal 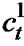 that is transmitted using transmit antenna i for 1≤i≤n. The n signals are transmitted simultaneously, each from a different transmit antenna, and all signals have the same transmission period.
that is transmitted using transmit antenna i for 1≤i≤n. The n signals are transmitted simultaneously, each from a different transmit antenna, and all signals have the same transmission period.
The signal at each receive antenna is the sum of the n transmitted signals contaminated by a noise and corrupted by Rayleigh fadings. We assume that the elements of the signal constellation are normalized by a factor of , where Eb is the bit energy, so that the average energy of the constellation is the unity. A decision is based on the received signals at each receive antenna 1≤j≤r. The signal
, where Eb is the bit energy, so that the average energy of the constellation is the unity. A decision is based on the received signals at each receive antenna 1≤j≤r. The signal 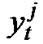 received by antenna j at time t is given by
received by antenna j at time t is given by
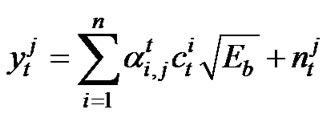 (2)
(2)
where the noise 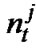 at time t is a complex Gaussian random variable with a zero-mean and variance N0/2 per dimension, independent for all j and t. The coefficient
at time t is a complex Gaussian random variable with a zero-mean and variance N0/2 per dimension, independent for all j and t. The coefficient 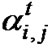 is the path gain from transmit antenna i to receive antenna j at time t. We are interested in the behavior of the block space-time codes that are optimally constructed for slow fading as channel dynamics change to independent path gains for every i, j and t.
is the path gain from transmit antenna i to receive antenna j at time t. We are interested in the behavior of the block space-time codes that are optimally constructed for slow fading as channel dynamics change to independent path gains for every i, j and t.
A maximum-likelihood sequence detector is applied for decoding. We assume ideal channel state information; thus, the path gains  , i=1,2,…n j=1,2,…r are precisely known to the receiver. Since
, i=1,2,…n j=1,2,…r are precisely known to the receiver. Since 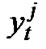 is the received signal at receive antenna j at time t, the branch metric for a transition labeled
is the received signal at receive antenna j at time t, the branch metric for a transition labeled  is given by
is given by
 (3)
(3)
Viterbi decoding is then applied to obtain the path with the lowest accumulated metric.
2.2. Conventional Serial Code
Convolutional coding is applied to each data stream as shown in Figure 2. The encoded symbols are serialto-parallel converted and fed to the modulator. The required bandwidth is equivalent to the block space-time code, although the bandwidth expansion produced by the encoder can be reduced considerably less than the reciprocal of the code rate [15]. We use the convolutional code with the code rate (1/R), the constraint length (K), and the generators equal to 1/2, 3 and [5 7] in octal, respectively [16]. This code has a free distance (dfree) equal to 5. The two 4-state diagram of this code is shown in Figure 1. The code can be described in terms of a sequence of binary inputs. The output, 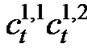 from the first encoder at time t is given by
from the first encoder at time t is given by
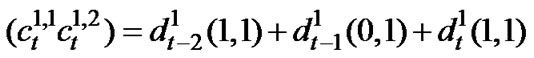 (4)
(4)
Modulo 2 addition is performed to obtain the encoder output pairs. Likewise, the output of the second encoder  can be generated. The encoders’ outputs are serial-to-parallel converted and fed to the modulator. The signal constellation employed here is 16-QAM for a single transmit antenna and the signal points are labeled by the elements of Z16. Considering that 16-QAM and 4-PSK display approximately 5 dB difference for Eb/N0≥0 dB, these modulation schemes are more favorable for the block space-time code system. Nevertheless, our results show that the conventional serial code system can outperform the block space-time code in some channel characteristics.
can be generated. The encoders’ outputs are serial-to-parallel converted and fed to the modulator. The signal constellation employed here is 16-QAM for a single transmit antenna and the signal points are labeled by the elements of Z16. Considering that 16-QAM and 4-PSK display approximately 5 dB difference for Eb/N0≥0 dB, these modulation schemes are more favorable for the block space-time code system. Nevertheless, our results show that the conventional serial code system can outperform the block space-time code in some channel characteristics.
The output of a 16-QAM modulator can be represented as a complex number,
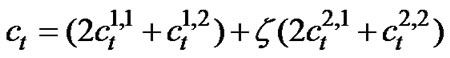 (5)
(5)
where ζ=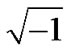 . The signal
. The signal 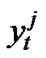 received by antenna j at time t is given by
received by antenna j at time t is given by
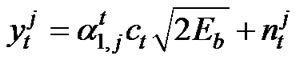 (6)
(6)
where 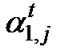 is the path gain from the single transmit antenna to receive antenna j at time t. Notice that we scaled the transmit bit energy to maintain the same average bit energy in both systems for fair comparison. For Viterbi decoding, we replace Equation (3) with
is the path gain from the single transmit antenna to receive antenna j at time t. Notice that we scaled the transmit bit energy to maintain the same average bit energy in both systems for fair comparison. For Viterbi decoding, we replace Equation (3) with
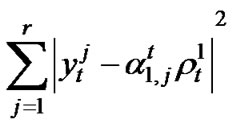
 (7)
(7)
3. Performance Analysis
3.1. Block Space-Time Code
From Figure 1, the codeword (0, 2, 2, 0) has the free distance from the all-zero codeword, (0, 0, 0, 0). The free distance is defined as the minimum Hamming weight of all possible codewords. For moderate and high signal-to-noise ratios, it is well known that the free-distance term in the union bound on the BER performance dominates the bound [17,18]. Assuming ideal channel state information, the probability of transmitting c=(0, 0, 0, 0) and deciding in favor of e=(0, 2, 2, 0) at the decoder is
 (8)
(8)
where l is the block length, N0/2 is the noise variance per dimension,

and
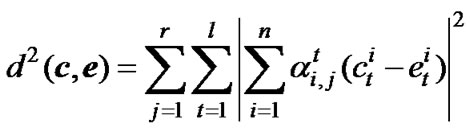 (9)
(9)
For r =1
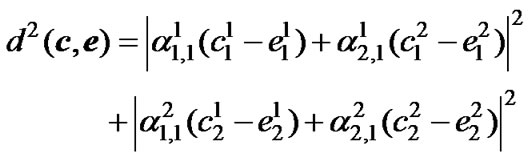 (10)
(10)
Applying c= (0, 0, 0, 0) and e= (0, 2, 2, 0),
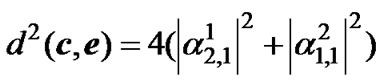 (11)
(11)
Since 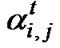 is Rayleigh fading, the probability density function (pdf) of
is Rayleigh fading, the probability density function (pdf) of 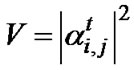 can be shown as [19]
can be shown as [19]
 (12)
(12)
to maintain the same average received power without fading. U(v) is the unit step function. With r receiving antennas and
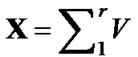
the pdf of X can be represented as a Gamma distribution with the parameter, 2r, as [19]
 (13)
(13)
Therefore,
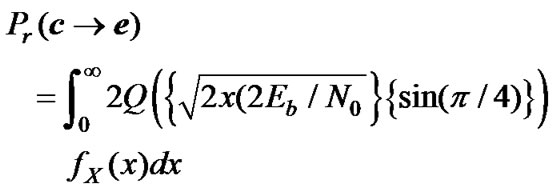 (14)
(14)
In Equation (14), we applied the approximation of the symbol error probability of QPSK [20],
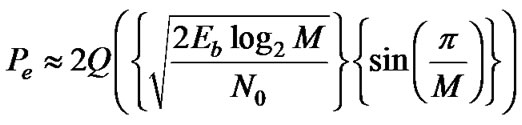 (15)
(15)
with M=4. Therefore, the probability of the bit error can be found as [17]
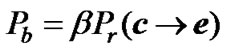 (16)
(16)
where
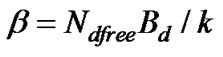
Bd and k are the number of nonzero information bits and the total number of information bits, respectively, on the dfree path. The error coefficient, Ndfree, is the total number, or multiplicity, of the free distance code word. For the chosen codewords, c=(0, 0, 0, 0) and e=(0, 2, 2, 0), Ndfree, Bd and k are 1, 1 and 4, respectively.
3.2. Conventional Serial Code
From Figure 1, the codeword, (3, 1, 3) has the free distance from the all-zero codeword, (0, 0, 0). Therefore, the probability of transmitting c=(0, 0, 0) and deciding in favor of e=(3, 1, 3) can be obtained as in Equation (8) with d2(c,e) as follows for r=1:
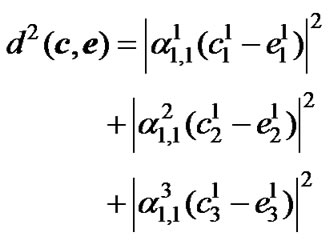 (17)
(17)
Using c =(0, 0, 0)and e=(3, 1, 3),
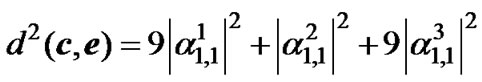 (18)
(18)
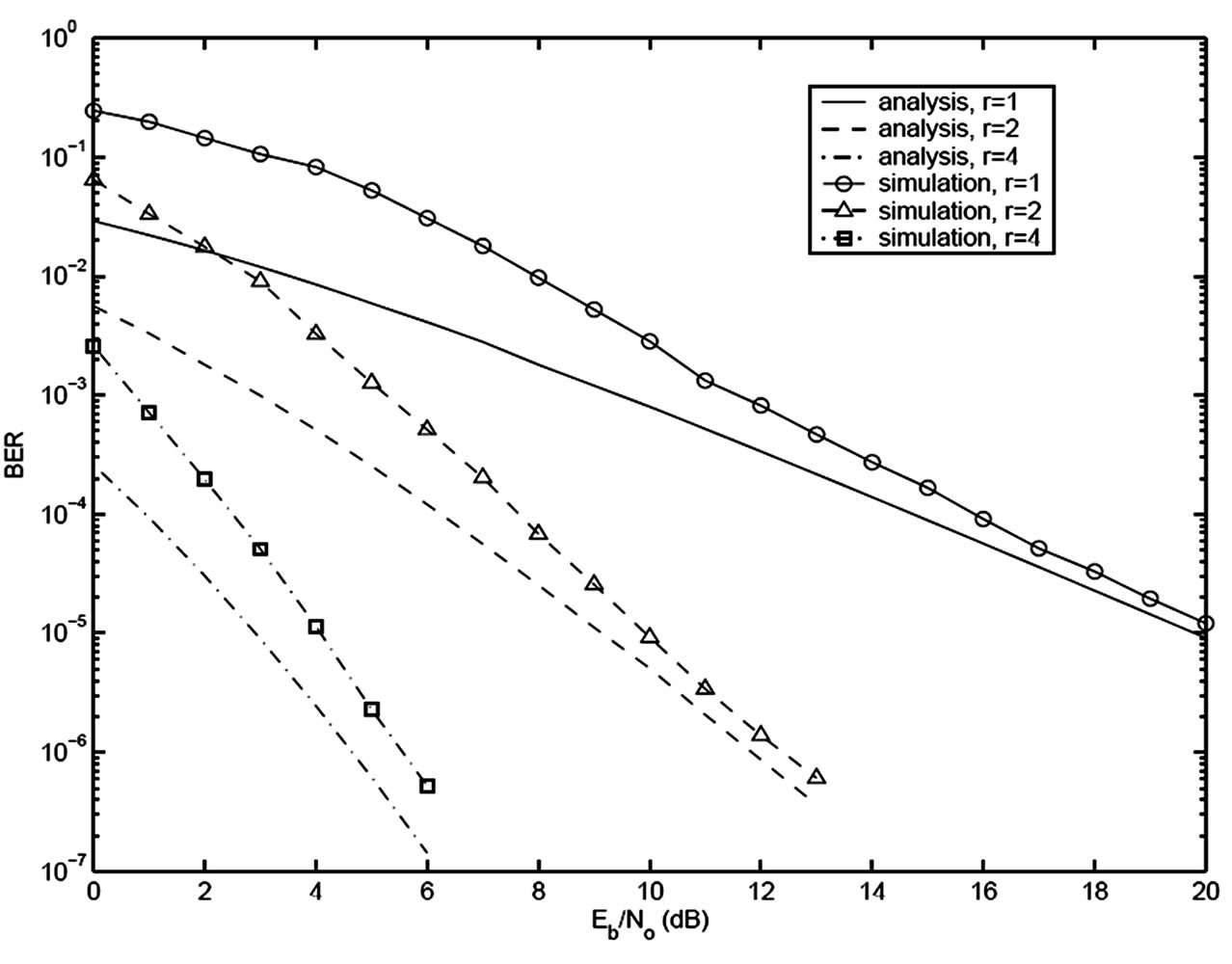
Figure 3. Block space-time code, two transmit antennas, 8 states, 4-PSK, 1, 2 and 4 receive antennas, Rayleigh.
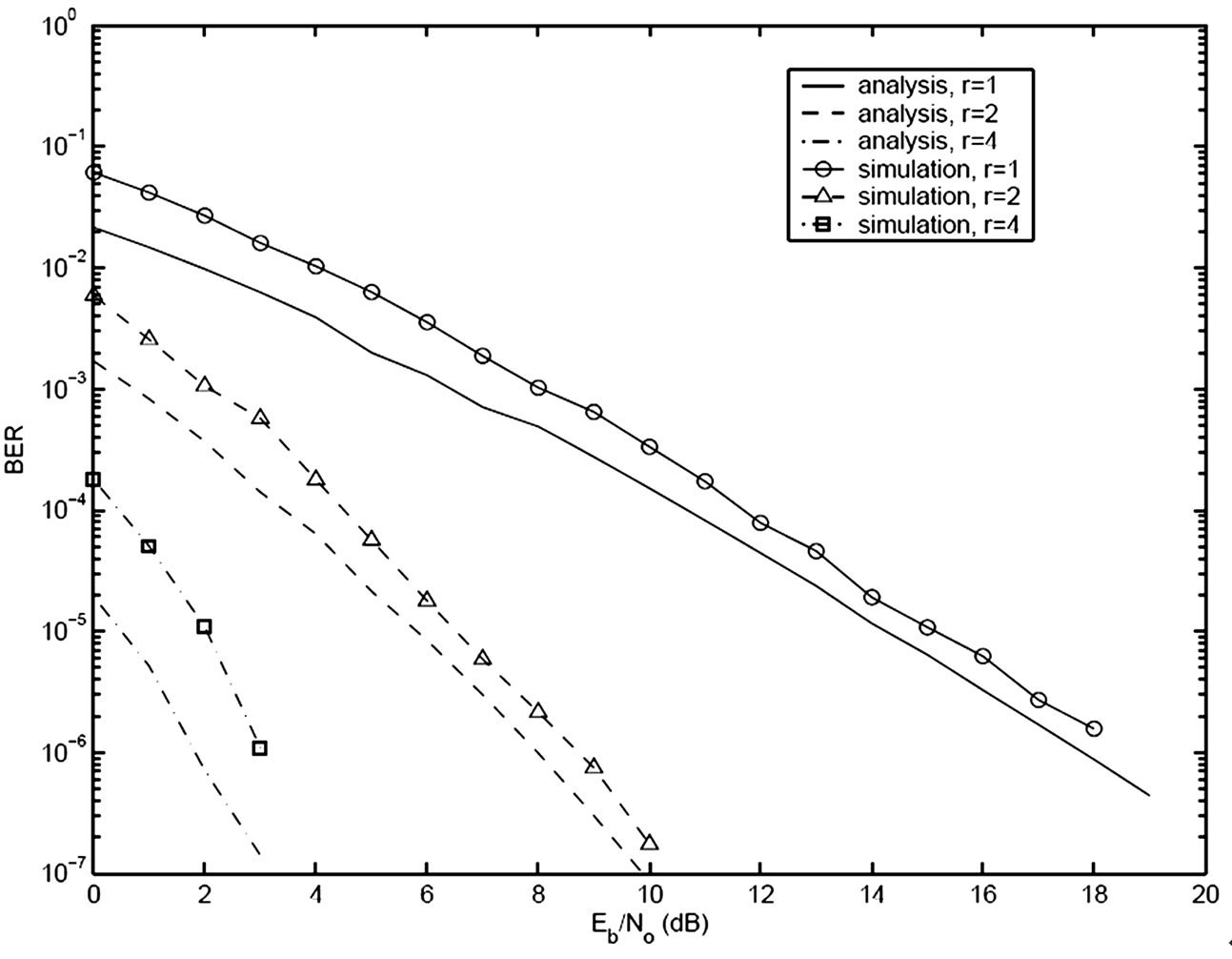
Figure 4. Convolutional code, single transmit antenna, two 4 states, 16-QAM, 1, 2 and 4 receive antennas, Rayleigh.
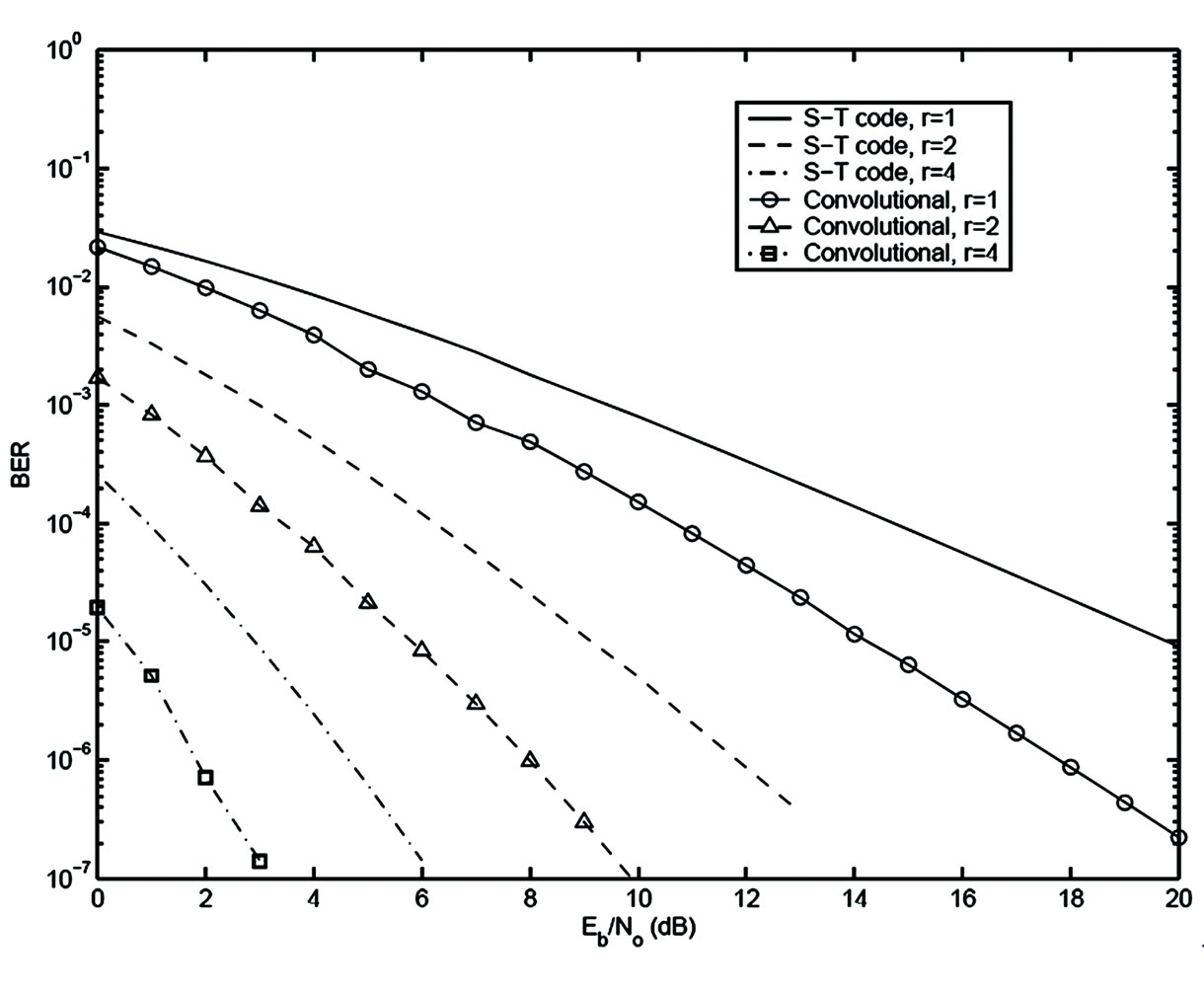
Figure 5. Analytical BER of block space-time code and convolutional code, 1, 2 and 4 receive antennas, Rayleigh.
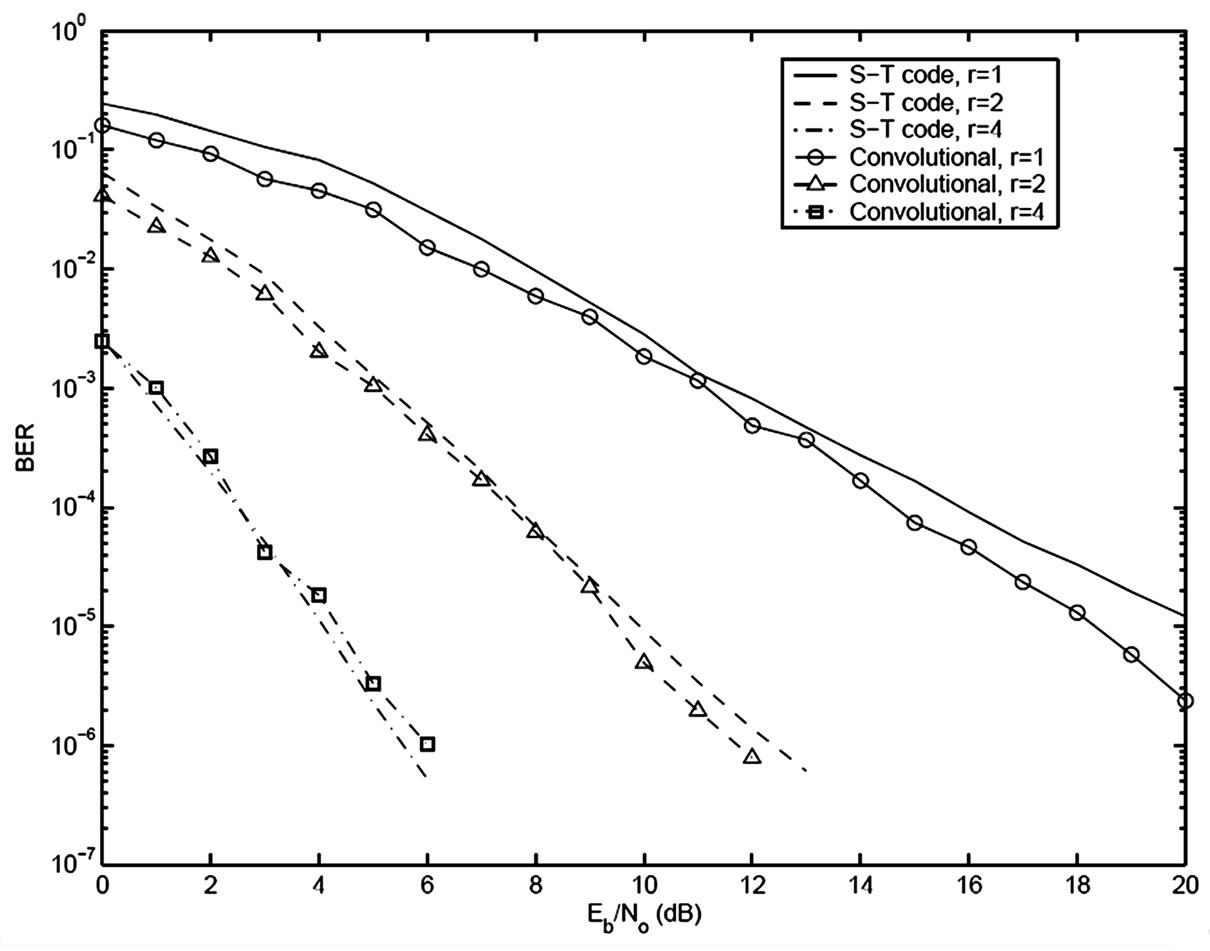
Figure 6. Simulation BER of block space-time code and convolutional code, a half average transmit power for convolutional code, 1, 2 and 4 receive antennas, Rayleigh.
With r receiving antennas, the pdf of the above equation can be represented as the combination of two random variables,
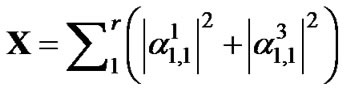
and
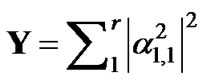 Consequently [19],
Consequently [19],
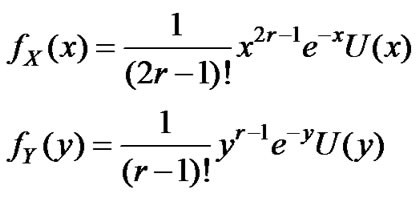 , and (19)
, and (19)
Therefore, the probability of bit error is
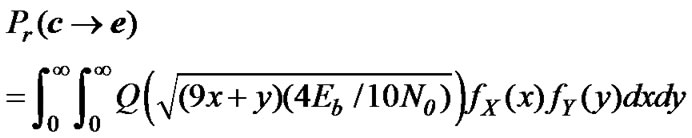 (20)
(20)
In Equation (20), we employ the approximation of the symbol error probability,  , for 16- QAM modulation [20]. The probability of the bit error is obtained from Equation (16), where Ndfree , Bd and k are 1, 1 and 3 respectively.
, for 16- QAM modulation [20]. The probability of the bit error is obtained from Equation (16), where Ndfree , Bd and k are 1, 1 and 3 respectively.
4. Simulation Results
We assume that the perfect channel state information is available at receive antennas in the following simulations. We consider the dynamic channel characteristics of independent fading for every bit interval. In Figure 3, the simulation BER and the analytical BER of the block space-time code with 8-state, 4-PSK and two transmit antennas are compared in Rayleigh fading channels for one, two and four receive antennas. The simulation BER approaches the analytical BER at high signal-to-noise ratios (SNR). With a larger number of receive antennas, the rate of the approach becomes faster. With two or more receive antennas, the difference between the simulation and the analysis is less than 1 dB for SNR≥6 dB. The receive antenna diversity significantly improves the system performance as expected. The BER performance of two four-state convolutional codes and a 16-QAM system with a single transmit antenna is displayed in Figure 4. The simulation BER rapidly approaches the analytical BER. The BER difference is less than 1 dB for all SNR. We observe similar effects of receive antenna diversity as in the block space-time codes. The analytical results of the two systems are shown in Figure 5. We can see that the BER of the conventional serial code is better than the block space-time code for all SNR under the same bandwidth, average transmits power, data rate and a similar processing complexity as channel dynamics reach to independent fading in each bit interval. The difference becomes larger at high SNR. We show the simulation BER of the block space-time code and the conventional serial code in Figure 6. Half of the average transmit power of the block space-time code is assigned to the conventional serial code transmission. Now we observe that the BER of both systems is equivalent. Our results show that for the same Eb/N0 , the performance of the block space-time code may not be as good as the conventional convolutional code for some channel features. As channel dynamics reach fast fading, a coded single antenna scheme can collect as much diversity as desired by suitably choosing the free distance of code. Block space-time codes are most useful in slow fading when temporal diversity is not available. The advantage of the block space-time code can be diminished significantly as wireless channel approach fast fading.
5. Conclusions
In this paper, we show that the block space-time coding gain can be degraded below the conventional channel coding with a single transmit antenna for some channel characteristics. Our results suggest that there is a need for a robust space-time code in rapidly changing wireless channels. Our future work is to develop SESS block space-time code. Due to the inherent time diversity in SESS, we expect SESS block space-time code to provide a robust performance in dynamic wireless channels.
6. Acknowledgements
This work was supported in part by the contract award FA9550-08-1-0393 from the U.S. Air Force Office of Scientific Research. Thanks are due to Dr. J. A. Sjogren whose support has allowed the authors to investigate the feasibility of self-encoded block space-time code in dynamic wireless fading channels.
7. References
[1] V. Tarokh, N. Seshadri, and A. R. Calderbank, “Space-time codes for high data rate wireless communication: Performance criterion and code construction,” IEEE Transactions on Information Theory, Vol. 44, No. 2, pp. 744–765, March 1998.
[2] S. Alamouti, “A simple transmit diversity technique for wireless communications,” IEEE Journal on Selected Areas in Communications, Vol. 1, No. 16, pp. 1451– 1458, 1998.
[3] V. Tarokh, H. Jafarkhani, and A. R. Calderbank, “Space-time block coding for wireless communications: Performance results,” IEEE Journal on Selected Areas in Communications, Vol. 17, No. 3, pp. 451–460, March 1999.
[4] S. Baro, G. Bauch, and A. Hansmann, “Improved codes for space-time trellis-coded modulation,” IEEE Communications Letters, Vol. 4, No. 1, pp. 20–22, January 2000.
[5] H. E. Gamal and A. R. Hammons, “On the design of algebraic space-time codes for MIMO block-fading channels,” IEEE Transactions on Information Theory, Vol. 49, No. 1, pp. 151–163, January 2003.
[6] H. E. Gamal and A. R. Hammons, “On the design and performance of algebraic space-time codes for BPSK and QPSK modulation,” IEEE Transactions on Communications, Vol. 50, No. 6, pp. 907–913, June 2002.
[7] A. Song, G. Wang, W. Su, and X. G. Xia, “Unitary space-time codes from Alamouti’s scheme with APSK signals,” IEEE Transactions on Wireless Communications, Vol. 3, No. 6, pp. 2374–2384, November 2004.
[8] G. J. Foschini and M. J. Gans, “On limits of wireless communications in a fading environment when using multiple antennas,” Wireless Personal on Communications, Vol. 6, No. 3, pp. 311–335, March 1998.
[9] E. Biglieri, G. Caire, and G. Taricco, “Limiting performance of block-fading channels with multiple antennas,” IEEE Transactions on Information Theory, Vol. 47, No. 4, pp. 1273–1289, May 2001.
[10] I. Sason, S. Shamai, and D. Divsalar, “Tight exponential upper bounds on the ML decoding error probability of block codes over fully interleaved fading channels,” IEEE Transactions on Communications, Vol. 51, No. 8, pp. 1296–1305, August 2003.
[11] L. Nguyen, “Self-encoded spread spectrum and multiple access communications,” Proceedings of the IEEE 6th International Conference on Spread Spectrum Technology & Applications, ISSSTA2000, Vol. 2, pp. 394–398, NJIT, NJ, September 6–8, 2000.
[12] J. H. Jung, W. M. Jang, and L. Nguyen, “Self-encoded multiple access multiuser convolutional codes in uplink and downlink cellular systems,” International Journal of Communications, Network and System Science, Vol. 2, No. 4, pp. 249–257, July 2009.
[13] Y. S. Kim, W. M. Jang, Y. Kong, and L. Nguyen, “Chip-interleaved self-encoded multiple access with iterative detection in fading channels,” Journal of Communications and Networks, Vol. 9, No. 1, pp. 50–55, March 2007.
[14] K. Hua, W. M. Jang, and L. Nguyen, “Cooperative self encoded spread spectrum in fading channels,” International Journal of Communications, Network and System Science, Vol. 2, No. 2, pp. 91–96, May 2009.
[15] D. Divsalar and M. K. Simon, “Spectral characteristics of convolutionally coded digital signals,” IEEE Transactions on Communications, Vol. COM-28, No. 2, pp. 173–186, February 1980.
[16] J. G. Proakis, Digital Communications, 4th Edition, pp. 492, McGraw Hill, 2001.
[17] S. Lin and D. J. Costello, Error Control Coding, 2nd Edition, PEARSON Prentice Hall, Upper Saddle River, NJ, 2004.
[18] L. C. Perez, J. Seghers, and D. J. Costello, “A distance spectrum interpretation of Turbo codes,” IEEE Transactions on Information Theory, Vol. 42, No. 6, pp. 1698– 1709, Part I, November 1996.
[19] A. Papoulis and S. U. Pillai, Probability, Random Variables and Stochastic Processes, 4th Edition, pp. 87, 190, McGraw Hill, 2002.
[20] B. P. Lathi, Modern Digital and Analog Communication Systems, 3rd Edition, pp. 612–614, Oxford University Press, New York, 1998.

