Journal of Intelligent Learning Systems and Applications
Vol.06 No.04(2014), Article ID:50481,8 pages
10.4236/jilsa.2014.64012
Computational Approaches for Biomarker Discovery
Malik Yousef1,2, Naim Najami1,3, Loai Abedallah2,4, Waleed Khalifa1,2
1The Institute of Applied Research, The Galilee Society, Shefa Amr, Israel
2Computer Science, The College of Sakhnin, Sakhnin, Israel
3Department of Biology, The Academic Arab College of Education, Haifa, Israel
4Department of Mathematics, University of Haifa, Haifa, Israel
Email: malik.yousef@gmail.com
Academic Editor: Dr. Steve S. H. Ling, University of Technology Sydney, Australia
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 August 2014; revised 28 September 2014; accepted 6 October 2014
ABSTRACT
Computational biology plays a significant role in the discovery of new biomarkers, the analyses of disease states and the validation of potential biomarkers. Biomarkers are used to measure the progress of disease or the physiological effects of therapeutic intervention in the treatment of disease. They are also used as early warning signs for various diseases such as cancer and inflammatory diseases. In this review, we outline recent progresses of computational biology application in research on biomarkers discovery. A brief discussion of some necessary preliminaries on machine learning techniques (e.g., clustering and support vector machines―SVM) which are commonly used in many applications to biomarkers discovery is given and followed by a description of biological background on biomarkers. We further examine the integration of computational biology approaches and biomarkers. Finally, we conclude with a discussion of key challenges for computational biology to biomarkers discovery.
Keywords:
Computational Biology, Biomarker Discovery, Machine Learning

1. Introduction
Machine learning is the subfield of artificial intelligence which focuses on methods to construct computer programs that learn from experience with respect to some class of tasks and a performance measure [1] .
Machine learning enables one to generate automatic rules based on observation of the appropriate examples by the learning machine. However, the selection and design of the features that will be considered in order to represent each example for the learning process are very important and influence the classifier performance [2] .
Each instance in any dataset used by the machine learning methods is presented by a sequence of features, where each instance has the same number and types of features. The features can be categorical (i.e. gender), numerical (i.e. weight, size, age), and Boolean (i.e. sick? married?). So, the algorithms of the machine learning were asked to explain the relationships between the features in the data.
There are two major settings of learning schemes in machine learning. One is called unsupervised learning, where no prior information is given to the learner regarding the data or the output. It studies how systems can learn to represent particular input data in a way to find natural partitions (grouping/clustering) of patterns. Clustering is a simple classical method of the unsupervised learning, which partitions the data set into clusters, so that the data in each subset share some common trait according to some defined distance measure.
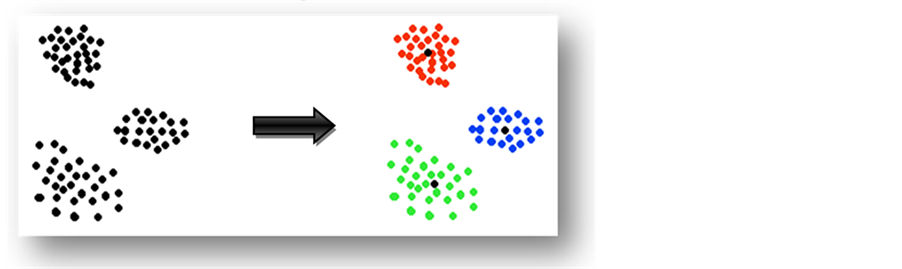
The main goal of clustering is to reduce the amount of data by grouping similar data items together. Most of the unsupervised learning methods use a measure of similarity between patterns in order to group them into clusters. The simplest of these involves defining a distance between patterns. For patterns whose features are numeric, the distance measure can be ordinary Euclidean distance between two instances, or Manhattan distance or any other similarity function. Figure 1 describes a simple example where a given set of sample points is clustered into three clusters around three different centers. It was noted that the clustering algorithm got data where no prior information was given. Moreover, the centers and clusters shapes were unknown, and then the learner studied the data and clustered it into three clusters as shown in the example.
Clustering methods [3] - [8] can be divided into four basic types:
Exclusive clustering (e.g., K-means algorithm [9] ).
Overlapping clustering (e.g., fuzzy C-means algorithm [10] and improved by Bezdek [11] ).
Hierarchical clustering (e.g., hierarchical clustering algorithm which was defined by Johnson in 1967 [12] ).
Probabilistic (e.g., expectation-maximization (EM) algorithm [13] ).
In the other setting, which is a termed supervised learning, the instances are given with known labels; its main goal is to build a classifier which then makes predictions about future instances to assign their class labels. The dataset will be divided into two partitions: one as a training dataset, and the second as a testing data set. The classifier was built according to the training dataset and its performance was measured by the performance of the classifier over the testing dataset. The example in Figure 2 has two classes (red class and blue class) and the classifier was asked to classify the black square point. In this case, if the classifier classifies the new instances according to the first nearest neighbor, then the black square will be classified as a blue class.
Some of the popular classification algorithms are:
Decision trees are trees that classify instances by sorting them based on feature values. Each node in a decision tree represents a feature in an instance to be classified, and each branch represents a value that the node can assume. Instances are classified starting at the root node and sorted based on their feature values [14] .
Support vector machines (SVMs) are a learning machine developed by Vapnik [15] . The performance of this algorithm, as compared to other algorithms, has proven to be particularly useful for the analysis of various classification problems, and has recently been widely used in the bioinformatics field [16] - [18] . Linear SVMs are usually defined as SVMs with linear kernel. The training data for linear SVMs could be linear non-separable and then soft-margin SVM could be applied. Linear SVM separates the two classes in the training data by producing
Figure 1. Data samples clustered into three clusters around three different centers.
the optimal separating hyper-plane with a maximal margin between class 1 and class 2 samples (Figure 3). Given a training set of labeled examples  where
where 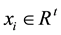 and
and , the support vector machines (SVMs) find the separating hyper-plane of the form
, the support vector machines (SVMs) find the separating hyper-plane of the form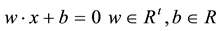 .
.
Here, w is the “normal” of the hyper-plane. The constant b defines the position of the hyper-plane in the space. One could use the following formula as a predictor for a new instance: 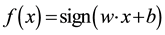 (for more information see Vapnik [15] ).
(for more information see Vapnik [15] ).
2. Biomarker-Biological Background
A biomarker is a gene, protein/peptide or metabolite present in a biological system, used to indicate a physiological or pathological state that can be recognized or monitored [19] - [21] . Biomarker discovery is a challenging process; a good biomarker has to be sensitive, specific and its test highly standardized and reproducible.
Genomic studies provide scientists with methods to quickly analyze genes and their products en masse. DNA microarray technologies permit systematic approaches to biological discovery that has begun to have a profound impact on biological research, pharmacology, and medicine. The ability to obtain quantitative information about the complete transcription profile of cells promises to be an exceptionally powerful means to explore basic biology, diagnose disease, facilitate drug development, tailor therapeutics to specific pathologies, and generate databases with information about living processes [22] .
Figure 2. An example of how the classifiers work.
Figure 3. A simple linear support vector.
Gene expression studies bridge the gap between DNA information and trait information by dissecting biochemical pathways into intermediate components between genotype and phenotype. These studies open new avenues for identifying complex disease genes and biomarkers for disease diagnosis and for assessing drug efficacy and toxicity.
For years, scientists studied one gene at a time and genes were indeed studied in isolation from the larger context of other genes. Nowadays, genomics studies the genome of organisms as a whole. It is based on high- throughput techniques allowing a wide picture of gene characteristics. The most popular high throughput techniques are arrays, which are an orderly arrangement of a great number of samples allowing large-scale studies (http://www.gene-chips.com/).
The first arrays were made using DNA samples. This is the genomic area, which emerged from the sequencing of genomes from many organisms. The development of the first arrays to study a great number of genes at a time started many years ago [23] and has widely expanded since then. But now, we can array DNA and RNA probes, proteins, antibodies and even biological samples allowing new types of research. Furthermore, other types of high throughput techniques are currently developing, for instance to study metabolites.
Genomics is thus linked to the development of new biotechnology which covers a broad field of disciplines (biology, computer science, chemistry, physics, and engineering) and which converge and work in synergy to advance rapidly. Genomics involves the identification of organism’s genes and understanding how the genes work using new biotechnological approaches [24] .
Recent advances in genomics are bringing about a revolution in our understanding of the molecular mechanisms of phenotypes, including the complex interplay of genetic and environmental factors [25] .
Genomics divided into two basic areas, structural genomics and functional genomics (also called post-ge- nomic area) [26] . In the former, the target of research is DNA which corresponds to the genetic background of organisms. Structural genomics is therefore clearly related to genetics. In functional genomics, the targets of research are the key molecules which give life to the cells: RNA, proteins and also metabolites (which are both biologically active molecules within cells and tissues). Functional genomics allows the detection of genes that are turned on/off at any given time depending on environmental factors.
Today, genomics has induced two new paradigms in biology. The first paradigm is a new approach allows the study of the complex network through which genes and proteins communicate. It implies the combination of expertise from biologists, engineers, chemists, and computer scientists. This multidisciplinary approach allows the development of systems biology. The second paradigm is a direct consequence of more available information derived from genomics studies. The raw data needs to be analyzed and then to be used in the systemic approach indicated above. This led the development of bioinformatics which needs the use of computers to manage biological information.
The practical applications of gene expression analyses are numerous and only beginning to be realized. One particularly powerful application of gene expression analyses is biomarker identification, which can be used for disease risk assessment, early detection, prognosis, prediction response to therapy, and preventative measures is a challenging task for cancer prevention and the improvement of treatment outcomes. Approaches to cancer biomarker discovery include genomic, epigenomic, transcriptomic, and proteomic analyses.
Current efforts in the laboratory focus on the identification of biomarkers in chronic lymphocytic leukemia, lung cancer and colon cancer. Among the biomarkers we consider are plasma microRNAs (miRNAs). miRNAs are a class of small RNAs that function as regulators of gene expression. Alteration of gene expression patterns due to dysregulation of miRNAs is a common theme in tumorigenesis. High concentrations of cell-free miRNAs originating from the primary tumor have been found in the plasma of cancer patients, and several lines of evidence indicate that plasma miRNAs are associated with specific vesicles called exosomes. Plasma miRNAs have emerged as a promising source of cancer biomarkers [27] .
A recent discovery of quantifiable circulating cancer-associated miRNAs, expose the immense potential for their use as novel minimally invasive biomarkers for breast and other cancers [28] .
In this section, structural genomics and the different fields of functional genomics (RNA studies, proteomics, metabolomics) will be first detailed for the reader to better understand what genomics is, before the description of the two new paradigms in biology derived from genomics (systemic approaches, bioinformatics).
3. Computational Approaches for Biomarker Discovery
DNA microarray technologies permit systematic approaches to biological discovery that has begun to have a profound impact on biological research, pharmacology, and medicine. The ability to obtain quantitative information about the complete transcription profile of cells promises to be an exceptionally powerful means to explore basic biology, diagnose disease, facilitate drug development, tailor therapeutics to specific pathologies, and generate databases with information about living processes [22] .
Gene expression studies bridge the gap between DNA information and trait information by dissecting biochemical pathways into intermediate components between genotype and phenotype. These studies open new avenues for identifying complex disease genes and biomarkers for disease diagnosis and for assessing drug efficacy and toxicity.
The practical applications of gene expression analyses are numerous and only beginning to be realized. One particularly powerful application of gene expression analyses is biomarker identification, which can be used for disease risk assessment, early detection, prognosis, prediction response to therapy, and preventative measures.
4. Computational Biomarker (Features) Selection
Classification of samples from gene expression datasets usually involves small numbers of samples and tens of thousands of genes. The problem of selecting those biomarker genes that are important for distinguishing the different sample classes being compared poses a challenging problem in high dimensional data analysis and the potential biomarkers are important in improvement in diagnostics and therapeutics development. A variety of methods to address these types of problems have been implemented [29] - [35] . These methods can be divided into two main categories: those that rely on filtering methods and those that are model-based or so-called wrapper approaches [29] [31] .
W. Pan [35] has reported a comparison of different filtering methods, highlighting similarities and differences between three main methods. The filtering methods, although faster than the wrapper approaches, are not particularly appropriate for establishing rankings among significant genes, as each gene is examined individually and correlations among the genes are not taken into account. Although wrapper methods appear to be more accurate, filtering methods are presently more frequently applied to data analysis than wrapper methods [31] .
Li and Yang [36] compared the performance of support vector machine (SVM) algorithms and ridge regression (RR) for classifying gene expression datasets and also examined the contribution of recursive procedures to the classification accuracy. Their study explicitly shows that the way in which the classifier penalizes redundant features in the recursive process has a strong influence on its success. They concluded that RR performed best in this comparison and further demonstrate the advantages of the wrapper method over filtering methods in these types of studies.
Guyon et al. [37] compared the usefulness of RFE (for SVM) against the “naïve” ranking on a subset of genes. The naïve ranking is just the first iteration of RFE to obtain ranks for each gene. They found that SVM-RFE is superior to SVM without RFE and also to other multivariate linear discriminant methods, such as linear discriminant analysis (LDA) and mean-squared-error (MSE) with recursive feature elimination. See Figure 4(b) for the procedure of SVM-RFE.
Xiong, Fang et al. [38] Propose a general framework to incorporate feature (gene) selection into pattern recognition in the process to identify biomarkers. Using this framework, they develop three feature wrappers that search through the space of feature subsets using the classification error as measure of goodness for a particular feature subset being “wrapped around”: linear discriminant analysis, logistic regression, and support vector machines.
Yousef, Jung et al. [39] , describe a new method for gene selection and classification, which is comparable to or better than some methods which are currently applied. Their method (SVM-RCE) combines the K-means algorithm for gene clustering and the machine learning algorithm, SVMs [15] , for classification and gene cluster ranking. The SVM-RCE method differs from related classification methods in that it first groups genes into correlated gene clusters by K-means and then evaluates the contributions of each of those clusters to the classification task by SVM. One can think of this approach as a search for those significant clusters of gene which have the most pronounced effect on enhancing the performance of the classifier. See Figure 4(a) that illustrates the procedure of SVM-RCE. Moreover, Lin-Kai [40] propose an improved method of SVM-RCE called ISVM-RCE. ISVM-RCE eliminates genes within the clusters instead of removing a cluster of genes when the number of clusters is small. Six data sets are used to test the performance of ISVM-RCE and compared their performances with SVM-RCE and linear-discriminant-analysis-based RFE (LDA-RFE). The results show that ISVM-RCE

Figure 4. (a) Recursive cluster elimination (RCE) procedure with SVM; (b) Recursive feature elimination (RFE) procedure with SVM.
greatly reduces the time cost of SVM-RCE, meanwhile obtains comparable classification performance as SVM-RCE, while LDA-RFE is not stable.
Recently, Grate [41] has described a technique for discovering small sets of genes (3 or less). The technique is based on brute force approach of exhaustive search through all genes, gene pairs and some cases triple of genes. The combination is analyzed with classification method looking for those combinations that form training error-free classifiers.
Robustness of biomarkers is an important issue, as it may greatly influence subsequent biological validations. In addition, a more robust set of markers may strengthen the confidence of an expert in the results of a selection method. Abeel [42] has proposed a general framework for the analysis of the robustness of a biomarker selection algorithm. The framework is based on ensemble feature selection, where multiple feature selections are combined in order to increase the robustness of the final set of selected features. The proposed methodology is evaluated on four microarray datasets showing increases of up to almost 30% in robustness of the selected biomarkers, along with an improvement of about 15% in classification performance. A different approach to deal with inconsistent cancer biomarkers due to bioinformatics artifacts, was proposed by [43] . The approach is based on using multiple data sets from microarrays, mass spectrometry, protein sequences, and other biological knowledge in order to improve the reliability of cancer biomarkers. The study presents a novel Bayesian network (BN) model which integrates and crosses-annotates multiple data sets related to prostate cancer. The computational results show that the method is able to find biologically relevant biomarkers with highest reliability [44] .
Some data is composed from multiple category or classes. For such a data a special methods of biomarker selection is required. [45] has proposed classification method is based on two schemes: error-correcting output coding (ECOC) and pairwise coupling (PWC). The biomarker pattern for distinguishing each disease category from another one is achieved by the development of an extended Markov blanket (EMB) feature selection method.
The study of [46] demonstrates that the machine learning approach can be used to detect a small subset of biomarker genes from high dimensional datasets and generate a classifier for multiple classes. A multiclass support vector machine (MC-SVM) method and an unsupervised K-mean clustering method were applied to independently refine the classifier, producing a smaller subset of 39 and 30 classifier genes, separately, with 11 common genes being potential biomarkers.
Yousef et al. [47] developed a new algorithm called recursive network elimination (RNE) with SVM. The main idea is to integrate network information with recursive feature elimination based on SVM. First, filter one thousand genes selected by t-test from training set so that only genes that map to a gene network database remain. Then to the remaining genes the gene expression network analysis tool (GXNA) [48] is applied to form n clusters of genes that are highly connected in the network. Using these clusters linear SVM is used to classify the samples and a weight is assigned to each cluster based on its significance to the classification. The clusters with less information are removed while retaining the remainder for the next classification step. This process is repeated until an optimal classification result is attained.
5. A Comparative Performance
Pirooznia, M. et al. [49] conducted a study to compare the performance (with cross validation) of different machine learning algorithm such as SVM, RBF Neural Nets, MLP Neural Nets, Bayesian, Decision Tree and Random Forrest methods. Additionally, the efficiency of the feature selection methods including support vector machine recursive feature elimination was compared. The data set consists from eight different binary (two class) microarray datasets. The performance was very well and in average higher than 90%. As expected, this study shows that in most cases the accuracy is improved with feature selection. Additionally, this study reports about stability of the top 50, 100, 200 genes with SVM-RFE. Actually those genes will be serving later as a biomarker for diagnostic diseases.
Yousef et al. [39] compare the performance of SVM-RCE against the popular SVM-RFE method to reported in most cases that SVM-RCE is with better results as in average of 6 datasets is 96% while SVM-RFE with 92% accuracy.
6. Conclusions
In this review, we proposed many computational approaches which are critical for mining high-dimensional data in order to effectively discover biomarkers. Best data mining approach would to integrate different approaches to arrive at an effective algorithm; however most of the suggested methods ignore existing biological knowledge and treat all the genes equally. Information about gene networks or pathways should be incorporated into a classifier to improve both the predictive performance and interpretability of the resulting biomarker genes as suggested by [47] and [50] .
Moreover, we suggest developing more algorithms that incorporate biological knowledge, extracted from existing database with the procedure of feature selection to have more accurate biological results.
Acknowledgements
This study was supported by The College of Sakhnin and The Institute of Applied Research―The Galilee Society. Also this study was supported by a grant from the Ministry of Science, Israel.
Competing Interests
No competing interests.
References
- Mitchell, T. (1997) Machine Learning. McGraw-Hill, New York.
- Malik Yousef, N.N. and Khalifav, W. (2010) A Comparison Study between One-Class and Two-Class Machine Learning for MicroRNA Target Detection. Journal of Biomedical Science and Engineering, 3, 347-252. http://dx.doi.org/10.4236/jbise.2010.33033
- Jain, A.K. and Dubes, R.C. (1988) Algorithms for Clustering Data. Prentice Hall, Englewood Cliffs.
- Hartigan, J. (1975) Clustering Algorithms. Wiley, New York.
- Tryon, R.C. and Bailey, D.E. (1973) Cluster Analysis. McGraw-Hill, New York.
- Sneath, P.H.A. and Sokal, R.R. (1973) Numerical Taxonomy. Freeman, San Francisco.
- Anderberg, M.R. (1973) Cluster Analysis for Applications. Academic Press, New York.
- Jardine, N. and Sibson, R. (1971) Mathematical Taxonomy. Wiley, London.
- MacQueen, J.B. (1967) Some Methods for Classification and Analysis of Multivariate Observations. Proceedings of 5-th Berkeley Symposium on Mathematical Statistics and Probability, 1, 281-297.
- Dunn, J.C. (1973) A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. Journal of Cybernetics, 3, 32-57. http://dx.doi.org/10.1080/01969727308546046
- Bezdek, J.C. (1981) Pattern Recognition with Fuzzy Objective Function Algoritms. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4757-0450-1
- Johnson, S.C. (1967) Hierarchical Clustering Schemes. Psychometrika, 32, 241-254. http://dx.doi.org/10.1007/BF02289588
- Dempster, A.P., Laird, N.M. and Rubin, D.B. (1977) Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society, 39, 1-38.
- Yuan, Y. and Shaw, M.J. (1995) Induction of Fuzzy Decision Trees. Fuzzy Sets and Systems, 69, 125-139. http://dx.doi.org/10.1016/0165-0114(94)00229-Z
- Vapnik, V. (1995) The Nature of Statistical Learning Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4757-2440-0
- Donaldson, I., Martin, J., De Bruijn, B., Wolting, C., Lay, V., Tuekam, B., Zhang, S.D., Baskin, B., Bader, G., Michalickova, K., Pawson, T. and Hogue, C.W.V. (2003) PreBIND and Textomy―Mining the Biomedical Literature for Protein-Protein Interactions Using a Support Vector Machine. BMC Bioinformatics, 4, 11. http://dx.doi.org/10.1186/1471-2105-4-11
- Pavlidis, P., Weston, J., Cai, J. and Grundy, W.N. (2001) Gene Functional Classification from Heterogeneous Data. Proceedings of the 5th Annual International Conference on Computational Biology, Montreal, 22-25 April 2001, 249- 255.
- Haussler, D. (1999) Convolution Kernels on Discrete Structuresed. Technical Report UCSCCRL-99-10, Baskin School of Engineering, University of California, Santa Cruz.
- Novak, K. (2006) Taking out the Trash. Nature Reviews Cancer, 6, 92. http://dx.doi.org/10.1038/nrc1807
- Novak, K. (2006) Marked Aggression. Nature Reviews Cancer, 6, 96. http://dx.doi.org/10.1038/nrc1806
- Goymer, P. (2006) Different Treatment. Nature Reviews Cancer, 6, 94-95. http://dx.doi.org/10.1038/nrc1808
- Young, R.A. (2000) Biomedical Discovery with DNA Arrays. Cell, 102, 9-15. http://dx.doi.org/10.1016/S0092-8674(00)00005-2
- Hergenhahn, M., Muhlemann, K., Hollstein, M. and Kenzelmann, M. (2003) DNA Microarrays: Perspectives for Hypothesis-Driven Transcriptome Research and for Clinical Applications. Current Genomics, 4, 543-555. http://dx.doi.org/10.2174/1389202033490231
- ESRC (Economic and Social Research Council) (2002) Genomics Scenario Project 2. Overview and Forecasts of the Applications of Genomics. http://www.cric.ac.uk/cric/projects/genomics/overview.pdf
- Collins, F.S., Green, E.D., Guttmacher, A.E. and Guyer, M.S. (2003) A Vision for the Future of Genomics Research. Nature, 422, 835-847. http://dx.doi.org/10.1038/nature01626
- Eggen, A. (2003) Basics and Tools of Genomics. Outlook on Agriculture, 32, 215-217. http://dx.doi.org/10.5367/000000003322740531
- Jeffrey, S.S. (2008) Cancer Biomarker Profiling with microRNAs. Nature Biotechnology, 26, 400-401. http://dx.doi.org/10.1038/nbt0408-400
- Heneghan, H.M., Miller, N., Lowery, A.J., Sweeney, K.J. and Kerin, M.J. (2010) MicroRNAs as Novel Biomarkers for Breast Cancer. Journal of Oncology, 2010, Article ID: 950201.
- Wang, Y., Tetko, I.V., Hall, M.A., Frank, E., Facius, A., Mayer, K.F.X. and Mewes, H.W. (2005) Gene Selection from Microarray Data for Cancer Classification―A Machine Learning Approach. Computational Biology and Chemistry, 29, 37-46. http://dx.doi.org/10.1016/j.compbiolchem.2004.11.001
- Li, T., Zhang, C.L. and Ogihara, M. (2004) A Comparative Study of Feature Selection and Multiclass Classification Methods for Tissue Classification Based on Gene Expression. Bioinformatics, 20, 2429-2437. http://dx.doi.org/10.1093/bioinformatics/bth267
- Inza, I., Larrañaga, P., Blanco, R. and Cerrolaza, A.J. (2004) Filter versus Wrapper Gene Selection Approaches in DNA Microarray Domains. Artificial Intelligence in Medicine, 31, 91-103. http://dx.doi.org/10.1016/j.artmed.2004.01.007
- Zhang, X.G., Lu, X., Shi, Q., Xu, X.Q., Leung, H.C.E., Harris, L.N., et al. (2006) Recursive SVM Feature Selection and Sample Classification for Mass-Spectrometry and Microarray Data. BMC Bioinformatics, 7, 197. http://dx.doi.org/10.1186/1471-2105-7-197
- Duan, K.B., Rajapakse, J.C., Wang, H.Y. and Azuaje, F. (2005) Multiple SVM-RFE for Gene Selection in Cancer Classification with Expression Data. IEEE Transactions on NanoBioscience, 4, 228-234. http://dx.doi.org/10.1109/TNB.2005.853657
- Yang, X.W., Lin, D.Y., Hao, Z.F., Liang, Y.C., Liu, G.R. and Han, X. (2003) A Fast SVM Training Algorithm Based on the Set Segmentation and k-Means Clustering. Progress in Natural Science, 13, 750-755. http://dx.doi.org/10.1080/10020070312331344360
- Pan, W. (2002) A Comparative Review of Statistical Methods for Discovering Differentially Expressed Genes in Replicated Microarray Experiments. Bioinformatics, 18, 546-554. http://dx.doi.org/10.1093/bioinformatics/18.4.546
- Li, F. and Yang, Y.M. (2005) Analysis of Recursive Gene Selection Approaches from Microarray Data. Bioinformatics, 21, 3741-3747. http://dx.doi.org/10.1093/bioinformatics/bti618
- Guyon, I., Weston, J., Barnhill, S. and Vapnik, V. (2002) Gene Selection for Cancer Classification Using Support Vector Machines. Machine Learning, 46, 389-422. http://dx.doi.org/10.1023/A:1012487302797
- Xiong, M., Fang, X. and Zhao, J. (2001) Biomarker Identification by Feature Wrappers. Genome Research, 11, 1878- 1887.
- Yousef, M., Jung, S., Showe, L.C. and Showe, M.K. (2007) Recursive Cluster Elimination (RCE) for Classification and Feature Selection from Gene Expression Data. BMC Bioinformatics, 8, 144. http://dx.doi.org/10.1186/1471-2105-8-144
- Luo, L.K., Huang, D.F., Ye, L.J., Zhou, Q.F., Shao, G.F. and Peng, H. (2011) Improving the Computational Efficiency of Recursive Cluster Elimination for Gene Selection. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 8, 122-129. http://dx.doi.org/10.1109/TCBB.2010.44
- Grate, L. (2005) Many Accurate Small-Discriminatory Feature Subsets Exist in Microarray Transcript Data: Biomarker Discovery. BMC Bioinformatics, 6, 97. http://dx.doi.org/10.1186/1471-2105-6-97
- Abeel, T., Helleputte, T., Van de Peer, Y., Dupont, P. and Saeys, Y. (2009) Robust Biomarker Identification for Cancer Diagnosis with Ensemble Feature Selection Methods. Bioinformatics, 26, 392-398. http://dx.doi.org/10.1093/bioinformatics/btp630
- Deng, X., Geng, H. and Ali, H.H. (2007) Cross-Platform Analysis of Cancer Biomarkers: A Bayesian Network Approach to Incorporating Mass Spectrometry and Microarray Data. Cancer Informatics, 3, 183-202.
- Huang, H.C., Jupiter, D. and VanBuren, V. (2010) Classification of Genes and Putative Biomarker Identification Using Distribution Metrics on Expression Profiles. PLoS ONE, 5, e9056. http://dx.doi.org/10.1371/journal.pone.0009056
- Oh, J.H., Kim, Y.B., Gurnani, P., Rosenblatt, K.P. and Gao, J.X. (2008) Biomarker Selection and Sample Prediction for Multi-Category Disease on MALDI-TOF Data. Bioinformatics, 24, 1812-1818. http://dx.doi.org/10.1093/bioinformatics/btn316
- Li, Y., Wang, N., Perkins, E.J., Zhang, C.Y. and Gong, P. (2010) Identification and Optimization of Classifier Genes from Multi-Class Earthworm Microarray Dataset. PLoS ONE, 5, e13715. http://dx.doi.org/10.1371/journal.pone.0013715
- Yousef, M., Ketany, M., Manevitz, L., Showe, L.C. and Showe, M.K. (2009) Classification and Biomarker Identifica- tion Using Gene Network Modules and Support Vector Machines. BMC Bioinformatics, 10, 337. http://dx.doi.org/10.1186/1471-2105-10-337
- Nacu, S., Critchley-Thorne, R., Lee, P. and Holmes, S. (2007) Gene Expression Network Analysis and Applications to Immunology. Bioinformatics, 23, 850-858. http://dx.doi.org/10.1093/bioinformatics/btm019
- Pirooznia, M., Yang, J.Y., Yang, M.Q. and Deng, Y.P. (2008) A Comparative Study of Different Machine Learning Methods on Microarray Gene Expression Data. BMC Genomics, 9, S13. http://dx.doi.org/10.1186/1471-2164-9-S1-S13
- Tai, F. and Pan, W. (2007) Incorporating Prior Knowledge of Predictors into Penalized Classifiers with Multiple Penalty Terms. Bioinformatics, 23, 1775-1782. http://dx.doi.org/10.1093/bioinformatics/btm234