Journal of Intelligent Learning Systems and Applications
Vol.6 No.2(2014), Article ID:45591,17 pages
DOI:10.4236/jilsa.2014.62006
Adaptive Fuzzy Sliding Mode Controller for Grid Interface Ocean Wave Energy Conversion
Adel A. A. Elgammal
Utilities Engineering Department, The University of Trinidad and Tobago UTT, Trinidad and Tobago, West Indies
Email: adel_elgammal@ieee.org
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 January 2014; revised 1 February 2014; accepted 8 February 2014
ABSTRACT
This paper presents a closed-loop vector control structure based on adaptive Fuzzy Logic Sliding Mode Controller (FL-SMC) for a grid-connected Wave Energy Conversion System (WECS) driven Self-Excited Induction Generator (SEIG). The aim of the developed control method is to automatically tune and optimize the scaling factors and the membership functions of the Fuzzy Logic Controllers (FLC) using Multi-Objective Genetic Algorithms (MOGA) and Multi-Objective Particle Swarm Optimization (MOPSO). Two Pulse Width Modulated voltage source PWM converters with a carrier-based Sinusoidal PWM modulation for both Generatorand Grid-side converters have been connected back to back between the generator terminals and utility grid via common DC link. The indirect vector control scheme is implemented to maintain balance between generated power and power supplied to the grid and maintain the terminal voltage of the generator and the DC bus voltage constant for variable rotor speed and load. Simulation study has been carried out using the MATLAB/Simulink environment to verify the robustness of the power electronics converters and the effectiveness of proposed control method under steady state and transient conditions and also machine parameters mismatches. The proposed control scheme has improved the voltage regulation and the transient performance of the wave energy scheme over a wide range of operating conditions.
Keywords:Grid integration, Wave Energy Conversion Systems, Self-Excited Induction Generator (SEIG), Vector Control, Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Sliding Mode Control (SMC), Fuzzy Logic Control (FLC), Membership Function Tuning

1. Introduction
Producing energy from renewable energy resources such as solar, wind, ocean, micro-hydro, biomass, etc. is becoming a necessity because of the continuous increasing of world energy demand of electrical power and continuous depreciation of conventional energy resources like oil, gas and coal. Since the abundance of wave power potential and its pollution-free nature, wave energy seems to be one of the attractive and exploitable alternative energy sources in the world today [1] -[4] . Globally, the theoretical potential of ocean energy has been estimated over 100,000 TWh/year which is about 100 times the total hydroelectricity generation of the whole planet, (as a reference, the world’s electricity consumption is around 16,000 TWh/year) [5] [6] . There are many different technologies converting ocean wave power into electrical power, such as Oscillating Water Columns (OWCs), marine and tidal current energy, ocean thermal energy, energy from salinity gradients (osmosis), and cultivation of marine biomass. However, the OWC-type wave-energy-harnessing method is considered as one of the best techniques to convert wave energy into electricity [5] . However, the economic performance of the WECS is still far from competitive and significant scope exists for the improvement of the capacity factor using the intelligent control systems [7] . Three-phase self-excited induction generators (SEIG) are widely used for generating power from renewable energy sources, such as wave, wind and small hydro for standalone and grid-connected applications. SEIG has many advantages over the DC generators and the synchronous generator such as its low cost, simple construction, absence of DC power supply for field excitation, brushless (squirrel-cage rotor), ruggedness, maintenance-free structure, simple control, self-protection against short-circuits and large overload and good dynamic response and accurate torque control when vector control techniques are used. However, the major disadvantage of SEIG is poor voltage and frequency regulation under varying prime mover speed, excitation capacitor and load characteristics [8] [9] . A number of schemes based on field oriented control have been suggested for regulating the terminal voltage. The stator flux oriented vector control with additional decoupling compensation for vector control in the stator flux orientation for wind turbine driven isolated induction generator has been presented in [10] . In [11] , a field-oriented controller has been used to excite the stand-alone induction machine efficiently, minimizing copper and iron losses, and to regulate the generated voltage for variable speed and load. The voltage control of the induction generator using rotor field-oriented control for small-scale AC and DC power applications has been given in [12] . An advanced solution for the problem of the variation of the terminal dc voltage due to the variation of the wind speed of the turbine or changing the load has been presented in [13] . The proposed solution provided an effective method of control based on fuzzy logic of the dc bus voltage based on an indirect rotor flux control strategy of the induction generator.
Fuzzy Logic Control System (FLCs) is a rule-based expert system with the ability to emulate a human’s subjective decision-making model through its linguistic rules [14] . While the fuzzy rules are relatively easy to derive from human experts, the fuzzy membership functions (MFs) are difficult to obtain. A fuzzy system can improve its performance by further tuning the fuzzy membership functions and selecting suitable fuzzification and defuzzification methods. The tuning means that, after we construct linguistic rules, the membership functions are altered and reconstructed by adjusting the difference between the inferred value and the control output to have a minimum value [15] . Differential evolution (DE) is a population-based method and generally considered as a parallel stochastic direct search optimizer which is very simple, precise, fast as well as robust algorithm. The main advantage of DE is its capability in solving optimization problems which require optimization process with non-linear and multi-modal objective functions. Recently, intelligent computation techniques based on genetic algorithms (GAs), tabu search algorithm, simulated annealing (SA) and particle swarm optimization (PSO) have been successfully used as optimization tools in various research areas, including the automatic tuning process of MFs. An adaptive neural network (NN) based fuzzy inference system was used to learn the mapping between the inputs and outputs to generate a Sugeno-type of fuzzy system [16] . A quantum NN was presented in [17] to learn the data space of a Tagaki-Sugeno (TSK) fuzzy controller. A back-propagation with recursive leastsquares and square-root filter methods has been proposed to learn the parameters of the fuzzy control system [18] [19] . A genetic learning algorithm has been proposed to optimize the type-2 fuzzy neural network parameters [20] [21] . GA has been used in tuning both the fuzzy MFs and the fuzzy rule bases [22] [23] in the areas of mobile robotics. The optimization of the MF parameters of a type-2 Mamdani FLS was presented in [24] based on fuzzy genetic architecture. Recently, the swarm optimization techniques, particle swarm optimization (PSO) and Ant Colony (AC) techniques have been proposed to automatically tune the FLC parameters and the membership function [25] -[33] . The sliding mode control theory (SMC) based on the variable structure system can be the good choice especially for the complicated environment and systems with uncertainty disturbance [34] . The sliding mode control is robust to plant uncertainties, parameters variations and insensitive to external disturbances. It is widely used to obtain good dynamic performance of controlled systems.
This paper describes the application of the MOGA and MOPSO for the automatic design of the scaling factors and the membership function parameters of a Mamadani-type fuzzy sliding mode control system in order to find the best intelligent controller associated to the flux oriented control technique for a variable speed wave turbine driven SEIG interfaced to the grid. A number of fitness functions are defined to measure the performance of the proposed controllers such as minimizing the mean square errors of the DC voltage, DC current, the Root Mean Square (RMS) of the AC line voltage and the frequency. Since these objectives are conflicting, multi-objective optimization is used to find a Pareto front from which a desired optimal operating state can be chosen. This is done using MOPSO and MOGA to determine the optimal gains for the SMC controllers of both the generatorside converter and the Grid-side converter of the SEIG. For the purpose of comparing the improvement obtained in the system dynamic performance with the application of the MOPSO and MOGA procedures to design the SMC controller gains, these results are compared with those obtained using a classical regulator SMC and a Fuzzy Logic Controller. A complete simulation model is developed for such machine under variable speed operation using MATLAB Simulink environment. Simulation results show that the proposed design approach is efficient to find the optimal design of the SMC controller and therefore improves the transient performance of the WECS over a wide range of operating conditions. This paper is organized as follows: Section II presents the SEIG and WECS mathematical model description as the systems to be studied and controlled. Section III shows the dynamic simulations of the studied system to evaluate the performance of the proposed controllers subject to a three-phase fault and load disturbances. Finally, specific important conclusions of this paper are drawn in Section IV.
2. Modeling of the Studied System
2.1. System Configuration
Figure 1 shows the system configuration of the proposed block diagram of the power circuit and control strategy for SEIG converting power from the wave to deliver power into the electric grid with constant frequency and RMS of the AC line voltage for a large range of wave variation. The proposed AC/DC converter is designed to convert the variable-frequency variable-voltage power generated by the SEIG AC power to regulated DC power. The regulated DC power can charge a battery set and supply DC loads. Then DC power is delivered to the DC side of the three-phase inverter to be converted into a three-phase AC power for the AC loads and for the grid connection. To overcome the problem of the variation of the terminal dc voltage when the variation of the wave speed of the turbine or when changing the load, there is provided an effective method of control based on fuzzy logic sliding mode control system of the dc bus voltage. Direct vector control strategy with rotor flux orientation with high dynamic performance has been used in this paper for voltage and frequency control of grid-connected SEIG for both DC and AC power applications. The induction generator rotor flux is controlled by the d-axis stator current and the q-axis stator current controls the delivering active stator power. This method is used to control the electrical torque of the SEIG driven by a variable speed wave turbine, where different forms of wave speed variation effect taken into consideration. The simulation studies for different transient conditions such as phase to phase short circuit fault, sudden application and removal of both AC and DC loads have been carried out to demonstrate the effectiveness of the scheme.
2.2. Generator-Side Converter Control
The generator-side converter was implemented so that the field-oriented current control loop controls the rotor flux and the machine torque, as shown in Figure 2. The rotor flux can be controlled by controlling the d-axis rotor current. The machine torque can be independently controlled by controlling the q-axis rotor current. These controls are implemented by two FLC-SMC controllers in each control loop. The rotor flux lr and the machine torque Te can be represented as functions of the individual current components. Therefore, the reference values of idr and iqr can be determined directly from the lr and Te commands. In the rotor flux control loop of the gene-

Figure 1. Schematic representation of wave energy converter with SEIG full-controlled induction generator.

Figure 2. Generator-side converter control.
rator side converter, the actual signal of the rotor flux (lr) is compared
with it’s the command
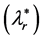 to form the rotor flux error signal. The rotor flux error is fed to the FLC-SMC
controller to generate the reference signal of the d-axis current component
to form the rotor flux error signal. The rotor flux error is fed to the FLC-SMC
controller to generate the reference signal of the d-axis current component
 of the compensator reference AC current. In the torque control loop of the generator
side converter, the actual torque is compared with the reference torque to generate
the error signal which is passed through the FLC-SMC controller to generate the
reference signal for the q-axis current component
of the compensator reference AC current. In the torque control loop of the generator
side converter, the actual torque is compared with the reference torque to generate
the error signal which is passed through the FLC-SMC controller to generate the
reference signal for the q-axis current component . The principal vector
control parameters
. The principal vector
control parameters
 and
and , which are DC values in synchronously rotating
frame, are converted to stationary frame with the help of unit vectors (cosqe
and sinqe) generated from flux vector signals
, which are DC values in synchronously rotating
frame, are converted to stationary frame with the help of unit vectors (cosqe
and sinqe) generated from flux vector signals
 and
and . The instantaneous three-phase reference
currents
. The instantaneous three-phase reference
currents
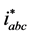 are generated by transforming the reference d-q components
are generated by transforming the reference d-q components
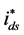 and
and
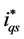 in the stator-flux oriented reference frame. The actual threephase currents signals
iabc are then compared with their reference signals
in the stator-flux oriented reference frame. The actual threephase currents signals
iabc are then compared with their reference signals
 to generate the error signals, which are passed through the hysteresis current controller
to form the switching signals. They are then used by the PWM module to generate
the IGBT gate control signals to drive the IGBT converter. The main task of the
hysteresis current controller in current regulated PWM inverters is to force the
current vector in the three phase load according to a reference trajectory. The
basic implementation of hysteresis current control is based on deriving the switching
signals from the comparison of the current error with a fixed hysteresis band. This
control is based on the comparison of the actual phase current with the hysteresis
band around the reference current associated with that phase. Three hysteresis bands
of the width ±h are defined around each reference value of the phase currents
to generate the error signals, which are passed through the hysteresis current controller
to form the switching signals. They are then used by the PWM module to generate
the IGBT gate control signals to drive the IGBT converter. The main task of the
hysteresis current controller in current regulated PWM inverters is to force the
current vector in the three phase load according to a reference trajectory. The
basic implementation of hysteresis current control is based on deriving the switching
signals from the comparison of the current error with a fixed hysteresis band. This
control is based on the comparison of the actual phase current with the hysteresis
band around the reference current associated with that phase. Three hysteresis bands
of the width ±h are defined around each reference value of the phase currents . The error of each phase current is controlled
by a two level hysteresis comparator. The goal is to keep the actual value of the
currents within their hysteresis bands all the time.
. The error of each phase current is controlled
by a two level hysteresis comparator. The goal is to keep the actual value of the
currents within their hysteresis bands all the time.
2.3. Grid-Side Converter Control
The grid-side converter is also vector-controlled using direct vector control and
synchronous current control in the inner loops. Figure
3 shows the overall control scheme of the grid-side converter. The main
objective of the grid-side converter is to keep the dc-link voltage constant regardless
of the magnitude and direction of the rotor power. The control of the grid-side
converter are organized in two loops; a DC-link current control loop, which controls
the current through the grid filter, and DC-link voltage control loop that controls
the dc-link voltage. This implies that the dc-link voltage control loop has to act
on the d component of the grid-filter current. An outer DC voltage control loop
is used to keep the DC link voltage constant. The actual signal of the dc-link voltage
(Vdc) is compared with its command
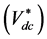 to form the error signal, which is passed through the FLC-SMC controller to generate
the reference signals for the d-axis current component
to form the error signal, which is passed through the FLC-SMC controller to generate
the reference signals for the d-axis current component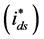 . In the second loop,
the actual signal of the line current (Vab) is compared with the reference
line current
. In the second loop,
the actual signal of the line current (Vab) is compared with the reference
line current
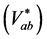 to form the line current error signal, which is passed through the FLC-SMC controller
to generate the reference signals for the q-axis current component
to form the line current error signal, which is passed through the FLC-SMC controller
to generate the reference signals for the q-axis current component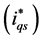 . The instantaneous
three-phase reference stator currents
. The instantaneous
three-phase reference stator currents
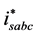 are generated by transforming the reference d-q components
are generated by transforming the reference d-q components
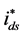 and
and
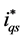 in the stator-flux oriented reference frame. The actual three-phase stator currents
signals isabc are then compared with their reference signals
in the stator-flux oriented reference frame. The actual three-phase stator currents
signals isabc are then compared with their reference signals
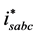 to generate the error signals, which are passed through the hysteresis current controller
to form the switching signals. They are then used by the PWM module to generate
the IGBT gate control signals to drive the IGBT converter.
to generate the error signals, which are passed through the hysteresis current controller
to form the switching signals. They are then used by the PWM module to generate
the IGBT gate control signals to drive the IGBT converter.
2.4. Fuzzy Logic Control-Based SMC Controller (FLC-SMC) Structure
Sliding mode control (SMC) is a technique derived from Variable Structure Theory. The basic idea of SMC controller is to force the tracking error e(t), after a finite time of reaching phase, to approach the sliding surface S(t) containing the system operating point and and then move along the sliding surface to the origin. SMC controllers proved their capability to handle nonlinear and time varying systems, high accuracy and robustness with respect to various internal and external disturbances.
The sliding surface S(t) is defined with the tracking error e(t) and its integral
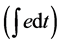 and rate of change (ė) as [35]:
and rate of change (ė) as [35]:
 (1)
(1)
where λ0, λ1, λ2 > 0 are positive real constants.
The overall design procedure of the combined FLC as a supervisory control with the adaptive SMC controller using the MOGA and the MOPSO is illustrated in Figure 4. The fuzzy sliding mode controller is proposed in order to eliminate the reaching time, the tracking error and the chattering problem. The main advantage of this method is that the robust behavior of the system is guaranteed and the performance of the system in the sense of removing chattering is improved [34] [36] . The parameter values (scaling factors, membership functions, rule term base) of the fuzzy sliding mode controller can be chosen by the MOGA and the MOPSO in such a way to obtain the best system behavior with respect to specific criteria. The SMC parameter settings (k, l0, l1, l2) are generated by fuzzy inference, which provides a nonlinear mapping from the error signal e (difference between system output and reference signal and defined as e(k) = Reference (k) – Output (k)) and the first-order difference of error signal De which is defined as Δe(k) = e(k) – e(k – 1). Note that the input variables to the fuzzy controller (E and DE) are transformed by multiplying the error (e) and the first-order difference of error signal (De) by the scaling factors β1 and β2 whose role is to allow the fuzzy controller to “see” the external world to be controlled.
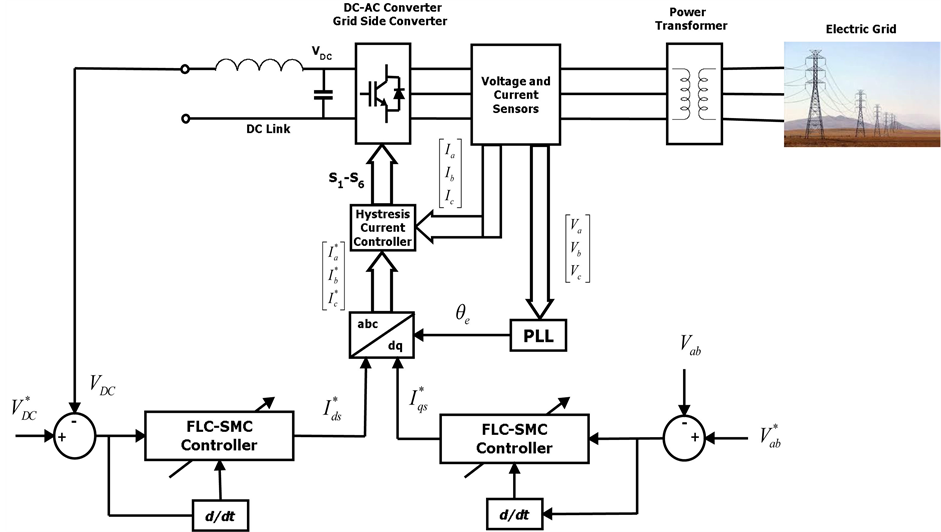
Figure 3. Grid-side converter control.
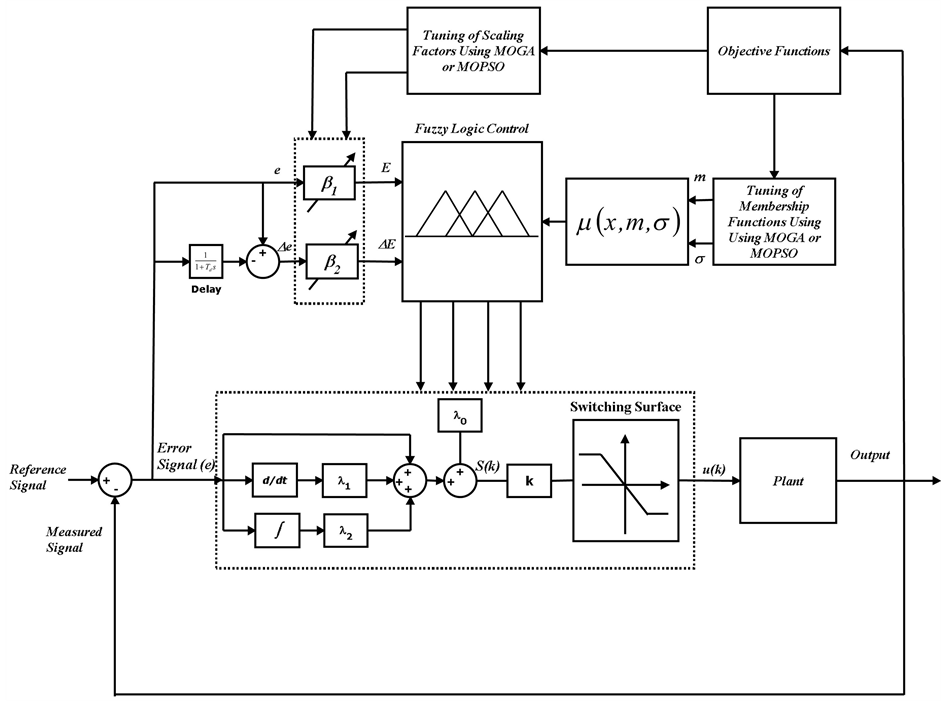
Figure 4. Schematic of the PSO-based scaling factors-tuning of the fuzzy PID controller.
In this paper, the adaptation of the adequate values for the scaling and gain factors of each SMC-type FLC structure is done the MOPSO and the MOGA to find the optimal parameters of the SMC controllers to optimize the proposed fitness functions. In the DC-side and the AC-side control loops, there are four SMC controllers and each of them has four gains (k, l0, l1, l2) and two scaling factors β1 and β2. The sliding hyper-plane highly depends upon dynamics of error and change in error so that we have to consider this variable as input to the fuzzy logic module for updating all gains. The designed fuzzy logic controller has two inputs and four outputs. The inputs are system error (e) and the change of the system error (de/dt) in a sample time, and outputs are the sliding mode controller gains (k, l0, l1, l2). In the proposed FLC, the membership functions of the input variables are assumed to be the Gaussian form [37]:
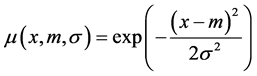 (2)
(2)
where m is the mean (or the center of the membership function) and s is the deviation (or the width of the membership function) of each MF. The set of rules which define the relation between the input and output of fuzzy controller can be found using the available knowledge in the area of designing the system. These rules are defined using the linguistic variables. The membership functions for the inputs and outputs for the fuzzy controller are shown in figures 5-7. Tables 1-4 show the control rules that used for fuzzy self-tuning of SMC controller. Where, NB: negative big, NM: negative medium, NS: negative small, ZE: zero, PS: positive small, PM: positive medium and PB: positive big. VB: very big, B: big, MB: medium big, ZE: zero, M: medium, S: small, MS: medium small.
3. Digital Simulation Results
The wave model of Figure 8 is adopted to generate a specific power reference and validate the good power tracking performances and therefore confirm the effectiveness of the proposed control strategy based on MOPSO and MOGA. In the grid-side and the generator side converters control loops, there are four SMC controllers and each of them has a sliding surface slope l1, a hitting gain (k) and an intercept l0 of sliding hyper-plane. The be-
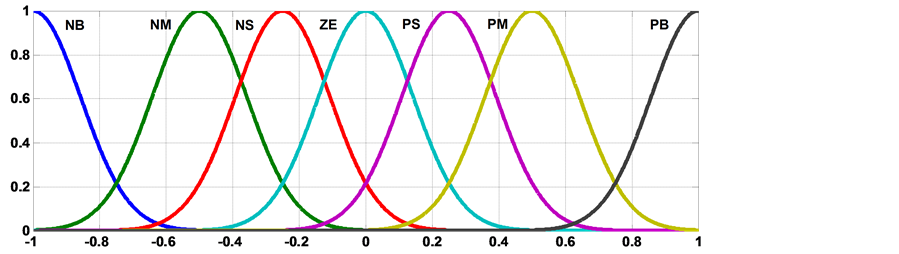
Figure 5.Initial membership functions of inputs (e, Δe).

Figure 6. Initial membership functions of outputs (l0, l1, and l2)

Figure 7. Initial membership functions of output gain k.
Table 3. Initial rule bases for tuning l2.
|
Δe/e |
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
NB |
ZE |
MS |
S |
M |
MB |
VB |
VB |
|
NM |
MS |
MS |
MB |
MB |
MB |
VB |
VB |
|
NS |
S |
MB |
B |
MB |
VB |
VB |
VB |
|
ZE |
M |
MB |
MB |
MB |
VB |
VB |
VB |
|
PS |
B |
MB |
VB |
VB |
VB |
VB |
VB |
|
PM |
MB |
VB |
VB |
VB |
VB |
VB |
VB |
|
PB |
VB |
VB |
VB |
VB |
VB |
VB |
VB |
Table 4. Initial rule bases for tuning k.
|
Δe/e |
NB |
NM |
NS |
ZE |
PS |
PM |
PB |
|
NB |
VB |
VB |
VB |
VB |
VB |
VB |
VB |
|
NM |
VB |
VB |
MB |
MB |
MB |
VB |
VB |
|
NS |
B |
B |
B |
B |
MB |
MB |
VB |
|
ZE |
ZE |
S |
ZE |
MS |
S |
S |
S |
|
PS |
B |
B |
B |
B |
MB |
MB |
VB |
|
PM |
VB |
VB |
MB |
MB |
MB |
VB |
VB |
|
PB |
VB |
VB |
VB |
VB |
VB |
VB |
VB |
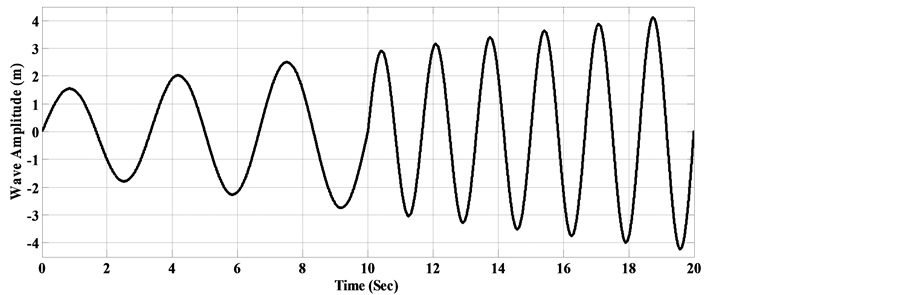
Figure 8. The wave model.
havior of the converters depends on these parameters of the SMC control system. If the controllers are tuned properly, it is possible to improve the gride-side and generator-side converter’s performance during the transient disturbances. For the same operation condition, the MOGA and MOPSO were used to adapt the scaling factors and the membership functions of the FLC to obtain the optimal gains for the SMC controller of the generator-side and the grid-side converters. To compare the improvement obtained in the system dynamic performance with the application of the MOPSO and MOGA procedures to design the FLC-SMC controller gains, these results are compared with those obtained using the traditional SMC and FLC-SMC.
The quality of the gains adjustment is measured by an index that represents the weighted sum of the Normalised Mean Square Error (NMSE) deviations between output plant variables and desired values. This way the objective to improve the system performance during the transient disturbances will be obtained by specifying optimal values for the controller gains. The NMSE deviations between output plant variables and desired values are defined as:
 (3)
(3)
 (4)
(4)
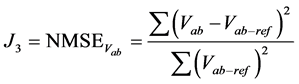 (5)
(5)
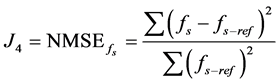 (6)
(6)
The SOPSO and the SOGA obtain a single global or near optimal solution based on a single weighted objective function. The weighted single objective function (Jo) combines several objective functions using specified or selected weighting factors as follows:
 (7)
(7)
where α1 = 0.25, α2 = 0.25, α3 = 0.25, α4 = 0.25 are selected weighting factors. J1, J2, J3, J4 are the selected objective functions. The weighting factors in the objective function (Jo) are used to satisfy different design requirements. If a large value of α1 is used, then the objective is to minimize the error of the DC link voltage. On the other hand, the MOPSO and the MOGA finds the set of acceptable (trade-off) Optimal Solutions. This set of accepted solutions is called Pareto front. These acceptable trade-off multi-level solutions give more ability to the user to make an informed decision by seeing a wide range of near optimal selected solutions.
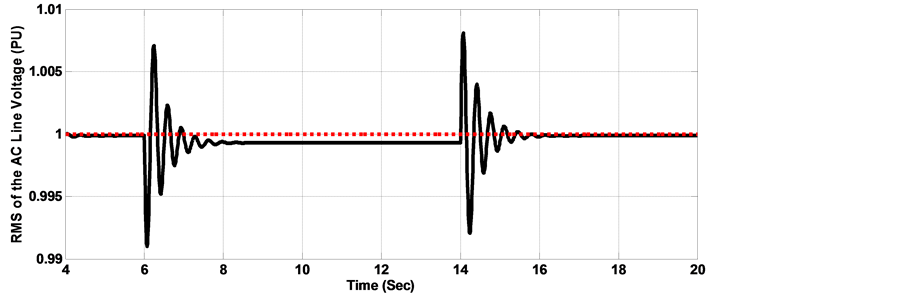
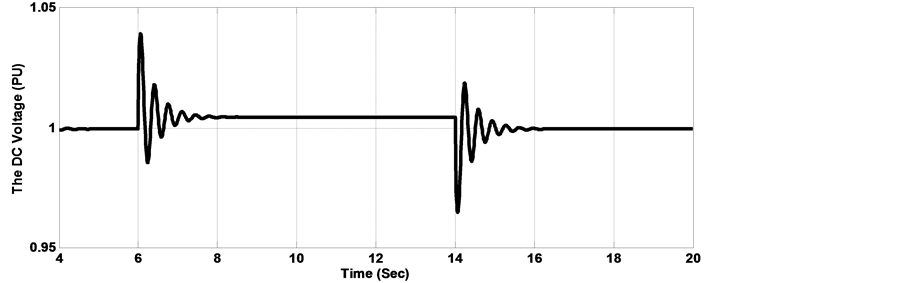
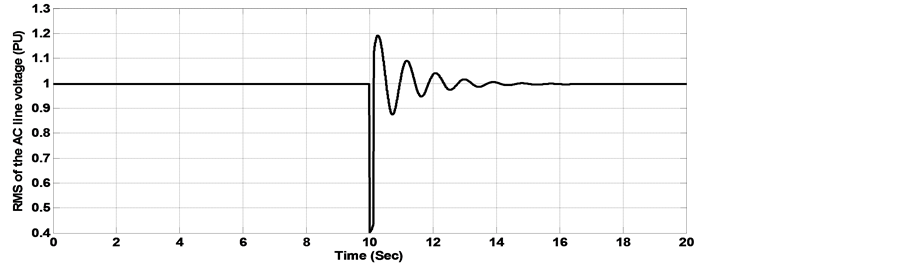
In the calculation of the optimal gains by the MOGA and the MOPSO procedures, the objective is to improve the overall dynamic performance of the proposed wave energy system using the SEIG when it is subjected to severe electrical disturbances and faults in the electrical network. The dynamic simulations were carried out for two cases. In the first case, a step load change was carried out from 0.5 pu to 1 pu at time 6 s and lasting 8 s. in the second simulation case, a phase to phase short circuit was carried out next to the generator bus at time t = 10 s, lasting for 0.1 s. The RMS of the AC line voltage voltage dynamic behavior with load disturbance is shown in Figure 9. It is observed that with the use of traditional SMC and FLC-SMC controllers, the terminal voltage presents deeper sag and larger oscillations as compared with those controllers with gains adjusted by the proposed MOPSO and MOGA procedures. In figure 10, a significant reduction in the maximum overshoot and the oscillations of the DC voltage can easily be observed when MOPSO and MOGA are implemented with FLC-SMC controller as compared with the conventional controllers. Figure 11, Figure 12 show the dynamic performance of the RMS of the AC line voltage and the voltage of the DC bus with phase to phase short circuit. It is observed that in the case when FLC-SMC controllers with gains adjusted by MOPSO and MOGA are used, the AC and DC voltages present smaller settling time and oscillations as compared with the SMC and FLC-SMC controllers, consequently contributes towards maintaining the converter in operation during the fault period. Table 5Table 6System dynamic behavior comparison with 50% step load disturbance.
show the system behavior comparison using the traditional SMC, FLC-SMC, MOGAFLC-SMC and MOPSO-FLC-SMC controllers with constant load, step load disturbance and phase to phase short circuit. In these results, we note that the AC and DC voltage regulation is obtained using the proposed
 (a)
(a)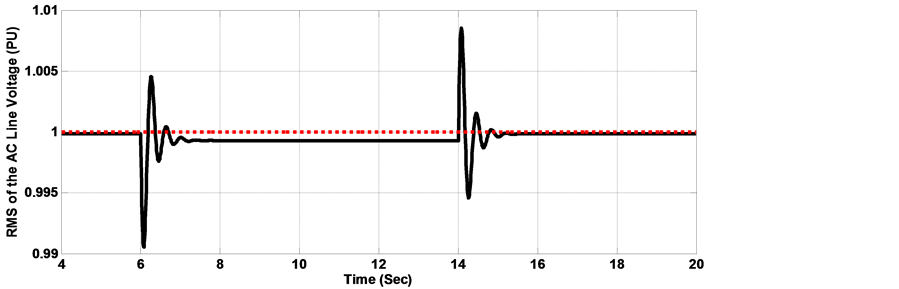 (b)
(b) (c)
(c) (d)
(d)
Figure 9. RMS of the AC line voltage with load disturbance (a) Response with classical SMC controller, (b) Response with FLC-SMC controller, (c) Response with MOGA-FLC-SMC controller, (d) Response with MOPSO-FLC-SMC controller.
 (a)
(a)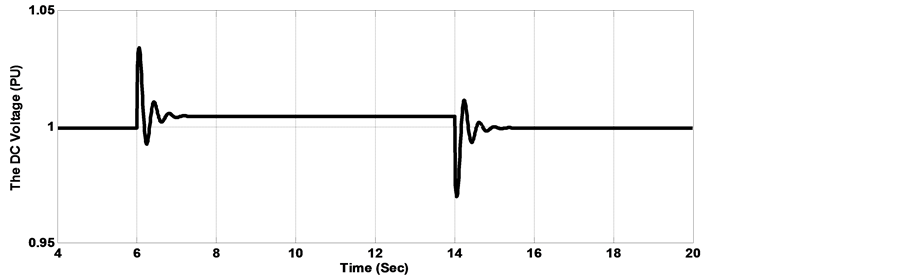 (b)
(b) (c)
(c)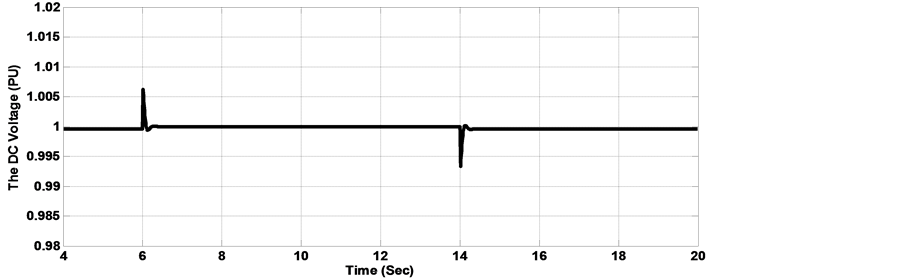 (d)
(d)
Figure 10. DC voltage with load disturbance (a) Response with classical SMC controller, (b) Response with FLC-SMC controller, (c) Response with MOGA-FLC-SMC controller, (d) Response with MOPSO-FLC-SMC controller.
 (a)
(a)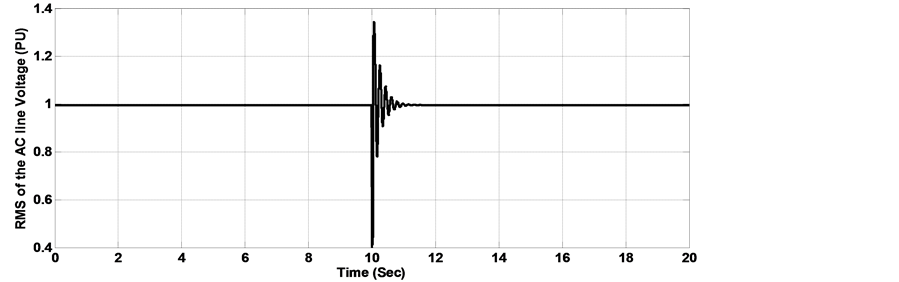 (b)
(b)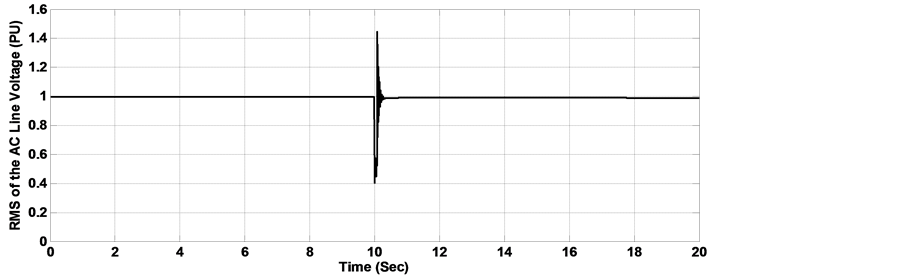 (c)
(c)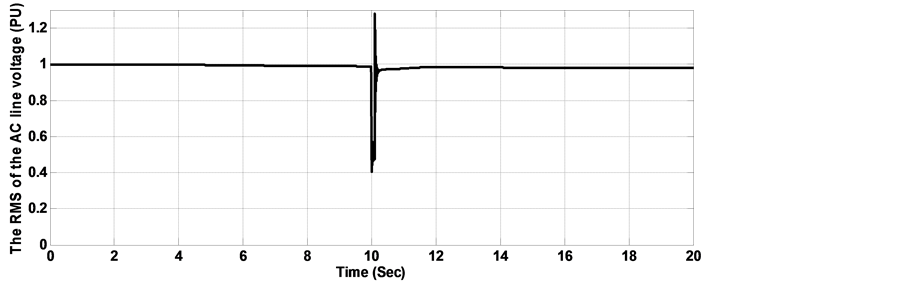 (d)
(d)
Figure 11. RMS of the AC line voltage with phase to phase fault (a) Response with classical SMC controller, (b) Response with FLC-SMC controller, (c) Response with MOGA-FLCSMC controller, (d) Response with MOPSO-FLC-SMC controller.
 (a)
(a) (b)
(b) (c)
(c)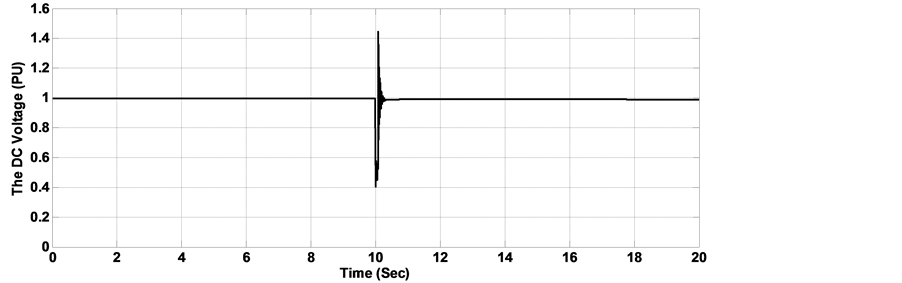 (d)
(d)
Figure 12. DC voltage with phase to phase fault (a) Response with classical SMC controller, (b) Response with FLC-SMC controller, (c) Response with MOGA-FLC-SMC controller, (d) Response with MOPSO-FLC-SMC controller.
MOPSO and MOGA algorithms controllers in spite of the presence of disturbances such as step changing of the load and short circuit fault.
4. Conclusion
This paper has presented the modeling and simulation of wave energy driven self-excited induction generator which feeds power to the utility grid. The adaptive fuzzy tuning control strategy was applied to the sliding mode controller for adopting the controller parameters according to the tracking error to both the dc-link voltage and ac line voltage regulation. The estimation of sliding slope, intercept of sliding surface and hitting gain can be solved by implementation of fuzzy logic control tuner based on the particle swarm optimization (PSO) algorithm and Genetic Algorithm (GA) to enhance the system performance which is insensitive to the parameter variations and disturbance effects. The indirect field-oriented mechanism was implemented for the control of the SEIG to regulate the dc-link voltage of the ac/dc power converter and the AC line voltage of the DC/AC power inverter with robust control performance. Simulation studies are carried out and compared the results obtained with the proposed optimal tuned FLC-SMC controller parameters design using MOPSO and MOGA with those using conventional variable structure SMC controller and fuzzy sliding mode control FLC-SMC controllers. The simulation results verified the effectiveness and robustness of the proposed tuning technique and it was comparatively superior to conventional SMC and FLC-SMC in the sense of the transient performance of the wave energy system over a wide range of operating conditions. The future work is to support the system by the PSO MPPT controller which can perform as a shunt active power filter as well as a wave energy extractor.
References
- Halamay, D., Brekken, T., Simmons, A. and McArthur, S. (2011) Reserve Requirement Impacts of Large-Scale Integration of Wind, Solar and Ocean Wave Power Generation. IEEE Transactions on Sustainable Energy, 2, 321-328. http://dx.doi.org/10.1109/TSTE.2011.2114902
- Fusco, F. and Ringwood, J. (2010) Variability Reduction through Combination of Wind and Waves: An Irish Case Study. Energy, 35, 314-325. http://dx.doi.org/10.1016/j.energy.2009.09.023
- Yang, X., Song, Y., Wang, G. and Wang, M. (2010) A Comprehensive Review on the Development of Sustainable Energy Strategy and Implementation in China. IEEE Transactions on Sustainable Energy, 1, 57-65. http://dx.doi.org/10.1109/TSTE.2010.2051464
- Wang L. and Chen, Z.-J. (2010) Stability Analysis of a Wave-Energy Conversion System Containing a Grid-Connected Induction Generator Driven by a Wells Turbine. IEEE Transactions on Energy Conversion, 25, 555-563.
- Modesto A., Mikel, A., Aitor, J.G. and Izaskun, G. (2011) Modeling and Simulation of Wave Energy Generation Plants: Output Power Control. IEEE Transactions on Industrial Electronics, 58, 105-117.
- Benelghali, S. Benbouzid, M.E.H. and Charpentier, J.F. (2007) Marine Tidal Current Electric Power Generation Technology: State of the Art and Current Status. Proceedings of the 2007 IEEE IEMDC, Antalya, 2, 1407-1412.
- Francesco F. and Ringwood, J.V. (2013) A Simple and Effective Real-Time Controller for Wave Energy Converters. IEEE Transactions on Sustainable Energy, 4, 21-30.
- Geng H., Xu, D., Wu, B. and Huang, W. (2011) Direct Voltage Control for a Stand-Alone Wind-Driven Self-Excited Induction Generator with Improved Power Quality. IEEE Transactions on Power Electronics, 26, 2358-2368.
- Jayaramaiah, G.V. and Fernandes, B.G. (2004) Analysis of Voltage and Frequency Controller for Grid Connected 3-Φ Self-Excited Induction Generator Using Current Controlled Voltage Source Inverter. TENCON 2004. 2004 IEEE Region 10 Conference, 3, 468-471.
- Manel O., Mohamed, B., Ali, K. and Maher, C. (2011) Investigation on the Excitation Capacitor for a Wind Pumping Plant Using Induction Generator. Smart Grid and Renewable Energy, 2, 116-125.
- Seyoum, D. Rahman, M.F. and Grantham, C. (2003) Terminal Voltage Control of a Wind Turbine Driven Isolated Induction Generator Using Stator Oriented Field Control. Proceedings of IEEE Power Electronics Conference and Exposition-APEC, 2, 846-852.
- Leidhold, R. Garcia, G. and Valla, M.I. (2002) Field-Oriented Controlled Induction Generator with Loss Minimization. IEEE Transactions on Industrial Electronics, 49, 147-156. http://dx.doi.org/10.1109/41.982258
- Ahmed A., Mohamed, B., Mohamed, A., Hassane, M. and Mohamed, M. (2013) Fuzzy Controller for Self-Excited Induction Generator Used in Wind Energy Conversion. Renewable and Sustainable Energy Conference (IRSEC), 2013 , 206-211.
- Hosseini, R. Qanadli, S.D., Barman, S., Mazinani, M., Ellis, T. and Dehmeshki, J. (2012) An Automatic Approach for Learning and Tuning Gaussian Interval Type-2 Fuzzy Membership Functions Applied to Lung CAD Classification System. IEEE Transactions on Fuzzy Systems, 20, 224-234.
- Fang G., Kwok, N.M. and Ha, Q. (2008) Automatic Fuzzy Membership Function Tuning Using the Particle Swarm Optimization. Pacific-Asia Workshop on Computational Intelligence and Industrial Application, 2, 324-328.
- Jang, J.S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transactions on Systems, Man, and Cybernetics, 23, 665-685. http://dx.doi.org/10.1109/21.256541
- Lin C.J., Chen, C.H. and Lee, C.Y. (2006) TSK-Type Quantum Neural Fuzzy Network for Temperature Control. International Mathematical Forum, 1, 853-866.
- Mendez, G. Cavazos, A., Soto, R. and Leduc, L. (2006) Entry Temperature Prediction of a Hot Strip Mill by a Hybrid Learning Type-2 FLS. Journal of Intelligent & Fuzzy Systems, 17, 583-596.
- Mendel, J.M. (2004) Computing Derivatives in Interval Type-2 Fuzzy Logic Systems. IEEE Transactions on Fuzzy Systems, 12, 84-98. http://dx.doi.org/10.1109/TFUZZ.2003.822681
- Lee, C., Hong, J., Lin, Y. and Lai, W. (2003) Type-2 Fuzzy Neural Network Systems and Learning. International Journal of Computational Cognition, 1, 79-90.
- Wang, C. Cheng, C. and Lee, T. (2004) Dynamical Optimal Training for Interval Type-2 Fuzzy Neural Network (T2FNN). IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 34, 1462-1477. http://dx.doi.org/10.1109/TSMCB.2004.825927
- Pratihar D.K., Deb, K. and Ghosh, A. (1999) A Genetic-Fuzzy Approach for Mobile Robot Navigation among Moving Obstacles. International Journal of Approximate Reasoning, 20, 145-172. http://dx.doi.org/10.1016/S0888-613X(98)10026-9
- Mucientes M., Moreno, D.L., Bugarin, A. and Barro, S. (2007) Design of a Fuzzy Controller in Mobile Robotics Using Genetic Algorithms. Applied Soft Computing, 7, 540-546. http://dx.doi.org/10.1016/j.asoc.2005.05.007
- Cazarez-Castro, N.R., Aguilar, L.T. and Castillo, O. (2010) Fuzzy Logic Control with Genetic Membership Function Parameters Optimization for the Output Regulation of a Servomechanism with Nonlinear Backlash. Expert Systems with Applications, 37, 4368-4378. http://dx.doi.org/10.1016/j.eswa.2009.11.091
- Kennedy J. and Eberhart, R. (1995) Particle Swarm Optimization. Proceedings of IEEE International Conference on Neural Networks, 4, 1942-1948.
- Karakuzu, C. (2008) Fuzzy Controller Training Using Particle Swarm Optimisation for Nonlinear System Control. ISA Transactions, 47, 229-239. http://dx.doi.org/10.1016/j.isatra.2007.09.003
- Niu, B., Zhu, Y., He, X. and Shen, H., (2008) A Multiswarm Optimizer Based Fuzzy Modeling Approach for Dynamic Systems Processing. Neurocomputing, 71, 1436-1448. http://dx.doi.org/10.1016/j.neucom.2007.05.010
- Mukherjee, V. and Ghoshal, S.P. (2007) Intelligent Particle Swarm Optimized Fuzzy PID Controller for AVR System. Electric Power Systems Research, 77, 1689-1698. http://dx.doi.org/10.1016/j.epsr.2006.12.004
- Lin, C. and Hong, S. (2007) The Design of Neuro-Fuzzy Networks Using Particle Swarm Optimisation and Recursive Singular Value Decomposition. Neurocomputing, 71, 271-310. http://dx.doi.org/10.1016/j.neucom.2006.12.016
- Esmin, A.A.A., Aoki, A. and Lambert-Torres, G. (2002) Particle Swarm Optimisation for Fuzzy Membership Functions Optimisation. Proceedings of 2002 IEEE International Conference on Systems, Man, and Cybernetics, Hammamet, 6-9 October 2002.
- Esmin, A.A.A. and Lambert-Torres, G. (2006) Fitting Fuzzy Membership Functions Using Hybrid Particle Swarm Optimization. Proceedings of 2006 IEEE International Conference on Fuzzy Systems, Vancouver, 2112-2119. http://dx.doi.org/10.1109/FUZZY.2006.1681993
- Martínez-Marroquín, R., Castillo, O. and Soria, J. (2009) Particle Swarm Optimization Applied to the Design of Type-1 and Type-2 Fuzzy Controllers for an Autonomous Mobile Robot. In: Melin, P., Kacprzyk, J. and Pedrycz, W., Eds., Bio-Inspired Hybrid Intelligent Systems for Image Analysis and Pattern Recognition (Studies in Computational Intelligence 256), Springer, Berlin, 247-262.
- Castillo, O. Martinez-Marroquin, R., Melin, P., Valdez, F. and Soria, J. (2012) Comparative Study of Bio-Inspired Algorithms Applied to the Optimization of Type-1 and Type-2 Fuzzy Controllers for an Autonomous Mobile Robot. Information Sciences, 192, 19-38. http://dx.doi.org/10.1016/j.ins.2010.02.022
- Navaneethakkannan, C. and Sudha, M. (2013) Comparison of Conventional & PID Tuning of Sliding Mode Fuzzy Controller for BLDC Motor Drives. 2013 International Conference on Computer Communication and Informatics (ICCCI 2013), Coimbatore, 4-6 January 2013, 1-6.
- Khelfi, M.F., Daikh, F.Z. and Chaouch, D.E. (2013) Sliding Mode with Neuro-Fuzzy Network Controller for Inverted Pendulem. IEEE International Conference on Industrial Technology (ICIT 2013), Cape Town, 25-28 February 2013, 193-198.
- Lakhekar G.V. (2012) Tuning and Analysis of Sliding Mode Controller Based on Fuzzy Logic. International Journal of Control and Automation, 5, 93-110.
- Fang, G., Kwok, N.M. and Ha, Q. (2008) Automatic Fuzzy Membership Function Tuning Using the Particle Swarm Optimisation. IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, 19-20 December 2008, 324-328. http://dx.doi.org/10.1109/PACIIA.2008.105


