Journal of Intelligent Learning Systems and Applications
Vol.6 No.1(2014), Article ID:42566,10 pages DOI:10.4236/jilsa.2014.61001
Fuzzy-Weighted Similarity Measures for Memory-Based Collaborative Recommender Systems
Electrical Engineering Department, Faculty of Engineering and Architecture, Ibb University, Ibb, Yemen.
Email: mohamad.alshamri@gmail.com, nlashwal@yahoo.com
Copyright © 2014 Mohammad Yahya H. Al-Shamri, Nagi H. Al-Ashwal. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Mohammad Yahya H. Al-Shamri, Nagi H. Al-Ashwal. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 9th, 2013; revised November 9th, 2013; accepted November 16th, 2013
KEYWORDS
Collaborative Recommender Systems; Pearson Correlation Coefficient; Cosine Similarity Measure; Mean Difference Weights Similarity Measure; Fuzzy Weighting
ABSTRACT
Memory-based collaborative recommender system (CRS) computes the similarity between users based on their declared ratings. However, not all ratings are of the same importance to the user. The set of ratings each user weights highly differs from user to user according to his mood and taste. This is usually reflected in the user’s rating scale. Accordingly, many efforts have been done to introduce weights to the similarity measures of CRSs. This paper proposes fuzzy weightings for the most common similarity measures for memory-based CRSs. Fuzzy weighting can be considered as a learning mechanism for capturing the preferences of users for ratings. Comparing with genetic algorithm learning, fuzzy weighting is fast, effective and does not require any more space. Moreover, fuzzy weightings based on the rating deviations from the user’s mean of ratings take into account the different rating scales of different users. The experimental results show that fuzzy weightings obviously improve the CRSs performance to a good extent.
1. Introduction
Web services grow very fast letting Web users in a difficult position to select from a huge number of choices. This creates an argent need for Web personalization tools that help users navigate Web easily in a personalized way. Collaborative recommender system (CRS), the most successful Web personalization tool [1-6], recommends a given active user items to people with similar tastes and preferences liked in the past. Today, recommender systems become a must in many Web applications. Amazon, eBay, MovieLens and many others use some types of recommender systems [2-5]. In real life, we cannot expect users to come across or have heard of each of the products (items) they might like.
Out-of-the-box recommendation is the most important feature of CRSs which allows CRS recommends a diverse set of items to an active user based on the tastes and past preferences of his set of neighbors. This set of neighbors play an important role in the CRS success [1,2,6]. As long as the neighborhood set is close and representative to the active user, the CRS suggestions will be more valuable. Hence, a great attention has to be paid for selecting the set of neighbors. Actually CRS constructs the set of neighbors based on a similarity measure which has to reflect the most important factors between the two users in consideration. Consequently, the similarity computation phase for any CRS plays the heart role for its success. Different similarity measures often lead to different sets of neighbors for a given active user and thus a good similarity measure will be that one producing a close set of neighbors for that active user.
The existing similarity measures for memory-based CRS based their work on the users’ raw declared ratings or on the deviation of these ratings from the mean ratings of the users. However, the tastes of users for ratings differ from time to time and the actual employed rating scale differs from user to user. Therefore the raw declared ratings need to be weighted so that a weighted rating scale is obtained for all users. Most of the previous weighting work for Pearson correlation coefficient was focusing either on genetic algorithm (GA) [7,8] or on trust and reputation as similarity modifiers [9]. However, GA approach takes a long time for training and forces the system to store the evolved weights which are an extra load for the system. Other weighting techniques like significance weighting using trust and variance weighting for discerning user’s interest for items are studied by Herlocher et al. [10]. Sometimes the inverse user frequency is used for distinguishing universally liked items from less common items [11]. The contribution of the universally liked items is decreased as they are not useful for capturing similar users while the contribution of the less common items is increased as they are useful for capturing similar users.
This paper proposes fuzzy weightings for the most popular similarity measures for memory-based CRS. Fuzzy weighting increases the effectiveness of the similarity measure for capturing close set of neighbors without loading the CRS in time or in space. Consequently, the CRS accuracy gets enhanced. The main contributions of this paper are three-folds.
Ÿ A methodology for fuzzifying rating values and rating deviation values is proposed.
Ÿ Fuzzy weightings for the most popular similarity measures of memory-based CRS are proposed.
Ÿ Fuzzy mean difference weights similarity measure is introduced.
The rest of this paper is organized as follows: an introduction to some similarity measures of memory-based CRS is given in Section 2. Section 3 explores the answer to two main questions for fuzzy weighting. The two questions are What and How to fuzzify? Fuzzy-weighted similarity measures for memory-based CRS are introduced in Section 4. The experimental methodology and results for the proposed approaches with the traditional approaches are presented in Section 5. Finally, we conclude our work in the last section.
2. Similarity Measures for Memory-Based CRS in Literature
Formally, CRS has 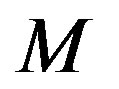 users,
users, 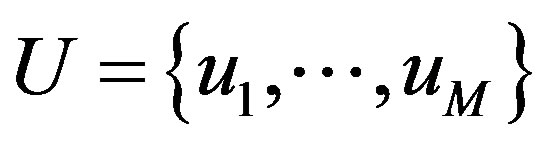 , having preferences for certain items such as products, news, web pages, books, movies, restaurants, destinations, or CDs. The user’s degree of preference for an item is represented by a rating that is obtained explicitly from the user directly or inferred implicitly from the users’ navigation behavior. For example, if an Amazon customer views information about a product, the system can infer that they are interested in that product, even if they don’t buy it [1,2,6]. Each user
, having preferences for certain items such as products, news, web pages, books, movies, restaurants, destinations, or CDs. The user’s degree of preference for an item is represented by a rating that is obtained explicitly from the user directly or inferred implicitly from the users’ navigation behavior. For example, if an Amazon customer views information about a product, the system can infer that they are interested in that product, even if they don’t buy it [1,2,6]. Each user 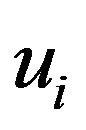 rates a subset of items
rates a subset of items 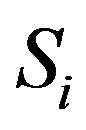 from the
from the 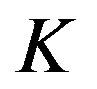 items,
items, 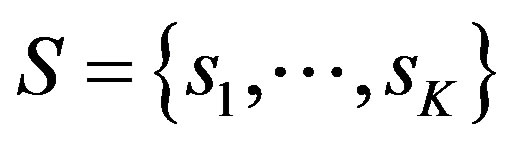 , of the system. The declared rating of user
, of the system. The declared rating of user  for an item
for an item 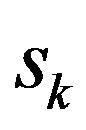 is denoted by
is denoted by 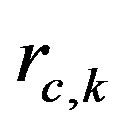 and the user’s average rating is denoted by
and the user’s average rating is denoted by  . The set of users cross the set of items form a user-item matrix which is called sometimes a utility matrix [1,2,6].
. The set of users cross the set of items form a user-item matrix which is called sometimes a utility matrix [1,2,6].
The set of ratings for each user forms the user profile which has to be compared to other users’ profiles based on a predefined similarity measure. The similarity between two users is a measure of how closely they resemble each other. Once similarity values are computed, the CRS system ranks users according to their similarity values with the active user to extract a set of neighbors for him. According to the set of neighbors, the CRS assigns a predicted rating to all the items seen by the neighborhood set and not by the active user [2,6]. The predicted rating, 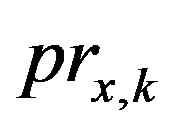 , indicates the expected interestingness of the item
, indicates the expected interestingness of the item 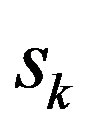 to the user
to the user 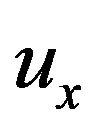 .
.
The most popular similarity measure for memory-based CRS is the Pearson correlation coefficient (PCC) [1,2,6]. PCC computes the similarity between two users, 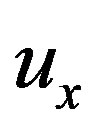 and
and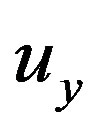 , based only on the common ratings,
, based only on the common ratings, 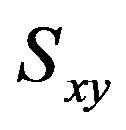 , both users have declared. The PCC is given by:
, both users have declared. The PCC is given by:
 (1)
(1)
The CRS’s literature described also the cosine similarity measure [2,6], which treats each user as a vector in the items’ space and then takes the cosine of the angle between the two vectors as a similarity measure between the two users.
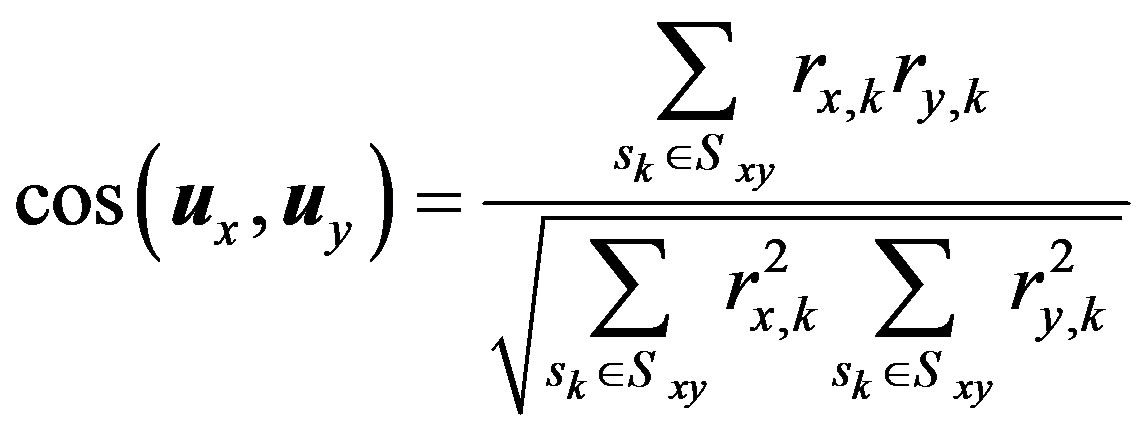 (2)
(2)
Many other efforts explore different similarity measures for memory-based CRS. Breese et al. [11] evaluated the predictive accuracy of different similarity measures for CRS. They concluded that Pearson correlation coefficient outperforms the other measures. Fuzzy concordance/discordance principle is used in [12] as a similarity measure which measures the pros and cons separately and then the overall statement about a given pair of users is obtained by balancing the pros and cons within the set of criteria. Recently, Bobadilla et al. [7] proposed the mean difference weights similarity measure. This similarity measure calculates the average of the two users’ rating difference weights. These weights are evolved using GA; however, they can be assumed fixed to the mean of each difference weight interval that have been proposed in [7].
 (3)
(3)
Bobadilla et al. [7] divide Formula (3) by the difference between the maximum and minimum values of the rating scale. However, this factor is not necessary because Formula (3) already divides the weights by their number. The numerator cannot exceed 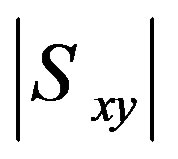 in any way since
in any way since 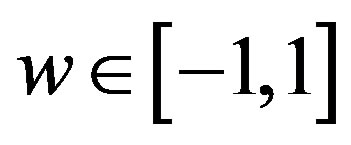 . The only effect this factor has is reducing the similarity values which in turn will reduce the contribution of each neighbor’s rating in the aggregation process. Moreover, the learning intervals of GA used by [7] are small. This will degrade the usefulness of GA learning process.
. The only effect this factor has is reducing the similarity values which in turn will reduce the contribution of each neighbor’s rating in the aggregation process. Moreover, the learning intervals of GA used by [7] are small. This will degrade the usefulness of GA learning process.
3. What and How to Fuzzify?
Weighting some variables of the user profile is an effective way to capture the users’ different tastes for the CRS rating scale. However, most of the previous work based this weighting on GA as a learning technique. Although GA can focus on the good items while removing bad ones or reducing their impact but it requires a long time for learning the weights and a large space for storing them later. Moreover, these weights have to be recalculated periodically to capture the users’ changing tastes over time. Therefore GA is a good way if we have time and space.
We argue that a simple and effective way will be that one uses fuzzy logic to get these weights by employing some variables of the user profile. This leads to fuzzyweighted similarity measures for memory-based CRS. Having you agreed to use fuzzy logic instead of GA for evolving weights. Two main questions arise, What and How to fuzzify? The answer to these two questions depends on the nature of the user profile. The user profile of memory-based CRS consists of a set of ratings for a subset of the system’s items. Accordingly, we have four main variables for the user profile, namely, the ratings themselves, the mean of these ratings, the rating deviation of each rating from the user’s mean rating, and the user total number of ratings.
The rating and the rating deviation variables are very close to the user’s taste for the rating scale. However, these ratings have less value if the user’s number of ratings is too small. Thus the user rating and the rating deviation variables are the more appropriate candidate to be fuzzified if the ratings are somehow dense. Normally, the user ratings follow a fixed rating scale which is usually a discrete rating scale while the rating deviation takes a continuous range. This nature of both variables will determine the fuzzy sets suitable for each one of them. Figures 1 proposes some fuzzy sets for a 5-point rating scale for the rating variable. Figure 1(a) represents each rating as a triangular fuzzy set that can be named very bad, bad, good, very good and excellent. Figure 1(b) gives three fuzzy sets for ratings that can be named bad (trapezoidal), neural (triangular) and good (trapezoidal). This representation treats rating 1 and 2 similarly as bad ratings and ratings 4 and 5 as good ratings. However, this is not always true especially for those users paying more attention for their votes. This situation getting worse with the two trapezoidal fuzzy sets of Figure 1(c) which groups ratings 1 and 2 as bad ratings and ratings 3, 4 and 5 as good ratings. Figure 1(d) seems to be more appropriate representation because it grades the membership values of ratings between two fuzzy sets bad and good sets.
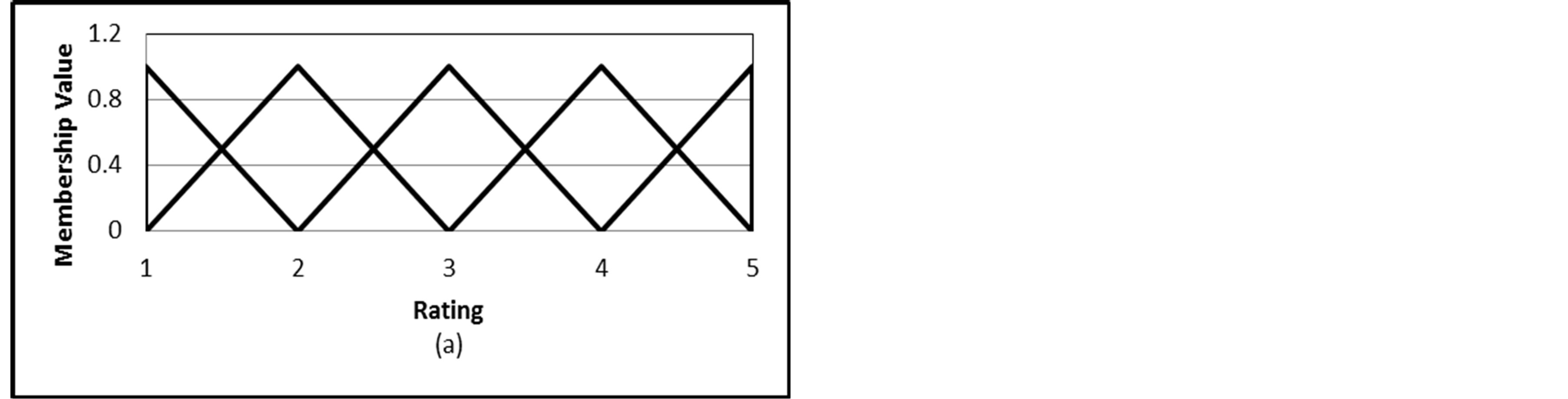

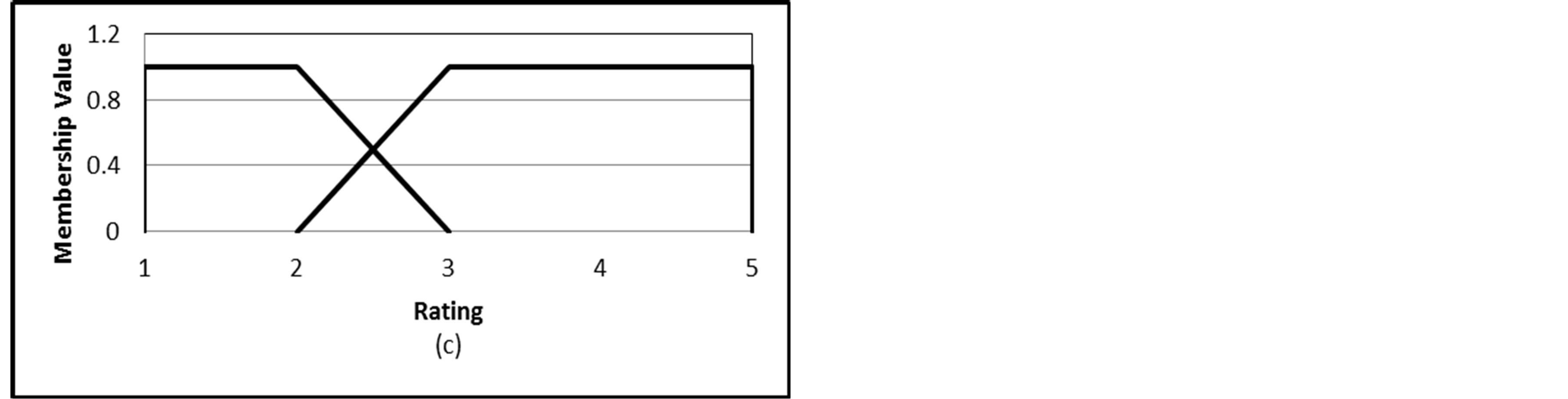
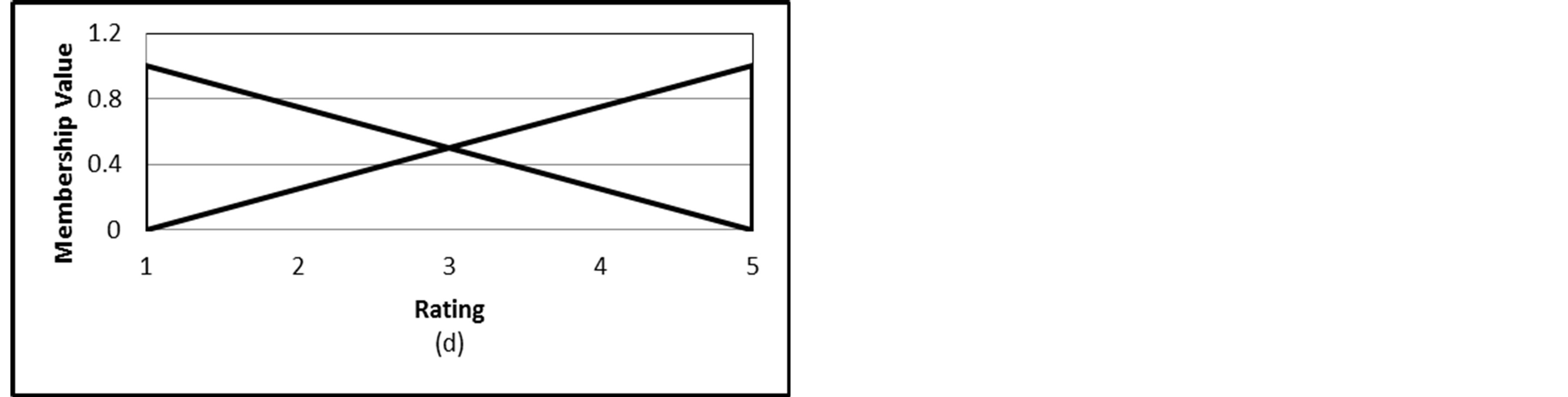
Figure 1. Different choices of fuzzy sets for the rating variable.
On the other hand, rating deviation values have a continuous range from a negative maximum to a positive maximum based on the rating scale nature. For a 5-point rating scale, the deviation value starts from −4 (rating 1 - rating 5) to 4 (rating 5 - rating 1). Accordingly, the range of choices for fuzzy sets representing deviation values is wider and more flexible than that of ratings themselves. Figure 2 proposes some possible fuzzy sets for the deviation value for a CRS with a 5-point rating scale. Figures 2(a) and (b) give nine and five triangular fuzzy sets for the deviation scale, respectively. The nine fuzzy sets seem to be large number while the five fuzzy sets are more acceptable. Instead of the five triangular fuzzy sets we can use five trapezoidal fuzzy sets as given in Figure 2(c). The trapezoidal fuzzy sets give flexibility for some values to be indifferent. This is more suitable for deviation values rather than rating values. The last option is Figure 2(d) which maps the deviation scale into three trapezoidal fuzzy sets. However, due to the long continuous and range of deviation values, the trapezoidal five fuzzy sets seem to be more appropriate than the other three ones.
To answer the second question we have to keep in mind that each profile variable has a crisp value. This value has to be mapped to fuzzy sets through membership values. That means each crisp value has to be mapped to a vector of membership values where the vector length is determined by the number of fuzzy sets representing that variable [13]. For example, each crisp value of rating, 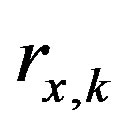 , will get a 2-tuple membership values (2-tuple vector) to the two bad and good fuzzy sets of Figure 1(d) as defined by the following membership functions.
, will get a 2-tuple membership values (2-tuple vector) to the two bad and good fuzzy sets of Figure 1(d) as defined by the following membership functions.
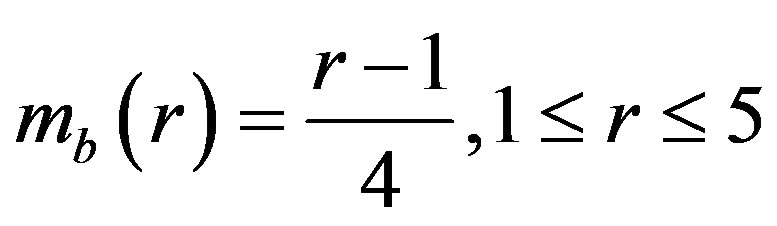 (4a)
(4a)
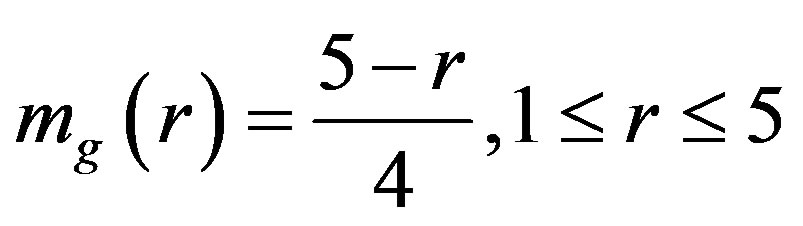 (4b)
(4b)
For example, if  then the corresponding 2-tuple membership vector will be
then the corresponding 2-tuple membership vector will be  . Based on the membership vectors, we can get the fuzzy weight,
. Based on the membership vectors, we can get the fuzzy weight, 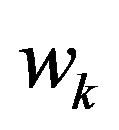 , for the
, for the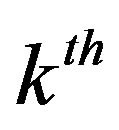 common item as [14]:
common item as [14]:
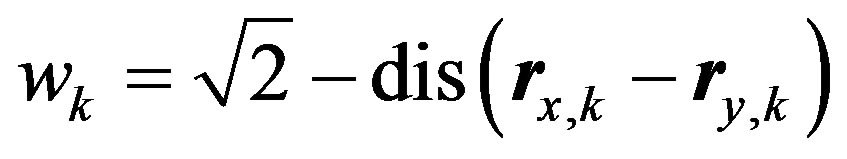 (5)
(5)
where 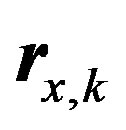 is the membership vector for
is the membership vector for  value and
value and 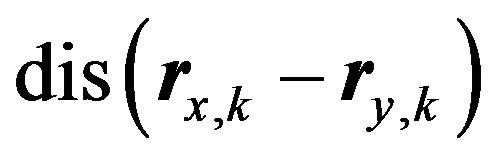 is any vector distance metric. In this paper, Euclidean distance function [13-15] is used for this purpose. In general
is any vector distance metric. In this paper, Euclidean distance function [13-15] is used for this purpose. In general  and
and  are two membership vectors of size
are two membership vectors of size  (in this paper
(in this paper 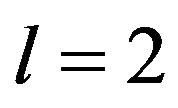 ).
).
 (6)
(6)
where 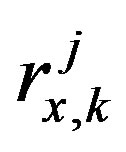 is the membership value of
is the membership value of 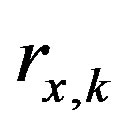 to its
to its 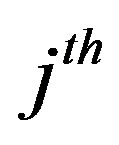 fuzzy set. We subtract
fuzzy set. We subtract 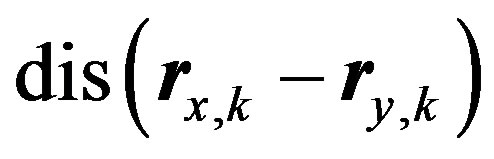 from
from 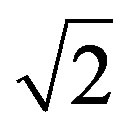 in
in

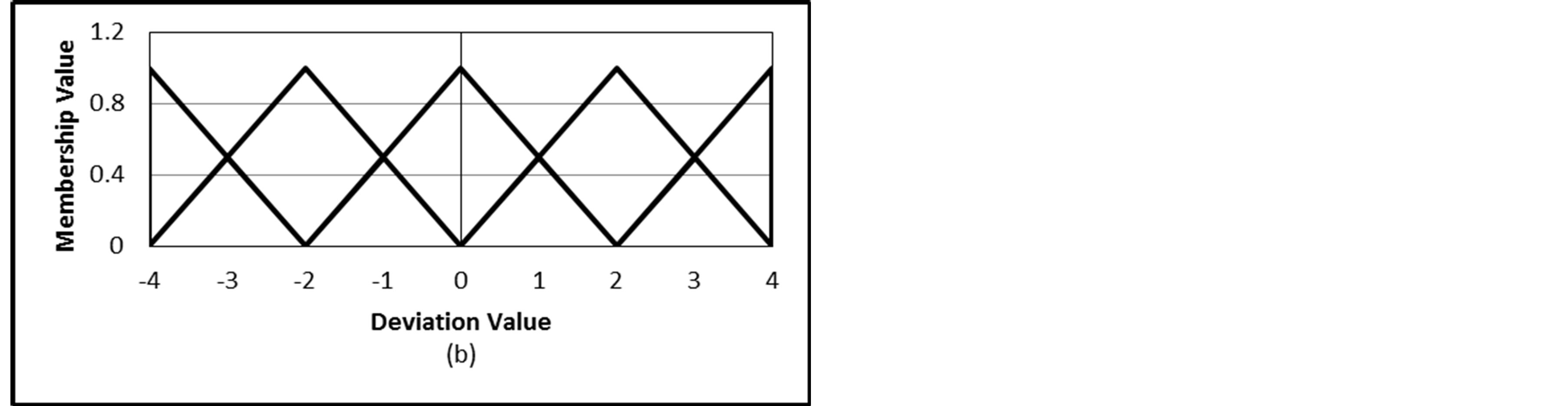
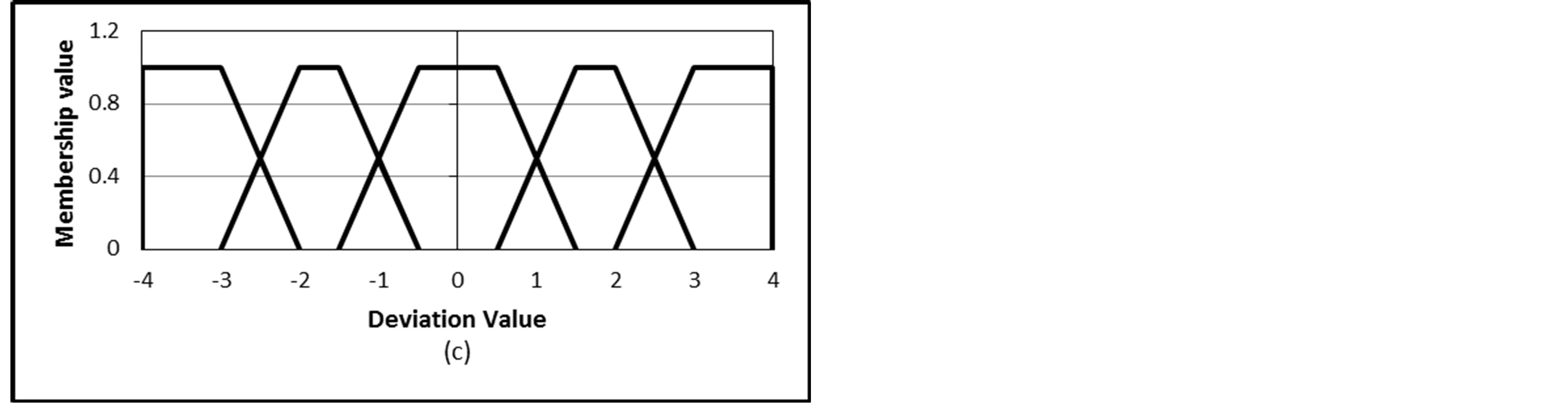
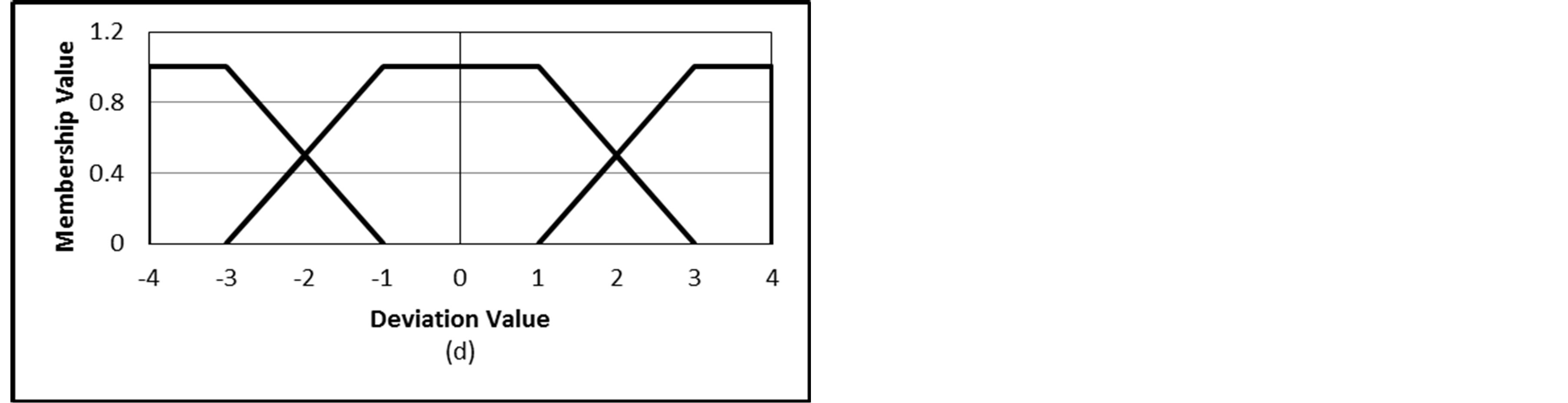
Figure 2. Different choices of fuzzy sets for the rating deviation variable.
Formula (5) because 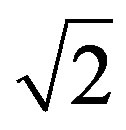 is the maximum distance value that we can get from Formula (6) [in this case the two deviation values belong to two different fuzzy sets with a unity membership value to each one of them, for example
is the maximum distance value that we can get from Formula (6) [in this case the two deviation values belong to two different fuzzy sets with a unity membership value to each one of them, for example 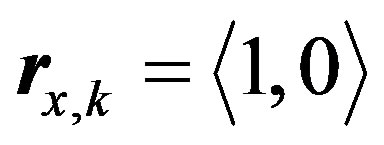 and
and 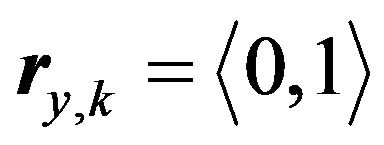 ]. For fuzzifying the rating deviation values,
]. For fuzzifying the rating deviation values, 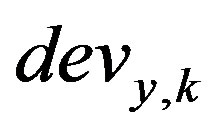 , we define five fuzzy sets for each deviation value (Figure 2(c)). The membership values for these fuzzy sets are defined as follows [14]:
, we define five fuzzy sets for each deviation value (Figure 2(c)). The membership values for these fuzzy sets are defined as follows [14]:
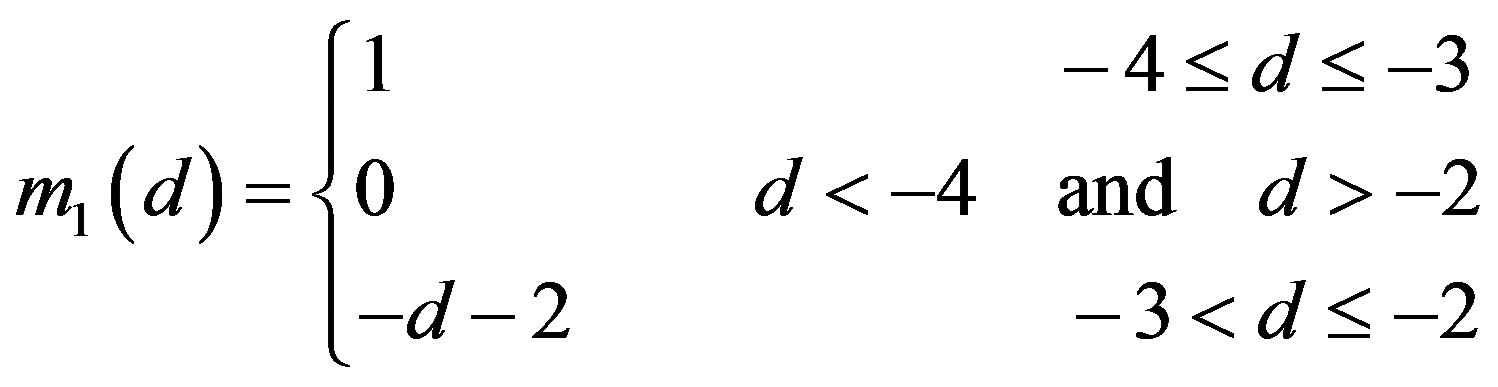 (7a)
(7a)
 (7b)
(7b)
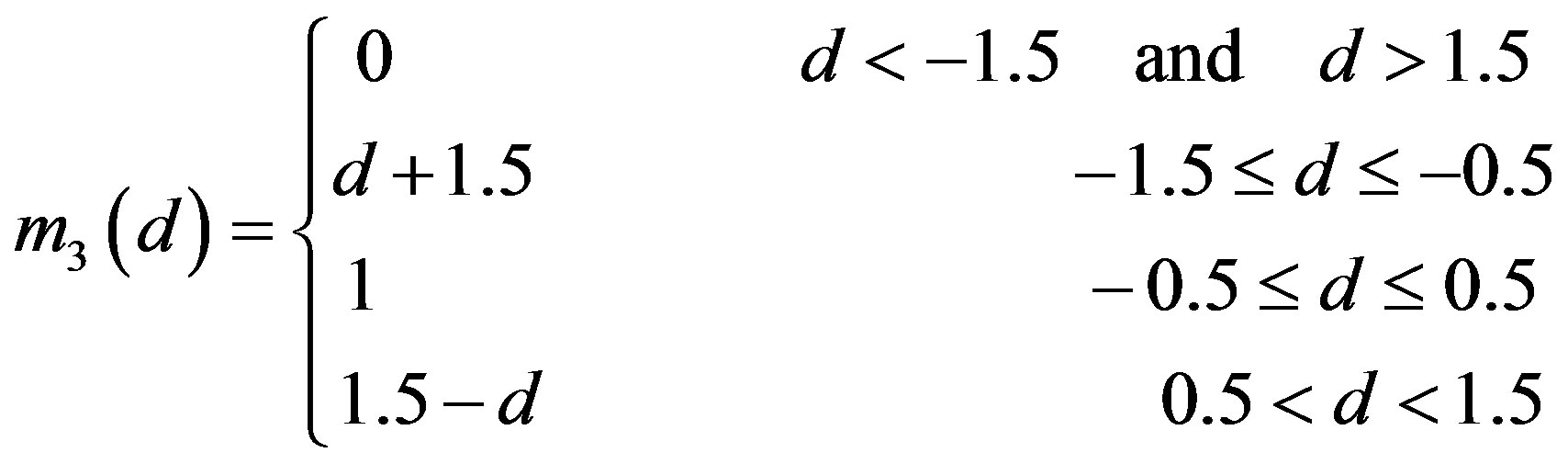 (7c)
(7c)
 (7d)
(7d)
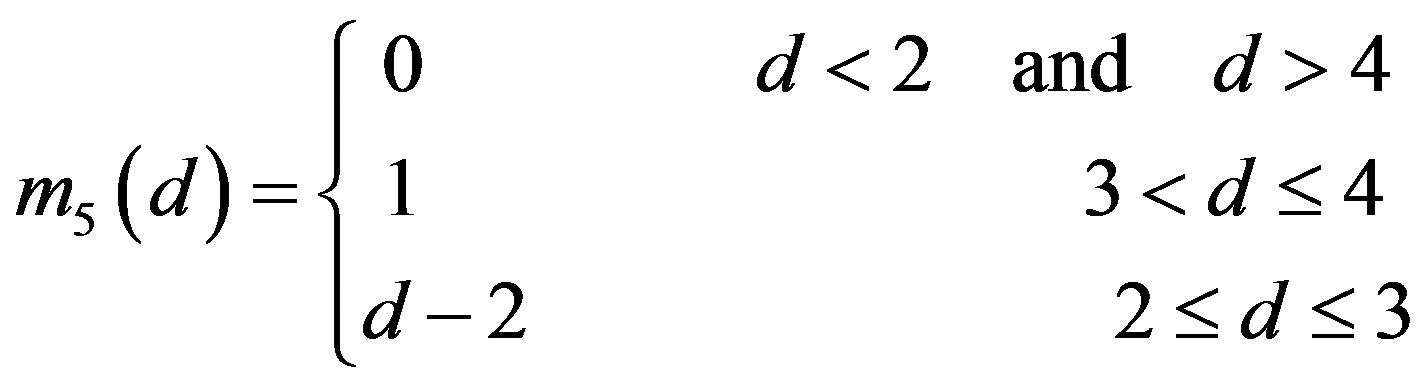 (7e)
(7e)
Accordingly, each deviation value will get a 5-tuple membership values (5-tuple vector) to the five fuzzy sets. For example, if , then the corresponding 5-tuple membership vector will be
, then the corresponding 5-tuple membership vector will be 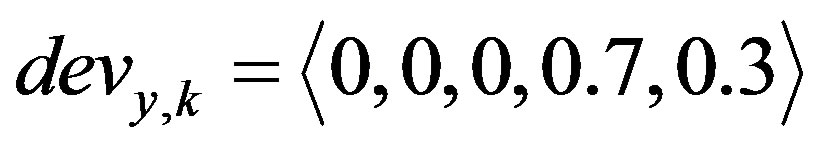 . The fuzzy weight,
. The fuzzy weight, 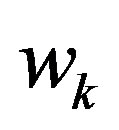 , for the
, for the 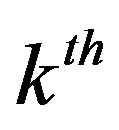 common item is obtained by Formulae (8) and (9) as done before for the rating values.
common item is obtained by Formulae (8) and (9) as done before for the rating values.
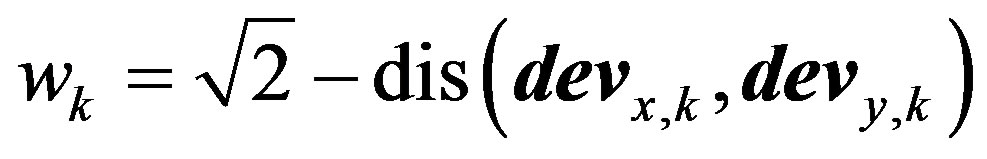 (8)
(8)
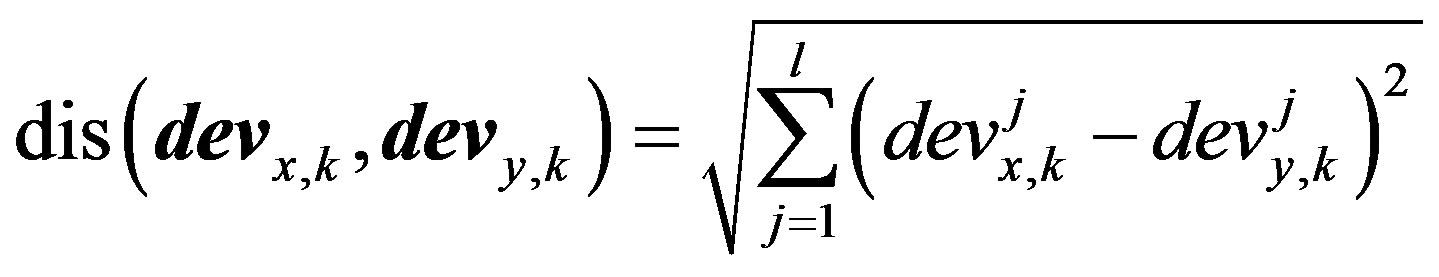 (9)
(9)
where 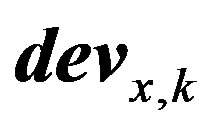 is the membership vector for
is the membership vector for 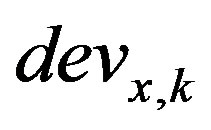 value. In general
value. In general 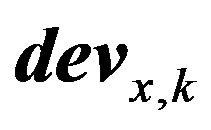 and
and 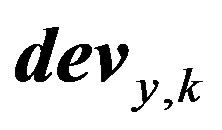 are two vectors of size
are two vectors of size 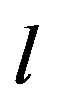 (in this paper
(in this paper 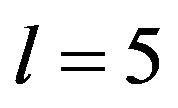 ) where
) where  is the membership value of the
is the membership value of the  value to its
value to its 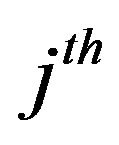 fuzzy set. An example of two deviation values belonging to two different fuzzy sets with a unity membership value to each one of them is
fuzzy set. An example of two deviation values belonging to two different fuzzy sets with a unity membership value to each one of them is 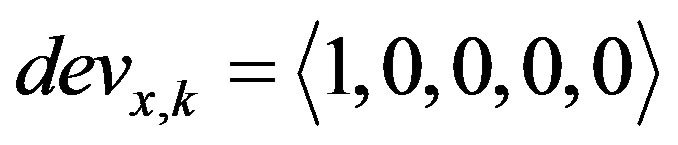 and
and 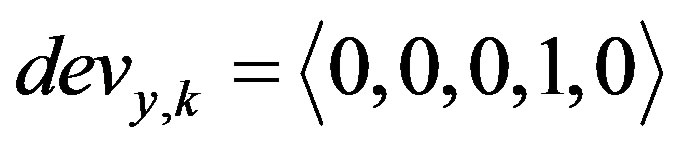 .
.
4. Fuzzy-Weighted Similarity Measures for Memory-Based CRS
Usually, weighting the similarity measure is done by introducing a weight, 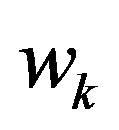 , to its numerator. The way of calculating these weights determines the weighting name. Consequently, the fuzzy-weighted cosine similarity measure and fuzzy-weighted Pearson correlation coefficient are defined as below:
, to its numerator. The way of calculating these weights determines the weighting name. Consequently, the fuzzy-weighted cosine similarity measure and fuzzy-weighted Pearson correlation coefficient are defined as below:
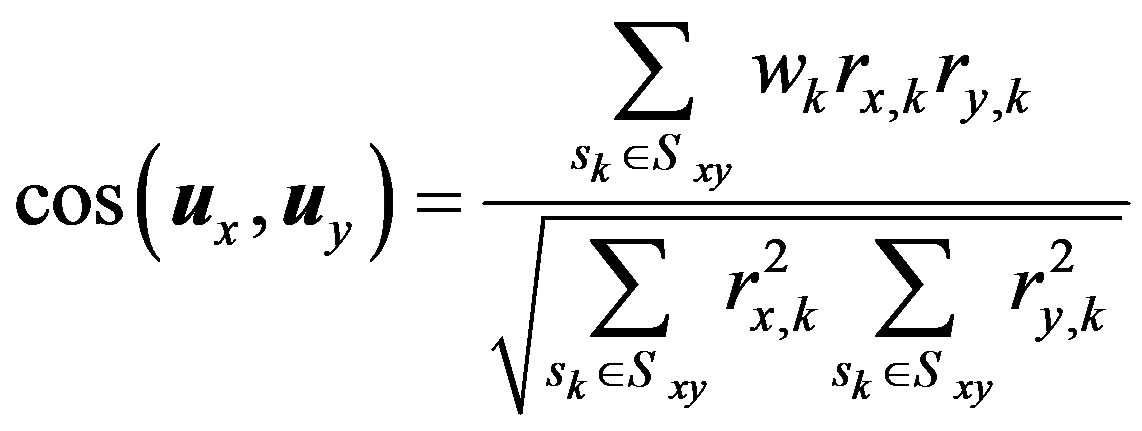 (10)
(10)
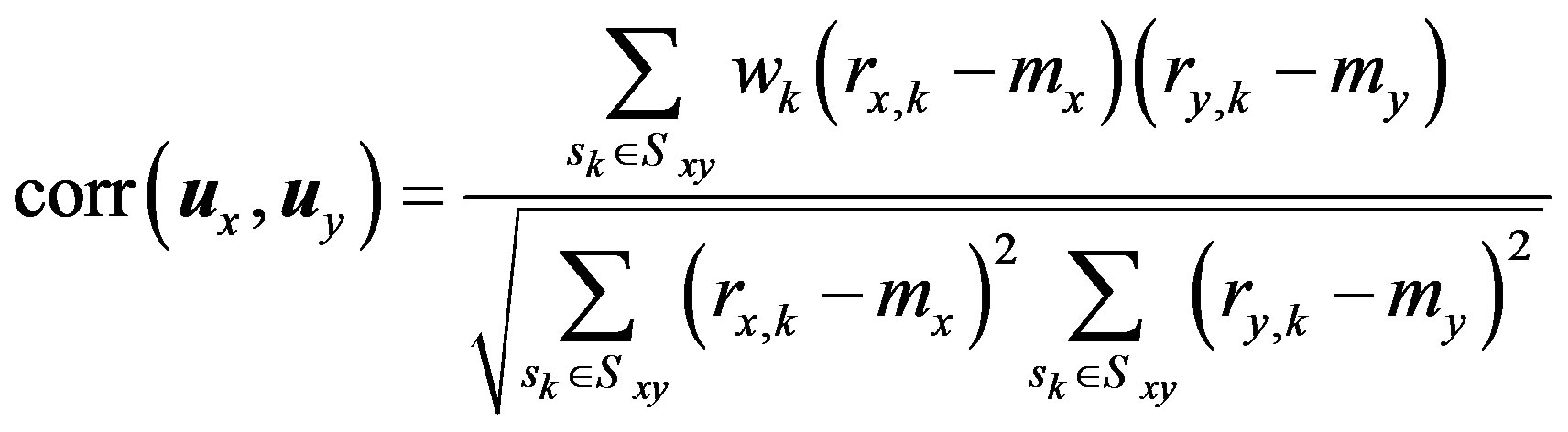 (11)
(11)
For both similarity measures, the fuzzy weights can be obtained based on the raw ratings themselves or based on the rating deviations. The direct rating values ignore the user’s taste and preferences for the rating scale while the rating deviations implicitly take the users’ different rating scales into consideration. Therefore we expect that the fuzzy weighting based on the rating deviations will perform better than the fuzzy weighting based on the raw ratings.
The third similarity measure we have examined is the mean difference weights similarity measure which gives an indirect way for calculating the similarity between users. The main idea for this similarity measure is how to get weights for the differences before summing up these weights. Bobadilla et al. [7] uses GA weights. However, fuzzy logic offers a very good alternative for calculating these weights without the headache of GA learning. The time complexity of GA learning depends on the number of users, number of items and the number of iteration required if a predefined threshold of the fitness function is not satisfied. For space complexity, GA learning process requires the system to store as large as the utility matrix for GA weights. On the other hand, fuzzy weighting calculates weights on-the-fly. The system needs to store these weights only at the implementation stage. The time complexity of calculating the fuzzy weights depends on the lengths of the vectors 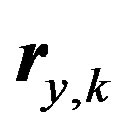 and
and . This time can be assumed constant as the lengths of the vectors
. This time can be assumed constant as the lengths of the vectors 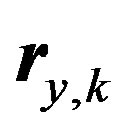 and
and  are constants for a given system. A more general mean difference weights similarity measure can be rewritten in terms of the difference,
are constants for a given system. A more general mean difference weights similarity measure can be rewritten in terms of the difference, 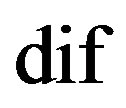 , as below.
, as below.
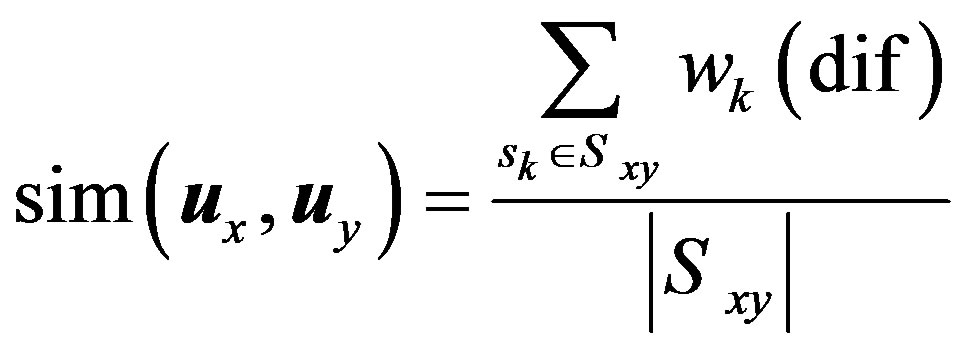 (12)
(12)
The difference can take many forms based on the underlying variable. In this paper, the difference can be obtained between the raw ratings or between the rating deviations from their corresponding rating means.
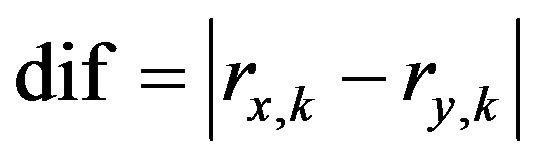 (13)
(13)
 (14)
(14)
The same reasoning for preferring PCC over cosine similarity measure is applicable here for preferring the difference of the rating deviations over the difference of the ratings themselves. This paper examines two options for calculating the difference fuzzy weights. The first option uses the two fuzzy sets for ratings depicted in Figure 1(d) (Formula (4)). The corresponding fuzzy weights are calculated using Formulae (5), and (6). The second option uses the five fuzzy sets for rating deviation values depicted in Figure 2(c) (Formula (7)). The corresponding fuzzy weights are calculated using Formulae (8), and (9). The two options get fuzzy weights without going through a comprehensive GA learning.
5. Experimental Evaluation
5.1. Dataset Selection and Formation
We conduct our experiments using the one million MovieLens dataset [16]. This dataset consists of 1,000,209 ratings by 6040 users on 3900 movies. Table 1 illustrates the distribution of the users of this dataset according to the number of each user’s declared ratings. Consequently, the total dataset is divided into three datasets, DataSet1, DataSet2, and DataSet3 according to the user’s total ratings. To mimic the whole dataset, we randomly select 500 users out of 6040 total users such that 50% (250 users) are selected from DataSet1, 40% (200 users) are selected from DataSet2, and 10% (50 users) are selected from DataSet3 [14].
Keeping in mind the actual users’ distribution, we subdivide the resulting dataset into 5 mutually exclusive folds, fold(1), …, fold(5), each of which having the same size, 100 users (20% of the total). Each fold mimics the whole dataset distribution where 50 users, 40 users, and 10 users are belonging to DataSet1, DataSet2, and DataSet3, respectively. Training and testing are performed 5 times where in iteration-i, fold(i) is reserved as the test set (20%) and the remaining folds are collectively used to train the system (80%). That is in Split-1 dataset, fold (2), …, fold(5) collectively serve as the training set while fold(1) is the test users; Split-2 is trained on fold(1), fold(3), …, fold(5) and tested on fold(2); and so on [15]. Thus each fold is used the same number of times for training and once for testing. The number of total users, total training users, and total active users are 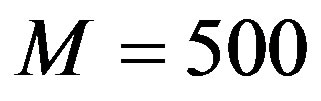 ,
, 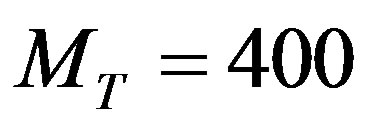 , and
, and 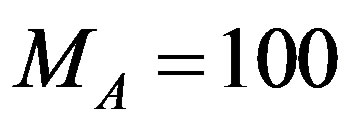 , respectively.
, respectively.
During the testing phase, the set of declared ratings, 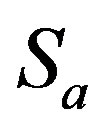 , by an active user,
, by an active user, 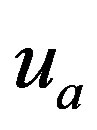 , are divided randomly into two disjoint sets, namely training ratings
, are divided randomly into two disjoint sets, namely training ratings 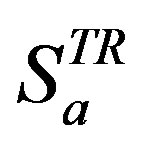 (34%) and test ratings
(34%) and test ratings 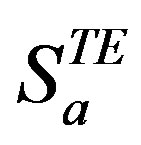 (66%) such that
(66%) such that 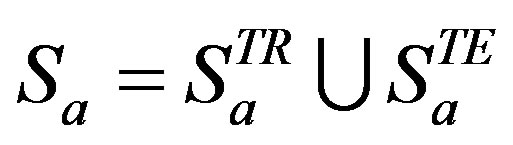 . The CRS treats
. The CRS treats 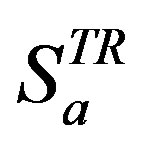 as the only declared ratings while
as the only declared ratings while 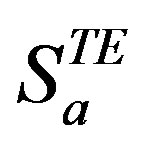 are
are

Table 1. The one million MovieLens dataset users’ distribution.
treated as unseen ratings that the system would attempt to predict for testing the CRS performance.
5.2. Evaluation Metrics
The performance of each CRS is evaluated using coverage, percentage of the correct predictions (PCP), and mean absolute error (MAE) [2,17,18]. Coverage is the measure of the percentage of items for which a CRS can provide predictions. We compute the active user coverage as the number of items for which the CRS can generate predictions for that user over the total number of unseen items. The split coverage over all active users is given by:
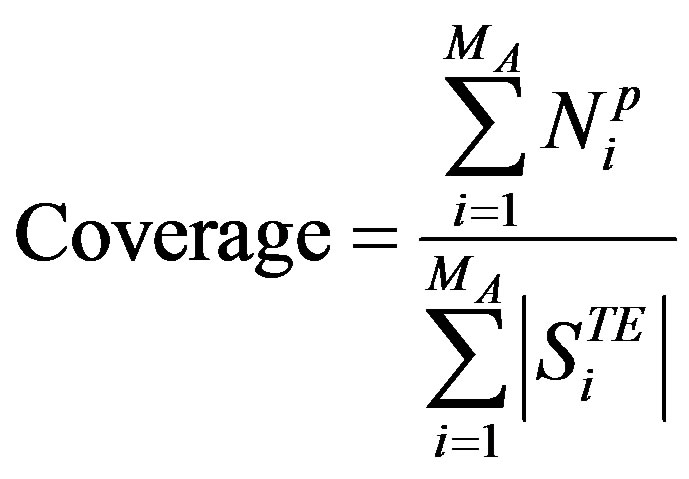 (15)
(15)
Here,  is the total number of predicted items for user
is the total number of predicted items for user 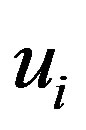 . The PCP of the active user [2,17,18] is the percent of the correctly predicted items by CRS for a given active user to the total number of items in the test ratings set of that user. The set of correctly predicted items for a given user and the split PCP over all active users are defined by the following formulae:
. The PCP of the active user [2,17,18] is the percent of the correctly predicted items by CRS for a given active user to the total number of items in the test ratings set of that user. The set of correctly predicted items for a given user and the split PCP over all active users are defined by the following formulae:
 (16)
(16)
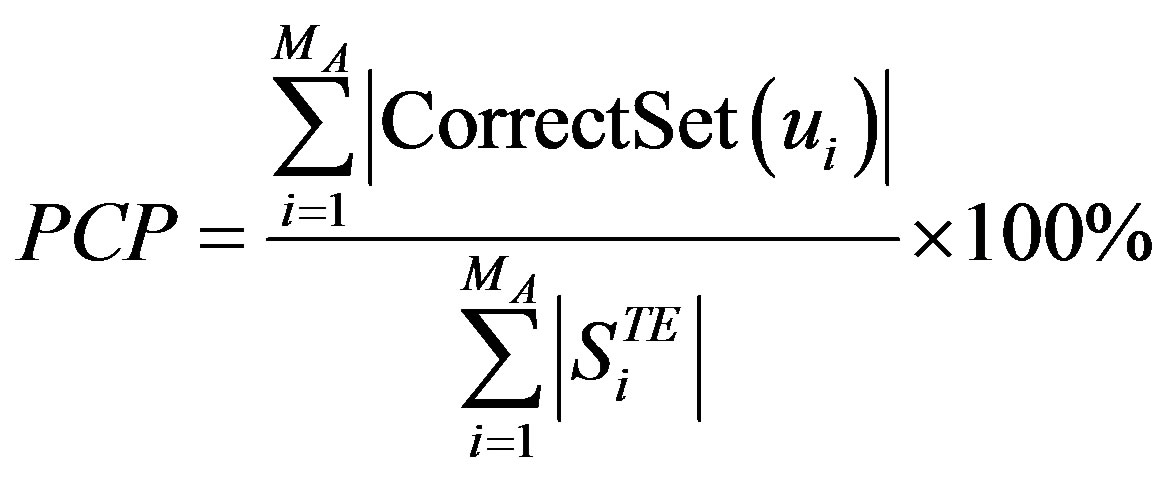 (17)
(17)
The MAE measures the deviation of predictions generated by the CRS from the true ratings specified by the active user [17,18]. The split MAE over all active users 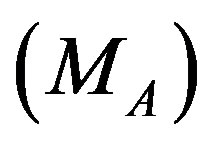 is given by:
is given by:
 (18)
(18)
Low coverage value indicates that the CRS will not be able to assist the user with many of the items he has not rated while lower MAE corresponds to more accurate predictions of a given CRS. Over all splits we compute PCP (coverage) by summing all correct predictions (predictions) over all active users over all splits and divided it by the sum of all testing set sizes of all active users over all splits. The MAE over all splits is the average of all splits’ MAEs.
5.3. Experiments
Our experiments assume that the number of common items between the active user and any training user has to be at least five to include this training user in the neighborhood set of that active user. By this assumption we guarantee that there is an acceptable history between the two users. Otherwise the similarity between the two users may be 100% even if they have only one common item. This data is too small to draw any reliable conclusions about the users’ similarity. Moreover, the misleading high correlations lead to neighbors that are terrible predictors for the active user.
The neighborhood set size, NSS = {10, ∙∙∙, 100} is varied from 10 to 100 by a step size of 10 each time to show the effect of NSS on the memory-based CRS performance. The Resnick’s prediction formula [1,2,6] is used for predictions which scales the contribution of each neighbor’s rating by his similarity to the given active user.
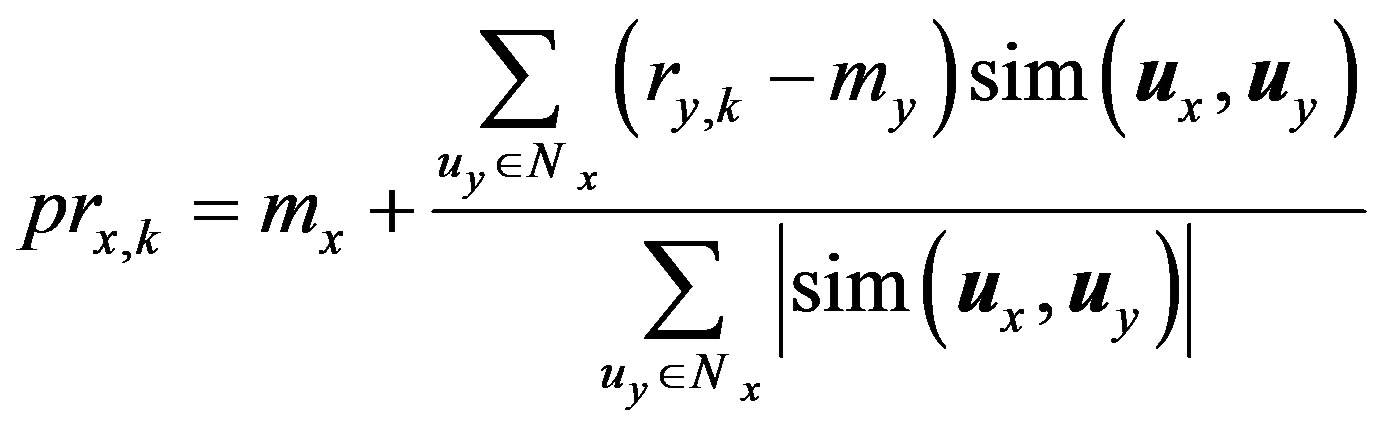 (19)
(19)
All the experiments are conducted on the 500 users’ dataset formed in Subsection 5.1. This paper implements eight experiments based on the formula used for comparing users. The first experiment uses PCC (Formula (1)) for similarity computation and we call this CRS as Correlation-Based RS (CBRS). The second experiment uses Cosine Vector similarity measure (Formula (2)) for similarity computation and we call this CRS as Cosine Vector RS (CVRS). The list of the conducted CRS experiments, their similarity measures, and their shortcuts are listed in Table 2.
5.4. Analysis of the Results
The PCP, MAE, and coverage over all active users and over all splits for all the examined memory-based CRSs are presented in Tables 3 to 5. The results of Tables 3 and 4 show that FPRS outperforms all the examined CRSs in terms of PCP, and MAE. However, FWRS outperforms all the examined CRSs in terms of coverage as Table 5 shows. Both FPRS and FWRS use the rating deviation values for evolving fuzzy weights. The per-
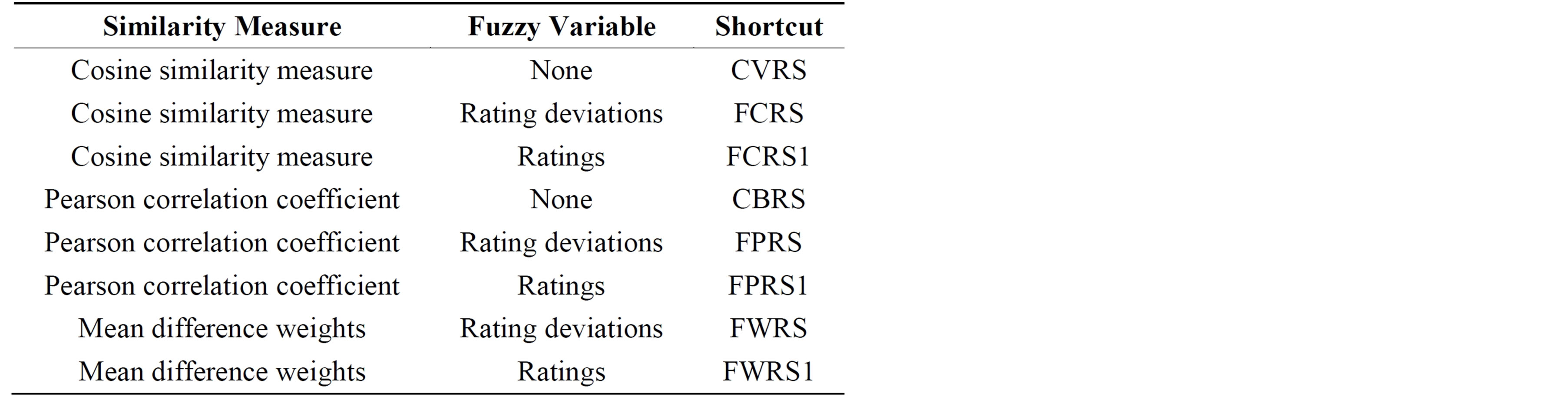
Table 2. Different CRS experiments and their shortcuts.
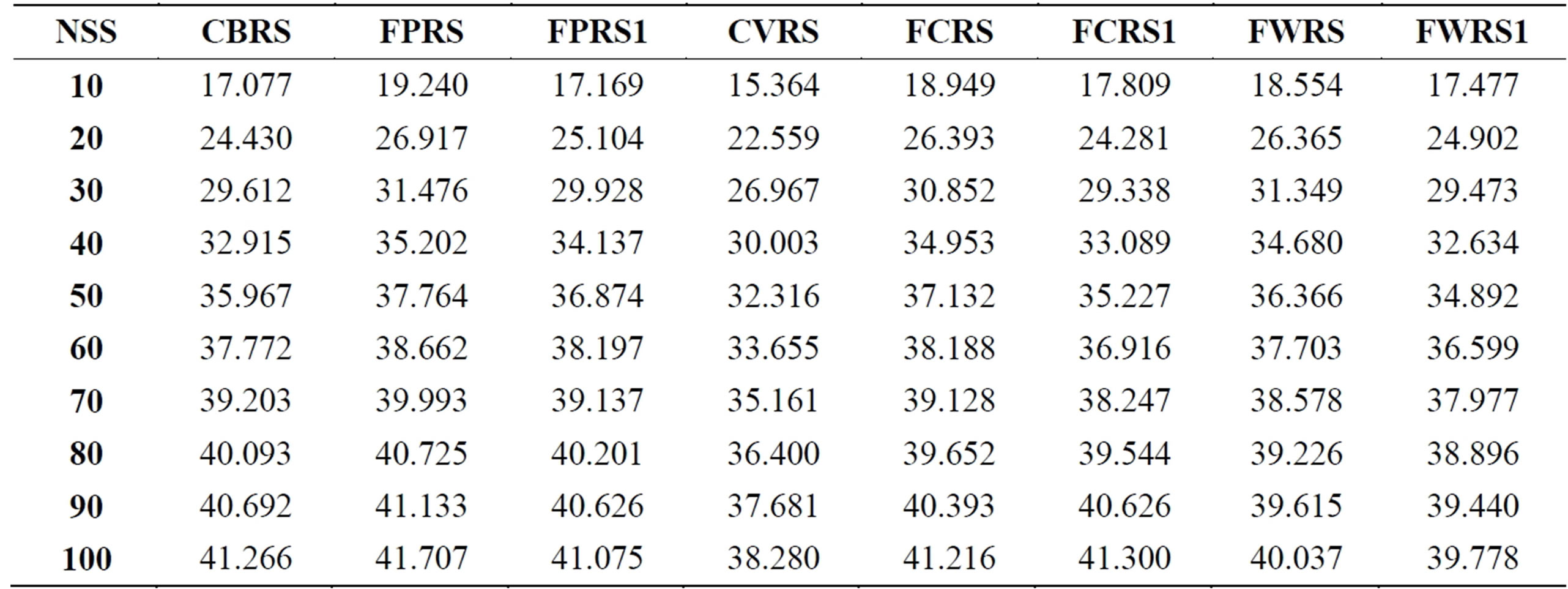
Table 3. PCP values for the different CRSs for many neighborhood set sizes.
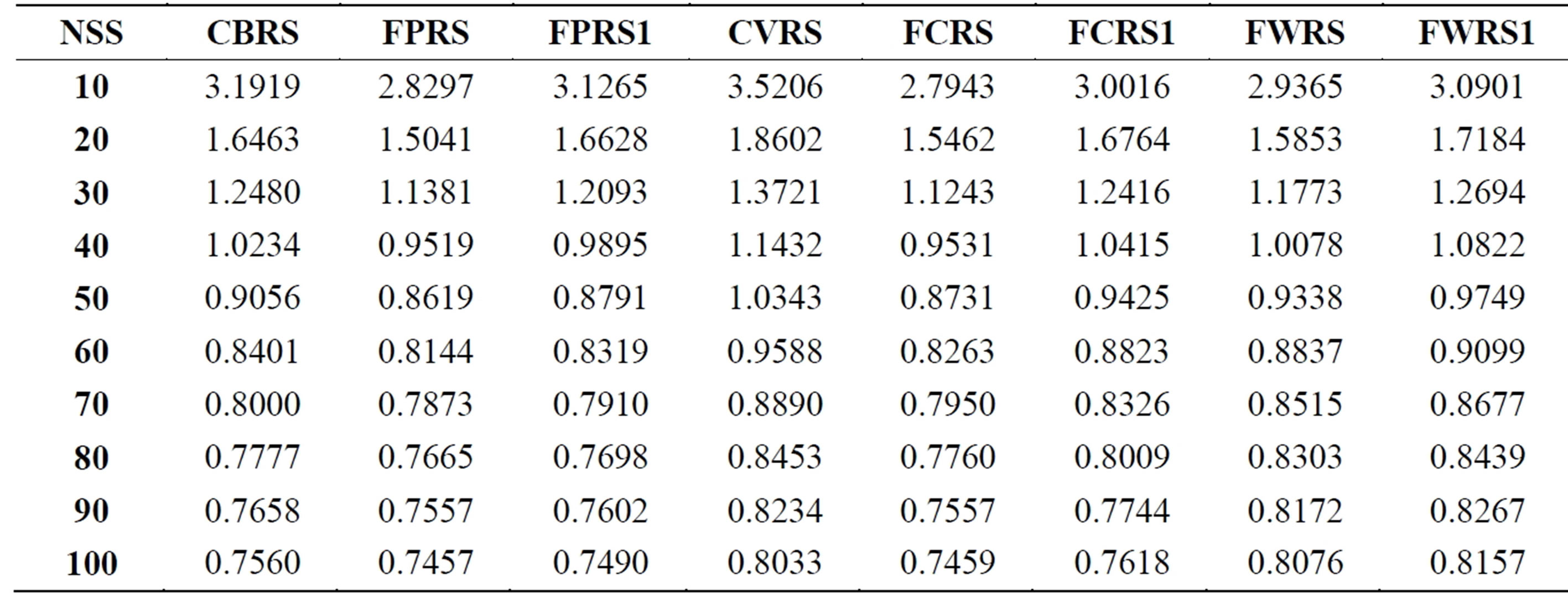
Table 4. MAE values for the different CRSs for many neighborhood set sizes.
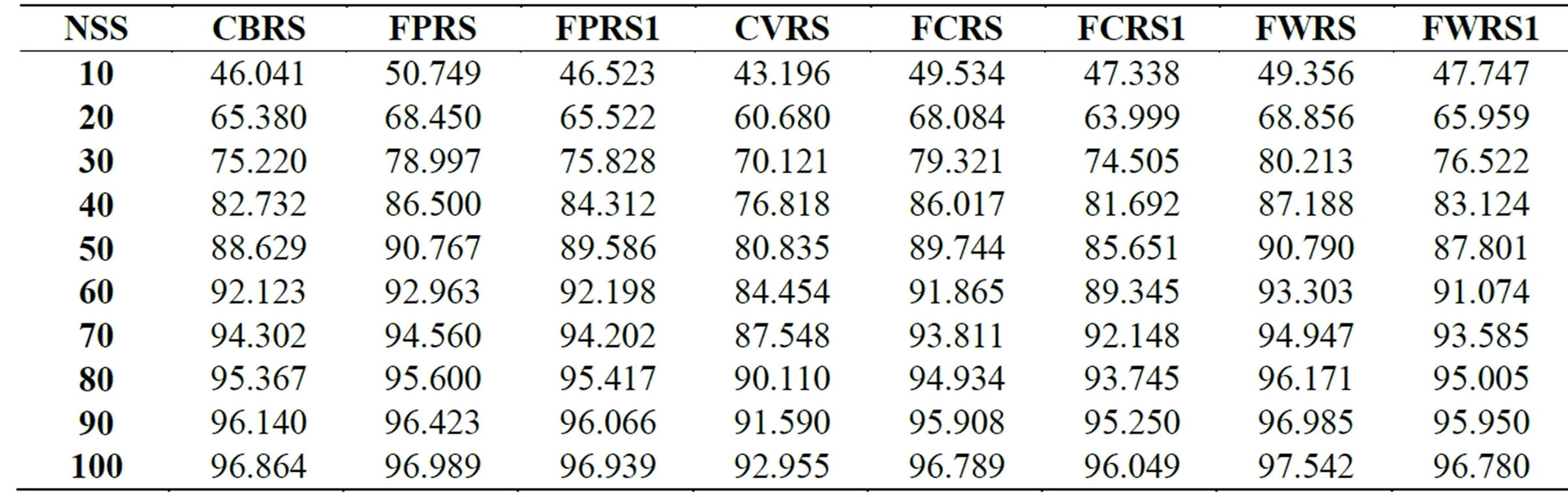
Table 5. Coverage values for the different CRSs for many neighborhood set sizes.
formance of the mean difference similarity measure [7] with fuzzy weighting is close to that of FCRS and FPRS even it does not go through a long and expensive GA learning.
Figures 3 to 8 depict PCP, MAE, and coverage results of the traditional approaches with their fuzzy weighting approaches. On the other side, Figures 6 to 8 compare different fuzzy weighting approaches for the examined memory-based CRSs. The experimental results show that CVRS performs the worst and the results indicate that all the proposed variants even poor ones outperform CVRS for all aspects and all NSSs. This is because CVRS relies directly on the raw ratings themselves. The raw ratings depend on each user’s rating scale and on his mood and taste. Thus comparing one user’s raw rating with another user’s raw ratings will not give a good indication of their similarity. This problem is alleviated somehow with CBRS which uses the rating deviation from each user’s mean of ratings instead of his direct raw ratings.
Once fuzzy weighting is introduced to CVRS, its performance is improved in all aspects. The improvement degree depends on the fuzzy variable used for weighting. For example, FCRS1 outperforms CVRS but not CBRS because its fuzzy variable for weighting is the user-dependent raw ratings. However, FCRS outperforms both CVRS and CBRS as its fuzzy variable for weighting is the rating deviations which alleviate the rating scale variations of different users.
The higher PCP and coverage values of the proposed approaches obviously illustrate that better sets of likeminded users are found and therefore the accuracy of the CRS gets enhanced. The PCP and coverage values for all CRSs increase as 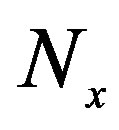 increases for all CRSs while the MAE values decreases as
increases for all CRSs while the MAE values decreases as  increases.
increases.
MAE starts high because only a few numbers of items can get predictions. For small neighborhood set sizes, there is a big improvement for FPRS, FCRS, and FWRS in all aspects. This improvement narrows as neighborhood set size increases. The performances of FPRS, FCRS, and FWRS seem very close with a small advantage for FPRS. This implies that the similarity measure choice has less effect as the fuzzy weighting variable is the deviation values.
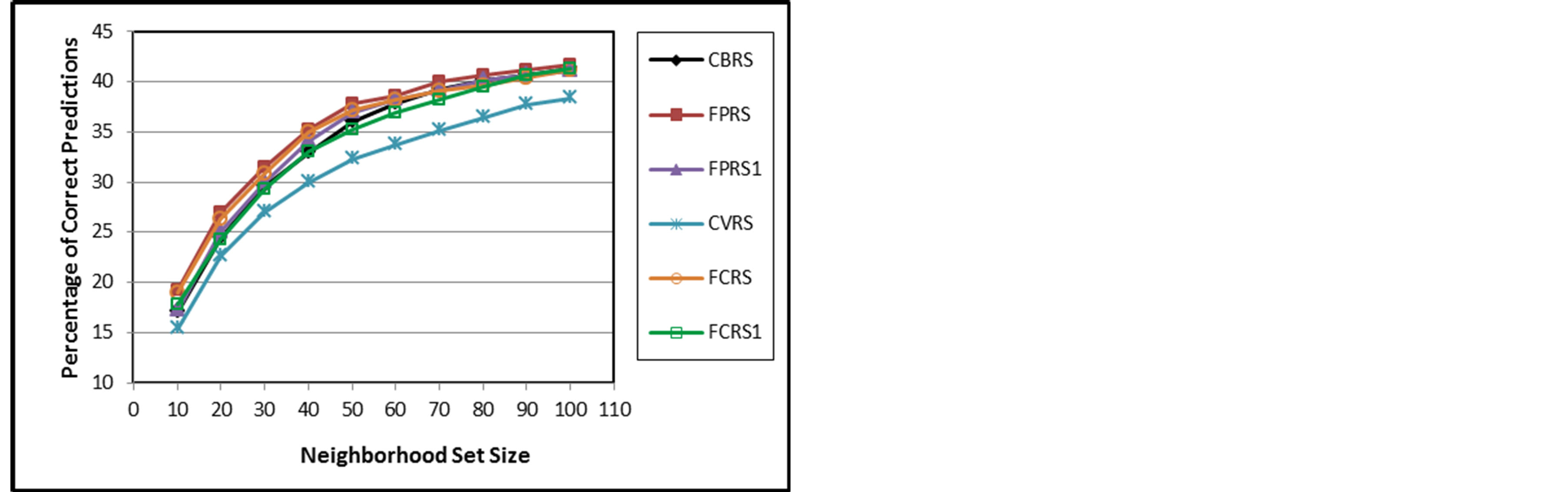
Figure 3. PCP of CBRS, FPRS, FPRS1, CVRS, FCRS, and FCRS1.
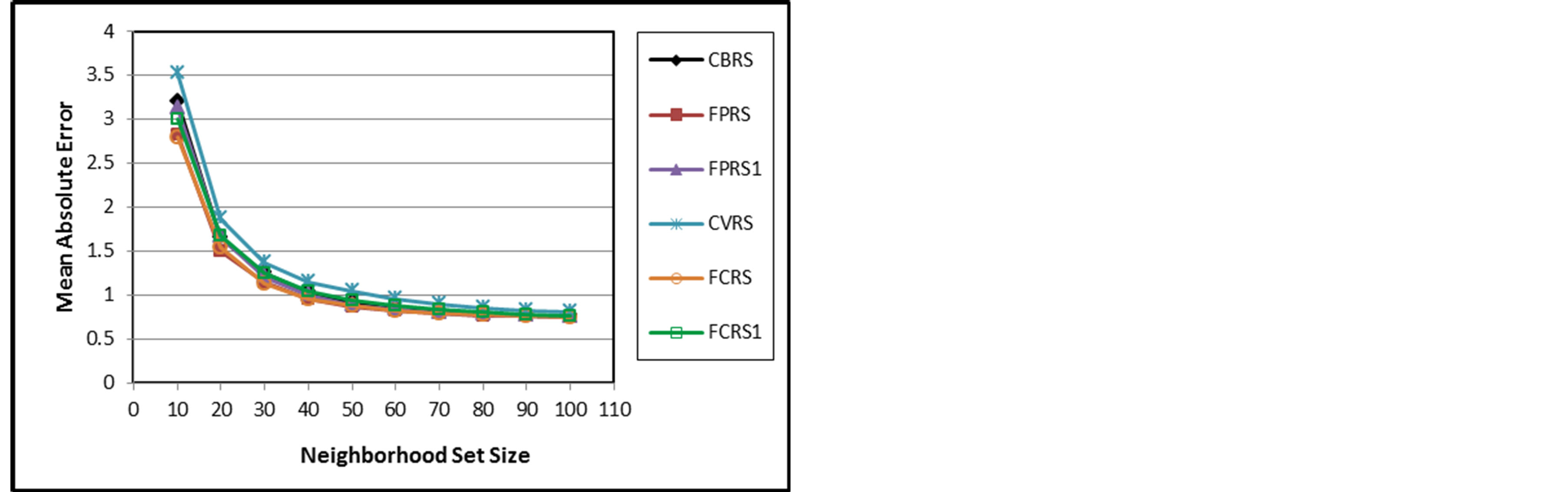
Figure 4. MAE of CBRS, FPRS, FPRS1, CVRS, FCRS, and FCRS1.
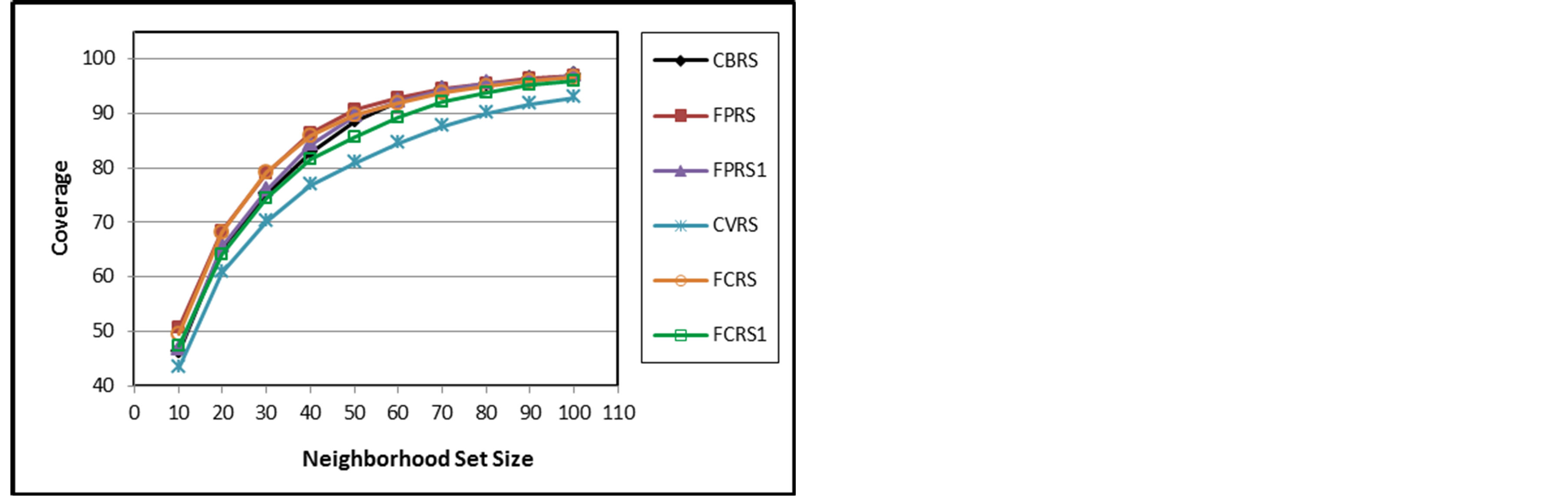
Figure 5. Coverage of CBRS, FPRS, FPRS1, CVRS, FCRS, and FCRS1.

Figure 6. PCP of FPRS, FPRS1, FCRS, FCRS1, FWRS, and FWRS1.
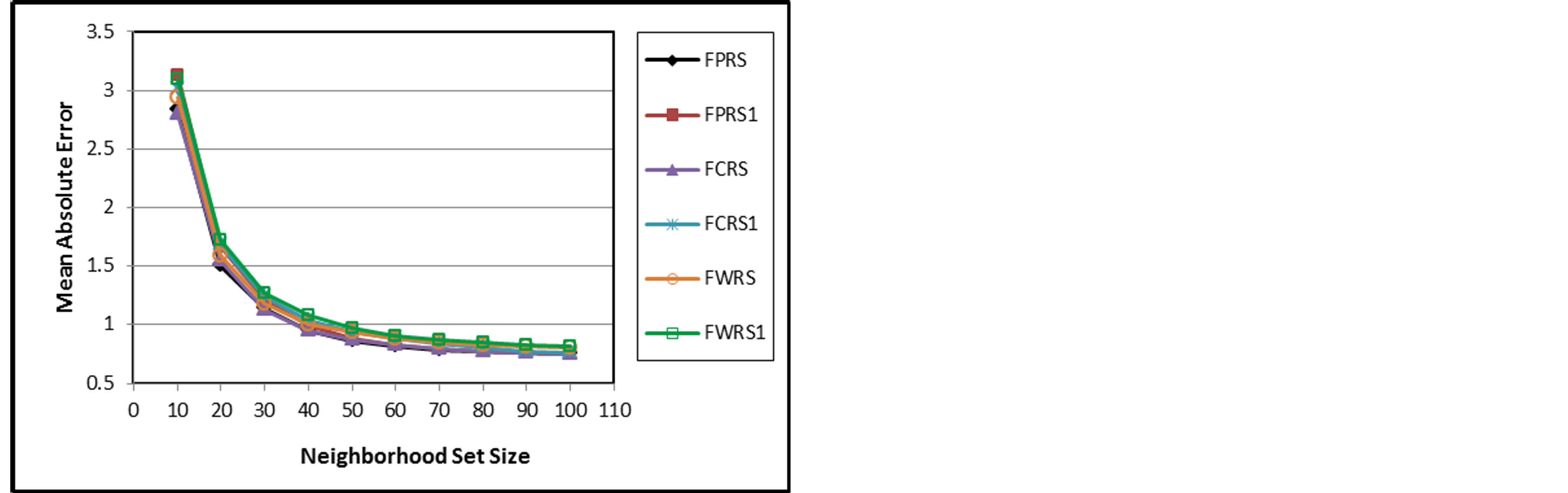
Figure 7. MAE of FPRS, FPRS1, FCRS, FCRS1, FWRS, and FWRS1.
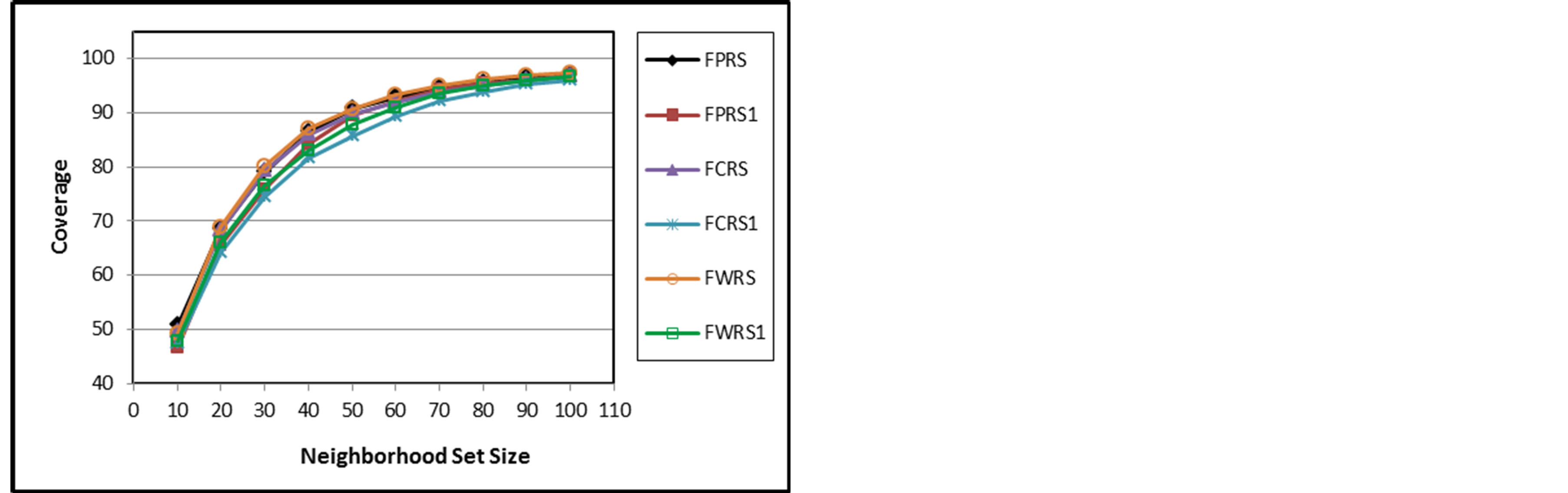
Figure 8. Coverage of FPRS, FPRS1, FCRS, FCRS1, FWRS, and FWRS1.
6. Conclusions
Different users of CRS usually give different weightings for their declared ratings. Thus many methods have been proposed for introducing weights to the similarity measure. Instead of utilizing GA for small intervals which degrades the usefulness of GA such as used in [7], the proposed fuzzy weightings give easy ways to get each user fuzzy weights for different rating values and rating deviation values. This weighting is not fixed and will be changed by changing the neighbor. Moreover, the proposed fuzzy weighting is efficient in terms of time and space complexities. An extra advantage of the fuzzy weighting derived from the user rating deviations is that it avoids the users’ different rating scales problem.
Experimental results show that fuzzy weighting improves the CRS performance irrespective of the fuzzy weighting variable where the fuzzy-weighted similarity measures outperform their traditional counterparts in terms of PCP, coverage, and mean absolute error. The fuzzy weighting performance advantage increases as we use rating deviations instead of ratings themselves. This paper maps crisp values to membership vectors to get the fuzzy weights. However, other fuzzy techniques can be used for calculating these weights. This is left for the future work.
REFERENCES
- J. Bobadilla, F. Ortega, A. Hernando and A. Gutiérrez, “Recommender Systems Survey,” Knowledge Based Systems, Vol. 26, 2013, pp. 109-132. http://dx.doi.org/10.1016/j.knosys.2013.03.012
- G. Adomavicius and A. Tuzhilin, “Toward the Next Generation of Recommender Systems: A Survey of the Stateof-the-art and Possible Extensions,” IEEE Transaction on Knowledge and Data Engineering, Vol. 17, No. 6, 2005, pp. 734-749. http://dx.doi.org/10.1109/TKDE.2005.99
- D. Goldberg, D. Nichols, B. M. Oki and D. Terry, “Using Collaborative Filtering to Weave an Information Tapestry,” Communication of the ACM, Vol. 35, No. 12, 1992, pp. 61-70. http://dx.doi.org/10.1145/138859.138867.
- U. Shardanand and P. Maes, “Social Information Filtering: Algorithms for Automating ‘Word of Mouth’,” Proceedings of the Conference on Human Factors in Computing Systems (CHI’95), Denver, May 1995, pp. 210-217. http://dx.doi.org/10.1145/223904.223931
- B. Miller, I. Albert, S. Lam, J. Konstan and J. Riedl, “MovieLens Unplugged: Experiences with an Occasionally Connected Recommender System,” Proceedings of the International Conference on Intelligent User Interfaces, 2003.
- J. B. Schafer, D. Frankowski, J. Herlocker and S. Sen, “Collaborative Filtering Recommender Systems,” In: P. Brusilovsky, A. Kobsa and W. Nejdl, Eds., The Adaptive Web, LNCS 4321, Springer-Verlag, Berlin Heidelberg, 2007, pp. 291-324.
- J. Bobadilla, F. Ortega, A. Hernando and J. Alcala, “Improving Collaborative Filtering Recommender System Results and Performance Using Genetic Algorithms,” Knowledge Based Systems, Vol. 24, No. 8, 2011, pp. 1310-1316. http://dx.doi.org/10.1016/j.knosys.2011.06.005.
- S.-H. Min and I. Han, “Optimizing Collaborative Filtering Recommender Systems,” In: P. S. Szczepaniak and A. Niewiadomski, Eds., AWIC 2005, LNAI 3528, SpringerVerlag, Berlin Heidelberg, 2005, pp. 313-319.
- K. K Bharadwaj and M. Y. H. Al-Shamri, “Fuzzy Computational Models for Trust and Reputation Systems,” Electronic Commerce Research and Applications, Vol. 8, No. 1, 2009, pp. 37-47. http://dx.doi.org/10.1016/j.elerap.2008.08.001
- J. Herlocker, J. Konstan, A. Borchers and J. Riedl, “An Algorithmic Framework for Performing Collaborative Filtering,” Proceedings of the 22nd annual International ACM SIGIR Conference on Research and Development in Information Retrieval, 1999, pp. 230-237. http://dx.doi.org/10.1145/312624.312682.
- J. Breese, D. Heckerman and C. Kadie, “Empirical Analysis of Predictive Algorithms for Collaborative Filtering,” Proceedings of the 14th Conference on Uncertainty in Artificial Intelligence, Madison, 1998, pp. 43-52.
- M. Y. H. Al-Shamri and K. K. Bharadwaj, “A Hybrid Preference-Based Recommender System based on Fuzzy Concordance/Discordance Principle,” Proceedings of the third Indian International Conference on Artificial Intelligence (IICAI’07), Pune, 2007, pp. 301-314.
- M. Y. H. Al-Shamri and K. K. Bharadwaj, “Fuzzy-Genetic Approach to Recommender Systems Based on a Novel Hybrid User Model,” Expert Systems with Applications, Vol. 35, No. 3, 2008, pp. 1386-1399. Http://dx.doi.org/10.1016/j.eswa.2007.08.016
- M. Y. H. Al-Shamri and N. H. Al-Ashwal, “Fuzzy Weighted Pearson Correlation Coefficient for Collaborative Recommender System,” Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS13), Angers, 2013, pp. 409-414. http://dx.doi.org/10.5220/000441240409041
- J. Han and M. Kamber, “Data Mining, Concepts and Techniques,” 2nd Edition, Morgan Kaufmann Publishers, 2006.
- http://www.movielens.umn.edu
- E. Vozalis and K. G. Margaritis, “Analysis of Recommender Systems’ Algorithms,” Proceedings of the sixth Hellenic-European Conference on Computer Mathematics and its Applications (HERCMA), Athens, 2003.
- J. L. Herlocker, L. A. Konstan, L. G. Terveen and J. T. Riedl, “Evaluating Collaborative Filtering Recommender Systems,” ACM Transaction on Information Systems, Vol. 22, No. 1, 2004, pp. 5-53. http://dx.doi.org/10.1145/963770.963772

