Journal of Intelligent Learning Systems and Applications
Vol.5 No.2(2013), Article ID:31425,17 pages DOI:10.4236/jilsa.2013.52008
Analysis of Students’ Misconception Based on Rough Set Theory
![]()
Graduate Institute of Educational Measurement and Statistics, National Taichung University of Education, Taichung, Chinese Taipei.
Email: sheu@mail.ntcu.edu.tw, et104979et104979@gmail.com, tsai.chenbin@msa.hinet.net, darkdreams0802@gmail.com, dangthanh7502@yahoo.com, nagai@kamakuranet.ne.jp
Copyright © 2013 Tian-Wei Sheu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 27th, 2013; revised April 25th, 2013; accepted May 2nd, 2013
Keywords: Misconception; Rough Set Theory; Interpretive Structural Model; Diagnostic Assessment; Structural Graph
ABSTRACT
The study analyzed students’ misconception based on rough set theory and combined with interpretive structural model (ISM) to compare students’ degree of two classes. The study then has provided an effective diagnostic assessment tool for teachers. The participants were 30 fourth grade students in Central Taiwan, and the exam tools were produced by teachers for math exams. The study has proposed three methods to get common misconception of the students in class. These methods are “Deleting conditional attributes”, “Using Boolean logic to calculate discernable matrix”, and “Calculating significance of conditional attributes.” The results showed that students of Class A had common misconceptions but students of Class B had not common misconception. In addition, the remedial decision-making for these two classes of students is pointed out. While remedial decision-making of two classes corresponded to structural graph of concepts, it can be found the overall performance of the Class B was higher than Class A.
1. Introduction
“Misconception” is also called as the “Alternative Conception” or the “Alternative Frame”. A number of scholars have shown that before a formal education, students have possessed the systematic structure of science phenomena. There is a basic difference between systematic structure and learning knowledge structure [1]. The Ministry of Education [2] of Taiwan has emphasized that teachers should investigate reason of the mistake which student easily make in learning. In recent years, the diagnostic teaching has been developing. Many experiments based on diagnostic teaching have been implemented [3-6].
There are many methods to do cognitive diagnosis. In quantitative approaches, although the Item Response Theory is frequently used, the requirement of a large sample size is existing limitation of the theory. In quailtative approaches, interview is common way. However, teachers are often unable to do individual remedial teaching because of a limited number of teachers. Moreover, in order to identify misconceptions in learning, then make an accurate diagnosis of student’s problems, a number of scholars have designed various kinds of diagnostic tests [7,8]. However, the development of one validity and reliability testing program requires the process of interview, paper-pencil test items design, pretest, and revise. This process consumes time, budget as well as resource. Therefore, it is difficult to operate above methods in teaching site and teachers cannot receive feedback from the diagnostic exams on time.
In order to overcome the problems mentioned above, unlike previous psychometric research, this study has analyzed students’ response based on rough set theory. Rough set theory is a very practical subject. It is the mathematical tools and proposed in 1982 by Pawlak to process vagueness and uncertainty. Rough set theory has been rapidly developed in recent years. It is an important method in artificial intelligence and cognitive science and often used in the medical field and industrial management. For example, Yeh and Cheng [9] applied rough set theory to classify appendicitis. They found that through the approximation sets and reduct, the multiattribute diseases can be well classified. In addition, rough set theory has fruitful results in many fields, particularly in approximate reasoning [10], mathematical logic analysis and reduct [11-13], building of predictive models [14], decision support system [15-19] and other areas. Many studies have shown that the use of rough set theory not only formulate a clear decision-making projects [12], but also enhance the effectiveness of the research while doing optimization [19,20]. Among them, the research related to education of Qu and Wang [16] provided a basis of personalized teaching strategies in distance learning website by analysis of reduct and attribute significance.
Rough set theory assume analyzed objects set implicit knowledge itself and knowledge is considered to be a classification ability for the object [21]. The main aim of rough set theory is to retrieve the rules in information system though difference set of lower and upper approximations in set theory and the concept of conditional probability [22-26]. Information system is composed from various objects and their corresponding attributes. The rules can describe each object under the conditional attribute which can be classified. Rough set theory can get the same knowledge as the original decision-making system without losing any information. At this time, the state has a minimum condition attributes, and maintain the simplest form which has same classification ability as the original decision-making system [21]. Relative to the probability statistics, the empirical theory of fuzzy sets and other mathematical tools, rough set theory not only can find objects relationship but also have an advantage which other theories have not. Statistic needs the probability distribution, the empirical theory needs basic trust given, fuzzy sets needs membership function, but rough sets do not obey any assumptions. It means that rough sets do not need quantity description given in advance of certain characteristics or attributes or probability distribution related statistics [21].
In view of the above reasons, although the rough set theory is rarely used in education, but its characteristics (Rough set theory does not obey any assumptions and can get the same knowledge as the original decisionmaking system under not lose any information.) are very suitable for small class teaching in the stage. Therefore, the study analyzed students’ misconception based on rough set theory and combined with interpretive structural model (ISM). The sample of the study was 30 fourth grade students in Central Taiwan, and the exam tools were produced by teachers for math exams. This study analyzed individual misconceptions of two classes, set appropriate remedial teaching decision-making according various degree, and combined ISM structural graph to compare degree of two classes in order to provide teachers an effective tool while doing teaching diagnosis.
2. Fundamental Theory
In this section, researchers do a brief introduction of fundamental theory used, including Rough Set Theory, and Interpretive Structural Modeling.
2.1. Rough Set Theory
Rough set theory is proposed in 1982 by Pawlak. It is a mathematical tool to deal with problems of vagueness and uncertainty [21]. It does not need to give quantity description or statistical probability distribution of some characteristics or attributes in advance and do not have to obey any assumptions. Rough set theory assumes that objects set analyzed itself imply the knowledge and knowledge is considered to be a classification ability of the object. The main purpose is to extract rules which can describe each object classified under which attributes from information system, the rules [27,28]. The following are the important concepts of rough set theory [21]:
2.1.1. Information System (IS)
Generally, the information posed by objects of study and its characteristics is known as an information system (IS), also known as the approximation space. Formally, information systems is a four-tuple, defined as 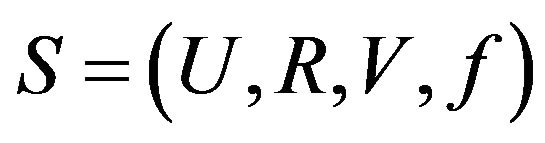 , for short
, for short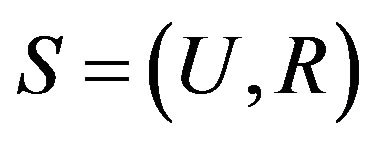 .
.
 : It is universe, a non-empty finite set of unit, written
: It is universe, a non-empty finite set of unit, written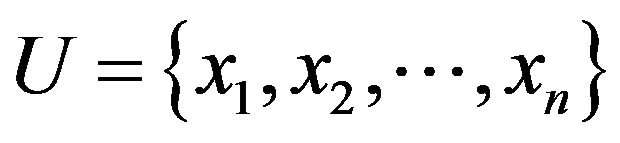 .
.
 : It is a non-empty finite set of attributes, written
: It is a non-empty finite set of attributes, written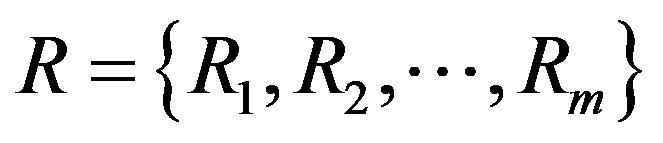 .
.
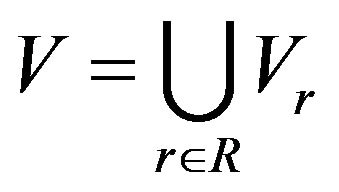 is written
is written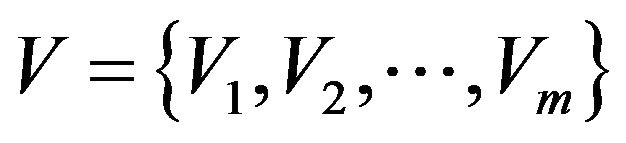 , where Vi is the range of attribute
, where Vi is the range of attribute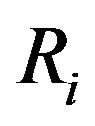 .
.
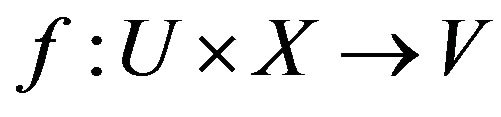 is an information function,
is an information function, 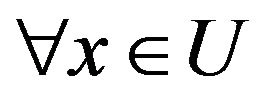 ,
,  , there is
, there is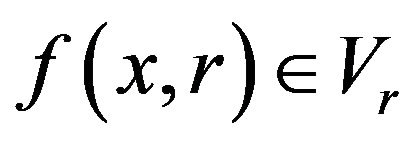 .
.
If attribute sets R can be further broken down into condition attribute C and decision attribute D, and when it satisfies , Information set can also be called a decision system or decision table (Table 1). If decision table contains only one decision attribute, it is called a single decision-making. Otherwise, it is called multi-decision.
, Information set can also be called a decision system or decision table (Table 1). If decision table contains only one decision attribute, it is called a single decision-making. Otherwise, it is called multi-decision.
2.1.2. Indiscernibility Relation
Indiscernibility relation use 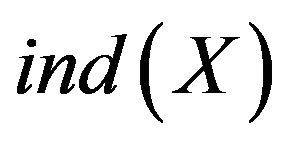 represented and is an equivalence relation. U is divided into a finite number of equivalent set. It is indiscernibility between objects in each equivalent set. The first step of classification in the rough set is using
represented and is an equivalence relation. U is divided into a finite number of equivalent set. It is indiscernibility between objects in each equivalent set. The first step of classification in the rough set is using 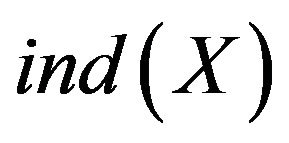 to construct the basic set. It
to construct the basic set. It

Table 1. Decision system.
is expressed as a mathematical model
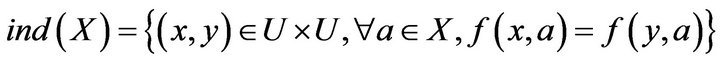 where
where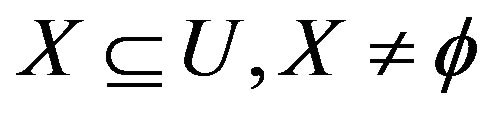 .
.
2.1.3. Upper Approximation and Lower Approximation
Positive domain 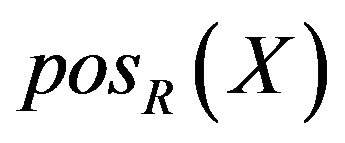 or lower approximation of X is a set of elements which completely determined to classify set X in U under R. It is defined as
or lower approximation of X is a set of elements which completely determined to classify set X in U under R. It is defined as
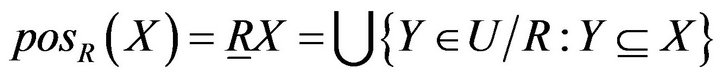 .
.
Negative domain 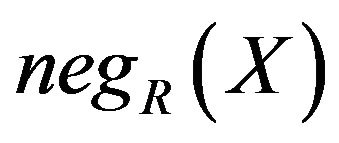 or Upper approximation of X is a set of elements which could not completely determined to classify set X in U under R. It is defined as
or Upper approximation of X is a set of elements which could not completely determined to classify set X in U under R. It is defined as
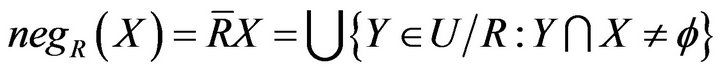 .
.
If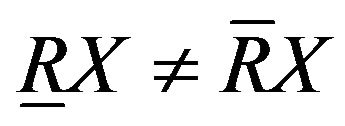 , boundary
, boundary 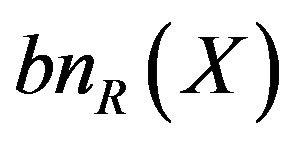 exists. Boundary is a set of elements which probably classify set X in U under R. It means the set neither completely determined to classify set X nor completely determined to classify set
exists. Boundary is a set of elements which probably classify set X in U under R. It means the set neither completely determined to classify set X nor completely determined to classify set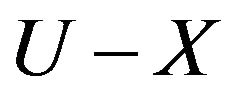 . It is defined as
. It is defined as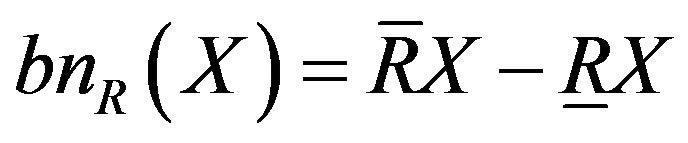 .
.
2.1.4. Dispensable and Independent
R is a set in equivalence relations. While , if
, if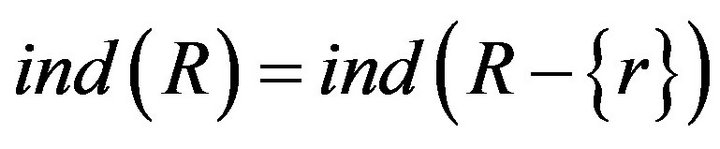 , it is said
, it is said 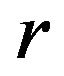 in R can be omitted. On the contrary, if
in R can be omitted. On the contrary, if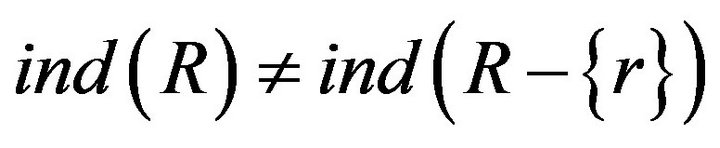 , it is said
, it is said 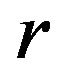 in R can be independent.
in R can be independent.
2.1.5. Dependents and Significant of Attributes
Assume in decision system, positive domain 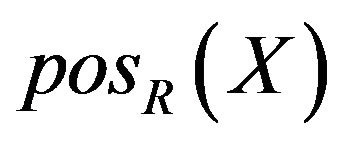 of decision attribute D under condition attribute C is divided by knowledge of C. It is defined as
of decision attribute D under condition attribute C is divided by knowledge of C. It is defined as
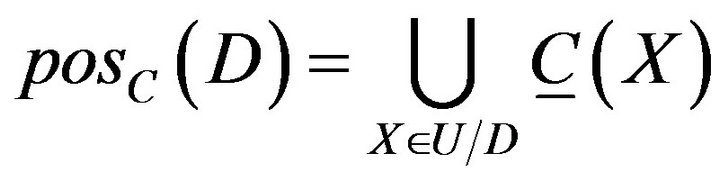 . And dependent of attribute
. And dependent of attribute 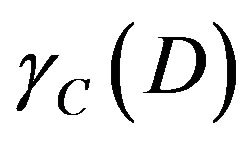 means dependence of decision attribute D on condition attribute C. It is defined as
means dependence of decision attribute D on condition attribute C. It is defined as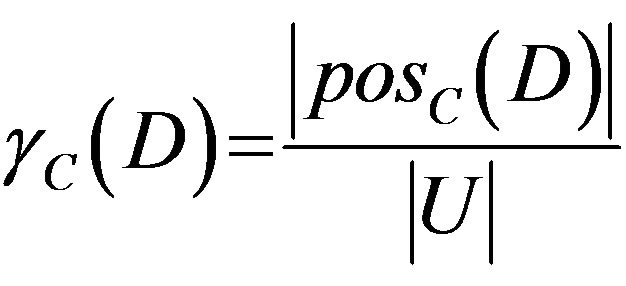 .
.
While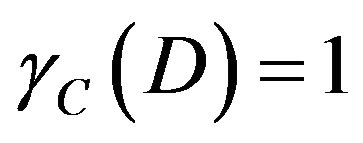 , it is said D is completely derivable under C; while
, it is said D is completely derivable under C; while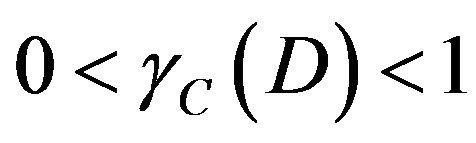 , it is said D is partial derivable under C; while
, it is said D is partial derivable under C; while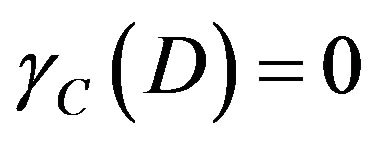 , it is said D is not completely derivable under C. Dependent of attribute can decide significant of attribute. The usual practice is deleteing a attribute
, it is said D is not completely derivable under C. Dependent of attribute can decide significant of attribute. The usual practice is deleteing a attribute 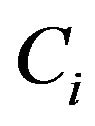 and calculating the impact of positive domain under C. It is defined as
and calculating the impact of positive domain under C. It is defined as
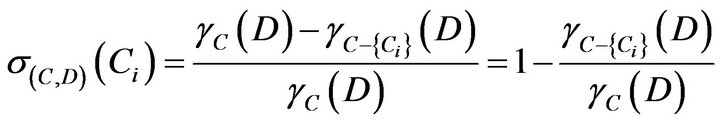 .
.
2.1.6. Reduct and Core of Rough Sets
For decision system given, if 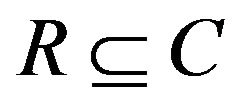 is independent and
is independent and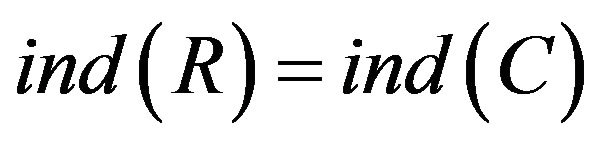 , it is said R is a reduct
, it is said R is a reduct 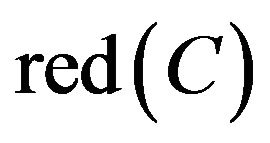 of C. An attribute set maybe have various reduct. Intersection of reduct is said core of C, represented
of C. An attribute set maybe have various reduct. Intersection of reduct is said core of C, represented 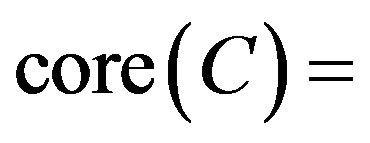
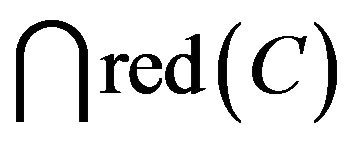 . Core can be interpreted as the most important part of knowledge, can not delete while reduct.
. Core can be interpreted as the most important part of knowledge, can not delete while reduct.
2.1.7. Decision Rule Having the Most Efficient
After calculations of reduct and core in decision system, rules can be extracted by the reduction of the decision system. The type of rules is if “characteristic value after reduction of sentence” then “a classification of decision attribute”. These rules express extracted knowledge from raw data.
2.2. Interpretive Structural Modeling (ISM)
Interpretive Structural Modeling (ISM) is proposed in 1976 by Warfield. The mathematical analysis transforms the relationship between the different types of elements into the associated constructor class diagram in a complex system [29]. While analyzing, using the Hierarchical Digraph in Graphic Theory describes the relationship between different types of elements. As a result, ISM transform fragmental and abstractive elements into the specific and comprehensive associated constructor class diagram in a complex system to clarify the structure of the complex situations [30].
While calculating, the relationship between the various elements must be arranged. Causality analysis table is established by binary matrix. Binary data of “1” and “0” means that the elements of related or unrelated. The matrix is represented by symbol A. To use Graphic Theory, the adjacency matrix A plus the unit matrix I becomes “contains its own causality matrix” represented by symbol B. Though 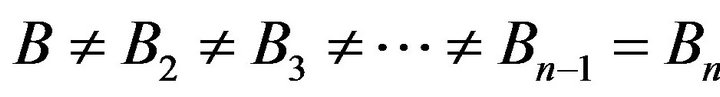 (Bn expresse B multiplied by n times), B is trasformed into reachable matrix represented by symbol T. It means
(Bn expresse B multiplied by n times), B is trasformed into reachable matrix represented by symbol T. It means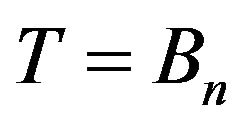 . Finally, all the structural elements in the event are transformed into the associated structural hierarchy chart to obtain a distribution position of various structural elements [29].
. Finally, all the structural elements in the event are transformed into the associated structural hierarchy chart to obtain a distribution position of various structural elements [29].
In recent years, the studies of applying ISM in education are very much. Such as making structural graph of learning interest factors in mathematics, and proposing guidance programs for students of different learning [31], structured analysis of the teaching content [32], proposing learning path of concepts by combining students’ misconceptions and ISM structural graph of concepts [33].
In this study, ISM structural graph of concepts is made by teaching content. By corresponding remedial decision-making of two classes to the ISM structural graph of concepts, researchers compared degrees of two classes. This method is an innovative method which is different from the traditional method of using the average.
3. Research Methods
In this section, researchers first do reliability test in order to ensure the data is quite reliable and then drew research procedures.
3.1. Reliability Test of Data
This paper took two fourth grade classes in the same school for example. The number of items was 24, the average of students of each class was 15, and the number of concepts were 7. Before analyzing, the researchers first test reliability of students’ responses for two classes. The results showed that Cronbach’s α value of Class A is 0.854 and Cronbach’s α value of Class B is 0.849. These data represent high reliability.
3.2. Research Procedures
The study analyzed students’ misconception based on rough set theory and combined with ISM to compare students’ degree of two classes. Research structure was shown in Figure 1.
4. Results and Discussion
Based on research structure, this section divides into several parts. About problems, researchers analyze the structural graph of concepts based on ISM. About students’ responses of Class A and B, researchers analyze the SCD table, find common misconceptions, and then formulate the remedial decision-making. Finally, researchers compare students’ degree of two classes.
4.1. Production and Analyses of the Structural Graph of Concepts Based on ISM
In this section, researchers used the ISM model to build the problems’ structural graph of concepts. The study used seven concepts of fraction in fourth grade math. The relationship between concepts is shown as in Table 2. Number “1” reflects the connection between two concepts and the lack of connection is indicated as “0”.
Researchers used ISM software to estimate a matrix calculation to obtain the causal linking structure between concepts which was the ISM structural graph of concepts (Figure 2). From Figure 2, structural graph of concepts has 5 layers, the lowest layer is the basic concept of this unit, and the top layer is the most difficult concept. When teachers teach this unit, there are three distinct teaching sequences, including C1 ® C2 ® C4 ® C6, C1 ® C2 ® C3 ® C5 ® C6 and C1 ® C2 ® C3 ® C5 ® C7.
4.2. SCD Table of Class A
First, teachers judged the correlation between concept and problem. If there is a connection between concept and problem, then a corresponding column will reflect the number “1” and a lack of connection will show a “0” (Table 3). In this paper, students of two classes did same test, so they had the same problem-concept relationship.
Students’ responses of Class A are shown in Table 4. “1” represents students answered correctly, “0” represents students answered incorrectly. In this paper, if students’ score was lower than average score, researchers
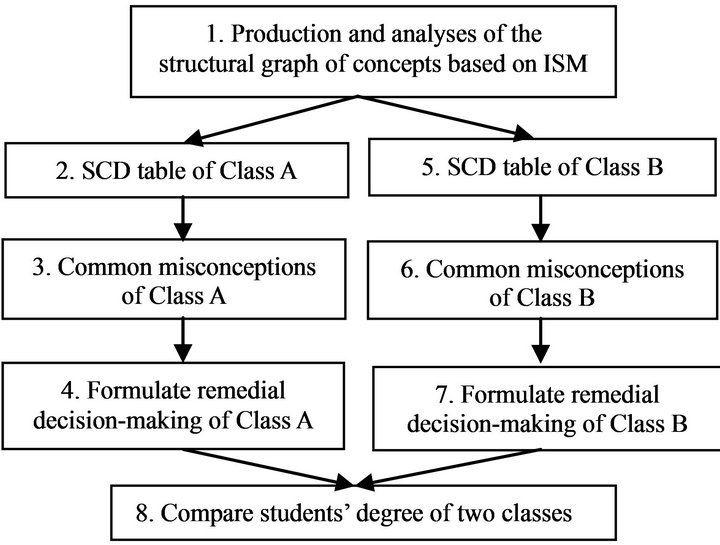
Figure 1. Research structure.
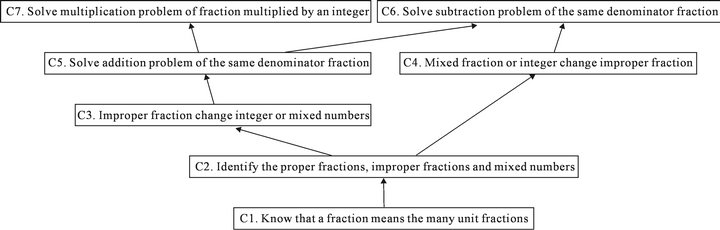
Figure 2. The structural graph of concepts.
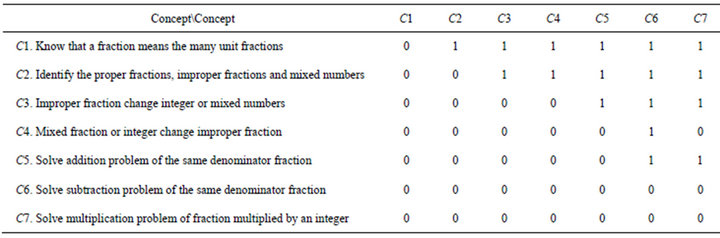
Table 2. Concept-concept relationship.
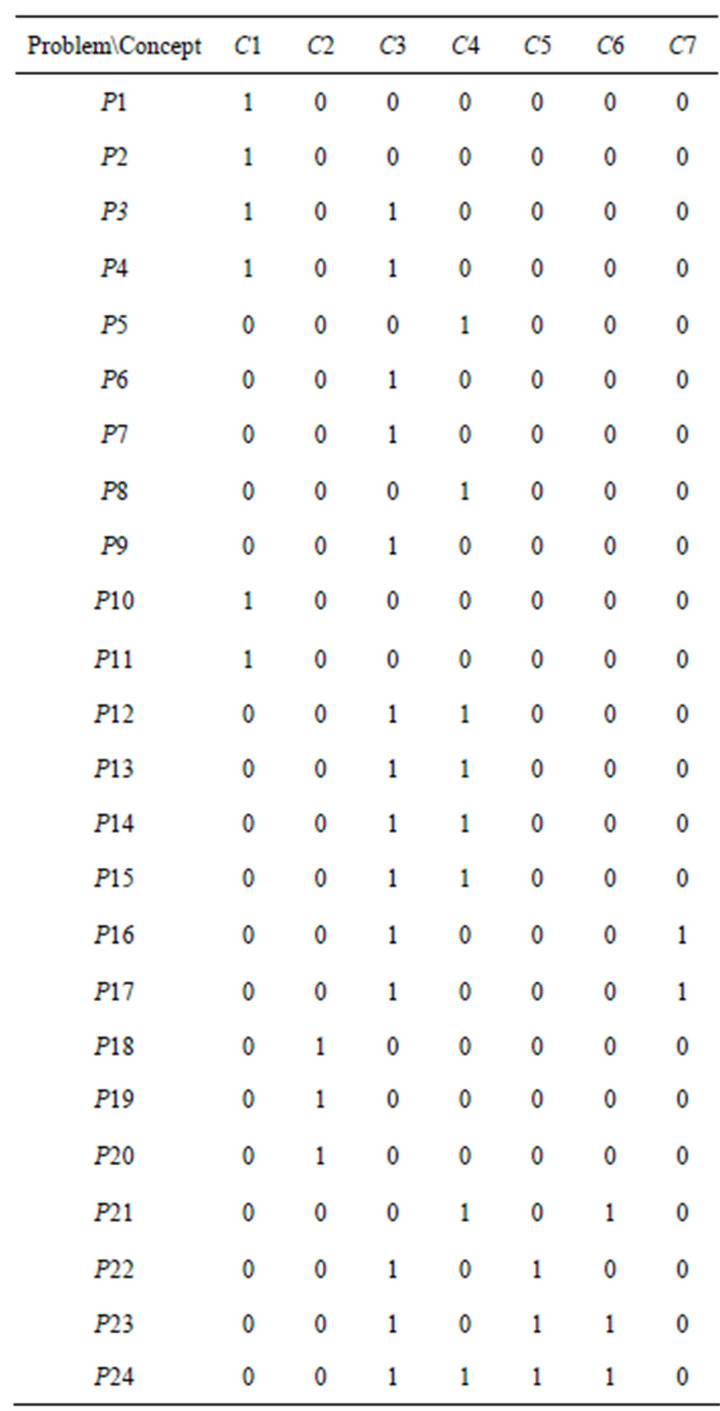
Table 3. Problem-concept relationship.
set for students who need remedial teaching. Because average score is very close to 22 points, students who get 22 points were set. Finally, researchers judged the students who need remedial teaching are A−2, A−3, A−8, A−14, and A−15.
In this paper, SCD table was formulated based on IS of rough set theory. SCD table is decision system, where S represents the students; Condition attributes C represents concepts that are required learning in this unit; decision attribute D represents whether teachers do remedial teaching. Before formulating SCD table, SC table must first be needed (Table 5). SC table was obtained by combining problem-concept relationship (Table 3) and students’ responses of Class A (Table 4). It represents the number of incorrect responses in C1 to C7, respectively. For example: In Table 4, researchers can find A−5 had wrong response in P17, and C3 and C7 must be equipped to answer correctly. Thus, a corresponding column will reflect the number “1” in SC table of Class A.
In SC table, the number of some concepts that students answered incorrectly was a great difference. If doing rough set computing according SC table, the rules could not be obtained. In other words, it is unable to identify common misconceptions of the students. Thus in this paper, researchers assumed if students answered incurrectly once at a certain concept, then it can be regarded as to got the wrong answer accidentally; if students answered incorrectly more than twice at a certain concept, then it can be regarded as to have the misconception. Based on the hypothesis, SC table was converted to SCD table (Table 6). In SCD table, students answered incorrectly more than twice and then a corresponding column will reflect the number “1”; it will be showed a “0”, conversely.
The indiscernibility relation can be obtained according to the rough set theory. It is equivalence relation of S under the condition attributes. The result of the calculation is as follows.
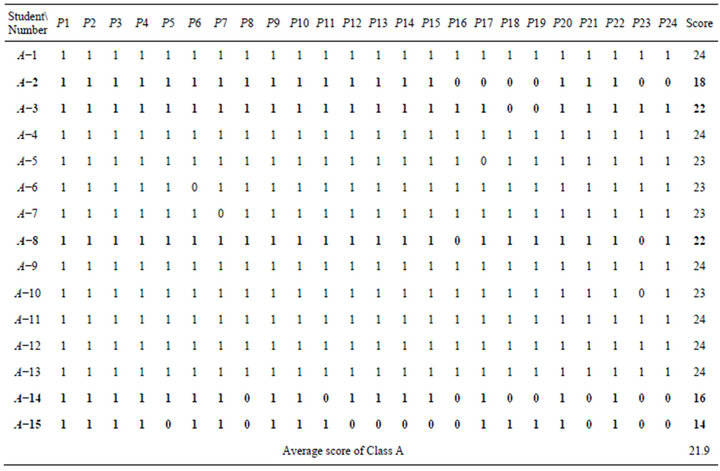
Table 4. Students’ responses of Class A.
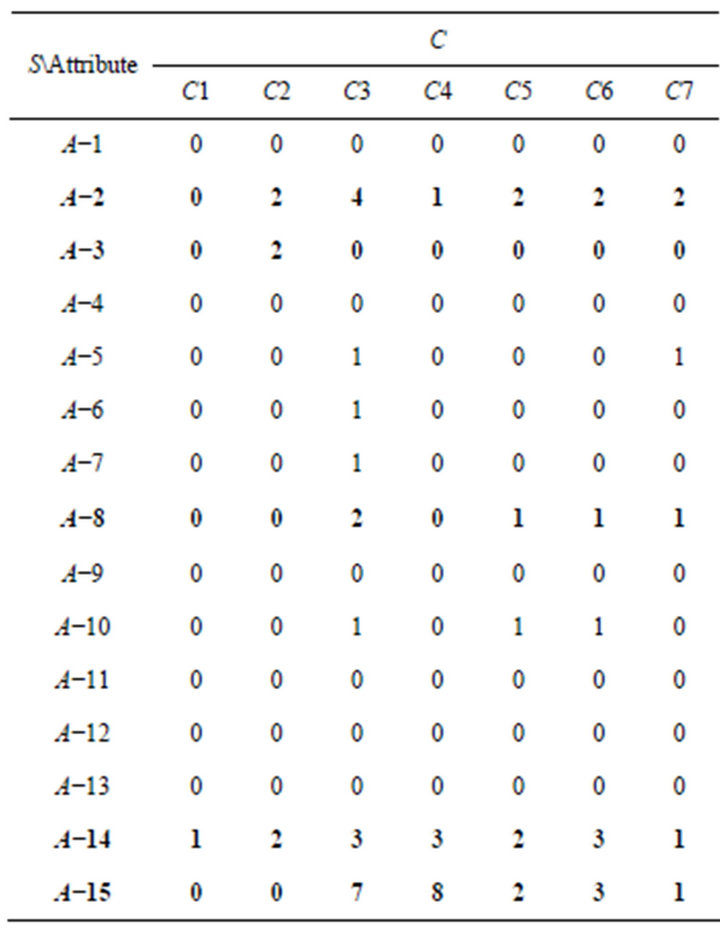
Table 5. SC table of Class A.
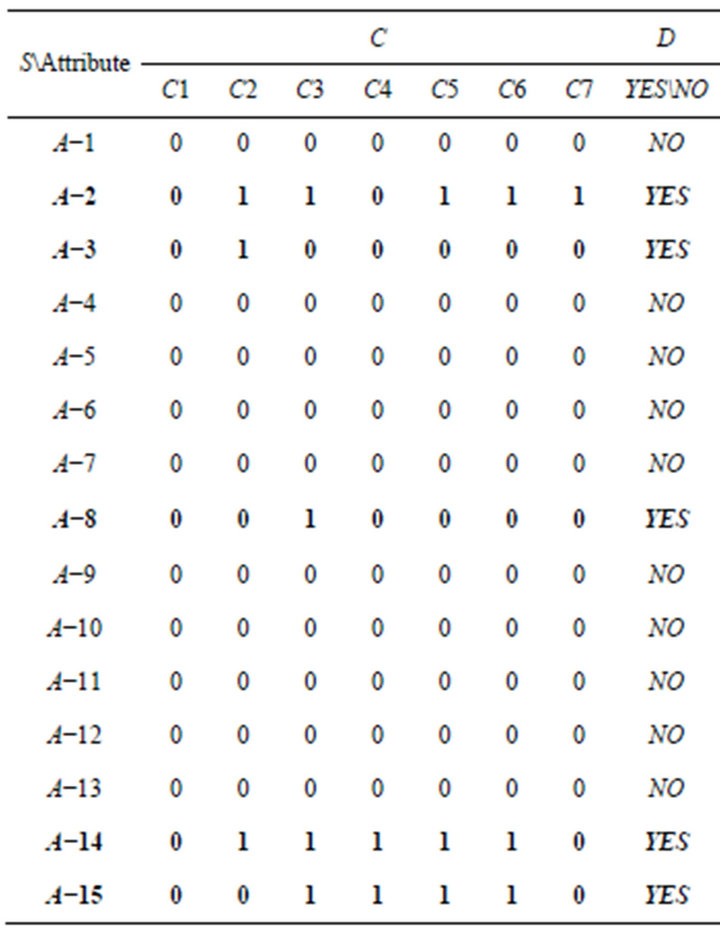
Table 6. SCD table of Class A.
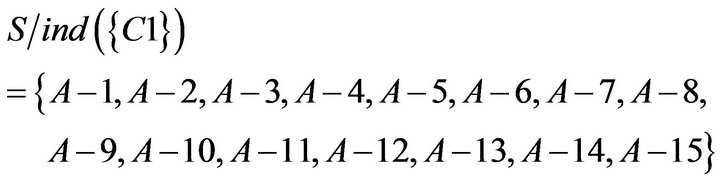
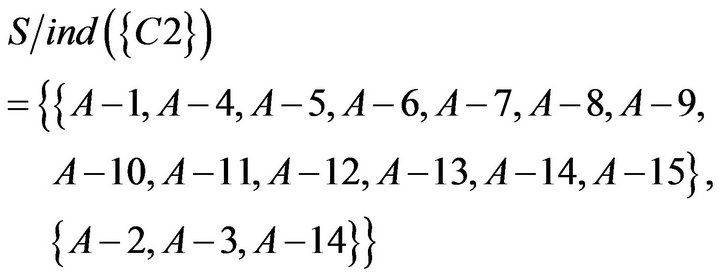
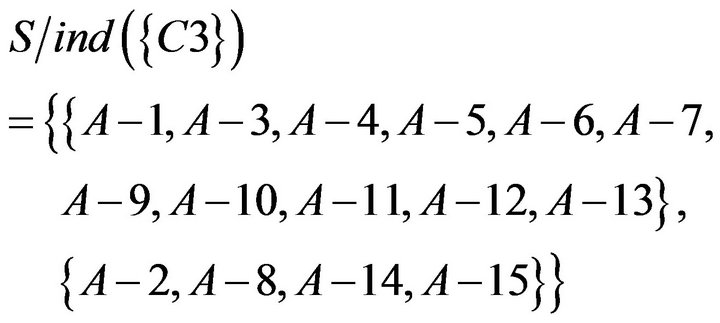
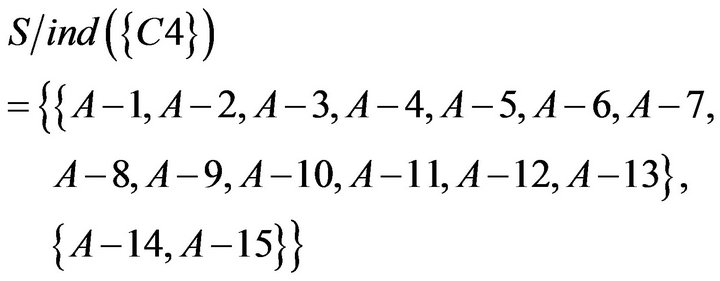
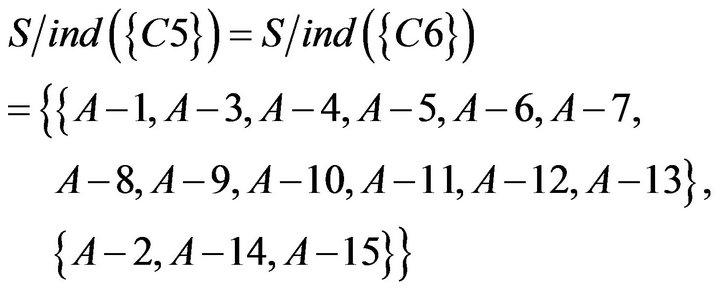
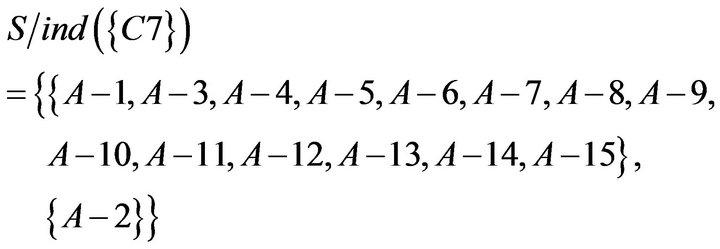
To take the intersection from 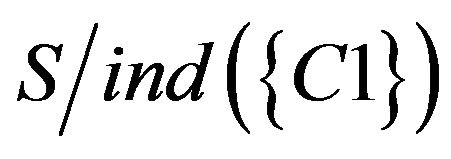 to
to
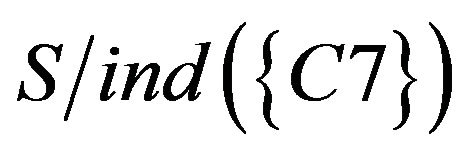 , equivalence relations of S were obtained. It represents students of Class A were classified as six categories based on C1 to C7. The result of the calculation is as follows.
, equivalence relations of S were obtained. It represents students of Class A were classified as six categories based on C1 to C7. The result of the calculation is as follows.

If D is YES, to calculate equivalence relation based on conditional probability and indiscernibility relation can obtain the following results.
If
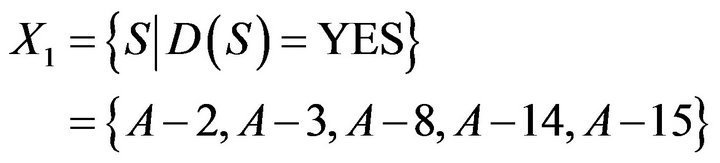
Upper approximation and the lower approximation are
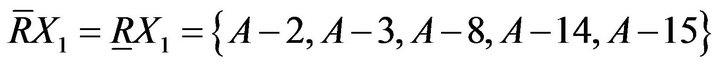
Boundary is 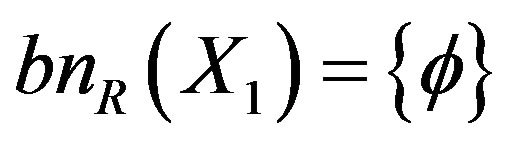
Complement is
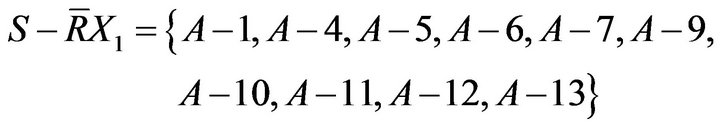
Similarly, if D is NO, to calculate equivalence relation based on conditional probability and indiscernibility relation can obtain the following results.
If
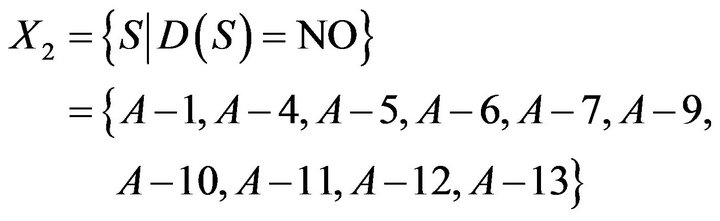
Upper approximation and the lower approximation are
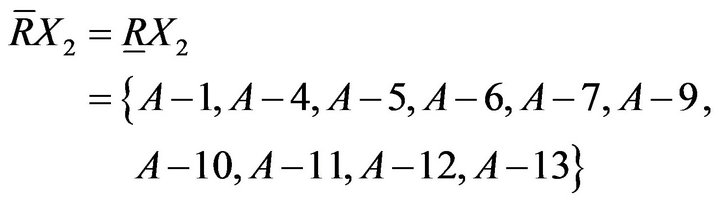
Boundary is 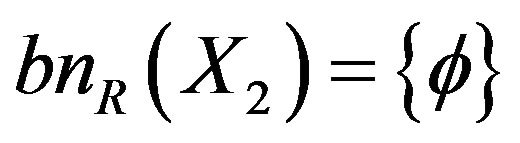
Complement is
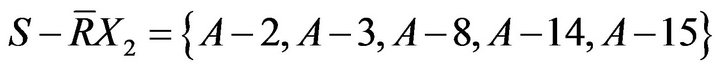
Results of the above calculations were drawn as Figure 3. A−2, A−3, A−8, A−14, and A−15 who need remedial teaching can be determined in Class A; A−1, A−4, A−5, A−6, A−7, A−9, A−10, A−11, A−12, and A−13 who need not remedial teaching can be determined in Class A. In addition, it is no sure whether remedial students in Class A.
4.3. Common Misconceptions of Class A
In order to find core of Class A, researchers do reduce of
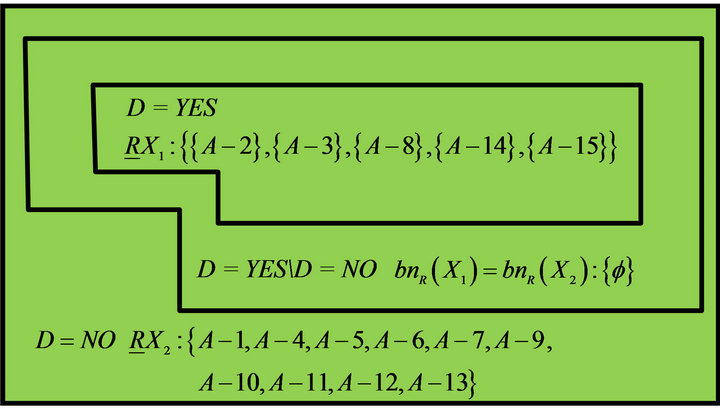
Figure 3. A distribution of students of Class A.
SCD table of Class A according to rough set theory. Core means common misconception of Class A. Three ways were provided as cross-validation while calculating.
First, researchers reduce data of SCD table. According to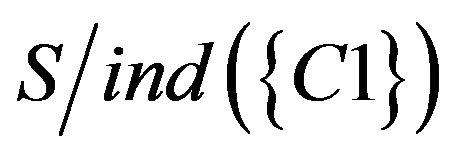 , students could not be divided into two groups and
, students could not be divided into two groups and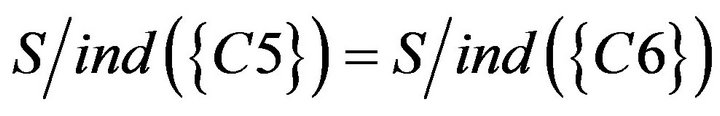 , hence SCD table be simplified (Table 7).
, hence SCD table be simplified (Table 7).
4.3.1. Deleting a Condition Attribute
The first way is to delete a condition attribute in SCD summary table and to check whether there will be new conflicts. The following is the result of deleting and checking of each attribute. Researchers delete C2 and C4 as an example (Tables 8 and 9). After deleting C2, there was a new contradiction between A−1 and A−3. It represented C2 could not be omitted.
1) After deleting C3, there was a new contradiction between A−1 and A−8. It represented C3 could not be omitted.
2) After deleting C4, there was no new contradiction. It represented C4 can be omitted.
3) After deleting C6, there was no new contradiction. It represented C6 can be omitted.
4) After deleting C7, there was no new contradiction. It represented C7 can be omitted.
By the analysis, C2 and C3 could not be omitted. 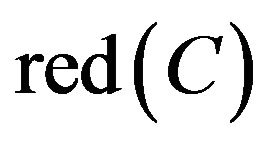 maybe were all sets containing C2 and C3. From SCD summary table of Class A, the student can be classified correctly and remedial teaching decision can be made whether just based on C2 and C3. Hence
maybe were all sets containing C2 and C3. From SCD summary table of Class A, the student can be classified correctly and remedial teaching decision can be made whether just based on C2 and C3. Hence 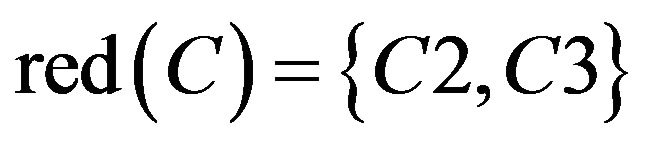 . It means
. It means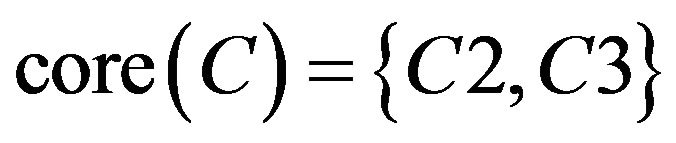 .
.
4.3.2. Using Boolean Logic to Calculate Discernable Matrix
The second way is to use Boolean logic to calculate discernable matrix. First, discernable matrix of Class A must be established. The researchers compared between students through the two-phase way and recorded different condition attributes in the matrix. For example, in Table 7, after comparing student A−1 and A−2, they have
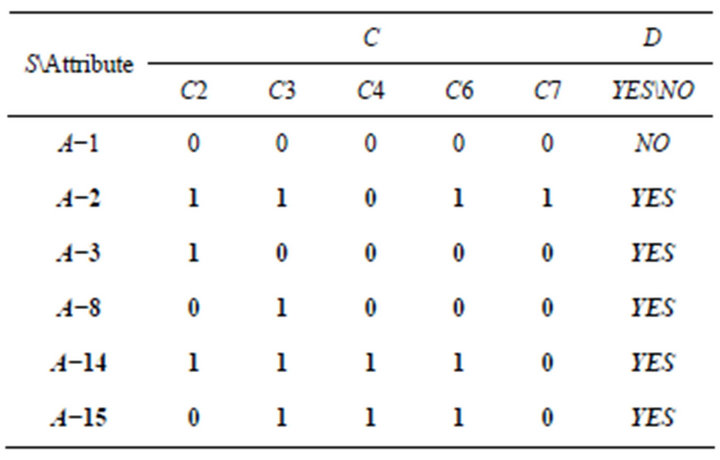
Table 7. SCD summary table of Class A.
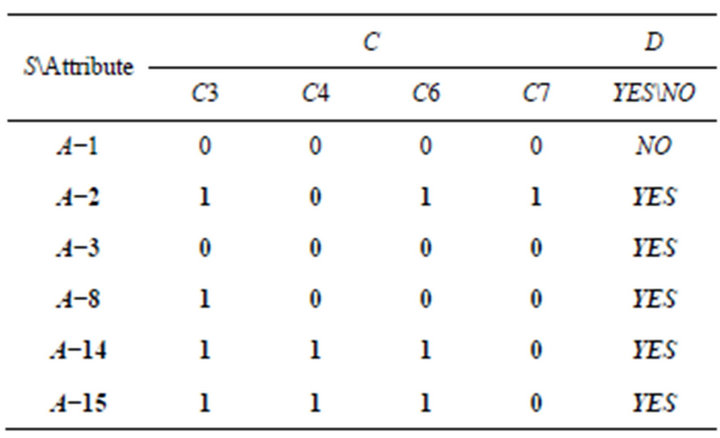
Table 8. Deleting C2.
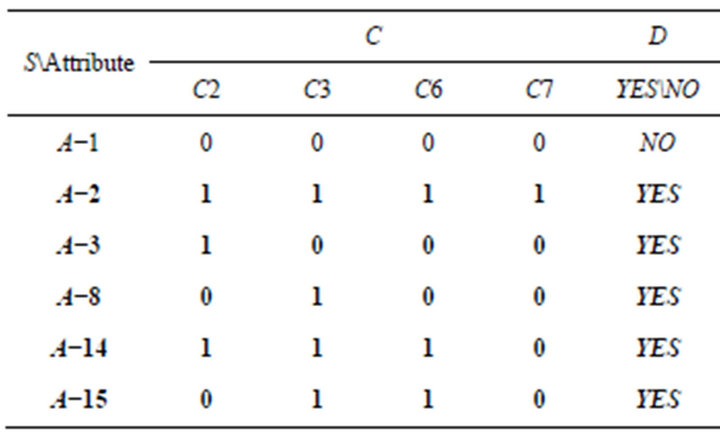
Table 9. Deleting C4.
difference in C2, C3, C6, and C7. And so on, Table 10 can be completed.
By discernable matrix, the union of each student and other students can be calculated. It means that student maybe produce misconception in that concept. And then, to take the intersection of all union in the matrix is possible 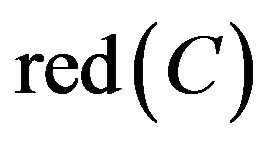 of Class A. Result of the calculation is as follows.
of Class A. Result of the calculation is as follows.
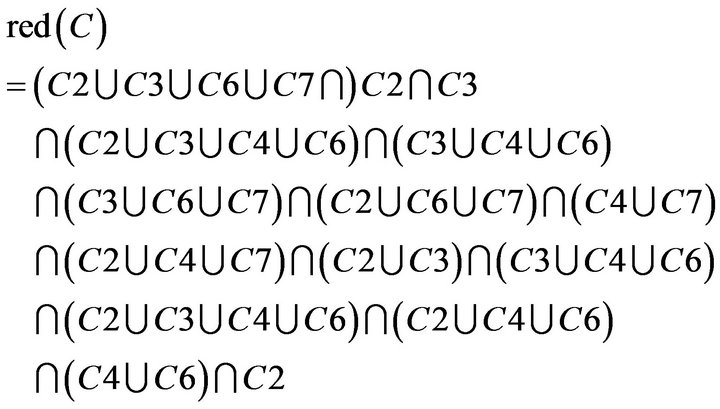
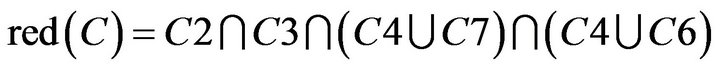
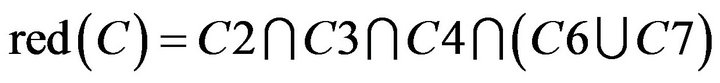
If attribute set is dependent, the smallest set of attribute is . Based on this rule,
. Based on this rule,
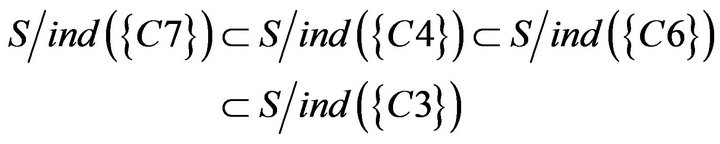
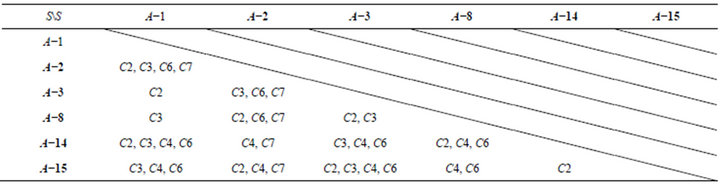
Table 10. Discernable matrix of Class A.
It can be obtained from indiscernibility calculation in SCD summary table of Class A while decision attribute D is YES (The calculation process is as follows.). Hence C4, C6, and C7 were not included in the ,
, 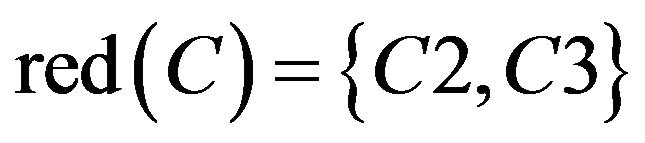 is obtained. It represented
is obtained. It represented 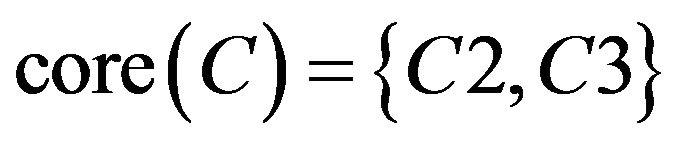 .
.
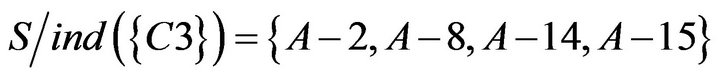
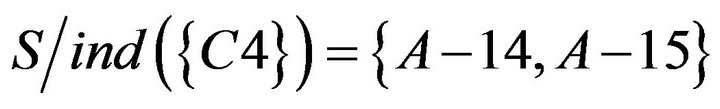
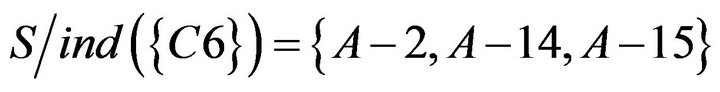
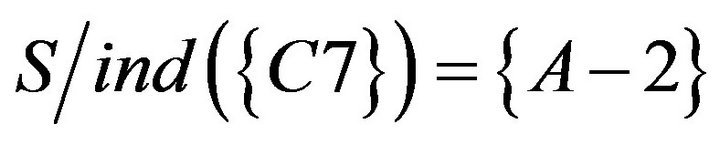
4.3.3. Calculating Significant of Condition Attributes
Using dependent of attribute can decide significant of attribute. The caculation of significant is removing a attribute 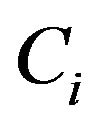 from C and finding the influencing degree of
from C and finding the influencing degree of 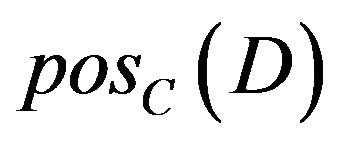 generated by C. Before calculating significant, dependent must be first calculated.
generated by C. Before calculating significant, dependent must be first calculated.
First, 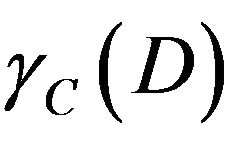 must be calculated. And then
must be calculated. And then 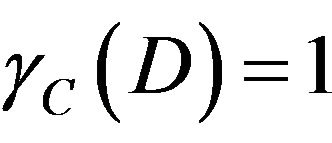 is obtained. The calculation process is as follows.
is obtained. The calculation process is as follows.


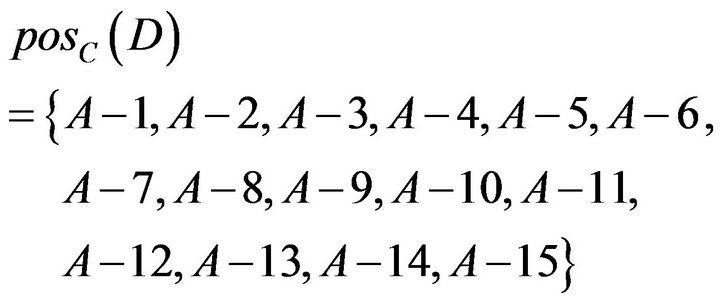
Substituting formula of dependent,
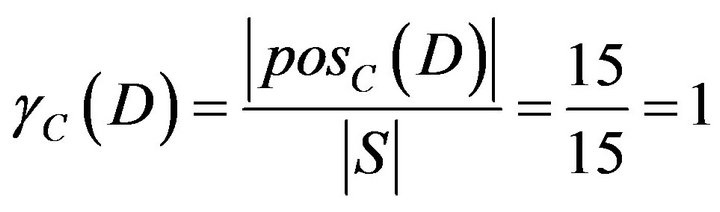
Then calculating 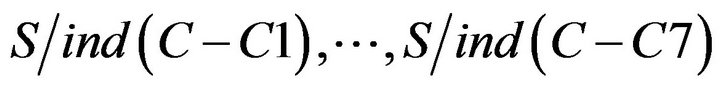 individually. The calculation process are as follows.
individually. The calculation process are as follows.
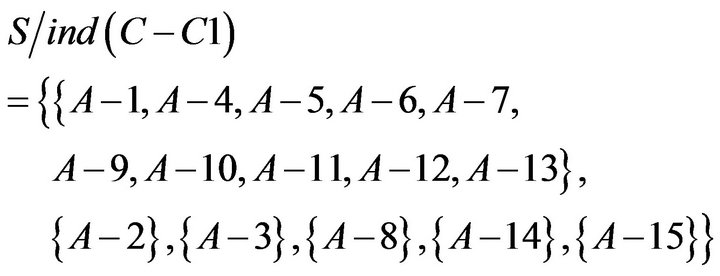

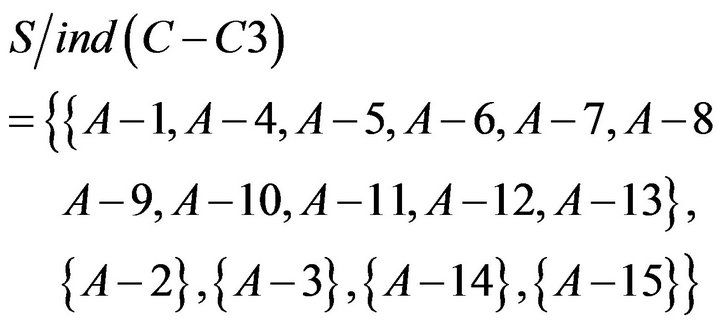

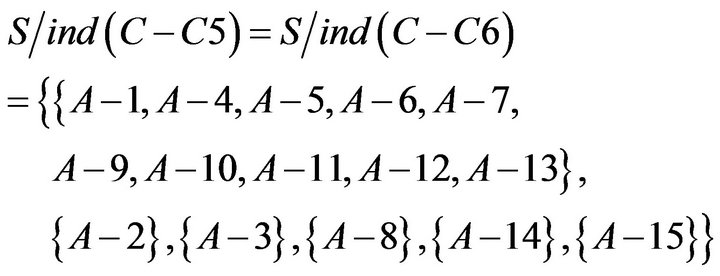

To imitate the calculation of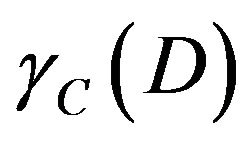 , using of
, using of 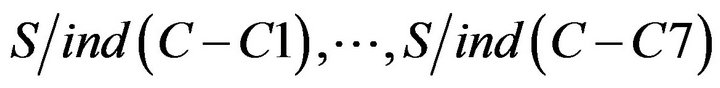 , and
, and 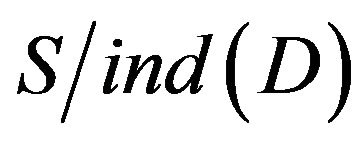 calculate individually
calculate individually 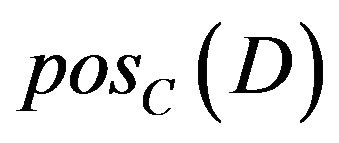 removing a attribute. After that, dependent of each attribute is obtained based on formula of dependent. Dependent of each attribute is shown in Table 11.
removing a attribute. After that, dependent of each attribute is obtained based on formula of dependent. Dependent of each attribute is shown in Table 11.
Finally, the dependent of each attribute substitutes formula of significance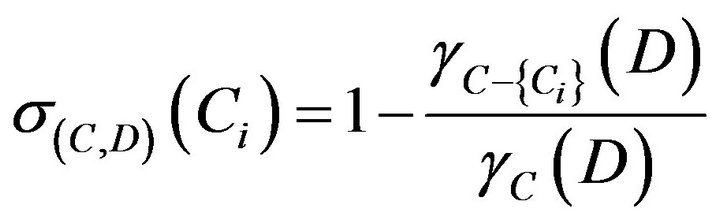 , researchers got sequence of significance that is C1 = C4 = C5 = C6 = C7 < C3 = C2. Significance of each attribute is shown in Table 12.
, researchers got sequence of significance that is C1 = C4 = C5 = C6 = C7 < C3 = C2. Significance of each attribute is shown in Table 12.
From Table 12, C1, C4, C5, C6, and C7 were redundant and could be removed. Researchers got 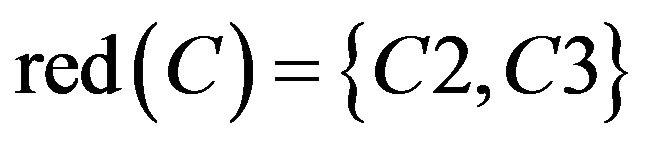 , so
, so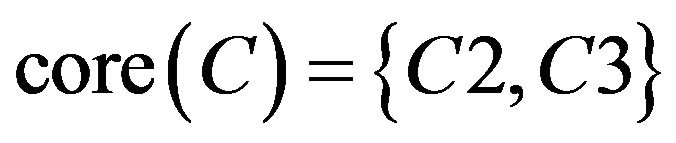 .
.
The calculation of the above three got the same results. It showed students of Class A had common misconception in C2 and C3 in fraction of unit. In Class A, teacher can do remedial teaching directly for two parts “Identify the proper fractions, improper fractions and mixed numbers” and “Improper fraction change integer or mixed numbers”.
4.4. Formulate Remedial Decision-Making of Class A
By the analysis of Class A, it was seen C2 and C3 could not be omitted. In order to do the remedial teaching more efficiently, researchers extracted rules according two condition attributes. In this paper, 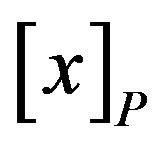 said that sets of students having same attribute value about attribute P.
said that sets of students having same attribute value about attribute P.
About Student A-1, reduct is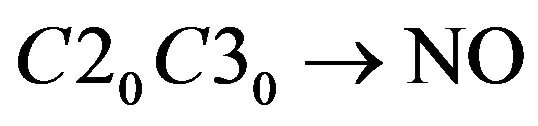 . The calculation is shown as following.
. The calculation is shown as following.
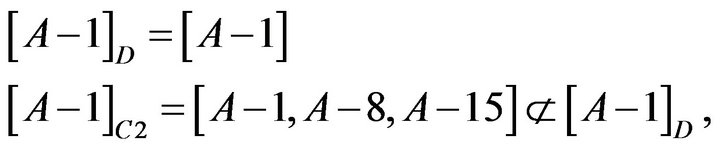
so C3 could not be omitted.
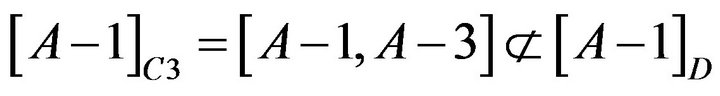 so C2 could not be omitted.
so C2 could not be omitted.
About Student A−2 and A−14, reduct is 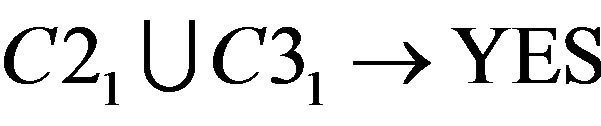 . The calculation is shown as following.
. The calculation is shown as following.

Table 11. Dependent of each attribute.

Table 12. Significant of each attribute.
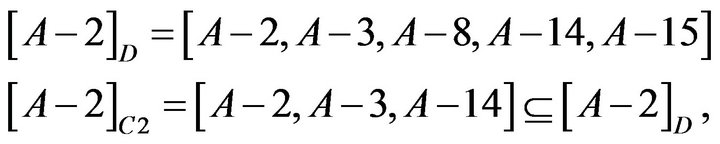
so C3 could be omitted.
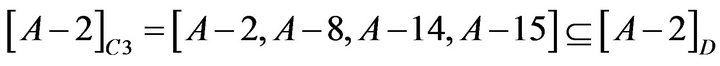 so C2 could be omitted.
so C2 could be omitted.
About Student A−3, reduct is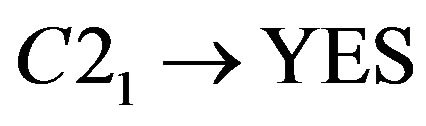 . The calculation is shown as following.
. The calculation is shown as following.
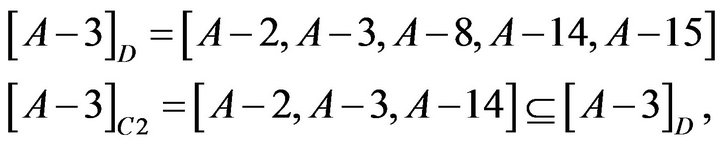
so C3 could be omitted.
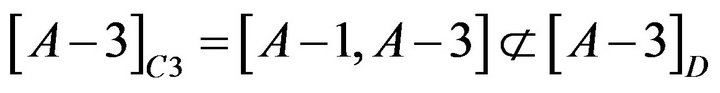 so C2 could not be omitted.
so C2 could not be omitted.
About Student A−8 and A−15, reduct is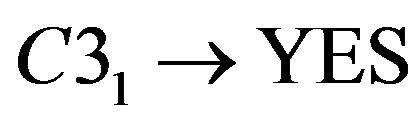 . The calculation is shown as following.
. The calculation is shown as following.
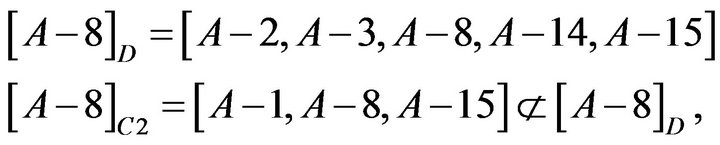
so C3 could not be omitted.
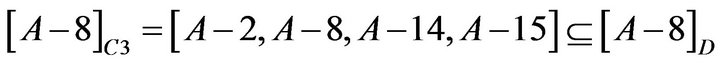 so C2 could be omitted.
so C2 could be omitted.
Take union of reduct of each student above, remedial decision-making of Class A obtained is the following two points:
1) If C2 = 1 or C3 = 1, then student needs remedial teaching.
Based on the ISM structural graph of concepts, C2 is simpler than C3. Therefore, in the remedial process, teachers can adjust remedial instruction according to the students’ level. If students have a lower level, remedy of C2 can be given first; if students have a higher level, remedy of C3 can be given directly.
2) If 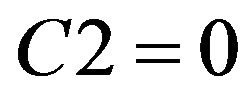 and
and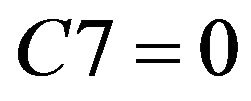 , then student do not need remedial teaching.
, then student do not need remedial teaching.
4.5. SCD Table of Class B
Similarly, students’ responses of Class A are shown in Table 13. “1” represents students answered correctly, “0” represents students answered incorrectly. If students’ score was lower than average score, researchers set for students who need remedial teaching. Researchers judged the students who need remedial teaching are B−1, B−8, and B−9.
Similarly, SCD table was formulated based on IS of rough set theory. As previously mentioned, SC table must first be needed (Table 14) before formulating SCD table. SC table was obtained by combining problemconcept relationship (Table 3) and students’ responses of
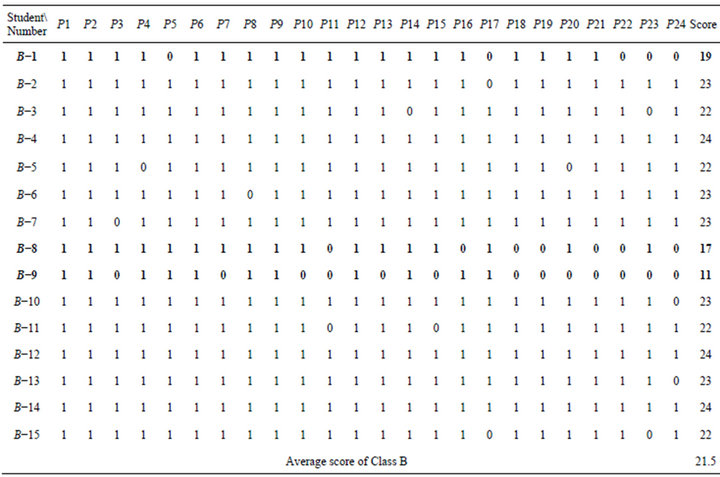
Table 13. Students’ responses of Class B.
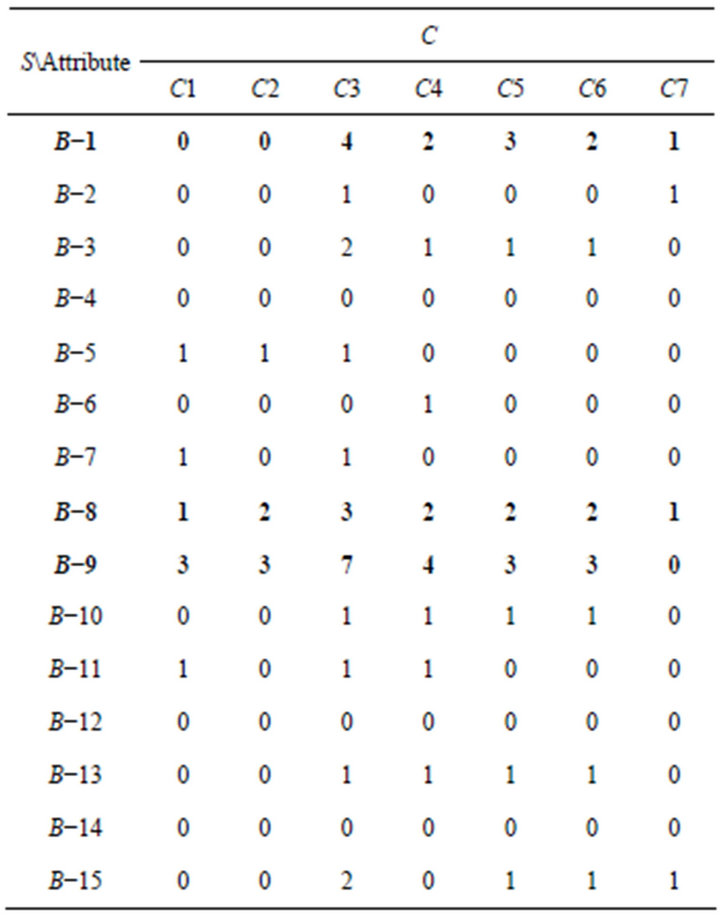
Table 14. SC table of Class B.
Class B (Table 13). It represents the number of incorrect responses in C1 to C7, respectively.
According previous mode, SC table was converted to SCD table (Table 15). In other words, if students answered incorrectly once at a certain concept, then it can be regarded as to get the wrong answer accidentally; if students answered incorrectly more than twice at a certain concept, then it can be regarded as to have the misconception.
Similarly, the indiscernibility relation can be obtained according to the rough set theory. It is equivalence relation of S under the condition attributes. The result of the calculation is as follows.
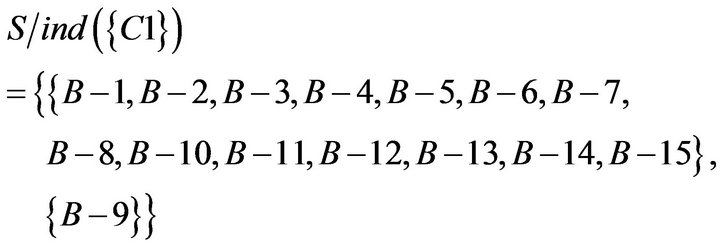
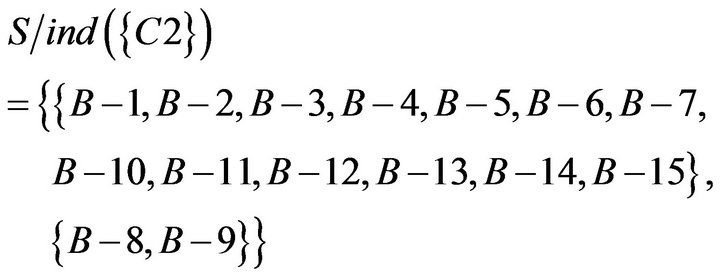
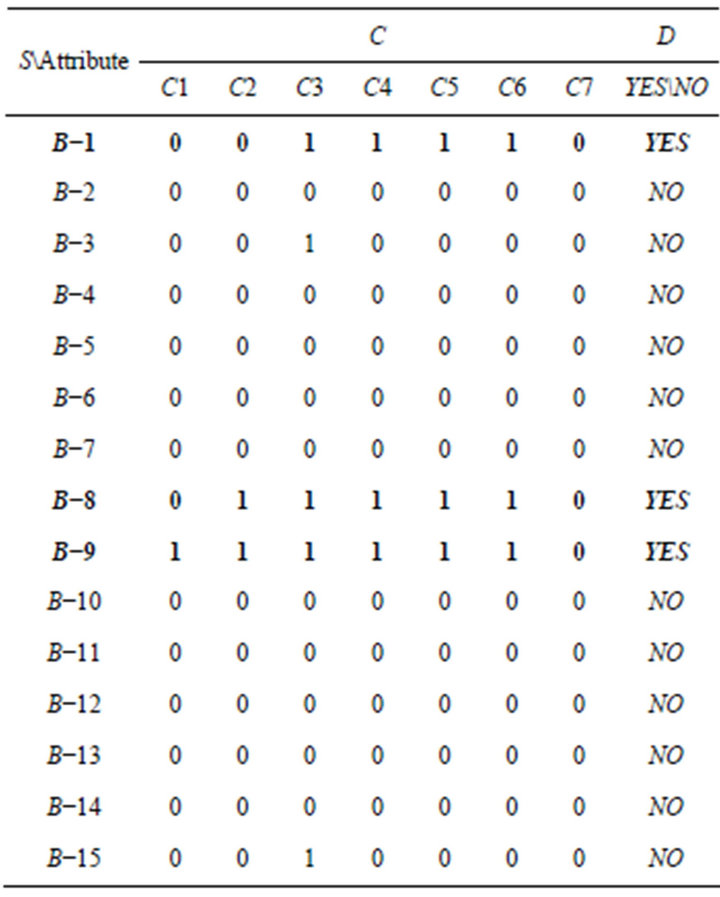
Table 15. SCD table of Class B.
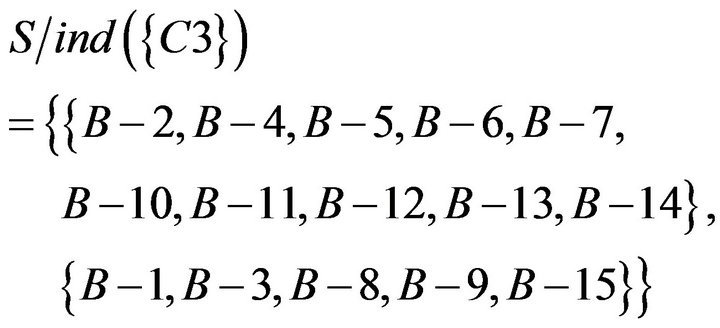
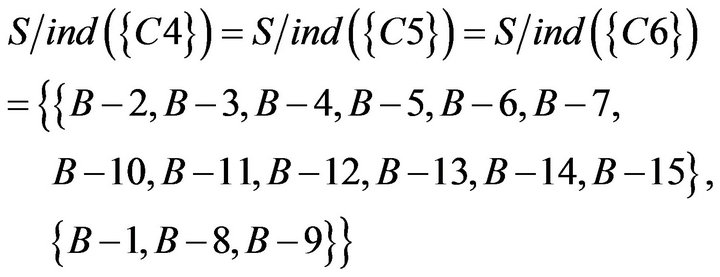
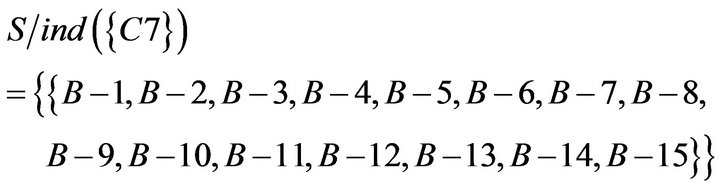
To take the intersection from 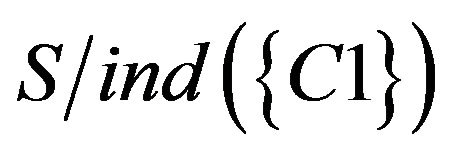 to
to 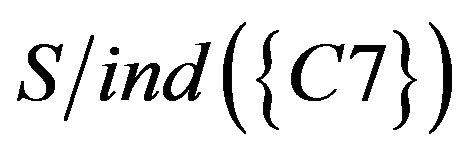 , equivalence relations of S was obtained. It represents students of Class A were classified as five categories based on C1 to C7. The result of the calculation is as follows.
, equivalence relations of S was obtained. It represents students of Class A were classified as five categories based on C1 to C7. The result of the calculation is as follows.

If D is YES, to calculate equivalence relation based on conditional probability and indiscernibility relation can obtain the following results.
If 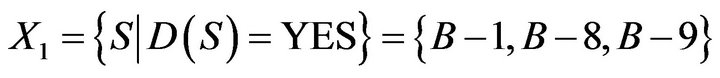
Upper approximation and the lower approximation are 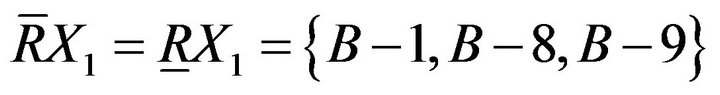
Boundary is 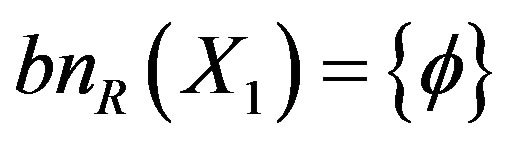
Complement is
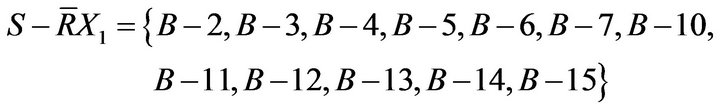
Similarly, if D is NO, to calculate equivalence relation based on conditional probability and indiscernibility relation can obtain the following results.
If
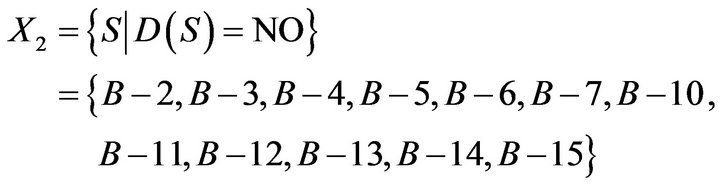
Upper approximation and the lower approximation are
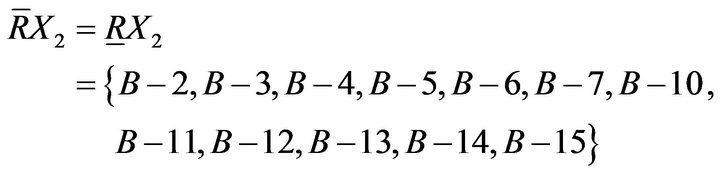
Boundary is 
Complement is
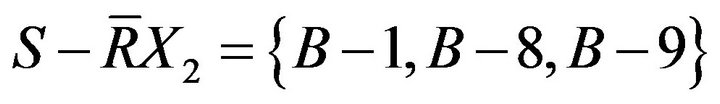
Results of the above calculations were drawn as Figure 4. B−1, B−8, and B−9 who need remedial teaching can be determined in Class B; B−2, B−3, B−4, B−5, B−6, B−7, B−10, B−11, B−12, B−13, B−14, B−15 who need not remedial teaching can be determined in Class B. In addition, it is no sure whether remedial students in Class B.
4.6. Common Misconceptions of Class B
In order to find core of Class B, researchers do reduct of SCD table of Class B again according to rough set theory. Core means common misconception of Class A. Simi-
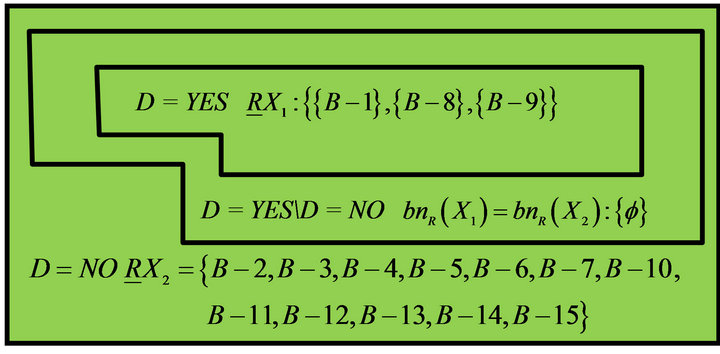
Figure 4. A distribution of students of Class B.
larly, three methods were provided as cross-validation while calculating.
First, researchers reduce data of SCD table. Because 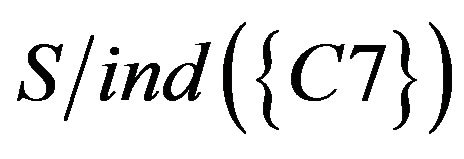 could not divide students into two groups and
could not divide students into two groups and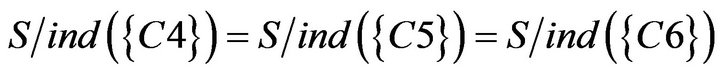 , SCD table be simplified (Table 16).
, SCD table be simplified (Table 16).
4.6.1. Deleting a Condition Attribute
The first way is deleting a condition attribute of SCD summary table and checking whether there will be new conflicts. The steps were the same as Class A. The following results were obtained after calculation.
1) After deleting C1, there was no new contradiction. It represented C1 can be omitted.
2) After deleting C2, there was no new contradiction. It represented C2 can be omitted.
3) After deleting C3, there was no new contradiction. It represented C3 can be omitted.
4) After deleting C6, there was a new contradiction between B−1 and B−3. It represented C6 could not be omitted.
By the analysis, C6 could not be omitted. 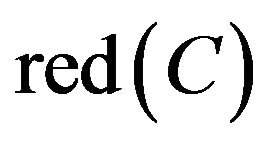 maybe was all sets containing C6. From SCD summary table of Class B, it is easy to correctly classify students and to decide whether remedial teaching just only based on C6.
maybe was all sets containing C6. From SCD summary table of Class B, it is easy to correctly classify students and to decide whether remedial teaching just only based on C6.
Due to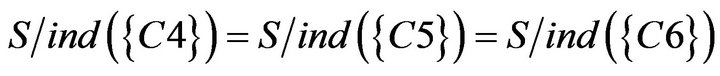 , so
, so 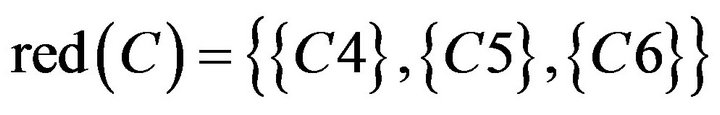 and
and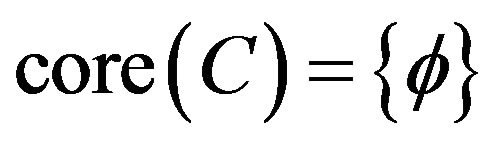 .
.
4.6.2. Using Boolean Logic to Calculate Discernable Matrix
The second way is using Boolean logic to calculate discernable matrix. Similarly, discernable matrix of Class A must be established. The researchers compared between students through the two –phase way and recorded different condition attributes in the matrix. And so on, Table 17 can be completed.
By discernable matrix, the union of each student and other students can be calculated. And then, to take the intersection of all union in the matrix is possible 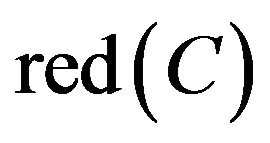 of Class B. Result of the calculation is as follows.
of Class B. Result of the calculation is as follows.
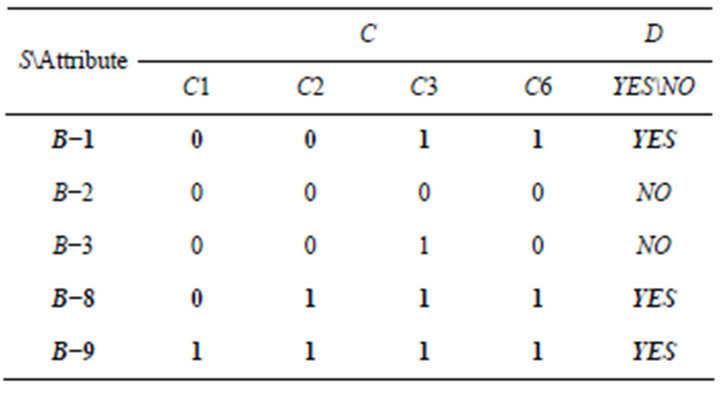
Table 16. SCD summary table of Class B.
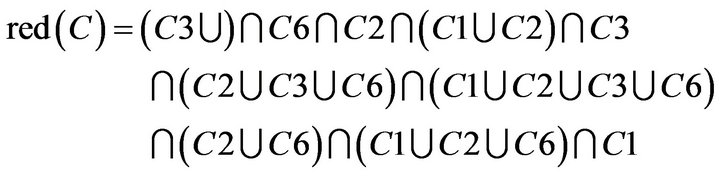
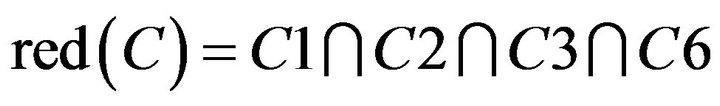
If attribute set is dependent, the smallest set of attribute is . Based on this rule,
. Based on this rule,
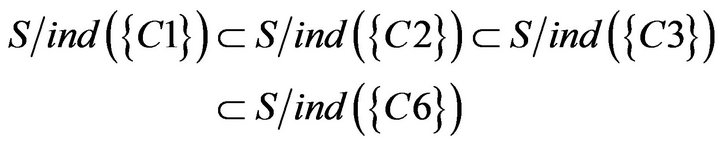
it can be obtained from indiscernibility calculation in SCD summary table of Class B while decision attribute D is YES (The calculation process is as follows.). Hence C1, C2, and C3 were not included in the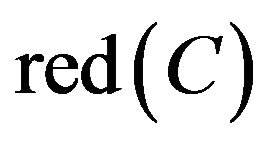 . In addition to
. In addition to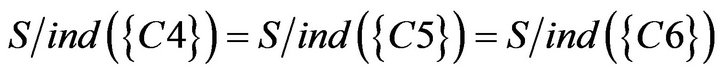 , so
, so  and
and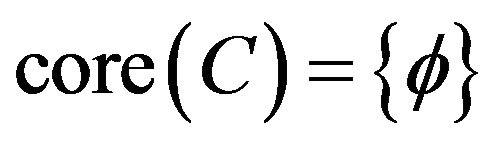 .
.
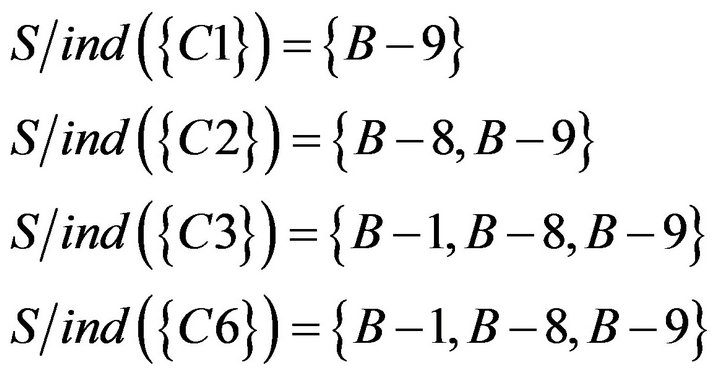
4.6.3. Calculating Significant of Condition Attributes
To imitate the analysis of the Class A, using dependent of attribute can decide significant of attribute. Before calculating significant, dependent must be first calculated. Similarly, 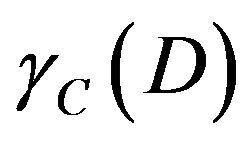 must be calculated. And then
must be calculated. And then 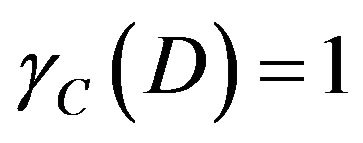 is obtained. The calculation process is as follows.
is obtained. The calculation process is as follows.
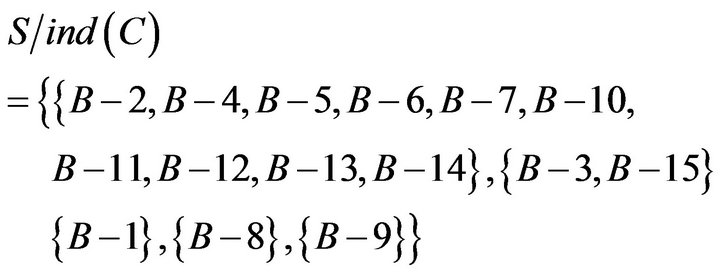
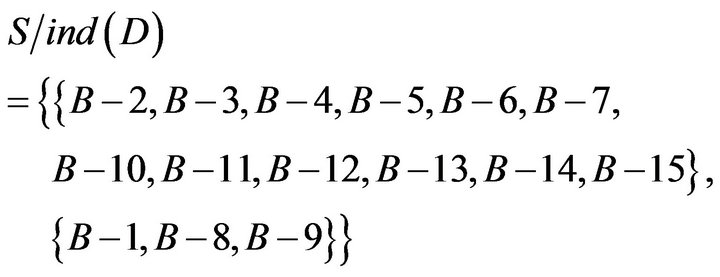
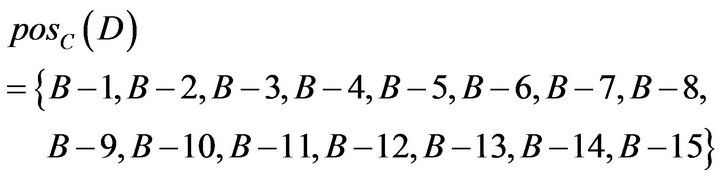
Substituting formula of dependent,
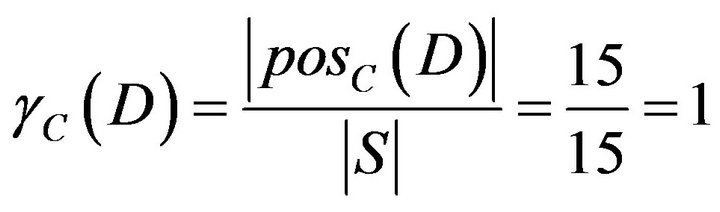

Table 17. Discernable matrix of Class B.
Then calculating
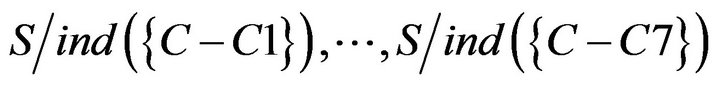
individually. The calculation process are as follows.
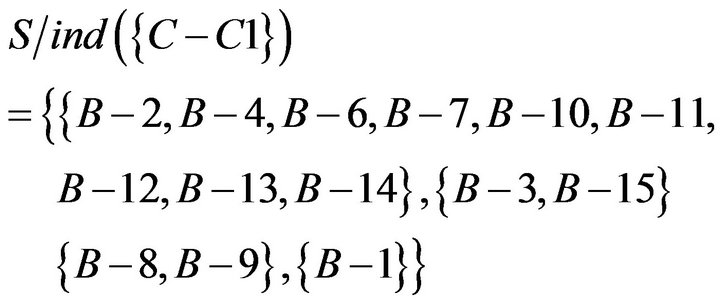
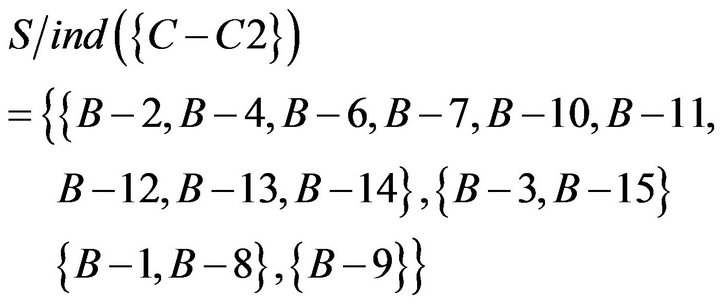
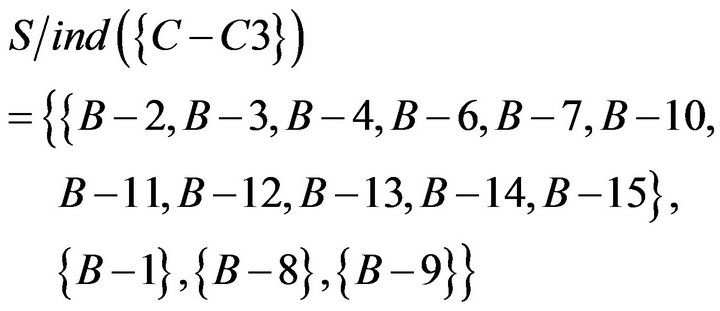
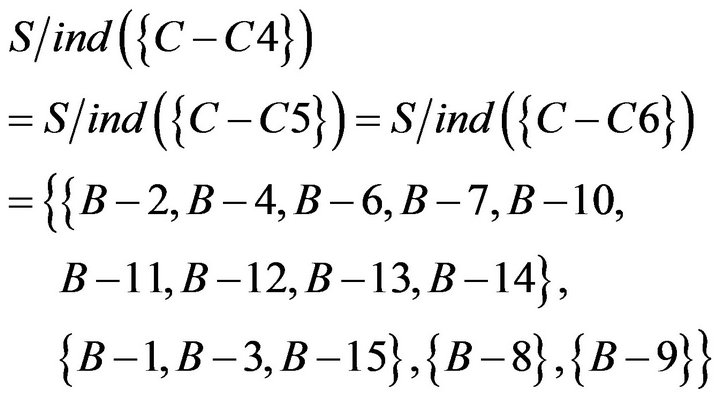
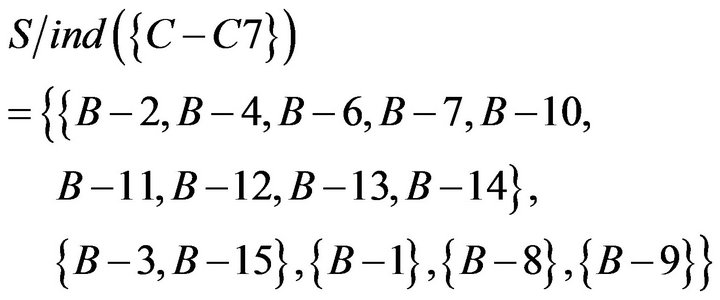
Then, using of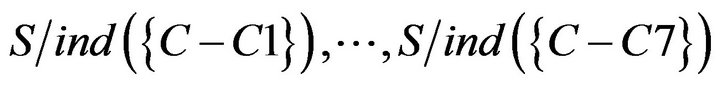 , and
, and 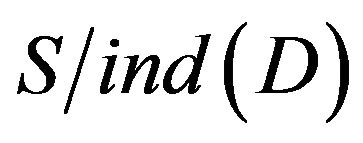 calculate individually
calculate individually 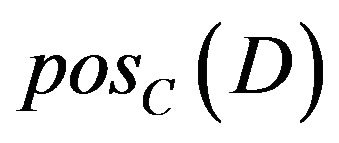 removing a attribute. After that, dependent of each attribute is obtained based on formula of dependent. Dependent of each attribute is shown in Table 18.
removing a attribute. After that, dependent of each attribute is obtained based on formula of dependent. Dependent of each attribute is shown in Table 18.
Finally, the dependent of each attribute substitutes formula of significant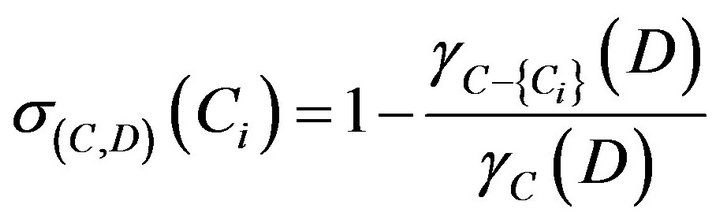 , researchers got sequence of significant that is C1 = C2 = C3 = C7 < C4 = C5 = C6. Significant of each attribute is shown in Table 19.
, researchers got sequence of significant that is C1 = C2 = C3 = C7 < C4 = C5 = C6. Significant of each attribute is shown in Table 19.
From Table 19, C1, C2, C3 and C7 were redundant and could be removed. But because of
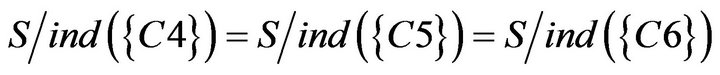 Class B had three reduct
Class B had three reduct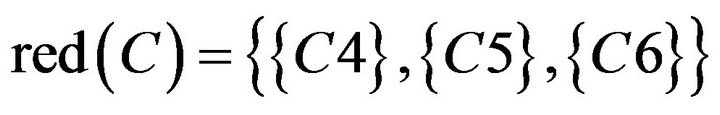 . It means
. It means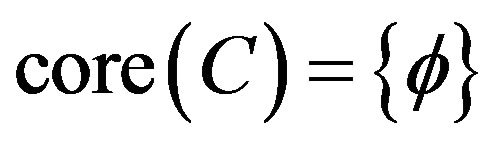 .
.
Three calculation ways above got the same results again. It showed that students of Class B had possible misconception in C4 or C5 or C6 but had not common misconception in fraction of unit. That means, teacher must do remedial teaching directly for three parts “Mixed fraction or integer change improper fraction”, “Solve addition problem of the same denominator fraction”, and “Solve subtraction problem of the same denominator fraction” in Class B.
4.7. Formulate Remedial Decision-Making of Class B
Similarly, by the analysis of Class B, it was seen C4, C5, and C6 could not be omitted. In order to do the remedial teaching more efficiently, researchers extracted rules according three condition attributes. In this paper, 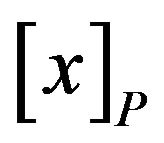 also indicated that sets of students have same attribute value about attribute P.
also indicated that sets of students have same attribute value about attribute P.
About Student B−1, B−8, and B−9, reduct is 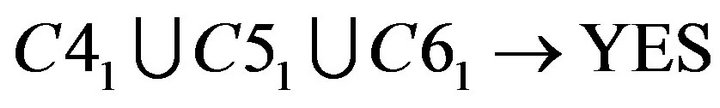 . The calculation is shown as following.
. The calculation is shown as following.
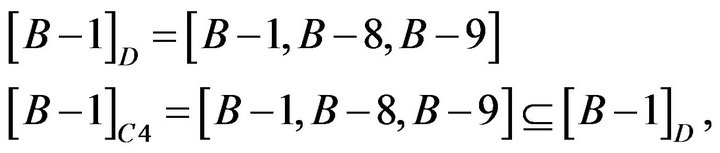
so C5 and C6 could be omitted.
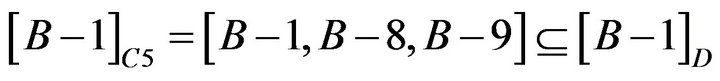 so C4 and C6 could be omitted.
so C4 and C6 could be omitted.
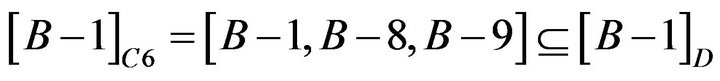 so C4 and C5 could be omitted.
so C4 and C5 could be omitted.
About Student B−2 and B−3, reduct is 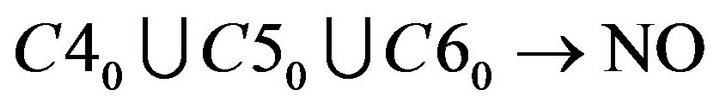 . The calculation is shown as following.
. The calculation is shown as following.
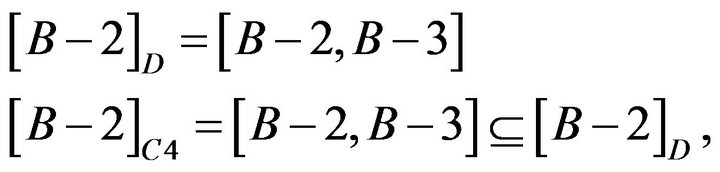
so C5 and C6 could be omitted.
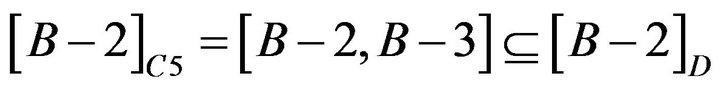 so C4 and C6 could be omitted.
so C4 and C6 could be omitted.
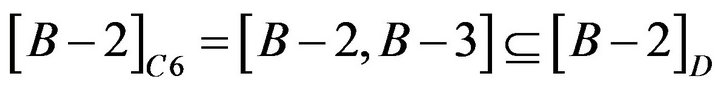 so C4 and C5 could be omitted.
so C4 and C5 could be omitted.
Take union of reduct of each student above, remedial decision-making of Class B obtained is the following two points:
1) If 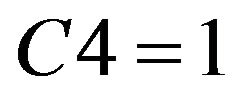 or
or 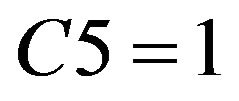 or
or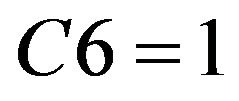 , then student needs remedial teaching.
, then student needs remedial teaching.
Based on the ISM structural graph of concepts, C6 is simpler than C4 and C5. Therefore, in the remedial process, teachers can adjust remedial instruction according to the students’ level. If students have a lower level, remedy of C4 or C5 can be given first; if students have a higher level, remedy of C6 can be given directly.
2) If 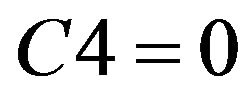 or
or 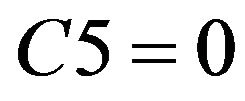 or
or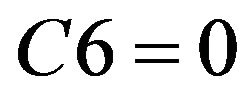 , then student do not need remedial teaching.
, then student do not need remedial teaching.
4.8. Compare Students’ Degree of Two Classes
In accordance with the traditional way, only from the average of two classes, the difference of two classes is insignificant. However, though caculating reduct and core of rough set theory and corresponding remedial decision-making of two classes to the ISM structural graph of concepts, it was found that Class B overall performance is higher than the Class A. By decision content, basic concept of students of Class A is weaker, because that students needed to remedy concepts of the lower layer C2 or C3 (Red part of Figure 5). And basic concept of students of Class B is stronger, because that students needed to remedy concepts of the higher layer C4 or C5 or C6 (Green part of Figure 5).
5. Conclusions
The study analyzed students’ misconception based on rough set theory and combined with interpretive structural model (ISM). The sample of the study was 30 fourth grade students in Central Taiwan, and the exam tools were produced by teachers for math exams. This study firstly suggested three ways to get the common misconception of the students in class, then based on the difference level of each class to make appropriate remedial teaching decision and finally combines with ISM structural graph to compare the degree of two classes in order to provide teachers an effective tool for teaching

Table 18. Dependent of each attribute.

Table 19. Significant of each attribute.

Figure 5. To compare remedial decision-making of two classes.
diagnosis. The results are as follows:
1) The ISM structural graph of concepts has 5 layers in fraction of unit. When teachers teach this unit, there are three distinct teaching sequences, including C1 ® C2 ® C4 ® C6, C1 ® C2 ® C3 ® C5 ® C6 and C1 ® C2 ® C3 ® C5 ® C7.
2) According to information system of rough set theory, this study differed from previous studies which analyzed students’ responses directly. This study establishes SC table based on the combination between problemconcept relationship and students’ responses. It represents the incorrect responses in C1 to C7, respectively. SCD table is a combination of SC table and researchers’ decision-making. The physical significance of the SCD table represents students whether have misconception in concept C1 to C7, as well as teachers whether judge the need for remedial teaching.
3) Based on calculation of indiscernibility relation, a distribution of students is obtained. From the distribution, researchers can determine the students who need remedial teaching, the students who do not need remedial teaching, and the students who could not determine the need for remedial teaching in class. According to results of two classes, it is not sure whether remedial students in two classes.
4) This study provided three methods to get common misconception of the students in class. These three methods are “Deleting a condition attribute”, “Using Boolean logic to calculate discernable matrix”, and “Calculating significance of condition attributes”. Reduct and core will be obtained after calculating, core represents common misconception of students in class.
5) Form caculating reduct and core, it showed students of Class A had common misconception in C2 and C3 in fraction of unit. In Class A, teacher can do remedial teaching directly for two parts “Identify the proper fractions, improper fractions and mixed numbers” and “Improper fraction change integer or mixed numbers”. Therefore, researchers extracted rules based on three attributes in SCD summary table of Class A, remedial decision-making of Class A obtained is the following two points: a) If C2 = 1 or C3 = 1, then student needs remedial teaching. b) If C2 = 0 and C7 = 0, then student do not need remedial teaching.
6) Form caculating reduct and core, it showed students of Class B had possible misconception in C4 or C5 or C6 but had not common misconception in fraction of unit. It means, teacher must do remedial teaching directly for three parts “Mixed fraction or integer change improper fraction”, “Solve addition problem of the same denominator fraction”, and “Solve subtraction problem of the same denominator fraction” in Class B. Therefore, researchers extracted rules based on three attributes in SCD summary table of Class B, remedial decision-making of Class B obtained is the following two points: a) If C4 = 1 or C5 = 1 or C6 = 1, then student needs remedial teaching. b) If C4 = 0 or C5 = 0 or C6 = 0, then student do not need remedial teaching.
7) After corresponding remedial decision-making of two classes with the ISM structural graph of concepts, it was found that Class B overall performance is superior than the Class A. students of Class A needed to remedy concepts of the lower layer C2 or C3 and that of Class B needed to remedy concepts of the higher layer C4 or C5 or C6.
8) Because this analysis method is based on rough set theory, inputted data must be discrete data. If data analyzed are continuous data, it must be discretizationed before analysis.
REFERENCES
- M. H. Chiu, “Reflections and Implications of Research on Conceptual Change,” Chinese Journal of Science Education, Vol. 8, No. 1, 2000, pp. 1-34.
- Ministry of Education, “Grade 1-9 Curriculum Guidelines,” Ministry of Education, Taipei, 2003.
- C. Y. Chen, “The Influence of Teaching Confrontation Style on Key Concepts of Elementary School Students,” Bulletin of Educational Psychology, Vol. 36, No. 4, 2005, pp. 375-393.
- D. C. Yang and S. M. Hung, “The Study of Remedial Instruction on Fraction,” Journal of Educational Research and Development, Vol. 4, No. 2, 2008, pp. 85-118.
- S. C. Wen, “A Study of Integrated Diagnostic Teaching on Fractions for Elementary Fifth-Grade Students,” Chinese Journal of Science Education, Vol. 19, No. 5, 2011, pp. 383-408.
- J. K. Lannin, D. D. Barker and B. E. Townsend, “How Students View the General Nature of Their Errors,” Educational Studies in Mathematics, Vol. 66, No. 1, 2007, pp. 43-59. doi:10.1007/s10649-006-9067-8
- C. C. Lee and S. C. Hu, “An On-Line Assessment and Misconception Correction Tool for Students Learning Fundamental Mathematics,” Journal of National Taichung University: Mathematics, Science & Technology, Vol. 23, No. 1, 2009, pp. 1-28.
- H. K. Tsai, C. C. Chen and H. P. Chang, “A Study of the Relationship between High School Students’ Force Diagrams and Equation Representations in Problem Solving,” Chinese Journal of Science Education, Vol. 18, No. 2, 2010, pp. 155-175.
- J. S. Yeh and C. H. Cheng, “Refining Rough Set for Applying Classification of Appendicitis,” The Journal of Taiwan Association for Medical Informatics, Vol. 14, No. 2, 2005, pp. 1-16.
- H. Wang, M. Zhou and Z. William, “A New Approach to Establish Variable Consistency Dominance—Based Rough Sets Based on Dominance Matrices,” 2012 International Conference on Intelligent System Design and Engineering Application, Sanya, 6-7 January 2012, pp. 48-51. doi:10.1109/ISdea.2012.636
- Y. Ren, T. Xing, Q. Quan and X. Chen, “Attributes Knowledge Reduction and Evaluation Decision of Logistics Centre Location Based on Rough Sets,” 2011 4th International Conference on Intelligent Computation Technology and Automation, Shenzhen, 28-29 March 2011, pp. 67-70. doi:10.1109/ICICTA.2011.24
- K. Zaras, J. C. Marin and B. Boudreau-Trude, “Dominance-Based Rough Set Approach in Selection of Portfolio of Sustainable Development Projects,” American Journal of Operations Research, Vol. 2, No. 4, 2012, pp. 502- 508. doi:10.4236/ajor.2012.24059
- G. Ke, L. Mingwu, F. Yong and Z. Xia, “A Hybrid Model of Rough Sets and Shannon Entropy for Building a Foreign Trade Forecasting System,” 2011 4th International Joint Conference on Computational Sciences and Optimization, Yunnan, 15-19 April 2011, pp. 7-11.
- C. J. Lai and K. L. Wen, “Application of Rough Set Approach to Credit Screening Evaluation,” Journal of Quantitative Management, Vol. 12, No. 1, 2005, pp. 69-78.
- D. Chao and P. Sulin, “The BSC Alarm Management System Based on Rough Set Theory in Mobile Communication,” 2011 7th International Conference on Computational Intelligence and Security, Hainan, 3-4 December 2011, pp. 1557-1561.
- A. N. Hossam, “A Probabilistic Rough Set Approach to Rule Discovery,” International Journal of Advanced Science and Technology, Vol. 30, 2011, pp. 25-34.
- Z. Qu and X. Wang, “Application of Clustering Algorithm and Rough Set in Distance Education,” 2009 1st International Workshop on Education Technology and Computer Science, Wuhan, 7-8 March 2009, pp. 489-493. doi:10.1109/ETCS.2009.117
- A. S. Salama and H. M. Abu-Donia, “Generalizations of Rough Functions in Topological Spaces by Using PreOpen Sets,” Journal of Intelligent Learning Systems and Applications, Vol. 4, No. 2, 2012, pp. 127-134. doi:10.4236/jilsa.2012.42012
- J. Shen, J. Wang and H. Ai, “An improved Artificial Immune Systembased Network Intrusion Detection by Using Rough Set,” Communications and Network, Vol. 4, No. 1, 2012, pp. 41-47. doi:10.4236/cn.2012.41006
- X. Zhang and W. Xu, “Rough Computational Approach to UAR Based on Dominance Matrix in IOIS,” Intelligent Information Management, Vol. 3, No. 4, 2011, pp. 131- 136. doi:10.4236/iim.2011.34016
- K. L. Wen, M. Nagai, T. C. Chang and H. C. Wang, “An Introduction to Rough Set Theory and Application,” Chuan Hwa Publishing Ltd., Taipei, 2008.
- Z. Pawlak, “Rough Sets,” International Journal of Computer and Information Sciences, Vol. 11, No. 5, 1982, pp. 341-356. doi:10.1007/BF01001956
- Z. Pawlak, “Drawing Conclusions from Data—The Rough Set Way,” International Journal of Intelligent Systems, Vol. 16, No. 1, 2001, pp. 3-11. doi:10.1002/1098-111X(200101)16:1<3::AID-INT2>3.0.CO;2-I
- Z. Pawlak, “Rough Set Theory and Its Applications,” Journal of Telecommunications and Information Technology, Vol. 3, 2002, pp. 7-10.
- Z. Pawlak, “Rough Sets and Intelligent Data Analysis,” Information Science, Vol. 147, No. 1-4, 2002, pp. 1-12. doi:10.1016/S0020-0255(02)00197-4
- Y. Y. Yao, “Probabilistic Approaches to Rough Sets,” Expert System, Vol. 20, No. 5,2003, pp. 287-297. doi:10.1111/1468-0394.00253
- Z. Pawlak, “Rough Sets, Decision Algorithms and Bayes’ Theorem,” European Journal of Operational Research, Vol. 136, No. 1, 2002, pp. 181-189. doi:10.1016/S0377-2217(01)00029-7
- Z. Pawlak, “Decision Algorithms and Flow Graphs; a Rough Set Approach,” Journal of Telecommunications and Information Technology, Vol. 3, 2002, pp. 98-101.
- J. N. Warfield, “Societal Systems Planning, Policy and Complexity,” John Wiley & Sons Inc., New York, 1976.
- J. N. Warfield, “Interpretive Structural Modeling (ISM) Group Planning & Problem Solving Methods in Engineering,” John Wiley & Sons Inc., New York, 1982.
- T. W. Sheu, T. L. Chen, J. W. Tzeng, C. P. Tsai and M. Nagai, “Analyzing the Structure of Factors Influencing of Learning Interest in Mathematics,” International Journal of Kansei Information, Vol. 3, No. 2, 2012, pp. 103-120.
- P. Y. Tsai and C. J. Chung, “The Study of Applying Interpretive Structural Modeling in Instructional Structural Design,” Educational Research & Information, Vol. 11, No. 2, 2003, pp. 1-40.
- T. W. Sheu, J. W. Tzeng, C. P. Tsai and T. L. Chen, “Applying Problem-Concept Chart Combined with Structural Analysis to Investigate the Learning Misconcept—Simple Equation with One Variable for Example,” Journal of Grey System, Vol. 15, No. 1, 2012, pp. 55-66.

