Journal of Intelligent Learning Systems and Applications
Vol.07 No.01(2015), Article ID:53451,9 pages
10.4236/jilsa.2015.71001
A Novel Fuzzy Membership Partitioning for Improved Voting in Fault Tolerant System
Akhilesh Pathak, Tarang Agarwal, Anand Mohan
Department of Electronics Engineering, Institute of Technology, Banaras Hindu University, Varanasi, India
Email: pathak.akhilesh@gmail.com, agarwaltarang07@gmail.com, amohan@bhu.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 December 2014; accepted 20 January 2015; published 22 January 2015
ABSTRACT
This paper presents a novel technique for improved voting by adaptively varying the membership boundaries of a fuzzy voter to achieve realistic consensus among inputs of redundant modules of a fault tolerant system. We demonstrate that suggested dynamic membership partitioning minimizes the number of occurrences of incorrect outputs of a voter as compared to the fixed membership partitioning voter implementations. Simulation results for the proposed voter for Triple Modular Redundancy (TMR) fault tolerant system indicate that our algorithm shows better safety and availability performance as compared to the existing one. However, our voter design is general and thus it can be potentially useful for improving safety and availability of critical fault tolerant systems.
Keywords:
Fault Tolerance, Fault Masking, Threshold, Fuzzy Voting, Majority Voting, Safety, Availability

1. Introduction
The fault tolerant systems frequently use hardware redundancy along with a voter to achieve enhanced operational availability of critical mission oriented systems against predefined set of faults. One of the most commonly used methods is based on static redundancy technique incorporating Triple-Modular Redundancy (TMR) [1] [2] where a majority voter determines the correct output value. In digital voting scheme, the determination of exact majority vote is straight forward, however, while finding the majority consensus among the outputs of redundant analog modules of a TMR requires determination of majority considering two closest matching analog outputs of the redundant analog modules. For example, it is very difficult to obtain an exact match between the outputs of replicated analog sensors of a fault tolerant data acquisition system or if the output is generated by diversely implemented software using floating point arithmetic. Therefore the design and performance of analog fault tolerant systems has been deeply focusing on development of improved voter design which can use “hard threshold” or “soft threshold” based voter implementation [3] - [6] . The hard threshold based voter implementations determine the majority consensus among the outputs of redundant analog modules using mid-value, fixed threshold, or history based weighted average threshold [4] [7] - [9] . The mid-value selector voting algorithm [7] generates voted output by considering the mid values of the outputs of redundant modules; fixed threshold voting [8] scheme generates majority output if the absolute difference between the outputs of different pairs of redundant modules is less than a prefixed value. The history based weighted average voting [9] [10] calculates the output with the help of weighted average. Here each redundant module is assigned a weight value depending upon its performance record and the weighted average is used to determine the voted output. Thus this method also uses a hard threshold value to decide the agreeability of individual modules with other modules. Therefore all hard threshold methods use a fixed threshold value for making majority decision which makes the majority voter non-adaptable against larger differences between outputs of redundant modules/changes in their output range. This is because the error in the voted output with respect to the desired output of the voter increases for larger differences between outputs of redundant modules/changes in their output range. Thus hard voting schemes become unsuitable for TMR voter implementation under these situations. Alternatively, soft threshold based fuzzy voters [3] can be used to tackle the voter’s accuracy problem due to large output and range variations of the redundant voter modules. These voters convert the mod value of relative differences into fuzzy membership and apply fuzzy rules to generate consensus output from the voter. The fuzzy voters perform better than hard threshold voting schemes having fixed threshold but it proves ineffective beyond moderate differences between outputs of redundant modules. In addition to this, the fuzzy voters do not perform satisfactorily in offering constant error in the voted output for multi band agreement tolerances as needed in flight control computers [11] - [13] .
This paper presents an improved design of fuzzy voter based on adaptive fuzzy membership boundaries of the mod values of the differences between analog outputs of the redundant modules and its range. The availability and safety performance of the proposed voter design is evaluated through MATLAB simulation studies and it is shown that our voter design is potentially useful for handling larger mod differences (>1.5) between the outputs of redundant analog channels. It offers 20% error reduction in the voted output as compared to the fuzzy voter suggested by Shabgahi [3] , 12% higher availability, and 18% improvement in safety. Section 2 describes the basic concepts of the fuzzy voter [3] [14] followed by the proposed design of the voter in Section 3. Section 4 presents MATLAB simulation of the proposed fuzzy voter along with different varied differences between outputs of the redundant modules. The simulation results indicating the error minimization in the voted output along with achievable improvements in availability and safety are also discussed in this section. Section 5 contains the conclusion indicating the major outcome and its benefit in design of fault tolerant avionic systems.
2. Fuzzy Voter Concepts
Fuzzy voters [3] are used to eliminate the limitations of fixed threshold TMR voting logic discussed in Section 1. Figure 1 shows the block schematic of a 3-input  fuzzy voter which contains fuzzifier and defuzzyfier to generate the weights for calculating a weighted average output
fuzzy voter which contains fuzzifier and defuzzyfier to generate the weights for calculating a weighted average output 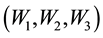 from the voter.
from the voter.
The fuzzification is achieved by transforming the numerical differences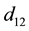 ,
, 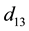 , and
, and 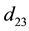 between the input pairs
between the input pairs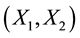 ,
, 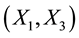 , and
, and 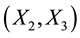 into fuzzy membership for each pair
into fuzzy membership for each pair  having numerical difference
having numerical difference 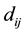 such that the fuzzy membership follows a triangular functions [3] as shown in Figure 2. Here, the fuzzy difference variable are represented by a set of membership grades
such that the fuzzy membership follows a triangular functions [3] as shown in Figure 2. Here, the fuzzy difference variable are represented by a set of membership grades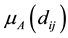 , where A: {small, medium, large}.
, where A: {small, medium, large}.
Referring Figure 2, the variables and fuzzy membership functions considering the difference between two voter inputs:  can be defined as below:
can be defined as below:
Symmetry: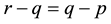 , where p, q and r are real numbers and
, where p, q and r are real numbers and 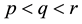
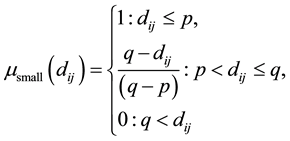 (1)
(1)
Figure 1. Block schematic of 3-input fuzzy voter.
Figure 2. Representation of membership grades


Equations (1)-(3) describe the functions for small, medium, and large membership grades respectively.
2.1. Defining the Fuzzy Agreeability of Each Input
For each of the input

2.2. Fuzzy Rules to Find out Agreeability of Each Input
Table 1 shows the rule matrix to find out agreeability of each input with other inputs.
Where 





Table 1. Rule matrix used for fuzzy input variables.
Figure 3. Representation of output fuzzy variable membership grades
2.3. Calculating the Voted Voter Output
The fuzzified value of agreeability is converted in to numerical value of weight 
3. Proposed Fuzzy Voter
The existing fuzzy voter considered fixed fuzzy partitioning parameter i.e. the values of parameter p, q and r are fixed. While the values of parameters p, q and r will not be optimum for all values of input ranges for example for very small magnitude of inputs, the value of p, q and r should be less as the accuracy tolerance between generated output and correct output will be less and for larger magnitude of input, the values of p, q and r could be high. so a modified fuzzy voting unit has been proposed in this paper where the value of output from voting unit is calculated with the same method as in the above fuzzy voting unit but the values of fuzzy partitioning will not be fixed, they will change themselves according to the input values and the numerical values of differences between them. The value of p is chosen considering the maximum and minimum of the input values and the minimum of the distance between input pairs. Figure 4 shows the block schematic of improved fuzzy voter:
The value of parameter p is calculated on the basis of fuzzy classification and values of q and r will be multiple of p, the fuzzy classification of p is achieved with three parameters as a, b, and c and their functions have been defined for module output ranging from {0 - 25}, while the partitioning of these parameters can be changed according to the application and the ranges of inputs.
The fuzzy membership a (Figure 5) which is defined as
The fuzzy membership b (Figure 6) which is defined as
The fuzzy membership c (Figure 7) which is defined as
The fuzzy membership function for output variable p (Figure 8) is categorized in four memberships as {small, medium, high, vhigh}.
The fuzzy membership for output p is:
The value of p is categorized in four memberships values {small, medium, high, vhigh} which are governed by the fuzzy rules formulated as under.
1) if (c is small) and (b is small) then (p is small);
Figure 4. Block schematic of 3-input improved fuzzy voter.
Figure 5. Definition of membership functions of variable a.
Figure 6. Definition of membership functions of variable b.
Figure 7. Definition of membership functions of variable c.
Figure 8. Definition of membership functions of output p.
2) if (c is small) and (b is medium) then (p is medium);
3) if (c is small) and (b is large) then (p is medium);
4) if (a is small) and (c is medium) then (p is medium);
5) if (a is medium) and (b is small) and (c is medium) then (p is high);
6) if (a is medium) and (b is medium) and (c is medium) then (p is medium);
7) if (a is medium) and (b is large) and (c is medium) then (p is medium);
8) if (a is large) and (b is small) and (c is medium) then (p is high);
9) if (a is large) and (b is medium) and (c is medium) then (p is medium);
10) if (a is large) and (b is large) and (c is medium) then (p is high);
11) if (a is small) and (c is large) then (p is medium);
12) if (a is medium) and(b is small) and (c is large) then (p is medium);
13) if (a is medium) and(b is medium) and (c is large) then (p is medium);
14) if (a is medium) and (b is large) and (c is large) then (p is high);
15) if (a is large) and (c is large) then (p is vhigh).
Rule No. 1 to 3 deals with cases where difference between at least two inputs are small it implies that there is a reasonably high degree of agreeability therefore p is categorized as either small or medium depending upon maximum value of inputs. Rules 4 to 10 define conditions when minimum of differences in inputs is in medium range, here the value of p will be either medium or high depending on the distance between minimum and maximum of the inputs. Similarly rules 11 to 15 have been formulated to deal with poor agreeability between set of inputs i.e. when minimum of differences in inputs is in large range, here the value of p will be either medium, high or vhigh depending on the distance between minimum and maximum of the inputs.
Based on the above parameters and the set of fuzzy rules the value of p will be in range {0.2 - 0.9} and the values of q and r are arrived at as multiples of p i.e. 

The defuzzification method used to calculate value of p is centroid method.
The output y will be calculated in same way as proposed in previous section but now the values of fuzzy partitioning parameters will not be fixed, they will adapt themselves according to inputs values and their differences.
4. Simulation Experiments
4.1. Experiment 1
The first experiment proves that the voted output generated by improved fuzzy voter is more closed to the actual output as compared to fuzzy voter proposed in [3] . Table 2 shows the output of the improved fuzzy voter and reference fuzzy voter [3] for 10 independent cases where the correct output value is 1 and where all the channels are subjected to errors.
4.2. Experiment 2
To compare the performance of improved fuzzy voter with reference fuzzy voter, the parameters used for simulation experiments are listed below:
The input to modules: sinusoidal function 
Table 2. Comparison of results of both the voters.
The errors has been injected in any two modules using a random generator with uniform distribution with amplitude from the interval {−emax +emax}.
Here the value of correct input will range from (0 - 20), the accuracy threshold value (ATV) will be different for different magnitudes of inputs, ATV is the max error allowed from the true output value and it is defined as:
if
else if
else if
where 
Reference fuzzy voter has been designed by taking following values:
The improved fuzzy voter uses same values for u, v, and w i.e.
The voter output can be interpreted as correct, incorrect, or benign output. For each voter, the results of 104 voting cycles are performed. And 


The availability A will be defined as:
And safety S will be defined as:

Simulation Results of Experiment 2:
Figure 9(a) and Figure 9(b) show availability and safety plots respectively where one module is fault free and the faults in two modules have been injected randomly by uniform distribution in range {−emax +emax}. The x-axis is the max error injected in the two modules. Results show that our improved fuzzy voter gives 1% - 8% better availability and 1% - 5% better safety as compared to reference fuzzy voter proposed in [3] .
Figure 10(a) and Figure 10(b) show availability and safety plots respectively when one module is fault free, the error in second has been injected randomly by uniform distribution in range {−emax +emax}. The x-axis is the max error injected in the second module. The third module is more faulty in which error has been injected randomly by uniform distribution in range {−5 +5}. Results show that our improved fuzzy voter gives 1% - 12% better availability and 1% - 18% better safety as compared to reference fuzzy voter proposed in [3] .
5. Conclusion
A fuzzy voter proposed by Shabgahi has been studied for its performance in various conditions. The fuzzy voter


Figure 9. (a) Performance comparison of voters in terms of availability when two modules are equally faulty; (b) Performance comparison of voters in terms of safety when two modules are equally faulty.
falls short of expectations with respect to safety and availability parameters for larger errors, so here we proposed an improvement to the fuzzy voter. The proposed modification considers dynamic partitioning parameter variation in a given range which can be chosen depending on the system requirements. The study shows that the


Figure 10. (a) Performance comparison of voters in terms of availability when one module is less faulty and the other is more faulty; (b) Performance comparison of voters in terms of safety when one module is less faulty and the other is more faulty.
proposed improved fuzzy voter yields better results as compared to the existing voter. This scheme can be adapted to different operational conditions of the system by varying the accuracy requirements and fuzzy partitioning parameters. The future work envisaged in this area is to integrate various other techniques like history based module selection, TMR with spare etc. into the fuzzy voters to further improve the availability and reliability of the systems.
References
- Von Neumann, J. (1956) Probabilistic Logics and Synthesis of Reliable Organisms from Unreliable Components. In: Shannon, C.E. and McCarthy, J., Eds., Automata Studies, in Annals of Mathematical Studies, No. 34, Princeton University Press, Princeton, 43-98.
- Ross, T.J. (2008) Fuzzy Logic with Engineering Applications. Wiley Student Edition.
- Latif-Shabgahi, G. and Hirst, A.J. (2005) A Fuzzy Voting Scheme for Hardware and Software Fault Tolerant Systems. Fuzzy Sets and Systems, 150, 579-598. http://dx.doi.org/10.1016/j.fss.2004.02.014
- Agarwal, T., Pathak, A. and Mohan, A. (2011) A Novel Hybrid Voter Using Genetic Algorithm and Performance History. International Journal of Artificial Intelligence and Expert Systems, 2, 117-125.
- Manic, M. and Frincke, D. (2001) Towards the Fault Tolerant Software: Fuzzy Extension of Crisp Equivalence Voters. IECON’01: The 27th Annual Conference of the IEEE Industrial Electronics Society.
- Latif-Shabgahi, G., Tokhi, M.O. and Taghvaei, M. (2005) Voting with Dynamic Threshold Values for Real-Time Fault Tolerant Control Systems.
- Krstic, M.D., Stojcev, M.K., Djordjevic, G.Lj. and Andrejic, I.D. (2005) A Mid-Value Select Voter. Microelectronics Reliability, 45, 733-738. http://dx.doi.org/10.1016/j.microrel.2004.07.006
- Parhami, B. (1994) Voting Algorithms. IEEE Transactions on Reliability, 43, 617-629. http://dx.doi.org/10.1109/24.370218
- Lala, P.K. (1984) Fault Tolerant and Fault Testable Hardware Design. BS Publications.
- Latif-Shabgahi, G., Bass, J.M. and Bennett, S. (2001) History-Based Weighted Average Voter: A Novel Software Voting Algorithm for Fault-Tolerant Computer Systems. 9th Workshop Parallel and Distributed Processing, 402-409.
- Parhami, B. (1992) Optimal Algorithm for Exact, Inexact and Approval Voting. FTCS-22: 22nd International Symposium on Fault Tolerant Computing, Boston, July 1992, 404-411.
- Hopgood, A. (2001) Intelligent Systems for Engineers and Scientists. 2nd Edition, CRC Press, Boca Raton.
- Minichino, M., Ciancamerla, E., Chiaradonna, S. and Bondavalli, A. (2000) An Experience of Dependability Assessment of a Typical Industrial Safety-Critical PLC. http://bonda.cnuce.cnr.it/Documentation/Reports/Doc2000/PDF00/C48.pdf
- Nurmi, H. (2003) A Fuzzy Solution to a Majority Voting Game. Fuzzy Sets and Systems, 2, 187-198.
















