Wireless Sensor Network
Vol.08 No.06(2016), Article ID:67241,8 pages
10.4236/wsn.2016.86009
Generalized Electromagnetic Pollution Monitoring Using WSN
Sara Nouh1, Nada Elgaml2, Nora Ali2, Ahmed Khattab2, Ramez Daoud1, Hassanein Amer1
1Electronics & Communications Engineering Department, American University in Cairo, Cairo, Egypt
2Electronics & Communications Engineering Department, Cairo University, Giza, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 March 2016; accepted 6 June 2016; published 9 June 2016
ABSTRACT
Wireless Sensor Networks (WSN) have recently become one of the major research areas in the wireless communication field and are implemented in a variety of applications. One of these applications that will be tackled in this paper is monitoring electromagnetic (EM) pollution that is mostly caused by a variety of wireless devices that we use in our daily life. This paper presents a generic algorithm that uses a WSN to monitor EM hazardous emissions and reports variation caused by four violators. Additionally it calculates the network’s lifetime and simultaneously studies the effect of random parameters and their distributions on the network. Finally the different combinations of the random parameters and the altered distributions are compared together to achieve the combination that can prolong the network’s lifetime.
Keywords:
WSN, EM Pollution, Monitoring, Random Distribution

1. Introduction
Recently Wireless Sensor Networks have been an attractive field, since they could be implemented in a huge number of applications. Different examples of these applications could be alarm systems, office and home automation, traffic control, civil infrastructure, environmental monitoring, personal health and many others [1] . Nowadays electromagnetic (EM) radiations are increasing tremendously due to the wide expansion of smartphones and wireless devices [2] . Moreover, people are exposed to other EM radiations due to the existence of several wireless networks, such as Global System for Mobile communications (GSM), Universal Mobile Telecommunications System (UMTS) and Wi-Fi, and the existence of FM Radio, TV, power systems and transmission powers [3] . Nevertheless, there is an increased demand of building wireless infrastructures, in order to provide higher data bandwidth and better coverage [4] . Therefore, concerns have risen due to the fact that these radiations could affect the personal health and hence, the need for monitoring these radiations has grown [4] . Possible hazardous effects of EM pollution could be cancer, leukemia and neuropsychological disorders [5] .
This paper proposes a WSN-based framework to monitor these emissions and report any security violation; still the aim of this paper is not only to monitor the excessive electromagnetic waves, but also to prolong the WSN network’s lifetime. The framework presented here is more general and more flexible than the one presented in [6] , several parameters are modeled as random variables instead of constants. Furthermore, several case studies are analyzed to illustrate the use of the generalized framework.
The rest of the paper is organized as follows. Section 2 presents some background information regarding the system presented in [6] . Section 3 introduces the proposed framework and the main three parameters that affect the network’s lifetime. Section 4 examines the use of different random distributions for the three main parameters. It is worth mentioning that the scope of this paper is only limited to measuring the EM pollution. Finally, Section 5 concludes the paper.
2. Relevant Background and Related Work
As previously mentioned, there is always the desire of increasing the wireless infrastructure due to the need of a better coverage and higher bandwidth. A simple example of that is the mobile base stations of different service providers, where multiple signals could overlap together causing higher EM exposure [2] . Additionally, some countries do not have regulations to limit the placement of antennas on offices or residential buildings [7] . Hence, this paper presents a simple wireless sensor network model based on [6] that can monitor the electromagnetic violation of four base stations from four different service providers. It is assumed that the frequency polluters (F1, F2, F3 and F4) are placed on each side of a 100 × 100 m2 area as illustrated in Figure 1. The sensors are distributed uniformly in the 100 × 100 m2 area; in order to make sure that the whole area is covered and also match the most commonly used applications.
There are 100 narrow band sensors inside this area and 25 sensors are associated to each frequency polluter as in Figure 1. It is assumed that in the case of violation only 11 sensors out of 25 that are close to their frequency polluter are the ones who sense the violation. In general, the 25 sensors should cover the whole area and report any violation. However, for simplicity and due to the fixedness of the polluter’s transmitting power, only the closest sensors to the frequency polluter are allocated to it. Hence, 11sensors have been chosen to report any violation. However, if the transmitting power is varied, the number of associated sensors could be changed accordingly.
Figure 1. Placement of wireless sensors that correspond to each frequency.
The sensors in this model could either be active sensors, which sense the violation, or network masters (NM), which gather the data from the sensors and send it to the sink. Having a network master, also known as a Cluster Head (CH) in wireless sensor networks, has been introduced in LEACH and LEACH C [8] [9] , in order to optimize the utilized energy in the network. This idea was also improved further in [10] by first having an optimized number of cycles of each NM, where each sensor could be an NM several times during the network’s lifetime. The second algorithm was to calculate an optimized number of cycles for each NM, but each sensor could be NM only once. In [6] [11] , this idea was developed further, so that each sensor, starting from the center and going in a circular order, could be an NM depending on a predefined threshold. If the sensor has enough energy above this threshold, it could act as an NM for several cycles, as long as it has enough energy to do so. When it depletes its required energy to act as an NM, the next sensor in row will be examined if it has enough remaining energy above the threshold that could enable it to act as an NM. The threshold for choosing the NM is based on a maximum threshold technique that was studied in [6] with several other techniques. It was then derived that the maximum threshold is the most practical threshold technique that could be used in this model.
While the NM selection is occurring, the sensors are continuously monitoring the power levels of their frequency polluters. This is done using the watchdog algorithm, where the sensors only send their data to the NM, when they detect violation. Other than that, when there is no violation, each sensor should send an “alive” data packet, every predefined period, in order for the sink to detect the network’s failure by the death of the first node. The predefined period in this paper is chosen as in [6] , which is every three cycles, where one cycle is equivalent to one hour.
3. Generalized Framework
The event by event algorithm used in [6] is developed in order to monitor frequency pollution. Four different frequencies as previously mentionedF1, F2, F3 and F4 are introduced and each one of them is assumed to be an operator that causes violation. The frequency polluter was placed at each side of the 100 × 100 m2 network area resulting in a total number of four polluters. There was a specified schedule for this system, meaning that the first frequency polluter violates during the last six hours of the day and on the next day the second polluter violates during the last six hours of the second day and so on. This process repeats itself every four days and upon that is the lifetime of the total network measured. Such an event by event algorithm is not very flexible to capture any diverse and dynamic network change. Therefore, in this paper, a new generic framework is developed in order to add flexibility to [6] and make it more applicable for diverse situations. The same parameters that were used in [6] [8] - [11] are going to be used in this proposed generalized framework and they are listed below:
Network size: 100 ´ 100 m2
Number of Sensors (N): 100 Sensors
Initial Energy: 2J
Transmitter/Receiver Electronics (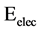 ): 50 nJ/bit
): 50 nJ/bit
Transmitter Amplifier (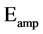 ): 100 pJ/bit/m2
): 100 pJ/bit/m2
Path Loss factor (n): 2
Aggregation Energy (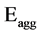 ): 5 nJ/bit/Signal
): 5 nJ/bit/Signal
Data packet size sent by active nodes to NM (K): 64 bits
Data packet size sent by the NM to the sink (K1): 512 bits
Data packet size equivalent to sensing power levels (K2): 1 bit
Sink location: field center
Distribution: Homogeneous Density (Figure 1)
The event by event algorithm in [6] is not a generic system, since the main parameters used are fixed parameters. Those parameters are the starting time of the violation, the duration of the violation and the number of polluters per day. Random variables are going to be used for each parameter in the suggested framework. Each one of them will be described separately as follows.
3.1. Starting Time
In the event by event algorithm, the staring time of the violation was at 6pm everyday and it lasted for six hours. This has been modified in the proposed algorithm to be a random starting time between 12 am, which is the beginning of the day, until 6 pm. Since the violation duration is 6 hours, the last starting time has to be 6 pm, so that when the violation starts at that time it will not extend over the following day.
Matlab [12] functions are used here to generate a stream of random numbers between 0 and 18 for each frequency polluter using different random distributions, such as uniform, Gaussian, and exponential distributions.
3.2. Violation Duration
The violation duration for each polluter was six hours as stated before. Using Matlab [12] the duration period becomes a random number between one and six hours. Thus, a violator could violate for one hour or more, but the maximum violation period is tied by the previous assumption in the event by event algorithm, which is six hours. However, the flexibility of this new generic framework allows the possibility of changing this assumption and replacing it by the desired violation period.
3.3. Number of Polluters Per Day
Previously, in the event by event algorithm it was assumed that each violator will violate on a separate day and each will repeat violation every four days. For instance F1 will violate on day one, F2 on day two, F3 on day three, F4 on day four, and the cycle repeats again,F1 on day five and so on. Here, the number of violators per day became unknown. This means that a minimum of one violator and a maximum of four violators can violate on the same day. Looking at the example of having two polluters violating on the same day, these polluters can be F1 and F2, F1 and F3, F1 and F4, F2 and F3, F2 and F4 or F3 and F4. The total number of combinations here will be:
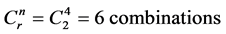 (1)
(1)
where n is the total number of polluters and r is the number of polluters violating on the same day. Consequently if three violators will violate on the same day then we will have 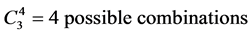 of random polluters per day.
of random polluters per day.
Changing the above three parameters that were used as fixed assumptions in the algorithm used in [6] and making them random makes the electromagnetic pollution monitoring technique more flexible and more suitable for different situations and applications.
3.4. Combining the Three Random Variables together Using Different Distributions
In order to add more flexibility to the newly proposed framework, it is designed to accommodate the randomness of the three above-mentioned parameters at the same time. Meaning that according to preference, one can choose to make for example the starting time and the violation duration random at the same time, or have all three parameters be random simultaneously. Different combinations can be chosen to simulate real life examples.
Additionally, different distributions will be introduced to the framework in order to expand its flexibility and meet the requirements of different applications. For simplicity the uniform distribution will be used as the default random distribution. However, one can also choose between the Gaussian and the exponential distribution according to the desired scenario. Certainly it is also possible for every parameter to have a different random distribution than the other or to choose the same distribution for all parameters. Figure 2 shows an overview of the Generalized Framework. Next different scenarios will be examined to show the usage of the new algorithm.
4. Examined Scenarios
In this section, several scenarios are examined to showcase the capabilities of the proposed algorithm. When monitoring EM pollution different situations can occur. Using this framework, it is easier to simulate these situations, since the main aim of proposing this framework is to make [6] generic and applicable for many scenarios and applications. Most of the assumptions are the same as in [6] , meaning that there are four violators; each of them is placed on one side of the network area. As mentioned before, these violators have fixed criteria when they breach, where each one of them violates only for six hours per day starting with F1 on the first day, then F2 on the second and so on and they repeat every four days. These six hours used to be the last six hours within the day. This scenario yielded a lifetime of 162,296 cycles and for further use, this lifetime will be referred to as the default lifetime.
Figure 2. Flowchart of the generalized framework.
One of the common scenarios that one can compare to the previous default example is the effect of having four violators breaching at the same time. It is not possible to examine such scenario with the system in [6] , however using the proposed framework it can be easily tested. It will be assumed that F1, F2, F3 and F4 are violating everyday, while all other parameters are fixed as follows: starting time = 6 pm, duration = six hours. This will result in a total lifetime of 122,977 cycles, which is a decrease by 24.227% compared to the default scenario. One would expect that having four violators per day compared to one violator, would automatically decrease the lifetime by 75%. However, this is not the case here, because of using the watchdog technique, where every three cycles all sensors should send to the network master a packet indicating that they are alive. Additionally, the number of network masters will differ in both cases, as on one day four polluters violating and exploiting from the sensors more energy than in the case of having one polluter per day. Accordingly, the calculated consumed energy using the distances between each network master and each sensor will be different in both scenarios. All these factors contribute to the 24.227% decrease in lifetime compared to the expected 75% with four violators per day,
Next the effect of randomness on lifetime is going to be obtained by removing all fixed assumptions and considering each parameter as a random variable with different distributions.
4.1. Effect of Starting Time Randomness on Lifetime
There are three main parameters in the algorithm in [6] that can be changed from fixed variables to random variables using the new proposed framework. These parameters are the starting time and the duration of the violation and at last the number of polluters violating per day. Therefore their effect on lifetime after being random variables needs to be deeply investigated in order to identify the dominant parameter that affects the lifetime mostly.
The first parameter, which is the starting time, will be examined separately. The starting time will be a random variable with uniform distribution from (1 - 19), which is equivalent to 1 am until 6 pm. The limit is at 6pm because the maximum duration violation (six hours) should not spill into the next day. The other two parameters will remain the same as the default case; the number of violators per day will be one starting with F1, F2 etc. and repeating every four days. Also the violation duration will remain six hours. This will result in a lifetime of 162,304 cycles, which has increased the default lifetime by only eight cycles. Since the 0.0049% increase of lifetime is very small, this shows that changing the starting time parameter to a random variable will result in an insignificant increase of the network’s the lifetime.
4.2. Effect of Number of Polluters vs. the Duration Randomness on Lifetime
Since it was shown in the previous section that the starting time, as a random variable, does not have a significant effect on lifetime, it will remain as a fixed variable. Furthermore, the other two parameters the duration and the number of polluters per day, will be investigated further to identify the most effective variable on lifetime. A simple experiment will be simulated, where in scenario (a) it will be assumed that the number of polluters per day is fixed in each case, having F1 fixed everyday and hence there are four cases to simulate all possible situations. Meanwhile, the duration is a random variable uniformly distributed between (1,4). Only four hours are considered here in order to have a fair comparison between both parameters. The results of this experiment are shown in Table 1.
The results show that changing the number of polluters from 1 - 4 does not show a significant change on lifetime. The lifetime only differs by 0.01% to 2.2%. The same experiment will be repeated, but this time the duration will be fixed, while the number of polluters will be a random variable uniformly distributed form (1,4). This will yield to the following results in Table 2.
Table 1. Scenario (a)
Table 2. Scenario (b)
Scenario (b) shows that the duration variable has a huge effect on the lifetime. When 1-4 polluters violate for only one hour per day, the default lifetime will increase by 12.02%. Also when comparing the different cases A, B, C, and D, one can obtain a significant change in lifetime between 7.53% and 17.36%. Hence, the duration parameter has the most notable effect on lifetime.
4.3. Effect of Changing Random Distribution on Lifetime
Through the previous experiments, the duration parameter has proven to yield a significant effect on lifetime when it is changed. Therefore, different distributions will be investigated next with the duration parameter as a random variable. Thus, the same scenario (b) will be implemented again but using Gaussian and exponential distributions, in addition to the existing uniform distribution. The results of this attempt will be as shown in Table 3.
In order to have a fair comparison, the same mean is used in all three distributions. The Gaussian distribution shows a better outcome than the uniform distribution, while the exponential distribution yields a higher lifetime compared to the Gaussian and the uniform distribution. Comparing the exponential distribution to the uniform distribution, it has increased the lifetime by a factor of 3.97% to 5.57%. Nevertheless this increase is not very significant and this is due to the low range of samples, since the random variable only varies between 1 and 4. Therefore, a wider range will be investigated next.
4.4. Effect of Changing Random Distributions on Lifetime with a Wider Range of Variables
In this example, case D in Table 3 will be examined more thoroughly and will be called scenario (d); four violators are violating everyday and the starting time is at 1 am, in order to be able to have a wider range of duration. Henceforth, the duration will be a random variable from (1,23). Using the same distributions that were used before, Table 4 shows the results of this experiment:
It is clear that the results follow the same trend like scenario (c). The uniform distribution has the least lifetime, while the exponential distribution has the highest lifetime. The Gaussian distribution lies between both of them, but is closer to the uniform distribution lifetime. The difference between the uniform and Gaussian distribution is about 3.4%, while the difference between the uniform and exponential distribution is 13.08%. This is more than a double increase compared to scenario (c). The reason for that is that the wide range of random variable has revealed the real effect of the random distribution on the duration parameter.
Table 3. Scenario (c)
Table 4. Scenario (d)
5. Conclusions
Wireless Sensor Networks are used in several applications that involve monitoring, controlling and tracking. In this paper a wireless sensor network-based framework was developed to monitor the EM emissions transmitted from frequency polluters. The framework developed here is more flexible and generic compared to previous systems in the literature; since all main parameters are treated as random variables. The main parameters are the starting time of the violation, the duration of the violation and at last the number of polluters violating per day.
To illustrate the use of the proposed framework, several case studies were investigated. It was identified through several simulations that the duration parameter is the most affective parameter and its variation can increase the network’s lifetime between 7.53% and 17.36%. Moreover, the change of random distributions used for the parameter’s random variables was investigated further through the examined scenarios. The outcome was that using the exponential distribution compared to the uniform distribution could prolong the network’s lifetime by 13.08%. Finally, it is very important to note that using a wider range for each random variable will always yield better results, when comparing parameters together.
Cite this paper
Sara Nouh,Nada Elgaml,Nora Ali,Ahmed Khattab,Ramez Daoud,Hassanein Amer, (2016) Generalized Electromagnetic Pollution Monitoring Using WSN. Wireless Sensor Network,08,85-92. doi: 10.4236/wsn.2016.86009
References
- 1. Mikhaylov, K., Tervonen, J., Heikkil, J. and Knskoski, J. (2012) Wireless Sensor Networks in Industrial Environment: Real-Life Evaluation Results. 2012 2nd Baltic Congress on Future Internet Communications (BCFIC), Vilnius, 25-27 April 2012, 1-7.
http://dx.doi.org/10.1109/bcfic.2012.6217971 - 2. Viani, F., Donelli, M., Oliveri, G., Trinchero, D. and Massa, A. (2011) A WSN-Based System for Real-Time Electromagnetic Monitoring. 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, 3-8 July 2011, 3129-3132.
http://dx.doi.org/10.1109/aps.2011.5997195 - 3. Djuric, N., Prsa, M., Kasas-Lazetic, K. (2011) Serbian Remote Monitoring System for Electromagnetic Environmental Pollution. Acta Electrotehnica, Proceedings of the 4th International Conference on modern Power Systems MPS 2011, Cluj-Napoca, 17-20 May 2011, 140-142.
- 4. Derr, K. and Manic, M. (2015) Wireless Sensor Networks-Node Localization for Various Industry Problems. IEEE Transactions on Industrial Informatics, 11, 752-762.
http://dx.doi.org/10.1109/TII.2015.2396007 - 5. Das, H., Gogoi, K. and Chatterjee, S. (2015) Analysis of the Effect of Electric Field Due to High Voltage Transmission Lines on Humans. 2015 1st Conference on Power, Dielectric and Energy Management at NERIST (ICPDEN), Itanagar, 10-11 January 2015, 1-4.
http://dx.doi.org/10.1109/icpden.2015.7084491 - 6. Abou El Seoud, D., Nouh, S., Abbas, R.A., Ali, N.A., Daoud, R.M., Amer, H.H. and El Sayed, H.M. (2010) Monitoring Electromagnetic Pollution Using Wireless Sensor Networks. Proceedings of the 15th International Conference on Emerging Technologies and Factory Automation ETFA, Bilbao, September 2010.
- 7. Stacenko, L. and Anna, A. (2015) Monitoring of Levels of Electromagnetic Radiation from Base Station Antennas. 2015 International Siberian Conference on Control and Communications (SIBCON), Omsk, 21-23 May 2015, 1-3.
http://dx.doi.org/10.1109/sibcon.2015.7147299 - 8. Heinzelman, W., Chandrakasan, A. and Balakrishnan, H. (2000) Energy-Efficient Routing Protocols for Wireless Microsensor Networks. Proceedings of the 33rd Hawaii International Conference on System Sciences (HICSS), Maui, 4-7 January 2000.
http://dx.doi.org/10.1109/HICSS.2000.926982 - 9. Heinzelman, W., Chandrakasan, A. and Balakrishnan, H. (2002) An Application Specific Protocol Architecture for Wireless Micro sensor Networks. IEEE Transactions on Wireless Communications, 1, 660-670.
http://dx.doi.org/10.1109/TWC.2002.804190 - 10. Botros, S., El Sayed, H.M., Amer, H.H. and El-Soudani, M.S. (2009) Lifetime Optimization in Hierarchical Wireless Sensor Networks. Proceedings of the 14th International Conference on Emerging Technologies and Factory Automation, ETFA, Mallorca, 22-25 September 2009, 1-8.
http://dx.doi.org/10.1109/etfa.2009.5347016 - 11. Nouh, S., Abbas, R.A., Abou El Seoud, D., Ali, N.A., Daoud, R.M., Amer, H.H. and El Sayed, H.M. (2010) Effect of Node Distributions on Lifetime of Wireless Sensor Networks. Proceedings of the IEEE International Symposium on Industrial Electronics ISIE, Bari, July 2010.
- 12. Official Site for MATLAB.
http://www.mathworks.com




