Wireless Sensor Network
Vol.07 No.07(2015), Article ID:57881,16 pages
10.4236/wsn.2015.77008
A Packet-Interleaving Scheme Using RS Code for Burst Errors in Wireless Sensor Networks
Tsang-Ling Sheu, Yen-Hsi Kuo, Zi-Tsan Chou*
Department of Electrical Engineering, National Sun Yat-Sen University, Kaohsiung Taiwan
Email: sheu@ee.nsysu.edu.tw, ysk@atm.ee.nsysu.edu.tw, *ztchou@mail.ee.nsysu.edu.tw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 May 2015; accepted 10 July 2015; published 13 July 2015
ABSTRACT
In this paper, we propose a packet-interleaving scheme (PIS) for increasing packet reliability under burst errors in wireless sensor networks (WSN). In a WSN, packet errors could occur due to weak signal strength or interference. These erroneous packets have to be retransmitted, which will increase network load substantially. The proposed PIS, encoding data using Reed-Solomon (RS) codes, can classify data into two different types: high-reliability-required (HRR) data and non-HRR data. An HRR packet is encoded with a short RS symbol, while a non-HRR packet with a long RS symbol. When an HRR and a non-HRR packet arrive at a sensor, they are interleaved on a symbol-by-symbol basis. Thus, the effect of burst errors (BE) is dispersed and consequently the uncorrectable HRR packets can be reduced. For the purpose of evaluation, two models, the uniform bit-error model (UBEM) and the on-off bit-error model (OBEM), are built to analyze the packet uncorrectable probability. In the evaluation, we first change the lengths of BE, then we vary the shift positions in a BE period, and finally we increase the number of correctable symbols to observe the superiority of the proposed PIS in reducing packet uncorrectable probability.
Keywords:
WSN, RS Code, Burst Errors, Interleaving, Packet Uncorrectable Probability

1. Introduction
Along with the increasing requirements for living quality and home security, sensors have been widely deployed inside or outside a building to collect environmental information, such as temperature, humidity, image, motion picture, etc. To effectively deliver the collected data back to a control center for further analysis, a wireless sensor network (WSN) [1] -[3] is usually built. However, packet transmission over a WSN may encounter intermittent errors due to weak signals or interferences. The erroneous packets, if comprising of text or numbers, such as temperature or humidity, would require packet re-transmission, which surprisingly increases network load. Thus, the motivation of this paper is to increase transmission reliability over a WSN, which has recently attracted many researchers’ attention.
Basically, previous researches on transmission reliability over a WSN can be divided into three major categories: reliable routing, information coding, and network coding. In the first category, to increase the transmission reliability after data are collected by a sensor node, relay nodes (RNs) are employed. For examples, H. Chebbo, et al. [4] modified IEEE 802.15.4 MAC frames. The authors added one bit in the frame control field, with which whether it is necessary to build a tree by RNs or just build a simple star, can be determined. Moreover, R. Sampangi, et al. [5] utilized RNs to divide sensors into several cluster networks. Since the distance from a sensor to its cluster head is reduced, the quality of data transmission is greatly improved. To protect the routing path, S. Kim, et al. [6] utilized both coding and retransmission schemes once the established path fails. However, in these schemes, it is inevitable that end-to-end packet delay will increase accordingly due to multiple-hop forwarding.
Thus, in the second category, instead of developing reliable routing, the authors switch their interests to information coding. For examples, E. Byrne, et al. [7] designed a coding scheme which can increase the probability of successful decoding based on graph theory. Y. Hamada, et al. [8] proposed a scheme to reduce packet error rate by using Luby Transform (LT) codes [9] . Their proposed schemes have achieved small complexity of O(n); yet too many packets are required for retransmission when bit error rate is high. Thus, K. Ishibashi, et al. [10] proposed embedded forward error control (FEC) technique which utilizes RS (Reed Solomon) code to reduce packet error rate. Similarly, M. Busse, et al. [11] can recover lost chunk by using Fountain code and Raptor code. To increase data reliability and processing speed, K. Yu, et al. [12] designed new FEC which protects header and payload, respectively. Similarly, M. Srouji, et al. [13] proposed a reliable data transfer scheme which can adjust the lengths of redundancy code based on the successful receiving rate at the downstream node.
In the third category, to increase transmission reliability, researchers focus on network coding. For examples, to increase the probability of successfully recovering the transmitted data, G. Arrobo, et al. [14] proposed cooperative network coding. Similarly, A. Taparugssanagorn, et al. [15] proposed unequally error protection (UEP) scheme. In UEP, data are classified into two types: medical and non-medical. Only medical data are EX-ORed, while non-medical data are not. However, in UEP, it is not guaranteed that a downstream sensor node can always decode data successfully. Thus, I. Salhi, et al. [16] proposed another reliable coding scheme where a relay node can produce much better packet combination through the exchange of neighboring table and topology interference information. Finally, Z. Kiss, et al. [17] tried to combine two coding techniques, RS coding and network coding. Once a relay node receives data packets transmitted from all the downstream sensor nodes, it begins to chop every data packet into smaller segments. Each segment is encoded into two symbols using RS codes. The two symbols are then converted to two checking blocks before data transmission. A receiving node can therefore increase the probability of correct data by decoding these two checking blocks.
Unlike the previous research work, where the authors focused on reliable routing, information coding, and network coding, in this paper, we propose a packet interleaving scheme (PIS) to reduce the impact of burst errors (BE) on high-reliability-required (HRR) data in WSNs. BE is defined as a sequence of transmitted bits which may encounter errors in continuous bit pattern. Although Reed-Solomon (RS) codes [18] , which encode data in a block-by-block fashion, may correct bit errors in a certain constraints, it may not be economically worthy in dealing with burst errors when the number of consecutive bit errors exceeds a threshold. In other words, it makes the overhead of redundancy codes become unacceptable. Hence, to increase packet correctable probability in a WSN, the proposed PIS first classifies the collected data into two different types: HRR data and non-HRR data. An HRR packet is encoded with a short RS symbol, while a non-HRR packet with a long RS symbol. When an HRR and a non-HRR packet arrive at a sensor, they are interleaved on a symbol-by-symbol basis. The noticeable benefit from the packet interleaving is that the burst errors are dispersed and the uncorrectable probability of HRR packets is significantly reduced.
The remainder of this paper is organized as follows. In Section 2, we introduce RS codes employed in a WSN. In Section 3, the proposed PIS and its operations are described. In Section 4, an analytical model is built using two bit-error models, the uniform bit-error model (UBEM) and the on-off bit-error model (OBEM). Finally, conclusions are drawn in Section 5.
2. Reed-Solomon Codes
2.1. Forward Error Correction
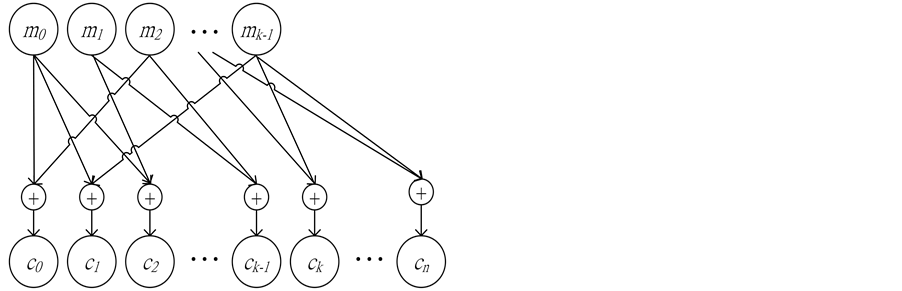
Forward Error Correction (FEC) codes have been widely used in today’s unreliable communication system, such as wireless networks, to reduce bit error rate (BER). The basic principle behind FEC is to generate redundancy code by encoding the user data; the former is then appended to the latter before transmission. At the receiver, user data together with the redundancy code are examined so that a certain pattern of bit errors can be corrected. FEC is composed of two categories, convolution code (CC) and block code (BC) [3] . The former has been applied to the transmission for continuous data, such as video streaming. Encoding process in CC requires relatively larger memory to store the previous, the current, and the upcoming information. As shown in Figure 1(a), each symbol in the k symbols, 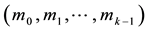 is Exclusive-ORed with the previous or the upcoming symbols. As a result, n symbols
is Exclusive-ORed with the previous or the upcoming symbols. As a result, n symbols 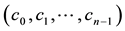 are produced from k symbols. BC, on the other hand, has been used in encoding discrete data on the basis of block by block. Thus, BC is more applicable to a sensor network, where data, such as temperature, moisture, etc., are collected discretely in a block size. The basic idea behind BC is to encode k-symbol information with a division operation. Redundancy codes with n-k symbols,
are produced from k symbols. BC, on the other hand, has been used in encoding discrete data on the basis of block by block. Thus, BC is more applicable to a sensor network, where data, such as temperature, moisture, etc., are collected discretely in a block size. The basic idea behind BC is to encode k-symbol information with a division operation. Redundancy codes with n-k symbols, 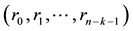 , are generated after the division operation. Before the transmission to an upper stream node, the n-k symbols are attached to the original k symbols, as shown in Figure 1(b).
, are generated after the division operation. Before the transmission to an upper stream node, the n-k symbols are attached to the original k symbols, as shown in Figure 1(b).
2.2. RS Encoding
1) It is well known that Reed-Solomon (RS) code is one of the most popular block codes. RS Code is usually represented by 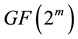 , where GF is the Galois Field [19] and m denotes the number of bits in a symbol. Alternatively, RS code can be represented by (n, k), where
, where GF is the Galois Field [19] and m denotes the number of bits in a symbol. Alternatively, RS code can be represented by (n, k), where 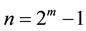 denotes the total number of symbols encoded, k is number of symbols for user data, and (n-k) denotes the number of redundancy symbols. Hence,
denotes the total number of symbols encoded, k is number of symbols for user data, and (n-k) denotes the number of redundancy symbols. Hence,
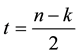 denotes the number of erroneous symbols that can be corrected.
denotes the number of erroneous symbols that can be corrected.
2) Let us briefly review the operations of RS codes. Before a message is transmitted using RS encoding, the message is segmented into a number of m-bit symbols. The k m-bit symbols can be represented by a polynomial:
 A generator polynomial,
A generator polynomial, 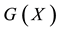 , is defined as
, is defined as  which is used to calculate a parity polynomial,
which is used to calculate a parity polynomial, ; i.e.,
; i.e.,  Finally, codeword,
Finally, codeword, 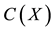 , is calculated by
, is calculated by 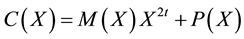 . The coefficients of polynomial
. The coefficients of polynomial  are the final encoded data to be transmitted.
are the final encoded data to be transmitted.
3) For example, a RS code has  and
and  or (n, k) = (7, 3); i.e., a message is segmented into a num-
or (n, k) = (7, 3); i.e., a message is segmented into a num-

Figure 1. Convolution code versus block code. (a) Convolution Code; (b) Block Code.
ber of 3-bit symbols. The 8 different symbols and their binary representations are shown in Table 1.
We assume the original user data is 9 bits: 001 010 011. Since a symbol consists of 3 bits and

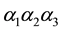
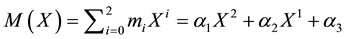

Parity polynomial is computed as 

2.3. RS Decoding
Due to noise or interference, data may encounter bit errors over wireless link. Let R(X) be the data received, C(X) be the data transmitted, and E(X) be the data in error. Thus, we have,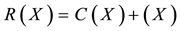
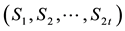
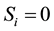
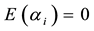
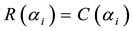
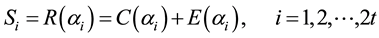
If bit errors do occur, error locations and error values are required computation. Assume there are v errors appear at the locations,


Next, if we can find 
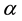
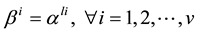

Table 1. An example of RS code with 8 symbols.
Thus, the polynomial of error locations can be expressed as shown in Equation (4).

To compute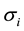
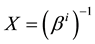

sults to Equation (5), where 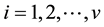
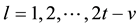


Expanding Equation (6), the result is shown in Equation (7).
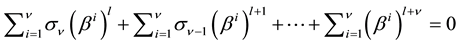
From Equation (3) and Equation (7), we can derive Equation (8).
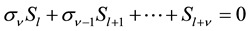
Substituting 

Equation (9) can be expressed by a matrix equation as shown in Equation (10). By applying the operation of inverse matrix, we can compute
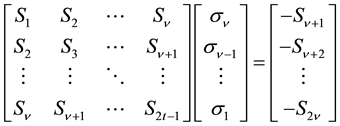
Substituting 

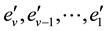
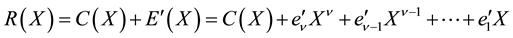
Let 
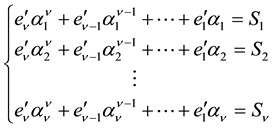
Since Equation (12) has 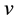
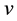
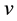
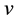

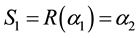

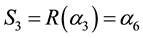
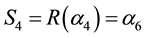


By multiplying an inverse matrix on both sides in Equation (13), we have derive Equation (14). Next, if we substitute 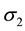

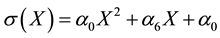
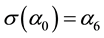
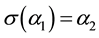

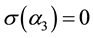
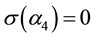
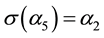


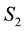


Since 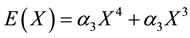

3. Packet Interleaving Scheme
3.1. WSN with Multi-Hop Tree Structure
In a wireless sensor network (WSN), a coordinator is the sink which gathers all the data collected from other distant sensor nodes. To facilitate data gathering from all the sensor nodes, it is very constructive that the coordinator and the sensor nodes will collaborate to build a multi-hop tree structure (MTS), as shown in Figure 2. In an MTS-based WSN, data collected by a sensor node will be forwarded hop-by-hop to the coordinator. Thus, by fully utilizing a branch node of the MTS, in this paper, we propose a packet interleaving scheme (PIS) based on RS codes to reduce the impact of burst errors on packet uncorrectable probability.
3.2. Packet Interleaving
In the proposed PIS, packets collected by a sensor node are classified into two different types: high-reliability required (HRR) packet and non-HRR packet. An HRR packet is defined as a packet which requires for retransmission, if uncorrectable burst errors exist. Payload in an HRR packet consists of numerical data, such as temperature, moisture, luminance, etc. This type of packet has relatively shorter data length (usually, a couple of bytes) and each uncorrectable HRR packet requires for retransmission. Hence, it is better to employ a shorter-length symbol (in this paper, we use m = 4) to encode an HRR packet with shorter data length. On the other
Figure 2. WSN with multi-hop tree structure.
hand, payload in a non-HRR packet consists of non-numerical data, such as video, audio, etc. This type of packet has relatively longer data length (usually, in the order of kilo bytes) and each uncorrectable non-HRR packet may not require for retransmission. Thus, it is better to employ longer-length symbol (in this paper, we use m = 8) to encode a non-HRR packet with longer data length.
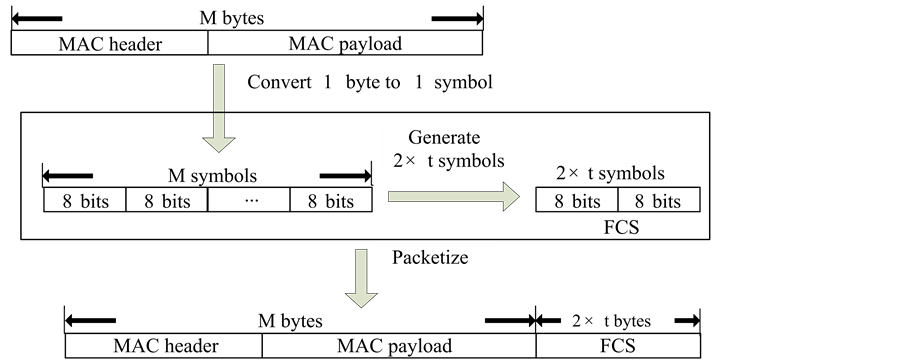
As it is illustrated in Figure 3, an HRR packet is encoded with a shorter-length RS symbol (i.e., m = 4). First,
an M-byte MAC-layer header and payload is converted to 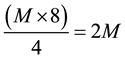
symbol. Thus, we have the length of a codeword is n, where

a codeword is
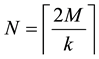
packet (header plus payload). The total redundancy code (or FCS) is therefore equal to 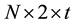

Similarly, as it is illustrated in Figure 4, a non-HRR packet is encoded with a longer-length symbol (m = 8).
An M-byte MAC-layer header and payload is converted to 
symbol. Since the length of a codeword, 
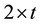
When both an HRR and a non-HRR packet are received by a branch node in a tree-structured WSN, these two packets are interleaved on a symbol-by-symbol basis, as shown in Figure 5. The interleaved packet is then forwarded to an upper stream node, which performs decoding and correction process. However, as shown in Figure 6, an interleaved packet may not be correctable, if it encounters burst errors where the number of total errors is greater than t. In the proposed PIS, by separating the interleaved single packet back to their original two packets, each individual packet may become correctable. This is because the number of errors in each separated packet is highly possible to be smaller than t.
4. Mathematical Model and Analysis
In RS codes, whether or not a coded packet is correctable is mainly determined by the number of erroneous symbols. In this section, to study the robustness and the error-correction capability of the proposed PIS, we build two mathematical models for comprehensive numerical simulations. The first one is referred to as uniform bit error model (UBEM), while the second one is referred to as on-off bit error model (OBEM). The first model assumes the errors occur evenly on the coded packets. The second model assumes the errors may occur continuously
Figure 3. An HRR packet encoded with a shorter-length symbol (m = 4).
Figure 4. A non-HRR packet encoded with a longer-length symbol (m = 8).
Figure 5. Packet interleaving on a symbol-by-symbol basis.
Figure 6. Burst errors dispersed on two symbols.
in a burst length.
4.1. UBEM
Let 


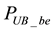
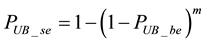
Next, let us define two more parameters, 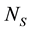

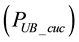
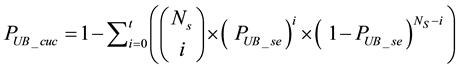
In Equation (18), we know in a codeword if the number of symbol errors is smaller than t, then the codeword is correctable. Thus, the uncorrectable probability of a codeword can be summed up from
are 
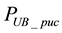
Since there are 

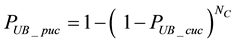
4.2. OBEM
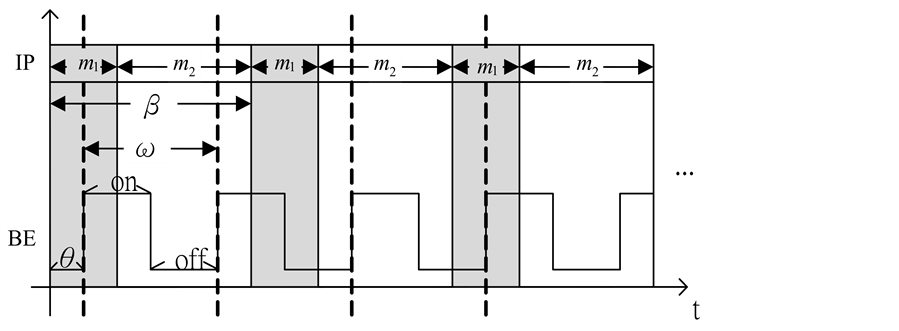
The on-off bit error model (OBEM) is illustrated in Figure 7. All the parameters used in the analysis are defined in Table 2. A burst error (BE) period is defined as two consecutive bit error intervals where high bit errors ap-
Figure 7. On-Off bit error model.
Table 2. Parameters used in OBEM.
pear first and then followed by low bit errors. Notice that 

First, we define 
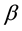

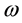




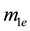



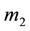
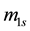
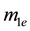
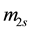
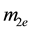
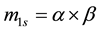

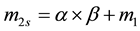
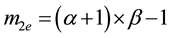
For simplicity, the four parameters, 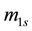

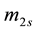




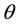
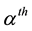
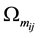
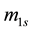
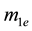
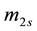


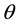
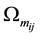
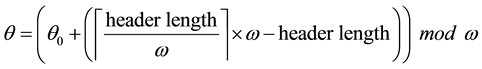

After we found the right-shift position between an IP and a BE, we can categorize the symbol errors into four cases, as illustrated from Figure 8(a) to Figure 8(d). Case 1 in Figure 8(a) shows whether or not a symbol may occupy one BE or two BE periods, their start bit and stop bit of a symbol all appear at the high-bit-error interval. Case 2 in Figure 8(b) shows only the start bit of a symbol appears at the high-bit-error interval. Case 3 in Figure 8(c) shows whether or not a symbol may occupy one BE or two BE periods, neither the start bit nor the stop bit appear at the high-bit-error interval. Finally, Case 4 in Figure 8(d) shows only the stop bit of a symbol appears at the high-bit-error interval. Actually, the four different cases of symbol errors can be constrained by eight inequalities with four parameters, 



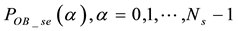
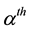

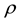
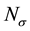
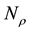
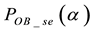

Now, we can compute 

Case 1:

Figure 8. Four cases of symbol errors in terms of the start and stop bits.
Table 3. Four cases of symbol errors with 8 constraints.
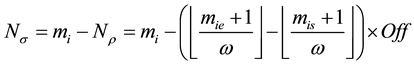
Case 2:
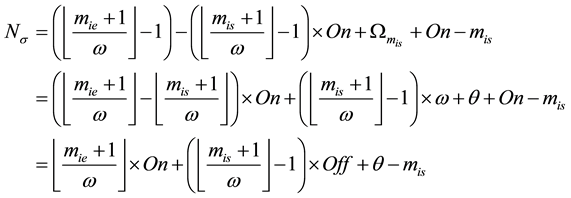
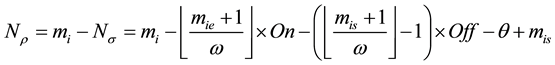
Case 3:
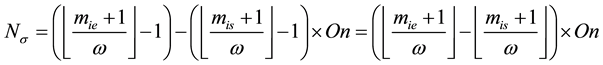

Case 4:

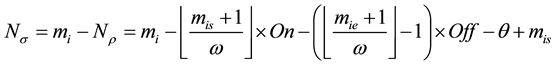
By substituting 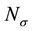
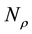
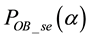
After we compute the symbol-error probability for the four different cases, our next step is to derive the uncorrectable probability of a codeword and the uncorrectable probability of a packet. We know there are 

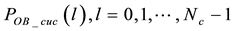
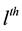
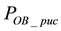
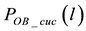



5. Numerical Simulations
In OBEM, to study the influences of the four parameters, (i) the length of high bit errors (i.e., the On period), (ii) the length of low bit errors (i.e., the Off period), (iii) the right-shift position (i.e.,
Table 4. Four cases of symbol-error probabilities.
Table 5. Parameter settings.
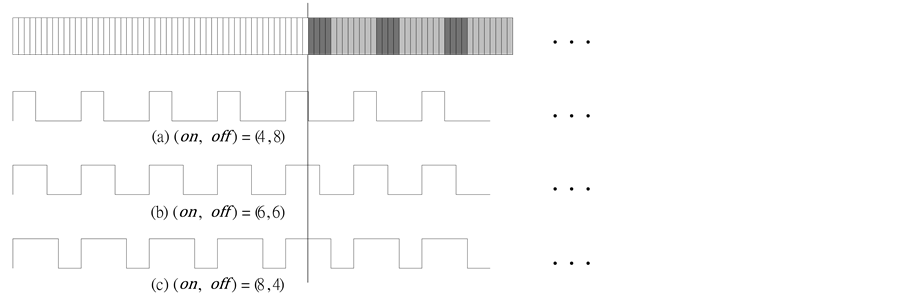
Prior to studying the influences of the three different On-Off lengths on packet uncorrectable probability, we illustrate three scenarios in Figure 9. When the length of On period is shorter, as shown in Figure 9(a), an HRR packet encoded with a shorter length of symbol (m = 4, dark-shaded portion) completely falls in the Off period, while a non-HRR packet encoded with a longer length of symbol (m = 8, light-shaded portion) just has a few bits fall in the Off period. When the length of the On period is increased to 6 bits, which is equal to the length of the Off period, as shown in Figure 9(b), half of the HRR packet falls in the On period. The error-bit coverage for an HRR packet becomes even worse when the On period is increased to 8 bits, as shown in Figure 9(c). As it can be seen, a whole symbol of an HRR packet is now covered by the On period, while only half of a symbol of a non-HRR packet is covered by the On period.
Impact of Correctable Symbols
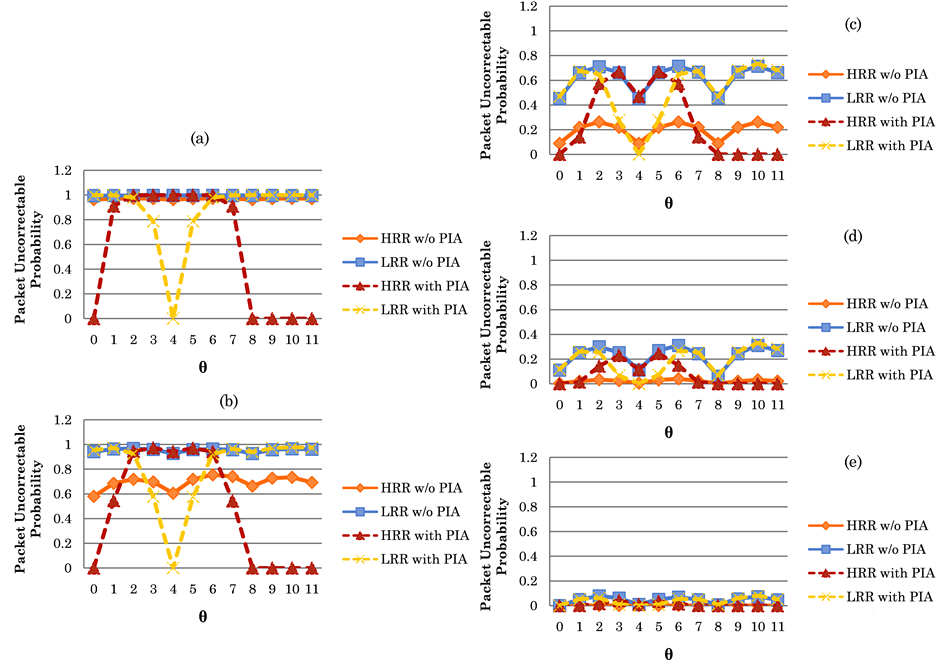
First, we are interested in studying the impact of increasing the number of correctable symbols when the length of high bit errors is shorter than the length of low bit errors; i.e., On = 4 bits and Off = 8 bits. As shown in Figures 10(a) to 10(e), we observe the variations of packet uncorrectable probability 

From Figure 10, we can observe that both the packet uncorrectable probabilities 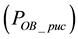
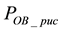
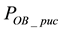



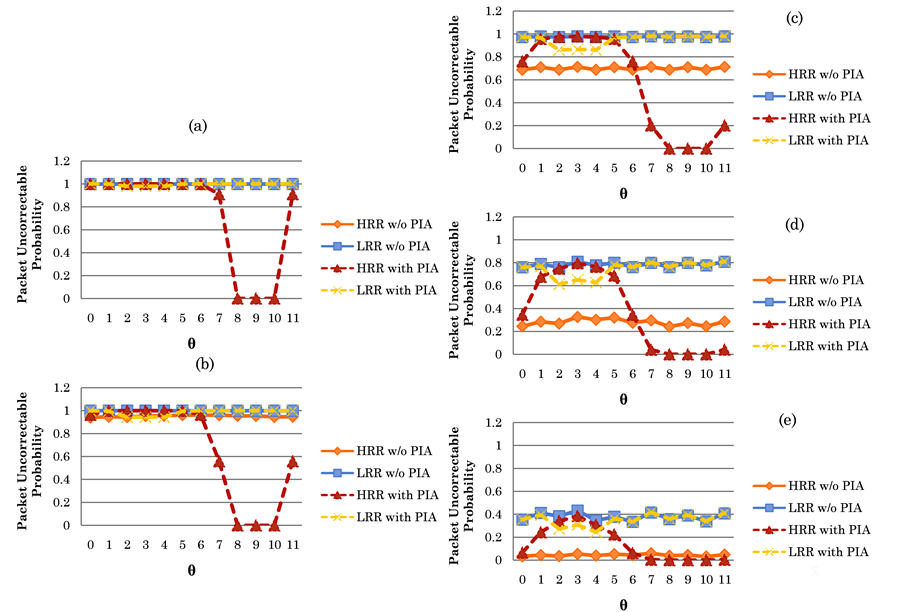
From Figure 11(a) to Figure 11(e), we show the packet uncorrectable probabilities when the on period (6 bits) is equal to the Off period (6 bits). It is not surprising to notice that, for the corresponding t values (t = 1 to 5), the four curves in Figure 11 are much higher than those four curves in Figure 10. The reason is quite straightforward, since the period of high bit errors (i.e., the On period) is increased from 4 bits to 6 bits. However, on average the proposed PIS can effectively reduce packet uncorrectable probability, as it is compared to the curves without using PIS. In particular, we can observe that, no matter what the value t is, the curves of HRR with PIS can be reduced to near zero when 

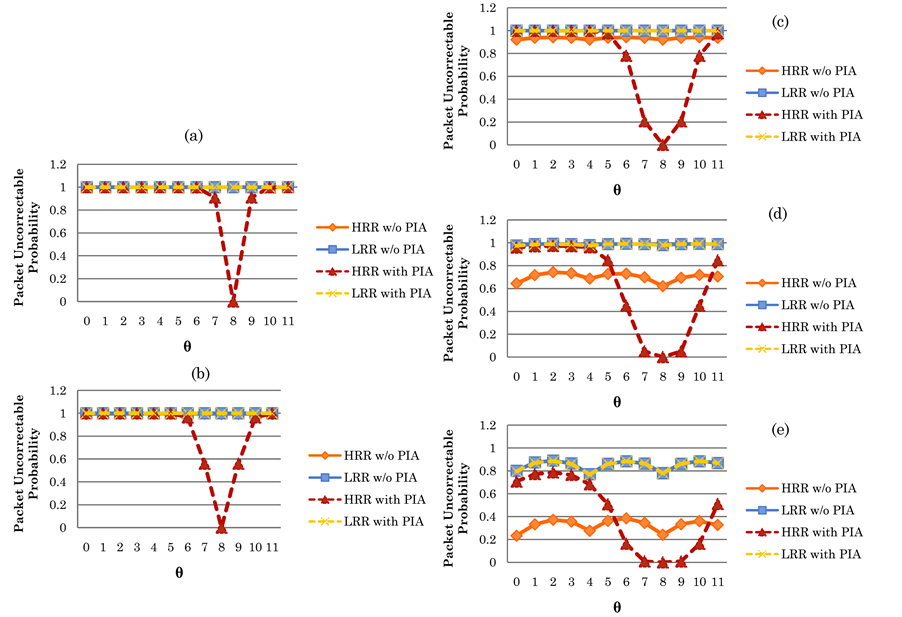
From Figure 12(a) to Figure 11(e), we show the packet uncorrectable probabilities when the on period (8 bits) is longer than the Off period (4 bits). It is interesting to notice that when t is larger than 3 and 
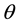
Figure 9. Influences of three On-Off lengths on the packet errors.
Figure 10. Variations of packet uncorrectable probability (on is smaller than off).
is no advantage achieved by using the proposed PIS.
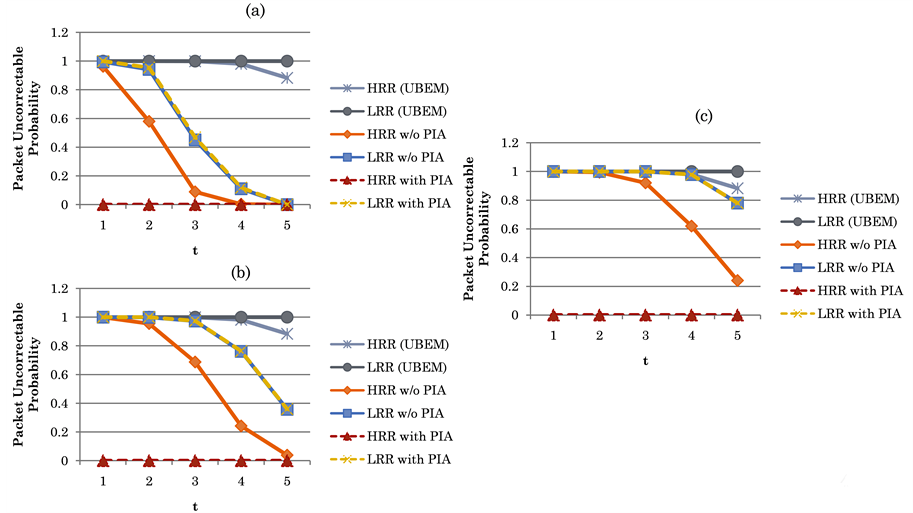
From Figure 13(a) to Figure 13(c), we show the comparisons in packet uncorrectable probabilities between UBEM and OBEM. First, we observe that in UBEM it does not make any big difference whether or not using the proposed PIS, since in UBEM every bit receives the same error probability. Second, we observe that packet uncorrectable probability in UBEM is relatively higher than that in OBEM. Notice that the curves of UBEM and the curves of OBEM vary along with the following two parameters: (i) when the number of correctable symbols (t) increases from 1 to 5, the curves of UBEM dissever very quickly from those of OBEM; and (ii) when the right-shift position 
Figure 11. Variations of packet uncorrectable probability (on is equal to off).
Figure 12. Variations of packet uncorrectable probability (on is larger than off).
Figure 13. Packet uncorrectable probability in UBEM vs in OBEM. (a) (On, Off, θ) = (4, 8, 0); (b) (On, Off, θ) = (6, 6, 8); (c) (On, Off, θ) = (4, 8, 8)
sult is that no matter how we increase the period of high bit errors (i.e., we increase the on period from 4 bits in 13(a) to 6 bits in 13(b), and finally to 8 bits in 13(c)), HRR with PIS in OBEM always exhibits the lowest packet uncorrectable probability (near zero, in some cases). The relatively lower packet uncorrectable probability for HRR packets has demonstrated that the proposed PIS can successfully protect HRR packets from burst errors, while at the same time it does not sacrifice non-HRR packets from large uncorrectable bit errors.
6. Conclusion
In this paper, we have presented a packet interleaving scheme (PIS) using RS code to reduce packet uncorrectable probability under burst errors in wireless sensor networks. In PIS, the collected data are classified into HRR and non-HRR. An HRR packet is encoded with a shorter RS symbol, while a non-HRR packet with a longer RS symbol. One of the contributions of this paper is right in that an HRR and a non-HRR packet are interleaved on a symbol-by-symbol basis, which effectively disperses the burst errors among an interleaved packet. Consequently, the packet uncorrectable probability of an HRR packet can be significantly reduced. In the performance evaluation, we built two mathematical models, UBEM and OBEM. From the thorough numerical simulations, we have demonstrated that, no matter how we adjust the period of high bit errors, the proposed PIS behaves more resilient to burst errors in OBEM than in UBEM. Finally, we have revealed that, by carefully adjusting the period of high bit errors and the right-shift positions, the proposed PIS can reduce the uncorrectable probability of HRR packets to near zero.
Acknowledgements
The authors would like to thank the reviewers, whose valuable comments helped improve the presentation of this paper. Additionally, the authors would like to thank Prof. Tsang-Ling Sheu’s assistant, Miss Yi-Ying Ke for her cautious redrawing of the figures which helped improve the quality of the paper. This study is supported under the three grant numbers: (1) NSC 102-2221-E-110-036-MY2 of MoST, Taiwan, (2) 103-EC-17-A-03-S1- 214, of MOEA, Taiwan, and (3) NHRI-EX103-10142EI, Taiwan.
Cite this paper
Tsang-LingSheu,Yen-HsiKuo,Zi-TsanChou, (2015) A Packet-Interleaving Scheme Using RS Code for Burst Errors in Wireless Sensor Networks. Wireless Sensor Network,07,83-99. doi: 10.4236/wsn.2015.77008
References
- 1. Barac, F., Yu, K., Gidlund, M., Akerberg, J. and Bjrkman, M. (2012) Towards Reliable and Lightweight Communication in Industrial Wireless Sensor Networks. Proceedings of the INDIN 2012: IEEE 10th International Conference on Industrial Informatics, Beijing, 25-27 July 2012, 1218-1224.
http://dx.doi.org/10.1109/indin.2012.6300846 - 2. Marinkovic, S. and Popovici, E. (2009) Network Coding for Efficient Error Recovery in Wireless Sensor Networks for Medical Applications. Proceedings of the 1st International Emerging Network Intelligence, Sliema, 11-16 October 2009, 15-20.
http://dx.doi.org/10.1109/emerging.2009.22 - 3. Sklar, B. (2001) Digital Communications: Fundamentals and Applications. 2nd Edition, Prentice Hall, Upper Saddle River.
- 4. Chebbo, H., Abedi, S., Lamahewa, T.A., Smith, D.B., Miniutti, D. and Hanlen, L. (2010) Reliable Body Area Networks Using Relays: Restricted Tree Topology. Proceedings of the 2012 International Conference on Computing, Networking and Communications (ICNC), Maui, 30 January-2 February 2010, 82-88.
http://dx.doi.org/10.1109/iccnc.2012.6167540 - 5. Sampangi, R.V., Urs, S.R. and Sampalli, S. (2011) A Novel Reliability Scheme Employing Multiple Sink Nodes for Wireless Body Area Networks. Proceedings of the 2011 IEEE Symposium on Wireless Technology and Applications (ISWTA), Langkawi, 25-28 September 2011, 162-167.
http://dx.doi.org/10.1109/iswta.2011.6089401 - 6. Kim, S., Fonseca, R. and Culler, D. (2004) Reliable Transfer on Wireless Sensor Network. Proceedings of the 1st Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, Santa Clara, 4-7 October 2004, 449-459.
- 7. Byrne, E., Manada, A., Marinkovic, S. and Popovici, E. (2011) A Graph Theoretical Approach for Network Coding in Wireless Body Area Networks. Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings (ISIT), Saint Petersburg, 31 July-5 August 2011.
http://dx.doi.org/10.1109/isit.2011.6034156 - 8. Hamada, Y., Takizawa, K. and Ikegami, T. (2012) Highly Reliable Wireless Body Area Network Using Error Correcting Codes. Proceedings of the 2012 IEEE Radio and Wireless Symposium, Santa Clara, 15-18 January 2012, 231-234.
http://dx.doi.org/10.1109/rws.2012.6175351 - 9. Luby, M. (2002) LT Codes. Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, 16-19 Novenber 2002, 271-280.
http://dx.doi.org/10.1109/sfcs.2002.1181950 - 10. Ishibashi, K., Ochiai, H. and Kohno, R. (2008) Embedded Forward Error Control Technique (EFECT) for Low-Rate but Low Latency Communications. IEEE Transactions on Wireless Communications, 7, 1456-1460.
http://dx.doi.org/10.1109/TWC.2008.060573 - 11. Busse, M., Haenselmann, T. and Effelsberg, W. (2007) Energy-Eficient Data Dissemination for Wireless Sensor Networks. Proceedings of the 5th Annual IEEE International Conference on Pervasive Computing and Communications Workshops, White Plains, 19-23 March 2007.
http://dx.doi.org/10.1109/percomw.2007.44 - 12. Yu, K., Barac, F., Gidlund, M., Akerberg, J. and Bjorkman, M. (2012) A Flexible Error Correction Scheme for IEEE 802.15.4-Based Industrial Wireless Sensor Networks. Proceedings of the 2012 IEEE International Symposium on Industrial Electronics (ISIE), Hangzhou, 28-31 May 2012, 1172-1177.
http://dx.doi.org/10.1109/isie.2012.6237255 - 13. Srouji, M.S., Wang, Z. and Henkel, J. (2011) RDTS: A Reliable Erasure-Coding Based Data Transfer Scheme for Wireless Sensor Networks. Proceedings of the 2011 IEEE 17th International Conference on Parallel and Distributed Systems, Tainan, 7-9 December 2011, 481-488.
http://dx.doi.org/10.1109/icpads.2011.104 - 14. Arrobo, G.E. and Gitlin, R.D. (2011) Improving the Reliability of Wireless Body Area Networks. Proceedings of the 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Boston, 30 August-3 September 2011, 2192-2195.
http://dx.doi.org/10.1109/iembs.2011.6090413 - 15. Taparugssanagorn, A., Ono, F. and Kohno, R. (2010) Network Coding for Non-Invasive Wireless Body Area Networks. Proceedings of the 2010 IEEE 21st International Symposium on Personal, Indoor and Mobile Radio Communications Workshops, Istanbul, 26-30 September 2010, 134-138.
http://dx.doi.org/10.1109/pimrcw.2010.5670413 - 16. Salhi, I., Ghamri-Doudane, Y., Lohier, S. and Roussel, G. (2011) Reliable Network Coding for ZigBee Wireless Sensor Networks. Proceedings of the 8th IEEE International Conference on Mobile Ad-Hoc and Sensor Systems, Valencia, 17-22 October 2011, 135-137.
- 17. Kiss, Z.I., Polgar, Z.A., Stef, M.P. and Bota, V. (2012) Network Coding Solution for Improving Transmission Reliability in Wireless Sensor Networks Employed in Industrial Monitoring. Proceedings of the 35th International Conference on Telecommunications and Signal Processing (TSP), Prague, 3-4 July 2012, 190-195.
http://dx.doi.org/10.1109/tsp.2012.6256280 - 18. Reed, I.S. and Solomon, G. (1960) Polynomial Codes over Certain Finite Fields. Journal of the Society of Industrial and Applied Mathematics, 8, 300-304.
http://dx.doi.org/10.1137/0108018 - 19. Lidl, R. and Niederreiter, H. (1997) Finite Fields. Cambridge University Press.
NOTES
*Corresponding author.