Wireless Sensor Network
Vol.07 No.05(2015), Article ID:56658,7 pages
10.4236/wsn.2015.75005
Distributed Target Location in Wireless Sensors Network: An Approach Using FPGA and Artificial Neural Network
Mauro Rodrigo Larrat Frota e Silva*, Glaucio Haroldo Silva de Carvalho, Dionne Cavalcante Monteiro, Leomário Silva Machado
Exact and Natural Sciences Institute, Faculty of Computer Science, Federal University of Pará, Belém, Brazil
Email: *maurolarrat@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2015; accepted 23 May 2015; published 26 May 2015
ABSTRACT
This paper analyzes the implementation of an algorithm into a FPGA embedded and distributed target location method using the Received Signal Strength Indicator (RSSI). The objective is to show a method in which an embedded feedforward Artificial Neural Network (ANN) can estimate target location in a distributed fashion against anchor failure. We discuss the lack of FPGA imple- mentation of equivalent methods and the benefits of using a robust platform. We introduce the description of the implementation and we explain the operation of the proposed method, followed by the calculated errors due to inherent Elliott function approximation and the discretization of decimal values used as free parameters in ANN. Furthermore, we show some target location estimation points in function of different numbers of anchor failures. Our contribution is to show that an FPGA embedded ANN implementation, with a few layers, can rapidly estimate target location in a distributed fashion and in presence of failures of anchor nodes considering accuracy, precision and execution time.
Keywords:
Wireless Sensors Network, RSSI, FPGA, Artificial Neural Network, Distributed Localization Methods

1. Introduction
Distributed target location algorithms provide lower power consumption and fault tolerance of sensors during the localization process when compared with centralized localization algorithms [1] . The main difference between these two types of localization algorithms is the local of occurrence of the processing target location information. In distributed localization, the target sends its location information to (at least) two or more base stations in the network (or anchor nodes), so that the execution of processing is distributed between these ones, in order that the locating procedure provides a reasonable estimative in case of failure of one of the base stations. The target location information can be obtained in various ways, as shown in the related works, by means of sensors which are adjacent to them (likelihood based) or by techniques based on measured distances (time of arrival, angle of arrival, received signal strength indicator, etc.) by the transmitted signals.
This work considers the characteristics of Artificial Neural Network, such as its ability of offering a reasonable approximation in presence of some absence of feeding information and the parallel processing of its units. The inputs of ANN are associated with the RSSI of each anchor nodes and the outputs are in form of 2-D coordinates in a plane surface. With our proposed method, at least two inputs are necessary to estimate, with some accuracy and precision, the location of a target. Considering the embedded level of our method, we just need to implement one neuron and replicate it to the desired architecture of the ANN in a modular fashion.
The embedded platform chosen to build in the ANN is the FPGA. With that we could achieve 6 × 10−7 s at each processing unit of the ANN. Considering parallel advantage architecture, the layer of the ANN is executed at same time. The FPGA is a reconfigurable platform that operates at 50 MHz and is very affordable nowadays. It is designed to operate process in parallel so it has equivalency to the ANN. There are many vendors and low costs FPGAs to fit any design problem. Our proposed method is implemented in the compact and tiny DE0-Nano’s solution from Altera, to show that it does not need a lot of resources to be built. There are many works that discuss the advantages of ANN implementations on applied in target location, rarely using FPGA as an applied platform. We focus on ANN embedded locating methods implemented in related works, but we emphasize that the ANN based locating target is a wide area of research and the hardware implementation is a branch we have pointed to; [2] discourses a parallel and distributed ANN platform model for target location; [3] uses an ANN embedded method for target tracking; [4] proposes a non-embedded generalized regression ANN together with a Centroid simulation method in a RSSI target location problem. Other papers on ANN and RSSI based methods can be found in [5] -[7] .
This paper contributes to showing a practical experiment implemented in a FPGA together with ANN applied in distributed target location in WSN and the advantages associated with this method, and how it fits to solve most known issues on distributed localization. We go beyond the limit of simulation to show new details and considerations of the applied method by analysing the characteristics intrinsic of this implementation. Section 2 shows some recent related works that use a set of complex algebraic techniques, common used to distributed localization, to estimate the target location, as well as some works that make use of Artificial Neural Network to estimate the target location. Section 3 details the methodology of our work. Section 4 shows our results and Session 5 presents our conclusions.
2. Related Works
In [8] a practical experiment is carried out in an 8 × 6.4 m indoor area with furniture. To locating targets, an ANN method is software embedded into an Arduino platform which makes use of Xbee as radio modules. The measured RSS signal operates in 256 bps and follows the IEEE 802.15.4 standard through Zigbee protocol. The RSSI is acquired through the proprietary Application Interface implemented into the Zigbee. The results showed compare the time spent considering six training methods, including the training method we used in our work (Resilient Backpropagation Algorithm―RBP), and the total average error which each training method did show. The error is in the form of average distance location error, comparing the known position with the estimated one. They show the Leven berg-Marquardt method (LM) as the best training algorithm based on the total average error, and the RBP being the third, with an error of 0.98. They cited that when the memory and time spent for training is not so relevant, the BP and variants could be used. In comparison, our results achieved a total error of 0.14 related to the RBP method. In fact, after the training method conclusion, the implemented ANN matrix is not affected in the estimated process. The lower training error is considered an advantage as we lead with the quantization error due to the hardware implementation and function approximation. Despite the authors cite the time constraint to be considered in a real-time solution they didn’t comment about the time the method they proposed takes to process; just associate the size/topology of the proposed ANN as a function of the time execution.
In [9] a more powerful microcontroller BS2PX-IC is used to embedded an ANN to locate a mobile robot. The microcontroller can operate with 125 kbps serial communication through the Wavetrend 433 MHz radio. They considered one ANN for estimating each coordinate, with just one hidden layer, as the previous reference did. The indoor environment of this experiment is about 2 m2. They suggest complement the locating process with additional frameworks, as sonar GPS and additional angle information, but such improvement reflects in aggregating cost to project, to not mention to the increase of power consumption. The results show the errors in function of tracking and angle of the mobile robot, being the tracking RMSE equal to 0.06 and the angle RMSE about 0.12. It is highlighted the difficulties in implementing ANN with more than one output (ordered pair) and more than one hidden layer (more stored information) due to the platform limitations, even if real-time response is required. We consider it as an embedded software implementation dependency problem in references.
In [10] an ANN is embedded in a PIC18f452 microcontroller to estimate the position of a mobile robot. Except they use infrared sensor, the objective is the same: imbuing the best ANN generated through the best training method into a hardware platform and approximate the position of a target given the reading of sensors as inputs. The LM training algorithm showed the lowest training error before others training methods. It is not clearly how the authors tested the proposed method in practice, unless the measures about 90 × 80 cm in the graphical results. The ANN modeled has one input, one hidden layer (with three neurons) and one output. The authors cite the limitation about processing time and memory associated to the chosen hardware platform. The ANN as a position estimator has stated itself an attractive choice, but the platform in which it is implemented has significant implications.
More references on implementing an ANN to estimate targets position can be found in, [11] -[14] . In the next section we explain our methodology and the main characteristics of the proposed method.
3. Methodology
The proposed method considers the real outdoor experiment and the data base acquired from [15] . The data base consists of a set of 6-tuples containing the inputs and outputs of ANN, respectively, the RSSI from anchor nodes and the ordered pair representing the position of the target in a plane. In resume, it consists of four anchor nodes spaced in an out door environment measuring 20 × 22 m2. The anchors receive a broadcast message from one target node located in some region inside this environment. The anchor nodes take the RSSI from that message and apply it to the proposed method. All anchor nodes are in line-of-sight with the target node. The scenario does not offer any obstacle to the signal other than the temperature and humidity as noise parameters. We choose this scenario appropriately to show how the method works.
In the next, we show how the method was implemented and moreover how it works algorithmically.
3.1. Method Implementation
We begin with the data treatment and ANN training algorithm, followed by deciding the ANN topology to be implemented in the FPGA. We consider four anchor nodes that will sequentially operate in the method, transmitting their distributed processing in an ordered path from anchor one to anchor four. To simulate failures on third and fourth anchor nodes, the 21000 data base samples were replicated twice, resulting in a total of 63000 samples. Thereby, we could implicitly apply zeros in the RSSI of replicated samples, related exclusively to the input of fourth anchor node and related exclusively to the input of third and fourth anchor nodes. We assume that, if the third anchor node fails, the fourth anchor fails together, as they will not receive the ordered distributed processing from the third anchor node.
The data base was divided in 75% for training and 25% for testing samples. The training and testing were preceded through the R language through the neural net package, using the Resilient Propagation (Rprop+) algorithm for training. Table 1 shows the parameters assumed in the training step.
We assumed the Universal Approximation Theorem [16] to decide the topology of the ANN, related to number of hidden layers and neurons contained in each one. Our ANN has four inputs, two hidden layers containing four neurons each of them and one output layer containing two neurons.
Each anchor node was implemented in a FPGA Altera™ DE0-nano [17] using VHDL. The chosen platform is recently developed and is affordable as an educational development board. It is considerable tiny in size in comparison with others bigger plat forms that include same resources. The 50 MHz processing capacity offered by DE0-nanogives us assuredness to concentrate in enforcing ANN features without worrying with timing or
Table 1. Parameters for ANN training.
processing issues.
To be implemented in synthesizable form, the free parameters generated for the ANN were converted to a fixed point format [18] , in which the integer part is a 10 bits two’s complement and the mantissa has 6 bits. The total 16 bits is sufficient to convert the bigger number (or lesser) of the free parameters.
The activation function of neurons is approximated using the Elliott activation function [19] , as shown in Equation (1).
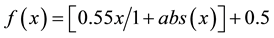 (1)
(1)
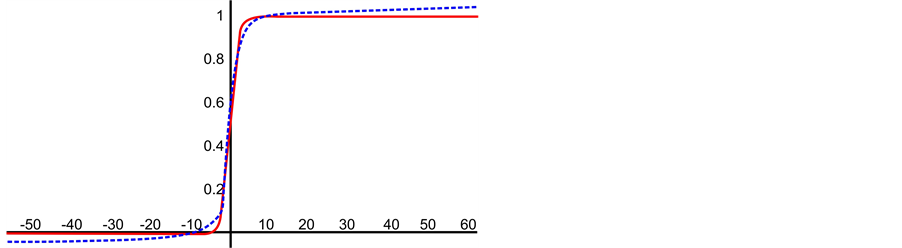
This approximation is due to the Log Sigmoid function being not synthesizable in hardware, i.e., it can’t be implemented because of its logarithm component. In other hand, Elliott function is ease applicable in training ANN due to its simple first derivative, which is used in versions of Back propagation training method. We can visualize the related approximation between the Log Sigmoid and the Elliott activation functions in Figure 1.
To evaluate how close the Elliott can approximate to the Log Sigmoid we computed in each function the interval considered into activation function in the ANN [0; 1] at a step resolution of 0.001. The RMSE of the output of the Elliott function, at these conditions, is equal to ±0.13462, so we can addict this error in the total error of our proposed method.
The description of ANN inside the FPGA is divided in modules: a neuron module, a layer module and an ANN module. The FPGA implementation allows the neurons at same layer being executed in parallel, achieving performance.
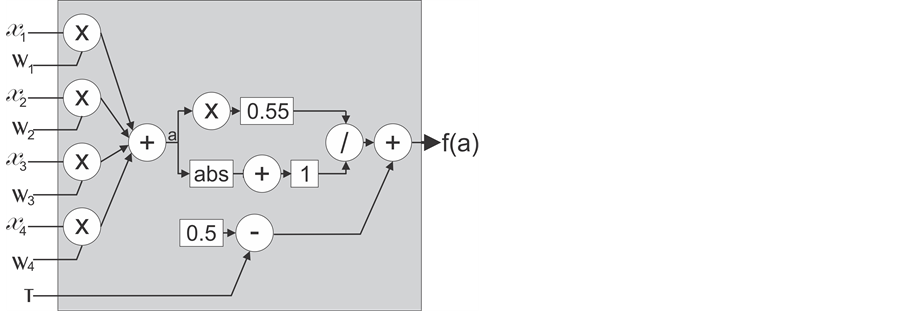
The neuron was implemented to execute the Elliott function’s fundamentals calculation in parallel, as the dependent results do not conflict. The products of summations occur in parallel, followed by the parallel calculation in the dividend and the divisor, then, the resultant summation with the constant, as stated in Figure 2.
In Figure 2, 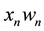 are the products of input and free parameters that is summed and passed to the Elliott Function as the resultant a. The threshold T is a constant subtracted from the constant 0.5 summed in Elliott function, this subtraction occurs in parallel with the rest of operations. Each parallel operation was descripted in an individual flagged process in VHDL, with executes as soon as the dependent operations conclude.
are the products of input and free parameters that is summed and passed to the Elliott Function as the resultant a. The threshold T is a constant subtracted from the constant 0.5 summed in Elliott function, this subtraction occurs in parallel with the rest of operations. Each parallel operation was descripted in an individual flagged process in VHDL, with executes as soon as the dependent operations conclude.
The two hidden layers and the output layers were designed as VHDL components formed by the neuron units. So, the complete ANN was designed as a component formed by the layers. This design allowed the connections being implemented by easily binding the component parts.
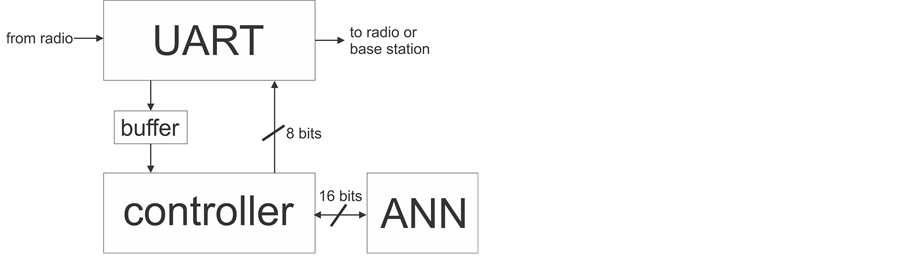
The anchor nodes, containing the ANN, can communicate with each other through the IEEE 802.15.4 Xbee radio standard athwart the 115.200 kbps UART communication. The oversampling is implemented in VHDL to integrate the 1.8 KHz UART frequency with the 50 MHz from the DE0-Nano.
In a top level VHDL modular design, our propose method can be described as a controller, a transceiver and ANN module, all implemented in each anchor node. The controller is modeled as a Moore finite state machine that is responsible for managing data transmission and ANN control. The implemented system can be seen as shown in Figure 3.
In the next section we describe the proposed method as an algorithm.
3.2. Method Description
The method considers one testing target. The target sends a broadcast message which is received on the four anchors. All anchors calculate the RSSI of the broadcast message through the power signal received. For
Figure 1. Relation between the continuous Log Sigmoid (in red) and the Elliott (in blue) functions.
Figure 2. Neuron block diagram.
Figure 3. The block diagram of the whole system.
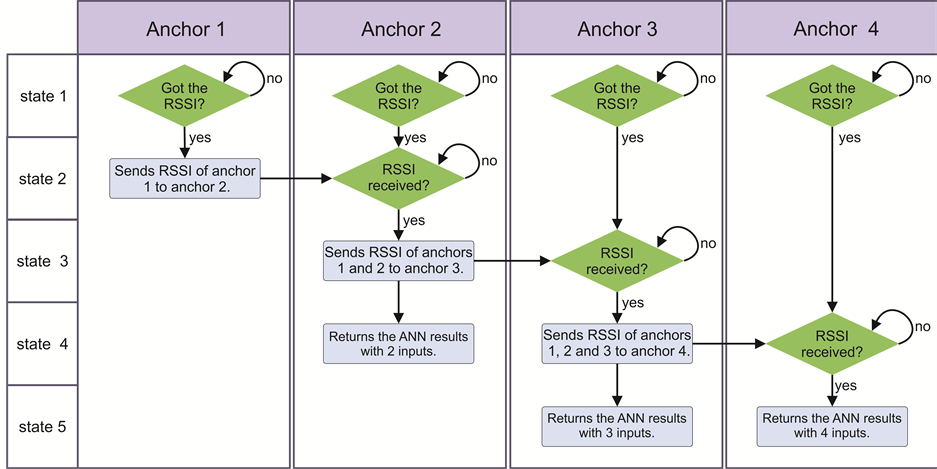
simplicity, we associate a token to identify the beginning anchor in the process. In an ideal case, the first anchor node sends its RSSI to the second anchor node, and the second anchor sends its RSSI and the RSSI of the first anchor to the third anchor. The third anchor sends the three RSSI to the fourth anchor.
As can be seen in Figure 4, the proposed method can be divided in seven mainly steps, vertically processed in each anchor node. The processing at same step is to be executed in parallel between anchors. If the fourth anchor node fails, the method can offer two estimated position (from anchor two and anchor three). If the third anchor fails, the method is still offering some reasonable response through second anchor. An optional but not implemented extension could be the last anchor (third or fourth) node returning the estimated position to the previous anchor. So the previous anchor can calculate some chosen media over the results, improving the accuracy and precision. The contribution of our proposed method is to explore the ANN to estimate with at least two inputs, different those methods based in triangulation, which needs at least three inputs.
In the next section we show our results and the errors associated to the anchor failures.
Figure 4. Flowchart of the proposed method.
4. Results
We took 25% of samples for testing the ANN and calculated the RMSE considering no failure and the failure of third or third and fourth anchors. Table 2 shows the RMS calculated in meters.
We can calculate the total RMSE of the method as being the summation of the training RMSE associated with anchor failure and the RMSE of the discretized free parameters due to hardware implementation. This relation is expressed in Equation (2).
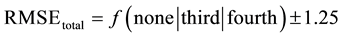 (2)
(2)
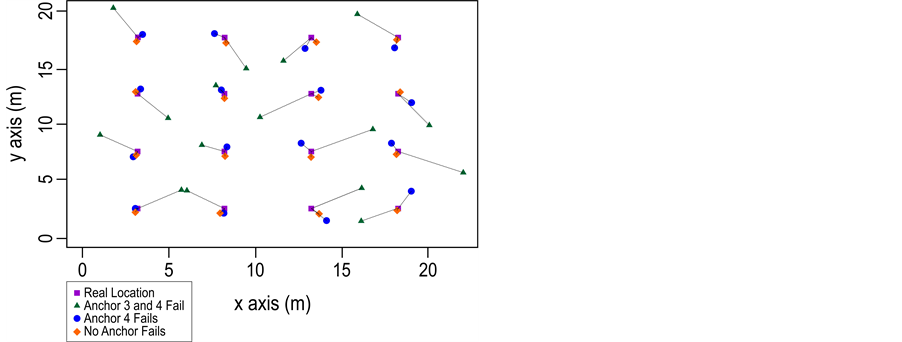
The function f in Equation (2) represents the RMSE considering anchor failures from Table 2. The constant 1.25 is the discretization RMSE generated in the free parameters due to binary representation. Figure 3 shows some location points estimated in the region of 20 × 22 m, considering no failures and anchor’s failure for the related cases.
We can visually observe in Figure 5 the results for the three estimation cases. The estimation with no failures presents a high precision and the failure of just the fourth anchor is a good precision too, considering an approximation. The failure of the third (and consequently the fourth) anchor has a considerable imprecision.
Related with time execution, the neuron was simulated using the ModelSim™, from Altera™, and achieve a total time o execution of 1.75 × 10−7 seconds. This processing time is the same for each layer, as they execute all neurons in parallel. The total time execution of the ANN is 6.80 × 10−7. In fact, the time execution of our proposed method is related to the distance the signal propagates from the target to anchor nodes and between the anchor nodes themselves. The time execution of our proposed method is faster compared with the time transmission. The time transmission is an inherent problem related to any method in location problems, and the reduction time during the location method can contribute to decrease this issue.
5. Conclusions
This work shows how the ANN can still be applied in WSN localization problem, with good approximations, and points the reconfigurable platform (FPGA) offering a way to achieve performance. The proposed method can be extended for multiple channels, if possible, allowing the multiple execution of the same algorithm in the FPGA, with a quite adjustment. The number of anchor nodes could be increased and grouped for estimating as cluster heads, for example. The media may be calculated for the three ANN estimations for better accuracy. The flexibility of FPGA and the ANN implementation allows this work to be extended to another new experiments to get better results.
Figure 5. Visual testing results for 16 coordinates.
Table 2. The RMS error (m) considering no failures and failures of third and fourth anchors.
As future work we intend to perform location of multiple targets by applying this ANN to perform the task.
References
- Alhmiedat, T., Salem, A.O.A. and Taleb, A.A. (2013) An Improved Decentralized Approach for Tracking Multiple Mobile Targets through Zigbee WSNs. International Journal of Wireless & Mobile Networks, 5, 61-76. http://dx.doi.org/10.5121/ijwmn.2013.5305
- Liu, L.Q. (2012) A Parallel and Distributed Computing Platform for Neural Networks Using Wireless Sensor Networks. Ph.D. Thesis, The University of Toledo, Toledo.
- Din, A., Bona, B., Morrissette, J., Hussain, M., Violante, M. and Naseem, M.F. (2012) Embedded Low Power Controller for Autonomous Landing of UAV Using Artificial Neural Network. 10th International Conference on Frontiers of Information Technology (FIT), Islamabad, 17-19 December 2012, 196-203.
- Rahman, M.S., Park, Y. and Kim, K.-D. (2012) RSS-Based Indoor Localization Algorithm for Wireless Sensor Network Using Generalized Regression Neural Network. Arabian Journal for Science and Engineering, 37, 1043-1053. http://dx.doi.org/10.1007/s13369-012-0218-1
- Kumar, S., Jeon, S.M. and Lee, S.R. (2014) Localization Estimation Using Artificial Intelligence Technique in Wireless Sensor Networks. The Journal of Korea Information and Communications Society, 39C, 820-827. http://dx.doi.org/10.7840/kics.2014.39C.9.820
- Zheng, J. and Dehghani, A. (2012) Range-Free Localization in Wireless Sensor Networks with Neural Network Ensembles. Journal of Sensor and Actuator Networks, 1, 254-271. http://dx.doi.org/10.3390/jsan1030254
- Bhardwaj, S. (2013) ANN for Node Localization in Wireless Sensor Network. International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering, 2, 1724-1731.
- Kumar, S. and Lee, S.-R. (2014) Localization with RSSI Values for Wireless Sensor Networks: An Artificial Neural Network Approach. International Electronic Conference on Sensors and Applications, 1 June 2014. http://dx.doi.org/10.3390/ecsa-1-d007
- Sabto, N.A. and Mutib, K.A. (2013) Autonomous Mobile Robot Localization Based on RSSI. Journal of King Saud University―Computer and Information Sciences, 25, 137-143. http://dx.doi.org/10.1016/j.jksuci.2012.10.001
- Saad, A.-M.H.Y. and Alhady, S.S.N. (2014) Embedded Neural Network for Distance Recognition Using Distance Sensor. 1st International Conference of Recent Trends in Information and Communication Technologies, Universiti Teknologi Malaysia, Johor, Malaysia, 182-191.
- Gogolák, L., Pletl, S. and Kukolj, D. (2011) Indoor Fingerprint Localization in WSN Environment Based on Neural Network. Proceedings of the IEEE 9th International Symposium on Intelligent Systems and Informatics (SISY), Subotica, 8-10 September 2011, 293-296.
- Chen, C.-S. (2012) Artificial Neural Network for Location Estimation in Wireless Communication Systems. Sensors, 12, 2798-2817. http://dx.doi.org/10.3390/s120302798
- Neves, A., Fonseca, H.C. and Ralha, C.G. (2013) Location Agent: A Study Using Different Wireless Protocols for Indoor Localization. International Journal of Wireless Communications and Mobile Computing, 1, 1-6.
- Pajares, G. (2012) Sensors in Collaboration Increase Individual Potentialities. Sensors, 12, 4892-4896. http://dx.doi.org/10.3390/s120404892
- Larrat, M., Machado, L. and Monteiro, D.C. (2013) Performance Evaluation of Lateration, KNN and Artificial Neural Networks Techniques Applied to Real Indoor and Outdoor Location in WSN. Journal of Communication and Computer, 12, 72-81.
- Csáji, B.C. (2011) Approximation with Artificial Neural Networks. M.Sc. Thesis, Faculty of Sciences, Eötvös Loránd University, Budapest.
- Altera (2013) DE0 Nano User Manual v1.9.
- Bishop, D. (2010) Fixed Point Package User’s Guide.
- Sibi, P., Allwyn Jones, S. and Siddarth, P. (2013) Analysis of Different Activation Functions Using Back Propagation Neural Networks. Journal of Theoretical and Applied Information Technology, 47, 1344.
NOTES
*Corresponding author.