Wireless Sensor Network
Vol.5 No.9(2013), Article ID:36540,11 pages DOI:10.4236/wsn.2013.59020
Robust Cubic-Based 3-D Localization for Wireless Sensor Networks
School of Electrical & Electronic Engineering, Nanyang Technological University, Singapore City, Singapore
Email: hninyushwe@ntu.edu.sg, ehjchong@ntu.edu.sg
Copyright © 2013 Hnin Yu Shwe et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 11, 2013; revised August 8, 2013; accepted August 22, 2013
Keywords: Wireless Sensor Network; Localization Technique; 3 Dimensions
ABSTRACT
The rapid progress of wireless communication and the availability of many small-sized, light-weighted and low-cost communication and computing devices nowadays have greatly impacted the development of wireless sensor network. Localization using sensor network has attracted much attention for its comparable low-cost and potential use with monitoring and targeting purposes in real and hostile application scenarios. Currently, there are many available approaches to locating persons/things based on global positioning system (GPS) and radio-frequency identification (RFID) technologies. However, in some application scenario, e.g., disaster rescue application, such localization devices may be damaged and may not provide the location information of the survivors. The main goal of this paper is to design and develop a robust localization technique for human existence detection in case of disasters such as earthquake or fire. In this paper, we propose a 3-D localization technique based on the hop-count data collected from sensor anchors to estimate the location of the activated sensor mote in 3-D coordination. Our algorithm incorporates two salient features, cubic-based output and event-triggering mechanism, to guarantee both improved accuracy and power efficiency. Both simulation and experimental results indicate that the proposed algorithm can improve the localization precision of the human existence and work well in real environment.
1. Introduction
Wireless sensor network (WSN) is an emerging technology and now widely used in many application areas; including civil monitoring, environmental monitoring and so on. In these applications, a significant number of sensor nodes are deployed on a widely geographical area to form a sensor network [1]. In WSN, sensor nodes themselves are not connected to the Internet directly [2]. The main task of the sensor mote is to collect the date points from its surrounding environment at regular time interval, which transforms them into an electrical signal and disseminates the signal to the sink or base node via some reliable communication medium. The sink node is usually connected to the Internet and it is the interface between the user and the sensor network.
In WSNs, localization is necessary to allow end-users to know the locations of sensors which have been triggered by events or readings. While GPS can be incorporated within each mote in the WSN, it is often costly to implement this function if the WSN consists of large number of motes, which typically amount up to thousands [3]. To overcome this problem, the locations of some of the motes are made known beforehand and these motes are known as anchor motes [4]. These motes are often used in localization techniques to identify the location of the trigger motes or target motes [5].
Additionally, localization is a key issue in WSN since it is very important to provide the accurate location information in timely manner. For example, after a disaster such as fire or earthquake, WSN is very useful to detect the survivor existence in order to perform the rescue operation [6-8]. Quickly searching and rescuing survivors are key issues in many disasters since it can save lots of people’s life. Most of the current localization techniques based on WSN technologies provide the location information in 2-D coordination. That means we can only know the location of the objects with xand y-coordinates. In some situation, the height such as z-coordinate may be useful and important to us. For example, if we like to measure any crack or damage of the bridge, it may be useful to know the position with all x-, y-, and z-coordinates to identify the exact location of the damage in the bridge. In addition, it is complementary for disaster management tasks such as finding escape route and rescuing survivors as well. For example, in case of fire in a high building, we can simply find out the escape route in a certain floor with the use of 3-D location information.
According to the features that sensor networks have no space constraints, flexible distribution, mobile convenience and quick reaction, in this paper, we proposed a 3-D localization scheme that uses wireless sensor network to detect the human/object existence which is applicable in all types of rescue applications. Our proposed technique will provide the location of the object in a 3-D format. With the proposed algorithm, we can monitor the building based on sensor network, quickly find out the survivors after any disaster and perform the rescue operation in the most effective way.
The rest of the paper is organized as follows. We first briefly describe some related works in Section 2. Section 3 describes the key idea of our proposed method to obtain 3-D localization precision of the nodes. Theoretical and experimental results are presented in Section 4. Finally, we conclude the paper in Section 5.
2. Related Works
Currently, the localization techniques in WSN can be generally classified into three categories, range-based localization technique, range-free localization technique and mobile-beacon-based technique. All these techniques are considered 2-D location techniques because the output location information will be in terms of xand ycoordinates.
Range-based techniques are based on distance estimation between motes. In other words, range-based technique conducts complex measurements on distance or angle of arrival signals in order to estimate the target location by using sophisticated devices. Due to the expensive hardware cost, range-base technique is rarely used in WSN applications which require huge number of sensor nodes. In range-free techniques, on the other hand, the estimation of the target node position is solely based on the connectivity between non-anchor nodes and anchors [9]. In mobile-beacon-based technique, the position of the beacon mote is dynamically changing and the location of unknown mote is estimated by computing the range between the unknown mote and the mobile beacon. Our proposed localization technique belongs to the range-free technique and thus, in this section, we will briefly discuss about other range-free techniques which make use of similar assumptions.
2.1. DV-Hop Technique
In [10,11], D. Niculescu and N. Badri proposed a rangefree localization method called DV-Hop. This is the most basic range-free technique which employs a classical distance vector exchange so that all nodes in the network get the distances to different anchors in hop-count numbers. The basic idea is to transform the distance to all anchor nodes from hops to meters by using computed average size of a hop.
Accordingly, in DV-Hop, a mote will establish information of the locations and number of hops from this mote to other motes in the WSN. The mote will then make an approximation of the single-hop distance where the information is flooded throughout the WSN. Lastly, based on the location of anchor motes and the approximate single-hop distance, the mote will then be able to make an approximation of its own location. Refer to Figure 1, mote 1, M1, can estimate its distance from M2 and anchor 1, A1. Since the position of A1 is known to M1, M1 can estimate its location with respect to A1. The advantages of the DV-Hop scheme are its simplicity and the fact that it does not depend on measurement error. However, despite its simplicity, DV-Hop propagation method is only applicable to isotropic networks in which the properties of the graph are the same in all directions.
2.2. Monte-Carlo Localization Technique
The Monte Carlo Localization (MCL) is the first technique exclusively developed for tracking moving sensor nodes [12]. The key idea is to represent the posterior distribution of possible sensor locations using a set of weighted samples.
In MCL algorithm, time is divided into discrete time unit so that a moving node can be re-localized to the new position in each new time unit. The algorithm consists of two phases. During the initialization phase (time t = 0), a sensor node has no knowledge about its position. Therefore, a random N sample is selected within the deployment area, which form the first sample set L0. The following phase will then repeat itself at each time unit. At each following time step, the new set Lt is obtained based on both possible node movement and new observations on node’s connectivity to the anchors. This process can be further divided into two steps: prediction and filtering.
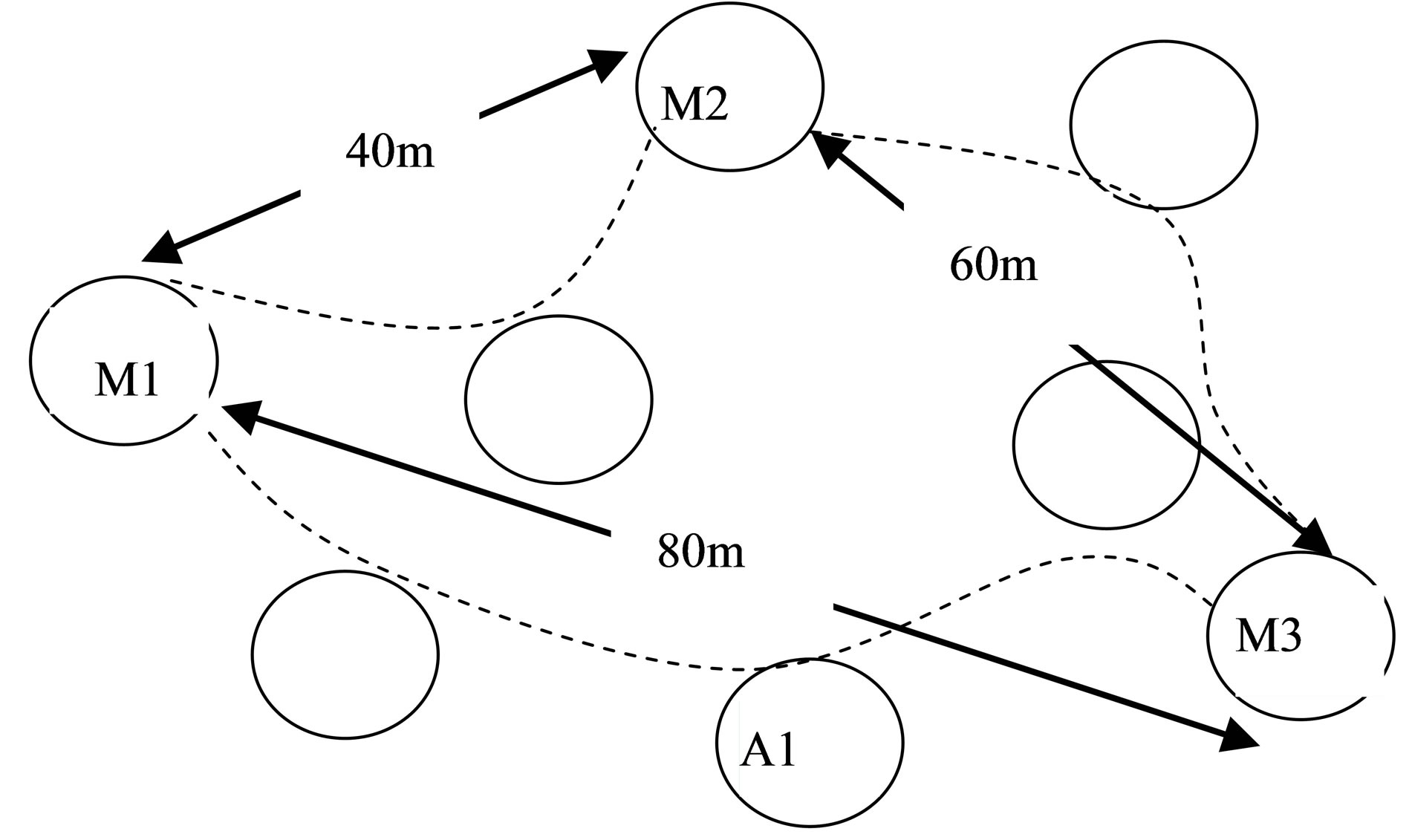
Figure 1. Example of DV-hop technique.
In prediction step, a node makes use of its previous location in Lt−1 together with the mobility model to obtain its new set of positions Lt. The algorithm assumes that the node has no knowledge about its speed and moving directions within the time unit, except that the maximum velocity is Vmax. Therefore, the new node position should lie within the circular region centered at 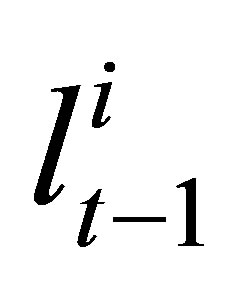 with radius Vmax. A new set of
with radius Vmax. A new set of 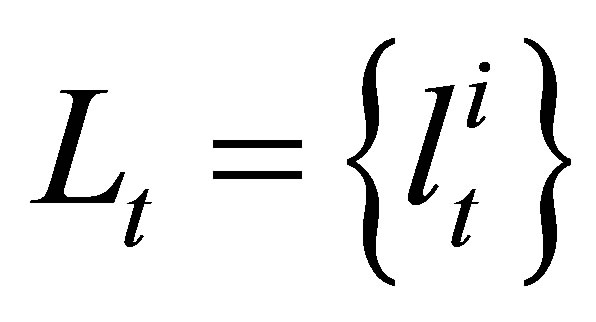 can be predicted in this way. However, the prediction step also reflects an increased uncertainty about the node’s position because Lt−1 contains many possible
can be predicted in this way. However, the prediction step also reflects an increased uncertainty about the node’s position because Lt−1 contains many possible 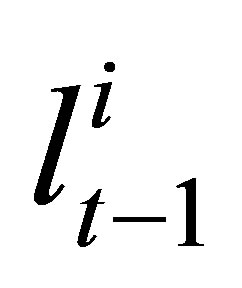 with unknown motion. Hence, a step which can eliminate some of the samples predicted from the previous step is also necessary.
with unknown motion. Hence, a step which can eliminate some of the samples predicted from the previous step is also necessary.
The following step is called filtering, in which the impossible calculated locations from the prediction process based on new observations between the mote and the anchors in the vicinity will be eliminated. The observation is based on the signal connectivity between node and anchor. If a node can receive signal from an anchor, it must fall within the detection range of the anchor. If a mote is unable to do so, it must be outside the range of the anchor. Any node that falls beyond the anchor range will be filtered out from the set Lt. However, since this process may cause the number of remaining possible positions to drop below N, resampling process is required so that N location samples can be maintained in each time step. The resampling is carried out by repeating prediction and filtering steps in each time unit. Iteration of these two processes will maintain a set of samples and, in the end, the node location estimation is done by taking the average of all N sample values in set Lt by the equation:
 (1)
(1)
2.3. Monte-Carlo Localization Boxed Technique
The Monte-Carlo Localization Boxed (MCB) technique [13] was developed based on the MCL technique. The major differences are the way of using anchor information and the method for drawing new samples. While MCL algorithm uses the two-hop anchor information in the filtering step, MCB algorithm muses both one-hop and two-hop anchor information in both prediction and filtering steps. In MCB, anchor information serves as a constraint to the area from which the samples are drawn. By reducing the area to sample from, a given number of N samples can be drawn more easily with less rejection probability in filtering step.
The initialization phase of MCB is the same as which in MCL; at t = 0 the node has no knowledge about its own position. An initial anchor box B0 is set up, from which the initial random sample set L0 is drawn. If the node is not connected to any anchor, the coordinates of the anchor box is 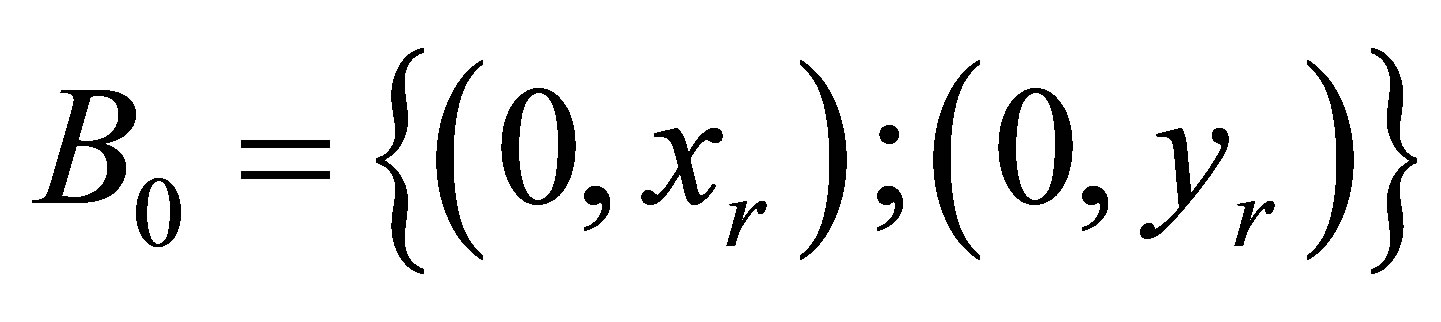 where xr and yr is the maximum x and y coordinate of the deployment area. Otherwise, the anchor box is built that covers the area where the anchors’ radio ranges will overlap. The coordinates of B0 is given as follows:
where xr and yr is the maximum x and y coordinate of the deployment area. Otherwise, the anchor box is built that covers the area where the anchors’ radio ranges will overlap. The coordinates of B0 is given as follows:
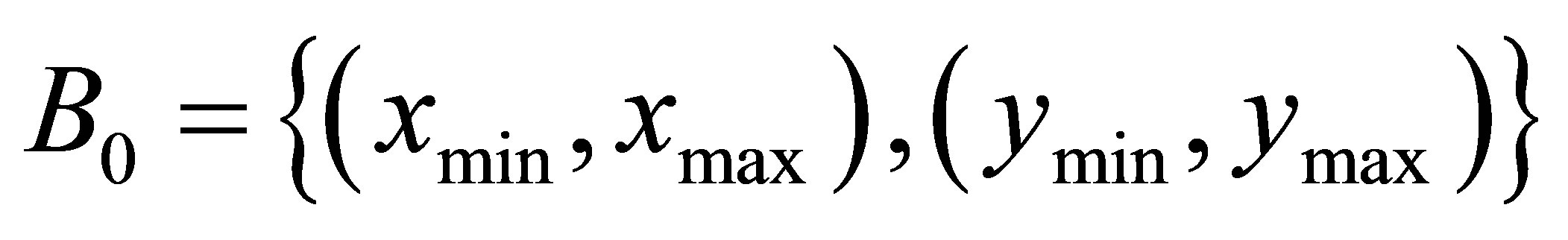 (2)
(2)
Let 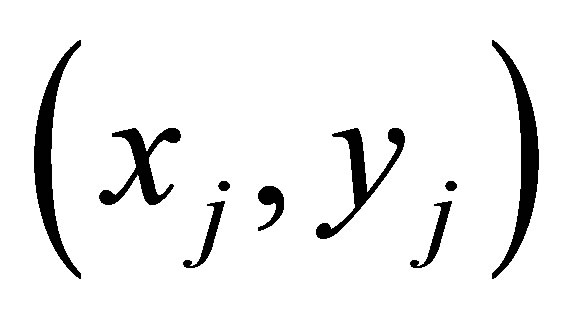 denotes the coordinate of anchor j. Hence, the coordinates of the four corners of B0 is also given by:
denotes the coordinate of anchor j. Hence, the coordinates of the four corners of B0 is also given by:
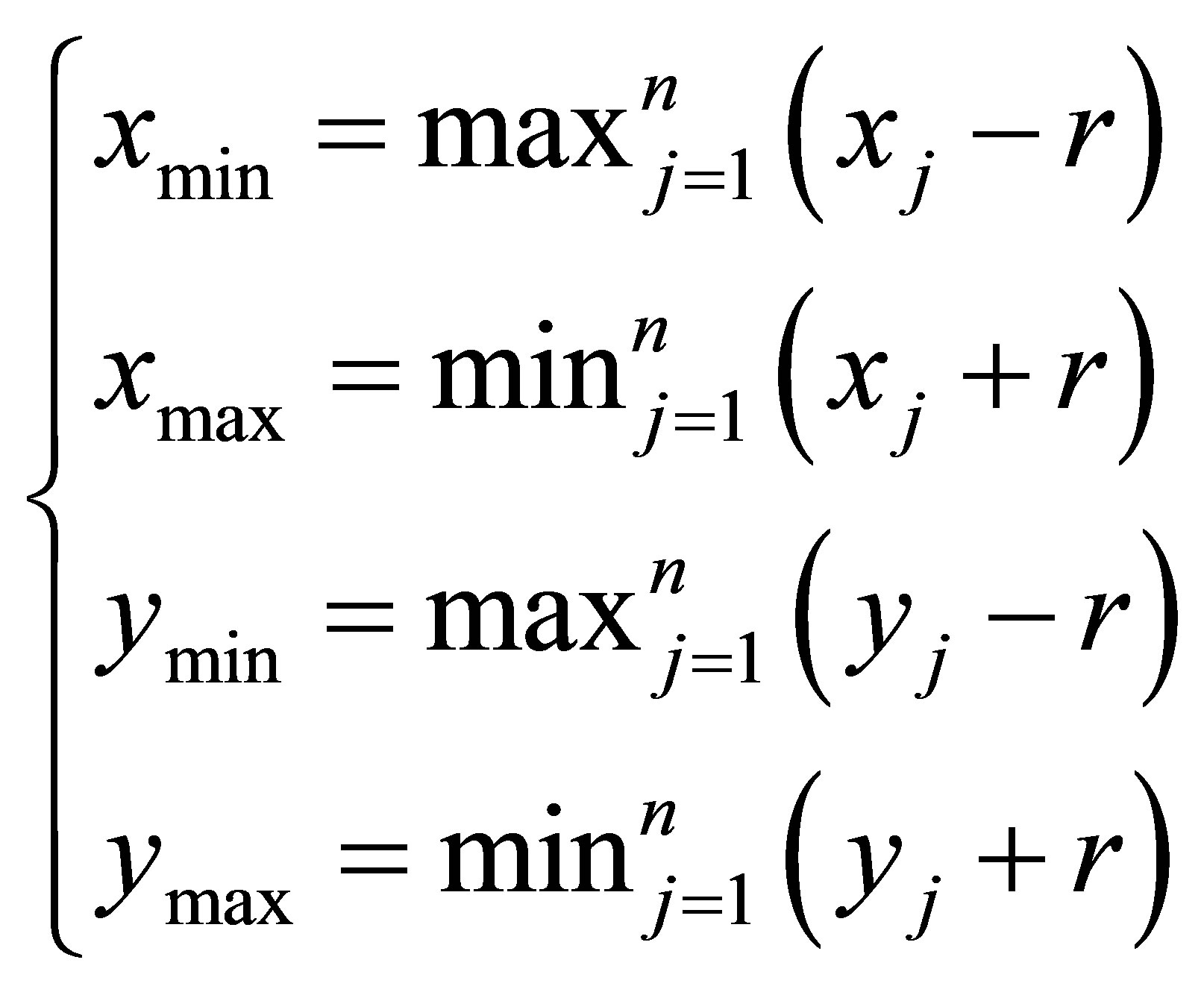 (3)
(3)
Figure 2 shows an example of how anchor box is created. At each new time interval, a new B0 is obtained and the overlap of this new B0 with the B0 obtained in the previous time interval will be the area in which the new location of the mote lies. If the value of anchor box vertex coordinates exceeds the border of deployment area, MCB algorithm will reset it to the coordinate value of the border.
3. Proposed 3-D Localization Technique
The basic idea of proposed technique is to break down the monitored 3-D space into an n × n × n grid structure and generates an output cube, a 3-D space, where the target node is located. In this localization technique, the coordinates of all anchor nodes are known in advance. It is assumed that there are a number of relay nodes that
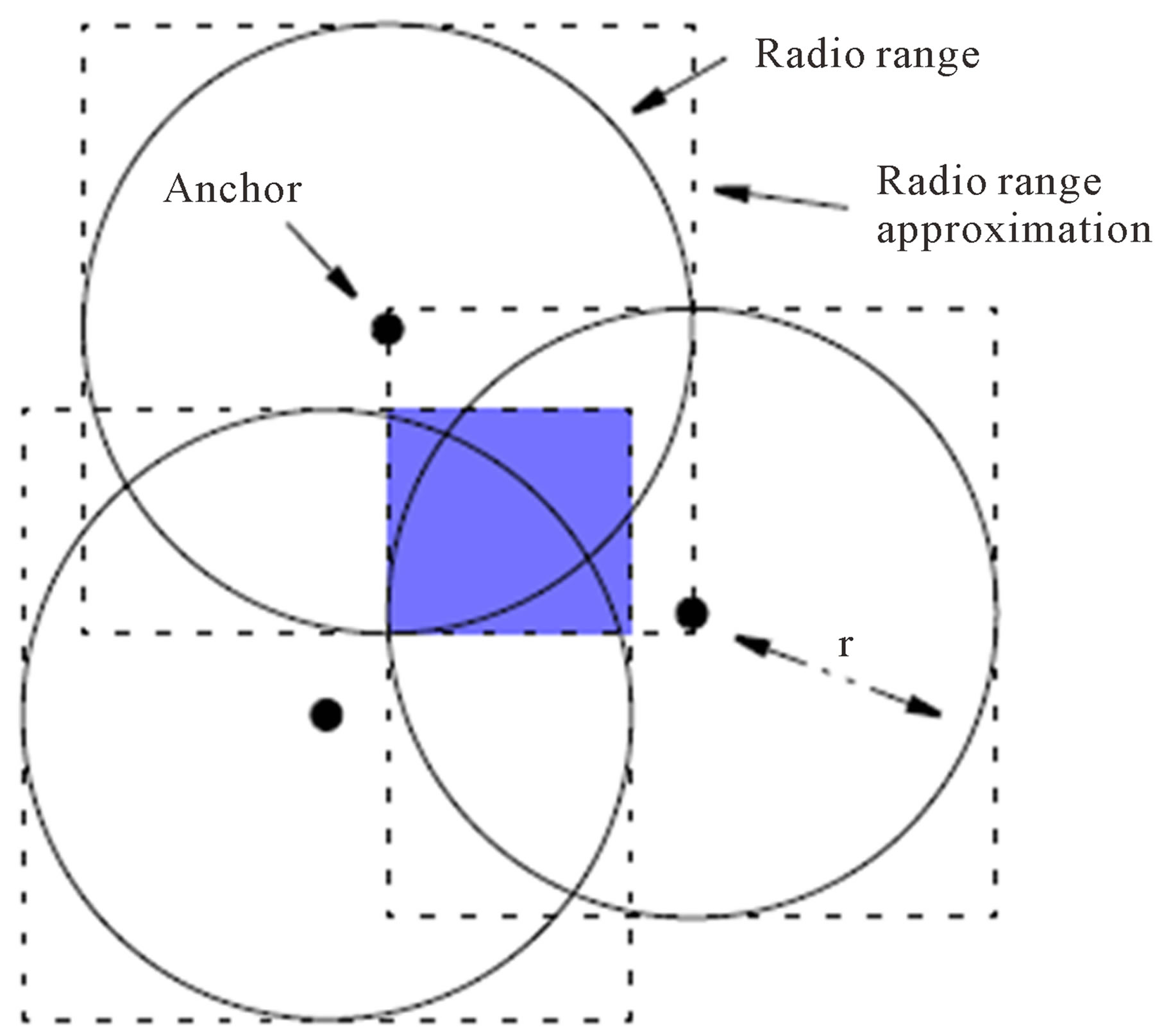
Figure 2. Anchor box established in MCB.
can relay the message from target node to each anchor. The transmission ranges of all relay nodes and anchors are the same and fixed. The localization is carried out by calculating the smallest numbers of hop-count from the target node to each anchor through a number of intermediate relay nodes. Thus, a shortest path routing is assumed. Based on that hop count information, the vertex coordinates and volume of output localizing cube, that cover the target node, can be found.
For this algorithm, the monitored 3-D space is enclosed within (0, 0, 0) and (Xs, Ys, Zs). The algorithm first divides the monitored space into an n × n × n grid structure and places eight fixed anchor nodes at eight corners. Figure 3 shows a 14 × 14 × 14 monitored space with eight anchors at each corner and several number of relay nodes. As shown in Figure 4, the dimension of each basic cube is r × r × r cubic unit and the diagonal length, d, of a cube is same as the transmission range, R, of the wireless nodes. Thus, the length, r, of one side of a cube, is given by:
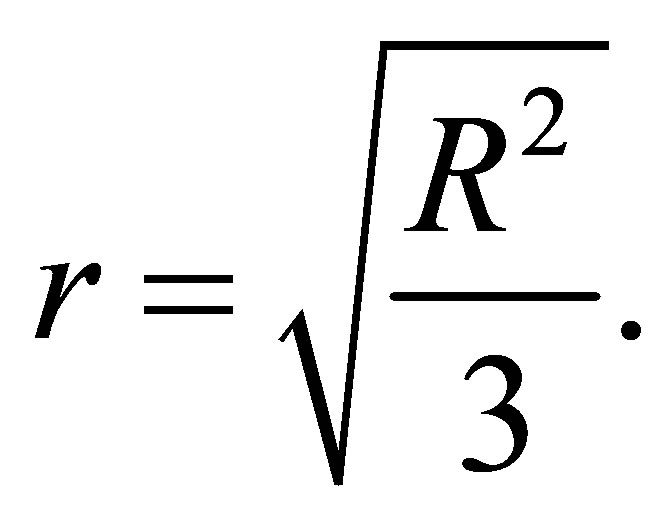 (4)
(4)
3.1. Assumption
Our proposed localization algorithm adopts similar assumptions as the MCL and MCB algorithm, which are:
1) Anchor motes, which are equipped with GPS or fixedly-placed at pre-known locations, are allowed to know their location all the time;
2) The transmission range of all anchors and relay nodes is identical and equal to R;
3) There is enough number of relay nodes inside the 3-D monitored space.
4) The number of hop count from target node to each
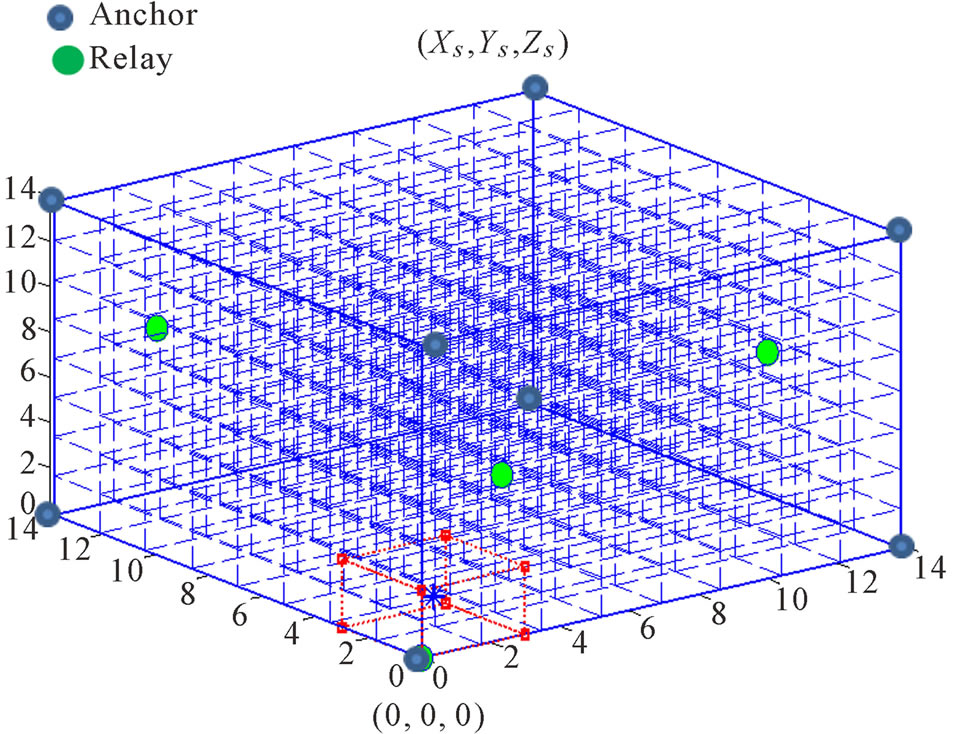
Figure 3. A 3-D monitored space with eight anchors.
anchor through the number of relay node is shortest. Thus, the shortest path routing is assumed to be used.
3.2. Finding Distance between Anchors and Target Node
In the first stage of this cubic-based 3D-localization technique, the distance between each anchor and the target node will be established in terms of X, Y and Z coordinates as in Figure 5. The shortest distance between two points, d, can be found by using the equation:
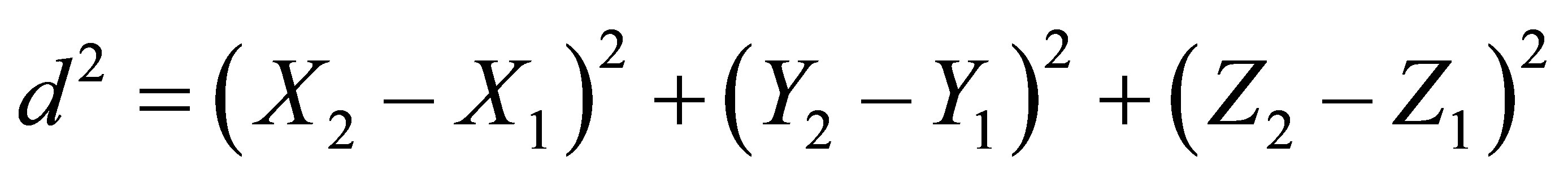 (5)
(5)
After obtaining the shortest distance between the target node and each anchor, we will be able to find the smallest number of hops from the target node to the respective anchor through relay nodes. The number, H, of hops, from the target node to each anchor can be found by the following relationship:
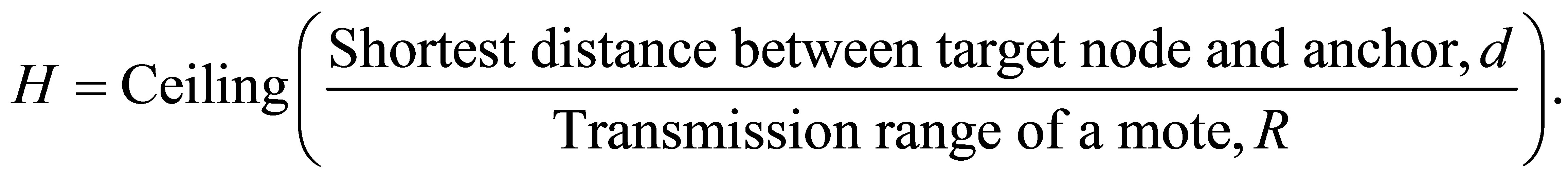
In WSN, it is assumed that the number of hop count from the target node to each anchor can be obtained through the intermediate relay nodes. Based on the hop count information collected from each anchor, we will have a set of hop-count data
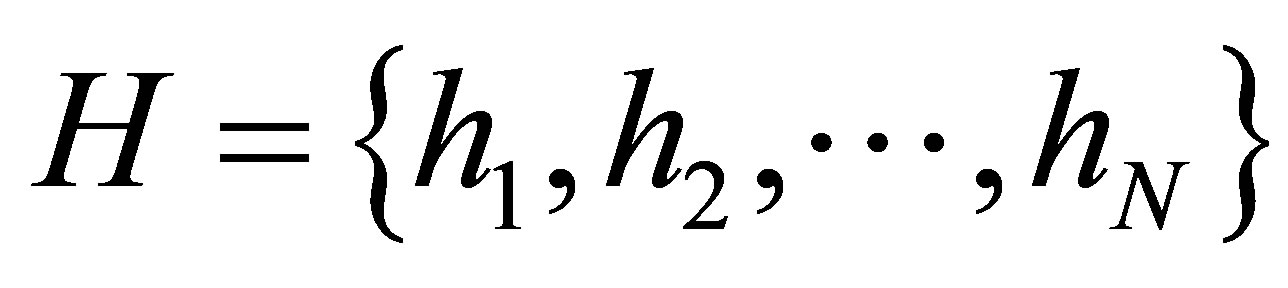
where hj is the number of hops from the target node to anchor mote j and N is the number of anchor motes. The output of the algorithm is a 3-D cube, B, which contains possible locations of the target node expressed in terms of x-, y-, z-coordinates (xmin, ymin, zmin) and (xmax, ymax, zmax) of the cubic space.
For the algorithm, the distance for 1 hop-count is set as being equivalent to the transmission range of a node. Hence, if
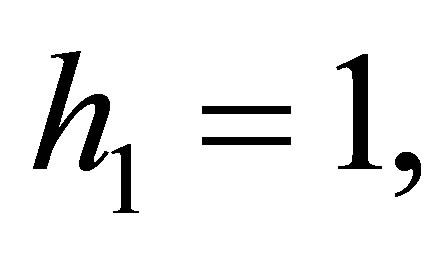
the target node must be inside the volume of 1-hop cubic space of Anchor 1. In this way, the hop count,
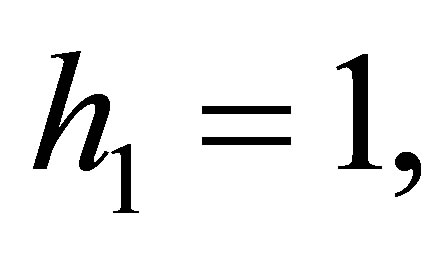
of Anchor 1 will in fact form a cube from the Anchor with the length of the diagonal of 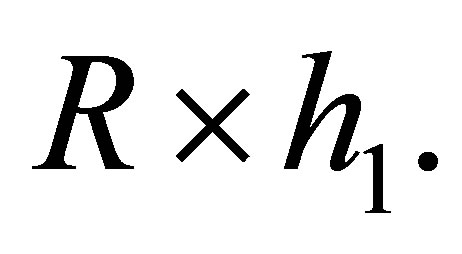
The algorithm will then determine a cube, Bj, which covers the target node. The output cube is a hj-hop count covered cube with Anchor j (Xj, Yj, Zj) located at one corner of the cube. The X, Y and Z coordinates of lower
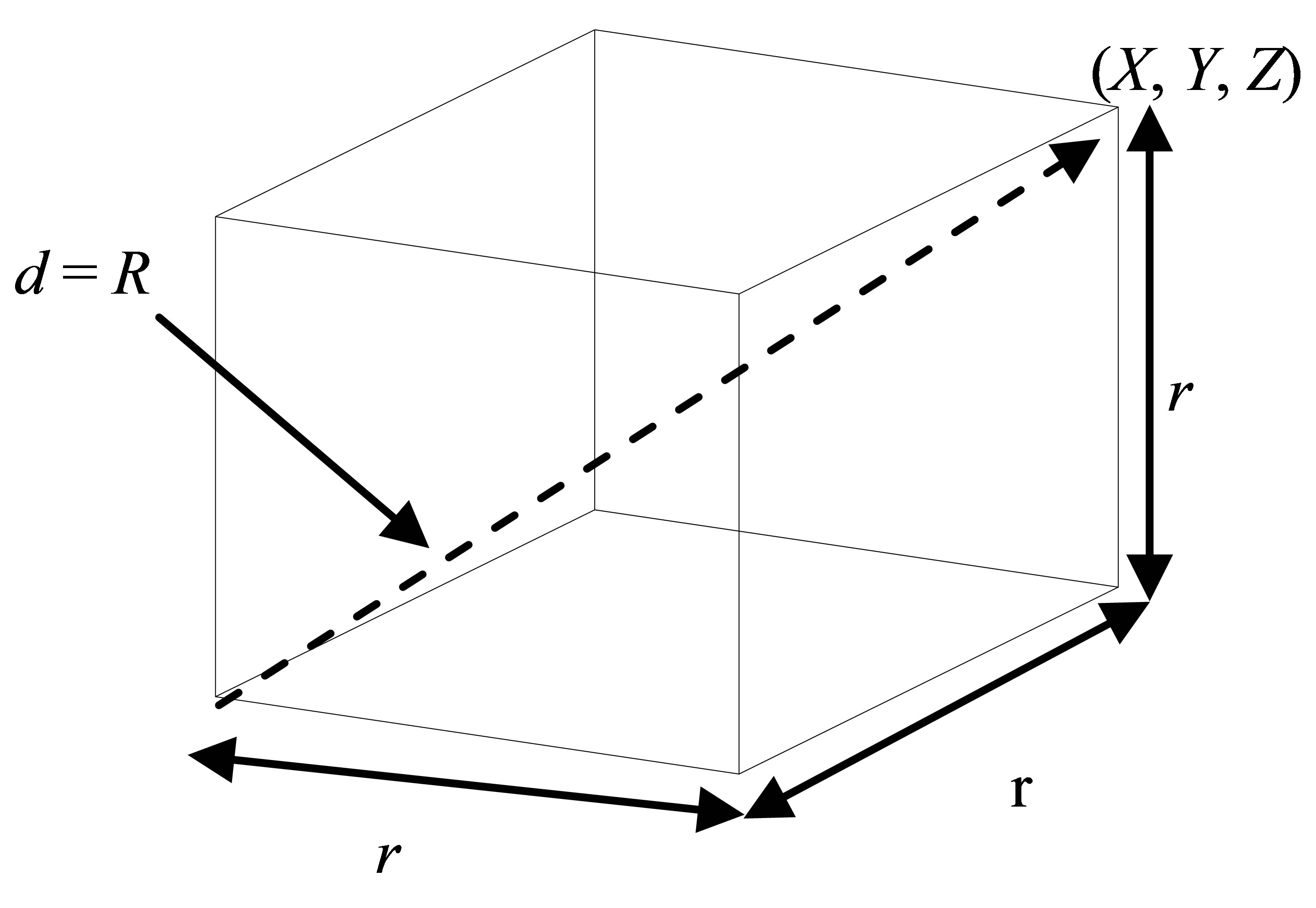
Figure 4. Illustration of one basic cube.
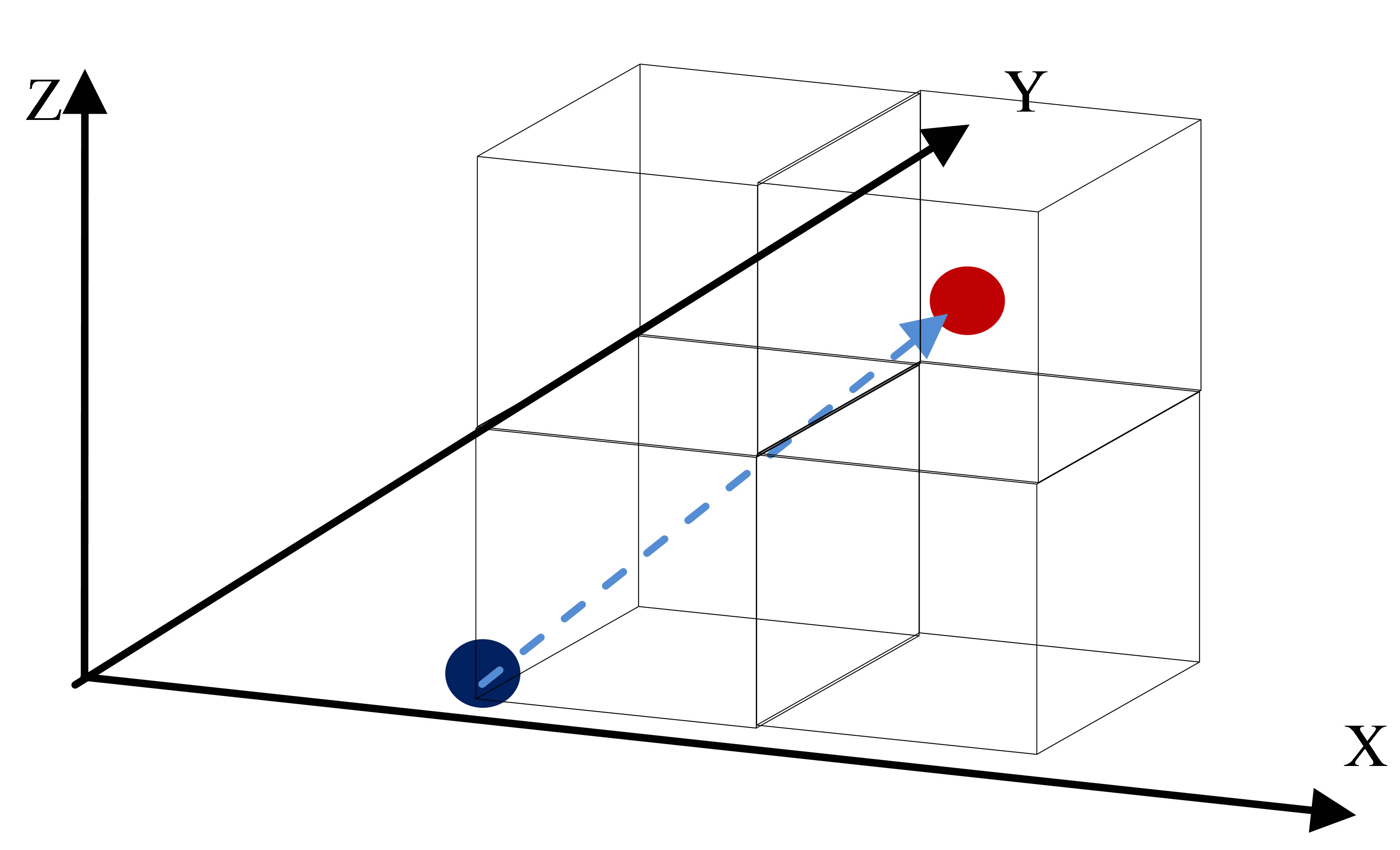
Figure 5. Finding distance between anchor mote and target node.
and upper corners of the output cube, Bj, are given by:
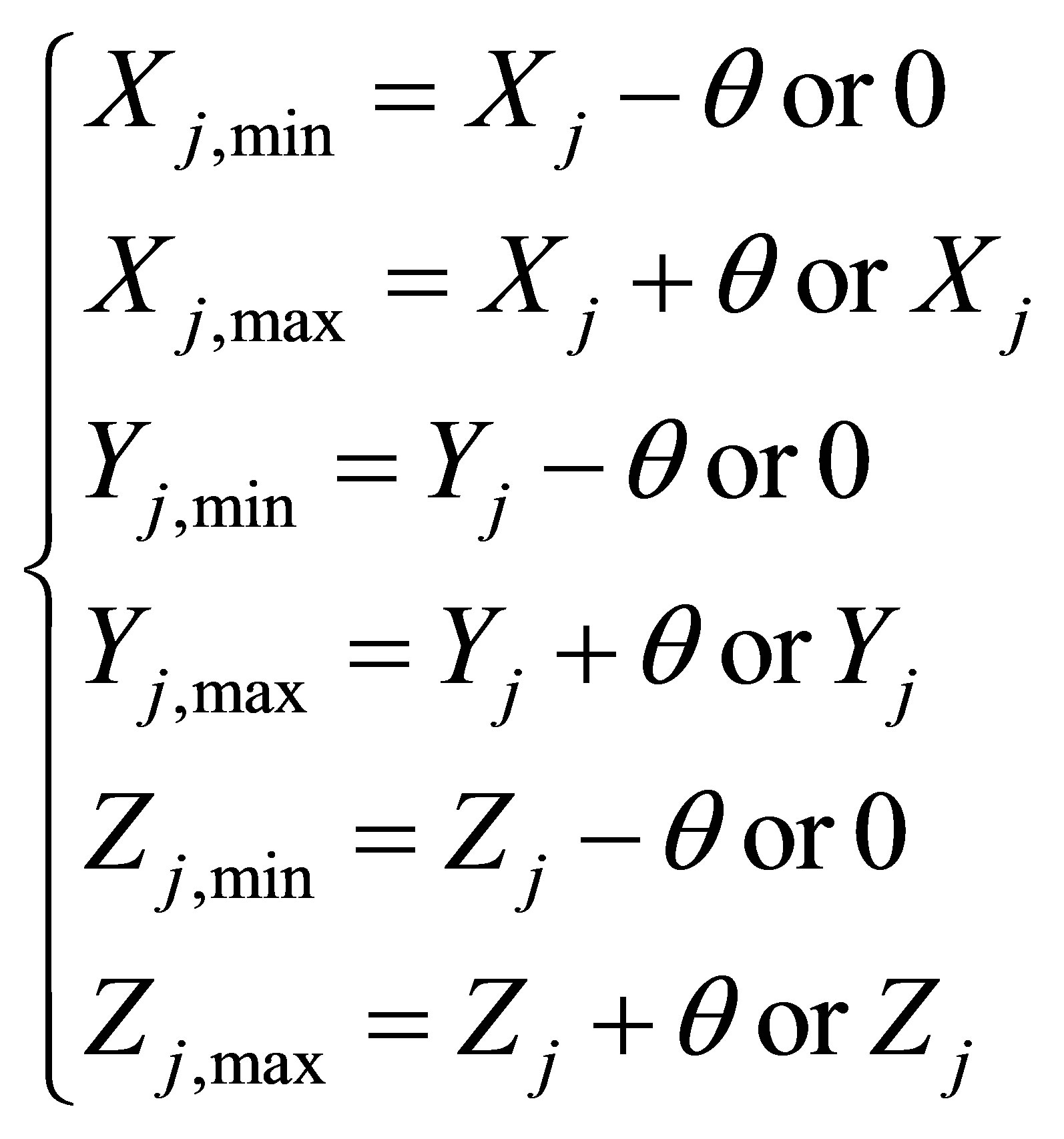 (6)
(6)
where
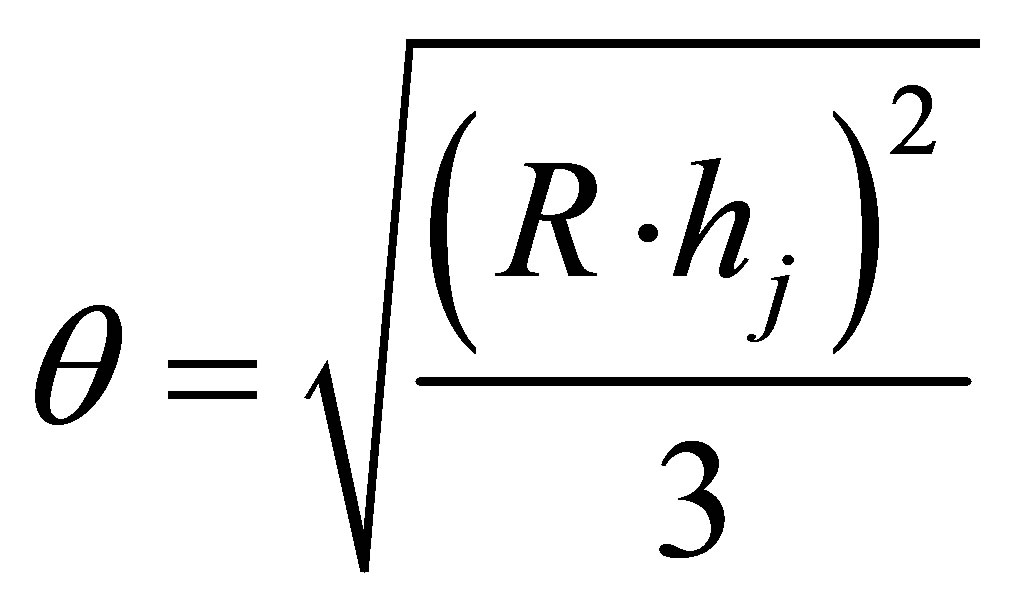 .
.
Figure 6 shows the output cube which contains the target node with lower and upper corner points as Anchor j and Point B, respectively.
3.3. Finding the Location of the Target Node
When we have more than one anchor nodes within the grid structure, we will receive a set of hop-count data, 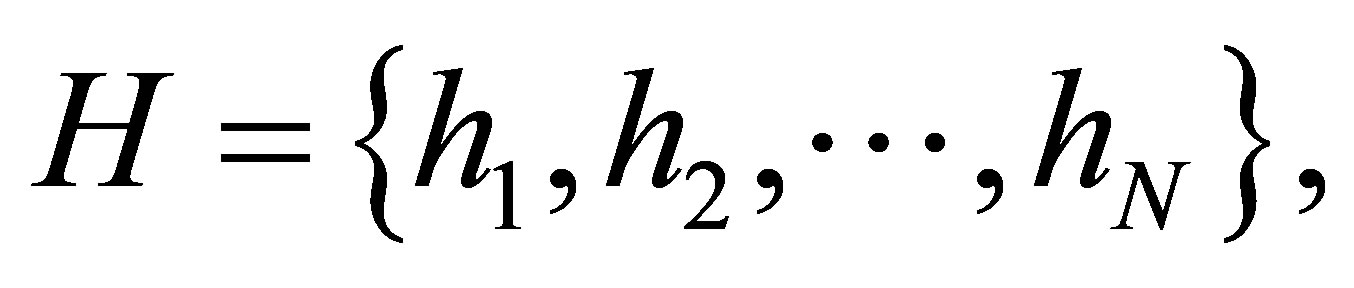 from N anchors. With each value of hj, we will be able to find a corresponding 3-D cube Bj for each anchor. By finding the overlapping volume of all the Bj, we will be able to determine the 3-D space B. Hence,
from N anchors. With each value of hj, we will be able to find a corresponding 3-D cube Bj for each anchor. By finding the overlapping volume of all the Bj, we will be able to determine the 3-D space B. Hence,
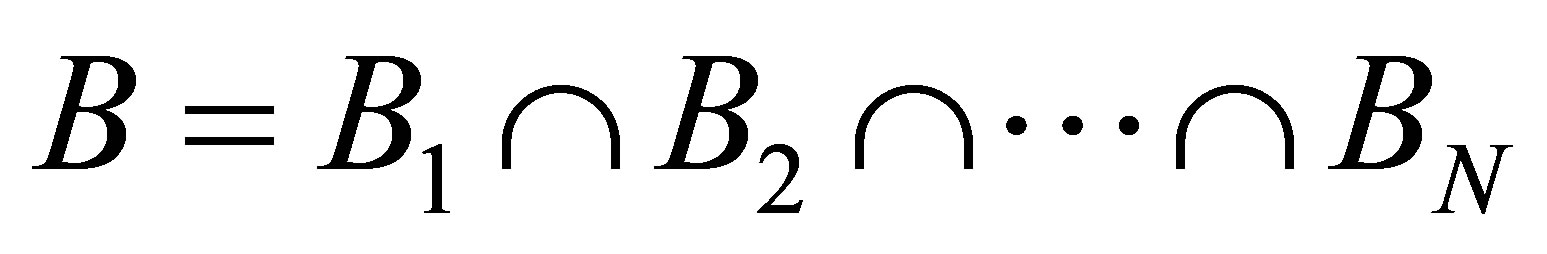 (7)
(7)
The 3-D cube B is the estimated cube which includes
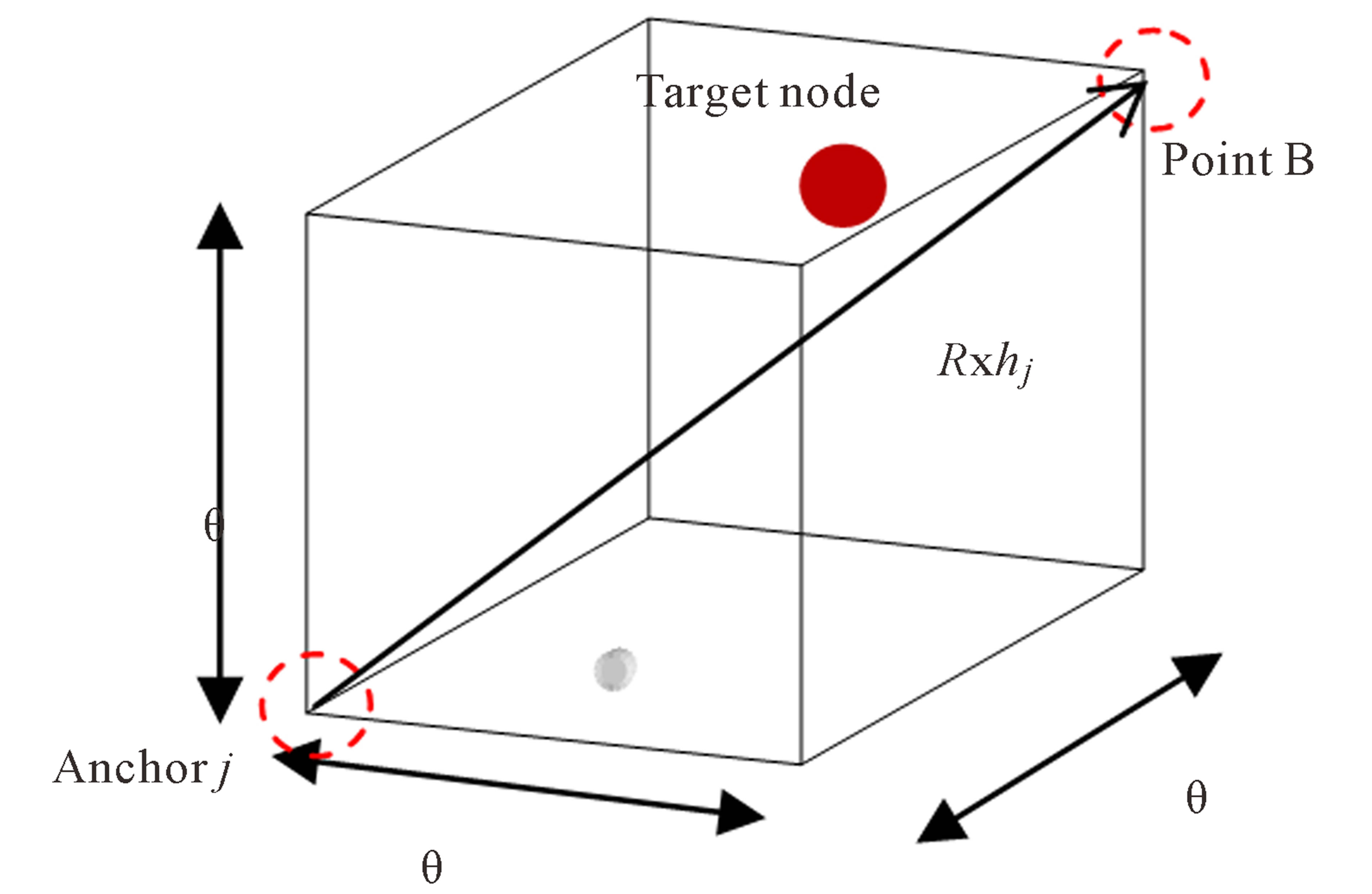
Figure 6. Output cube containing the target node.
the location of the target node. The upper bound and lower bound of X, Y and Z coordinates for this cube is given by:
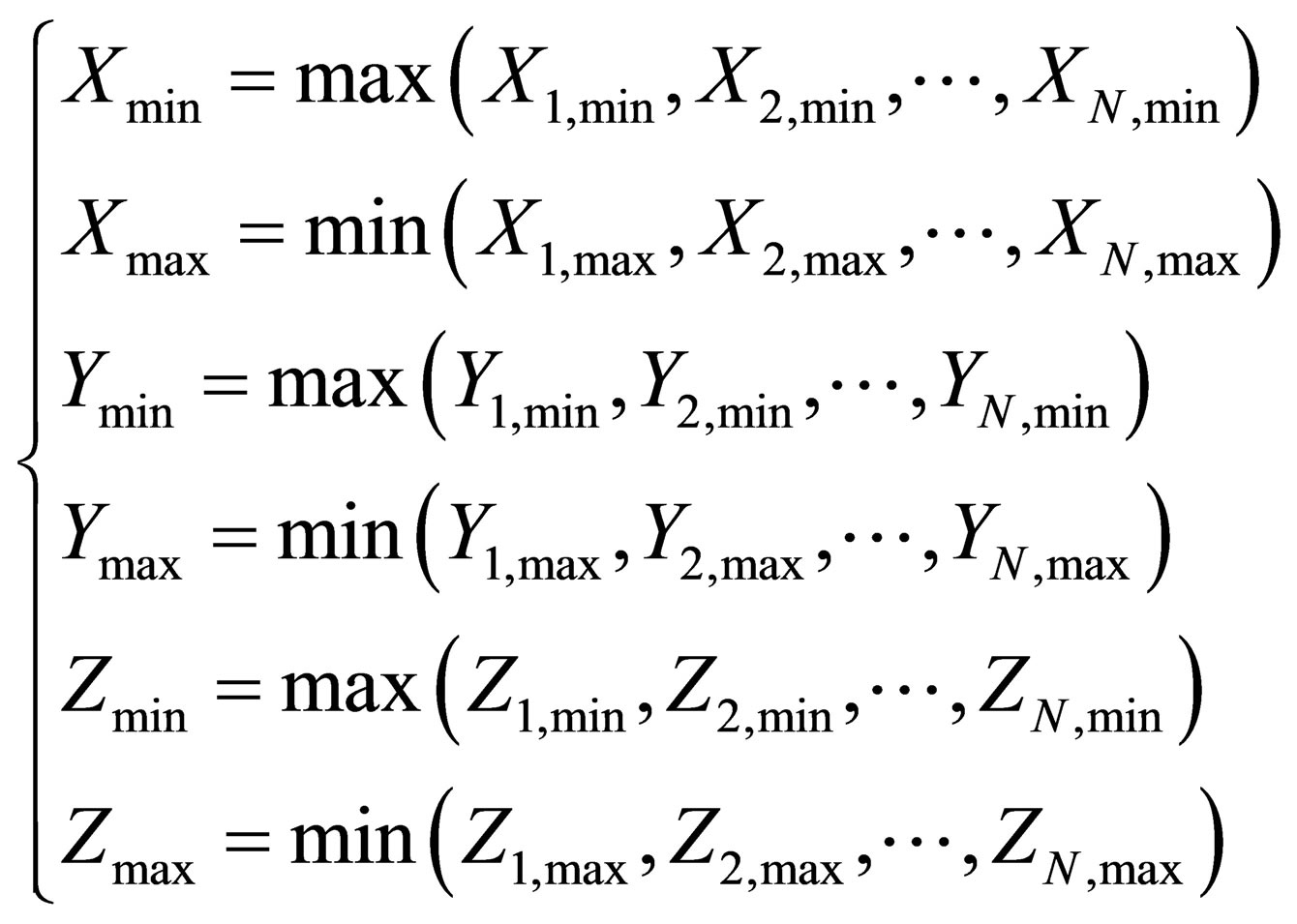 (8)
(8)
Based on this, we will be able to obtain the corresponding cube for each anchor. Assuming that we only have two anchors, we will obtain two cubes as shown in Figure 7 where the possible location of the target node is enclosed with the overlapped cube, red box. We will then find the common volume intersected by these two cubes and this will help us narrow down the possible cube volume which contains the target node. Point C is one corner of this cube which is the minimum point in terms of X, Y and Z coordinates and Point D is the corner directly opposite Point C which is the maximum point in terms of X, Y and Z coordinates. We will then proceed to find a possible 3-D space bounded with the red dotted box as shown in Figure 8 which shows the estimated cube contains the target node.
4. Simulation and Experimental Results
In this section, we will present both theoretical results obtained from Mat Lab simulation and experimental results using Crossbow wireless sensor components.
4.1. Simulation Setup
In this sub-section, we evaluate the performance of our proposed 3-D cubic-based localization algorithm based on Mat Lab simulation. For Mat Lab simulation, we set up the WSN as the parameters shown in Table 1.
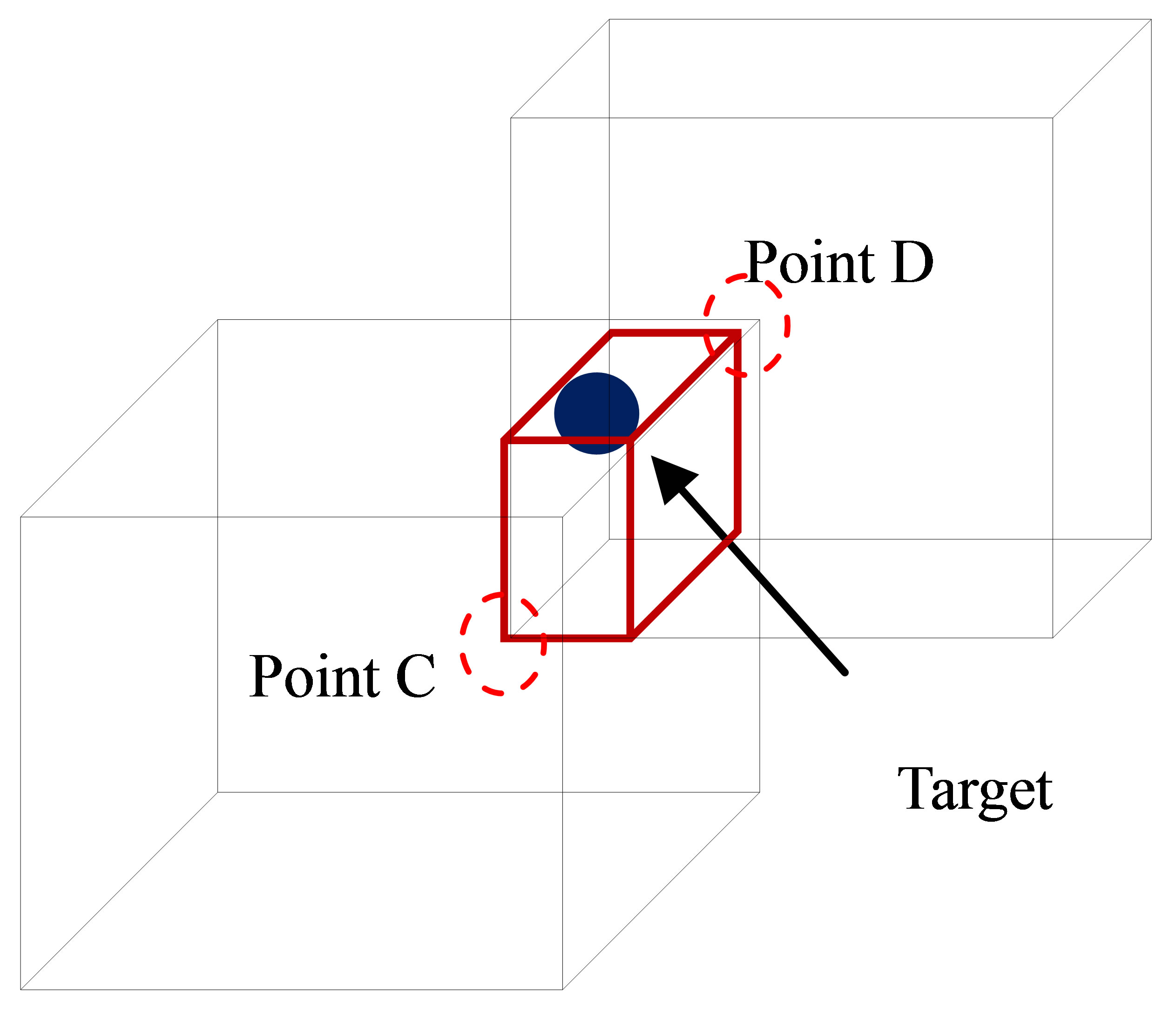
Figure 7. Obtaining red box containing possible location of target node.
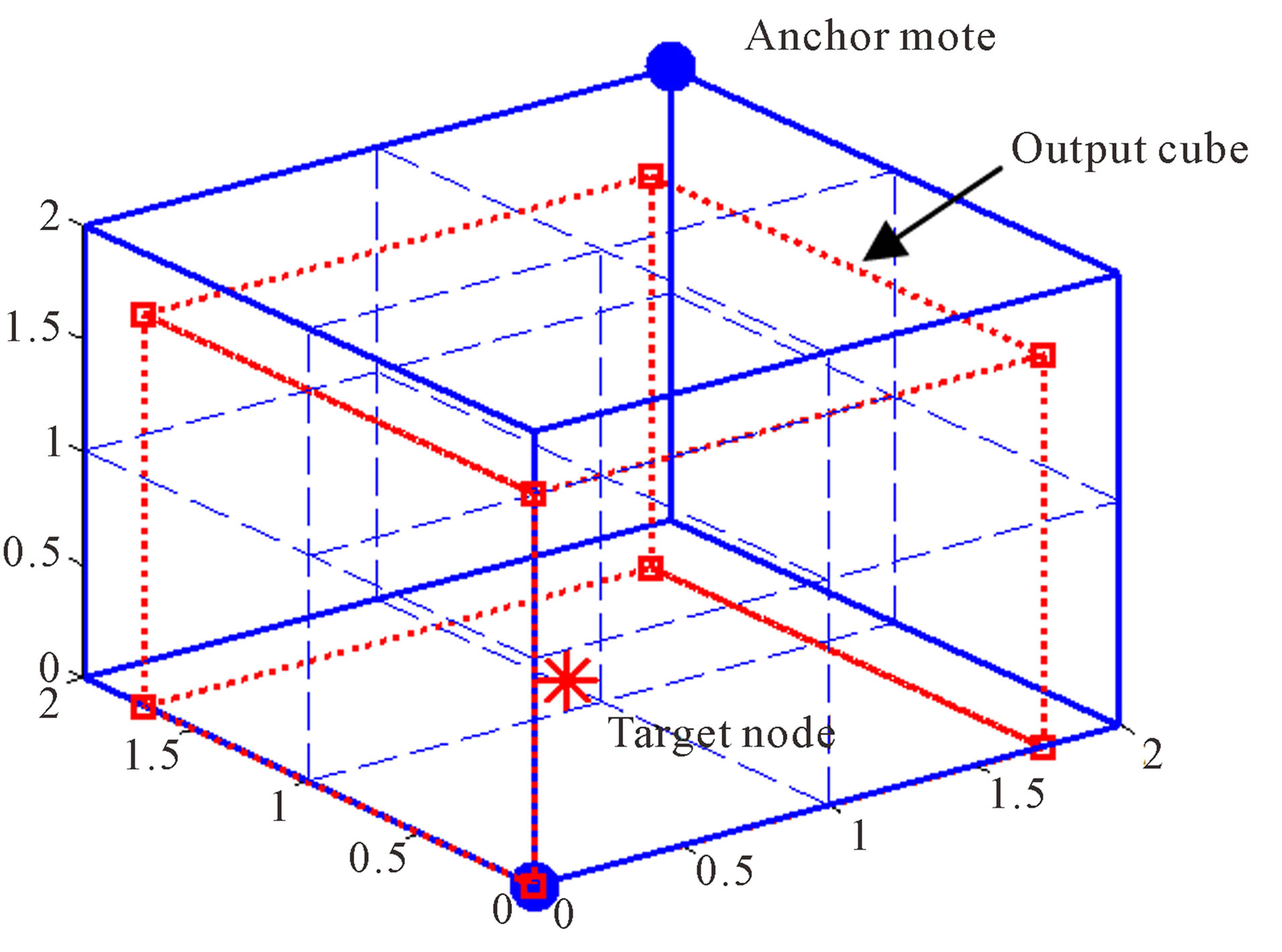
Figure 8. Estimated 3-D output cube to detect the target node.
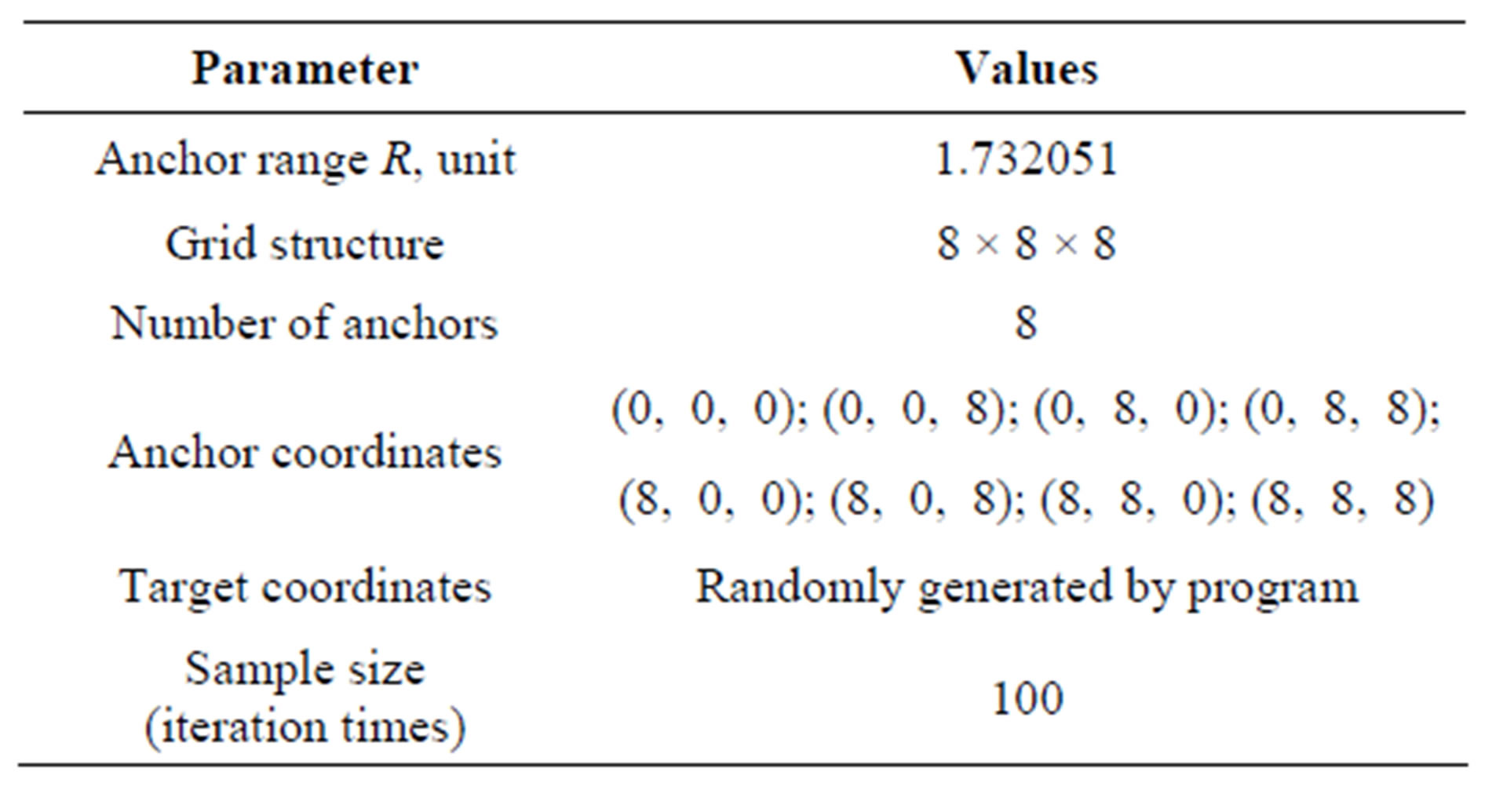
Table 1. WSN setup parameters.
4.2. Simulation Results
Different combinations of hop-count values and the corresponding output cube volumes are summarized in Table 2. The hop-count values shown in each row do not correspond to actual anchor number. It can be seen that, for 8 × 8 × 8 grid structure, only the hop-count values of 1 or 2 can give a smaller output cube volume which can contribute to higher localization accuracy.
From Table 2, there are two possible output cube volumes for the hop-count set (4, 4, 4, 4, 5, 5, 5, 5),

Table 2. Combination of hop-count values and the corresponding output cube volumes.
200.8602 and 237.6202. This is because there are different distributions of the four anchors with hi = 4. The two actual anchor numbers, (h1, h2, h3, h4, h5, h6, h7, h8), are (4, 4, 4, 5, 4, 5, 5, 5) and (4, 4, 5, 5, 4, 4, 5, 5). The simulation results for these two cases are shown in Figures 9 and 10, respectively. In the figures, the blue nodes indicate the anchors and the red asterisk indicates the location of the target node and the red dotted box indicates the output cubic space based on our proposed 3-D localization algorithm. Even though the hop-count set is the same for both cases, different spatial distribution of the anchor number has affected the output cube volume.
Next, weanalyse the effective output localization volume obtained from different combination of node’s transmission range, R, and grid structure, n × n × n as shown in Figures 11 and 12. In both figures, the x-axis refers n and the length of the grid increases with R. Figure 11 shows the average effective output localization volume for different n and R. For a fixed grid structure, n × n × n, as R increases, the output volume increases. This is because the grid size increases with R correspondingly. The growth of average effective output volume follows a
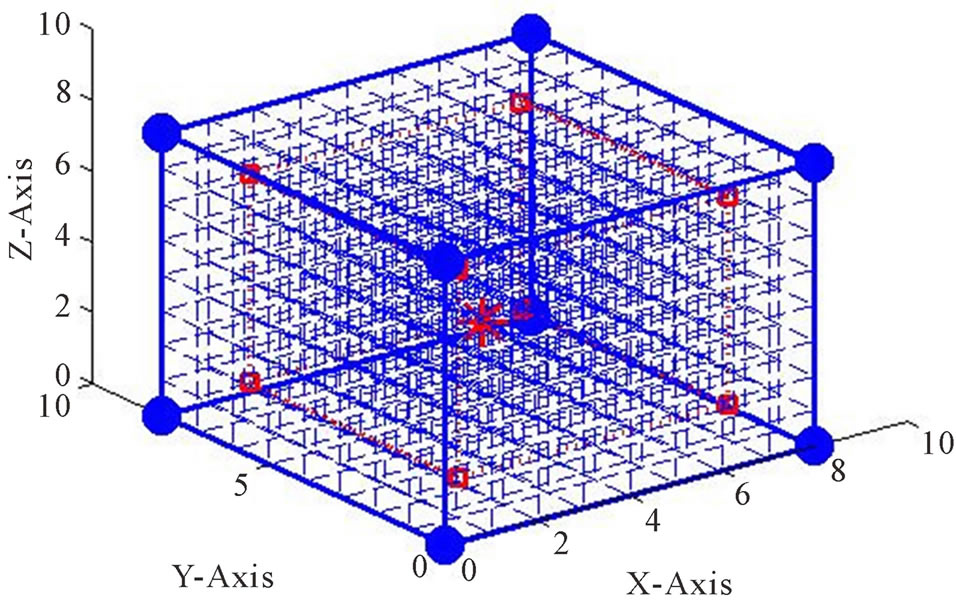
Figure 9. MATLAB simulation result for hop-count set (4, 4, 4, 5, 4, 5, 5, 5).
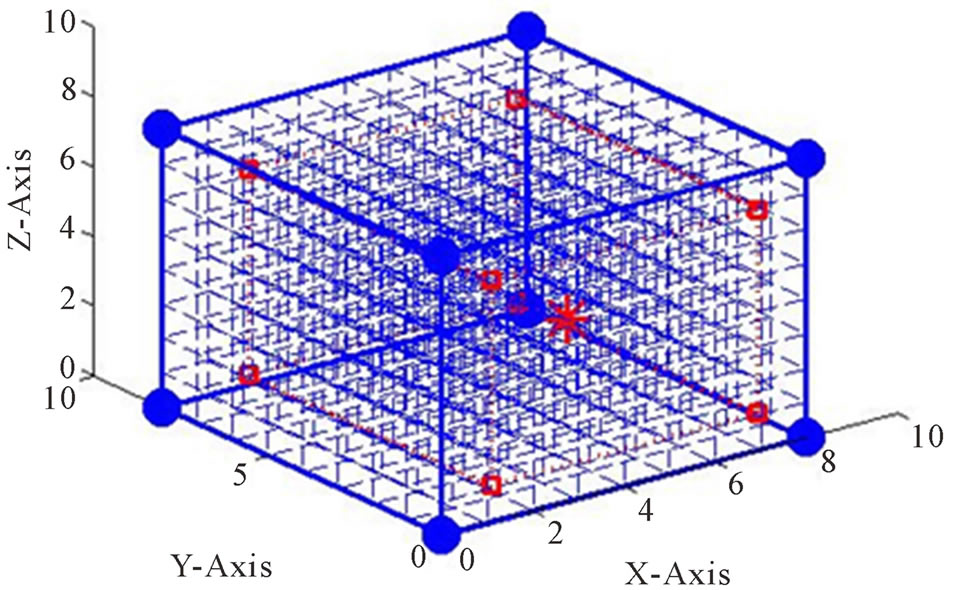
Figure 10. MATLAB simulation result for hop-count set (4, 4, 5, 5, 4, 4, 5, 5).
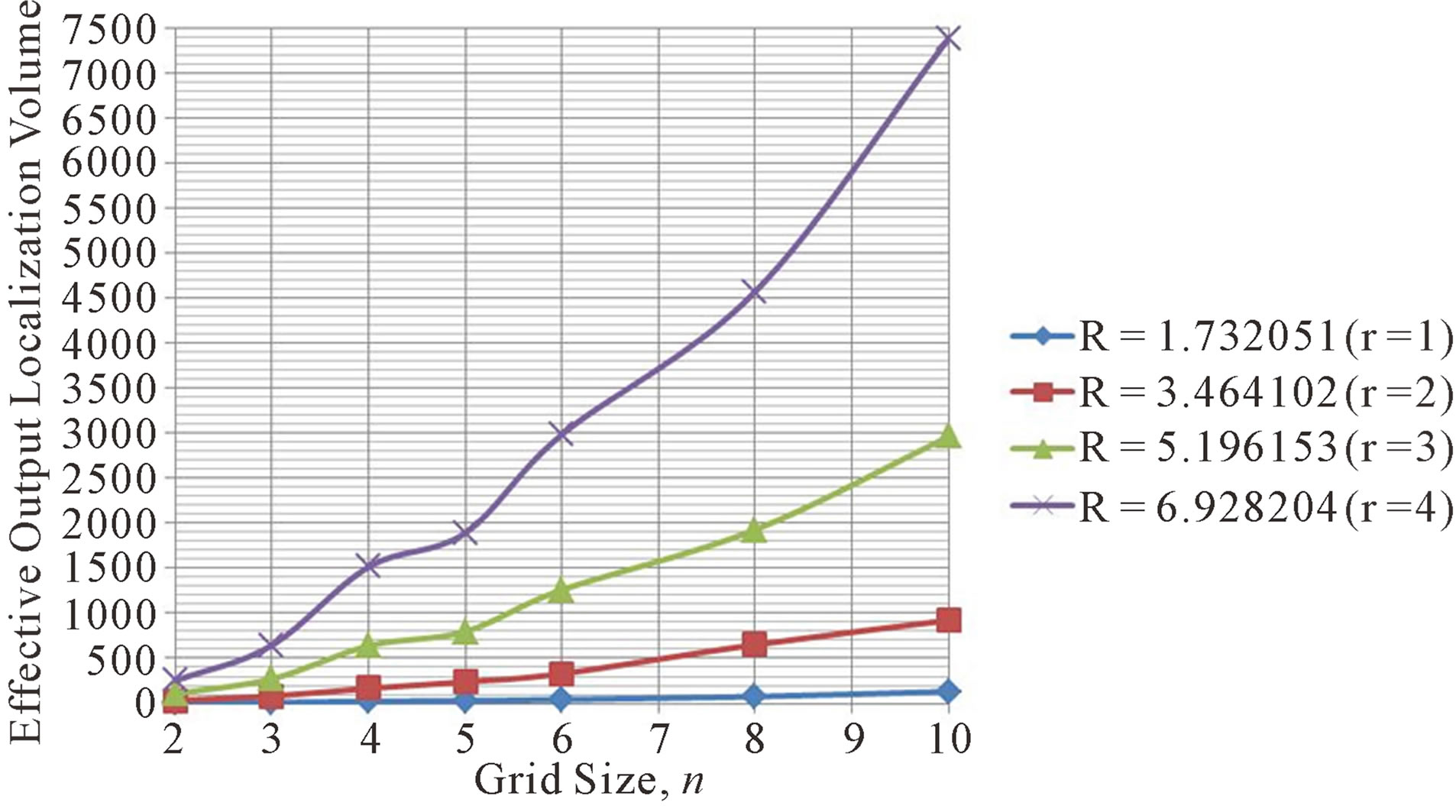
Figure 11. Average effective output localization volume for different n.
cubic relationship to the R, which implies a rapid drop in localization accuracy as well. The relationship can be expressed as:
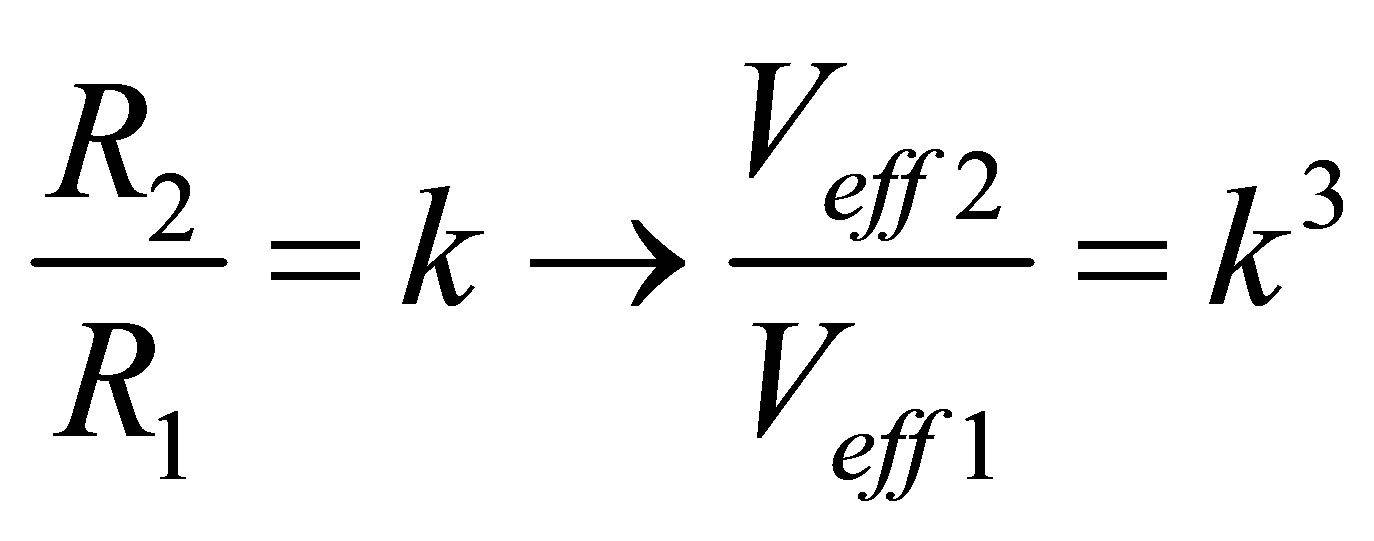 (9)
(9)
For a fixed R, the average effective output localization volume increases with n. That means the localization accuracy decreases with n. This is a reasonable observation because a larger n give more possibilities for a target node to be positioned.
Figure 12 shows the average percentages of the effective output localization volume to the total monitoring volume. The percentage of the average effective output localization volume to the total monitoring volume decreases with total monitoring volume. For example, for n = 10, the average percentage of the effective output localization volume to the total monitoring volume is about 10. The average output volume covering the target node is about 100 cubic units as compared to a total of 1000 cubic units of the monitoring volume.
Similar to Figures 11, Figure 13 shows the average effective output localization volume for different R with different n.
4.3. Hardware Requirements
Table 3 shows the hardware list for our test-bed. Further information about each hardware components can be referred to the Crossbow MICAz datasheet [14], MPRMIB user manual [15] and MTS/MDA sensor board user manual [16].
4.4. Experiment Setup
For this 3-D experiment, the WSN is set up such that we place the motes as far apart from each other as possible and model the monitored area as similar to a rectangular
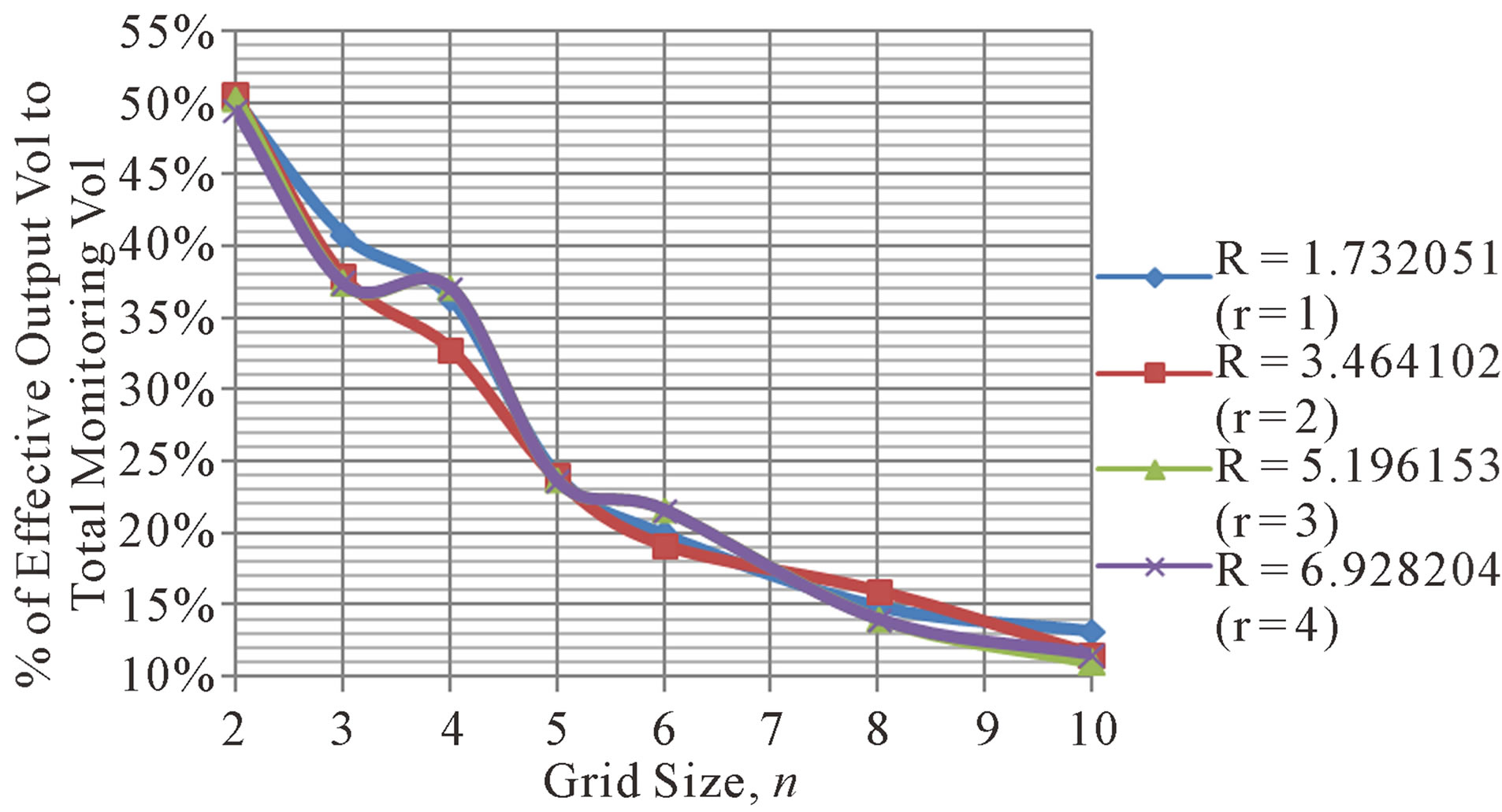
Figure 12. Average percentage of effective output localization volume to the monitoring region volume for different n.
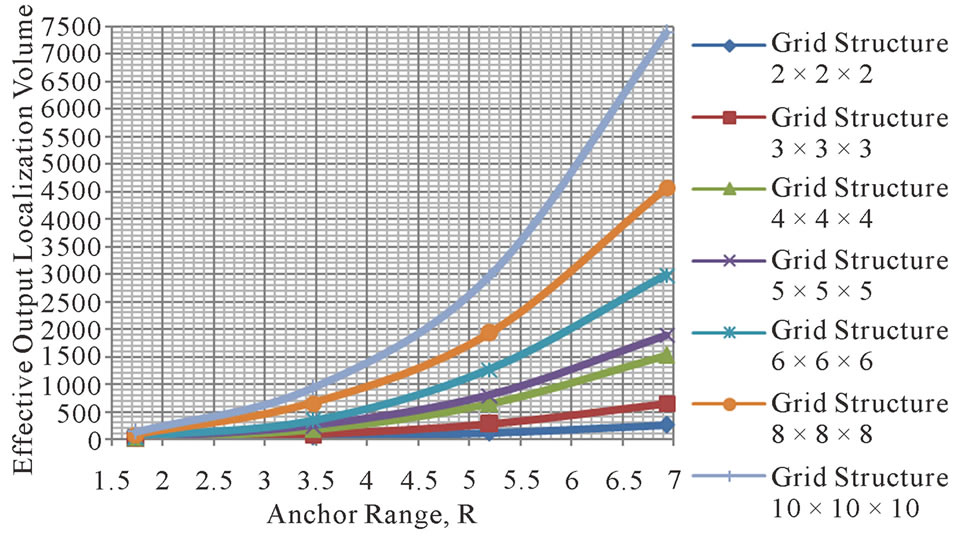
Figure 13. Average effective output localization volume for different R.
cube as possible. The motes are placed such that there is no major obstruction of line of sight between each of the motes. Seven motes are placed on benches and tables in the lab as shown in Figure 14. Their positions are shown in Table 4. Due to space constraint in the laboratory, the height difference between the motes placed at the highest and lowest height is just 0.9 m that is much smaller than the transmission range of a mote which is 3.2 m. But in our output we still use hop count from x, y and z direction to form a cubic space. We believe that our experiment is able to demonstrate the concept of 3-D localization.
Five experiments have been conducted to test the proposed 3-D localization technique. The locations of the target mote are shown in Table 5. Tables 6 to 10 show the hop count numbers from target node to 7 anchor motes obtained from both experimental and theoretical results.
Table 3. Hardware list.

Figure 14. Wireless sensor network setup in lab.
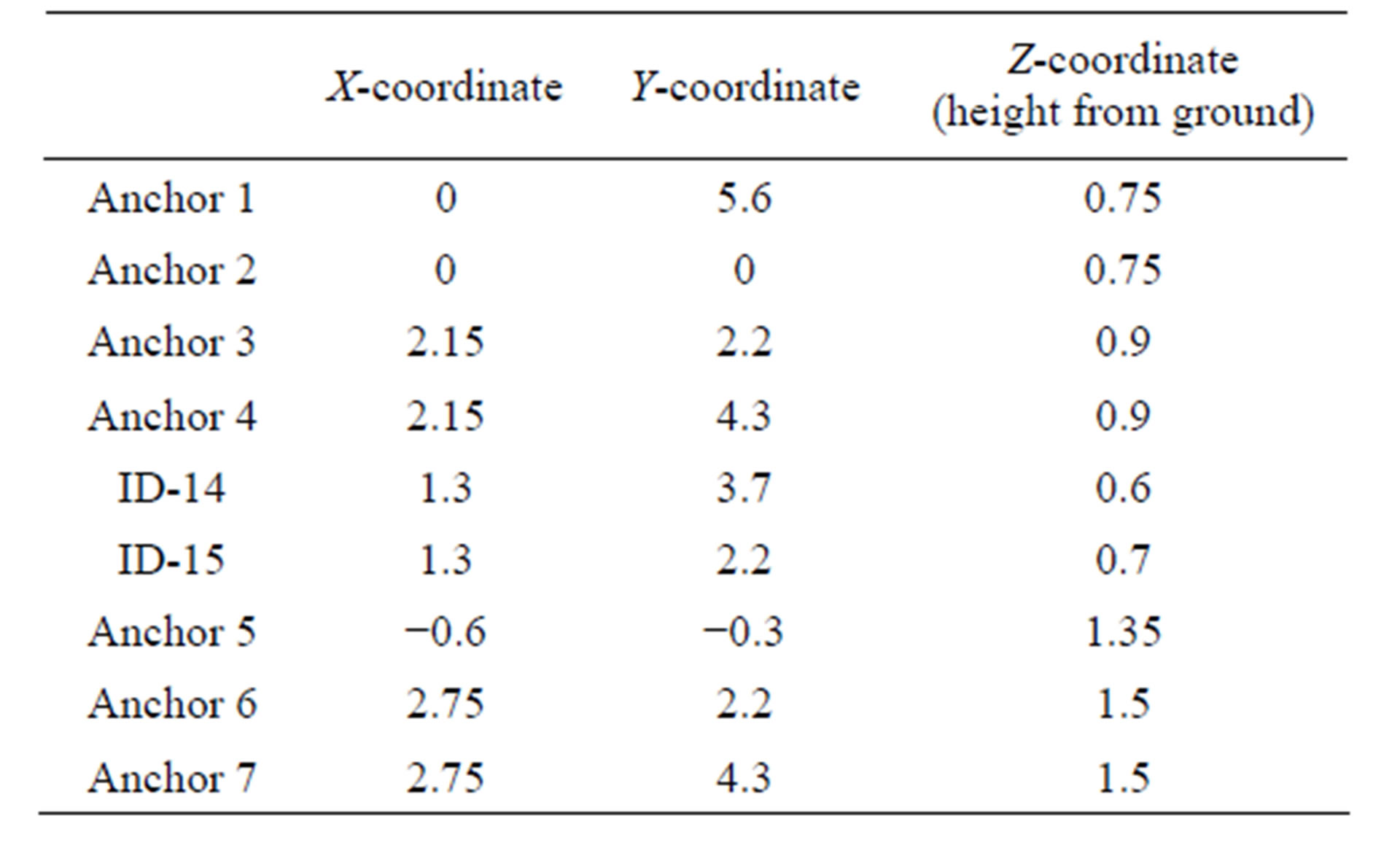
Table 4. Location of anchor and relay motes.
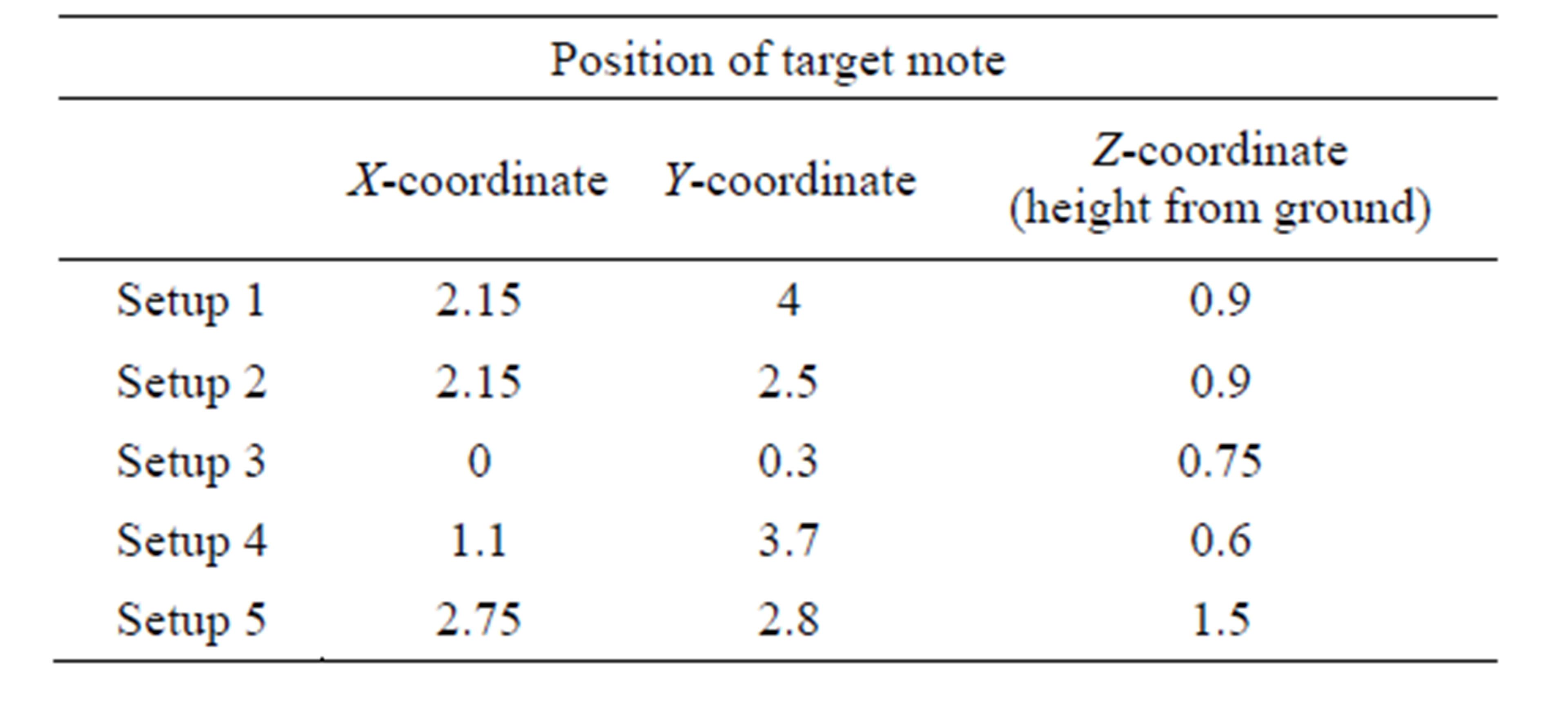
Table 5. Position of target mote in five different setups.
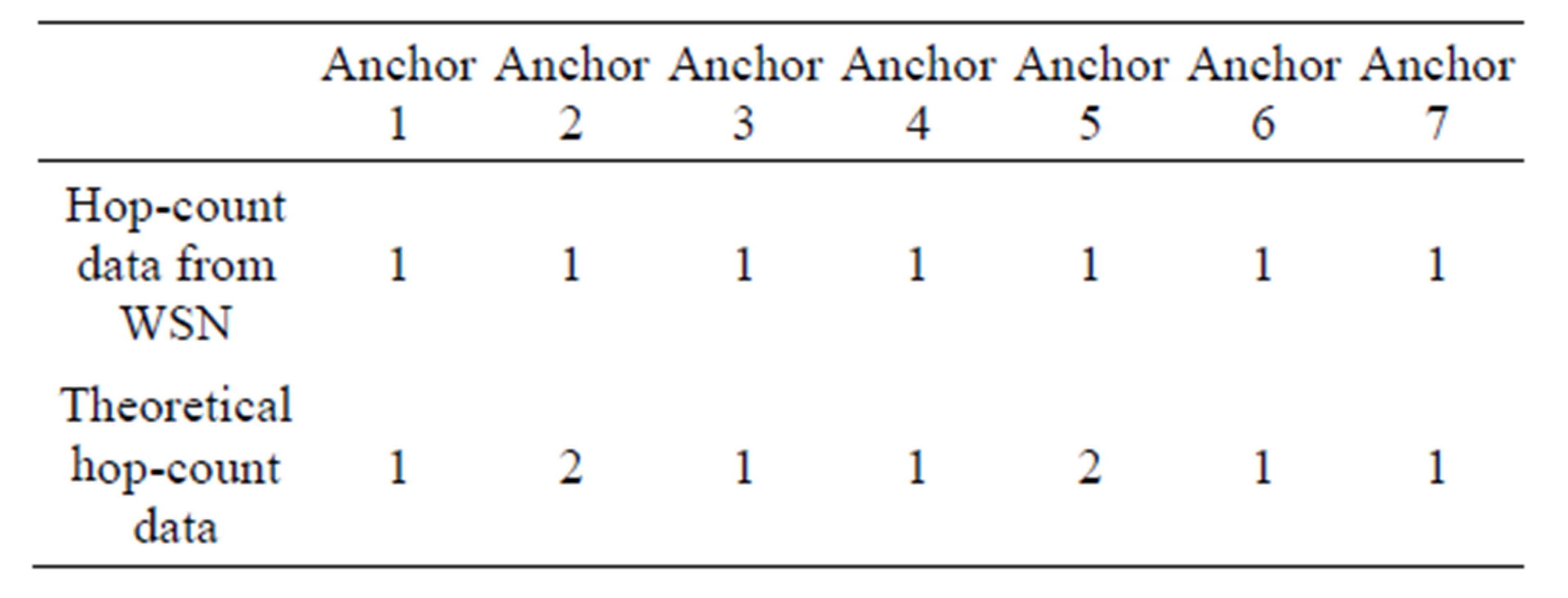
Table 6. Hop-count data for setup 1.
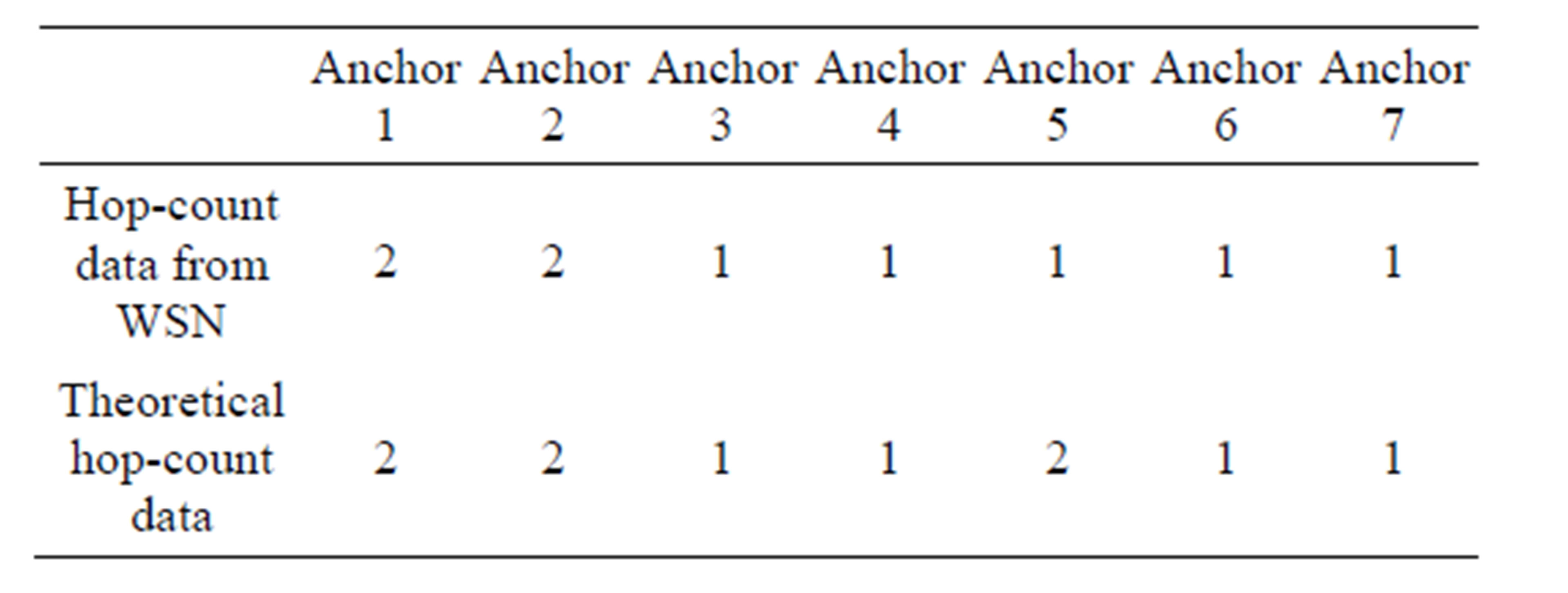
Table 7. Hop-count data for setup 2.
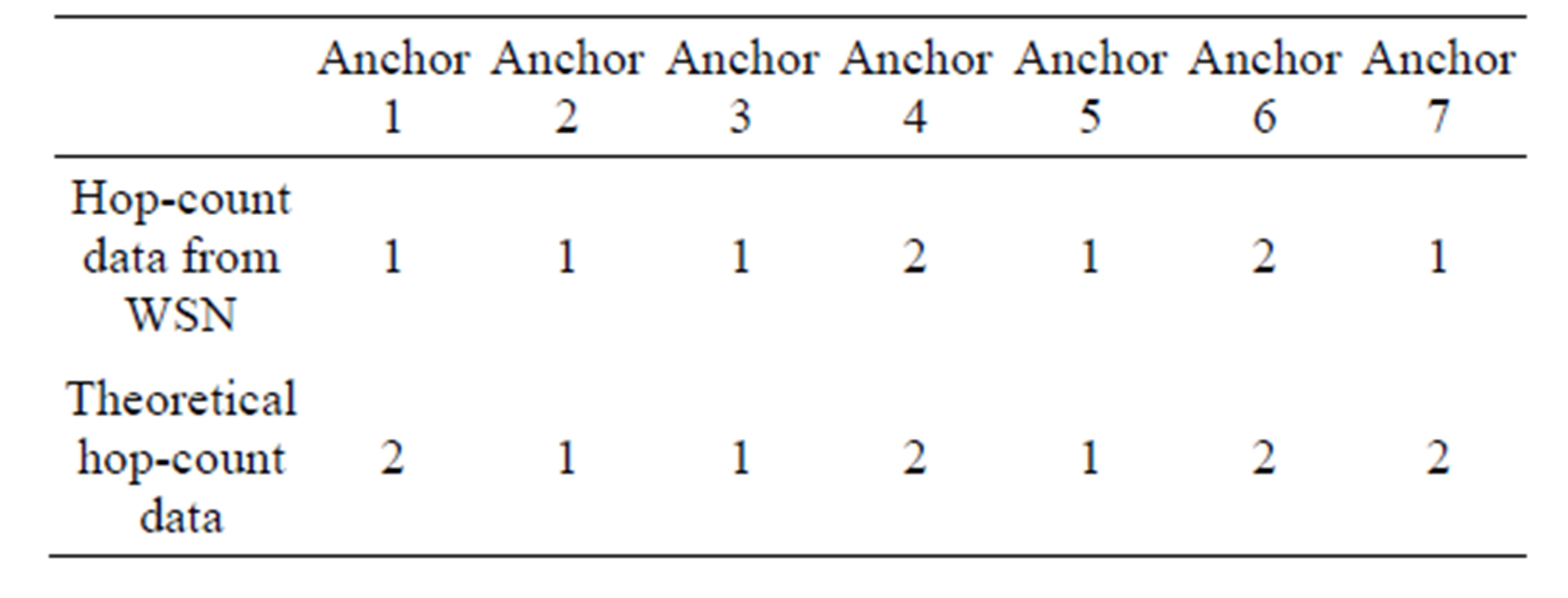
Table 8. Hop-count data for setup 3.
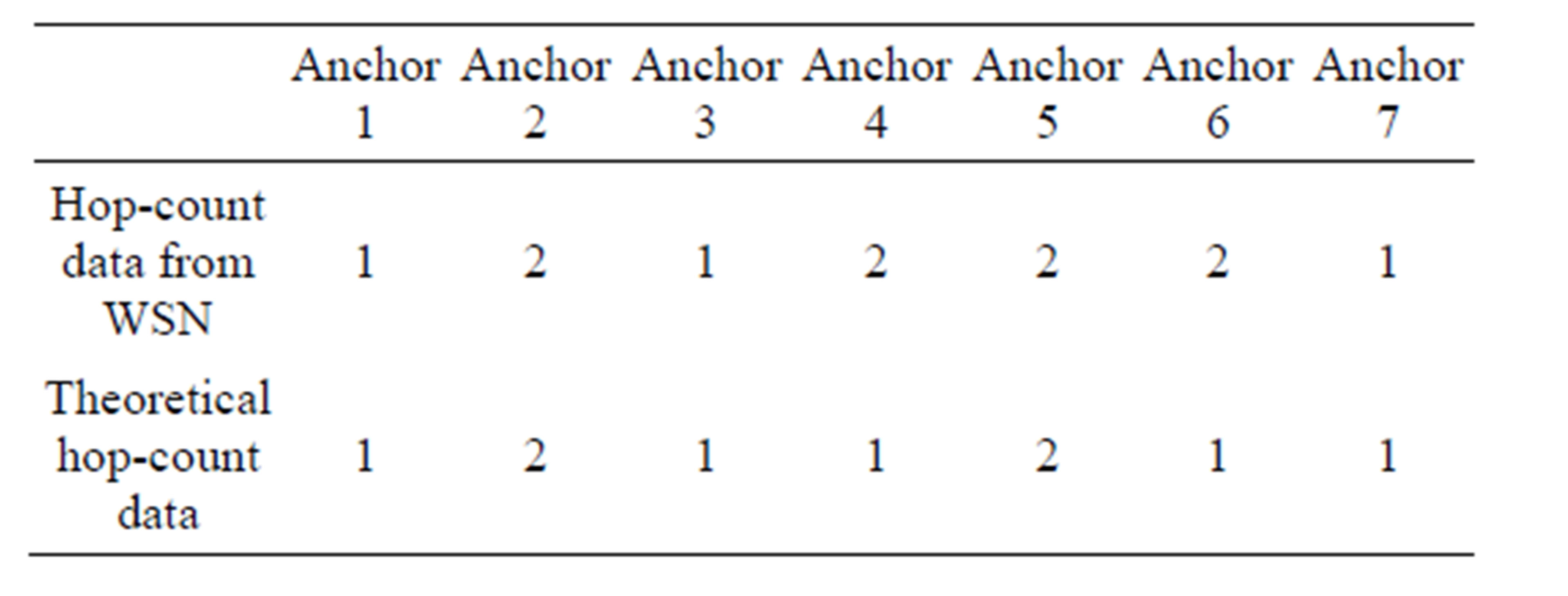
Table 9. Hop-count data for setup 4.
4.5. Experimental Results
In the following figures, the blue nodes indicate the anchor motes, the green motes indicate the relay motes, the red asterisk indicates the location of the target node and the red dotted box indicates the cubic space output based on our proposed localization algorithm.
Figure 15 shows the 3-D view for setup 1. The numbers in the figure refer the anchor number. The hop count numbers from both experimental and theoretical from target node to 7 anchor motes for setup 1 are shown in Table 6. It can be seen that they have some differences due to measurement errors caused by wireless channel environment. The top view of setup 1 is shown in Figure 16. It can be seen that the output red box does not cover the target node. It means our proposed 3-D localization technique does not identify the target node. The reason to have the incorrect estimated output cube is because the number of anchors is not enough and the measure error is coming from the wireless channel.
The results for setup 2 are shown in Figures 17 and 18. The hop count data for setup 2 is shown in Table 6. In Figures 17 and 18, it can be seen that the target node is inside the red cubic box. That means the target’s location can be found. The results for other three experiments are shown from Figures 19 to 24.
As we have seen from the figures above, some of the experiments are unable to correctly estimate the position of the target mote. It seems that the correctness of our proposed 3-D localization techniques depend on the location of the target node. In fact, this is not true. The inaccuracy of our localization algorithm can be explained as follows:
• One reason is due to insufficient number of anchors. Since more anchors will give more cubes to intersect each other, it can produce a smaller output cube to cover the target node.
Table 10. Hop-count data for setup 5.
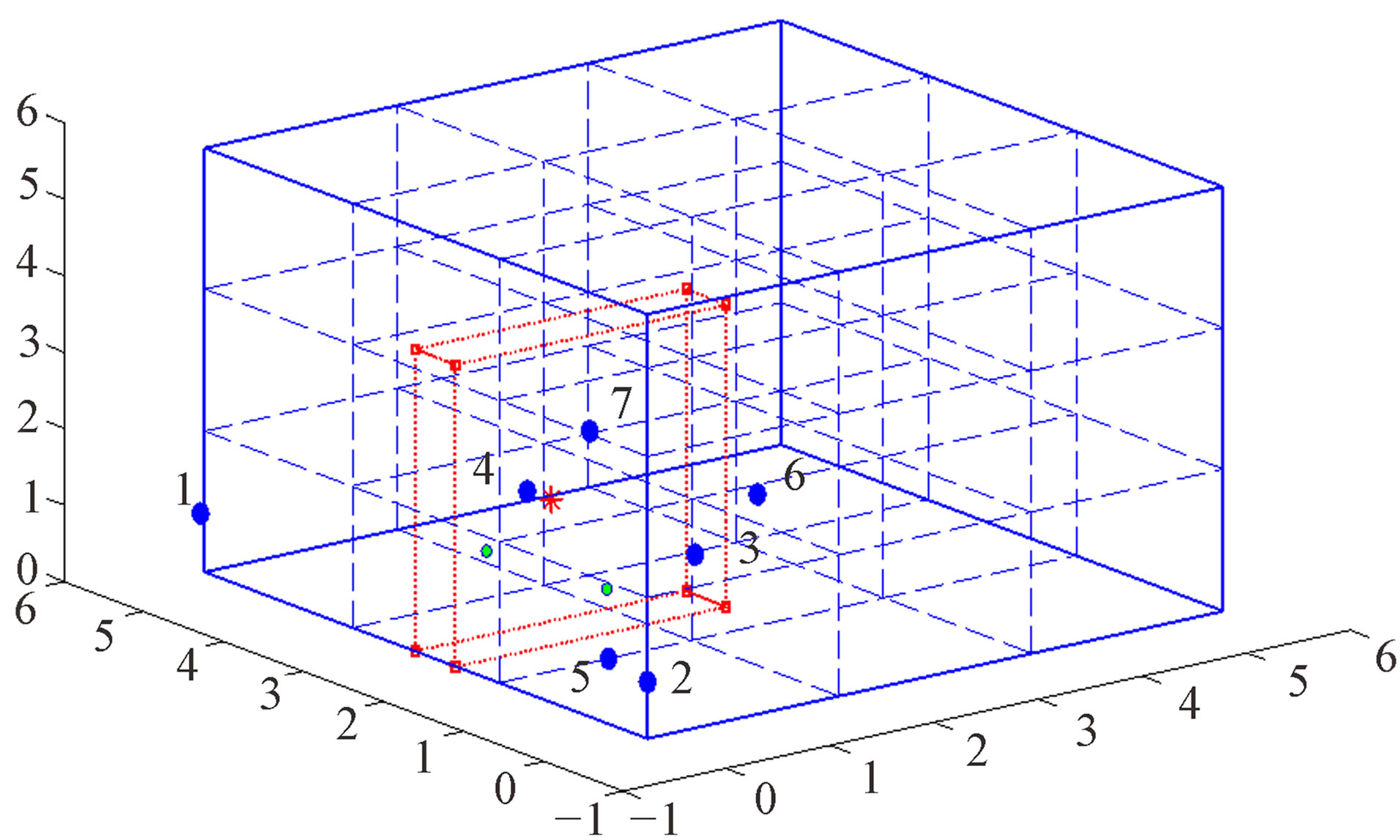
Figure 15. 3-D view for setup 1.
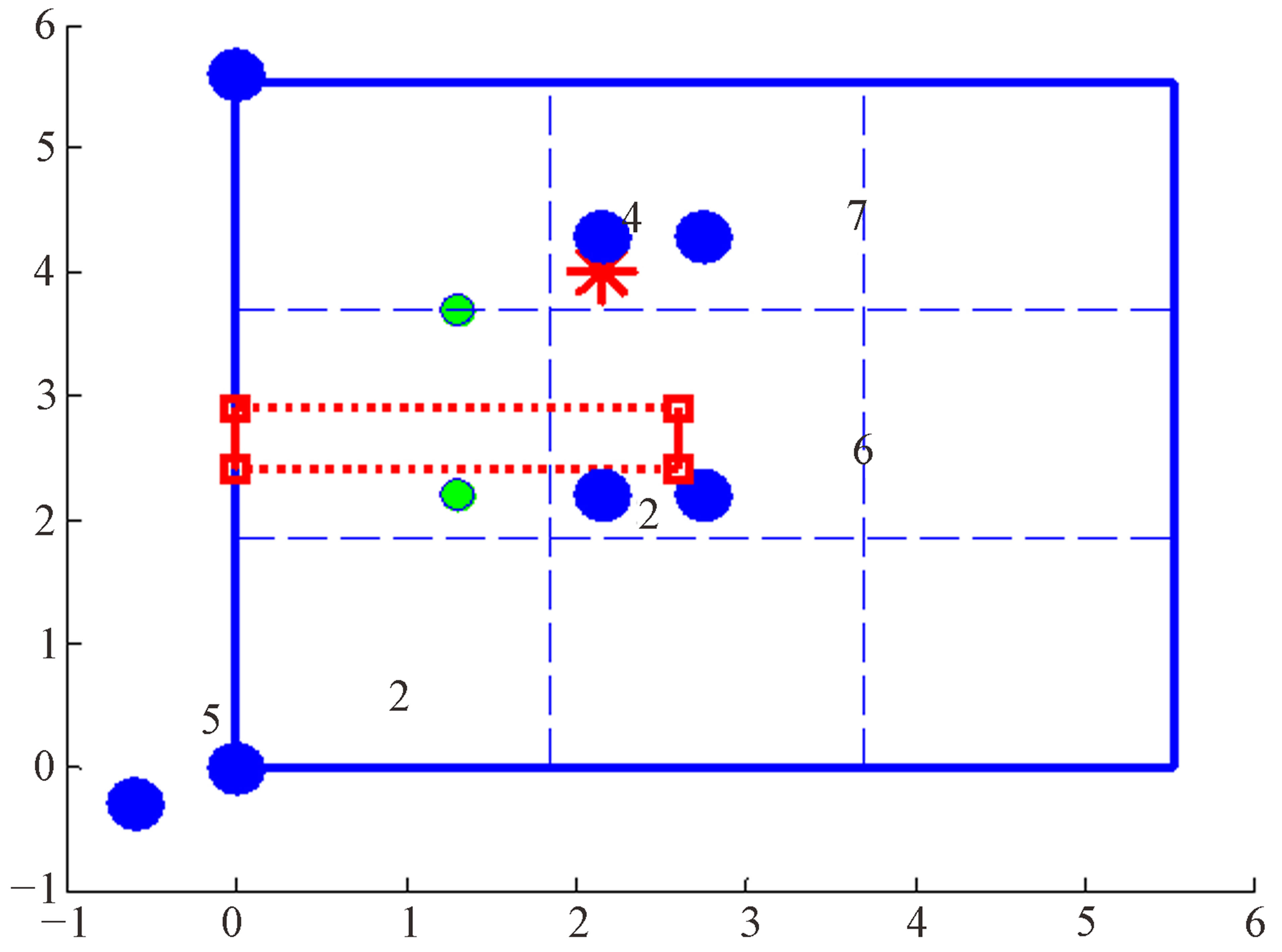
Figure 16. Top-down view for setup 1.
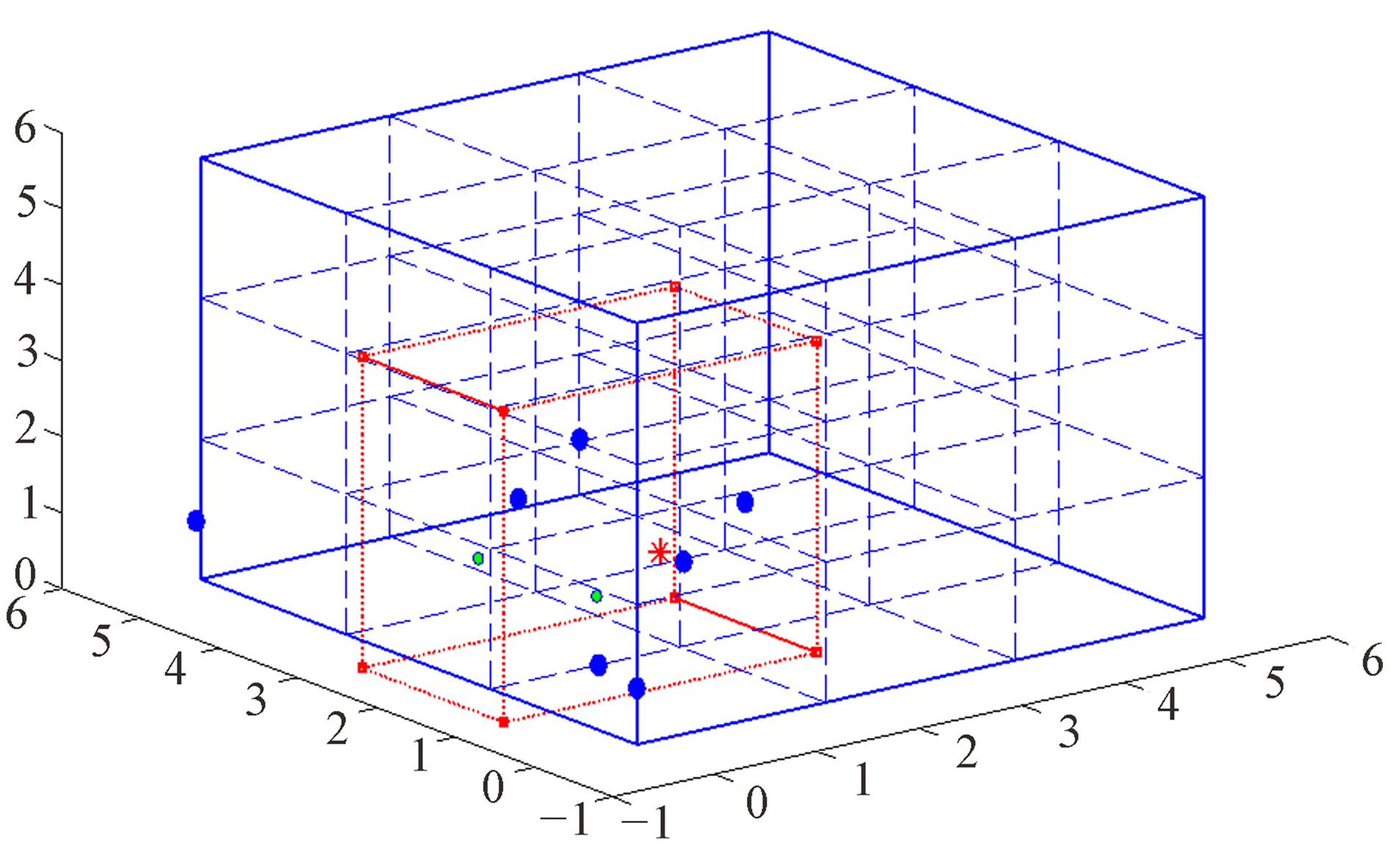
Figure 17. 3-D view for setup 2.
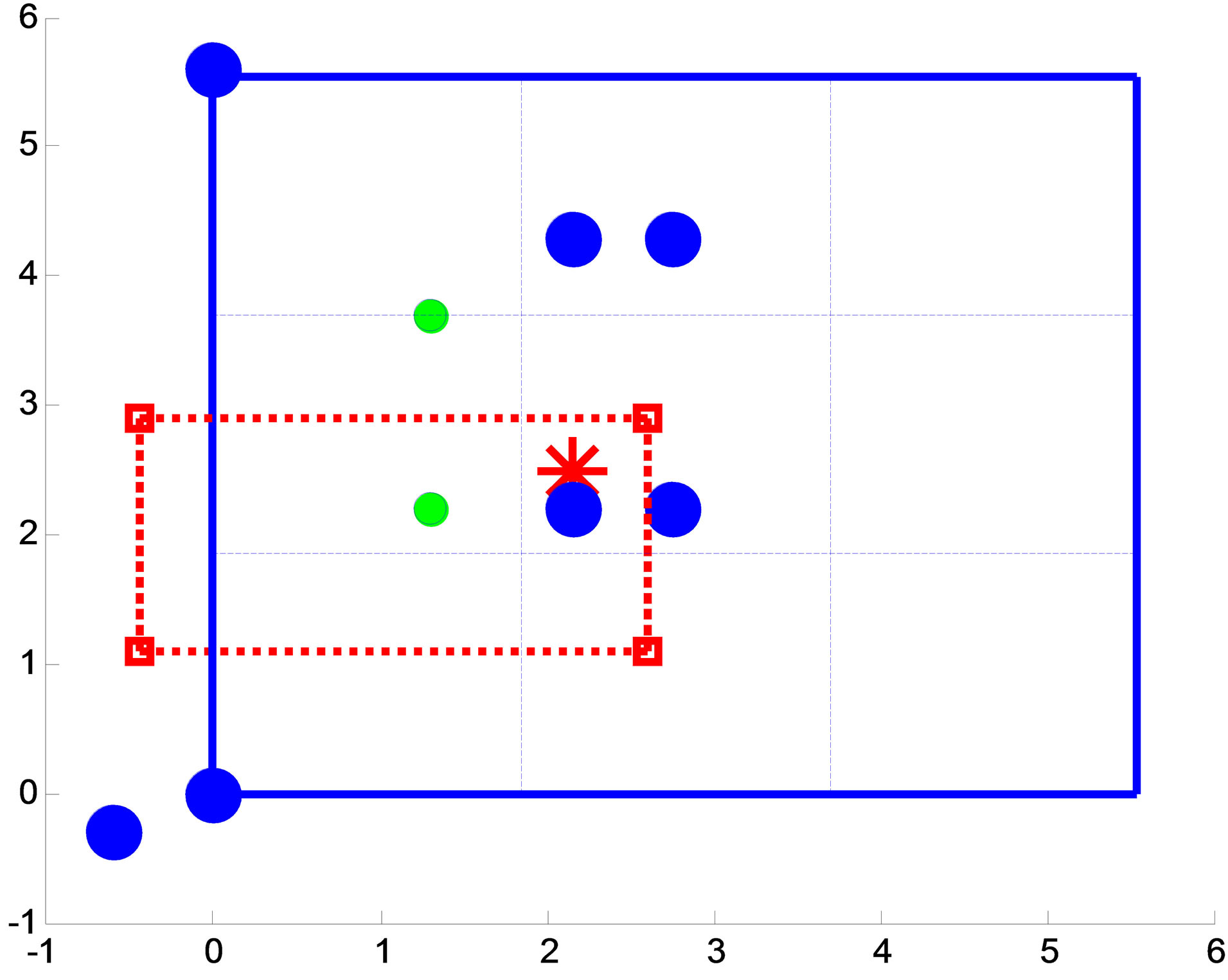
Figure 18. Top-down view for setup 2.
• As compared to the theoretical hop-count data based on calculations, the hop-count data that were received from experiment were different for all five setups. The different hop count between them is due to the insufficient number of relay nodes and the nature of wireless channel. Since the accuracy of our proposed
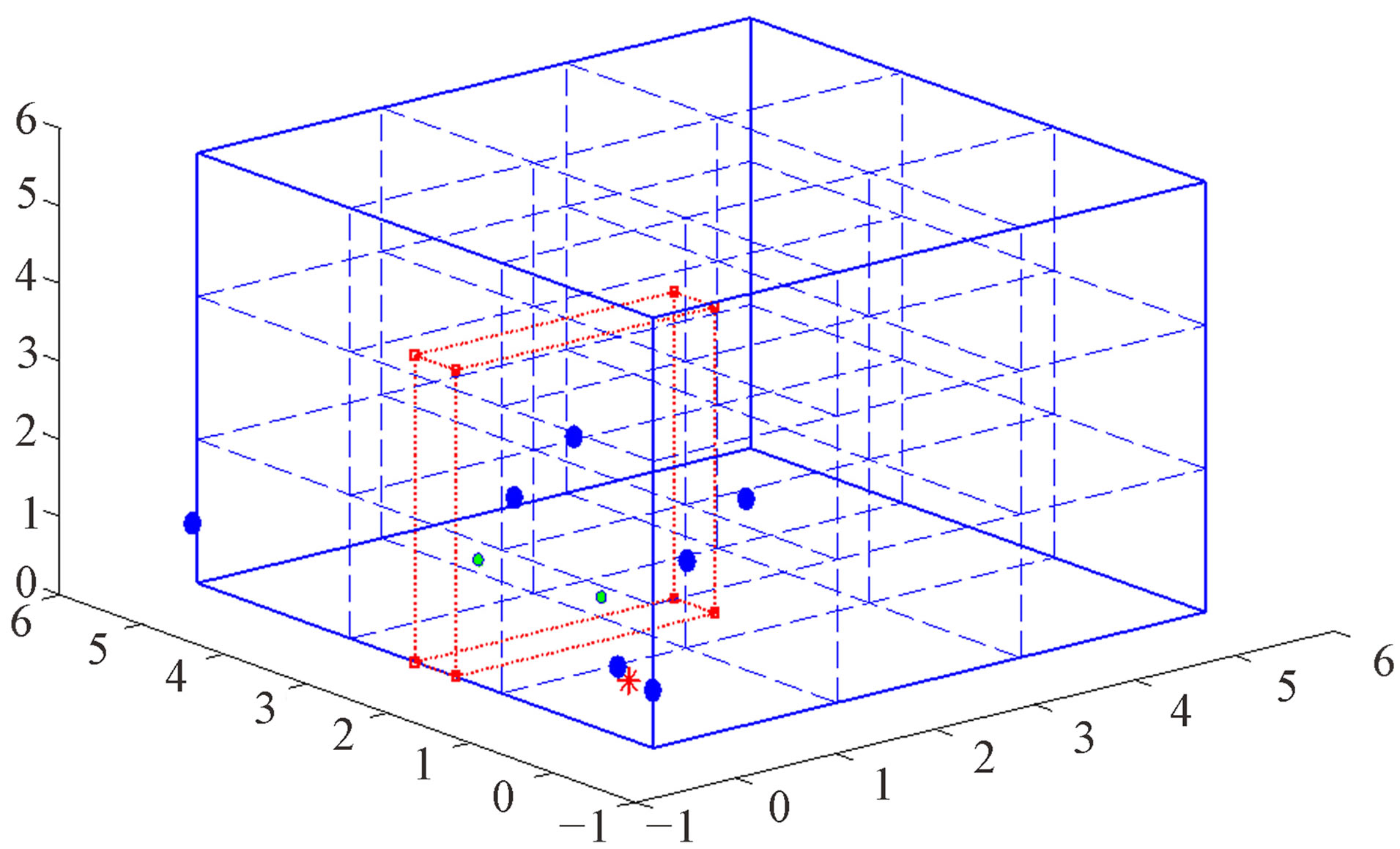
Figure 19. 3-D view for setup 3.
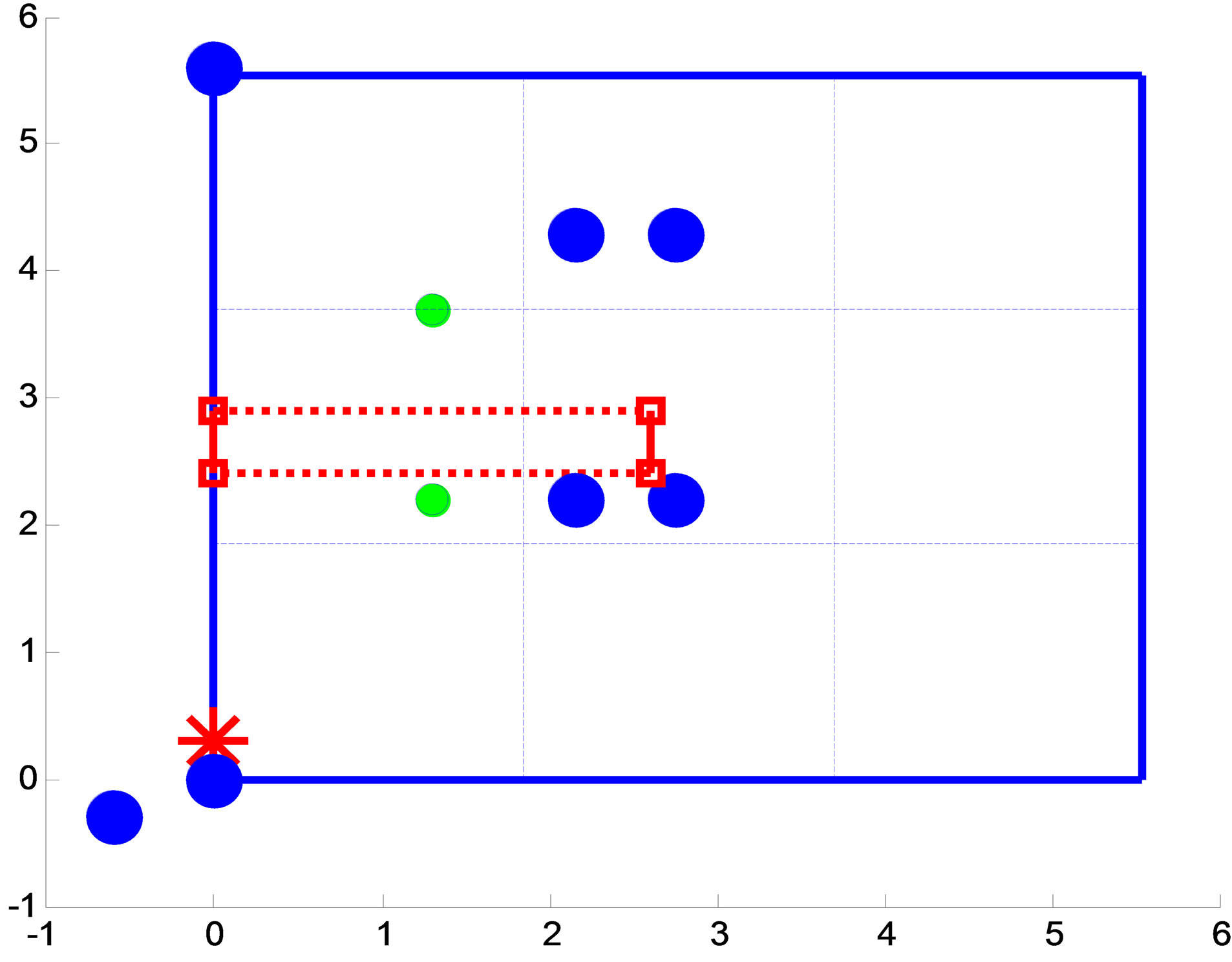
Figure 20. Top-down view for setup 3.
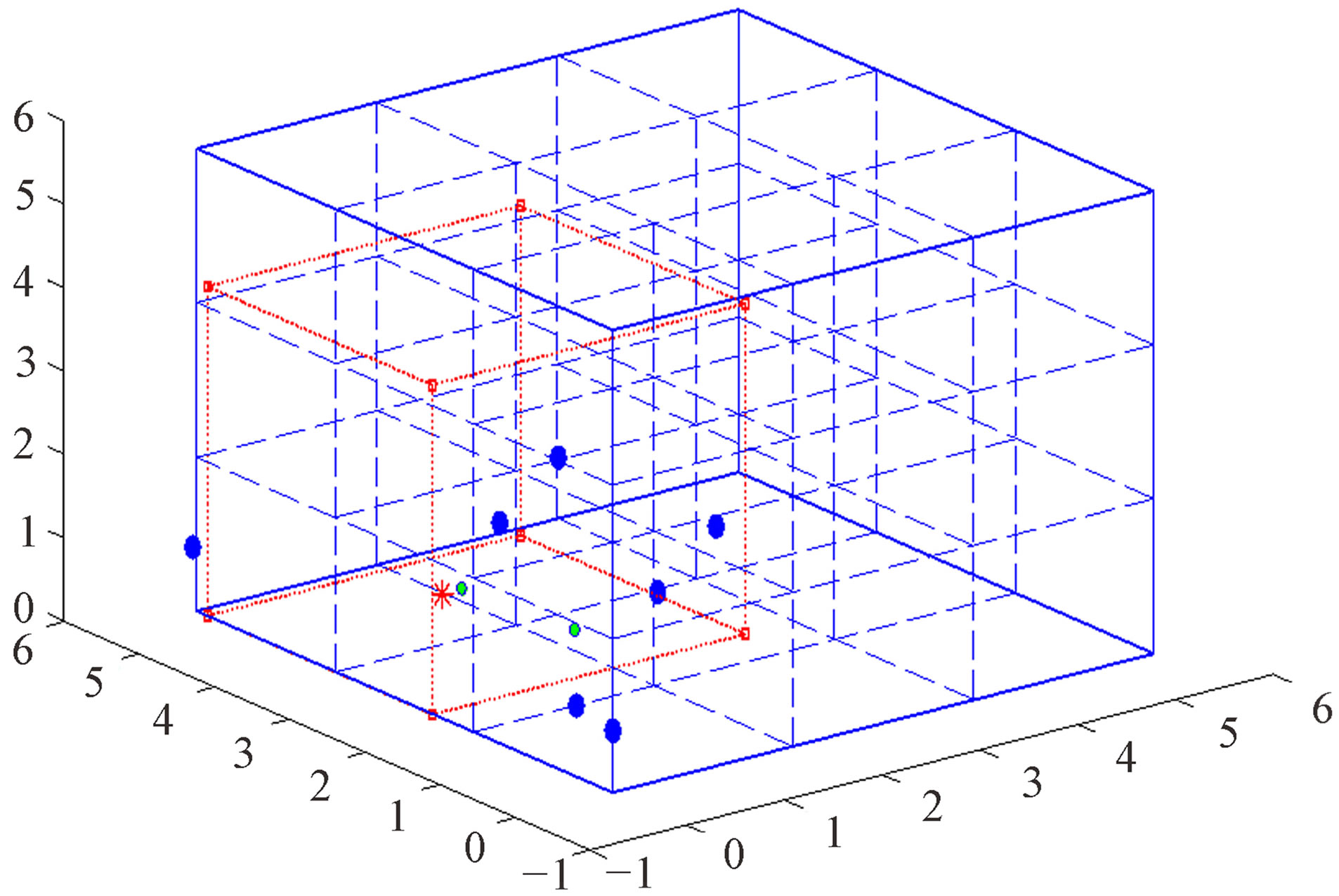
Figure 21. 3-D view for setup 4.
localization algorithm depends on the hop count, it is important to correctly estimate the location of the target mote.
• Another reason is due to different transmission range. We use the average number of transmission range of 3.2 m for theoretical calculation. However, the real transmission range is different for each anchor, relay motes and target mote. For example, for setup 3, since
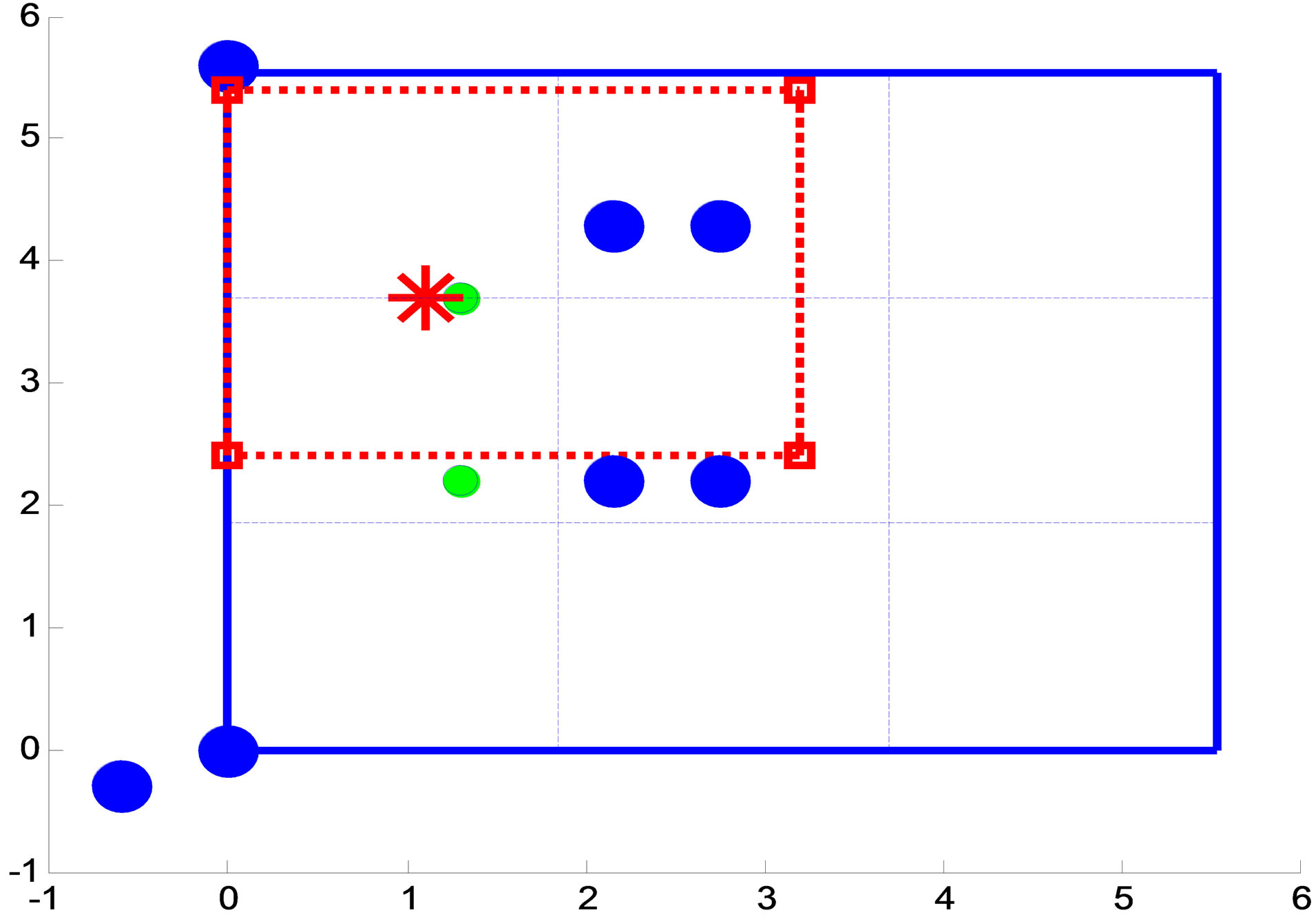
Figure 22. Top-down view for setup 4.
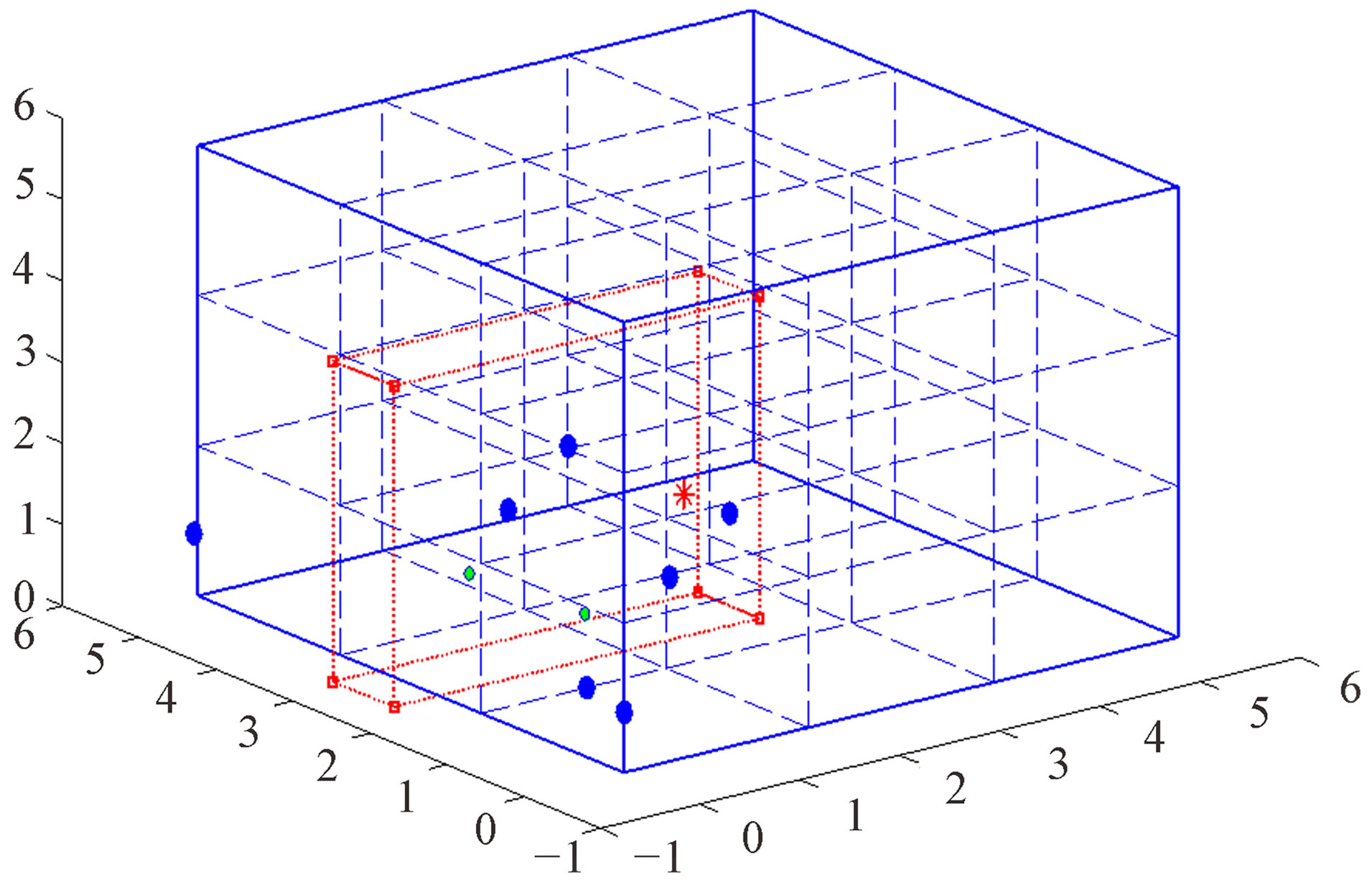
Figure 23. 3-D view for setup 5.
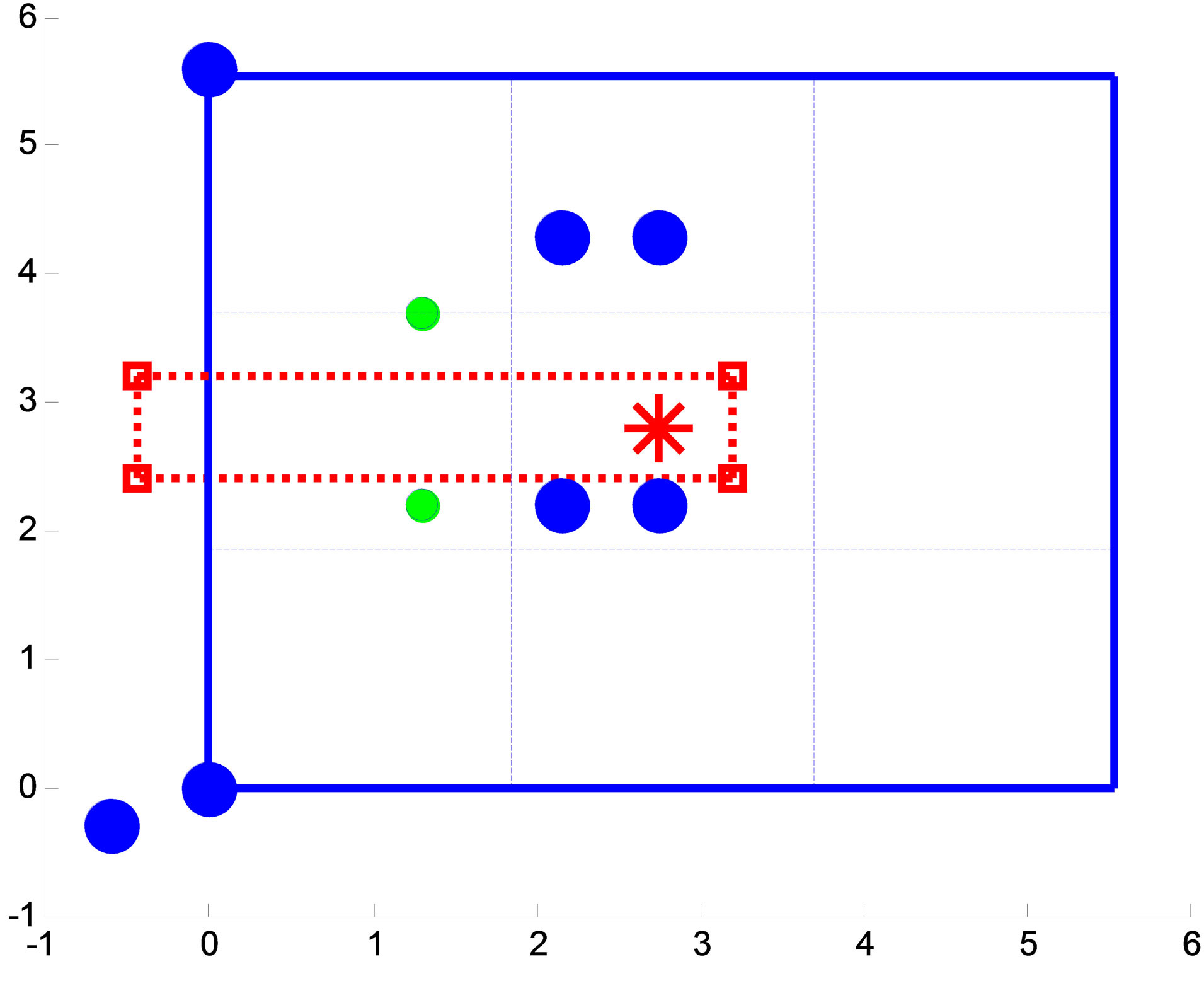
Figure 24. Top-down view for setup 5.
the target mote in about 5.3 metres away from Anchor 1, the theoretical hop-count for Anchor 1 should be 2. However based on the hop-count data collected from the experiment, the hop-count is 1. This shows that it is possible for the range of a mote to exceed what was previously measured.
• Another reason could be attributed to the presence of foreign objects in the laboratory where the experiment took place. This includes the presence of the student conducting this experiment and other laboratory users in the experimental area. All these ultimately lead to multi path effects of the radio signal which could have resulted in the motes having different range patterns under different circumstances.
Hence, the above factors might have ultimately caused the hop-count data collected from the WSN to be incorrect and leads to the result from the localization algorithm to be incorrect as well.
5. Conclusion
In recent times, search and rescue with modern localization techniques bring interest to the scientific and industrial sides. This paper presents a robust cubic-based 3Dlocalization technique particularly tailored for disaster rescue applications. By adopting cubic-based output and event-triggering mechanism, the proposed algorithm can reduce computational complexity, improve output accuracy and reduce power consumption. In this paper, we have presented our proposed idea and design application and performed the preliminary experiment on the proposed model. Furthermore, experiments have been conducted in which the proposed algorithm was implemented using Crossbow’s set of sensor hardware. Theoretical results show that our proposed 3-D localization algorithm can always identify the target node’s location. Then, we conduct the experiments inside a lab to test the accuracy of the algorithm. However, experimental results show that the proposed algorithm is unable to identify the target node in some cases. The reason is that the size of the experimental area is not large enough. We believe that if we conduct in a larger area and we can use a large transmission range for the wireless sensor, it can definitely increase the accuracy of our 3-D localization algorithm. Furthermore, in order to provide better accuracy, we will add some mobile anchors in our experiment.
REFERENCES
- F. Akyildiz, et al., “Wireless Sensor Networks: A Survey,” Computer Networks, Vol. 38, No. 4, 2002, pp. 393- 422. doi:10.1016/S1389-1286(01)00302-4
- H. Karl and A. Willig, “A Short Survey of Wireless Sensor Networks,” Technical Report TKN-03-018, Telecommunication Networks Group, Technical University, Berlin, 2003.
- C. K. Seow and S. Y. Tan, “Non Line of Sight Localization in Multipath Environment,” IEEE Transactions on Mobile Computing, Vol. 7, No. 5, 2008, pp. 647-660. doi:10.1109/TMC.2007.70780
- L. Hu and D. Evans, “Localization for Mobile Sensor Networks,” Proceedings of ACM MobiCom’04, Vol. 1, Philadelphia, 26 September-1 October 2004, pp. 45-57.
- A. Baggio and K. Langendoen, “Monte-Carlo Localization for Mobile Wireless Sensor Networks,” Ad Hoc Networks, Vol. 6, No. 5, 2008, pp. 718-733. doi:10.1016/j.adhoc.2007.06.004
- A. Ward, A. Jones and A. Hopper, “A New Location Technique for the Active Office,” IEEE Personal Communications, Vol. 4, No. 5, 1997, pp. 42-47. doi:10.1109/98.626982
- N. B. Priyantha, A. Chakraborty and H. Balakrishnan, “The Cricket Location-Support System,” Proceedings of ACM MobiCom’00, Vol. 1, Boston, 2000, pp. 32-43. doi:10.1145/345910.345917
- Y. Liu, J. P. Xing and R. Wang, “3D-OSSDL: Three Dimensional Optimum Space Step Distance Localization Scheme in Stereo Wireless Sensor Networks,” Advances in Intelligent and Soft Computing, Vol. 112, 2012, pp. 17-25. doi:10.1007/978-3-642-25194-8_3
- G. Mao, B. Fidan and B. D. O. Anderson, “Wireless Sensor Network Localization Techniques,” Computer Networks, Vol. 51, No. 10, 2007, pp. 2529-2553. doi:10.1016/j.comnet.2006.11.018
- D. Niculescu and N. Badri, “Ad-Hoc Positioning System (APS) Using AOA,” Proceedings of IEEE/ACM INFOCOM’03, Vol. 3, San Francisco, 30 March-3 April 2003, pp. 1734-1743.
- D. Niculescu and N. Badri, “DV Based Positioning in Ad Hoc Networks,” Journal of Telecommunication Systems, Vol. 22, No. 1-4, 2003, pp. 267-280. doi:10.1023/A:1023403323460
- D. Fox, W. Burgard, F. Dellaert and S. Thrun, “MonteCarlo Localization: Efficient Position Estimation for Mobile Robots,” Proceedings of the National Gonfemnce on Artificalntelligence, AAAI, 1999.
- A. Baggio and K. Langendoen, “Monte Carlo Localization for Mobile Wireless Sensor Networks,” Ad Hoc Networks, Vol. 6, No. 5, 2008, pp. 718-733.
- Crossbow Technology, “MICAz,” 2007.
- Crossbow Technology, “MPR-MIB Users Manual,” 2007.
- Crossbow Technology, “MTS/MDA Sensor Board Users Manual,” 2007.

