Journal of Water Resource and Protection
Vol.08 No.11(2016), Article ID:71115,20 pages
10.4236/jwarp.2016.811077
Comparison of Three Delineation Methods Using the Curve Number Method to Model Runoff
William D. Troolin, Katherine Clancy
College of Natural Resources, University of Wisconsin-Stevens Point, Stevens Point, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 6, 2016; Accepted: October 7, 2016; Published: October 10, 2016
ABSTRACT
Digital Elevation Models (DEMs) are spatial grids which are used to automate watershed boundary determination. Sinks are present within most DEMs. In order to easily process the watershed boundary, the sinks are reassigned to elevation equivalent to an adjacent cell. The derived DEM is called a “filled” DEM. Due to its relative simplicity, the use of the “filled” DEM is one of the most widely used methods to delineate watershed boundaries and works well in about 70 percent of the watersheds in the US. In landscapes with internal drainage, sinks may accurately represent these depressions. In this study, we compare two delineation methods that do not fill in sinks to another method that does fill in sinks. We examined ten gaged watersheds in Wisconsin and Minnesota. We found the spatial extent of the watersheds from the three methods were significantly different. To evaluate the delineation methods, we modeled ten runoff events using the Curve Number (CN) method and compared them to USGS gage discharge for each watershed. For small storms we found that there were no significant differences in the modeled runoff for three delineation methods. For large storms, we found the no-fill methods had a smaller error, but overall the difference was insignificant. This research suggests that capturing internal drainage by the delineation does not have much of an impact on the widely used CN model.
Keywords:
Geographic Information Systems, Runoff, Watershed Management, Curve Number

1. Introduction
Surface watershed delineation is the process of defining the boundary of the portion of the landscape that drains runoff to a particular point or outlet within the stream. Topography is the dominant feature used to distinguish the boundaries [1] . Areas of high elevation form the boundaries to determine the portion of the study area that drains to areas of lower elevation. In the last thirty years, there has been widespread development of elevation grids, which are called Digital Elevations Models (DEMs). Algorithms using DEMs have been developed to automate watershed delineation [2] - [7] . The most common method, the “standard fill method” (SFM), used for watershed delineation develops a flow direction grid derived from the DEM [3] [8] . Water is assumed to flow from a given cell to an adjacent cell associated with the steepest gradient. This gradient or flow direction is based on the D8 flow routing algorithm, [3] - [6] [9] that determines the steepest gradient based on a cell’s eight possible flow directions.
The D8 algorithm calculates the flow direction of every cell within the DEM by com- paring the elevations of the four adjacent cells and the four diagonal cells. The flow direction of the cell is assigned based on the maximum possible slope where the change in elevation is divided by the cell distance with a distance of one being used for the adjacent cells and a value of 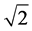 used for the diagonal grids [3] [7] [10] .
used for the diagonal grids [3] [7] [10] .
This process of determining the maximum slope generates a flow direction grid based on the DEM. DEMs have sinks or depressions that can be artifacts or errors of the raw data [5] [11] . These sinks are lower than the surrounding elevation. The D8 flow algorithm will not be able to assign a value to this cell, because it does not flow to any of the surrounding cells. This problem can result in a discontinuous flow network and an omission of areas of the watershed [12] [13] .
Depression-free DEMs are required to run the Hydrology and ArcHydro tools of ArcGIS [8] . To avoid generating these areas with no flow direction, an additional processing step is added before the flow direction grid is developed. This processing step is called “fill sinks” in ArcMap. The “fill sink” step works by increasing the sink’s elevation to the minimum elevation of the adjacent cell [3] [6] .
The filled DEM is used to generate a flow direction grid based on the D8 algorithm. The flow direction grid is then used to develop a flow accumulation grid, which serves as the model for digitized streams. Details on the ArcGIS stepwise watershed delineation process can be found in Khan et al., 2014 [8] . This method of watershed delineation is what we will refer to as the standard fill delineation method (SFM).
The widespread availability of DEMs and the D8 flow direction algorithm has made watershed delineation automation significantly more assessable, but the accurate modeling of watershed drainage is a complex process that is made more difficult by features such as continental glaciation, karst topography, thick sand layers, flat plains, and excessively arid regions (<20 cm of annual precipitation) [14] . These landscape features occur in approximately one third of the area within the conterminous United States, and encompass most of the Midwest [14] . Continental glaciation and karst topography create low topography and are highly correlated with wetlands and lakes that result in areas of internal drainage.
Areas of internal drainage can be divided into two basic categories: those that are capable of contributing surface runoff and those that are isolated from surface drainage networks, i.e. non-contributing [15] [16] . Internally drained areas that contribute to surface flow or groundwater in unexpected directions or unexpectedly fast timescales are generally a product of fractured bedrock, limestone karst topography, [17] [18] or anthropogenic modifications such as tile drainage [19] . Noncontributing areas serve more to store surface runoff rather than contribute it to the outlet and are characterized by a landscape with lakes and wetlands. Although the two types of internally drained areas are quite different, they can both lead to significant error in runoff and sediment estimates due to incorrect identification of contributing areas and runoff volumes [16] [18] [20] - [22] .
Using the SFM delineation in regions with continental glaciation, thick sand, and karst topography can mean the inclusion of noncontributing internally drained areas within a watershed [16] [23] . Many hydrologic processes such as runoff and sediment transport are modeled under the assumption that all areas of the watershed are contributing. Previous studies have developed methods of processing internally drained areas within watersheds [16] [20] [24] and examined the implementation of some strategies in a handful of watersheds [22] . Alternatives to the SFM delineation method requires additional processing and time, and for these reasons they not as widely used.
Few studies have been done to evaluate the accuracy of the SFM or compare it to other delineation methods [8] [25] [26] . The size, shape, and boundaries of the watersheds delineated by the different methods are expected to be different, but in order to determine which method works best, we needed to determine a method of comparison. In small watersheds this could be accomplished by detailed field studies that would need to be conducted over several seasons. In large watersheds, especially one involving multiple sites, this is not easily feasible.
The goal of our study is to compare and evaluate the SF delineation method to two other watershed delineation methods that process the delineation without filling the original DEM. We choose to compare the observed runoff (from a USGS gage) to model runoff using the modeled runoff using the curve number (CN) method for the three watershed delineation methods. We compared the delineation method’s modeled runoff to observed runoff at a US Geological Survey (USGS) gaging station for ten watersheds that have indicators of the presence of noncontributing internal drainage such as wetlands lakes, low relief. We hypothesize those watershed delineation methods that remove areas of internal drainage will have modeled values of runoff that are closer to observed values.
1.1. Delineation Methods
DEMs are inputs to all three delineation methods. Our DEMs are products of the USGS National Elevation Data (NED) with 10-m resolution [27] . The SFM is derived from a filled DEM, and this method assumes all parts of the watershed in the boundary will drain to the outlet. The two methods we present for comparison are the cut method (CM) and the Potentially Contributing Source Area method (PCSAM). Internal drainage can be defined many ways using landuse or wetland percent. For this study, we define internal drainage as the difference of the CM or PCSAM from the SFM. Both the CM and PCSAM attempt to account for areas of internal drainage; however, the complexity and additional data requirements associated with the PCSAM are significant.
The CM uses the outputs from the SFM filled DEM and the original DEM. An internal calculator within ArcMap called raster calculator is used to create a third layer of the difference between the filled DEM and the original DEM. The newly created grid has values of zero in the cells where the unfilled and filled DEM are the same; thus, these cells are not considered sinks. Cells which have a different elevation of the filled and unfilled DEM are considered sinks. Using the spatial analyst tool in ArcMap, the new grid is reclassified so that all the values of zero (not sinks) are reclassified with a value of one, and the sinks cells are reclassified as “no data”. This creates a DEM with “holes” cut out of it, hence the term “cut.” The watershed area and boundary derived from the SFM method are then used to mask or clip out the watershed from the newly derived “cut DEM”. This does not change the extent or shape of the watershed boundary. The watershed’s area will be decreased only by the amount of sinks identified. The advantages of this method are that it does not require any additional data inputs, all processes can be done in ArcMap, and it only requires the user to make two additional grids.
The Wisconsin Department of Natural Resources (WIDNR)’s Erosion Vulnerability Assessment for Agricultural Lands (EVAAL) attempts to identify internally drained areas that cannot contribute to soil loss by using a method that is similar to the CM [24] . To estimate if the sink will fill up and overflow, thus contributing to runoff at the outlet, the volume of each sink is determined and compared to a precipitation event. In order to accurately estimate the sink volume, high resolution Light Detecting and Ranging (LiIDAR) DEMs (1 m) are required and it only works on small watersheds (<2 km). LiDAR DEMs are not available at the writing of this publication for all watersheds in the study.
The PCSAM is more complex than the SFM and CM discussed above. It delineates the watershed by assuming the river and lands that have a slope upstream are part of the contributing area [16] [28] . The PCSAM was developed by Richards and Brenner, 2004 [16] and improved upon by Macholl et al., 2011 [22] . The PCSAM program is a FORTRAN program that operates outside of ArcMap to delineate watersheds based on raster data. Two input files in the float raster format are used in the PCSAM delineation: a DEM of the watershed region and an initial contributing area raster. Both inputs need to be created with the same extent, cell size, and projection in order for PCSAM to properly work. The initial contributing area input is based on a buffer around a stream network and connected wetlands. A buffer distance of 100 meters was used around streams to represent the floodplain. The 100-meter buffer distance was selected after examining multiple watershed DEMs with overlaid buffers to determine a limit that would not generally extend outward into unconnected areas. If the 100-meter buffer extended beyond the borders of the filled delineation, the buffer would be edited to fit fully within the filled watershed boundaries. This was done in order to avoid erroneously including portions of adjacent watersheds.
Wetlands and open water were extracted from the 2011 USGS National Land Cover Dataset [29] and converted to polygons. A “select by location” function was then performed to find wetland polygons connected to the stream buffer. These polygons were then merged and given a new attribute field named “PCSAM” with a value of 1. This initial contributing area was merged with a polygon of exactly the same extent and coordinate system as the DEM input. The resulting merged polygon was then converted to raster format with cell size and processing extent fixed to the DEM input.
1.2. Modeled Runoff: The CN Approach
We chose to use the CN method to model runoff because it is one of the most widely used runoff models [30] - [32] . The CN method has been used for several decades and tends to perform as well as or better than other runoff prediction methods [33] [34] . In studies where complex model calibration is not feasible, the CN method has been shown to perform as well as more complex models [35] .
The CN method calculates runoff depth (Q) from a given precipitation (P) and soil storage (S) (Equation (1)). The variable S is derived from the curve number (CN) (Equation (2)). The CN is an empirical variable that comes from a lookup table that requires landuse and hydrologic soil type to look up its value.
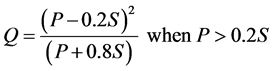 (1)
(1)
 (2)
(2)
An assumption of the CN method is that precipitation values less than 0.2 for S will not generate runoff. This assumption attempts to account for a concept of initial abstraction, which is obliquely defined as “precipitation not available for runoff” [36] . Physically initial abstraction refers to such processes as canopy interception. A value of 0.2 is the standard cited in the literature for S [32] [35] .
The CN values used in this project were derived from USGS National Land Cover Dataset [29] and US Department of Agriculture’s (USDA) hydrologic soil type from the Soil.
Survey Geographic Database (SSURGO) [37] . National land cover data are divided into thirty possible categories [29] . Hydrologic soil types are divided into four groups: A, B, C, and D. Group A represents sandy soils with the highest infiltration and least runoff, and group D represents clay rich soils with the lowest infiltration and greatest runoff. The method to derive the CN spatial grid combines both soil and landuse data and is described in Hernández-Guzmán and Ruiz-Luna, 2013 [38] . Land cover data [29] were only available at 30 m resolution, so the hydrologic soil data [37] was converted into a matching 30 m grid.
From the CN grid, a storage grid can be derived using the raster calculator and Equation (2). From the storage grid, a runoff grid can be determined using Equation (1) and an input of precipitation. The resulting grids all have resolutions of 30 m and were used to calculate runoff for each grid. We determined the storage (Equation (2)) for each precipitation event, and calculated a runoff for each grid which satisfied the assumption of the P > 0.2S (see Equation (1)). This method to calculate CN is described in McCuen, 2004 [39] . In particular, he warns of using an average value for diverse landuses with curve numbers
For example, agricultural landuse with a curve number 70 should not be averaged with forest landuse with a value of 50. This advice is contrary to Garen and Moore, 2005 [40] warning that curve number was not meant to be determined at the field scale. As our objective is to determine how the delineation affects runoff we find the McCuen, 2004 [39] interpretation more useful.
2. Study Sites
Ten watersheds in Wisconsin and Minnesota were selected as study sites (Figure 1) based on the availability of precipitation and discharge gage data, topography including noncontributing internal drainage, and land cover. Tile drainage was not present in the high agricultural watersheds and only minimally present in the northern forested watershed [41] . Watersheds containing wetlands, forests, and varying levels of agriculture and with at least ten years of gage data for both discharge and precipitation were selected. Major landuse categories are described for each watershed in Table 2. The stream network was not derived from the delineation, but rather it was obtained from the Wisconsin Department of Natural Resources [42] .
Figure 1. Watershed study sites in Wisconsin and Minnesota. The shapes are based on the SFM delineation. The watershed names are taken from the USGS gaging stations.
3. Methods
3.1. Precipitation and Discharge Data
Storms were selected based on both measured precipitation (NCDC, 2014) and the observed USGS discharge (USGS, 2013). Daily precipitation data were acquired from the National Climate Data Center (NCDC). We choose storms from June through September to remove the possibility of selecting snow, snowmelt, or rain on snow events. When possible, storms were modeled from a recent continuous dataset. Storms were selected that produced a response in the discharge gage data. Between five and ten suitable storms were modeled in each watershed depending on the number of suitable storms available [43] [44] .
Other considerations in storm selection were magnitude and independent storms. The magnitude of the storm not only had to produce a visible hydrograph response, but the storm also needed to be above the initial abstraction value of 0.2S for most areas of the watershed. Discharge response to precipitation needed to be independent of other events. If several precipitation events occurred close together, it would be impossible to partition a storm’s impact on the discharge. Storm events were deemed too close to model if they were separated by less than three days of precipitation. If an otherwise acceptable precipitation event was spread over two days, the two events were treated as one. Where multiple gages were in proximity to the watershed area, storm precipitation was determined by the Theissen polygon method [39] .
Daily mean discharge data at the outlet of each watershed were acquired from USGS gaging stations. Baseflow and direct flow were separated using the local minimum method with the HYSEP program [45] through the USGS Web Hydrograph Analysis Tool [46] .
3.2. Statistics
Results were analyzed both in terms of actual error ( ) and normalized error (m). To compare results from different delineations and different size watersheds, we normalized the error by the watershed’s area delineated by SFM. Normalized error was calculated with Equation (3), below:
) and normalized error (m). To compare results from different delineations and different size watersheds, we normalized the error by the watershed’s area delineated by SFM. Normalized error was calculated with Equation (3), below:
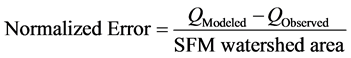 (3)
(3)
The model error in cubic meters was also examined for each individual storm across all watersheds in order to look for any trends that were not visible using average normalized error.
Storms were divided between large and small storms in order to examine the impact of storm size, with small storms being defined as less than 50 millimeters precipitation. The model error and normalized error from small storms, large storms, and storms of all sizes were each compared to percent internal drainage, drainage density, relief, and percent cover for land cover categories of agriculture, wetland, and forest.
The percent error was calculated based on Equation (4) as another metric to compare the modeled runoff between different watersheds with storm runoff volumes separated by orders of magnitude.
 (4)
(4)
The nonparametric Kendall Tau trend test is a statistical test that determines if a data set has monotonic increasing or decreasing trends. It was used in hydrologic studies [47] [48] to evaluate monotonic trends within the data and is documented and described in Helsel and Hirsch, 2002 [49] . We used it to compare normalized error versus precipitation, drainage density, relief, and percent cover for land cover categories of agriculture, wetland, and forest (alpha of 0.05). The Kendall Tau trends test was run in Minitab ver. 17 and requires a minimum of ten points.
4. Results
The watershed delineation areas are summarized in Table 1. The average area for CM was 84 percent of the SFM delineation. For PCSAM delineations on average 58 percent of the SFM area was delineated. The delineated areas were found to vary drastically between delineation methods in some cases. For example, for Allequash Creek (Figures 2(a)-(c)) the performance of the delineation methods was quite different.
The summary of the delineation methods watershed areas are noted in Table 1. The CM method removes any filled sinks from the watershed delineated by the SFM. The PCSA delineates from the stream network and directly connected wetlands, assuming
Table 1. Watershed areas for the three delineation methods: Standard Fill Method (SFM), Cut Area Method (CM), Potential Contributing Source Area Method (PCSAM). Stream miles were based upon the Wisconsin DNR 24 K Hydrography (WDNR, 2007). Drainage density is the number of stream miles divided by the watershed area. Additional the ratios of the watershed delineation areas are presented. The CM was usually close to the area generated by the SFM area with an average ratio of 0.85. The PCSA area was much lower than the SFM with an average ratio of 0.58.

Figure 2. (a) Represents the boundary of the watershed delineated by the standard fill method (SFM); (b) Depicts the surface water and wetlands which are inputs to the potentially; (c) Represents the PCSA method compared to the SFM.
that cells that flow toward the wetlands and stream network will be a part of the contributing area. In all cases, the CM and PCSA methods have smaller areas than the SFM. As mentioned in the methods section, the boundary or shape of the watershed for the CM is similar or the same as the SFM, while PCSA watershed delineation shape is often different. As noted in Table 1.
The drainage density for the PCSA were substantially higher than the other two delineations, but these results were directly associated with the watershed areas.
As described in the methods section, internal drainage is only defined for the CM and PCSAM. The SFM has all possible internal drainage filled, so it does not have internal drainage. The differences between the SFM and the other delineation methods represent the internal drainage of that method. Of interest in Table 1 is that the ratios of the CM and PCSA to SFM indicated some significant differences between the methods. On average the CM/SFM and PCSA/SFM values were 85 and 58 percent, respectively. The range of CM/SFM was 60 - 100 percent, while the PCSM/SFM was 20 - 95 percent.
In Table 2, we summarize the major landuse percentages for each watershed delineation method. Of note is wetland and open water makes up a larger percent for the PCSAM, but this is associated with wetlands and open water being initial inputs into the method. It is interesting in that the wetland and open water is less for the CM and the decrease is due to the sinks identifying wetlands depressions that were cut from the SFM delineation. In some watersheds, such as the Allequash, the difference in wetland and open water between the three methods is significant with the SFM having 35 percent, the CM identifying 30 percent, and the PCSAM identifying 50 percent. The Bear and White watersheds also have significant differences (>10%) in wetland and open water, while the White and Whittlesey Creek watershed have significant differences (>10%) in forest between delineation methods. Most other landuse categories within
Table 2. Watershed landuse for the three delineation methods.
the watersheds do not show a significant difference.
The average CN for each watershed are in Table 3. The CN for the watershed is based on the percent of landuse associated with a curve number. Higher CN values result in higher amounts of runoff, but generally the CN values for the delineation methods are similar. The largest differences are associated with how the delineation method captures the landuse. The Bear and Whittlesey Creek have the largest CN differences. A notable trend is that the PCSAM CN values are higher. This is associated with the PCSAM capturing less forest (where forest CNs are some of the lowest values, with ranges of 40 - 60) in the delineation.
In Figure 3(a) and Figure 3(b) we compare the ratios of the CM and PCSAM to the SFM for the different land cover types that are most likely associated with internal drainage (agriculture, forest, wetland). Though no significant trend exists, the PCSM/SFM shows a general increase in the ratio with increasing wetland. The wetlands in most
Table 3. CN for each landuse category were weighted by area and summarized for each watershed. Higher CN represent areas of higher runoff. The curve number values for each watershed were similar with small differences with the exception of the White and Whittlesey.


Figure 3. (a) Percent Land cover vs CM/SFM and (b) Percent Land cover vs PCSAM/SFM: The areas of watershed delineations methods are normalized by the SFM and compared to land cover. The CM the values fall between 60% - 100% of the watershed. The range for the PCSMA/SFM was much wider, between 20% - 95%.
of the watersheds are contiguous to the stream network; therefore, it is not surprising that watersheds with high percentages of wetlands would also have a higher PCSM/SFM ratio.
For both Figure 4(a) and Figure 4(b) and Figure 5(a) and Figure 5(b) we separated the normalized error by storm size. Large storms (over 50 mm) had both over and underestimates of the observed runoff while small storms overestimated the observed runoff. In Figure 4(a) and Figure 4(b) we compare the normalized error to percent agriculture associated with the delineation method. Although not a statistically significant trend, the error of the methods increases with increasing agriculture. For the majority of the watersheds, the methods performed similarly for both large and small storms.
Figure 5(a) and Figure 5(b) shows an opposite trend with the largest normalized correlated with smaller percentages of wetlands, but the trends are not statistically significant. The PCSAM method error is generally lower than the other two methods; usually the difference is less than three percent. The SFM and CM were typically within one percent of each other.


Figure 4. Normalized error vs watershed percent agriculture for large and small storms.


Figure 5. Normalized error vs percent wetland for large and small storms.
Additionally, we examined total relief and internal drainage (as defined in the methods section) and we did not find a relationship between the delineation methods. Overall the differences between the methods were minimal except in the case of watersheds with high agriculture and low wetland. In general, the PCSAM performed the best, especially in agricultural watersheds, but the differences were typically between 3% - 5% of the other two methods. The CM compared to the SFM did not reveal any significant differences. The Kendall Tau trend test indicated no significant trends (p > 0.5) for the standard error for drainage density, precipitation, or land cover percent for the three delineation methods (agriculture, forest, wetland).
5. Discussion
We initially hypothesized that the main variables impacting model performance would be watershed area, drainage density and percent internal drainage, with the SFM (that fill in sinks) experiencing the largest deviations from actual runoff totals [16] [22] . This was not the case for the watersheds studied, they instead did not show strong trends (Figure 4(a) and Figure 4(b) and Figure 5(a) and Figure 5(b)). In cases where modeled storm runoff was overestimated PCSAM delineations produced smaller overestimations. In cases of model underestimation, PCSAM had the highest magnitude normalized errors, but again, these differences were insignificant.
One likely reason for the similar performance of all models is the impact of intermittently overflowing internal drainage, particularly in areas containing wetland that may or may not be part of variable source areas depending on antecedent moisture levels [28] [31] [50] [51] . Based on the results of this study, it may be concluded that it is necessary to generate multiple PCSAs for a drainage network. Rain events of different magnitudes will have different potential contributing source areas. In addition, some areas such as wetlands may contribute or not contribute depending on the volume of water in them, leading to differences in observed runoff for storms of the same magnitude and duration. PCSAM delineations may be used as an additional tool when identifying variable contributing source areas. Identification of contributing areas is a complex problem that depends not only on topography but also on field scale variations in moisture and landcover along with other variables [28] [52] .
The CN model appears to perform differently for small and large storms when examining the model error in runoff volume versus storm size. This has also been encountered in previous studies [30] [35] [53] . As precipitation depth increases the SFM model appears to overestimate runoff volumes, while the CM and PCSAM delineations tend to underestimate for all storm sizes.
An answer to the antecedent moisture conditions has been to consider changes to the initial abstraction which is usually assumed to be 0.2 for S. The Spatial Analysis of surface Runoff in ArcGis (SARA) model by Hernández-Guzmán and Ruiz-Luna, 2013 [38] incorporates findings from Hawkins et al., 2008 [53] . Hawkins et al., 2008 [53] found that the curve number model initial abstraction varies from 0.0 to 0.49 depending upon storm size. The SARA model allows for the adjustment of initial abstraction in calculating runoff. Another solution has been to add a wetness index into existing runoff and water quality models such as SWAT that use curve number [31] [51] . Such adjustments to our study are beyond the scope of this study, but it would make for an interesting future study.
In this study, the largest errors were for the Pecatonica and Yahara watersheds, which are characterized by over 60 percent agriculture with few wetlands or forests. Recent studies such as Tessema et al., 2014 [54] indicate that CN models may not fully account for the impact of seasonally variable evapotranspiration on available storage. Antecedent moisture considerations may be problematic in heavily irrigated regions, and this may account for the high overestimation runoff. Given the high variability of agricultural land cover at a field scale, a correction factor or soil wetness index may be beneficial when modeling agriculture dominated watersheds as suggested by [31] [38] [51] .
The most notable finding upon examining the results is the similar performance of all three delineation methods for both large and small storms. All models experienced similar degrees of error; no model clearly outperformed the others. The lack of a significant performance difference between the delineation methods has also been found by at least one previous study on three watersheds in New York’s Catskill Mountains [55] . This study attempted to determine watershed source areas and used CN runoff models to compare results. Their findings show similar results for different modeled areas [55] .
One possible implication of this research is that methods that are more data intensive and time consuming such as PCSAM may not be worth the additional data preparation required for modeling runoff given the data resolutions currently available except for agricultural watershed. Earlier studies such as Richards and Brenner, 2004 [16] that focused on PCSAM noted the likely importance of high resolution (3 m) DEM data. High resolution data with cells of several meters or less were unavailable for Richard and Brenner’s 2004 [16] study and are still unavailable for many regions containing noncontributing internal drainage as of 2015. The current available thirty-meter resolution of land cover inputs also likely limits the impact of increasing DEM resolution.
6. Conclusions
Comparison of the different delineation methods appears to indicate that they may each be suited for different purposes. No one delineation method significantly outperformed the others in predicting watershed runoff with the CN given available data. Given the comparatively simple workflows, the SFM seems ideal for delineation for predicting storm runoff. Because sinks tend to overflow during large rain events, the more extensive delineations that fill sinks to some degree could better handle large storms.
PCSAM delineations that accurately delineate contributing areas will encompass larger areas around drainage networks as precipitation increases, leading to variable source areas based on topography. Multiple potential contributing source areas based on storm size could be useful in determining sources for non-point source pollution for different magnitude rain events. A similar method was employed by Schneiderman et al. (2007) [31] to determine areas capable of contributing non-point source pollution in a single watershed. Cut delineations may be useful as a tool used in conjunction with PCSA to quantify sink volumes in order to determine which sinks may overflow during given events. Previous studies such as Frankenberger et al. (1999) [28] and Van Liew et al. (2007) [52] have focused on the role of land cover and antecedent moisture in determining variable contributing source areas.
Another additional research question raised by this study and others is the role of DEM resolution in the accuracy of different delineation methods [16] [22] . The PCSA method is sensitive to small elevation changes and will likely produce more accurate delineations as cell size decreases [16] .
Based on the similar levels of model error seen between all delineation methods, raster resolution does not appear to be one of the most significant factors impacting runoff model error. It is important to note that in addition to the DEM, the resolution of land cover and soil data will require improvements to increase model accuracy. Currently both of these important variables are available only in resolutions even coarser than the ten meter DEM; for example, land cover data is available at thirty-meter resolution. As the delineation method performed similarly, the resolution of the DEM and the resulting watershed delineations do not appear to be key problem. Improvements in modeling will likely be tied to multiple factors including more complete and accurate data for precipitation, elevation, land cover, and antecedent moisture.
From a management perspective, the most important implication of the study results is when modeling runoff with the CN, the filled delineation method was not outperformed by other delineations. As the basis of watershed delineations used by landuse planners and regulators, this means adopting more time and data intensive processes will not necessarily provide increased accuracy with inputs of the resolutions currently available. Two areas where future studies are needed to evaluate the delineation methods and runoff are as follows: 1) regions where agriculture is the dominant landuse; and 2) extreme precipitation events where either the duration or intensity of the storm is unusual for the region.
Acknowledgements
The authors are grateful to the University of Wisconsin for provided a graduate stipend and to anonymous reviewers who improved this paper.
Cite this paper
Troolin, W.D. and Clancy, K. (2016) Comparison of Three De- lineation Methods Using the Curve Number Method to Model Runoff. Journal of Water Resource and Protection, 8, 945-964. http://dx.doi.org/10.4236/jwarp.2016.811077
References
- 1. Dunne, T. and Leopold, L.B. (1978) Water in Environmental Planning. WH Freeman and Co., New York.
- 2. Jenson, S. (1984) Automated Derivation of Hydrological Basin Characteristics from Digital Elevation Data. US Geological Survey Report 14-08-0001-20129, 10 p.
http://topotools.cr.usgs.gov/pdfs/automated-derivation-of-hydrologic-basin-characteristics-from-digital-elevatioin-model-data.pdf - 3. Jenson, S. and Domingue, J. (1998) Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. Photogrammetric Engineering and Remote Sensing, 54, 1593-1600.
- 4. Mark, D.M. (1984) Automated Detection of Drainage Networks from Digital Elevation Models. Cartographica, 21, 168-178.
http://dx.doi.org/10.3138/10LM-4435-6310-251R - 5. Martz, L. and Garbecht, J. (1992) Numerical Definition of Drainage Network and Subcatchment Areas from Digital Elevation Models. Computer Geosciences, 18, 747-761.
http://dx.doi.org/10.1016/0098-3004(92)90007-E - 6. O’Callaghan, J. and Mark, D. (1984) The Extraction of Drainage Networks from Digital Elevation Data. Computer Vision, Graphics, and Image Processing, 28, 323-344.
http://dx.doi.org/10.1016/S0734-189X(84)80011-0 - 7. Tarboton, D.G., Bras, R.L. and Rodriguez-Iturbe, I. (1991) On the Extraction of Channel Networks from Digital Elevation Data. Hydrological Processes, 5, 81-100.
http://dx.doi.org/10.1002/hyp.3360050107 - 8. Khan A., Richards, K., Parker, G., McRobie, A. and Mukhopadhyay, B. (2014) How Large Is the Upper Indus Basin? The Pitfalls of Auto-Delineation Using DEMs. Journal of Hydrology, 509, 442-453.
http://dx.doi.org/10.1016/j.jhydrol.2013.11.028 - 9. Morris, D. and Heerdegen, R. (1988) Automatically Derived Catchment Boundaries and Channel Networks and Their Hydrological Applications. Geomorphology, 1, 131-141.
http://dx.doi.org/10.1016/0169-555X(88)90011-6 - 10. Kiss, R. (2004) Determination of Drainage Network in Digital Elevation Models, Utilities and Limitations. Journal of Hungarian Geomathmatics, 2, 16-29.
- 11. Qian, J., Ehrich, R. and Campbell, J. (1990) DNESYS—An Expert System for Automatic Extraction of Drainage Networks from Digital Elevation Data. IEEE Transactions on Geoscience and Remote Sensing, 28, 29-45.
http://dx.doi.org/10.1109/36.45743 - 12. McCormack, J., Gahegan, M., Roberts, S., Hogg, J. and Hoyle, B. (1993) Feature Based Derivation of Drainage Networks. International Journal of Geographical Information Science, 7, 263-279.
http://dx.doi.org/10.1080/02693799308901956 - 13. Nikolakopoulos, K., Kamaratakis, E. and Chrysoulakis, N. (2006) SRTM vs ASTER Elevation Products. Comparison for Two Regions in Crete, Greece. Remote Sensing, 27, 4819-4838.
http://dx.doi.org/10.1080/01431160600835853 - 14. Hughes, R. and Omernik, J. (1981) Use and Misuse of the Terms Watershed and Stream Order. Warmwater Stream Symposium, American Fisheries Society, Bethesda, 1981, 320-326.
- 15. Troolin, W. (2015) Impacts of Delineation Methods on Modeled Runoff in Watersheds Containing Non-Contributing Internal Drainage. MSc Thesis, University of Wisconsin, Stevens Point.
- 16. Richards, P. and Brenner, A. (2004) Delineating Source Areas for Runoff in Depressional Landscapes: Implications for Hydrologic Modeling. Journal of Great Lakes Research, 30, 9-21.
http://dx.doi.org/10.1016/S0380-1330(04)70325-1 - 17. Alexander, E.C., Green, J.A. and Alexander, S.C. (2008) Plum Bottom Closed Depression Groundwater Trace Final Report. Administrative Report Submitted to the Door County Soil and Water Conservation Department, 13 p.
http://map.co.door.wi.us/swcd/Plum%20Bottom%20Groundwater%20Trace%20Final%20Report%20Jan%202008.pdf - 18. Taylor, C., Williamson, T., Newson, J., Ulery, R., Nelson, H. and Cinotto, P. (2012) Phase II Modification of the Water Availability Tool for Environmental Resources (WATER) for Kentucky: The Sinkhole-Drainage Process, Point-and-Click Basin Delineation, and Results of Karst Test-Basin Simulations. US Geological Survey Report 2012-5071, 56 p.
http://pubs.usgs.gov/sir/2012/5071/pdf/sir2012-5071.pdf - 19. Granato, G. (2012) Estimating Basin Lagtime and Hydrograph-Timing Indexes Used to Characterize Stormflows for Runoff-Quality Analysis. US Geological Survey Scientific Investigations Report 2012-5110, 47 p.
http://pubs.usgs.gov/sir/2012/5110/ - 20. Richards, P. and Noll, M. (2006) GIS-Based Riparian Buffer Management Optimization for Phosphorus and Sediment Loading. USGS Water Resources Research Report, 2005NY66B. 25 p.
http://water.usgs.gov/wrri/05grants/progress.completion_reports/NY/2005NY66B.pdf - 21. Phillips, R., Spence, C. and Pomeroy, J (2011) Connectivity and Runoff Dynamics in Heterogeneous Basins. Hydrological Processes, 25, 3061-3075.
- 22. Macholl, J., Clancy, K. and McGinley, P. (2011) Using a GIS Model to Identify Internally Drained Areas and Runoff Contribution in a Glaciated Watershed. Journal of the American Water Resources Association, 47, 114-125.
http://dx.doi.org/10.1111/j.1752-1688.2010.00495.x - 23. McDonnell, J., Sivanpalan, M., Vache, K., Dunn, S, Grant, G., Haggerty, R., Hinz, C., Hooper, R., Kirchner, J., Roderick, M., Selker, J. and Weiler, M. (2007) Moving beyond Heterogeneity and Process Complexity: A New Vision for Watershed Hydrology. Water Resources Research, 43, 7301-7306.
http://dx.doi.org/10.1029/2006WR005467 - 24. Nelson, T., Mazurek, D., Ruesch, A., Kempen, S. and Evans, D. (2014) Erosion Vulnerability Assessment for Agricultural Lands (EVAAL) Methods Documentation, Wisconsin DNR.
http://dnr.wi.gov/topic/Nonpoint/documents/EVAAL/EVAAL_Methods_v1_0.pdf - 25. Turcotte, R., Fortin, J., Rousseau, A., Massicotte, S. and Villeneuve, J. (2001) Determination of the Drainage Structure of a Watershed Using a Digital Elevation Model and a Digital River and Lake Network. Journal of Hydrology, 240, 225-242.
http://dx.doi.org/10.1016/S0022-1694(00)00342-5 - 26. Wu, S., Li, J. and Huang, G. (2008) A Study on DEM-Derived Primary Topographic Attributes for Hydrologic Applications: Sensitivity to Elevation Data Resolution. Applied Geology, 28, 210-223.
http://dx.doi.org/10.1016/j.apgeog.2008.02.006 - 27. USGS (US Geological Survey) (2001) NED (National Elevation Data) 2011 Elevation. SDE Raster Digital Data.
http://nationalmap.gov/elevation.html - 28. Frankenberger, J., Brooks, E., Walter, M. and Steenhuis, T. (1999) A GIS-Based Variable Source Area Hydrology Model. Hydrological Processes, 13, 805-822.
http://dx.doi.org/10.1002/(SICI)1099-1085(19990430)13:6<805::AID-HYP754>3.0.CO;2-M - 29. USGS (US Geological Survey) (2011) NLCD (National Land Cover Database) 2011 Land Cover. SDE Raster Digital Data. http://www.mrlc.gov
- 30. Hawkins, R. (1993) Asymptotic Determine of Runoff CNs from Data. Journal of Irrigation and Drainage Engineering, 19, 334-345.
http://dx.doi.org/10.1061/(ASCE)0733-9437(1993)119:2(334) - 31. Schneiderman, E., Steenhuis, T., Thongs, D., Easton, Z., Zion, M., Neal, A., Mendoza, G. and Walter, M. (2007) Incorporating variable source area hydrology into a curve-number based watershed model. Hydrological Processes, 21, 3420-3430.
http://dx.doi.org/10.1002/hyp.6556 - 32. McGinley, P., Freihoefer, A. and Mentz, R. (2013) Runoff Curve Numbers at the Agricultural Field-Scale and Implications for Continuous Simulation Modeling. Journal of the American Water Resources Association, 49, 1436-1443.
http://dx.doi.org/10.1111/jawr.12097 - 33. King, K., Arnold, J. and Binger, R. (1999) Comparison of Green-Ampt and CN Methods on Goodwin Creek Watershed Using SWAT. American Society of Agricultural Engineers, 42, 919-925.
http://dx.doi.org/10.13031/2013.13272 - 34. Ponce, V. and Hawkins, R. (1996) Runoff CN: Has It Reached Maturity? Journal of Hydrologic Engineering, 1, 11-19.
http://dx.doi.org/10.1061/(ASCE)1084-0699(1996)1:1(11) - 35. Michaud, J. and Sorooshian, S. (1994) Comparison of Simple versus Complex Distributed Runoff Models in a Midsized Semi-Arid Basin. Water Resources Research, 30, 593-605.
http://dx.doi.org/10.1029/93WR03218 - 36. NRCS (National Resources Conservation Services) (1986) Urban Hydrology for Small Watersheds. US Department of Agriculture-NRCS Technical Release, 55.
ftp://ftp.odot.state.or.us/techserv/Geo-Environmental/Hydraulics/Hydro/Manuals_and_Guidance/HDM%202011/Chapter_07_2011/Chapter_07_appendix_G/Urban_Hydrology_for_Small_Watersheds.pdf - 37. USDA (US Department of Agriculture) (2006) STASG Soil Data: US General Soil Map Tabular Data.
http://sdmdataaccess.nrcs.usda.gov/ - 38. Hernández-Guzmán, R. and Ruiz-Luna. A. (2013) SARA—An Enhanced Curve Number-Based Tool for Estimating Direct Runoff. Journal of Hydroinformatics, 15, 881-887.
http://dx.doi.org/10.2166/hydro.2013.145 - 39. McCuen, R. (2004) Hydrologic Analysis and Design. 3rd Edition, Pearson, Upper Saddle River, 888 p.
- 40. Garen, D. and Moore, D. (2005) Curve Number Hydrology in Water Quality Modeling: Uses, Abuses, and Future Directions. Journal of the American Water Resources Association, 41, 377-388.
http://dx.doi.org/10.1111/j.1752-1688.2005.tb03742.x - 41. Ruark, M., Panuska, J., Cooley, E. and Pagel, J. (2009) Tile Drainage in Wisconsin: Understanding and Locating Tile Drainage Systems. University of Wisconsin Extension (GWQ054), 4 p.
http://learningstore.uwex.edu/Assets/pdfs/GWQ054.pdf - 42. WDNR (Wisconsin Department of Natural Resources) (2007) 24,000 Hydrography Data, Version. 6.
- 43. NCDC (National Climate Data Center) (2014) NCDC Surface Data: Daily, US High Resolution-Cooperative, NWS.
http://www.ncdc.noaa.gov/oa/climate/climatedata.html#daily - 44. USGS (US Geological Survey) (2013) Geological Survey, National Water Information System: Web Interface, Surface Water for Wisconsin.
http://waterdata.usgs.gov/wi/nwis/rt - 45. Sloto R. and Crouse, M. (1996) HYSEP: A Computer Program for Streamflow Hydrograph Separation and Analysis. US Geological Survey Water-Resources Investigations Report.
- 46. Lim, K., Engel, B., Tang, Z., Choi, J., Kim, K., Muthukrishnan, S. and Tripathy, D. (2005) Automated Web GIS Based Hydrograph Analysis Tool, WHAT. Journal of the American Water Resources Association, 41, 1407-1416.
http://dx.doi.org/10.1111/j.1752-1688.2005.tb03808.x - 47. McCabe, G. and Wolock, D. (2002) A Step Increase in Streamflow in the Conterminous United States. Geophysical Research Letters, 29, 2185-2188.
http://dx.doi.org/10.1029/2002GL015999 - 48. Juckem, P., Hunt, R. anderson, M. and Roberson, D. (2008) Effects of Climate and Land Management Change on Streamflow in the Driftless Area of Wisconsin. Journal of Hydrology, 355, 123-130.
http://dx.doi.org/10.1016/j.jhydrol.2008.03.010 - 49. Helsel, D. and Hirsch, R. (2002) Statistical Methods in Water Resources. US Geological Survey, Techniques of Water-Resources Investigations Book, Vol. 4, Chapter A3, 522 p.
- 50. Ludden, A., Frink, D. and Johnson, D. (1983) Water Storage Capacity of Natural Wetland Depressions in the Devils Lake Basin of North Dakota. Journal of Soil and Water Conservation, 3, 45-58.
- 51. Easton, Z., Fuka, D., Walter, M., Cowan, D., Schneiderman, E. and Steenhuis, T. (2008) Re-Conceptualizing the Soil and Water Assessment Tool (SWAT) Model to Predict Runoff from Variable Source Areas. Journal of Hydrology, 348, 279-291.
http://dx.doi.org/10.1016/j.jhydrol.2007.10.008 - 52. Van Liew, M.W., Green, C.H. and Starks, S. (2007) Unit Source Area Data: Can It Make a Difference in Calibrating the Hydrologic Response for Watershed Scale Modeling? Journal of Soil and Water Conservation, 62, 162-170.
- 53. Hawkins, R., Ward, T., Woodward, D. and Van Mullem, J. (2008) CN Hydrology. American Society of Civil Engineers, Reston.
- 54. Tessema, S., Lyon, S., Setegn, S.G. and Mortberg, U. (2014) Effects of Different Retention Parameter Estimation Methods on the Prediction of Surface Runoff Using the SCS CN Method. Water Resources Management, 28, 3241-3254.
http://dx.doi.org/10.1007/s11269-014-0674-3 - 55. Lyon, S., Walter, M., Marchant, P. and Steenhuis, T. (2004) Using a Topographic Index to Distribute Variable Source Area Runoff Predicted with the SCS CN Equation. Hydrological Processes, 18, 2757-2771.
http://dx.doi.org/10.1002/hyp.1494



