Journal of Water Resource and Protection
Vol.06 No.17(2014), Article ID:51939,12 pages
10.4236/jwarp.2014.617143
Saturated Hydraulic Conductivity Changes with Time and Its Prediction at SAR and Salinity in Quevedo Region Soils
Abdelmonem Mohamed Amer1,2,3, Carmen Suarez3, Felix Valverde3, Roberto Carranza3, Leonardo Matute3, Gabriel Delfini3
1SENESCYT, Prometeo Project, Quito, Ecuador
2Department of Soil Science, Faculty of Agriculture, Menoufia University, Shebin El-Kom, Egypt
3Faculty of Agriculture, Quevedo State Technical University-UTEQ, Quevedo, Ecuador
Email: amer_abdel@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2014; revised 12 October 2014; accepted 5 November 2014
ABSTRACT
Darcy’s law is applied to describe the steady flow processes in which the flux remains constant with time along the conducting system. Due to the dispersion and migration of colloidal particles and lodging in the soil pores the reduction in hydraulic conductivity occurs with time in particular when the soil and the percolating solution are affected by electrolyte concentration. Hence, the aim of this study is to find empirical equations that can be used to predict the flux with time. Data for the effluent volume versus time (up to 6 hours) which was collected for three soils (located at Quevedo-Los Rios region) treated by two salt solutions (5 and 50 meq/l) with different SAR values were used to test certain mathematical forms of equations. Only four empirical equations were found to perfectly fit the data (flux vs time) whereas, fitting the calculated and measured data of the hydraulic conductivity for all soils produced regression factors R2 ≥ 0.99. So, these equations can be applied to predict the hydraulic conductivity and to characterize the flow process at saturated conditions of the studied soils with great confidence. The Hoerl function model was the best of all equations for application as the fitting degrees were almost perfect for all studied soils at 5 and 50 meq/l. It was observed for all equations that one of the fitting parameters would always represent the initial hydraulic conductivity (Kos) that was evaluated graphically at zero time by extrapolation.
Keywords:
Saturated Hydraulic Conductivity, Empirical Models, Effluent Volume and SAR, Linear & Nonlinear Flux

1. Introduction
The basic equation for describing the steady flow of water through columns of porous materials is represented by Darcy’s law:
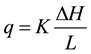 (1)
(1)
where, q is the flux or the effluent volume of the percolating solution per unit of area and time; K is the proportionality factor or hydraulic conductivity of the porous media; and 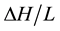 represents the total hydraulic head gradient. Then, if Q is the volume of solution vertically flowing through a column of porous material (L cm length with a cross sectional area of A cm2) under a constant hydraulic head (h cm), the flux in L・T−1 unit (cm/hr) can be calculated as:
represents the total hydraulic head gradient. Then, if Q is the volume of solution vertically flowing through a column of porous material (L cm length with a cross sectional area of A cm2) under a constant hydraulic head (h cm), the flux in L・T−1 unit (cm/hr) can be calculated as:
 (2)
(2)
thus,
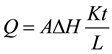 (3)
(3)
where,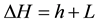 .
.
Equation (3) can be represented in a straight line whose slope is equal to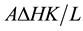 . It is, therefore, possible to determine the hydraulic conductivity as a parameter characterizing the flow process. Also, the slope of the linear equation is equal to K when the Equation (3) rearranged as follows:
. It is, therefore, possible to determine the hydraulic conductivity as a parameter characterizing the flow process. Also, the slope of the linear equation is equal to K when the Equation (3) rearranged as follows:
 . (4)
. (4)
However, the validity of Darcy’s law is determined by physical and/or chemical properties of either the porous media or the percolating solution and depends on the hydraulic head gradient applied [1] [2] . Also, Darcy’s law may only be applied to describe steady or stationary flow processes in which the flux remains constant with time along the conducting system [3] .
In the saturated soils, K is generally considered a constant, although it may change with time due to particle rearrangement within the soil matrix. Because of changes in the physical or chemical and structural state of the porous media, changes in the hydraulic conductivity may therefore occur during the flow process. Dikinya et al., (2008) [4] measured changes in hydraulic gradients 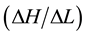 along the columns and outflow particle sizes and concentrations during pressure leaching with solutions of 100, 10 and 1 mmol/L NaCl. The lowest ionic strength has resulted in more reduced hydraulic conductivity and relatively more release of colloids associated with hydrodynamic shear and dispersion. Steady increases in hydraulic gradient
along the columns and outflow particle sizes and concentrations during pressure leaching with solutions of 100, 10 and 1 mmol/L NaCl. The lowest ionic strength has resulted in more reduced hydraulic conductivity and relatively more release of colloids associated with hydrodynamic shear and dispersion. Steady increases in hydraulic gradient 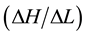 and corresponding decreases in relative saturated hydraulic conductivity
and corresponding decreases in relative saturated hydraulic conductivity 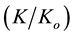 with time were observed for the soils under investigation. The decrease in
with time were observed for the soils under investigation. The decrease in 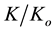 and increase in
and increase in 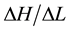 were clearly influenced by the size as well as the concentration of migrating particles in the porous medium. This was attributable to swelling and dispersion within the soil matrix at these concentrations.
were clearly influenced by the size as well as the concentration of migrating particles in the porous medium. This was attributable to swelling and dispersion within the soil matrix at these concentrations.
The effects of sodium adsorption ratio (SAR) and electrolyte concentration on hydraulic properties of soils and clays as well as the variations in the hydraulic conductivity as a function of exchangeable ion status of soils have been extensively studied [5] -[9] . Detailed information on salinity effects on soil-water properties under saturated conditions is also reported by Frenkel et al. (1978) [10] .
Dispersion and migration of colloidal particles, subsequently lodging in the soil pores, lead to reduction in hydraulic conductivity when the soil is slightly sodic and/or the percolating solution is low in electrolyte concentration. On the other hand, at high exchangeable sodium percentage (ESP) and salt concentration ˃ 5 meq/l, the swelling of clay is the main mechanism responsible for decreases in hydraulic conductivity [5] [11] [12] . These effects may therefore, progressively reduce hydraulic conductivity according to the particular type of soil or the chemical composition of the percolating solution.
High sodium adsorption ratios and low electrolyte concentrations cause a progressive reduction in the percolating rate, resulting in a non-linear relationship between effluent volume and time, i.e., Ks becomes not constant and the Darcy’s law, which characterizes steady or stationary flow processes, does not apply. So, the objectives of this study are: 1) to find some empirical equations that can correctly predict soil hydraulic conductivity, taking into consideration the changes in the physical or chemical and structural state of the porous media, which occur during the flow process; 2) to find the fitting parameters for the proposed empirical equations with respect to initial saturated hydraulic conductivity (Kos) at zero time; and 3) to study the effect of SAR of two salt solutions (5 and 50 meq/l) on the saturated hydraulic conductivity of tropical soils of Quevedo-Los Rios region.
2. Materials and Methods
To achieve the aim of this study, surface soil samples were collected at two locations to represent the Quevedo region of the Los Rios Province, Ecuador. The first location is the Felix Farm, about 30 km to Quevedo City. The second location is the INIAP Experimental Farm, Pichilingue-Quevedo. Disturbed and undisturbed soil samples were taken at a depth, 0 - 30 cm. The disturbed samples were air dried, gently crushed and sieved through a 2 mm sieve. Fractions below 2 mm were subjected to chemical and mechanical analysis. The undisturbed samples were used to determine bulk density and Hydraulic conductivity. Soil physical and chemical analyses, presented in Table 1, were done according to Black et al., (1965) [13] .
Two salt solutions (5 and 50 meq/l, representing ionic strength of 0.005 N and 0.05 N) with six SAR values; 0, 5, 10, 30, 50 and ˃50 or (∞) were prepared and employed in studying their effects on the saturated hydraulic conductivity of the previously mentioned soils.
Saturated hydraulic conductivity was determined by using undisturbed soil samples according to Klut’s method (1972) [14] . Schematic of the head-constant device that can be used for determination of the hydraulic conductivity is shown in Figure 1, whereas the hydraulic conductivity values were calculated according to Darcy’s law.
Table 1. Particle size distribution for the depth 0 - 30 cm of the studied soils.
*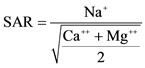 .
.
Figure 1. Classic schematic for the hydraulic conductivity method with constant head. Key: 1―standard flask; 2―car- rier; 3―table wood; 4―glass calyx; 5―glass tube on U form; 6―plastic diaphanous column; 7―glass calyx; 8― mineral avoirdupois.
The hydraulic gradient was kept constant during the experiments with a constant head device. All experiments were carried out to evaluate the effect of SAR and electrolyte (salt) concentrations on the drainage properties of studied soils. So, the effluent volume as a function of time was recorded.
Data for the effluent volume versus time (up to 6 hours) for the soils that treated with two salt solutions with six different SAR values was collected and used for testing a large number of the known forms of equations (26 models are listed in Table 2). Characteristic parameters of the proposed equations are the saturated hydraulic conductivity at zero time (Kos) and coefficients a, b, c that takes into account the progressive reduction in the initial hydraulic conductivity (Kos) of the soils.
The relationships between effluent volume and time were statistically analyzed to find the regression equations and then to find the initial hydraulic conductivity (Kos) as well as to find the fitting parameters of the empirical equations for predicting drainage rate from soil columns under saturated conditions. The measured data were fitted to all mathematical forms and the regression coefficients were calculated using a computer program named Curvefit by Thomas S. Cox, 1984. Only equations that predicted the effluent volume versus time with a correlation factor (R2) near unity was considered.
3. Results and Discussion
3.1. Characteristics of Flow Process and Empirical Models
To characterize the flow process, the saturated hydraulic conductivity  was calculated according to Darcy’s law as
was calculated according to Darcy’s law as



Table 2. Tested equations for best-fit of the measured data of effluent volume changes with time.
Table taken from a curve fitting computer program called Curvefit by Thomas S. Cox, 1984, based on equations listed in Curve fitting for programmable calculations by William M. Kolb. Published by IMTEC, P.O. Box 1402 Bowie MD 20716.
particles along the soil columns with subsequent plugging of conducting pores [5] [11] . For instance, data illustrated in Figure 2 and Figure 3 for the surface depth of the Felix Farm sandy loam soil show Linear relationships between effluent volume of percolating solution and time which were obtained at high electrolyte concentration (50 meq/l) with all SAR values except for low SAR values (0 and 5) which were nonlinear.
Also, nonlinear relationships were observed at low electrolyte concentration (5 meq/l) at SAR values 0, 5, 10 and 30 in the Felix Farm sandy loam soil as well as at SAR 5 and 10 for other heavier soils (INIAP farm). Thus indicate a variation or decrease in the initial hydraulic conductivity of the soil during the flow process.
The empirical equations (26 equations) were applied to fit the data for effluent volume vs time. These data were used for characterizing the flow process when hydraulic conductivity is not a constant factor under saturated conditions. However, this case is occurred when the Darcy’s equation does not produce a straight line but a curve with decreasing slope with time, following changes in the physical or chemical state of the soil during the percolating process.
The following empirical equations were observed to almost perfectly fit the experimental data:


Figure 2. Relationships between effluent volume {Q(L/AΔH)} and time for Felix Farm sandy loam soil (0 - 30 cm) as a function of SAR at 5 meq/l.
Figure 3. Relationships between effluent volume {Q(L/AΔH)} and time for Felix Farm sandy loam soil (0 - 30 cm) as a function of SAR at 50 meq/l.


where, Y is equal to
It should be noted that Y was not taken as the effluent volume Q but rather 


3.2. Initial Hydraulic Conductivity
The initial hydraulic conductivity (Kos) was observed to be presented in all the proposed equations as one of the constants of each equation. The presence of Kos as a part of all the used equations indicates that the initial hydraulic conductivity is assumed to stay constant if only no changes occur to the soil structure with time. Changes in the physical or chemical state of the soil during the percolation process will result in decreasing the value of Ks with time. Each of the four equations accounted for the decrease in Ks with time, and predicted the hydraulic conductivity change that reflects the current state of the soil.
Evaluation of the initial hydraulic conductivity (Kos) at time zero involves dividing by zero, so, it can be done graphically for the relation of 


And for electrolyte solution of 50 meq/l, they were:
As for the representation of the initial hydraulic conductivity (Kos) through the fitted parameters a, b, and c in the suggested four models, it was observed that the first model (Reciprocal Hyperbola) contained two constants a, and b, while Kos was noticed to equal the reciprocal of the constant b
Figure 4. Initial hydraulic conductivity (Kos) as obtained by extrapolation of Ks vs t curve at 5 meq/l with different SAR values for Felix Farm sandy loam soil.
Figure 5. Initial hydraulic conductivity (Kos) as obtained by extrapolation of Ks vs t curve at 50 meq/l with different SAR values for Felix Farm soil.
The fourth model by Aringhirri and Capurro (1994) [9] included only two constants Ks and a, where the Ks constant represented the initial hydraulic conductivity (Kos).
3.3. Calculated and Measured Hydraulic Conductivity
Hydraulic conductivity (Ks) values were calculated for the surface depth of the studied soils, using the four previous equations (models; 5, 6, 7 and 8). The calculated values were compared to the measured Kos values (Y vs t) and the R2 was recorded for all SAR values. The equations parameters for the sandy loam soil (Felix Farm) and regression equations are presented in Tables 3-6. However, only the regression equations for both INIAP soils were calculated for 0 - 30 cm depth at salt concentration treatments with concerned models. For instance, at 5 millieq/l treatment in Cacao farm-INIAP, the regression equations using the models of Reciprocal Hyperbola, Parpola, Hoerl function and Aringhirri & Capurro were as follows: Y = 1.003x + 0.2245, Y = 0.919x − 0.0289, Y = 0.999x + 0.1039, Y = 0.997x + 0.1623, respectively, while with treatment 50 millieq/l they were: Y = 0.954x + 0.6785, Y = 0.97x + 0.1507, Y = 0.969x + 0. 401, Y = 0.960x + 0.5354, respectively, whereas, Y represents calculated hydraulic conductivity (Ks) and x is the measured one (Kos). In the corn farm-INIAP, the regression equations at 5 millieq/l were: Y = 1.008x +0.0238, Y = 0.986x − 0.0051, Y = 1.003x + 0.0102, Y = 1.006x + 0.0175,
Table 3. Calculated fitting parameters of the Reciprocal Hyperbola equation at different SAR values for Felix Farm sandy loam soil.
Table 4. Parameters of the Parabola equation at different SAR values for Felix Farm soil.
Table 5. Calculated fitting parameters of the Hoerl function with SAR for Felix Farm soil.
Table 6. Parameters of the Aringhirri & Capurro equation at different SAR for Felix Farm soil.
and with 50 millieq/l they were; Y = 0.988x + 0.1494, Y = 0.966x − 0.0025, Y = 0.988x + 0.1073, Y = 0.988x + 0.1299, respectively.
However, the fitting R2 between calculated and measured values were greater than 0.99, which prove that the four equations can predict the actual data with great confidence. The Hoerl function model was the best of all models, where the fitting degree was almost perfect for all studied soils at 5 and 50 meq/l salt concentration.
3.4. Predicted Hydraulic Conductivity (Ks) as Influenced by SAR and Salt Concentration
The effect of SAR on the hydraulic conductivity and drainage properties of the studied soil samples at 5 and 50 meq/l electrolyte (salt) concentrations (equivalent to solutions of 0.005 N and 0.05 N ionic strength) is shown in Tables 7-9. The saturated hydraulic conductivity (Ks) was calculated according to Darcy’s equation as 
These results are in agreement with those findings by Santiwong et al., (2008) [15] , Levy and Mamedov (2002) [16] , Wissmeier and Barry (2009) [17] . Also, Arienzo et al., (2012) [18] , reported that solutions with sodium adsorption ratio (SAR) of 5 - 40, where the monovalent cation was Na+ or K+ and the divalent cation was Ca2+ or Mg2+ were used to leach the soil columns, at electrolyte concentrations ranging from 2.5 to 640 meq∙L−1. Percolating solutions with SAR caused a decrease in hydraulic conductivity as electrolyte concentrations reduced. They added that, when the Na+ solutions flowed through the soil column a greater cloudiness was observed in the percolate indicating that clay deflocculating and movement are factors leading to the reduced structural stability. Generally the obtained data of Ks showed that, the hydraulic conductivity was highest at time
Table 7. Hydraulic conductivity (Ks) changes with time at different SAR values in Felix Farm soil.
Table 8. Hydraulic conductivity (Ks) changes with time for different SAR values in INIAP-Cacao Field soil.
Table 9. Hydraulic conductivity (Ks) changes with time for different SAR values in INIAP-Corn field soil.
zero (Kos) and decreased sharply with increasing values of SAR, where the measured Ks values at the highest 
Also, the hydraulic conductivity values were higher at time zero (Kos) and decreased with times up to 6 hours at 5 and 50 meq/l for all SAR values under investigation. The rate of decrease was higher for 5 meq/l than 50 meq/l, where the Kos values at 5 meq/l were low compared with the same values at 50 meq/l for SAR values.
4. Conclusion
Dispersion and migration of colloidal particles, subsequently lodging in the soil pores, lead to reduction in saturated hydraulic conductivity (Ks), hence, the relation between effluent volume and time will be non-linear and Darcy’s law can’t be applied. This work aims to find other equations that can correctly predict the changing flux with time with respect to Darcy’s equation at non-linear flow. The changes in saturated hydraulic conductivity (Ks) with time were determined in three tropical soils located in Quevedo Region (Los Rios Province). The measured data of the investigated tropical soils were compared with that calculated by proposed equations. Initial hydraulic conductivity (Kos) has been involved with the equations that used for prediction of the change in K with time. Four empirical equations were observed to almost perfectly fit the experimental data: Reciprocal Hyperbola, Parabola, Hoerl function, Aringhirri and Capurro model. The Hoerl function model was the best of all models for application as the fitting degrees were almost perfect for all studied soils at 5 and 50 meq/l. Using Kos as a fitting parameter for all proposed equations indicates its stability if there are no changes in soil structure with time. Darcy’s equation along with the four models can predict soil hydraulic properties in a wide range of either electrolyte concentrations or SAR values. Hydraulic conductivity, Ks, was highest at time zero and decreased gradually with time (up to 6 hours). Also, Ks decreased sharply with increasing SAR values. The measured Ks values for all soils at the highest SAR value were only 7% - 13% of the measured Ks values at the lowest SAR value. The rate of decrease was higher for 5 meq/l than 50 meq/l electrolyte concentration of the percolation solution.
Acknowledgements
I am pleased to have the Prometheus Scholarship of the SENESCYT Prometeo Project of Ecuador during 2013/ 2014. The financial support of SENESCYT for this work is acknowledged.
References
- Amer, A.M. (2012) Water Flow and Conductivity into Capillary and Non-Capillary Pores of Soils. Journal of Soil Science and Plant Nutrition, 12, 99-112. http://dx.doi.org/10.4067/S0718-95162012000100009
- Amer, A.M. (2011) Prediction of Hydraulic Conductivity and Sorptivity in Soils at Steady-State Infiltration. Archives of Agronomy and Soil Science, 58, 1179-1194. www.tandfonline.com/loi/gags20 http://dx.doi.org/10.1080/03650340.2011.572877
- Hillel, D. (1980) Fundamental of Soil Physics. Academic Press, New York.
- Dikinya, O., Christoph, H. and Graham, A. (2008) Decrease in Hydraulic Conductivity and Particle Release Associated with Self-Filtration in Saturated Soil Columns. Geoderma, 146, 192-200. http://dx.doi.org/10.1016/j.geoderma.2008.05.014
- Pupinsky, H. and Shainberg, I. (1979) Salt Effects on the Hydraulic Conductivity of a Sandy Soil. Soil Science Society of America Journal, 43, 429-433. http://dx.doi.org/10.2136/sssaj1979.03615995004300030001x
- Metzger, L., Yaron, B. and Mingelgrin, U. (1983) Soil Hydraulic Conductivity as Affected by Physical and Chemical Properties of Effluents. Agronomie, 3, 771-778. http://dx.doi.org/10.1051/agro:19830808
- Yousaf, M., Ali, O.M. and Rhoades, J.D. (1987) Clay Dispersion and Hydraulic Conductivity of Some Salt-Affected Arid Land Soils. Soil Science Society of America Journal, 51, 905-907. http://dx.doi.org/10.2136/sssaj1987.03615995005100040013x
- Keren, R. and Singer, M.J. (1988) Effect of Low Electrolyte Concentration on Hydraulic Conductivity of Sodium/Cal- cium Montmorillonite-Sand System. Soil Science Society of America Journal, 52, 368-373. http://dx.doi.org/10.2136/sssaj1988.03615995005200020012x
- Aringhieri, R. and Capurro, M. (1994) Evaluating Saturated Hydraulic Conductivity of a Soil in Laboratory Investigations: An Empirical Model. Soil Science, 157, 77-83. http://dx.doi.org/10.1097/00010694-199402000-00002
- Frenkel, H., Goertzen, J.O. and Rhoades, J.D. (1978) Effects of Clay Type and Content, Exchangeable Sodium Percentage, and Electrolyte Concentration on Clay Dispersion and Soil Hydraulic Conductivity. Soil Science Society of America Journal, 42, 32-39. http://dx.doi.org/10.2136/sssaj1978.03615995004200010008x
- Felhender, R., Shainberg, I. and Frenkel, H. (1974) Dispersion and Hydraulic Conductivity of Soils in Mixed Solutions. Transactions on the 10th International Congress of Soil Science, 1, 103-112.
- Shainberg, I., Rhoades, J.D. and Prather, R.J. (1981) Effect of Low Electrolyte Concentration on Clay Dispersion and Hydraulic Conductivity of a Sodic Soil. Soil Science Society of America Journal, 45, 273-277. http://dx.doi.org/10.2136/sssaj1981.03615995004500020009x
- Black, G.A., Evans, D.D., White, J.L., Ensminger, L.E. and Clerk, F.E. (1965) Methods of Soil Analysis. Parts, 1 and 2. American Society of Agronomy, Madison.
- Klute, A. (1986) Methods of Soil Analysis. 2nd Edition, ASA and SSSA, Madison.
- Santiwong, S.R., Guan, J. and Waite, T.D. (2008) Effect of Ionic Strength and pH on Hydraulic Properties and Structure of Accumulating Solid Assemblages during Microfiltration of Montmorillonite Suspensions. Journal of Colloid and Interface Science, 317, 214-227. http://dx.doi.org/10.1016/j.jcis.2007.09.052
- Levy, G.J. and Mamedov, A.I. (2002) High-Energy-Moisture-Characteristics Aggregate Stability as a Predictor for Seal Formation. Soil Science Society of America Journal, 66, 1603-1609. http://dx.doi.org/10.2136/sssaj2002.1603
- Wissmeier, L. and Barry, D.A. (2009) Effect of Mineral Reactions on the Hydraulic Properties of Unsaturated Soils: Model Development and Application. Advances in Water Resources, 32, 1241-1254. http://dx.doi.org/10.1016/j.advwatres.2009.05.004
- Arienzo, M., Christen, E.W., Jayawardane, N.S. and Quayle, W.C. (2012) The Relative Effects of Sodium and Potassium on Soil Hydraulic Conductivity and Implications for Winery Wastewater Management. Geoderma, 174, 303-310. http://dx.doi.org/10.1016/j.geoderma.2011.12.012
- Amer, A.M. (2012) Infiltration Functions for Prediction of Water Sorptivity and Hydraulic Conductivity in Soils. Proceedings of the BALWOIS Conference, Ohrid, 28 May-2 June 2012.
- Brooks, R.H. and Corey, A.T. (1964) Hydraulic Properties of Porous Media. Hydrology Paper 3, Colorado State University, Fort Collins.
- Jayawardane, N.S., Christen, E.W., Arienzo, M. and Quayle, W.C. (2011) Evaluation of the Effects of Cation Combinations on Soil Hydraulic Conductivity. Australian Journal of Soil Research, 49, 56-64. http://dx.doi.org/10.1071/SR09222


















