Journal of Water Resource and Protection
Vol.4 No.4(2012), Article ID:18418,7 pages DOI:10.4236/jwarp.2012.44020
The Intra-Annual Variability of Discharge, Sediment Load and Chemical Flux from the Monitoring: The Yukon River, Alaska
1Faculty of Science, Hokkaido University, Sapporo, Japan
2Faculty of Fisheries Sciences, Hokkaido University, Hakodate, Japan
3International Arctic Research Center, University of Alaska, Fairbanks, USA
Email: *chikita@mail.sci.hokudai.ac.jp
Received February 13, 2012; revised March 11, 2012; accepted April 5, 2012
Keywords: Yukon River; Suspended Sediment Concentration; POC; PON; Sediment Load; Snowmelt Runoff; Glacier-Melt Runoff
ABSTRACT
The covered-ice breakup in subarctic to arctic rivers in the early snowmelt season often gives any damage to instruments monitoring physical and chemical factors of water. The serious condition has brought few time series data during the snowmelt runoff except the river stage or discharge. In this study, the contribution of snowmelt runoff to the discharge and sediment load is quantified by monitoring water turbidity and temperature at the lowest gauging station of US Geological Survey in the Yukon River, Alaska, for more than 3 years (June 2006 to September 2009). The turbidity was recorded by a self-recording turbidimeter with a sensor of infrared-ray back-scattering type, of which the window is cleaned by a wiper just before a measurement. The turbidity time series, coupled with frequent river water sampling at mid-channel, produce time series of suspended sediment (SS) concentration, particulate organic carbon (POC) concentration and particulate organic nitrogen (PON) concentration (mg∙L–1) by using the high correlation (R2 = 0.747 to 0.790; P < 0.001) between the turbidity (ppm) and the SS, POC and PON concentrations. As a result, the three-year time series (5 September 2006 to 4 September 2009) indicated that the snowmelt runoff, continuing about 40 days (late April or early May to early June), occupies 14.1% - 24.8% of the annual discharge (1.94 × 1011 to 2.01 × 1011 m3), 8.7% - 22.5% of the annual sediment load (3.94 × 107 to 5.08 × 107 ton), 11.6% - 23.7% of the annual POC flux (4.05 × 105 to 4.77 × 105 ton), and 10.3% - 24.5% of the annual PON flux (2.80 × 104 to 3.44 × 104 ton). In the snowmelt season, the peak suspended sediment concentration preceded the peak discharge by a few days. This probably results from the fluvial sediment erosion in the river channels.
1. Introduction
Many subarctic to arctic rivers are frozen in winter, and the snowmelt runoff starts in March or April, often accompanied by covered-ice breakup (URL http://aprfc. arh.noaa.gov/). The breakup ice could often give any damage to the equipment for monitoring physical and chemical factors of water by jamming rivers (URL http://www.denniskalma.com/ice.html). Hence, for such rivers, up to date, there are few time series data during the snowmelt runoff except for water level (or discharge). Thus, contributions of sediment load and chemical flux by snowmelt runoff to the annual ones have not been accurately quantified. Meanwhile, if subarctic to arctic river basins include glacierized subbasins, the river discharge, sediment load and chemical flux could be affected by glacier-melt runoff in summer. The subarctic Yukon river basin, occupied by 1% glacierized area [1], could produce relatively high sediment load, compared with rivers of the same scale order with no glacierized area, because of glacial bedrock erosion in Alaska Range, Wrangell Mts, etc. [2,3]. The relatively high sediment load may also produce relatively high particulate carbon (POC) and particulate organic nitrogen (PON) fluxes [2]. Thus, the temporal variability of sediment load is related to carbon and the other chemical cycles in a river basin and between the river basin and the sea. Runoff analyses for the Tanana River, a tributary of the Yukon River, by Wada et al. (2011) [3] revealed that, at the lowest gauging station (site TNN in Figure 1), the glacier-melt runoff from the glacierized regions accounts for 26% - 57% of the Tanana discharge in the glacier-melt season (June - September). According to the Landsat images of August 2005, the glacierized area is 9130 km2 (1.1% of the drainage area) upstream of the lowest gauging station (site PLS in Figure 1) of the Yukon River, and 3570 km2 (5.5% of the drainage area) upstream of site TNN in the Tanana River. Assuming that the mean glacier-melt runoff rate (mean discharge per unit area; mm∙day–1) at site TNN in June-September by Wada et al. (2011) [3] is equal to that at site PLS, the glacierized area upstream of site PLS, which is about 2.6 times as large as that upstream of site TNN, could produce the glacier-melt runoff to occupy 27% - 33% of the Yukon discharge over June-September. It is reported that the shrinkage of mountain glaciers due to global warming is most prevalent for the Alaskan glaciers [4,5]. Thus, the current and future glacier shrinkage may significantly decrease the Yukon discharge as a water resource. The turbidity monitoring has been conducted in streams as one of their water qualities [6], but few in large rivers such as the Yukon River. In this study, associated with river discharge to the ocean [7,8], the water turbidity and temperature of the Yukon River are monitored at the lowest gauging station (site PLS) of US Geological Survey (USGS) for more than three years, and the contribution of snowmelt runoffs to the annual river fluxes of water, sediment, POC and PON is evaluated.
2. Study Area and Methods
Most of the Yukon river drainage basin (area, 8.55 × 105 km2) belongs to the subarctic region south of the Arctic Circle (66˚33'N), and is occupied by 74.8% forest with discontinuous permafrost and 1% glacierized region of
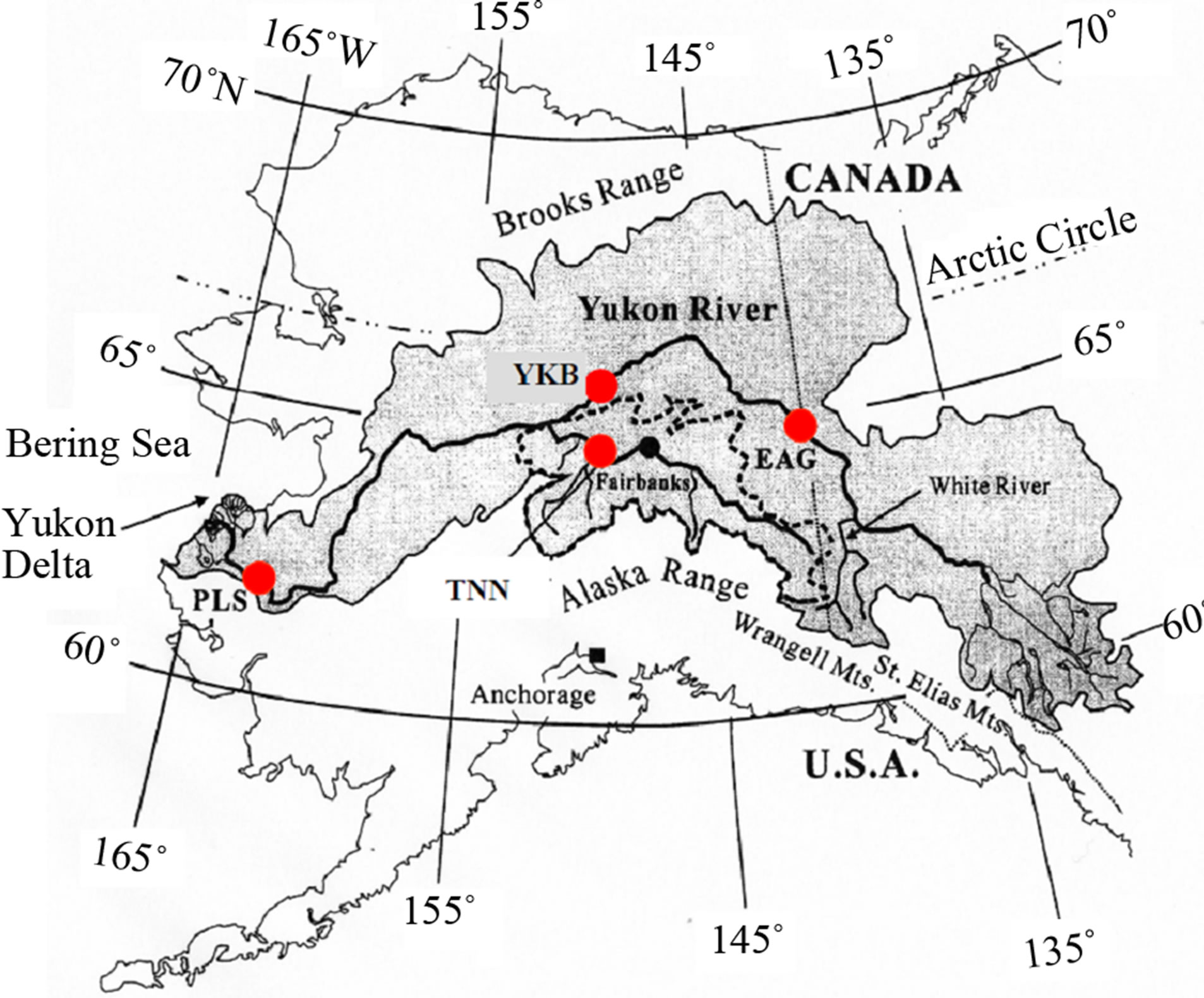
Figure 1. Locations of the Yukon River basin, Alaska (gray), and the lowest gauging station (site PLS) and the other two gauging stations (site YKB and site EAG ) of the US Geological Survey (USGS) along the Yukon River (modified after [9]). Site TNN is the lowest USGS gauging station of the Tanana River, a tributary of the Yukon River. The dashed line shows the water divide of the Tanana River basin.
Alaska Range, Wrangell Mts., St. Elias Mts., etc. (Figure 1) [1]. Water temperature and water turbidity were monitored at 1 hr intervals at site PLS in June 2006-September 2009 by fixing a temperature data logger (StowAway TidBiT ver.2, Onset Computer, Inc.: accuracy, ±0.1˚C) and a self-recording turbidimeter (model ATU3- 8M, Alec Electronics, Inc.; range, 0 - 20,000 ppm; accuracy, ±2% of measured value) (Figure 2). The turbidimeter has a sensor of infrared-ray back scattering type with a window cleaned every 1 hour by a wiper just before the measurement. The mooring-buoy system was fixed at about 60 m distant from the exposed bedrock below the USGS shelter on the right bank. Considering the low river stage in winter, the turbidimeter and temperature data logger was moored at about 1 m above the weight. The water turbidity (ppm) from the turbidimeter was converted into suspended sediment concentration (SSC: mg∙L–1) by using the relationship between the turbidity, x, and the SSC, y, from the water sampled simultaneously at mid-channel (y = 0.7656x + 59.733; R2 = 0.756, P < 0.001) (Figure 3). The relationship indicates near one-to-one correspondence. In order to know the representativeness of SSC and water temperature by the one-point method, during the monitoring, fluctuations of SSC and temperature across the river channel are assessed by lowering a TTD (turbidity-temperature-depth) profiler from a boat [9]. As a result, differences between recorded SSC and temperature and cross-sectionally averaged SSC and temperature were less than 50 mg∙L–1 and less than 0.2˚C, respectively, being independent of their magnitude. The small difference between the recorded SSC and the averaged SSC results from the fine suspended sediment of more than 90% silt and clay [9].
Frequent water sampling was conducted at mid-channel in June-September 2009. For suspended sediment, particulate organic carbon (POC) and particulate organic nitrogen (PON) contents in the water samples were obtained by filtering water samples with Whatman Grade GF/F glass microfiber filters (pore size: 0.7 μm) and

Figure 2. Mooring-buoy system of a turbidimeter and a temperature data logger at site PLS (Figure 1).
drying the filters. After weighing the dry filters, they were treated with hydrochloric acid to eliminate carbonate. Finally, POC and PON contents were detected by a mass spectrometer (Finnigan Delta V plus, Thermo Fisher Scientific, Inc.). There were definitely linear relationships between POC and PON concentrations (mg∙L–1) and SSC (R2 = 0.747 for POC concentration vs. SSC and R2 = 0.790 for PON concentration vs. SSC; P < 0.001) (Figure 4). Thus, the time series of SSC furnished those of POC and PON concentrations. The two regression lines in Figure 4 are almost parallel. Thus, the ratio of the POC to PON concentrations is approximately constant at 9.9. Daily mean discharge data were downloaded from the National Water Information System on the USGS web site (http://waterdata.usgs.gov/nwis/dv/? site_ no=15565447&agency_cd=USGS&referred_module=sw). The sediment load, POC flux and PON flux in kg∙s–1 were calculated by multiplying SSC and POC and PON concentrations (g∙L–1 in this calculation) by discharge (m3∙s–1), respectively.
Grain size analyses for the suspended sediment in the water samples and the river-bank sediment newly deposited in the glacier-melt season were conducted by the photo-extinction method with a centrifuge for particles of grain size d ≤ 44 μm (micrometers) and by the sieving method for d > 44 μm particles.
3. Results and Discussion
Figure 5 shows daily mean variations of (a) suspended sediment concentration (SSC) and water temperature, (b) discharge and sediment load, and (c) POC flux and PON flux at site PLS for a period of 19 June 2006-5 September 2009. As shown by the water temperature at almost 0˚C, the frozen conditions of the river appeared for 5 November 2006-8 May 2007, 18 October 2007-14 May 2008, and 14 October 2008-7 May 2009. The breakup of covered ice occurred for 3 - 5 days before the end of the completely frozen conditions by increasing the water level from snowmelt. The SSC for the frozen periods is

Figure 3. Relationship between water turbidity (ppm) and suspended sediment concentration (mg∙L–1).

Figure 4. Relationships between suspended sediment concentration, POC concentration and PON concentration (mg∙L–1).

Figure 5. Daily mean variations of (a) suspended sediment concentration (SSC) and water temperature; (b) Discharge and sediment load; and (c) POC flux and PON flux at site PLS for 19 June 2006-5 September 2009.
not stable year by year. This is probably due to the position of the turbidity sensor at a short distance below the covered ice and above the riverbed (Figure 2). Especially, for 18 March-1 April 2007 and 22 March-2 April 2008, the temperature recorded below 0˚C, indicating that the temperature data logger was frozen into ice (Figure 5(a)).
The snowmelt runoffs occurred for 25 April-1 June 2007 (38 days), 4 May-10 June 2008 (38 days) and 3 May-11 June 2009 (38 days). The initial and final days of the runoffs were here defined by the start of ascending discharge before the breakup and the end of the abruptly descending limb of sediment load, respectively (Figure 5(b)). The snowmelt runoff in 2007 was smallest in the three snowmelt periods. This results from relatively small snow depth (30 cm in Fairbanks), when the positive daily mean air temperature started in Fairbanks on 7 April 2007, compared with 38 cm on 31 March 2008 and 58 cm on 11 April 2009 (Figure 1) [Alaska Climate Research Center; URL http://climate.gi.alaska.edu/], though the magnitude and duration of snowmelt runoffs depend also on the temporal variation of air temperature. According to the discharge record since 1976, the annual peak discharge generally occurs in the snowmelt season [National Water Information System, USGS]. The annual peak discharge (15,340 m3∙s–1 on 12 May) in 2007 was the second lowest in the record. The annual peak discharge (29,730 m3∙s–1 on 24 May) in 2009 was the third largest since 1976, due to the relatively large snow depth and high air temperature [Alaska Climate Research Center]. The snowmelt sediment runoff started by a day to three days more slowly than the snowmelt runoff (Figure 5(b)), but, in the snowmelt season of 2008 and 2009, the peak sediment load preceded the peak discharge by three days and one day, respectively. In the snowmelt runoff of 2007, the peak sediment load lagged behind the peak discharge by two days.
In general, rainfall runoffs occur in mid-June to early October before the river freezing starts between late October and mid-November (see water temperature in Figure 5(a)), while the glacier-melt runoffs may appear in mid-June to early September during the positive air temperature in the glacierized regions. Thus, in the Yukon River basin or the tributary river basins with glacierized regions, the rainfall runoffs and glacier-melt runoffs could occur simultaneously in the summer season [2,3]. The SSC time series in Figure 5(a) indicate that weak rainfall runoffs occurred even in November after freezing.
Meanwhile, the sediment load, POC flux and PON flux of the Yukon River may vary in response to both the glacier-melt sediment runoff from the glacierized regions and the fluvial erosion of riverbed sediment from rainfalls [2]. According to the simulated results of Wada (2010) [2], the glacier-melt sediment load of the Tanana River occupies 76% - 94% of the total sediment load in June to September, while the POC flux from the glacierized regions and from the fluvial erosion in river channels account for 10% - 32% and 60% - 70% of the Tanana POC flux in the glacier-melt season, respectively. Each contribution of the glacier-melt and fluvial erosion to the sediment load, POC flux and PON flux of the Yukon River should also be quantified.
The suspended sediment and bank sediment at site PLS consists of more than 90 % silt (4 ≤ d < 63 μm) and clay (d < 4 μm) (Figure 6). The bank sediment, sampled on 8 September 2008, was very fresh, suggesting that it deposited during the relatively large sediment runoff in mid-August (Figure 5(b)). The bank sediment could be eroded by the snowmelt runoff in the next year, since no large sediment runoffs occurred after the mid-August.
Figure 7 shows relations between discharge and suspended sediment concentration (SSC) in the snowmelt runoffs of (a) 2007, (b) 2008 and (c) 2009. It is seen that the larger the snowmelt runoff, the clearer the hysteresis. The hysteresis seems to change the counterclockwise loop to the clockwise loop at the discharge of more than about 15,000 m3∙s–1. The simulations of Wada et al. (2011) [3] indicated that, in June - September of 2007 and 2008, the Tanana sediment load consisted of 87% and 76% glacier-melt sediment runoff from the glacierized regions, and 13% and 24% fluvial sediment erosion in the river channels, respectively. The glacier-melt does not yet start in the snowmelt season, because of the negative air temperature in the glacierized regions. Thus, the snowmelt sediment runoff is exclusively caused by the fluvial sediment erosion in the river channels, due to an increase in discharge. The clockwise hysteresis in Figures 7(b) and (c) suggests that, after the peak SSC, the amount of the riverbed sediment to be eroded was not enough (i.e., low sediment availability). In gravel-bed rivers, the clockwise hysteresis is frequently observed [10,11]. In the Yukon River, the 1% largest size (about 100 μm) of river-bank sediment is between 90 and 180 μm (Figure 6), where the smaller sediment, if it is unconsolidated, can be eroded simultaneously on the Sundborg diagram [12]. Thus, as the discharge increases in the snowmelt season, the coarsest and finer particles of the bed and bank sediments could be simultaneously eroded. The counterclockwise hysteresis in the weak snowmelt runoff of 2007 (Figure 7(a)) and in the early snowmelt runoff of 2009 (Figure 7(c)) indicates that the SSC increases with the discharge decreasing from ca. 15,000 m3∙s–1. This suggests that, at the discharge of about 15,000 m3∙s–1, some of about 100 μm or less particles started to move. At more than about 15,000 m3∙s–1, the particles of the whole size were possibly eroded with increasing SSC. Chikita (1996) [13] showed that, in case of the sufficient sediment availability for silt and clay particles, the SSC and discharge vary in phase at any time.

Figure 6. Cumulative grain size distributions of suspended and bank sediments sampled at site PLS.

Figure 7. Relations between discharge (m3∙s–1) and SSC (mg∙L–1) in the snowmelt runoffs of (a) 2007, (b) 2008 and (c) 2009.
We can estimate the annual Yukon river flux (Table 1) and the contribution (%) of the snowmelt runoff to the annual flux (Table 2) from the time series in Figure 5. We set a boundary of the year in early September when the glacier-melt drops down. As a result, the annual discharge, sediment load, POC flux and PON flux ranged from 1.94 × 1011 to 2.01 × 1011 m3, from 3.94 × 107 to 5.08 × 107 ton, from 4.05 × 105 to 4.77 × 105 ton, and from 2.80 × 104 to 3.44 × 104 ton, respectively, for the three years of 5 September 2006 to 4 September 2009. The snowmelt runoff, continuing for 38 days, occupied 14.1% - 24.8% of the annual discharge, 8.7% - 22.5% of the annual sediment load, 11.6% - 23.7% of the annual POC flux and 10.3% - 24.5% of the annual PON flux. The small snowmelt runoff in 2007 affected the magnitude of the annual sediment load, POC flux and PON flux and the contribution of snowmelt runoff to the three annual fluxes. On the base of frequent water sampling, Striegel et al. (2007) [14] indicated the annual POC flux at the mean of 7.48 × 105 ton yr–1 with a range of 5.77 × 105 to 1.10 × 106 ton∙yr-1 in the five years of 2001-2005. However, these values seem to be overestimated, since the mean annual POC flux in Table 1 is 4.52 × 105 ton∙yr–1. Milliman and Meade (1983) [7] estimated the annual sediment load of the Yukon River at 6.0 × 107 ton∙yr–1. This is reasonable in magnitude to our mean annual sediment load of 4.7 × 107 ton∙yr–1, though the recent

Table 1. Annual water discharge, sediment load, POC flux and PON flux (ton∙yr–1), and annual mean SSC, POC and PON concentrations (mg∙L–1) of the Yukon River.
shrinkage of Alaskan glaciers tends to decrease the glacial sediment yield. The contribution of the snowmelt runoff to the annual fluxes is relatively large in 2008 and 2009 (Table 2). Then, the contribution (%) of the snowmelt runoff to the annual water discharge is similar to its contribution to the annual sediment load, POC flux and PON flux. In this case, the contribution of the snowmelt runoff to the annual sediment load, POC flux and PON flux can be estimated only from the discharge data.

Table 2. Contribution of the snowmelt runoff to the annual flux.
4. Conclusion and Future Works
The monitoring of water turbidity and temperature and frequent water sampling at the lowest gauging station of USGS in the Yukon River furnished the time series of discharge, sediment load, POC flux and PON flux for more than 3 years. The relation between suspended sediment concentration and discharge during the snowmelt runoff exhibited a counterclockwise hysteresis in the small runoff of less than about 15,000 m3∙s–1, and a clockwise hysteresis in the larger runoff. The clockwise hysteresis suggests that the sediment supply is due to the fluvial erosion of riverbed and bank sediments. The annual sediment load calculated is reasonable in magnitude to that of Milliman and Meade (1983) [7], but the annual POC flux of Striegel et al. (2007) [14] is probably overestimated. As the next step, in order to identify the sources of sediment, POC and PON in the Yukon River, and to clarify physical and chemical processes in their erosion, transport and deposition, simulations for the time series of discharge, sediment load, POC flux and PON flux should be conducted by a lumped model such as the tank model [3] or a semi-distributed model such as the “SWAT” model (URL http://swatmodel.tamu.edu/software/ swat-model/) [15,16].
5. Acknowledgements
We are indebted to US Geological Survey, Fairbanks and Anchorage, for their welcome data supply and their great help in the field observations, especially to Dr. David F. Meyer and Mr. Charles S. Couvillion. We also thank Prof. Larry Hinzman, Director of the International Arctic Research Center (IARC), the University of Alaska Fairbanks (UAF) and Ms. Yoriko Freed at the office of IARC/UAF for their welcome support in our field survey. This study was financially supported by the Japan Aerospace Exploration Agency (JAXA).
REFERENCES
- T. P. Brabets, B. Wang and R. H. Meade, “Environmental and Hydrologic Overview of the Yukon River Basin, Alaska and Canada,” US Geological Survey Water-Resources Investigations Report 99-4204, 2000.
- T. Wada, “Sediment Load and Chemical Flux in the Subarctic Tanana River Basin, Alaska,” Ph.D. Thesis, Hokkaido University, Sapporo, 2010.
- T. Wada, K. A. Chikita, Y. Kim and I. Kudo, “Glacial Effects on Discharge and Sediment Load in the Subarctic Tanana River Basin, Alaska,” Arctic, Antarctic, and Alpine Research, Vol. 43, No. 4, 2011, pp. 632-648. doi:10.1657/1938-4246-43.4.632
- M. B. Dyurgerov and M. F. Meier, “Glaciers and the Changing Earth System: A 2004 Snapshot,” Occasional Paper 58, Institute of Arctic and Alpine Research, 2005.
- K. Matsuo and K. Heki, “Time-Variable Ice Loss in Asian High Mountains from Satellite Gravimetry,” Earth and Planetary Science Letters, Vol. 290, No. 1-2, 2010, pp. 30-36. doi:10.1016/j.epsl.2009.11.053
- V. G. Christensen, A. C. Ziegler and X. Jian, “Continuous Turbidity Monitoring and Regression Analysis to Estimate Total Suspended Solids and Fecal Coliform Bacteria Loads in Real Time,” Proceedings of the Seventh Federal Interagency Sedimentation Conference, Vol. 1, 2001, pp. 94-101.
- J. D. Milliman and R. H. Meade, “World-Wide Delivery of River Sediment to the Oceans,” Journal of Geology, Vol. 91, No. 1, 1983, pp. 1-21. doi:10.1086/628741
- J. D. Milliman and K. L. Farnsworth, “River Discharge to the Coastal Ocean: A Global Synthesis,” Cambridge University Press, Cambridge, 2011. doi:10.1017/CBO9780511781247
- K. A. Chikita, R. Kemnitz and R. Kumai, “Characteristics of Sediment Discharge in the Subarctic Yukon River, Alaska,” Catena, Vol. 48, No. 4, 2002, pp. 235-253. doi:10.1016/S0341-8162(02)00032-2
- Y. Kurashige, “The Mechanisms on Suspended-Sediment Supply to Rivers,” Ph.D. Thesis, Hokkaido University, Sapporo, 1992.
- Y. Kurashige, “Model for Pulling Up Fine Particles from Armour-Coated Gravel Bed in the Early Snowmelt Season,” Japanese Geomorphological Union, Vol. 6, No. 4, 1985, pp. 287-302.
- A. A. Sundborg, “The River Klaralven. A Study of Fluvial Processes,” Geografiska Annalar, Vol. 38, No. 3, 1956, pp. 238-316.
- K. A. Chikita, “Suspended Sediment Discharge from Snowmelt: Ikushunbetsu River, Hokkaido, Japan,” Journal of Hydrology, Vol. 186, No. 1-4, 1996, p. 295-313. doi:10.1016/S0022-1694(96)03021-1
- R. G. Striegel, M. M. Dornblaser, G. R. Aiken, K. P. Wickland and P. A. Raymond, “Carbon Export and Cycling by the Yukon, Tanana, and Porcupine Rivers, Alaska, 2001- 2005,” Water Resources Research, Vol. 43, No. 2, 2007. doi:10.1029/2006WR005201
- R. Srinivasan, X. Zhang and J. Arnold, “SWAT Ungauged: Hydrological Budget and Crop Yield Predictions in the Upper Mississippi River Basin,” Transactions of the ASABE, Vol. 53, No. 5, 2010, pp. 1533-1546.
NOTES
Corresponding author.

