Journal of Water Resource and Protection
Vol. 3 No. 1 (2011) , Article ID: 3769 , 11 pages DOI:10.4236/jwarp.2011.31001
N-Removal on Wastewater Treatment Plants: A Process Control Approach
1Department of Telecomunications and Systems Engineering, School of Engineering, Bellaterra, Spain
2Industrial Control Centre, University of StrathClyde, Glasgow, Scotland
3Control & Instrumentation Engineering Department, Faculty of Electrical Engineering, UTM Skudai, Johor, Malaysia
E-mail: Ramon.Vilanova@uab.cat, r.katebi@eee.strath.ac.uk, aliza@fke.utm.my
Received March 18, 2010; revised June 10, 2010; accepted September 12, 2010
Keywords: Wastewater Process Control, Nitrogen Removal, PID Control
ABSTRACT
A multilayered control design approach is proposed here. Starting with the Dissolved Oxygen (DO) control loop in the last aerated tank, the control of the recirculation sludge is added next. Once the limitations of this two-loop control strategy are highlighted, a cascade control loop is proposed. This cascade control is further enhanced by a feed-forward control action that makes use of influent ammonia concentration. The resulting cascade+feedforward control configuration achieves satisfactory nitrogen removal for the three influent operating conditions (dry, rain and storm).
1. Introduction
As a result of increased human activity, discharge of nutrients, including nitrogen (N) and phosphorus (P), into receiving waters represents one of the most serious environmental problems. This fact has motivated the need for enhanced operational strategies for wastewater treatment plants (WWTP). As strict regulations have been imposed on the Total Nitrogen level at the effluent of the WWTP, the Activated Sludge Process (ASP) with nitrification/denitrification stages has become the more popular and common. The ASP involves an anoxic stage followed by an aerobic zone and a settler from which the major part of the biomass is recycled to the anoxic basin. Their widespread use has motivated a number of studies in order to improve the functioning and understanding of ASPs. Among available techniques, the modeling and the control of these processes are known to be very efficient and can help the optimization of the water treatment process [1,2].
From a control point of view, as highlighted by [3], the main challenge can be stated in terms of a disturbance attenuation control problem. Furthermore, the problem faced is a multivariable nonlinear control problem of time-varying nature and ill-defined parameters. A summary of the problems associated with these processes is presented in [4].
For control of ASPs, the Dissolved Oxygen (DO) is recognized as a key variable and often used in real life applications. The DO level in the aerobic reactors has a direct influence on the microorganism’s activity that lives in the activated sludge. A proper DO concentration level has to be maintained by operation of the aeration mechanisms to supply enough oxygen to the microorganisms in the sludge, so organic matter is degraded and ammonium is converted to nitrate.
However aeration energy consumption is also a very important issue, being responsible for approximately the 50% of the energy consumption of the plant. Therefore an excessively high DO, which requires a high airflow rate, leads to high energy consumption. In addition excessive aeration may also deteriorate the sludge quality and high DO in the internally recirculated water will also make the denitrification less efficient. Therefore there are both economic and process efficiency reasons for appropriate management of the dissolved Oxygen. Sufficient aeration is used to ensure appropriate nitrification. This can be accomplished by either applying constant aeration flow rates, by controlling the DO concentration at prescribed set-points or by accommodating the DO set-point on the basis of the ammonia concentration on the last aerobic reactor. See for example [5-8]. As far as the denitrification part of the process is concerned this is usually controlled by using either the internal recirculation flow rate or by external carbon addition [9]. Different control approaches have been suggested in the literature, see [10,11] for example, that lead to quite complex solutions and hence not amenable to practical implementation.
The main purpose of this paper is to propose a process control oriented approach for enhancing N-removal. Most of the approaches found in the literature lack a methodological application procedure, where the tuning of the controller parameters (either simple PI/PID, predictive controller, optimal controllers, etc) is done in an ad-hoc way, and suffers from lack of concrete and well defined tuning approaches. This fact makes it difficult to implement the methods in real life applications. The novel control method and tuning of the controllers proposed here makes use of very simple and direct process information that can be obtained by application of realistic step tests on the control handles (instead of the more theoretical; and sometimes unrealistic pseudo-random binary signal). In order to have the results more close to reality, all the controller evaluation and simulation results are based on the IWA Benchmark Simulation Model Num. 1 (BSM1) proposed for the evaluation of control strategies in wastewater treatment plants [12]. The Benchmark is based on the most common wastewater treatment plant: a continuous flow activated sludge plant, performing nitrification and pre-nitrification. This study is strictly in agreement with the Benchmark methodology especially from the point of view of control and plant performance evaluation.
This paper is concerned with the design and development of simple but effective control structures for enhancing nitrogen (N) removal in activated sludge processes. Most of the approaches found in the literature lack a systematic method to tune the controller parameters and this is often carried out in an ad-hoc way, and hence suffers from a lack of repeatability, robustness and easy implementation. This fact makes it difficult to implement and use these methods in practice. The novel control method and tuning of the controllers proposed here makes use of very simple and direct process information that can be obtained by application of realistic step tests on the control handles. The final goal of the control is to improve the effluent quality and to trade-off such quality with the energy consumption and operating costs.
The rest of the paper is organized as follows. Next section presents the Benchmark model and the performance evaluation criteria used. Subsequent sections present the proposed control strategy, i.e. basic DO control loop in section 3, Two-loop Benchmark strategy in section 4, cascade control in section 5 and feed forward control enhancement in section 6. The paper ends with some conclusions and remarks for further study.
2. Benchmark Wastewater System
The Benchmark [12] defines a plant layout, a simulation model, influent loads, test procedures and evaluation criteria. The layout is relatively simple: it combines nitrification with denitrification, which is most commonly used for N-removal. The benchmark plant is composed of a five compartment reactor with an anoxic zone and a secondary settler. The nitrogen pollution enters the activated sludge tank as organic nitrogen and ammonia (mainly from the wastewater), and nitrate and nitrite nitrogen returning from the exit of the tank by the internal loop. This pollution is treated first by denitrification which takes place under anoxic conditions: at that point nitrates are transformed into gaseous nitrogen. In the aerobic phase, ammonia nitrogen is oxidized into nitrates (nitrification).
The plant layout can be seen in figure 1. The first two compartments makes up the anoxic zone with individual volume of 1000 m3, and 3 compartments create the aerobic

Figure 1. Benchmark WWTP layout1.
zone with individual volume of 1333 m3. The oxygen mass transfer coefficient rate, KLa, is set to 240 day-1, while the KLa at the last compartment is controlled in order to maintain the dissolved oxygen concentration at 2 mg/l. The flow rate of the internal recirculation, Qa is kept at 55338 m3/day. The flow rate of the sludge recirculation is 18446 m3/day and the excess sludge is removed from the settler at 385 m3/day. The IWA activated sludge model No. 1 (ASM1) [13] is used to describe the biological processes in the reactors. The secondary settler has a conical shape with the surface of 1500 m2 and the depth of 4 m. The secondary settler is modeled as a non-reactive, 10-layer process with a double exponential settling velocity model proposed by [14]. The complete description of the plant can be found in [12].
A basic proposed control strategy comprises two control loops to test the benchmark. The first loop is used to control the dissolved oxygen level in the final compartment of the reactor by manipulation of the oxygen transfer coefficient. The DO sensor is assumed to be ideal. The second loop deals with the control of the nitrate level in the last anoxic compartment by manipulation of the internal recycle flow rate. The nitrate sensor is assumed to have a time delay of 10 min; with a white noise. Within the Benchmark specification a set-point of 2 g/ m3 is specified for the DO and 1 g/m3 for the nitrate on the second tank. In this study the effect of sensor noise is not considered since it is always possible to design Kalman filters to refine the measurement [15].
2.1. Influent Data and Evaluation Procedure
To get an objective view of the performance of the applied control strategy in different situations, simulated influent data are available in three two-week files derived from real operating data for three different weather conditions: dry, rain and storm. Each one of these files contains 14 days of data at 15-min intervals. To calculate benchmark performance the plant is first run to steady state by simulating the plant with the defined constant influent file over a 150-day period. Then, the plant simulation continues by first applying 14 days of the dryinfluent weather file, followed by 14 days of dry, rain or storm influent file. The performance of the benchmark is then evaluated for the last 7 days of dynamic data.
2.2. Performance Evaluation
The performance evaluation is carried out at two different levels: controller and process levels. At the controller level, performance indexes are IAE (integral of absolute error) and ISE (integral of square error), maximal deviation from set point and error variance serve to evaluate wether the proposed control strategy has been applied properly.
At the second level effluent quality operating cost are defined. Effluent quality index represents the levies or fines to be paid due to the discharge of pollution in the receiving bodies. The performance of the plant is always evaluated for the last 7 days of dynamic simulations (from a total of 28 days) using the dry weather influent wastewater according to the benchmark definition. The Effluent Quality (EQ) is averaged over the 7-day observation period based on a weighting of the effluent loads of compounds:
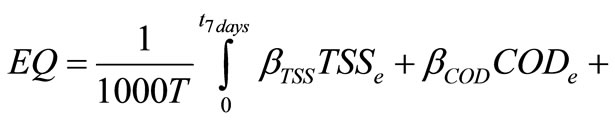
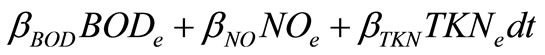 (1)
(1)
where EQ is the effluent quality index (kg poll. unit/day), βi are weighting factors that apply to the different effluent concentrations, TSSe the suspended solids concentration, CODe and BODe are the chemical and biological oxygen demands, NOe is the nitriteand nitrate-concentration and TKNe is the total N (all concentrations are in g/m3). The weighting factors are chosen according to [12] as it is shown in table 1.
It is seen that the larger weighting factors are those linked with nitrogen βNO and βTKN.
The Aeration Energy (AE) is of special interest determined by the following formula:
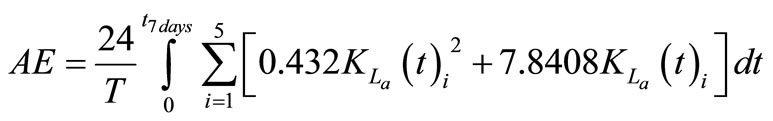 (2)
(2)
where KLa is the mass transfer coefficient in h-1 of the i-th compartment. The sludge production to be disposed is calculated from the total solid flow from wastage and the solids accumulated in the system over the 7-day period. The Pumping Energy (PE) is calculated as:
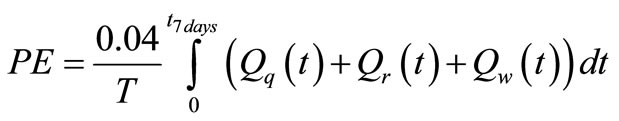 (3)
(3)
where Qa is the internal recirculation flow rate, Qr the sludge recirculation and Qw is the wastage flow rate, all expressed in m3/day.
3. DO5 Controller
In this section the design of the DO controller for the fifth aerated tank, DO5 is considered. Here, we will only

Table 1. Effluent quality index weighting factors.
be interested on the dynamics and performance of the DO controller. Later on we will use the tracking capabilities of such DO5 controller as the basis for an advanced control strategy where the DO5 set-point becomes time-varying and driven by a secondary controller that takes care of effluent quality.
For controller design purposes, a linear model is derived first. In order to facilitate the implementation of the controller as well as minimize impact on plant operation the required experiments to identify the models are designed as simple as possible. The experiment carried out is to drive the system to a steady state situation and to apply a 10% step change in the manipulated variable (KLa5 in this case). The resulting data is collected and used for identification. The linear process models were obtained using subspace identification techniques. The algorithm employed was N4SID [16], which exhibit robust numerical properties and relatively low computational complexity. As usual within the Process Control community, whenever possible, these models will be reduced to the usual First-Order-Plus-time-Delay (FOPTD) or even just First-Order (FO) in order to facilitate the application of simple controller tuning rules. Here the following First Order model is obtained:
 (4)
(4)
As the process model is of first order, a PI controller is to be used. For comparison purposes two approaches are followed: the Analytic Tuning (AT) presented in [17] and the Internal Model Control (IMC) design of [18]. These tuning approaches fall into the so called one-parameter tuning approaches. Therefore it is easy to relate the controller performance to the tuning parameter. In both cases, the tuning parameter is related to the desired closed-loop time constant. While in the IMC approach the tuning parameter, λ, is directly the desired time constant, for the AT method of [17], the tuning parameter, τc, is the ratio between the open-loop and (desired) closedloop time constants.
Table 2 shows the controller performance for different choices of the tuning parameter. To make the tunings comparable, the choice of the IMC controller tuning parameter is done as λ = τc Tp, Tp being the open-loop time constant. The table shows the controller performance as well as the corresponding information related to the effluent quality and operation costs. The regulation is performed under the dry influent conditions, and it is seen that, even the regulation performance can be increased by appropriate tuning, the final repercussion on effluent quality is only marginal. Therefore it seems that, from the point of view of effluent quality, any one of the previous tunings would provide almost the same result. However, as it will be seen later on, the need for a good DO5 control will arise when dealing with the cascade control approach and a time varying set-point will need to be tracked.
The PI controller tuned by applying the AT approach is a Two-Degree-of-freedom PI controller with parameters (for τc= 0.3): Kc = 323,92, Ti = 0,01 and β = 0,59. To have a more realistic comparison and also to show that the performance provided can be comparable to that of more advanced control strategies the performance of the DO5 control loop is also compared with the PI tuning suggested in [19], where the controller was tuned by applying an IAE optimization over all the 14 days running period. This approach however is very difficult to translate to another situation or even to a real plant where limited tests are allowed (the optimization is carried out by using the real influent data to the plant). The time responses for the last 7 days under the dry influent operating conditions are shown in figure 2.
Note that the behavior of the AT and IMC approaches is quite similar, but the variation of the IMC controller slightly larger in some cases. Therefore, for tight DO5 control the AT method seems more appropriate as it is able to provide more accurate disturbance attenuation with almost the same aeration energy. In fact control signals look almost identical.
Another advanced control approach is proposed in [20] where Model Predictive Control (MPC) is applied on the basis of a second order model. The tuning of the MPC controller becomes a trial and error procedure where the different tuning factors are selected by means of simulation
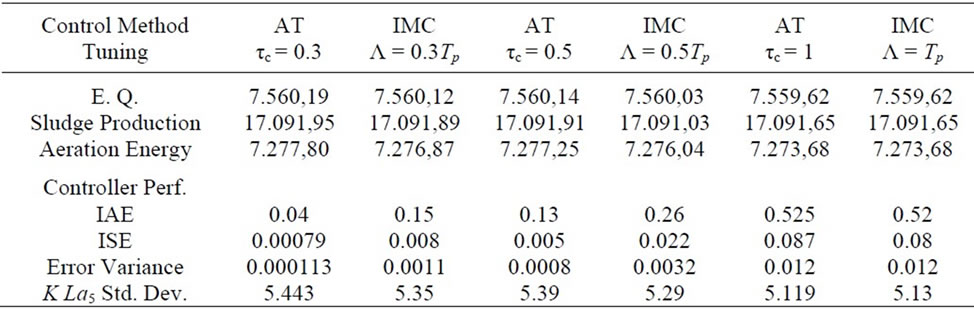
Table 2. DO5 Performance evaluation.

Figure 2. Comparison of the performance of AT and IMC design approaches for the control of DO5 concentration.
studies. Even the results are not reproduced here, authors in [20] report an IAE performance of about 0.089, an ISE value of 0.0026 and an error variance of 0.0196. Effluent quality characteristics are similar to the ones reported here. Therefore, from the controller performance point of view, the necessity of more complex control algorithms (sometimes more difficult to tune) is raised here where comparable and even superior performance is achieved by a well tuned PI controller.
4. Benchmark Control Strategy
As a complement to the DO5 control on the last aerated tank, the Benchmark framework proposes the control of the nitrate on the second tank, NO2, by using the internal recirculating flow, Qa. The NO2 controller will be tuned according to the AT approach but now using the corresponding identified model. The procedure follows the same lines as the one for the DO controller in the previous section and the model that will be used for control is:
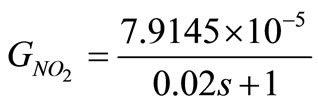 (5)
(5)
Different values of the tuning parameter τc are chosen and as it is seen from table 3 excessive bandwidth on this loop causes large variations in the control signals and generates higher values for the effluent quality index. Therefore the selection of τc = 1 may provide a good compromise. At this point, only the results corresponding to the AT tuning are shown, being those of the IMC approach slightly worse than this one. Time responses are
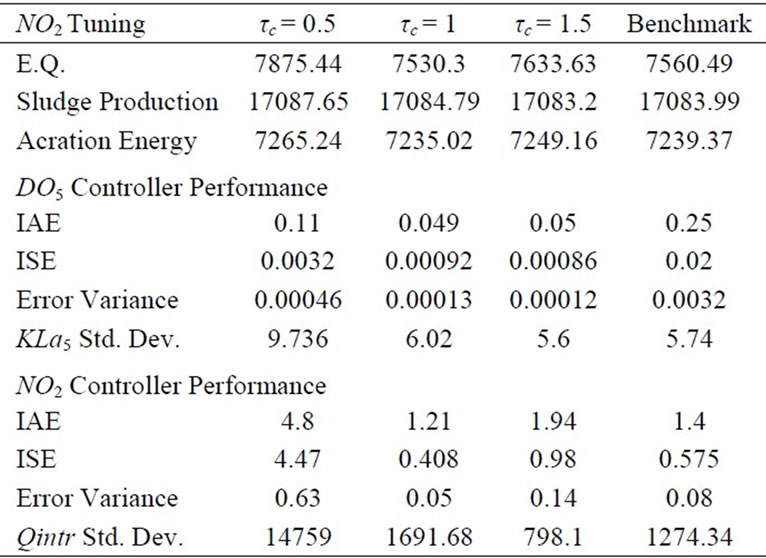
Table 3. Performance of the two-loop configuration by using the tuning τc = 0.3 for the DO5 loop. The column corresponding to the Benchmark uses the controller tunings provided in the Benchmark description.
shown in Figure 3 also showing the comparison with the performance of the PI controllers proposed in the Benchmark. As it is seen, the time responses are quite similar but the tight control on the dissolved oxygen achieves a final better effluent quality.
5. Cascade Control
In order to improve the effluent quality, a major goal of the control system is to keep the level of Nitrogen in the effluent as low as possible. To achieve this, instead of keeping the DO5 set-point constant, the rationale behind the cascade control approach is to generate a time-varying DO5 set-point; DO5ref on the basis of the nitrate concentration on the second anoxic tank. This scheme is assumed to better accommodate load variations as well as make a more rational use of aeration energy. Figure 4 shows the block diagram of this control configuration.
The inner-loop will be chosen as the AT tuned PI control found on the previous section. Therefore, due to the fast dynamics of the oxygen, as the time constant of the resulting inner-loop will be τc Tp = 0.003, the series connection of the inner-loop with the P2(s) transfer function will behave practically as P2(s). This observation simplifies the design of the outer loop controller; K2(s), on the basis of the model
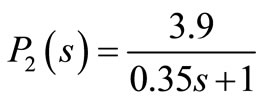 (6)
(6)
Note that under this control configuration, the only manipulated variable is the aeration rate in the fifth tank. The internal recirculation sludge is now kept constant to its steady value Qa = 55338 m3/d. As a first experiment the reference value for the NO2 concentration, NO2ref, is set to 2 mg/l, as in the previous experiments. By applying the AT tuning approach with a tuning choice of τc = 1 the resulting Effluent Quality index value was reduced to 6747.54, sensibly lower than the one achieved by using the two loop configuration as suggested in the Benchmark. Also the aeration energy was reduced to 6377.16. The main reason for such reductions is the time-varying DO5ref signal generated by the outer loop controller. Figure 5 shows the time evolution of the DO5ref and the actual DO5 value. It is observed that most of the time the required concentration is below the 2 mg/l, therefore requiring less aeration. Also as a consequence of this time-varying DO5 set-point, figure 5 also shows the concentration of Total Nitrogen (TN = TKN + NO) in the effluent. This uniform reduction, with respect to the
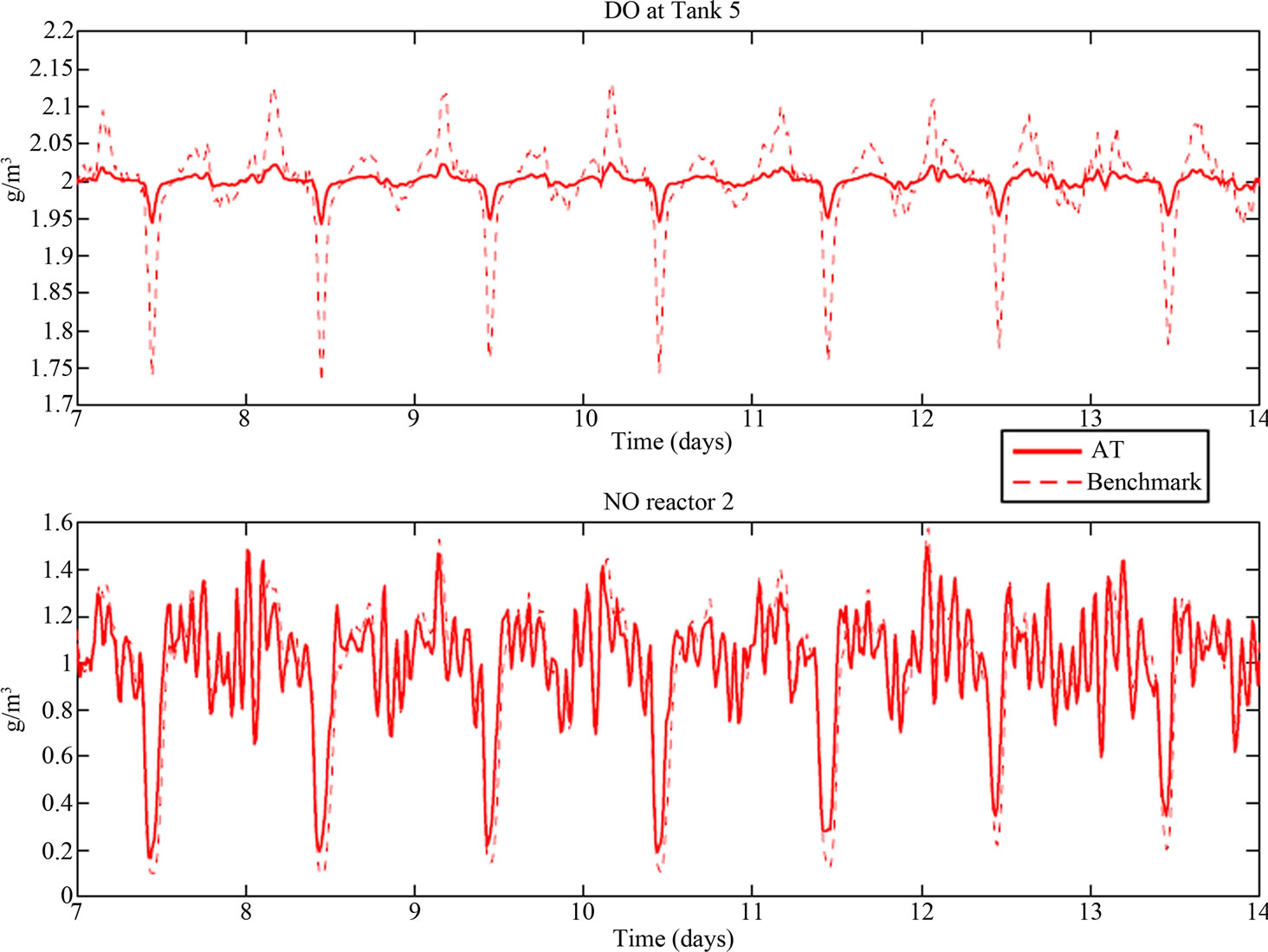
Figure 3. Time responses for the AT and Benchmark tunings of the DO concentration at the last aerated tank and NO at the second anoxic tank.

Figure 4. Cascade control scheme for time-varying DO setpoint generation.
levels achieved by the two-loop configuration, over time of the TN concentration is the main reason for the reduction of the Effluent Quality index value.
A complementary analysis has been conducted on the choice of the appropriate value for NO2ref as well as the impact on possible different tunings for the cascade controllers. As the AT tuning method is just driven by the desired speed of the closed-loop system, several combinations have been tested for NO2ref Î [1.5, 5]. It has been verified that a proper choice of the NO2ref can help to achieve good improvement in the Effluent Quality. As a result, the value NO2ref ≈ 2.25 represents a good compromise reference value. Figure 6 shows the effluent total nitrogen for the initial reference value of NO2ref = 2 and the value NO2ref = 2.25. It is noticed that even the change on the reference set-point is small; the TN is maintained below the required level. This improvement is accomplished at the expense of increasing the Aeration Energy to 6530.15 KWh/d. This increase is due to the required higher levels for the DO5 concentration as it is reflected on the generated DO5 set-point (see figure 5).
6. Inclusion of Feed forward Control Action
The preceding cascade based control performance analysis shows that it is difficult to reduce the TN concentration when high load of ammonia on the influent is present. Considerable peaks are still present on the effluent. In order to incorporate such situation into the control scheme, a feed forward control action from the influent ammonia is devised. To properly design such feed forward controller, a model of the dynamics from the ammonia influent to the nitrate of the second tank is needed. The block diagram of the resulting linear control system, by incorporating such disturbance model is shown in figure 7.
Firstly, the effect of the influent ammonia, NHin, on the nitrate concentration in the second tank, NO2, has to be identified. For such purpose, the same input profile provided for the dry influent operation is used as input data for 2 days. During these days, and with the plant operating in open loop, the NO2 concentration is recorded.

Figure 5. Time-varying DO set-point and actual value for the DO5 and time evolution of TN = TKN + NO on effluent.

Figure 6. Effluent Quality and Aeration energy index for the cascade controllers and NO2ref = 2 and the value NO2ref = 2.25.
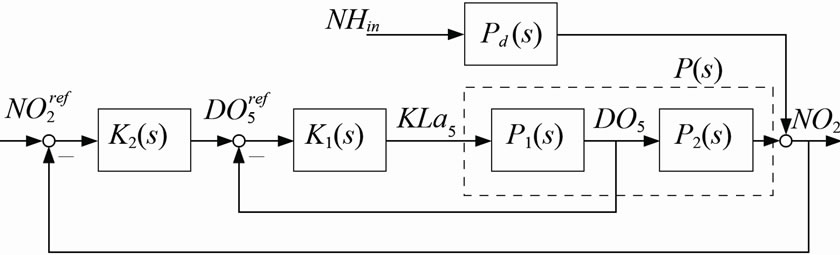
Figure 7. Cascade control scheme for time-varying DO setpoint generation.
By applying the subspace identification with N4SID [16], a fourth order model is identified. The obtained model is as follows:
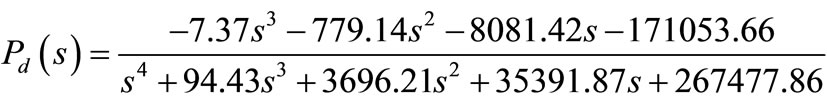 (7)
(7)
This Pd (s) model will be used for disturbance feed forward control compensation.
As far as manipulated variables are concerned, the same control handles, KLa5 and Qa, as before are considered. However, external carbon addition is also sometimes used as a manipulated variable in order to help the denitrification process. When the readily biodegradable carbon source is present on a limited quantity, (Sin), the denitrifiction process is not working efficiently. Therefore, carbon addition is usually also considered as a manipulated variable. This control action is achieved by complementing the Sin with respect to the, non-controlled, input concentration. Therefore external carbon addition is considered as the manipulated variable for nitrate reduction to be determined by the feed forward control action.
With the purpose of using Sin as the manipulated variable to help reducing the nitrate concentration for high influent ammonia load peaks, the dynamics from Sin to NO2 are needed. In order to highlight the simplicity of the approach, dynamics are identified to a first order model with transfer function.
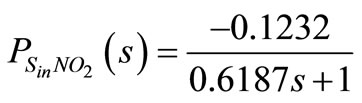 (8)
(8)
This model will be used to determine the feedforward controller, Qff (s), according to the following scheme: first we can use the disturbance model Pd (s) to predict the disturbance that will be caused by the influent ammonia on NO2 and take this quantity as the NO2 concentration that has to be counteracted by adding extra carbon. The resulting Qff (s) controller is computed as
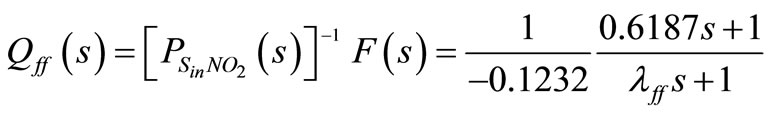 (9)
(9)
being λff the feed forward tuning parameter. Very low values for λff will introduce undesirable high frequency dynamics on the external carbon dosage. Therefore, a compromise value has to be chosen. According to the bandwidth of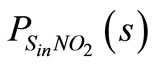 , a value of λff that starts to roll-off a decade above will perform dynamic inversion over the frequency range of interest and does not introduce too excessive high frequency dynamics. The evolution of the TN on effluent compared with the cascade results of the previous section as well as the total input carbon (SSin + added by feed forward) are shown in figure 8. As it can be seen an uniform improvement on the reduction of the N concentration is achieved. Table 4 summarizes the comparison among the three control structures by using the choice λff = 0.06 for the feed forward controller.
, a value of λff that starts to roll-off a decade above will perform dynamic inversion over the frequency range of interest and does not introduce too excessive high frequency dynamics. The evolution of the TN on effluent compared with the cascade results of the previous section as well as the total input carbon (SSin + added by feed forward) are shown in figure 8. As it can be seen an uniform improvement on the reduction of the N concentration is achieved. Table 4 summarizes the comparison among the three control structures by using the choice λff = 0.06 for the feed forward controller.
It is worth to remember that the design has been done under the dry influent conditions. To complement the evaluation of the proposed control configuration, a simulation study has been carried out that shows the performance under the rain influent and storm influent conditions. The combination cascade + feed forward is able to maintain the TN concentration in the effluent below the established limit (18 N mg/l) for all three operating conditions, whereas the cascade control, even achieves good performance on the dry influent situation, do not keep the concentration below 18 N mg/l in all cases.
7. Conclusions
In this paper a process control oriented strategy for N-removal is proposed. The final control configuration relies on a DO control loop for the last aerated tank. The set-point to this control loop is provided by an outer nitrate control loop that on the basis of the nitrate concentration in the second anoxic tank generates a time-varying set-point. These two loops are built up on a cascade control configuration that exhibits better plant performance

Table 4. Performance comparison of the different tested control strategies.
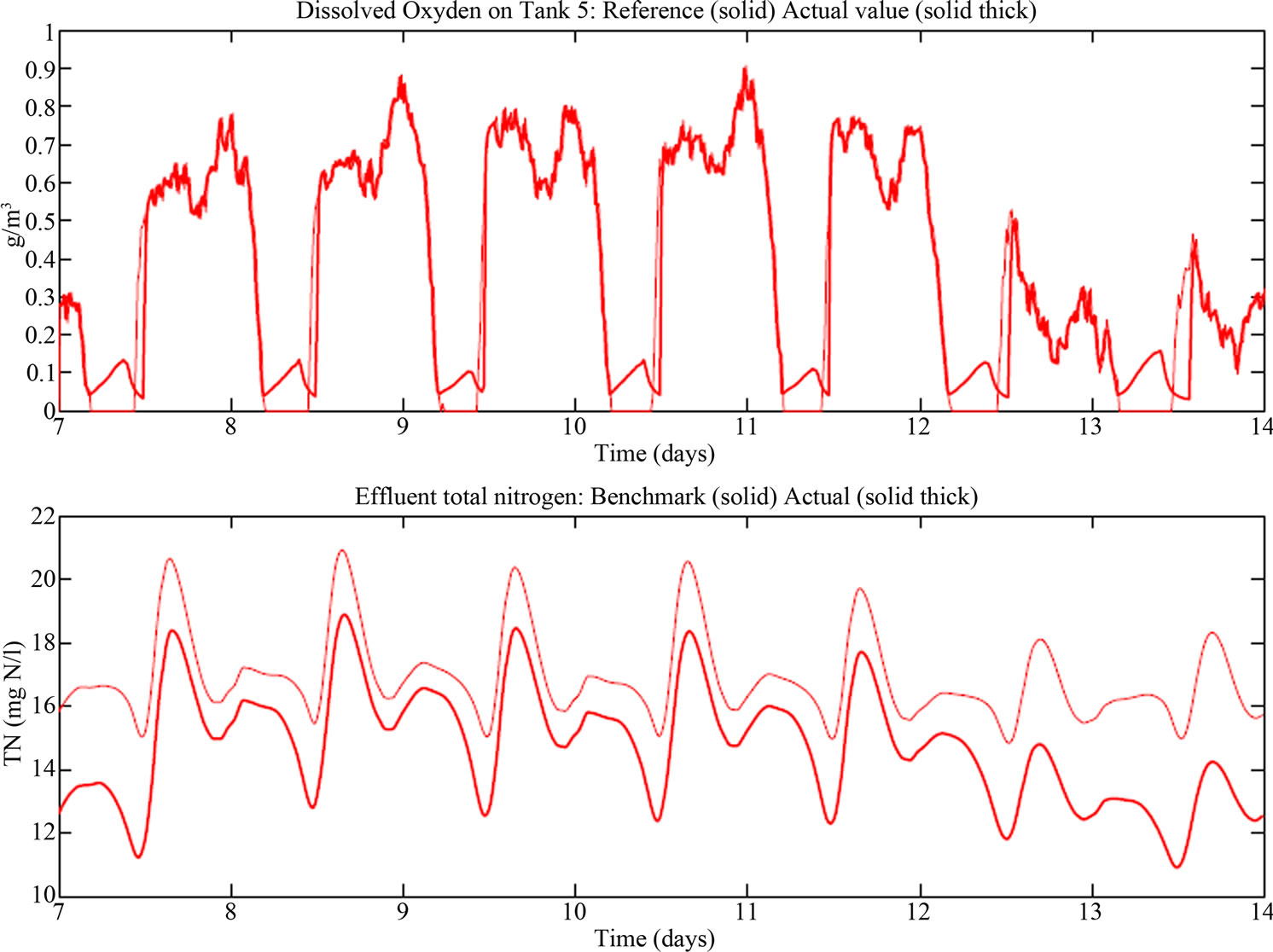
Figure 8. Evolution of the total nitrogen on effluent. Comparison of the cascade and cascade + feedforward control strategies.
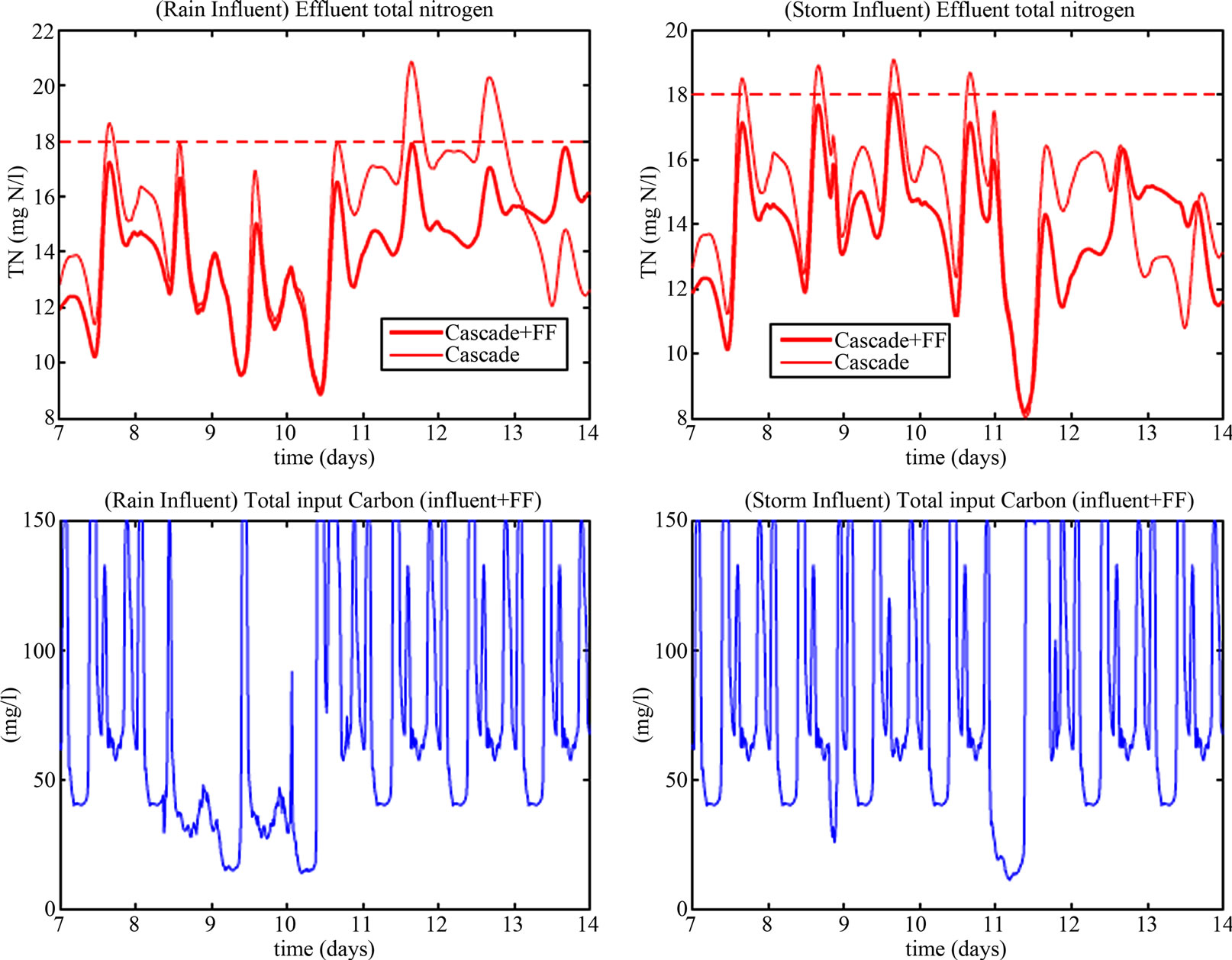
Figure 9. Nitrogen removal for te cascade and cascade+feedforward under the raininfluent and storminfluent conditions.
(in terms of effluent quality). It has been reported that appropriate choice of the reference value for this cascade control configuration (in fact the reference value for the nitrate concentration in the second tank) has clear effects on the final effluent quality index.
The cascade control configuration only uses aeration in the last tank as the manipulated variable. In order to reduce nitrate concentration when high influent load comes in, a feed forward control signal has been added to complement the task of the cascade control system. The resulting cascade + feed forward control configuration achieves satisfactory nitrogen removal for the three influent operating conditions (dry, rain and storm.)
The design of all the controllers has been carried out in terms of direct and readily available data by using simple step-tests. The control strategy is based on PI/PID type controller and hence the approach presented is more appealing for practical implementation. In addition, as the tuning approach is single parameter driven, fine tuning of the controller is possible and easy to apply.
A number of important questions remain open that may improve plant operation. The recirculation flow rate has not been manipulated. Therefore it remains as an additional control handle that may be determined to better enhance the plant performance. Also, the reference value for the nitrate concentration on the second tank has been fixed to a constant value. This reference value can also be interpreted as a manipulated variable that can be readjusted on-line in terms of the plant influent load. This readjustment may improve both plant efficiency and operation costs. All these aspects are currently under study and will be reported elsewhere.
8. Acknowledgements
This work has received financial support from the AECIPCI programs A/025100/08 and A/025100/09, the MICINN ProExt mobility program grant PR2008-0102 and from the Spanish CICYT program under grant DPI20- 07-63356.
REFERENCES
- J. F. Andrews, “Dynamic Models and Control Strategies for Wastewater Treatment Processes,” Water Research, vol. 8, 1974, pp. 261-289. doi:10.1016/0043-1354(74)90090-6
- P. Vanrolleghem, “On-Line Modelling of Activated Sludge Processes: Development of an Adaptive Sensor,” Thesis from the University of Gent, Belgium, 1994.
- L. J. S. Lukasse, K. J. Keesman and G. van Straten, “A Recursively Identified Model for the Short-Term Predictions of NH4/NO3 Concentrations in Alternating Activated Sludge Processes,” Journal of Process Control, vol. 9, 1999, pp. 87-100. doi:10.1016/S0959-1524(98)00037-7
- J. F. Andrews, “Dynamic Control of Wastewater Trement Plants,” Environmental Science Technology, vol. 28, 1994, pp. 434-440. doi:10.1021/es00058a004
- D. Vrecko, N. Hvala, and B. Carlsson, “FeedforwardFeedback Control of an Activated Sludge Process: A Simulation Study,” Water Science Technology, Vol. 47, No. 12, 2003, pp. 19-26.
- P. Ingildsen, “Realising Full-Scale Control in Wastewater Treatment Systems Using in Situ Nutrient Sensors,” Ph.D. Thesis, Department of Industrial Electrical Engineering and Automation, Lund University, Sweden, 2002.
- A. Stare, D. Vrecko and N. Hvala, “Comparison of Control Strategies for Nitrogen Removal in an Activated Sludge Process in Terms of Operating Costs: A Simulation Study,” Journal of Process Control, vol. 41, 2007, pp. 2004-2014.
- N. A. Wahab, R. Katebi and J. Balderud, “Multivariable Pid Control Design for Activated Sludge Process with Nitrification and Denitrification,” Biochemical Engneering Journal, vol. 45, No. 3, 2009, pp. 239-248. doi:10.1016/j.bej.2009.04.016
- Z. Yuan, A. Oehmen and P. Ingildsen, “Control of Nitrate Recirculation Flow in Predenitrification Systems,” Water Science and Technology, vol. 45, No. 4-5, 2002, pp. 29- 36.
- P. R. Barros and B. Carlsson, “Iterative Design of a Nitrate Controller Using an External Carbon Source in an Activated Sludge Process,” Water Science and Technology, vol. 37, No. 12, 1998, pp. 95-102. doi:10.1016/S0273-1223(98)00341-2
- M. Steffens and P. Lant, “Multivariable Control of Nutrient Removing Activated Sludge Systems,” Water Research, Vol. 33, 1999, pp. 2864-2878. doi:10.1016/S0043-1354(98)00521-1
- J. Copp, “IWA Task Group on Benchmarking of Control Strategies for WWTPs.” http://www.benchmarkwwtp.org/
- M. Henze, W. Gujer, M. C. van Loosdrecht and T. Mino, “Activated Sludge Models ASM1, ASM2, ASM2d and ASM3,” IAWQ Scientific and Technical Report No. 3, IAWQ, Great Britain, 2000.
- I. T. G. Patry and D. Nolasco, “A Dynamic Model of the Clarification Thickening Process,” Water Research, vol. 10, 1991, pp. 1263-1271.
- A. Iratni, R. Katebi, R. Vilanova and M. Mostefai, “On Estimation of Unknown State Variables in Wastewater Systems,” IEEE Conference on Emerging Technologies and Factory Automation, Palma, 22-25 September 2009. doi:10.1109/ETFA.2009.5347055
- P. V. Overschee and B. de Moor, “N4SID: Subspace Algorithms for the Identification of Combined Deterministic-Stochastic Systems,” Automatica, vol. 30, 1994, pp. 75-93. doi:10.1016/0005-1098(94)90230-5
- V. M. Alfaro, R. Vilanova and O. Arrieta, “Analytical Robust Tuning of PI controllers for First-Order-PlusDead-Time Processes,” In: 13th IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, 15-18 September 2008,.
- M. Morari and E. Zafirou, “Robust Process Control,” Prentice-Hall International, 1989.
- W. Zarrad, J. Harmand, M. Devisscher and J. Steyer, “Comparison of Advanced Control Strategies for Improving the Monitoring of Activated Sludge Processes,” Control Engineering Practice, vol. 12, 2004, pp. 323- 333. doi:10.1016/S0967-0661(03)00169-2
- B. Holenda, E. Domokos, A. Redey and J. Fazakas, “Dissolved Oxygen Control of the Activated Sludge Wastewater Treatment Process Using Model Predictive Control,” Computers and Chemical Engineering, vol. 32, 2008, pp. 1270-1278. doi:10.1016/j.compchemeng.2007.06.008
NOTES
1figure taken from http://www.benchmarkwwtp.org/

