Journal of Water Resource and Protection
Vol. 1 No. 6 (2009) , Article ID: 1070 , 10 pages DOI:10.4236/jwarp.2009.16046
Z-Transform Based Instantaneous Unit Hydrograph for Hilly Watersheds
1DHI (India) Water & Environment, New Delhi, India
2Department of Civil Engineering, Indian Institute of Technology Roorkee, Uttarakhand, India
E-mail: rai.raveendra@gmail.com, cspojha@rediffmail.com
Received June 17, 2009; revised July 16, 2009; accepted July 27, 2009
Keywords: IUH, ARMA Process, Z-Transform, Nash Model, Direct Runoff Hydrograph, Hilly Watershed
ABSTRACT
Present study emphasizes the applicability of linear theory concept onto hilly watersheds. For this purpose, Z-transform technique was used to derive the instantaneous unit hydrograph (IUH) from the transfer function of autoregressive and moving average (ARMA) type linear difference equation. Parameters of the ARMA type rainfall-runoff process were estimated by least-squares method. The derived IUH from Z-transform (i.e. ARMA-IUH) has been used to compute the hydrologic response i.e. direct runoff hydrograph (DRH). Further, the superiority of the proposed approach has been tested by comparing the results through the results obtained from the Nash-IUH. Analyzing the results obtained from ARMA-IUH and Nash-IUH for the two hilly watersheds of North Western Himalayas shows the applicability of the linear theory concept even in turbulent flow conditions which are frequently encountered in hilly terrains under similar conditions of flow.
1. Introduction
The rainfall-runoff process is nonlinear and dynamic with spatially distributed inputs and outputs. Watershed response is inherently spatial, non-linear and time-variant. However, linear models are frequently used for analysis of watershed response to rainfall, as they are mathematically more convenient to handle than non-linear models. The input-output mathematical models based on linear theory of hydrologic systems attempt to establish a link between two or more observed phenomena without detailed description of physical process under investigation. In hydrological context, the basin is regarded as the system in which an input of effective rainfall is transformed into an output of discharge at the basin outlet. Spolia and Chander [1] presented a discretely coincident form of the equal-reservoir cascade model [2]. A discrete linear cascade model was developed for hydrology using the cascade concept of the Auto Regressive Moving Average (ARMA)-type difference equation and derived the unit impulse response function as a discrete time function for a family of discrete-parametric models [3–4]. Wang and Wu [5] showed that discrete input data could be represented by means of unit step functions. Wang et al. [6] developed a rainfall-runoff model for small watersheds and an applied discrete excess rainfall-runoff model to calculate the hydrograph of a watershed from the excess rainfall under the concept of linear system.
Hilly terrains are generally encountered in many countries. Planning of water resources is equally important for such watershed. Often, very little attention has been given to these watersheds because of poor availability of hydrological data due to inaccessible terrains. In this work, data of two hilly watersheds are subjected to analysis using Z-transform technique, with the objective to study the rainfall-runoff process. Normally, rainfall-runoff process is treated as a linear system. However, it is perfectly not known whether this linearity also holds good for hilly watersheds. Thus, the intention is to analyze the data and see the applicability of using linear system concept in the modeling of rainfall-runoff in hilly terrains.
Hilly terrains normally possess larger roughness in comparison to the plane watersheds. This may be because of the nature of surface over which overland flow can take place. Piece of boulders, gravels is frequently encountered in the hilly regions. Also, a dense forests and scrubs may add to the roughness. Thus, it is equally important to test the linear behavior of the system even in conditions of terrains having normally higher roughness. In hilly terrains, due to higher roughness and large velocities of flow, the regime of flow is generally turbulent and applicability of linear system concept on hilly terrains remains unexplored.
Therefore, the present study has been carried out with an objective to test whether the system behaves in a linear manner even under several extreme and complex conditions of terrains and nature of flow.
2. Derivation of IUH
Since inception [7], the unit hydrograph approach has been very well established as a linear theory concept in surface water hydrology and is continuously used by the researchers. For more generalized form, an instantaneous unit hydrograph (IUH) approach has achieved considerable momentum [2,8–10]. Other than the conceptual models [2,10], the researchers investigated wide range of methodology to derive IUH [11]. Also, many transform techniques (viz., Harmonic series, Fourier transform, Laplace transform etc.) either in continuous time domain or discrete time domains have been successfully used in the derivation of IUH. The Z-transform method constitutes one of the transform methods that can be applied to develop the response functions as a discrete time function of linear difference equations [10–15]. The technique works under the premise that the rainfall-runoff process behaves as a linear system for which Z-transform of the direct runoff equals the product of the Z-transform of the transfer function and the effective rainfall. They have used higher order polynomial to analyzed the single storm event and derive the unit hydrograph ordinates by root selection from Argand diagram, which is a complicated and time consuming process. Therefore, in the present study analytical derivation of instantaneous unit hydrograph from the transfer functions of ARMA type difference equation using the Z-transform (ARMA-IUH) has been presented. The derived ARMA-IUH is then used to apply for the computation of direct runoff hydrographs. The relative performance of the proposed method has been tested by comparing it with the Nash-IUH model.
Therefore, the procedure for the derivation of ARMAIUH and Nash-IUH has been represented in the following section.
2.1. ARMA-IUH (p, q) Model
The current outflow at the watershed outlet would generally be expected to depend on inflows (excess rainfall) and outflows (direct runoff) of several time units back. Therefore, an autoregressive and moving average (ARMA) process of excess rainfall-direct runoff can be used to determine the transfer function of the watersheds. The autoregressive and moving average of order (p, q) (ARMA (p, q)) process of rainfall excess and direct runoff can be given as [16]:
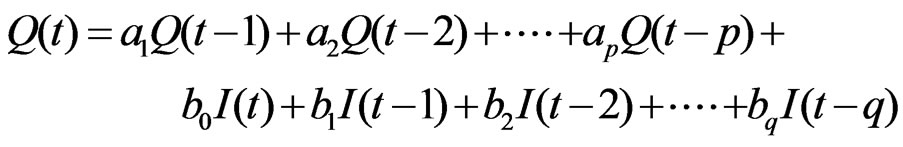 (1)
(1)
in which Q(t) is the direct runoff in m3/sec, I(t) is the excess rainfall intensity in m3/sec, 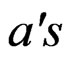 and
and 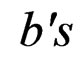 are the discrete time invariant parameters to be estimated and p and q are the order of the autoregressive and moving average (ARMA) processes respectively. For hydrologic applications, values of p and q must be selected through model identification and are generally less than four [17].
are the discrete time invariant parameters to be estimated and p and q are the order of the autoregressive and moving average (ARMA) processes respectively. For hydrologic applications, values of p and q must be selected through model identification and are generally less than four [17].
The Equation (1) can also be written using the back shift operator such that, 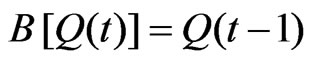 as [17]:
as [17]:
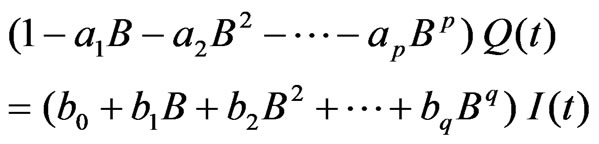 (2)
(2)
Equation (2) can be expressed in the form of transfer function as:
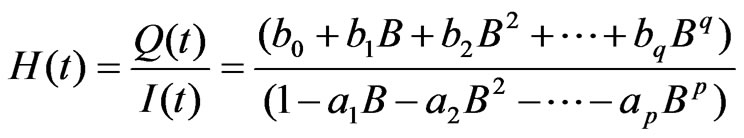 (3)
(3)
where, H(t) is the transfer function of ARMA(p, q) process of excess rainfall-direct runoff of the linear system.
2.1.1. Definition of Z-Transform
The Z-transform is one of the transform methods applied to the solution of linear difference equations. Difference equations are functional equations that define sequences and are the discrete counterparts of the differential equations. In many systems, the outputs are measured at discrete values of time, usually at nT, n = 0, 1, 2, ……., where T is the fixed positive number, usually referred to as the sampling period (it could be unity). Consider such a sequence {f(nT)} = 0, 1, 2, ………, which can be thought of as arising from a continuous waveform sampled at times nT, n = 0, 1, 2, ……. .The Z-transform of this sequence is defined as [18]:
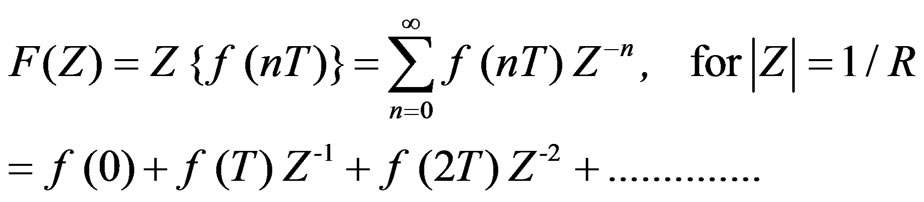 (4)
(4)
where, 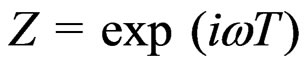 , R is the radius of convergence of the infinite series,
, R is the radius of convergence of the infinite series, 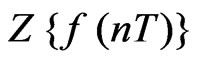 is the Z-transform of the sequence f (nT),
is the Z-transform of the sequence f (nT), 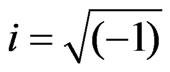 and
and 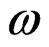 is the angular frequency.
is the angular frequency.
Here, in the manuscript the derivation of IUH was presented for the ARMA (2, 2) and ARMA (1, 1) processes using Z-transform technique according to the watersheds considered for the study.
2.1.2. IUH from ARMA (1, 1) Process [ARMA-IUH (1, 1)]
The transfer function of ARMA (1, 1) process of rainfall-runoff described by Equation (3) can be written as:
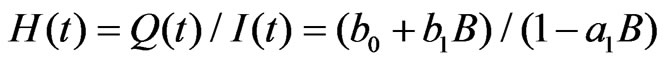 (5)
(5)
The Z-transform of Equation (5) is:
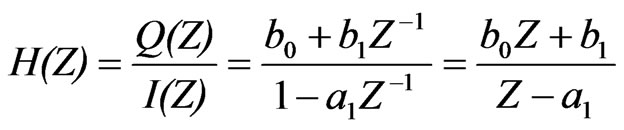 (6)
(6)
Division of Equation (6) throughout by Z gives:
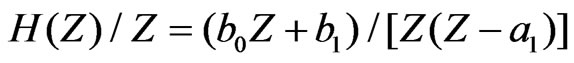 (7)
(7)
in which Q(Z) and I(Z) are the Z-transforms of Q(t) and I(t) sequences and H(Z) is the Z-transform of transfer function. The inverse Z-transform of H(Z) gives the unit impulse response function as:
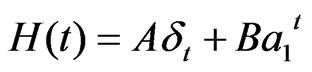 (8)
(8)
where: 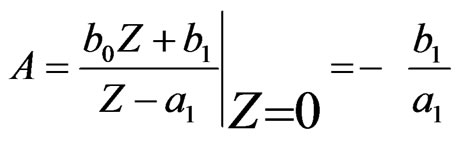 (9)
(9)
and: 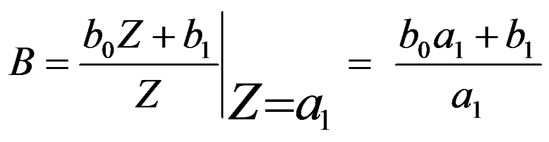 (10)
(10)
It should be noted that for t = 0, the unit impulse response function will be zero. Thus, substituting (t-1) in place of t for t = 1, 2, ….., n + 1 in the right side of the Equation (8), the unit impulse response function, h(t), of the watershed can be written as:
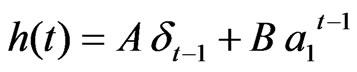 (11)
(11)
In Equation (11) which h(t) is the unit impulse response function (ARMA-IUH) at discrete time t and dt-1 is the Dirac delta function which is defined as:
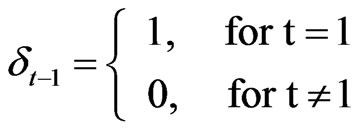 (12)
(12)
2.1.3. IUH from ARMA (2, 2) Process [ARMA-IUH (2, 2)]
The ARMA (2, 2) process of rainfall-runoff in its transfer function form described by Equation (3) can be written as:
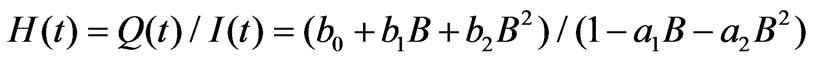 (13)
(13)
The Z-transform of Equation (13) is:
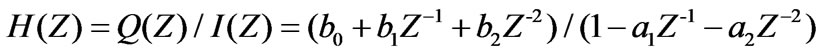 (14)
(14)
Equation (14) can be simplified as:
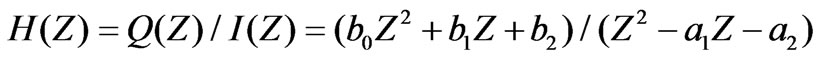 (15)
(15)
Equation (15) has been written after division by Z as:
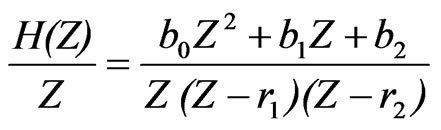 (16)
(16)
where: 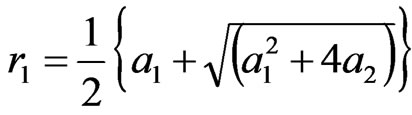 (17)/p>
(17)/p>
and:
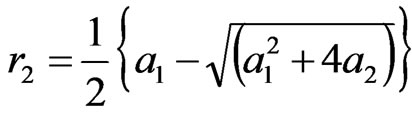 (18)
(18)
The partial fraction expansion of Equation (16) is:
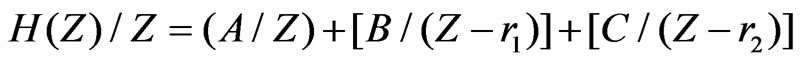 (19)
(19)
where: 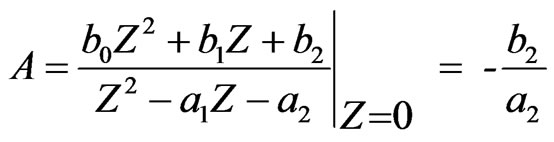 (20)
(20)
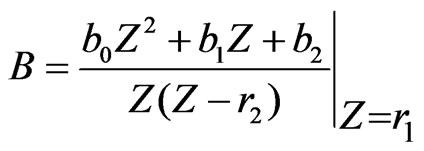 (21)
(21)
and,
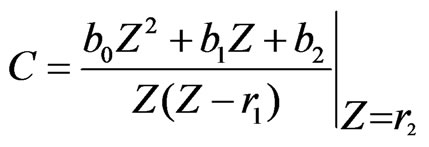 (22)
(22)
The inverse Z-transform of Equation (19) is as follows.
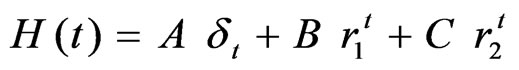 (23)
(23)
Therefore, the unit impulse response function (ARMA-IUH), h (t) will be expressed as follows.
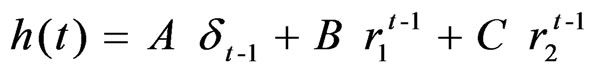 (24)
(24)
where:
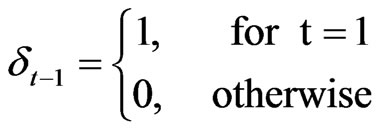 (25)
(25)
2.1.4. Parameter Estimation of ARMA (p, q) Process
Methods of fitting mathematical models to numerical data have been presented in a number of references [17, 19,20]. The least-square method was used to fit the model parameters of the ARMA (p, q) process from input (excess rainfall) and output (direct runoff) data. This method seeks estimators which minimize the sum of the squared residual or errors between the observed and calculated Q(t). Let the residual be e(t), then:
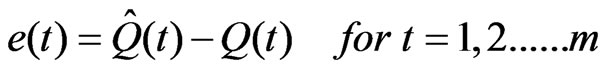 (26)
(26)
in which  and Q(t) are the observed and calculated value of the direct runoff data. The Equation (26) may be written in matrix form as follows.
and Q(t) are the observed and calculated value of the direct runoff data. The Equation (26) may be written in matrix form as follows.
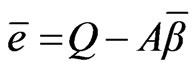 (27)
(27)
The components of the Equation (27) is given as follows.
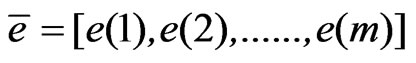 (28)
(28)
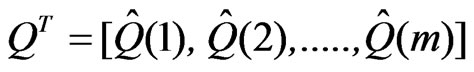 (29)
(29)
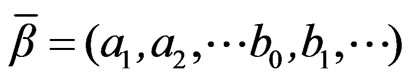 (30)
(30)
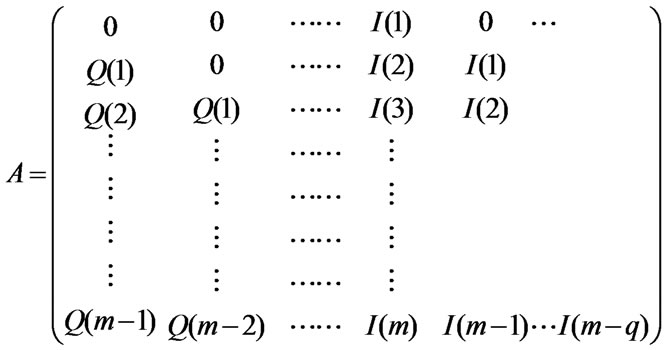 (31)
(31)
The least-square estimate of 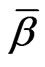 is the solution of Equation (27), that is:
is the solution of Equation (27), that is:
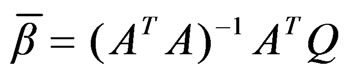 (32)
(32)
2.2. The Nash’s IUH
Nash [2,8] considered watershed as consisting of a series of n identical reservoirs and proposed a conceptual model by routing an instantaneous inflow through a series of linear reservoirs in the following form of the instantaneous unit hydrograph equation.
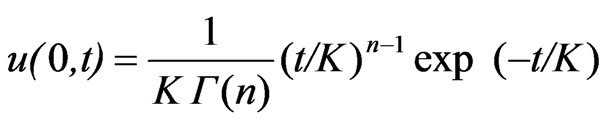 (33)
(33)
In above relationship, u (0, t) is the ordinate of instantaneous unit hydrograph (1/hr) at time t, K is storage constant (hr), t is the time in hours after the beginning of direct runoff (hr), Γ is the gamma function such that 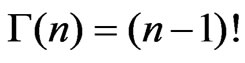 and n is the shape parameter. Equation (33) in terms of time to peak (tp) can be written as follows.
and n is the shape parameter. Equation (33) in terms of time to peak (tp) can be written as follows.
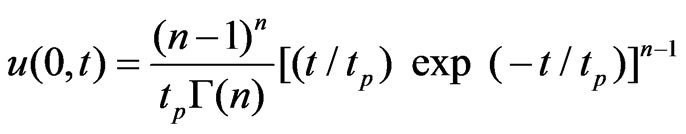 (34)
(34)
In the above relationship, tp is the time of peak flow ordinate.
2.2.1. Estimation of Shape Parameter n
The shape parameter, n was estimated for the corresponding values of dimensionless recession constant using the curve (Figure 1), the relationship between dimensionless recession constant and the hydrograph parameter, n. The dimensionless recession constant was estimated by using the following equation followed by plotting the recession curve of the actual direct runoff hydrograph on semi-logarithmic paper, with direct runoff hydrograph on the logarithmic scale, it was possible to fit a straight line to the part of the curve immediately following the crest segment of the hydrograph [21].
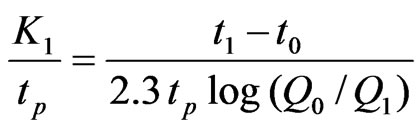 (35)
(35)
where tpis the time to peak, and Q0 and Q1 is the two values of the discharge and t1 and t0 are the corresponding two values of the time on the straight line in the semi-logarithmic plot.
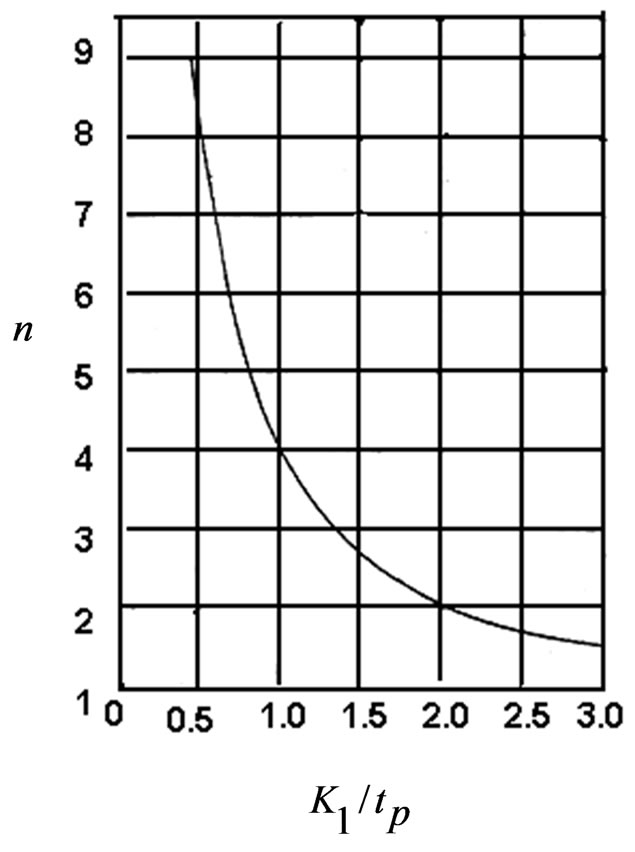
Figure 1. Relationship between dimensionless recession constant and hydrograph (Source: Wu et al., 1964).
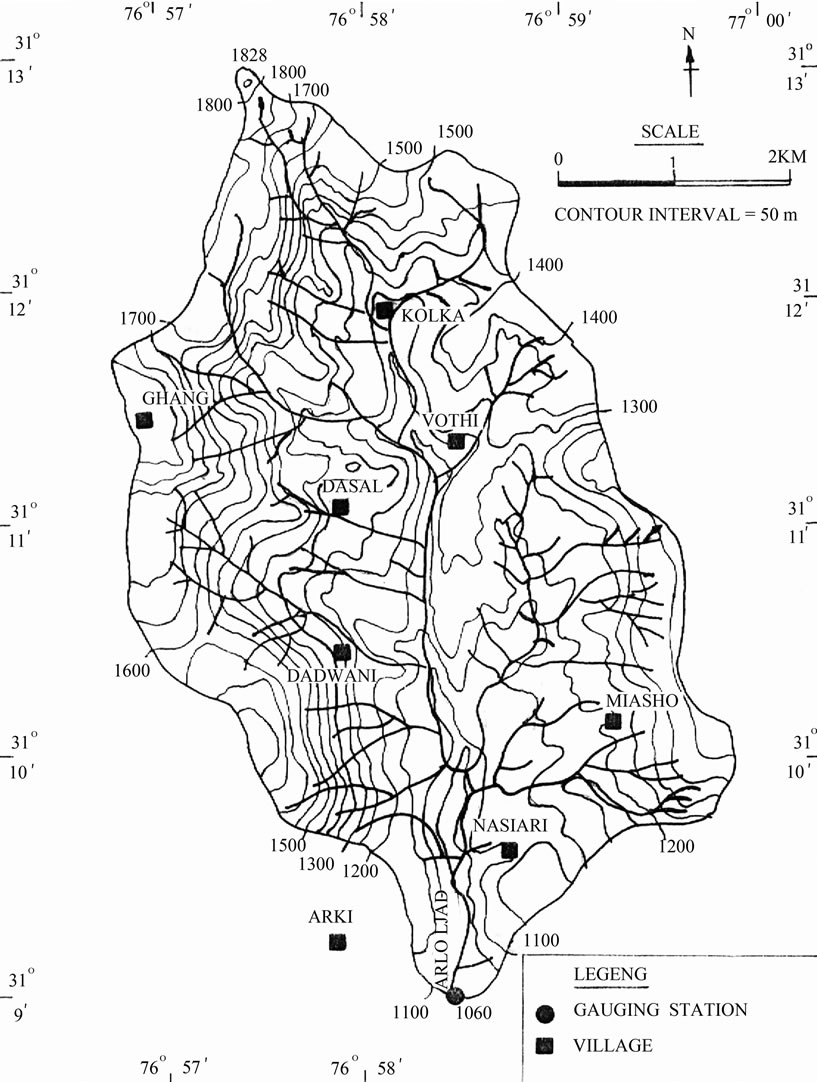
Figure 2. Drainage map of Arki watershed.
3. The Hilly Watersheds
Two watersheds (viz., Arki and Chaukhutia) of different topographic and land use conditions from North Western Himalayas have been picked up to test the concept of linearity. The Arki watershed (31° 8′ 58″ and 31° 12′ 58″ N latitude and 76° 56′ 50″ and 76° 59′ 50″ E longitude)
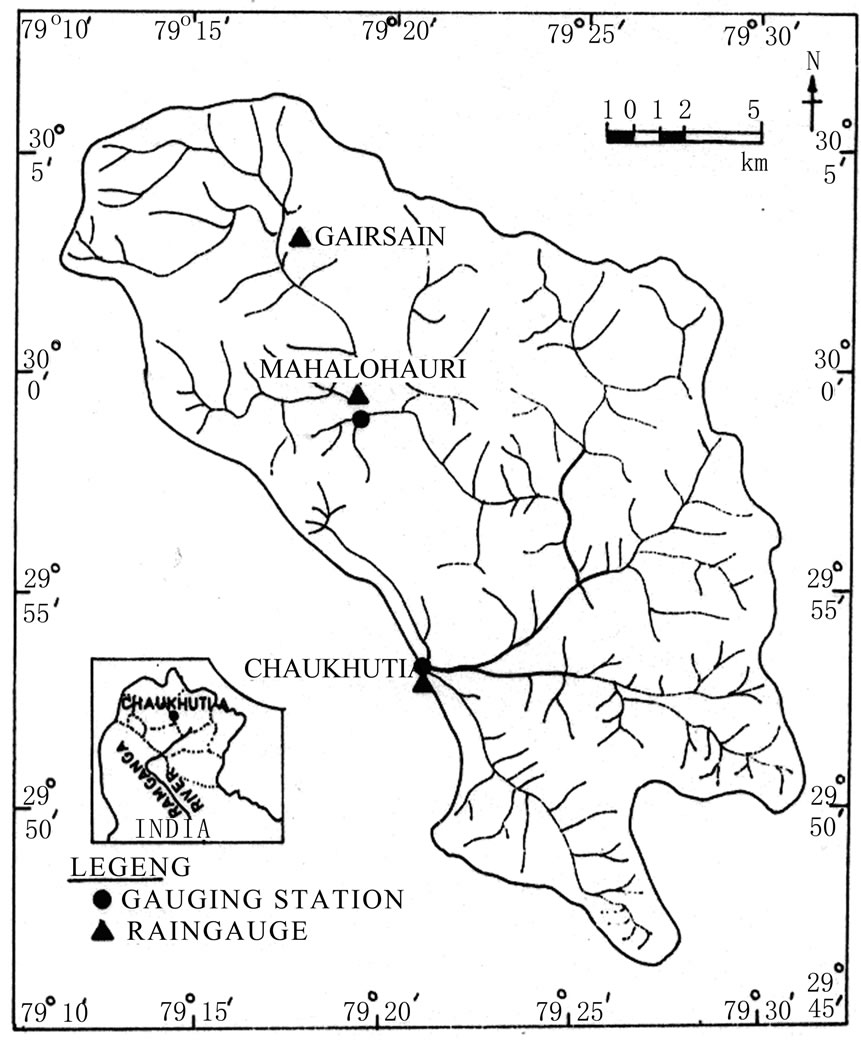
Figure 3. Drainage map of Chaukhutia watershed.
is a sub-watershed of Satluj river catchment comprising an area of 24.60 sq km and lies in Solan district of Himachal Pradesh (India) as shown in Figure 2. The watershed is more or less rectangular in shape and has a mean length of 7 km and width of 3.5 km. The maximum and minimum elevations of the watershed above mean sea level are 1828 m at the upstream end of Arki river and 1060 m at the gauging station near the Arki town respectively. The watershed lies in the upper Shivaliks and mid hills and has sub-temperate climate. The total annual rainfall recorded at different locations of the watershed varies from 800 mm to 2000 mm and about 78 percent of the total annual rainfall occurs during the monsoon season (mid June to mid September). The wa-tershed has hilly terrain with extremely undulating and irregular slopes ranging from relatively flat in valleys to
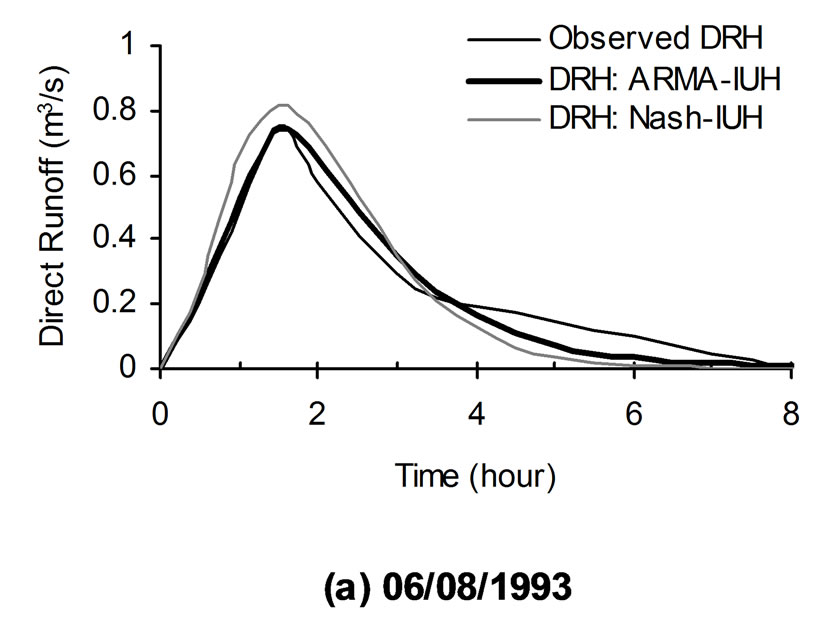
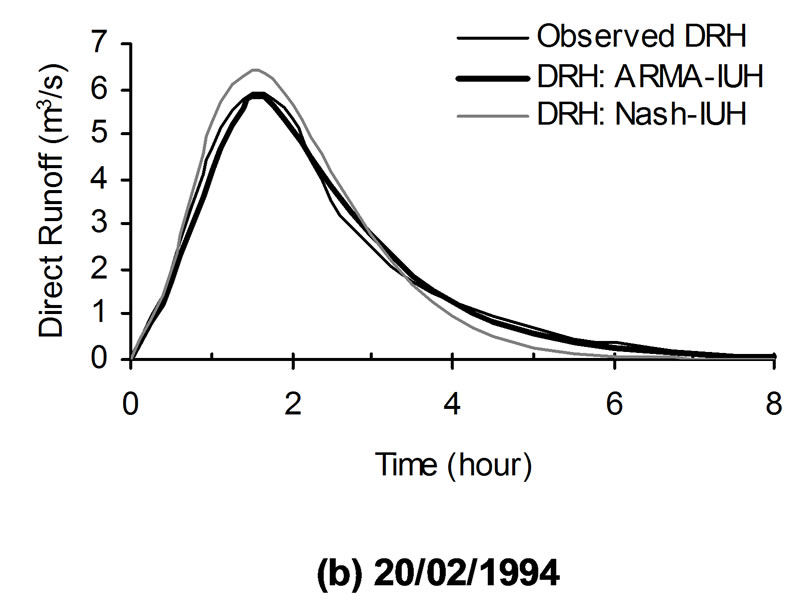
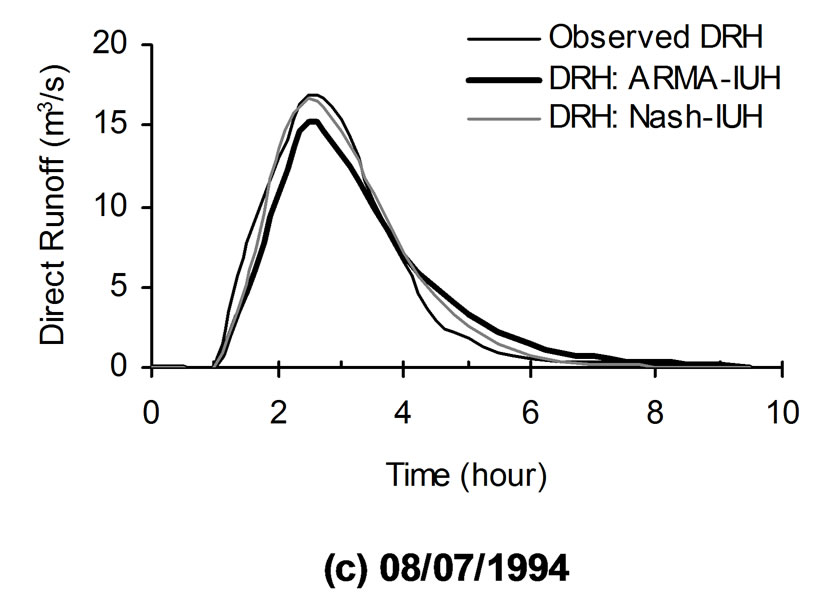
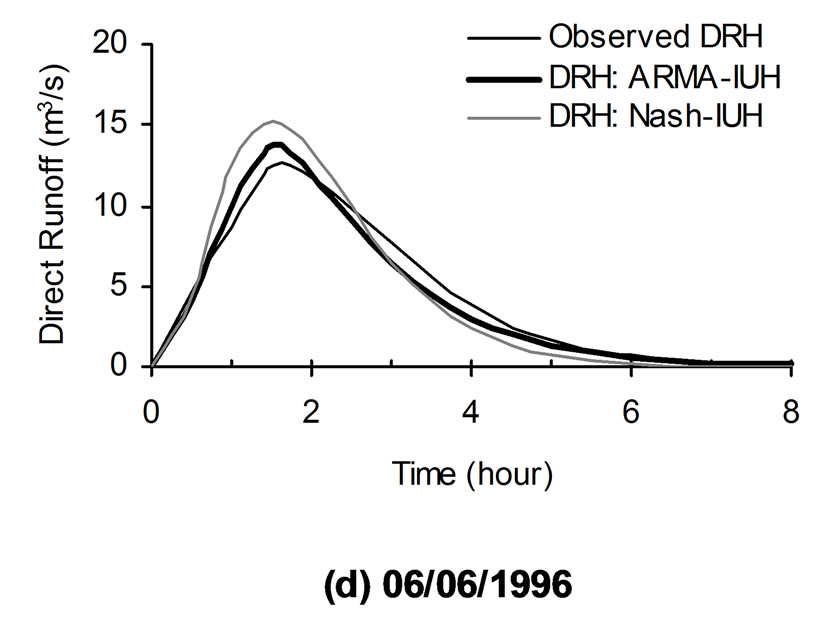
Figure 4. Comparison of observed and computed direct runoff hydrographs of sample storm events of Arki watershed.
quite steep slopes towards ridges with average slope of about 9 percent [22]. Whereas, the Chaukhutia watershed, a sub-watershed of Ramganga river catchment, a spring fed river originating from the mid-Himalayan ranges in Chamoli district of Uttaranchal (India) covering an area of 452.25 sq km and is located between 29° 46¢ 15² to 30° 6¢ N latitude and 79° 12¢ 15² to 79° 31¢ E longitude as shown in Figure 3. The Chaukhutia watershed is also approximately rectangular in shape and elongated in
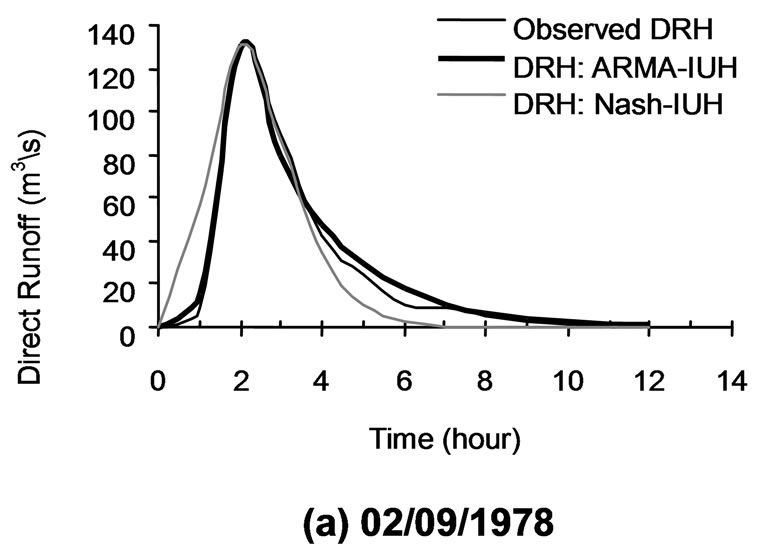

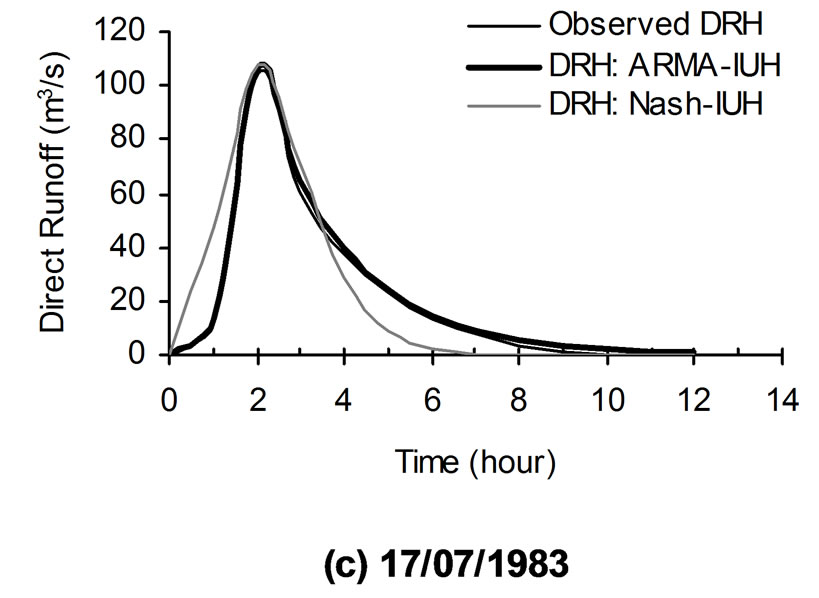
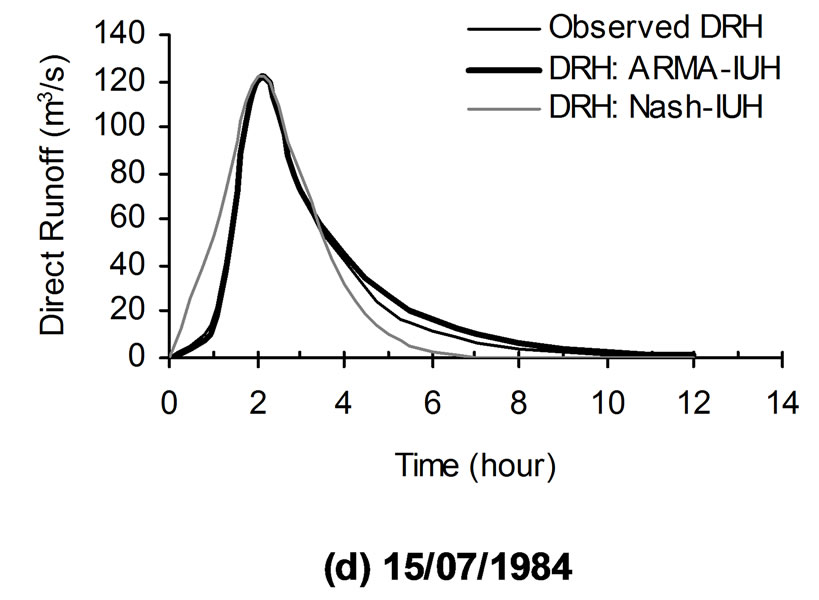
Figure 5. Comparison of observed and computed direct runoff hydrographs of sample storm events of Chaukhutia watershed.
north-south direction, has a maximum length (northsouth) of 30 km and width (west-east) of 16 km. The maximum and minimum elevations of the watershed are 3114 m at the upstream end and 929 m at the gauging station respectively. The slopes in the valley vary from 8-10 percent. The moderate hills lie between valley and steep hills with slopes varying from 10-50 percent while the slopes in the steep hills vary from more than 50 percent to almost vertical hills. The annual average precipitation in Chaukhutia watershed varies from 1084 mm to 1679 mm at different locations with mean annual precipitation of 1384 mm. From the total annual rainfall, about 75 percent occurs during the monsoon season from southwest monsoon. The climate of the Himalayan sub-watersheds varies from sub-tropical to sub-temperate with mean annual temperature of about 22°C. The mean annual minimum and maximum temperatures are 18°C and 30°C respectively. The monthly mean daily maximum temperature is highest (40°C) in the month of April whereas it is lowest (23°C) in December. The monthly mean daily minimum temperature is lowest (2°C) in January and highest (20°C) in August. The three distinct seasons in the area are: winter (October to March), summer (April–mid June) and monsoon (mid June-September). Severe frost occurs during nights from midDecember to mid-February when winter rains are deficient and damage fruits and vegetable crops grown in the watersheds.
Sixteen storm events that produced single peaked runoff hydrographs for the years 1993 to 1997 for Arki watershed and twenty storm events for the years 1976 to 1984 were analyzed to estimate the model parameters representing the watershed response. Almost all these events encountered a flow regime of turbulent flow around occurrence of peak flows. Direct runoff hydrographs were obtained by separating base runoff from total runoff hydrographs using the convex method suggested by Chow [23]. The volume of excess rainfall was determined by using the Φ-index method. The Φ-index method determines the horizontal line on rainfall hyetograph by iterative procedure such that the total depth of rainfall above it equals the resulting direct runoff [24].
As stated the objectives of the work is to confirm the applicability of the linear system concept for hilly watersheds in the runoff generation process. Towards this, the complexity of the system has been identified by the study of flow regime (i.e. laminar or turbulent flow) followed by the application of the methodology. For the application of the models, the data has been randomly divided into the calibration events and validation events. The parameters were estimated on the basis of the storm events used in calibration. The procedural details are discussed in next section for the Arki watershed and subsequently the results are presented for Chaukhutia watershed.
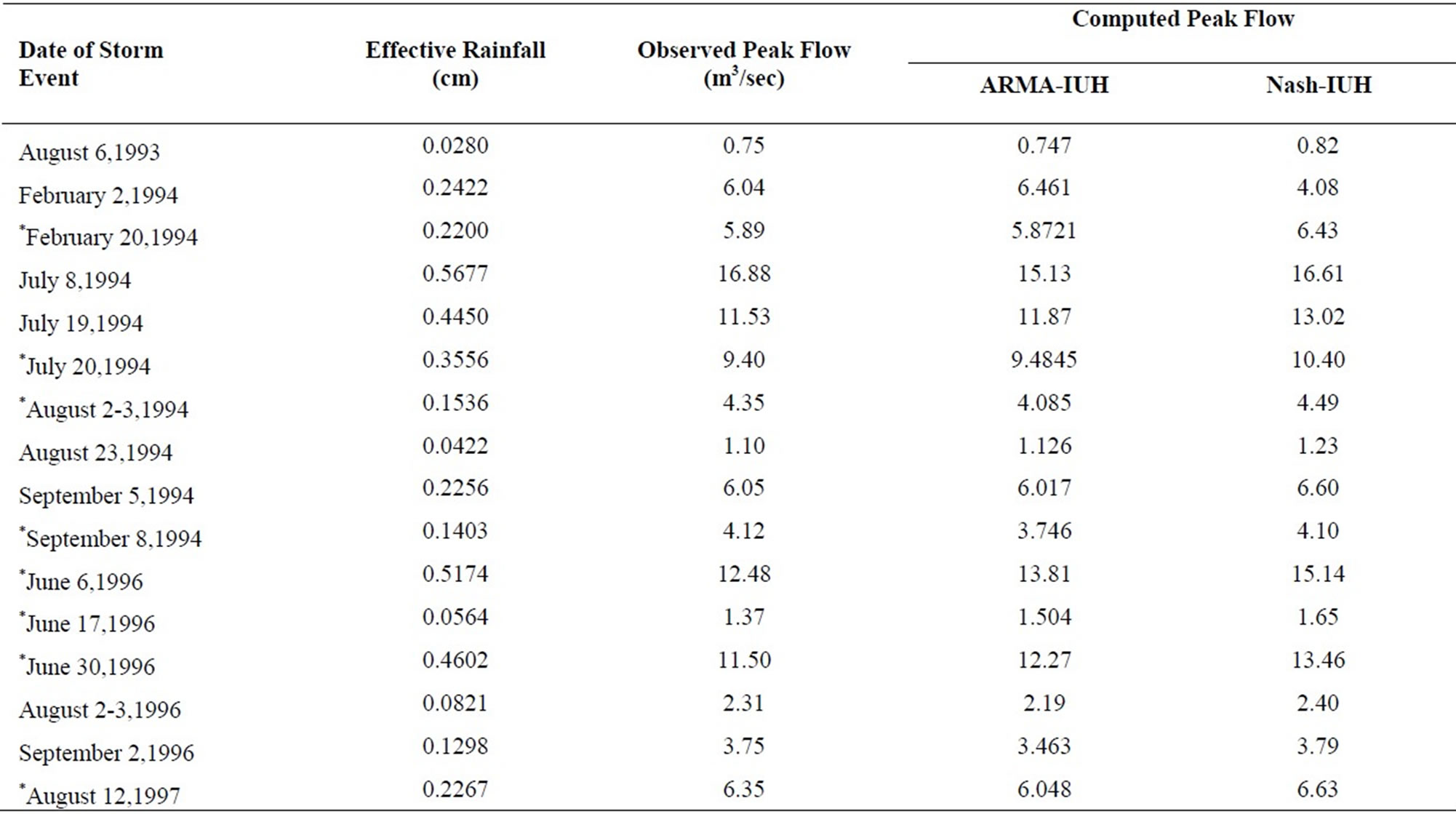
Table 1. Comparison of observed and computed peak flows for Arki watershed.

Table 2. Average estimated values of statistical measures for the models.
4. Results and Discussions
Eight out of sixteen storm events of Arki watershed were used to calibrate the model parameters. Analysis of these data revealed that the ARMA (2, 2) process was best fitted for Arki watershed. The average values of the parameters of ARMA (2, 2) process viz., a1, a2, b0, b1, and b2 for Arki watershed were estimated to be 1.05042, -0.25591, 0.117016, 0.156270 and 0.126858, respectively. These parameters were then used to develop an IUH based on ARMA (2, 2) [i.e. ARMA–IUH (2, 2)] and IUH is as follows.
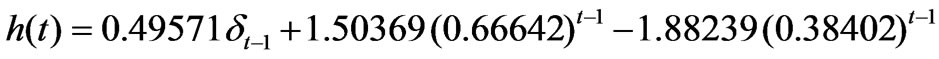 (36)
(36)
In the above relationship, t is the unit time step. The developed ARMA-IUH has been used to compute the direct runoff hydrographs using the convolution technique. The comparisons of computed direct runoff hydrographs along with the observed hydrograph for sample storm events are shown in Figure 4. The hydrograph parameter i.e. peak flow rate for all the storm events used in the analysis are given in Table 1. Along with the visual assessment of proposed model, the following statistical criteria have been employed to test the performance of the approach.
1) Coefficient of efficiency (CE) [25]
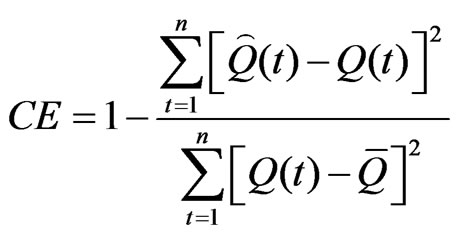 (37)
(37)
where  is the computed discharge,
is the computed discharge,  is the observed discharge,
is the observed discharge,  is average value of the discharge during the storm.
is average value of the discharge during the storm.
2) Relative error in estimated peak (EP)
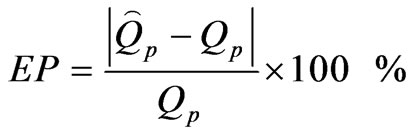 (38)
(38)
where 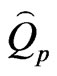 is the computed peak discharge and
is the computed peak discharge and  is the observed peak discharge.
is the observed peak discharge.
The average estimated values of the CE and EP for Arki watershed is given in Table 2.
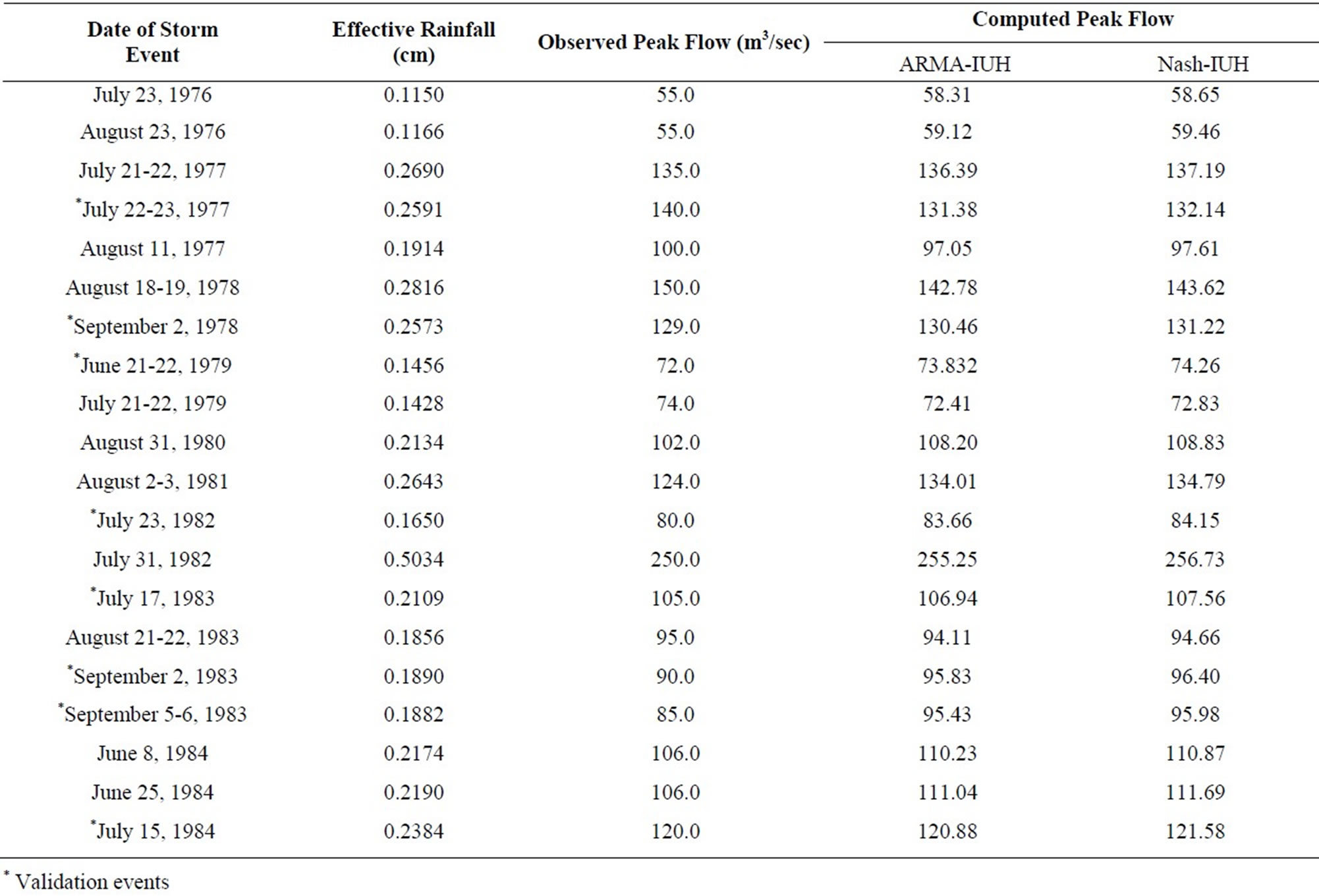
Table 3. Comparison of observed and computed peak flows for Chaukhutia watershed.
Similarly, the rainfall-runoff records of Chaukhutia watershed has been divided into two sets. Twelve out of twenty storm events were randomly selected for the calibration of the model parameters. Analysis of these datashows that the ARMA (1, 1) process found to best fitted. The average values of the parameters of ARMA (1, 1) (i.e. a1, b0 and b1) using the least-squares method (Equation 6) were found to be 0.60585, 0.04921 and 0.37349, respectively. Using these parameters, the derived ARMA-IUH for Chaukhutia watershed is given as follows.
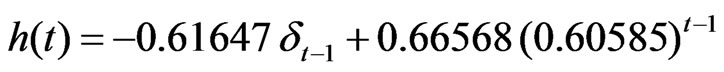 (39)
(39)
The developed ARMA-IUH has been used to compute the direct runoff hydrographs using the convolution technique. The comparisons of computed direct hydrographs along with the observed one are shown in Figure 5. The hydrograph parameter i.e. peak flow rate for all the storm events used in the analysis are given in Table 3. The average estimated values of two statistical criteria (i.e. CE and EP) are given in Table 2.
4.1. Comparison of ARMA-IUH with Nash-IUH
The validity of the proposed approach has been tested by comparing the results obtained through the Nash-IUH Model (Equation 34). For this purpose, the shape parameter (i.e. n) has been estimated adopting the procedure given by Wu et al. (1964) and time to peak (i.e. tp) has been obtained from the available storm event data of the two hilly watersheds. The calibration set of data have been used to estimate the value of n. The average estimated values of shape parameter n and the time to peak tp for Arki and Chaukhutia watersheds were determined to be 3.75 and 1.50 hours and 5.307 and 2.00 hours, respectively. Finally the obtained relationship of IUH for Arki watershed using Equation (34) is obtained as follows.
 (40)
(40)
In a similar fashion, the relationship obtained to define the Nash’s IUH (Equation 34) for Chaukhutia watershed is given as follows.
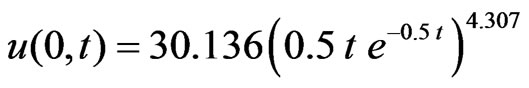 (41)
(41)
The derived relationships of instantaneous unit hydrographs using Nash model have been used to compute the direct runoff hydrographs for the available storm events of the two hilly watersheds. The comparison of the resulting direct runoff hydrographs from Nash model with the observed direct runoff hydrographs along with the DRH obtained from ARMA-IUH are shown in Figures 4 and 5 for Arki and Chaukhutia watersheds, respectively. The hydrograph parameter i.e. peak flow rate for all the storm events used in the analysis are given in Tables 1 and 3. Along with the visual assessment of proposed model, the statistical criteria (i.e. CE and EP) have been used and the average estimated values of these errors are given in Table 2.
5. Summary and Conclusions
In the present study, an attempt has been made to seek the applicability of linear theory on the complex hilly watersheds. For this purpose, transfer function derived from the ARMA type difference equation has been used for the derivation of IUH applying the Z-transform technique. The proposed ARMA-IUH has been used for computation of direct runoff hydrographs for two hilly watersheds viz. Arki and Chaukhutia watersheds. Further, the superiority of the proposed approach has been tested by comparing the responses obtained from the Nash-IUH. From the present investigation, following conclusion can be drawn.
1) Since, both the models have been developed from the linear theory concepts, i.e. ARMA-IUH is derived from the transfer function of the linear ARMA type difference equation and Nash-IUH was derived from the cascade of linear reservoirs, therefore, it is clear that the concept of linear theory is applicable to the hilly watersheds of complex hydrologic system.
2) It has been clearly observed from the Figures 4 and 5 as well as from Tables 1 through 3 that the proposed ARMA-IUH reproduced responses very close to the observed responses in comparison to that of Nash-IUH.
REFERENCES
- S. K. Spolia and S. Chander, “Modeling of surface runoff systems by an ARMA model,” Journal of Hydrology, Vol. 22, pp. 317–332, 1974.
- J. E. Nash, “The forms of the instantaneous unit hydrograph,” International Association of Science and Hydraulics Division, Proceedings of the American Society of Civil Engineers (ASCE), Vol. 104 (HY 2), pp. 262–276, 1957.
- K. M. O’Connor, “A discrete linear cascade model for hydrology,” Journal of Hydrology, Vol. 29, pp. 203–242, 1976.
- K. M. O’Connor, “Derivation of discretely coincident forms of continuous linear time-invariant models using the transfer function on approach,” Journal of Hydrology, Vol. 59, pp. 1–48, 1982.
- G. T. Wang and K. Wu, “The unit-step function response for several hydrological conceptual models,” Journal of Hydrology, Vol. 62, pp. 119–128, 1983.
- G. T. Wang, V. P. Singh, and F. X. Yu, “A rainfall-runoff model for small watersheds,” Journal of Hydrology, Vol. 138, pp. 97–117, 1992.
- L. K. Sherman, “Stream flow from rainfall by the unit-graph method,” Eng. News Rec., Vol. 108, pp. 501–505, 1932.
- J. E. Nash, “Systematic determination of unit hydrograph parameters,” Journal of Geophysical Research, Vol. 64, No. 1, pp. 111–115, 1959.
- J. C. Dooge, “A general theory of the unit hydrograph,” Journal of Geophysical Research, Vol. 64, No. 2, pp. 241–256, 1959.
- J. C. Dooge, “Linear theory of hydrologic Systems,” Technical Bulletin No. 1468, U.S. Department of Agriculture, Agricultural Research Service, Washington, D.C., 1973.
- V. P. Singh, “Hydrologic Systems: Rainfall-Runoff Modelling,” Vol. I, Prentice Hall, Englewood Cliffs, New Jersey, 1988.
- J. E. Turner, J. C. I. Dooge, and T. Bree, “Deriving the unit hydrograph by root selection,” Journal of Hydrology, Vol. 110, pp. 137–152, 1989.
- K. K. Singh, “Flood estimation for selected Indian river basins,” An unpublished Ph.D. Thesis, Kurukshetra University, Kurukshetra, India, 1997.
- C. S. P. Ojha, K. K. Singh, and D. V. S. Verma, “Single-storm runoff analysis using Z-transform,” Journal of Hydrologic Engineering, American Society of Civil Engineers (ASCE), Water Resources Engineering Division, Vol. 4, No. 1, pp. 80–82, 1999.
- R. K. Rai, M. K. Jain, S. K. Mishra, C. S. P. Ojha, and V. P. Singh, “Another look at Z-transform for deriving the unit impulse response function,” Water Resources Management, Vol. 21, No. 11, pp. 1829–1848, 2007.
- G. E. P. Box and G. M. Jenkins, “Time series analysis: Forecasting and control,” Revised Edition, Holden Day, San Francisco, California, 1976.
- V. T. Chow, “Hydrologic modeling – The seventh John R. Freeman memorial lecture,” Proceeding of Boston Society of Civil Engineers, Vol. 60, No. 5, pp. 1–27, 1972.
- E. J. Muth, “Transform Methods, with applications to engineering and operations research,” Prentice-Hall Inc., Englewood Cliffs, New Jersey, 1977.
- A. Gelb, Applied Optimal Estimation, MIT Press, Cambridge, Mass, 1974.
- G. T. Wang and Y. S. Yu, “Estimation of parameters of the discrete, linear, input-output model,” Journal of Hydrology, Vol. 85, pp. 15–30, 1986.
- I. P. Wu, J. W. Delleur, and M. H. Diskin, “Determination of peak discharge and design hydrographs for small watersheds in Indiana,” Bulletin Indiana Flood Control Resources Commission at Purde University, 1964.
- L. N. Singh and R. S. Rana, “Indigenous flora and soil-water conservation practices in Kandi region of Himachal Pradesh,” Directorate of Research, Himachal Pradesh Krishi Vishvavidyalaya, H. P. Palampur, 1998.
- V. T. Chow, Handbook of Applied Hydrology, McGraw Hill, New York, U.S.A., 1964.
- V. T. Chow, D. R. Maidment, and L. W. Mays, “Applied Hydrology,” McGraw-Hill Book Company, New York, 1988.
- J. E. Nash and J. V. Sutcliffe, “River flow forecasting through conceptual model. Part-3 A discussion of the principle,” Journal of Hydrology, Vol. 10, pp. 282–290, 1970.


