Journal of Software Engineering and Applications
Vol.5 No.7(2012), Article ID:19722,10 pages DOI:10.4236/jsea.2012.57051
Improving Class Cohesion Measurement: Towards a Novel Approach Using Hierarchical Clustering
![]()
Software Engineering Research Laboratory, Department of Mathematics and Computer Science, University of Quebec, Trois-Rivières, Canada.
Email: {Lazhar.Sadaoui, Mourad.Badri, Linda.Badri}@uqtr.ca
Received April 26th, 2012; revised May 23rd, 2012; accepted May 31st, 2012
Keywords: Object-Oriented; Classes; Cohesion; Similarity; Clustering; Metrics and Empirical Evaluation
ABSTRACT
Class cohesion is considered as one of the most important object-oriented software attributes. High cohesion is, in fact, a desirable property of software. Many different metrics have been suggested in the last several years to measure the cohesion of classes in object-oriented systems. The class of structural object-oriented cohesion metrics is the most investigated category of cohesion metrics. These metrics measure cohesion on structural information extracted from the source code. Empirical studies noted that these metrics fail in many situations to properly reflect cohesion of classes. This paper aims at exploring the use of hierarchical clustering techniques to improve the measurement of cohesion of classes in object-oriented systems. The proposed approach has been evaluated using three particular case studies. We also used in our study three well-known structural cohesion metrics. The achieved results show that the new approach appears to better reflect the cohesion (and structure) of classes than traditional structural cohesion metrics.
1. Introduction
Class cohesion is considered as one of the most important object-oriented (OO) software attributes. It is used to assess the design quality of classes. Class cohesion (more specifically, functional cohesion) is defined as the degree of relatedness between members of a class. In OO systems, a class should represent a single logical concept, and not to be a collection of miscellaneous features. OO analysis and design methods promote a modular design by creating high cohesive classes. However, improper assignment of responsibilities during the design phase can produce low cohesive classes with unrelated members. The reasoning is that such (poorly designed) classes will be difficult to understand, to test and to maintain.
Many different metrics have been suggested in the last several years to measure the cohesion of classes in OO systems. The class of structural cohesion metrics is the most investigated category of cohesion metrics. In this paper, we are focusing on this category of cohesion metrics. These metrics measure cohesion on structural information extracted from the source code. Although there have been several empirical studies performed on these metrics, no consensus has yet been reached as to which of these metrics best measures cohesion [1]. Furthermore, studies have noted that most of these metrics fail in many situations to properly reflect cohesion of classes [2-5]. Major existing structural cohesion metrics can give cohesion values that do not reflect actually the disparity of the code of a given class. These metrics, in fact, capture some links (from a structural point of view) between parts of code that can be conceptually unrelated. As stated by Marcus et al. in [5], these metrics give no clues whether a class is cohesive from a conceptual point of view (implements one or more concepts, for example). These weaknesses can lead, indeed, in various situations to some inconsistencies between the computed values of cohesion and the intuitively expected ones [3,4]. As a result, these metrics may not be completely reliable to be used to detect effectively weaknesses in the design (assignment of disparate roles to classes for example), or identify refactoring opportunities. The debate on cohesion metrics still continues and new definitions are proposed [3,5-14].
Existing cohesion metrics are directly or indirectly based on observations of the attributes referenced by the methods. The assessment of cohesion of classes is based on the notion of similarity between methods. Clustering (or unsupervised classification) methods are concerned with grouping objects based on their interrelationships or similarity [15]. Clustering is a data mining activity that aims to partition a given set of objects into groups (or clusters) such that objects within a group would have high similarity to each other and low similarity to objects in other groups [16-18]. The inferring process is carried out with respect to a set of relevant characteristics of the analyzed objects [18]. Clustering techniques have been widely used to support various software reengineering activities such as system partitioning [19], architecture recovery [20] and program restructuring [15,21-25]. Clustering techniques have also been used more recently in the area of aspect mining [18,26-30].
This paper aims at exploring the use of clustering techniques to improve the measurement of cohesion of classes in OO systems. We believe, indeed, that using clustering will better reflect the structure and the design quality of classes. Clustering provides, in fact, a natural way for identifying clusters of related methods based on their similarity. The paper proposes a new approach to measure the cohesion of individual classes within an OO system based on hierarchical clustering. The proposed approach has been evaluated using three particular case studies taken from the literature. We also used in our study three well-known structural cohesion metrics: LCOM [31], LCOM* [32] and TCC [33]. The achieved results show that the new approach appears to better reflect the cohesion (and structure) of classes than traditional structural cohesion metrics.
The rest of the paper is organized as follows: Section 2 presents a brief survey on major class cohesion metrics. Section 3 introduces the new approach we propose for the measurement of cohesion of classes in OO systems. Section 4 gives a simple example of application of our approach. Section 5 presents the case studies we used to evaluate our approach. Finally, Section 6 presents some conclusions and future research directions.
2. Object-Oriented Cohesion Metrics
Many metrics have been proposed in order to measure class cohesion in OO systems. The argument over the most meaningful of those metrics continues to be debated [8]. Major of proposed cohesion metrics are based on the notion of similarity between methods, and usually capture cohesion in terms of connections between members of a class. Based on the underlying information used to measure the cohesion of a class, there exist different classes of cohesion metrics [5]: structural metrics [31-36], semantic metrics [5,9,37], information entropy-based metrics [38], slice-based metrics [11], metrics based on data mining [39] and metrics for specific types of applications [40]. The class of structural cohesion metrics is the most investigated category of cohesion metrics. Structural cohesion metrics measure cohesion on structural information extracted from the source code. These metrics present, however, some differences in the definition of the relationships between members of a class. A class is more cohesive when a larger number of its instance variables are referenced by a method (LCOM* [32], Coh [34]), or a larger number of methods pairs share instance variables (LCOM1, LCOM2 [31], LCOM3 [36], LCOM4 [35], Co [35], TCC and LCC [33], DCD and DCI [41]). Several studies using the Principal Component Analysis technique have been conducted in order to understand the underlying orthogonal dimensions captured by some of these metrics [1,5,34,42]. Briand et al. [34] developed a unified framework for cohesion measurement in OO systems that classifies and discusses several cohesion metrics. Development of metrics for class cohesion assessment still continues [3,5-14,37].
3. Clustering Based Cohesion Measurement
3.1. Introduction
Clustering aims to differentiate groups inside a given set of objects. The resulting groups (clusters), distinct and non-empty, are to be built so that the objects within each cluster are more closely related to one another than objects assigned to different clusters. The clustering process is based on the notion of similarity (or dissimilarity) between the objects. The similarity between two objects x and y can be derived from the following measure [43]:
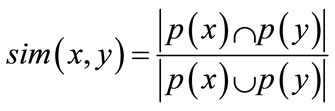 (1)
(1)
where p(x) and p(y) are the properties of the objects x and y respectively. The distance measure used for discriminating objects express the dissimilarity between them. A possible measure of distance can be defined as follows:
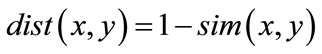 (2)
(2)
The generic concept of similarity (and dissimilarity) is presented in Bunge’s Ontology [44]. These concepts were first used in the area of OO software measurement by Chidamber & Kemerer [31]. In this paper, we are focussing only on hierarchical clustering. The hierarchical clustering methods represent a major class of clustering techniques [18]. There are two styles of hierarchical clustering algorithms: bottom-up and top-down. In our work, we use as a first attempt the bottom-up approach. Given a set of n objects, the bottom-up methods begin with n singletons (sets with one element), merging them until a single cluster is obtained. At each step, the most similar two clusters are chosen for merging [18]. The hierarchical clustering algorithm is implemented in several statistical analysis tools. In our case, we used the one integrated in XLSTAT1, a software for statistical and data analysis for Microsoft Excel.
3.2. Model Definition
In our approach, the objects to classify are the attributes and the methods members of the class. We focus, however, on the connectivity between methods. The resulting clusters are to be built so that the methods within each cluster are more closely related to one another than methods assigned to different clusters. Let C be a class. Let M = {m1, m2, ∙∙∙, mn} be the set of methods of the class and A = {a1, a2, ∙∙∙, ak} be the set of its attributes. Let p(mi) be the set of properties of the method mi, which includes the attributes of the class C referenced by the method mi and the methods of the class C invoked directly by the method mi. Let p(ai) be the set of properties of the attribute ai, which includes the methods of the class C using directly the attribute ai. The development of our model includes the following three main steps.
3.2.1. Constructing the Entities-Properties Matrix
Let EP be the entities-properties matrix, which represents the properties of the entities (attributes and methods) of the class C. This matrix is a binary square matrix (n + k)*(n + k), where n is the number of methods and k the number of attributes of the class C. It models the different relationships between the members of the class. There is a method-attribute relationship between a method mi and an attribute aj, if the attribute appears in the body of this method (EP(mi, aj) = 1 and EP(aj, mi) = 1). There is a method-method relationship between a method mi and a method mk if the method mk is invoked directly by the method mi (EP(mi, mk) = 1).
3.2.2. Performing a Hierarchical Clustering Algorithm
The EP matrix is provided as input for the hierarchical clustering algorithm of the XLSTAT tool in order to obtain multiple nested partitions of the entities of the class as a hierarchical tree. We used in our approach the Jaccard coefficient as similarity measure. The Jaccard metric seems to be the most intuitive for software entities. Moreover, as mentioned above, we used in our approach the bottom-up hierarchical clustering algorithm of XLSTAT. Given a set of n entities, the bottom-up algorithm begins with n singletons (sets with one method), merging them until a single cluster is obtained. At each step, the most similar two clusters are chosen for merging.
3.2.3. Determining the Optimal Number of Clusters
Determining the optimal number of clusters is equivalent to determining the optimal level of truncation of the hierarchical tree. The truncation criterion is often based on heuristics. There are several methods to determine the optimal number of clusters. Earlier works in this area include the rule of Hartigan [45], the indexes of Krzanowski and Lai [46] and the silhouette statistic suggested by Kaufman et al. [47]. More recent works include the “gap” method proposed by Tibshirani et al. [48] and the method of resampling based on prediction [49]. The comparison of these approaches is out of the scope of this paper. As our work is exploratory by nature, we used the automatic truncation of the hierarchical tree, integrated in XLSTAT. It determines the optimal number of clusters of the analyzed class. The approach adopted by the XLSTAT tool to determine the optimal number of clusters is based on entropy. Entropy measures how elements are distributed or assigned in each cluster. Low entropy corresponds to a better clustering.
3.3. Cohesion Measurement
Let C be a class. Let M = {m1, m2, ∙∙∙, mn} be the set of its methods. The number of pairs of methods is: [n∙(n − 1)/2]. Consider the undirected graph GC, resulting from the clustering, where the nodes represent the methods of the class C. There is an arc between two nodes if the corresponding methods belong to the same cluster. As mentioned earlier, from the point of view of clustering, each cluster contains only related methods. Therefore, all the pairs of methods within a cluster are related. Let EC be the set of connected components of the graph GC. It represents, in fact, the set of clusters. Let EA be the set of arcs in the graph GC. The approach we propose allows the calculation of two metrics:
• COHCL = |EA|/[n∙(n – 1)/2] Є [0, 1]. It gives the percentage of pairs of methods that are related.
• NCL = |EC|. It gives the number of clusters in the class. The NCL metric takes values greater than or equal to 1.
3.4. Interpretation
The COHCL metric gives, in fact, the degree of relatedness between the methods of the class. A low value of COHCL indicates that the methods of the class are poorly related, in spite of the fact that they may constitute a single group of related members. However, it may also indicate (in an implicit way) the existence of several (two or more) groups of connected methods. In fact, these different groups may reflect, in some cases, the disparateness of the roles (more than one concept) assigned to a class. In this case, we will be able to determine it only by reviewing the code. A low value of COHCL may be interpreted in different ways and reveals, in fact, various situations: 1) the methods of the class constitute a single group of connected methods but are however weakly related; 2) the roles assigned to the class are disparate; and 3) possibly both.
In practice, we may have two classes with comparable values of cohesion (let us assume 0.50): In the case of the first class, the methods are weakly related but constitute a single group of connected methods, and in the case of the second class the roles assigned to the class are unrelated which will be reflected in its implementation. Without the NCL metric, it’s only by reviewing the code that we will be able to determine it. The metric NCL (as an indicator of the disparity of the concepts implemented by the class) reveals in an explicit way this problem. Together, the two metrics reflect in several situations some design problems (weaknesses in the design). The case studies presented in Section 5 illustrate this dimension. The COHCL metric indicates the cohesion degree of the class. The NCL (taken with COHCL) helps in interpreting the results.
4. A Simple Example of Application
In order to better understand our approach, we present in this section a simple example of application. Consider the class C with: M(C) = {m1, m2, m3, m4, m5, m6, m7} the set of its methods and A(C) = {i1, i2, i3, i4, i5} the set of its attributes (instance variables). Let Uj be the set of attributes and methods used by the method mj. Suppose that the values of these sets in our example are: U1 = {i1, i2, i3, m3}, U2 = {i1, i2, m3}, U3 = {i1, i2}, U4 = {i1}, U5 = {i1, i4, i5}, U6 = {i4, i5}, and U7 = {i4}.
By applying the hierarchical clustering algorithm of XLSTAT, we obtain the dendrogram (hierarchical tree) given in Figure 1. We obtain two distinct clusters of methods (Figure 1): {m1, m2, m3, m4} and {m5, m6, m7}. All methods belonging to the same cluster are related. The graph GC modeling the connections between the methods of the class C resulting from the clustering is given in Figure 2. From the graph GC of Figure 2, we obtain: COHCL = 9/21 = 0.43 and NCL = 2.
5. Empirical Evaluation
In order to evaluate our approach, we consider as case studies three particular examples of classes (in Java) discussed in the literature in the area of maintenance, restructuring and aspect mining [50-52]. To facilitate comparison with our class cohesion measurement approach, we chose in our study three well-known structural cohesion metrics: LCOM [31], LCOM* [32] and TCC [33]. LCOM (Lack of COhesion in Methods) is defined as the number of pairs of methods in a class, having no common attributes, minus the number of pairs of methods having at least one common attribute. LCOM is set to zero when the value is negative. LCOM* is somewhat different from the LCOM metric. LCOM* is different also from the other versions of the LCOM metric proposed by Li et al. [36] and Hitz et al. [35]. It considers that cohesion is directly proportional to the number of instance variables that are referenced by the methods of a class. TCC (Tight Class Cohesion) is defined as the percentage of methods pairs, which are directly related. Two methods are directly related if they
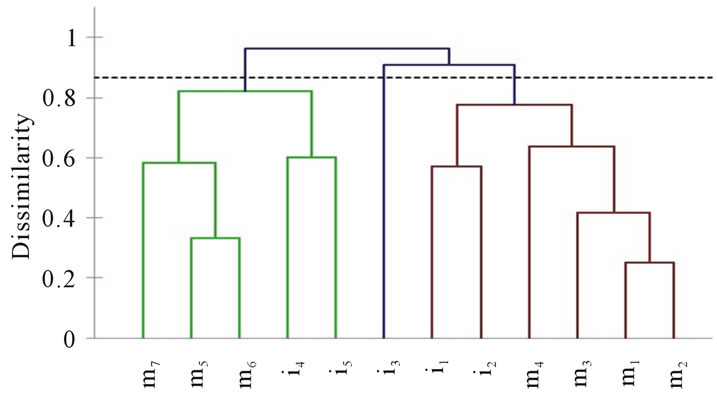
Figure 1. The dendrogram (hierarchical tree) of the class C.
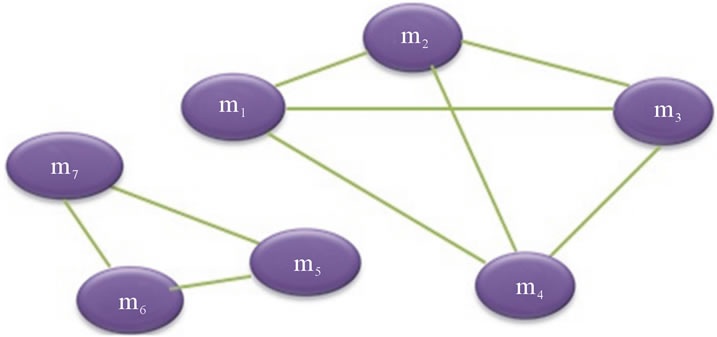
Figure 2. The graph GC corresponding to the class C.
both use either directly or indirectly a common instance variable. We used the Borland Together2 tool to compute the metrics LCOM, LCOM* and TCC. Moreover, we used the XLSTAT tool to perform clustering.
5.1. Observer Design Pattern
The Observer design pattern defines a “one to many” dependency between a subject and several observers [51]. When the subject object changes its state, all observers objects will automatically be notified and updated accordingly [53]. Figure 3 gives an OO implementation of this pattern [54]. It models a simple system of graphic figures elements in which a class Point share the same interface FigureElement with other classes. If a call to any of the methods prefixed by “set” on an object of type FigureElement is triggered, the observer object must be alerted in order to reflect the changes at the graphical representation. According to the object approach [53], the implementation usually requires that the subject (the observed object) must define a field (list) to provide mechanical registration and deregistration of interested observers (i.e. methods: attachObserver() and detachObserver()) and a notification method (i.e. informObserver ()).
From Figure 3 we can clearly see the limits of the object paradigm due to the duplication and tangling of code that were inevitable. Indeed, the class Point (and other classes not mentioned here) must integrate all the code fragment relating to the maintenance and reporting of observed objects in their implementations (pieces of code

Figure 3. An example of a partial implementation of the observer design pattern [54].
labelled C and D in Figure 3). Furthermore, we note the duplication resulting from calling the method informObservers() in order to report the change in an attribute to the observer object (piece of code labelled B). Moreover, we note the tangling of code in the same class (Point), between its main functionality (labelled A) mixed with the code for the notification mechanism of the observer we have described above (statements labelled B, C, D). This means that the class Point has been assigned more than one role [54]. Table 1 gives the values of the selected structural cohesion metrics. According to these values, the class is not cohesive.
By applying our approach, we obtain the dendrogram given in Figure 4. We obtain the following two clusters of methods: K1 = {setY(), setX, setXY()} and K2 = {informObserver(), attachObserver(), detachObserver()}. The three methods informObserver(), attachObserver() and detachObserver() are grouped in one cluster (K2), and the other methods i.e. setY(), setXY() and setX() are grouped in the other cluster (K1).
The graph of connections between methods, obtained after clustering, is given in Figure 5. As mentioned above, two methods classified in the same cluster are similar and therefore related. We obtain, therefore:
NCL = 2 and COHCL = 0.4.
The value of COHCL indicates that the methods of the class are weakly related. As the value of the metric NCL is equal to 2, this means that the class contains two dis-

Table 1. Values of selected structural cohesion metrics for the class Point.
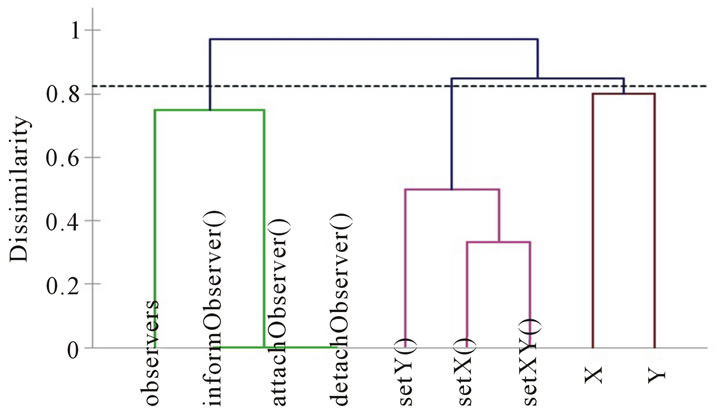
Figure 4. Dendrogram corresponding to the class Point.
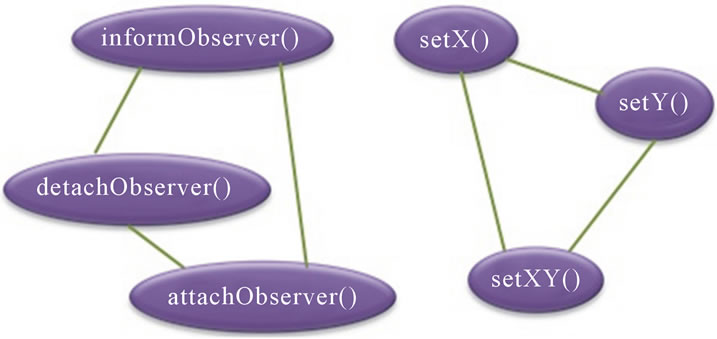
Figure 5. The graph GC corresponding to the class Point.
joint groups of connected methods (the two clusters k1 and k2). These results (COHCL and NCL) adequately reflect the structure (code) of the class given in Figure 3: two disparate roles, i.e. its primary role as point and a secondary role related to the management of the notification mechanism for observers objects. Despite the entanglement of the code on these two roles, the new approach was able to capture and isolate the related elements properly. Moreover, we note by the decomposition of clusters K1 and K2 that each cluster contains only methods concerning the same responsibility (concept). The cluster K1 includes elements of code A, while the cluster K2 includes elements of code B and C (Figure 3). The values of the metrics NCL and COHCL reflect properly the structure of the class than the structural cohesion metrics.
5.2. The Tangled Stack Class
This example is taken from [52]. It presents a class that defines the basic operations managing a stack (push, pop, check if the stack is empty or full) in addition to those related to a second functionality (display of its contents in a text field of a frame). The code of the class is shown in Figure 6. The parts of the code labelled (B, C and D) are related to the second functionality assigned to the class. Table 2 gives the values of the selected structural cohesion metrics. Metrics LCOM and TCC indicate a perfect cohesion. In contrary, the metric LCOM* indicates that the class presents a lack of cohesion (which is important according to LCOM*).
By applying our approach, we obtain the dendrogram given in Figure 7. We obtain the following two clusters of methods: K1 = {isEmpty(), isFull(), pop(), push(), top(), toString()} and K2 = {display()}. The graph of connections between methods, obtained after clustering, is given in Figure 8. We obtain the following values of cohesion: NCL = 2 and COHCL = 0.71. The value of the metric COHCL (0.71) indicates a relatively good cohesion. This is not the case for metrics TCC and LCOM, which indicate a perfect cohesion. According to the metric NCL (whose value is equal to 2), we have two disjoint groups of methods (k1 and k2).
Indeed, the class TangledStack as mentioned above has two distinct roles: its primary role as a stack and a secondary role related to the display mechanism in a GUI.
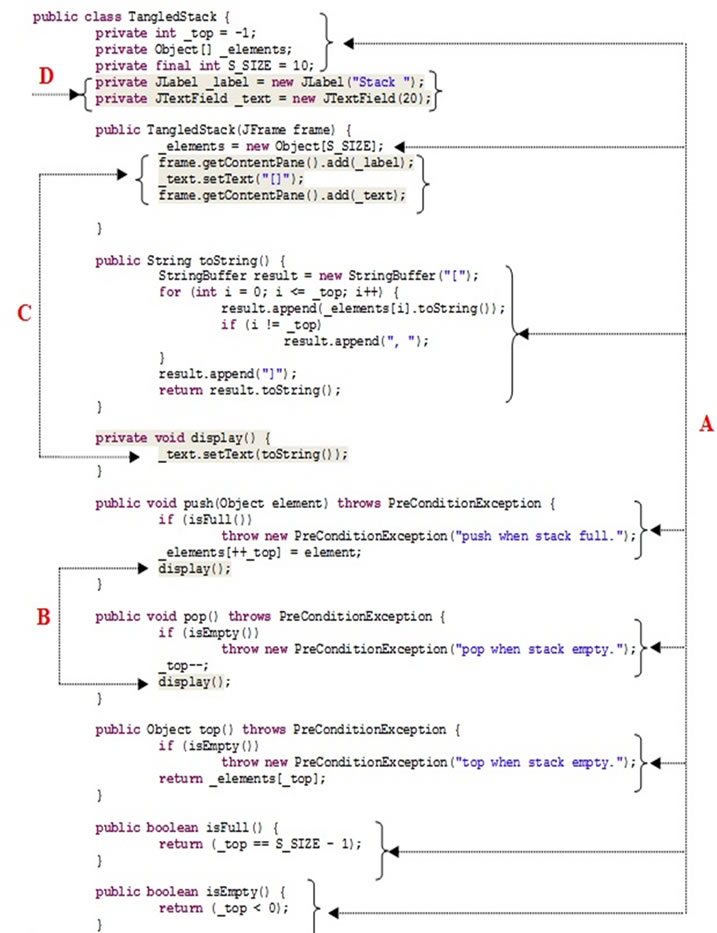
Figure 6. Code of the class TangledStack.

Table 2. Values of selected structural cohesion metrics for the class TangledStack.
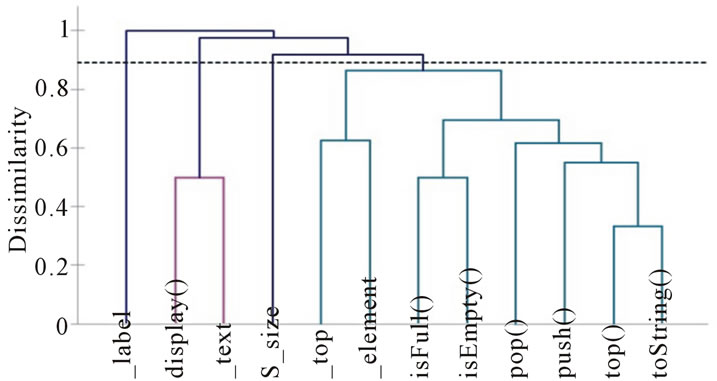
Figure 7. Dendrogram of the class TangledStack.
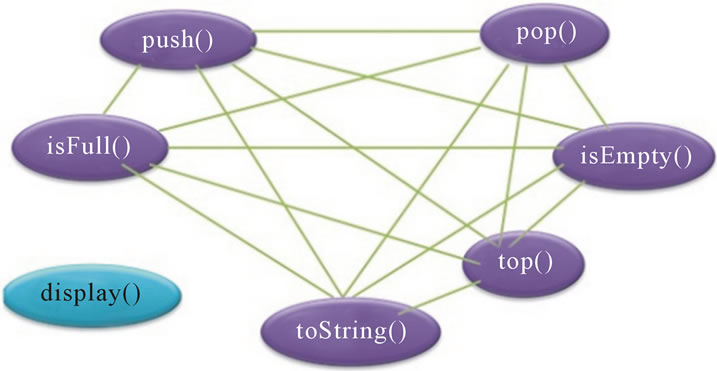
Figure 8. The graph GC corresponding to the class TangledStack.
The new approach effectively isolated the methods related to each role. Indeed, we note according to the decomposition of k1 and k2 that each cluster contains only methods relating to the same responsibility. Cluster k2 includes elements of code B (Figure 6), while cluster k1 includes the items of base code A of the standard class “Stack”. The values of the two metrics (COHCL and NCL), taken together, better illustrate the structure of the class. This is not the case with the other metrics. In the case of this example, it is also a crosscutting concern that overlaps with the main concern of the class Stack. An aspect-oriented solution was proposed by Monteiro in [52].
5.3. Chain of Responsibility Design Pattern
This example is taken from [50]. It was also discussed by Monteiro in [52]. Ideally, each class must provide a single role (contain a coherent set of responsibilities). Unfortunately, this is not always the case. It is also the case of superimposed roles as outlined by Hannemann and Kiczales in [51]. One symptom that can help to detect Double Personality in Java source code is implementation of interfaces [52]. Interfaces are a popular way to model roles in Java. When a class implements an interface modeling a role that does not relate to the class’ primary concern, the class smells of Double Personality [52].
The design pattern “Chain of Responsibility” allows to any number of classes to try to answer a query without knowing the capabilities of other classes on this query. Each time an object receives a message it can’t deal with, it delegates it to the next object in the chain. The purpose of this pattern is to create a process chain, encapsulated in objects, and to allow to propagate the call to this process in the chain, leaving to the object/process to decide whether the context is of its concern or not. Figure 9 shows a possible implementation of the Chain of Responsibility pattern by a class ColorImage.
The secondary role is modeled by the interface Chain, that all participant objects must implement (the related code of this role is shaded and referenced by labels B and C). The method addChain() adds another class to the chain of classes. The method getChain() returns the current object to which messages are sent. These two methods allow to modify the chain dynamically and to add additional classes in the middle of an existing chain [50]. The method sendToChain() sends a message to the next object in the chain.
This implementation causes a code tangling because the class has been assigned a second responsibility (handling of received messages and giving them to the following participant objects in the chain in case the current object could not handle the message). Otherwise, the class would be reduced to a very simple code just for the handling of color. Table 3 gives the values of the selected structural cohesion metrics. Metrics LCOM* and TCC indicate (is the case of this example also) a perfect
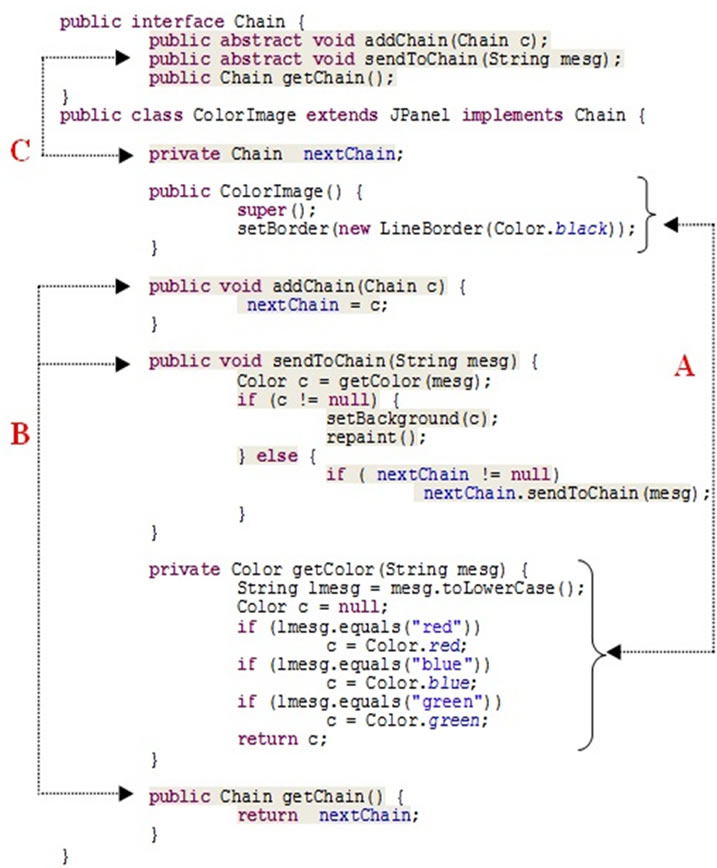
Figure 9. Example of implementation of the design pattern chain of responsibility (class ColorImage).
cohesion. In contrary, the metric LCOM indicates that the class presents a lack of cohesion.
By applying our approach, we obtain the dendrogram given in figure 10. We obtain the following two clusters of methods: K1 = {getColor()} and K2 = {addChain(), getChain(), sendToChain()}. The class ColorImage has two connected components. The graph of connections, obtained after clustering, is given in Figure 11. We obtain the following values of cohesion: NCL = 2 and COHCL = 0.5. This reveals a low cohesion in the class. Indeed, a simple inspection of the code will indicate that the class has two different roles.
Moreover, we can see by the decomposition of clusters k1 and k2 that each cluster contains only methods related to the same role. Cluster k2 includes elements of code B (Figure 11), while cluster k1 contains only elements of base code of the class ColorImage, which is the method getColor() (it means that there is no tangling of code in the same cluster). Once again, the values of the two metrics COHCL and NCL, taken together, better illustrate the structure of the class.
6. Conclusion and Future Work
This paper investigates the use of hierarchical clustering techniques to improve the measurement of cohesion of

Table 3. Values of selected structural cohesion metrics for the class ColorImage.
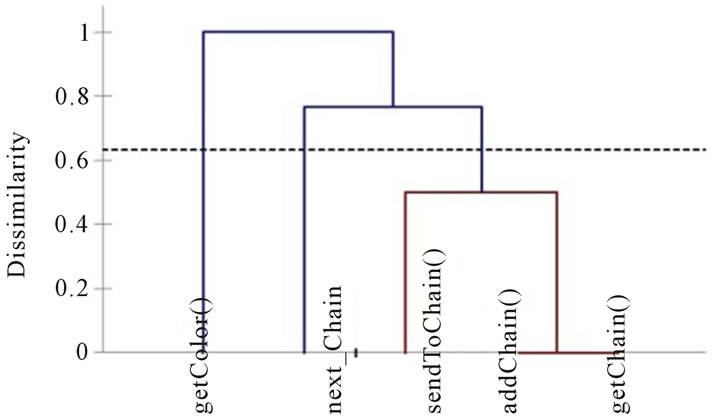
Figure 10. Dendrogram of the class ColorImage.
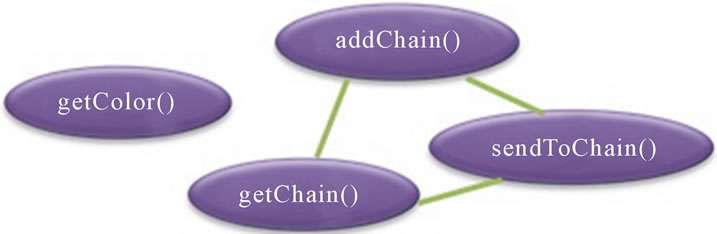
Figure 11. The graph GC corresponding to the class ColorImage.
classes in OO systems. Existing cohesion metrics are directly or indirectly based on observations of the attributes referenced by the methods. The measurement of cohesion of classes is based on the similarity between their methods. So, we used clustering to better identify clusters of related methods.
The proposed approach has been evaluated using three particular case studies taken from (maintenance, restructuring and aspect mining) literature. The achieved results show clearly that the new approach better reflects the structure and quality of the design of the evaluated classes than the selected traditional structural cohesion metrics. The approach was effectively able to detect the disparity between the roles implemented by the evaluated classes. It allows, in fact, better differentiating and classifying methods of a class into groups of related and cohesive methods. This capacity is mainly due to the potential of separation into cohesive groups offered by clustering techniques. According to the evaluated case studies and the obtained results, the new approach appears to better detect design problems, such as assigning disparate roles to a class, than traditional structural cohesion metrics.
The study performed in this paper should, however, be replicated using a large number of OO systems in order to draw more general conclusions. Indeed, the findings in this paper should be viewed as exploratory and indicative rather than conclusive. As future work, we plan to: extend the study by introducing other OO cohesion metrics, explore the use of the approach to support aspect-mining activities and finally replicate the study on data collected from a large number of OO software systems to be able to give generalized results.
7. Acknowledgements
The authors would like to acknowledge the support of this work by NSERC (National Sciences and Engineering Research Council of Canada) Grant.
REFERENCES
- L. H. Etzkorn, S. E. Gholston, J. L. Fortune, C. E. Stein, D. Utley, P. A. Farrington and G. W. Cox, “A Comparison of Cohesion Metrics for Object-Oriented Systems,” Information and Software Technology, Vol. 46, No. 10, 2004, pp. 677-687. doi:10.1016/j.infsof.2003.12.002
- H. Aman, K. Yamasaki, H. Yamada and M. T. Noda, “A Proposal of Class Cohesion Metrics Using Sizes of Cohesive Parts,” In: T. Welzer, et al., Eds., Knowledge-Based Software Engineering, IOS Press, Amsterdam, 2002, pp. 102-107.
- H. S. Chae, Y. R. Kwon and D. H. Bae, “Improving Cohesion Metrics for Classes by Considering Dependent Instance Variables,” IEEE Transactions on Software Engineering, Vol. 30, No. 11, 2004, pp. 826-832. doi:10.1109/TSE.2004.88
- H. Kabaili, R. K. Keller and F. Lustman, “Cohesion as Changeability Indicator in Object-Oriented Systems,” Proceedings of the 5th European Conference on Software Maintenance and Reengineering, Lisbon, 14-16 March 2001. doi:10.1109/CSMR.2001.914966
- A. Marcus and D. Poshyvanyk, “The Conceptual Cohesion of Classes,” Proceedings of the 21st International Conference on Software Maintenance, Budapest, 25-30 September 2005, pp. 133-142.
- L. Badri, M. Badri and G. A. Badara, “Revisiting Class Cohesion: An Empirical Investigation on Several Systems,” Journal of Object Technology, Vol. 7, No. 6, 2008, pp. 55-75. doi:10.5381/jot.2008.7.6.a1
- Z. Chen, Y. Zhou, B. Xu, J. Zhao and H. Yang, “A Novel Approach to Measuring Class Cohesion Based on Dependence Analysis,” Proceedings of the 18th International Conference on Software Maintenance, Timisoara, 12-18 September 2002.
- S. Counsell and S. Swift, “The Interpretation and Utility of Three Cohesion Metrics for Object-Oriented Design,” ACM Transactions on Software Engineering and Methodology, Vol. 15, No. 2, 2006, pp. 123-149. doi:10.1145/1131421.1131422
- A. De Lucia, R. Oliveto and L. Vorraro, “Using Structural and Semantic Metrics to Improve Class Cohesion,” Proceedings of the International Conference on Software Maintenance, Beijing, 28 September-4 October 2008.
- A. Marcus, D. Poshyvanyk and R. Ferenc, “Using the Conceptual Cohesion of Classes for Fault Prediction in Object-Oriented Systems,” IEEE Transactions on Software Engineering, Vol. 34, No. 2, 2008, pp. 287-300.
- T. M. Meyers and D. Binkley, “Slice-Based Cohesion Metrics and Software Intervention,” Proceedings of the 11th Working Conference on Reverse Engineering, Delft, 8-12 November 2004, pp. 256-265. doi:10.1109/WCRE.2004.34
- G. Woo, H. S. Chae, J. F. Cui and J. H. Ji, “Revising Cohesion Measures by Considering the Impact of Write Interactions between Class Members,” Information and Software Technology, Vol. 51, No. 2, 2009, pp. 405-417.
- Y. Zhou, B. Xu, J. Zhao and H. Yang, “ICBMC: An Improved Cohesion Measure for Classes,” Proceedings of the International Conference on Software Maintenance, Montréal, 3-6 October 2002.
- Y. Zhou, L. Wen, J. Wang, Y. Chen, H. Lu and B. Xu, “DRC: Dependence-Relationships-Based Cohesion Measure for Classes,” Proceedings of the 10th APSEC, Chiang Mai, 10-12 December 2003.
- T. A. Wiggerts, “Using Clustering Algorithms in Legacy Systems Remodularization,” Proceedings of the 4th Working Conference on Reverse Engineering, Washington, 6-8 October 1997. doi:10.1109/WCRE.1997.624574
- I. G. Czibula, G. Czibula and G. S. Cojocar, “Hierarchical Clustering for Identifying Crosscutting Concerns in Object-Oriented Software Systems,” Proceedings of the 4th Balkan Conference in Informatics, Thessaloniki, 17-19 September 2009.
- J. Han and M. Kamber, “Data Mining: Concepts and Techniques,” Morgan Kaufmann Publishers, Waltham, 2001.
- G. S. Moldovan and G. Serban, “Aspect Mining Using a Vector Space Model Based Clustering Approach,” Proceedings of Linking Aspect Technology and Evolution Workshop, Bonn, 20 March 2006, pp. 36-40.
- N. Anquetil, C. Fourrier and T. Lethbridge, “Experiments with Hierarchical Clustering Algorithms as Software Remodularization Methods,” Proceedings of the Working Conference on Reverse Engineering, Benevento, 23-27 October 1999.
- C.-H. Lung, “Software Architecture Recovery and Restructuring through Clustering Techniques,” Proceedings of the 3rd International Software Architecture Workshop, Orlando, 1-5 November 1998, pp. 101-104.
- I. G. Czibula and G. Czibula, “A Partitional Clustering Algorithm for Improving the Structure of Object-Oriented Software Systems,” Studia Universitatis Babes-Bolyai, Series Informatica, Vol. 3, No. 2, 2008.
- C. Lung, M. Zaman and A. Nandi, “Applications of Clustering Techniques to Software Partitioning, Recovery and Restructuring,” Journal of Systems and Software, Vol. 73, No. 2, 2004, pp. 227-244. doi:10.1016/S0164-1212(03)00234-6
- C.-H. Lung and M. Zaman, “Using Clustering Technique to Restructure Programs,” Proceedings of the International Conference on Software Engineering Research and Practice, Las Vegas, 21-24 June 2004, pp. 853-860.
- G. Serban and I. G. Czibula, “Restructuring Software Systems Using Clustering,” Proceedings of the 22nd International Symposium on Computer and Information Sciences, Ankara, 7-9 November 2007. doi:10.1109/ISCIS.2007.4456872
- G. Snelting, “Software Reengineering Based on Concept Analysis,” Proceedings of the European Conference on Software Maintenance and Reengineering, Zurich, 29 February-3 March 2000, pp. 1-8.
- G. S. Cojocar, G. Czibula and I. G. Czibula, “A Comparative Analysis of Clustering Algorithms in Aspect Mining,” Studia Universitatis Babes-Bolyai, Series Informatica, Vol. 4, No. 1, 2009.
- L. He and H. Bai, “Aspect Mining Using Clustering and Association Rule Method,” International Journal of Computer Science and Network Security, Vol. 6, No. 2A, 2006, pp. 247-251.
- G. Serban and G. S. Moldovan, “A New k-Means Based Clustering Algorithm in Aspect Mining,” Proceedings of 8th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, 26-29 September 2006, pp. 69-74. doi:10.1109/SYNASC.2006.5
- D. Shepherd and L. Pollock, “Interfaces, Aspects, and Views,” Proceedings of Linking Aspect Technology and Evolution Workshop, Chicago, 15 March 2005.
- D. Zhang, Y. Guo and X. Chen, “Automated Aspect Recommendation through Clustering-Based Fan-In Analysis,” Proceedings of the 23rd IEEE/ACM International Conference on Automated Software Engineering, l’Aquila, 15-19 September 2008, pp. 278-287.
- S. R. Chidamber and C. F. Kemerer, “A Metrics Suite for Object Oriented Design,” IEEE Transactions on Software Engineering, Vol. 20, No. 6, 1994, pp. 476-493. doi:10.1109/32.295895
- B. Henderson-Sellers, “Software Metrics,” Prentice Hall, Upper Saddle River, 1996.
- J. M. Bieman and B. K. Kang, “Cohesion and Reuse in an Object-Oriented System,” Proceedings of the Symposium on Software Reusability, Seattle, 23-30 April 1995, pp. 259-262. doi:10.1145/211782.211856
- L. C. Briand, J. Daly and J. Wusr, “A Unified Framework for Cohesion Measurement in Object-Oriented Systems,” Empirical Software Engineering, Vol. 3, No. 1, 1998, pp. 67-117. doi:10.1023/A:1009783721306
- M. Hitz and B. Montazeri, “Measuring Coupling and Cohesion in Object-Oriented Systems,” Proceeding of the International Symposium on applied Corporate Computing, Monterrey, 25-27 October 1995, pp. 25-27.
- W. Li and S. Henry, “Object-Oriented Metrics That Predict Maintainability,” Journal of Systems and Software, Vol. 23, No. 2, 1993, pp. 111-122. doi:10.1016/0164-1212(93)90077-B
- L. Etzkorn and H. Delugach, “Towards a Semantic Metrics Suite for Object-Oriented Design,” Proceedings of the 34th International Conference on Technology of Object-Oriented Languages and Systems, Xi’an, 30 October- 4 November 2000, pp. 7-80.
- E. B. Allen, T. M. Khoshgoftaar and Y. Chen, “Measuring Coupling and Cohesion of Software Modules: An Information-Theory Approach,” Proceedings of 7th International Software Metrics Symposium, London, 4-6 April 2001, pp. 124-134.
- C. Montes de Oca and D. L. Carver, “Identification of Data Cohesive Subsystems Using Data Mining Techniques,” Proceedings of International Conference on Software Maintenance, Bethesda, 16-19 November 1998, pp. 16-23.
- E. S. Cho, C. J. Kim, D. D. Kim and S. Y. Rhew, “Static and Dynamic Metrics for Effective Object Clustering,” Proceedings of Asia Pacific International Conference on Software Engineering, IEEE Computer Society, Washington, 1998, pp. 78-85.
- L. Badri and M. Badri, “A Proposal of a New Class Cohesion Criterion: An Empirical Study,” Journal of Object Technology, Vol. 3, No. 4, 2004, pp. 145-159. doi:10.5381/jot.2004.3.4.a8
- H. S. Chae, Y. R. Kwon and D. H. Bae, “A Cohesion Measure for Object-Oriented Classes,” Software Practice and Experience, Vol. 30, No. 12, 2000, pp. 1405-1431. doi:10.1002/1097-024X(200010)30:12<1405::AID-SPE330>3.0.CO;2-3
- F. Simon, S. Löffler and C. Lewerentz, “Distance Based Cohesion Measuring,” Proceedings of the 2nd European Software Measurement Conference, Amsterdam, 4-8 October 1999.
- M. Bunge, “Ontology I: The Furniture of the World,” Treatise on Basic Philosophy, Vol. 3, D. Reidel Publishing Company, Dordrecht, 1977.
- J. Hartigan, “Clustering Algorithms,” Wiley, New York, 1975.
- W. J. Krzanowski and Y. T. Lai, “A Criterion for Determining the Number of Groups in a Data Set Using Sum of Squares Clustering,” Biometrics, Vol. 44, 1988, pp. 23- 34. doi:10.2307/2531893
- L. Kaufman and P. J. Rousseuw, “Finding Groups in Data: An Introduction to Cluster Analysis,” Wiley-Interscience, New York, 1990. doi:10.1002/9780470316801
- R. Tibshirani, G. Walther and T. Hastie, “Estimating the Number of Data Clusters via the Gap Statistic,” Journal of the Royal Statistical Society B, Vol. 63, No. 2, 2001, pp. 411-423.
- S. Dudoit and J. Fridlyand, “A Prediction-Based Resampling Method for Estimating the Number of Clusters in a Dataset,” Genome Biology, Vol. 3, No. 7, 2002, Research 0036.1-0036.21.
- J. Cooper, “Java Design Patterns: A Tutorial,” Addison-Wesley, New York, 2000.
- J. Hannemann and G. Kiczales, “Design Pattern Implementation in Java and AspectJ,” Proceedings of the 17th Annual Conference on Object-oriented Programming Systems, Languages and Applications, Seattle, 4-8 November 2002, pp. 161-173.
- M. J. T. Monteiro, “Refactorings to Evolve Object-Oriented Systems with Aspect-Oriented Concepts,” Ph.D. Thesis, Universidade do Minho, Minho, 2005.
- E. Gamma, et al., “Design Patterns—Elements of Reusable Object-Oriented Software,” Addison-Wesley, New York, 1994
- St. Hanenberg and R. Unland, “A Proposal for Classifying Tangled Code,” 2nd AOSD-GI Workshop, Bonn, 21- 22 February 2002.
NOTES
1Hhttp://www.xlstat.com/U
2HUhttp://www.borland.com/U

