Journal of Biomedical Science and Engineering
Vol.10 No.05(2017), Article ID:76161,14 pages
10.4236/jbise.2017.105016
An Analytical Solution to Neumann-Type Mixed Boundary Poiseuille Microfluidic Flow in Rectangular Channel Cross-Sections (Slip/No-Slip) including a Numerical Technique to Derive It
Christiane Richter, Frederik Kotz, N. Keller, Tobias M. Nargang, Kai Sachsenheimer, Dorothea Helmer, Bastian E. Rapp*
Karlsruhe Institute of Technology (KIT), Istitute of Microstructure Technology (IMT), Eggenstein-Leopoldshafen, Germany

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 20, 2017; Accepted: May 13, 2017; Published: May 16, 2017
ABSTRACT
In most microfluidic applications, pressure-driven Poiseuille flow in a contained cross-section with no-slip boundary conditions is the underlying fluid- mechanical model. Solutions for this problem exist for many known cross- sections. We have recently demonstrated a simple method to solve the relevant Poisson equation using a finite difference scheme in a spreadsheet analysis tool such as Microsoft Excel. The numerical solutions obtained from such a spreadsheet are close-to-exact to the analytical solutions with errors on the order of only a few percent. However, there are numerous applications in microfluidics for which the no-slip boundary condition is not valid. Examples include drag-reducing air-retaining surfaces as well as open-channel flow. For these scenarios few to no analytical models exist. In this paper, we derive an analytical model for mixed boundary conditions (slip/no-slip) in two dimensions in a rectangular channel cross-section. We also demonstrate that the equivalent numerical solution can be derived conveniently by adaption of the spreadsheet. In general, mixed boundary-type flow scenarios are especially difficult to solve analytically whereas numerical solutions can be derived using Microsoft Excel within seconds.
Keywords:
Microfluidics, Numerics, Navier-Stokes Equation, Slip Condition, No-Slip Condition

1. Introduction
Many effects in microfluidics rely on the sound understanding of the underlying fluid mechanics of the flow. Compared to macroscopic and high Reynolds- number flows, the flow cases in microfluidics are usually significantly simpler due to the fact that most microfluidic applications are within the strictly laminar flow regime and the flow is assumed to be parallel. In addition, assuming a flow to be stationary and fully-developed allows dropping additional terms of the Navier-Stokes equation. The remaining, simplified version of the Navier-Stokes equation is a Poisson equation. As we have demonstrated recently, this equation can be solved using a numerical scheme based on a finite difference approach. This approach can be implemented conveniently in a spreadsheet analysis tool such as Microsoft Excel [1] . We have shown that the numerical solutions derived compare well to the analytical solutions for various flow cases including the flow in circular cross-sections (Hagen-Poiseuille flow) as well as in rectangular channel profiles. One of the most important points to consider when implementing a numerical scheme is the behaviour of the boundaries of the computational domain. In all of the cases discussed the flow was assumed to exhibit no-slip behaviour on the boundary, i.e., the flow velocity on the boundaries was assumed to be zero. This type of boundary condition is referred to as Dirichlet-type boundary condition where the value of the dependent variable (in this case the flow velocity 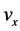 parallel to the axis of the channel) on the boundary is assumed to have a distinct value. However, many cases in microfluidics require Neumann-type boundary condition where the gradient of the dependent variable, i.e., the first derivative of the velocity profile, is assumed to obtain a certain value. The most important cases of Neumann-type boundary conditions are open surfaces where the shear stress of the fluid must be zero. This translates to a Neumann-type boundary condition where the gradient of the velocity profile is zero. Examples of this flow case include Couette flow as used, e.g., in plate/cone viscometers. Traditionally, slip-flow is an effect usually studied only at elevated temperatures [2] [3] . However, there are many cases in microfluidics where slip flow occurs. Examples include, e.g., in air-retaining drag-reducing Salvinia-type [4] [5] and superhydrophobic [6] surfaces with [7] or without surface textures [5] . In many of these cases, the flow exhibits mixed boundary conditions with one surface showing slip boundary behaviour whereas the opposing surface shows no-slip boundary behaviour. Deriving analytical solutions for flow cases exhibiting Neumann-type boundary conditions or even mixed boundary conditions is significantly more difficult. These cases are usually studied numerical solver packages [8] , lattice-Boltzmann or molecular dynamics simulations [9] .
parallel to the axis of the channel) on the boundary is assumed to have a distinct value. However, many cases in microfluidics require Neumann-type boundary condition where the gradient of the dependent variable, i.e., the first derivative of the velocity profile, is assumed to obtain a certain value. The most important cases of Neumann-type boundary conditions are open surfaces where the shear stress of the fluid must be zero. This translates to a Neumann-type boundary condition where the gradient of the velocity profile is zero. Examples of this flow case include Couette flow as used, e.g., in plate/cone viscometers. Traditionally, slip-flow is an effect usually studied only at elevated temperatures [2] [3] . However, there are many cases in microfluidics where slip flow occurs. Examples include, e.g., in air-retaining drag-reducing Salvinia-type [4] [5] and superhydrophobic [6] surfaces with [7] or without surface textures [5] . In many of these cases, the flow exhibits mixed boundary conditions with one surface showing slip boundary behaviour whereas the opposing surface shows no-slip boundary behaviour. Deriving analytical solutions for flow cases exhibiting Neumann-type boundary conditions or even mixed boundary conditions is significantly more difficult. These cases are usually studied numerical solver packages [8] , lattice-Boltzmann or molecular dynamics simulations [9] .
This paper will derive an analytical solution to mixed slip/no-slip boundary conditions in two dimensions in rectangular channel cross-sections. This case is the most common case in microfluidic systems. We will also show that the Microsoft Excel spreadsheet developed for solving no-slip boundary flow scenarios can be adapted to derive the same solution within seconds. This allows deriving solutions to mixed Neumann/Dirichlet boundary condition flow scenarios for a wide variety of cross-sections.
2. Rectangular Channel with Two-Dimensional Flow: No-Slip Boundary Conditions Along y-Axis and Mixed Boundary Conditions Along z-Axis
2.1. Analytical Solution
2.1.1. Simplified Navier-Stokes Equation for Poiseuille Flow
The fundamental equation for the Poiseuille flow in microfluidics is given by
 (1a)
(1a)
which can be written as
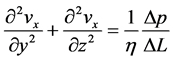 (1b)
(1b)
Details on the derivation can be found elsewhere [1] . Here the velocity 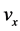 along the x-axis is the dependent variable,
along the x-axis is the dependent variable, 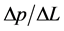 is the driving pressure drop and
is the driving pressure drop and 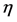 is the dynamic viscosity. y is the independent variable along the channel width W and z is the independent variable along the channel height H.
is the dynamic viscosity. y is the independent variable along the channel width W and z is the independent variable along the channel height H.
2.1.2. Homogeneous Solution
The solution to Equation (1) is derived by a separation of variables approach. For this we assume the dependent variable 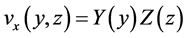 to be composed of two functions
to be composed of two functions 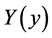 and
and 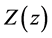 both of which depend on only one independent variable, respectively. Details on this procedure and the derived solutions can be found elsewhere [10] . We begin by finding the homogeneous solution to Equation (1) according to
both of which depend on only one independent variable, respectively. Details on this procedure and the derived solutions can be found elsewhere [10] . We begin by finding the homogeneous solution to Equation (1) according to
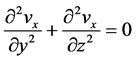 (2a)
(2a)
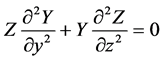 (2b)
(2b)
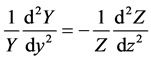 (2c)
(2c)
where we exploited the fact that 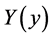 and
and 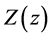 are functions of only one independent variable respectively. Equation (2c) will only be satisfied for arbitrary values of y and z if both sides of Equation (2c) result in a constant. We therefore obtain two ordinary differential equations from Equation (2c) which are given by
are functions of only one independent variable respectively. Equation (2c) will only be satisfied for arbitrary values of y and z if both sides of Equation (2c) result in a constant. We therefore obtain two ordinary differential equations from Equation (2c) which are given by
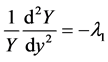 (3)
(3)
and
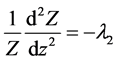 (4)
(4)
Details on these solutions can be found elsewhere [10] . For Equation (3) we have the boundary conditions 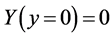 and
and 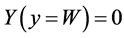 (both Dirichlet boundary conditions, no-slip) whereas for Equation (4) we have the boundary conditions
(both Dirichlet boundary conditions, no-slip) whereas for Equation (4) we have the boundary conditions 


and

Applying the boundary condition 







and the general solution to Equation (3) as

Applying the boundary condition 







and the general solution to Equation (4) as

The homogenous solution of Equation (1) is therefore given by

2.1.3. Inhomogeneous Solution
Using Equation (9) the inhomogeneous solution is obtained from Equation (1) as

where the right-hand side of Equation (10) (which is constant) must be converted to a two-dimensional Fourier series in order to derive 



In two-dimensions with 


The right-hand side of Equation (10) is therefore converted to a two-dimen- sional Fourier series using Equation (11) and setting 


where we have used the fact that the right-hand side requires only odd values of n. We can now determine the missing constants 

in which case the solution to Equation (1) is obtained from Equation (9) and Equation (12) as

where we introduce the channel aspect ratio r as

which allows us to rewrite Equation (13) to

and

with
Equation (13’’) is shown as a three-dimensional plot in Figure 1(a) normalized to the maximum velocity


2.2. Numerical Solution
2.2.1. Numerical Scheme
The numerical scheme used to solve Equation (1) is based on a finite difference approach and can be written as


where 






2.2.2. Implementing Neumann-Type Boundary Conditions
In order to replicate the scenario displayed in Figure 1(a) we need to implement
Figure 1. 3D flow profiles. Visualization of the analytical solutions to the flow case discussed in Section 2.1.3 (a) and Section 3.1.2 (b) given by Equation (13’’) and Equation (20), respectively. The Fourier series have been expanded to
Neumann-type boundary conditions on our computational domain in the spreadsheet (the used spreadsheet can be found in the supporting information). This can be done by setting the boundary value equal to the value of the neighbouring cell. This effectively implements a Neumann-type boundary condition, i.e., the gradient of the dependent variable will be zero. By adding an offset value according to
the gradient can be set to any desired offset value. For the case shown in Figure 1(a) we select the cells in the spreadsheet that represent the upper boundary (cells B1 to AO1). We then link the values of each of these cells to the value of the cell below it, respectively (cells B2 to AO2). We use a pressure gradient of −0.1 mbar/mm, a channel with a height and width of 100 µm, respectively, and use water as the fluid in question (viscosity 1 mPa×s). After completion of the recursive calculation Figure 2(a) is obtained.
2.3. Comparison of Analytical and Numerical Solution
Figure 2(b) shows the numerical output obtained from the spreadsheet in direct comparison with the analytical solution given by Equation (13’’) using the given values. As can be seen, the error is highest in areas of high gradients, predominantly in the edges of the cross-section. However, the solution should be sufficiently exact for most applications. In order to increase the exactness of the numerical solution, the step width h needs to be reduced further. For this, the resolution of the computational domain must be increased, i.e., the number of cells must be augmented. However, for most applications the given spreadsheet creates sufficiently exact results.
3. Two-Dimensional Flow Case Mixed Boundary Conditions along
3.1. Analytical Solution
3.1.1. Homogenous Solution
In the next step, we extend our discussion to channels with mixed boundary conditions along both channel axes. These types of channels have Dirichlet boundary condition for 






and

which yields the homogeneous solution
Figure 2. Numerical solutions for different boundary conditions. (a) Numerical output obtained from the Microsoft Excel spreadsheet for solving Equation (1) for cross-section with slip boundary condition (Neumann boundary condition) for



3.1.2. Inhomogeneous Solution
For the inhomogeneous solution the constant of the right-hand side in Equation (1) is again converted to a two-dimensional Fourier series with 




By comparison of coefficients between Equation (17) and Equation (18) 

in which case the general solution is obtained from Equation (17) as

Equation (20) is shown as a three-dimensional plot in Figure 1(b) normalized to the maximum velocity


3.2. Numerical Solution
Extending the previous example we will now discuss the flow case with mixed boundary conditions along both the y-axis as well as the z-axis. This flow case as zero-value Dirichlet boundary conditions for 



3.3. Comparison of Analytical and Numerical Solution
Figure 2(d) shows the relative error between the numerical solution obtained from the spreadsheet and the analytical solution given by Equation (20). As can be seen, the error is virtually non-existing in regions of small gradients, i.e., at the slip boundaries for 

4. One-Dimensional Flow Cases
As last examples we will illustrate that the spreadsheet can also be used to obtain solutions to one-dimensional flow cases.
Obviously, for all of these cases, analytical solutions exist and are described in the literature. This serves to illustrate that the numerical solutions obtained using the spreadsheet yield correct results also for these cases. The three flow cases addressed are shown in Figure 3.
4.1. Infinitesimally-Extended Channel Along y-Axis
The first case is the infinitesimally-extended channel displayed in Figure 3(a). This case is essentially a one-dimensional problem for which Equation (1) simplifies to


where the partial differentials can be converted to ordinary differentials because there is no change along the y-axis. The solution to Equation (21) can be obtained by integrating twice using the boundary values 


Compared to the scenarios discussed so far, this scheme is one-dimensional. This requires our two-dimensional spreadsheet to be converted to a one-dimen- sional problem. Numerically this is implemented by setting the boundary conditions on the left- and right-hand side of our domain from Dirichlet boundary conditions to Neumann boundary conditions. For this select the cells which represent the left-hand side of the boundary (cells A2 to A41 in the provided spreadsheet) and set them equal to the value of the right-hand side cell, respectively, by inserting the formula

Figure 3. Schematics of one-dimensional flow cases discussed. (a) Infinitesimally-ex- tended channel along the y-axis (Dirichlet boundary conditions for top and bottom boundary, zero boundary value for top and bottom boundary). (b) Couette flow (Dirichlet boundary conditions for top and bottom boundary, non-zero boundary value for top boundary, zero boundary value for bottom boundary). (c) Mixed boundary value case (Neumann boundary condition for top boundary, Dirichlet boundary condition for bottom boundary, zero boundary values for top and bottom boundary).
Likewise we select the cells of the right-hand side of the domain (cells AP2 to AP41 in the provided spreadsheet) and set them equal to the neighboring cells within the domain by inserting the formula
This effectively removes the second dimension from the numerical problem. Figure 4(a) shows the numerical solution displayed by the spreadsheet whereas Figure 4(b) shows the direct comparison between the numerical and the analytical solutions which show an exact match.
4.2. Couette Flow
The next flow scenario discussed is the one-dimensional Couette flow (see Figure 3(b)). For this scenario we again use Neumann boundary conditions along
Figure 4. Numerical solutions for one-dimensional flow cases. Numerical output obtained from the Microsoft Excel spreadsheet for solving Equation (1) for the three one-dimensional flow cases shown in figure 3 (a: Infinitesimally-extended channel; b: Couette flow; c: Mixed boundary conditions with no-slip condition for z=0 and slip condition for z = H). The color-coded outputs shown in (a/c/e) are the velocity profiles obtained from a microfluidic flow in a channel with 100 µm height. The flow in (a/e) is driven by a constant pressure drop of -0.1 mbar/mm whereas the flow in (c) is driven by a moving top boundary. All cases use water as fluid. The step width h of the numerical scheme was set to 2.5 µm, i.e., each cell represents a cross-section of 2.5 × 2.5 µm². (b/d/f) Comparison of the numerically obtained solutions (diamonds) with the analytical solutions (solid line) calculated using Equation (22) (b), Equation (24) (d) and Equation 25 (f), respectively. As can be seen the results are in good agreement.
the y-axis therefore reducing the flow scenario to one dimension. In comparison to Poiseuille flow, Couette flow is not driven by a pressure drop along the channel axis but by a movement of one of the boundaries (in our case the top boundary). In comparison to the flow scenarios discussed so far, Couette flow requires a non-zero Dirichlet boundary for


With the boundary conditions 


In the example in the spreadsheet we use
4.3. One-Dimensional Mixed Boundary Condition
As a third example, we will use a one-dimensional flow scenario with mixed boundary conditions along the y-axis (see Figure 3(c)). In this example, the lower boundary of the domain has a zero-value Dirichlet boundary (no-slip) whereas the upper boundary has a zero-value Neumann boundary (slip). This is the one-dimensional version of the case discussed in Section 3. Again we use Neumann boundary conditions on the left- and right-hand side boundaries of the domain therefore obtaining a one-dimensional flow. We set the value of the top boundary (cells A1 to AO1) equal to the values of the neighboring cell inside of the domain, respectively (cells A2 to AO2). This implements a Neumann boundary condition at the top of the domain. Again we use a pressure gradient of −0.1 mbar/mm, a channel height of 100 µm and water as the fluid in question (viscosity 1 mPa×s). After completion of the recursive calculation the output shown in Figure 4(e) is obtained.
The analytical solution to this flow scenario can be obtained by applying the boundary conditions 


The direct comparison between the numerical and the analytical solution is shown in Figure 4(f). As can be seen the numerical solution is again, close-to- exact.
5. Conclusion
In this paper, we extended the concept of using a spreadsheet analysis tool such as Microsoft Excel to solve the fundamental equation for Poiseuille flow, i.e., the simplified Navier-Stokes equation in arbitrary cross-sections in one and two dimensions implementing different boundary conditions. Besides zero-value and fixed-value Dirichlet boundary conditions (which are commonly used for implementing no-slip boundaries), we showed that simple modifications to the spreadsheet are sufficient to implement Neumann boundary conditions which set the gradient of the velocity profile to fixed values. These boundaries are required to implement slip boundaries which are commonly encountered on open surfaces or air-retaining substrates. We have shown that the solutions obtained within seconds from the spreadsheet compare very well to the analytical solutions obtained for three cases of one-dimensional flows: infinitesimally-extended channel, Couette flow and one-dimensional mixed boundary condition flow. In terms of two dimensional flows we provided analytical solutions to the case of a no-slip/no-slip boundary pair along the y-axis and a no-slip/slip boundary pair along the z-axis as well as a solution to the case of a no-slip/slip boundary pair along both the y- and the z-axis. In both cases, the numerical solutions obtained agree well with the analytical solutions. This underlies the potential of using simple-to-use spreadsheet analysis tools such as Microsoft Excel to derive important features such as the velocity profiles in arbitrary channel cross-sections instead of referring to expensive and difficult-to-use numerical solver packages. As we have shown this approach copes very well with different and even mixed boundary conditions and provides solutions within seconds even in cases where analytical solutions are rather difficult to derive.
Acknowledgements
This work was funded by the Bundesministerium für Bildung und Forschung (BMBF), funding code 03X5527 “Fluoropor”.
Cite this paper
Richter, C., Kotz, F., Keller, N., Nargang, T.M., Sachsenheimer, K., Helmer, D. and Rapp, B.E. (2017) An Analytical Solution to Neumann-Type Mixed Boundary Poiseuille Microfluidic Flow in Rectangular Channel Cross-Sec- tions (Slip/No-Slip) including a Numerical Technique to Derive It. J. Biomedical Sci- ence and Engineering, 10, 205-218. https://doi.org/10.4236/jbise.2017.105016
References
- 1. Richter, C., Kotz, F., Giselbrecht, S., Helmer, D. and Rapp, B. E. (2016) Numerics Made Easy: Solving the Navier–Stokes Equation for Arbitrary Channel Cross-Sections Using Microsoft Excel. Biomedical microdevices, 18, 1-8.
https://doi.org/10.1007/s10544-016-0070-2 - 2. Ngoma, G.D. and Erchiqui, F. (2007) Heat Flux and Slip Effects on Liquid Flow in a Microchannel. International Journal of Thermal Sciences, 46, 1076-1083.
https://doi.org/10.1016/j.ijthermalsci.2007.02.001 - 3. Yu, S. and Ameel, T.A. (2001) Slip-Flow Heat Transfer in Rectangular Microchannels. International Journal of Heat and Mass Transfer, 44, 4225-4234.
- 4. Barthlott, W., Schimmel, T., Wiersch, S., Koch, K., Brede, M., Barczewski, M. et al. (2010) The Salvinia Paradox: Superhydrophobic Surfaces with Hydrophilic Pins for Air Retention Under Water. Advanced Materials, 22, 2325-2328.
https://doi.org/10.1002/adma.200904411 - 5. Kavalenka, M.N., Vüllers, F., Lischker, S., Zeiger, C., Hopf, A., Rohrig, M., et al. (2015) Bioinspired Air-Retaining Nanofur for Drag Reduction. ACS Applied Materials & Interfaces, 7, 10651-10655.
- 6. Wang, C., Tang, F., Hao, P., Li, Q. and Wang, X. (2016) Experimental Study on the Drag Reduction Effect of a Rotating Superhydrophobic Surface in Micro Gap Flow Field. Microsystem Technologies, 1-8.
https://doi.org/10.1007/s00542-016-3097-7 - 7. Quéré, D., Lafuma, A. and Bico, J. (2003) Slippy and Sticky Microtextured Solids. Nanotechnology, 14, 1109.
https://doi.org/10.1088/0957-4484/14/10/307 - 8. Hlushkou, D., Kandhai, D. and Tallarek, U. (2004) Coupled Lattice-Boltzmann and Finite-Difference Simulation of Electroosmosis in Microfluidic Channels. International Journal for Numerical Methods in Fluids, 46, 507-532.
https://doi.org/10.1002/fld.765 - 9. Priezjev, N.V. (2007) Rate-Dependent Slip Boundary Conditions for Simple Fluids. Physical Review E, 75, p. 051605.
- 10. Rapp, B.E. (2016) Microfluidics: Modeling, Mechanics and Mathematics. Vol. 1, Elsevier, Cambridge.







