Journal of Biomedical Science and Engineering
Vol.6 No.5(2013), Article ID:31504,9 pages DOI:10.4236/jbise.2013.65065
Estimation of overall heat transfer coefficient of cooling system in RF capacitive hyperthermia
![]()
1Department of Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran
2Department of Medical Physics, Tehran University of Medical Science, Tehran, Iran
3Department of Medical Physics, Shahid Beheshti University, Tehran, Iran
Email: ali_aghayan@ymail.com
Copyright © 2013 Seyed Ali Aghayan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 30 March 2013; revised 2 May 2013; accepted 15 May 2013
Keywords: Estimation; Hyperthermia; Inverse Problem; Phantom; Overall Heat Transfer Coefficient
ABSTRACT
The study presented in this article involves the estimation of the overall heat transfer coefficient of cooling system in RF capacitive hyperthermia treatment using inverse problem based on the conjugate gradient method to provide improved distribution of temperature. The temperature data computed numerically from the direct problem using the finite difference time domain method are used to simulate the temperature measurements. The effects of the errors and sensor positions upon the precision of the estimated results are also considered. The results show that a reasonable estimation of the unknown can be obtained. Finally, measurements in a tissue-equivalent phantom are employed to appraise the reliability of the presented method. The comparison of computed data with measurements shows a good agreement between numerical and experimental results.
1. INTRODUCTION
Hyperthermia is the procedure to raise the temperature of tumor-loaded tissue to 40˚C - 43˚C and it is applied as an adjunctive therapy with various established cancer treatments such as radiotherapy and chemotherapy [1]. The quality and thus the effectiveness of treatment rely on the ability to control the absorbed power and thus the temperature distribution in the heterogeneous tissue. The water bolus is often used as an external applicator for solving the scattering problem and the improvement of power transmission into tissue and also to minimize thermal hot spots. The effect of the water coupling bolus on the temperature and the specific absorption rate (SAR) of tissue during hyperthermia treatment have been the main themes of a number of studies [2,3]. Griffiths et al. [4] and Reddy et al. [5,6] had shown that the power absorbed in the bolus decreases and that absorbed in the tissue or phantom increases with the increase in the bolus conductivity. They have used different concentrations of saline in bolus bags to vary the bolus conductivity. Neuman et al. [7] examined the effect of various thickness water bolus coupling layers on the SAR patterns from dual concentric conductor based on conformal microwave array superficial hyperthermia applicators. Sherar et al. [8] presented the design of a water bolus for external microwave applicators which increased the available treatment field size by removing the central hot spot caused by the increased power from the applicator in this region. They also used beam shaping bolus with array of saline-filled patches inside the coupling water bolus for superficial microwave hyperthermia [9]. Ebrahimi-Ganjeh et al. [10] numerically computed and compared both the SAR distributions and effective field size in the presence and absence of water bolus. The aim of the current study is to improve the ability of the cooling system; consequently the optimal temperature distribution inside the tissue can be obtained. To do this, the overall heat transfer coefficient (OHTC) of the cooling system is inversely estimated by means of the conjugated gradient method with adjoint equation (CGMAE). In the last two decades, CGMAE has been extensively used in the resolution of the general inverse heat transfer problems (IHTPs) with respect to the optimization procedure [11] especially in therapeutic applications [12-14]. None of the previous studies concerns to the estimation of the cooling system properties with CGM and its experimental validation. Although, the Levenberg-Marquardt and simplex methods are common techniques for solving optimization problems; but some of the advantages of the CGMAE are insensitive to the initial choice of unknown parameters and it does not require the priori information about the unknowns.
The most common approach for determining the optimal estimation of model parameters is to minimize an objective function. Here, the objective function was based on the criterion of the minimal square root of the difference between the measured temperature and the computed one. Temperature measurements taken at different sensor positions inside the phantom are considered available. CG-MAE is derived by perturbation principles that transform the inverse problem into the solution of three problems namely, the direct, the sensitivity and the adjoint problems, which will be discussed in details in the following sections. The governing equations are numerically solved by using the finite difference time domain (FDTD) method. In this study, we demonstrate that optimum heating conditions inside the phantom can be numerically attained by means of estimation of the OHTC associated with the cooling system. After describing the simulation model, we show the validity of the presented method by providing an experimental set-up in a tissueequivalent phantom.
2. MATERIALS AND METHOD
2.1. Direct Problem
To illustrate the methodology for developing expressions for the use in determining the unknown OHTC of the cooling system, we consider the Pennes bioheat equation [15]. The geometry of the model is shown in Figure 1. In the current study, we assumed that heat mainly propagates in the direction perpendicular to the surface. As a result, one-dimensional heat transfer is assumed. The temperature distribution inside the tissue,  , is given by the solution of the following equation:
, is given by the solution of the following equation:
 (1)
(1)
Subject to the following boundary conditions:
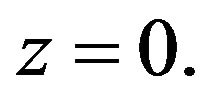
 (2)
(2)
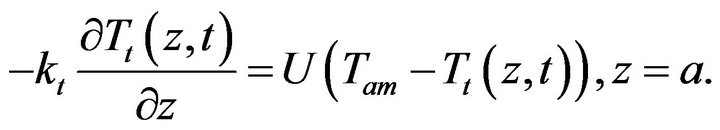 (3)
(3)
And the initial condition:
 (4)
(4)
where the OHTC of the cooling system is expressed with . Since the temperature distribution is very sensitive to the heat transfer between the cooling system and the tissue, the numerical value of
. Since the temperature distribution is very sensitive to the heat transfer between the cooling system and the tissue, the numerical value of  must be estimated appropriately. It can be easily shown that the expression of
must be estimated appropriately. It can be easily shown that the expression of  is obtained as follows [16]:
is obtained as follows [16]:
 (5)
(5)
here, 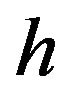 is the heat convection coefficient of water,
is the heat convection coefficient of water,  and
and  are thickness and thermal conductivity of the casing layer respectively.
are thickness and thermal conductivity of the casing layer respectively.
The volumetric EM power deposition averaged over time is calculated by:
 (6)
(6)
where,  is the electrical conductivity of the medium and
is the electrical conductivity of the medium and  is the amplitude (effective value) of the electric field (
is the amplitude (effective value) of the electric field (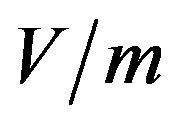 ). The spatial and temporal behavior of the electric field within the medium is governed by Maxwell’s equations.
). The spatial and temporal behavior of the electric field within the medium is governed by Maxwell’s equations.
2.2. Inverse Problem
In the inverse problem considered here, the OHTC of the cooling system is regarded as unknown, while the other quantities appearing in the formulation of the direct problem described above are assumed to be known precisely. In addition, transient temperature readings taken along the medium are considered available. The goal of the inverse analysis presented here is to estimate the unknown merely from the knowledge of these temperature

Figure 1. Cross section of (a) Control zone; (b) Cooling system.
readings. The solution of the present inverse problem is to be obtained in such a way that the following functional is minimized:
 (7)
(7)
We tend to achieve the continuous measured temperatures, 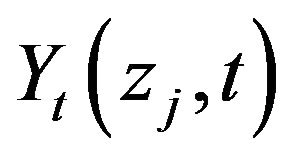 , at
, at  different sensor locations located at
different sensor locations located at 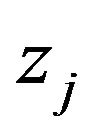 within the total time
within the total time 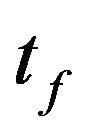 of the treatment process. The measured temperatures contain measurement errors. The estimated temperature,
of the treatment process. The measured temperatures contain measurement errors. The estimated temperature,  , and measured one, computed numerically from the solution of the direct problem given previously by using an estimated and exact
, and measured one, computed numerically from the solution of the direct problem given previously by using an estimated and exact , respectively. Similarly, our simulation tool can also be used to an optimization procedure. In order to develop expressions for the determination of the unknown
, respectively. Similarly, our simulation tool can also be used to an optimization procedure. In order to develop expressions for the determination of the unknown  a ‘‘sensitivity” and an ‘‘adjoint” problem are constructed as described below.
a ‘‘sensitivity” and an ‘‘adjoint” problem are constructed as described below.
2.3. Conjugate Gradient Method for Minimization
The unknown parameter,  , is estimated through the minimization of the functional
, is estimated through the minimization of the functional  by the following iteration process based on conjugate gradient method:
by the following iteration process based on conjugate gradient method:
 (8)
(8)
here,  is the step size and
is the step size and 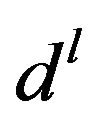 is the descent direction of the
is the descent direction of the  th iteration defined as follows:
th iteration defined as follows:
 (9)
(9)
The coefficient of conjugate gradient,  , is given by:
, is given by:
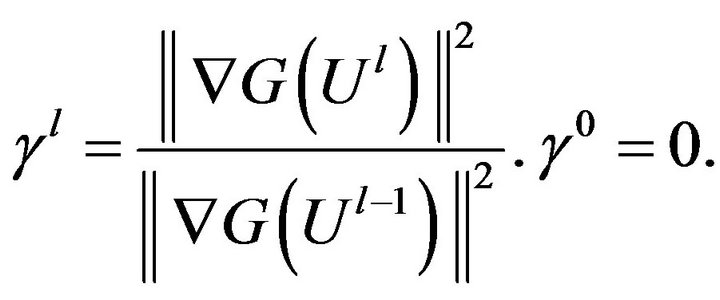 (10)
(10)
It is required to compute  and
and  to perform the process based on Equation (8). In the following sections we construct the sensitivity and adjoint problems, to develop expressions for the determination of these parameters.
to perform the process based on Equation (8). In the following sections we construct the sensitivity and adjoint problems, to develop expressions for the determination of these parameters.
2.4. Sensitivity Problem
It is assumed that when  undergoes a variation of
undergoes a variation of , then
, then  is perturbed by an amount
is perturbed by an amount . Then, replacing
. Then, replacing  and
and 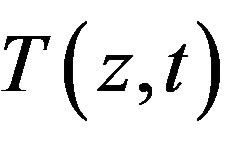 by
by ,
,  in the direct problem, and subtracting the original direct problem from the resulting expressions and ignoring the second order terms, the following sensitivity problem can be obtained:
in the direct problem, and subtracting the original direct problem from the resulting expressions and ignoring the second order terms, the following sensitivity problem can be obtained:
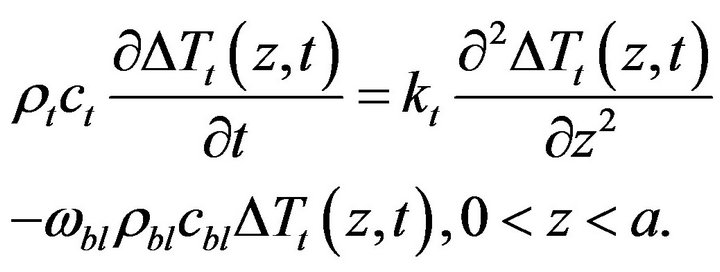 (11)
(11)
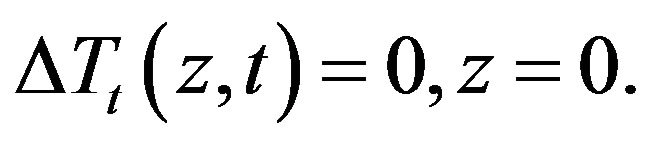 (12)
(12)
 (13)
(13)
 (14)
(14)
The functional  for the iteration
for the iteration 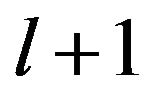 is obtained by rewriting Equation (7) as:
is obtained by rewriting Equation (7) as:
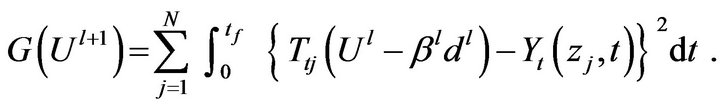 (15)
(15)
where, we replace  by the expression given by Equation (8). The temperature
by the expression given by Equation (8). The temperature  can be linearized by a Taylor expansion and then after some calculations the step size can be derived as [17]:
can be linearized by a Taylor expansion and then after some calculations the step size can be derived as [17]:
 (16)
(16)
2.5. Adjoint Problem and Gradient Equation
To obtain the adjoint problem, Equation (1) is multiplied by the Lagrange multiplier, . Also, the resulting expression is integrated over the time and the corresponding space domains. Then, the results are added to the right-hand side of Equation (7) as:
. Also, the resulting expression is integrated over the time and the corresponding space domains. Then, the results are added to the right-hand side of Equation (7) as:
 (17)
(17)
here,  is called the Lagrangian functional. The next step is to calculate the variation of
is called the Lagrangian functional. The next step is to calculate the variation of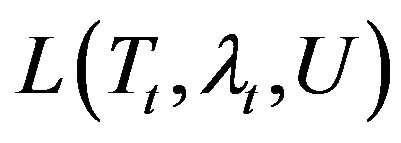 . Integration the second and third double integral terms by parts in the resulting equation for
. Integration the second and third double integral terms by parts in the resulting equation for 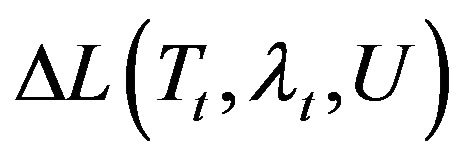 and using the boundary and initial conditions of the sensitivity problem the following adjoint problem for the Lagrange multiplier is obtained by allowing
and using the boundary and initial conditions of the sensitivity problem the following adjoint problem for the Lagrange multiplier is obtained by allowing  to go to zero by vanishing the integrands containing
to go to zero by vanishing the integrands containing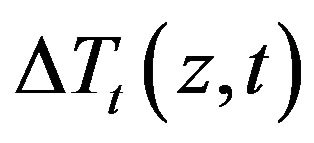 :
:
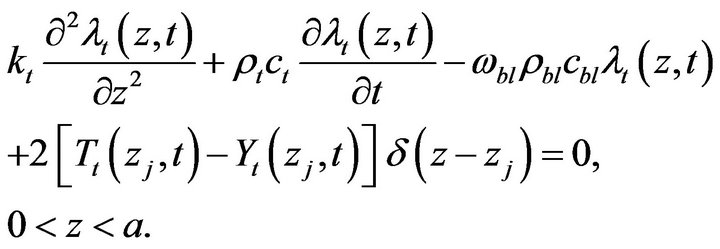 (18)
(18)
 (19)
(19)
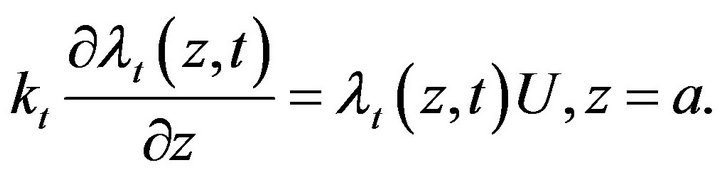 (20)
(20)
 (21)
(21)
Note that the adjoint problem is different from the standard initial value problem in that the final time condition at time  is specified instead of
is specified instead of . In the limiting process used to obtain the adjoint problem above, the following integral term is left:
. In the limiting process used to obtain the adjoint problem above, the following integral term is left:
 (22)
(22)
It can be shown that the gradient of residual functional, 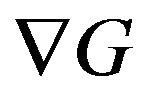 , has the following analytical expression [13-14,17]:
, has the following analytical expression [13-14,17]:
 (23)
(23)
2.6. Stopping Criterion and Computational Algorithm
The stopping criterion based on the discrepancy principle gives the CGM of parameter estimation an iterative regularization character. The stopping criterion is given by:
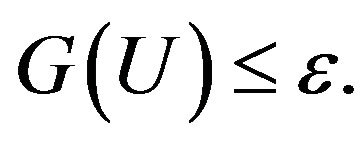 (24)
(24)
The tolerance  is chosen so that smooth solutions are obtained with measurements containing random errors. It is assumed that the solution is sufficiently accurate when:
is chosen so that smooth solutions are obtained with measurements containing random errors. It is assumed that the solution is sufficiently accurate when:
 (25)
(25)
where  is the standard deviation of measurement errors. Thus,
is the standard deviation of measurement errors. Thus,  is obtained from Equation (7) as:
is obtained from Equation (7) as:
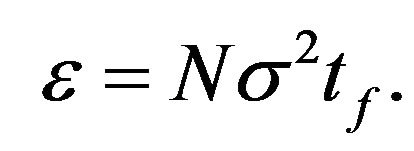 (26)
(26)
Then the stopping criterion is given by Equation (24) with  determined from Equation (26). The computational algorithm of the method is shown in Figure 2.
determined from Equation (26). The computational algorithm of the method is shown in Figure 2.
2.7. Computer Simulation
The computational algorithm presented above was programmed in Fortran 90 compiled through the software Compaq Visual Fortran Professional Edition to show the validity of the CGMAE method in the estimation of OHTC accurately with no prior information on it. Simulation was performed on a computer with an Intel Core i7 3.5 GHz and 16 Gb of RAM. Two approaches for analysis of the simulated data are discussed, in the first OHTC is estimated using exact data while in the second analysis is performed with noisy data. Generally, measurements containing random errors,  , are simulated by adding an error term to the computed exact temperatures,
, are simulated by adding an error term to the computed exact temperatures,  , in
, in
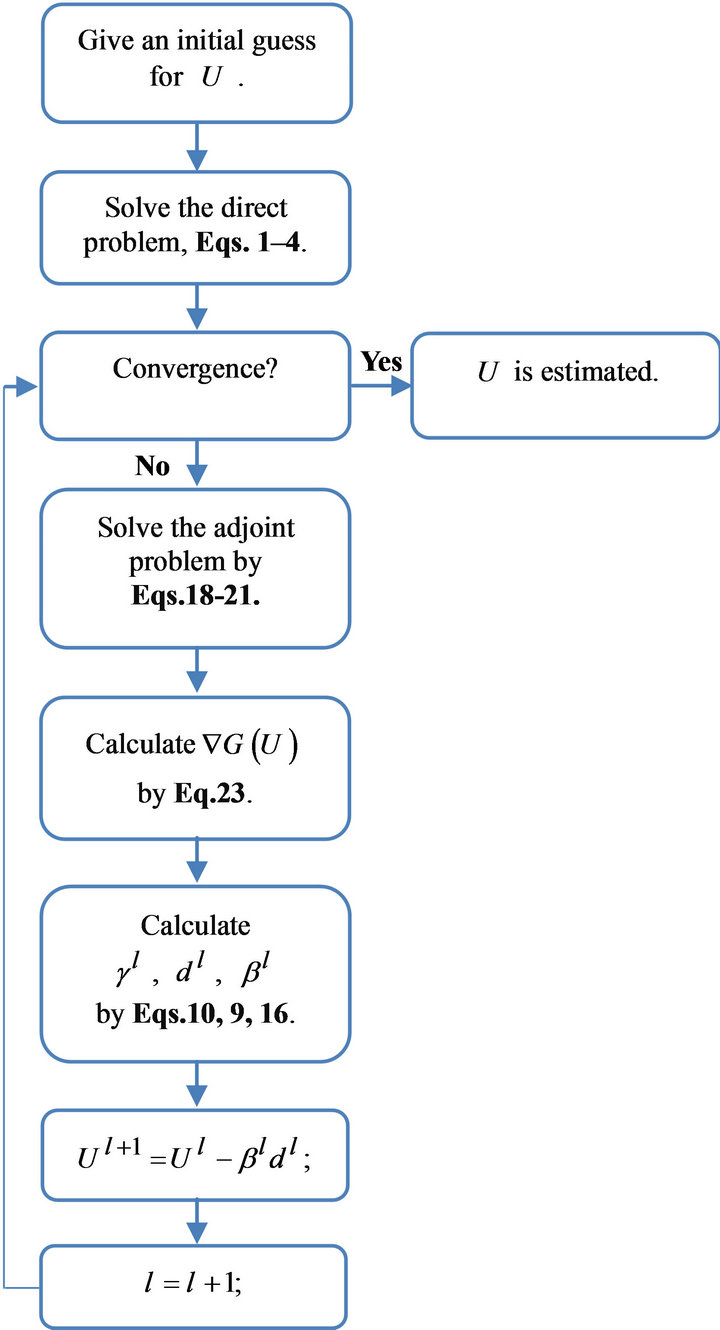
Figure 2. A block diagram of the CGM.
the following manner:
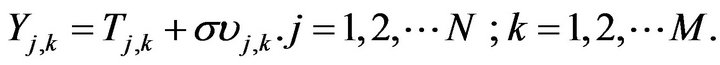 (27)
(27)
where σ is standard deviation of measurement errors and  is random error variable and will be within −2.576 to 2.576 for normally distributed errors with zero mean and 99% confidence bounds.
is random error variable and will be within −2.576 to 2.576 for normally distributed errors with zero mean and 99% confidence bounds.  is the number of sensors and
is the number of sensors and 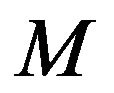 is the number of measurements taken with each sensor
is the number of measurements taken with each sensor , in the total time of the process. In order to illustrate the accuracy of the presented inverse analysis, noise was inserted in the measured temperatures with three different levels of standard deviations:
, in the total time of the process. In order to illustrate the accuracy of the presented inverse analysis, noise was inserted in the measured temperatures with three different levels of standard deviations:  (errorless),
(errorless), 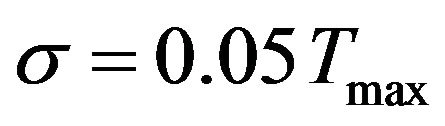 and
and 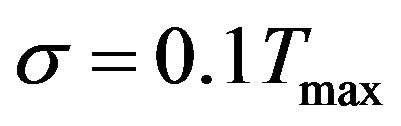 where
where  is the maximum measured temperature. We assumed the simulated exact value of OHTC as 145
is the maximum measured temperature. We assumed the simulated exact value of OHTC as 145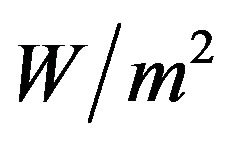 ˚C.
˚C.
For the simulation, a geometry as shown in Figure 1, has been considered. The typical data for different materials at the frequency of 8 are given in Table 1. Since our experimental verification are considered in the phantom, metabolism (
are given in Table 1. Since our experimental verification are considered in the phantom, metabolism ( ) and blood perfusion (
) and blood perfusion ( ) of tissue are neglected. It is clear that by considering this
) of tissue are neglected. It is clear that by considering this
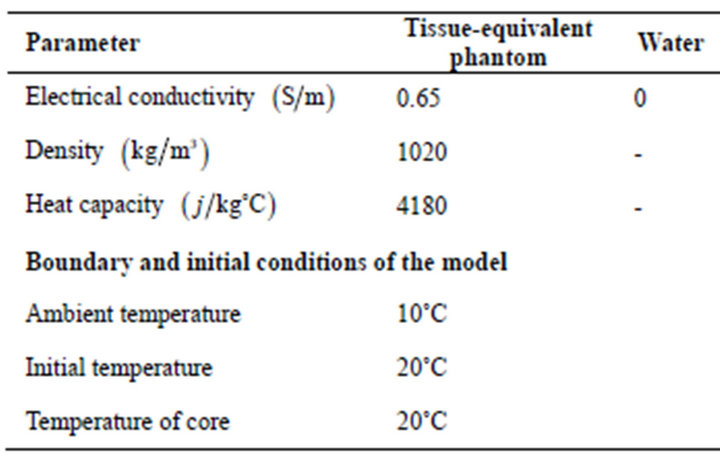
Table 1. Characteristics employed in the numerical simulation.
simplification, the foregoing equations are still reliable. In the present study, Maxwell’s equations as well as the direct, the sensitivity and the adjoint problems were solved using FDTD method with an implicit discretization in space and time. Uniform grid of 31 × 31 mesh is utilized for all results presented below. The final time, 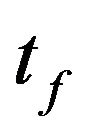 , is chosen 1200 s. Moreover, the computational precision (
, is chosen 1200 s. Moreover, the computational precision (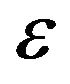 ) is set 10−5. The readings of three sensors located at the positions:
) is set 10−5. The readings of three sensors located at the positions: ,
,  and
and  are used for estimation of the unknown OHTC. In order to examine the ability of the proposed method, three initial guesses are chosen; one is close to the exact value and the two other ones are far from it.
are used for estimation of the unknown OHTC. In order to examine the ability of the proposed method, three initial guesses are chosen; one is close to the exact value and the two other ones are far from it.
2.8. Experimental Design Consideration
To validate the heating characteristics obtained in the simulation results, an experimental arrangement depicted in Figure 3, was prepared. A rectangular soft tissueequivalent agar phantom of 0.05 × 0.05 × 0.12 m3, composed of deionised-water (95.6 w/w%), NaN3 (0.4 w/w%) and agar (4 w/w%) was prepared [18]. A pair of plate electrodes, which made of aluminium and were 0.06 × 0.06 m2 connected to RF device through coaxial wires, was constructed. The heating system has been made of an ultrafast MOSFET driver (DEIC420) at 8 MHz and 50 W power supplied by half size clock oscillator (XO-52). The phantom was embedded by cooling system and heated with the RF applicator and then the temperature distribution along the Z-axis of the phantom was measured with thermometers. The cooling system consists of a very malleable plastic pocket with thermal conductivity of 0.14 w/w˚C and 0.15 × 0.055 × 0.01 m3 in size. It contains the deionised water and circulation system of water is provided with the aid of a controllable pump, which its flow rate can be changed. Thermometry system (Extech 421509) consists of Teflon-coated thermocouples was used to record the axial temperature distributions with a 0.5 cm equal increment in depth of phantom from its surface. The measured temperatures are continuously displayed on the computer screen with a reso-

Figure 3. Experimental setup used to measure temperature field inside the phantom produced from the RF applicator; (1) Phantom; (2) Water bolus; (3) Flow meters; (4) RF generator; (5) Thermometers; (6) Sensors.
lution of 0.1˚C. The interaction of electric fields generated between the parallel-opposed electrodes with the material causes the heat distribution through the phantom.
3. RESULTS AND DISCUSSIONS
3.1. Results of Computer Simulation
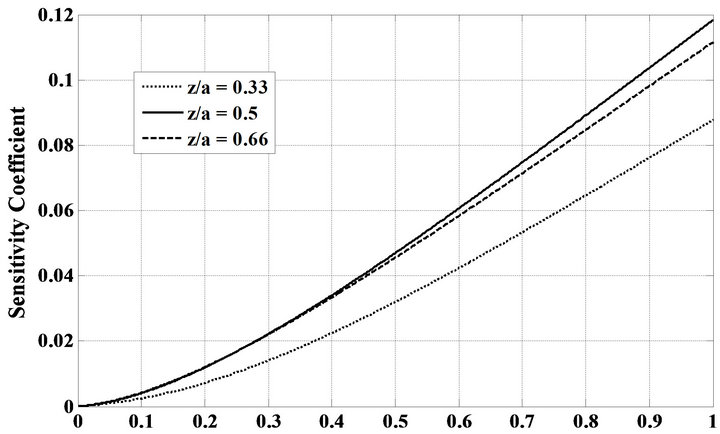
Before we attempt to solve the foregoing inverse problem, the timewise variation of the sensitivity coefficient with respect to parameter U was examined. This examination helps us to select the best sensor position in the effectiveness treatment by hyperthermia in the manner of the less invasive temperature measurement. It is clearly well known that large values of sensitivity coefficient will lead to a successful estimation of the unknown parameter. The sensitivity coefficient of the OHTC is computed by using the numerical solution of the direct problem. A sensor located at different dimensionless positions 0.33, 0.5 and 0.66 which are equivalent to ,
,  and
and  is studied. Figure 4 shows the variation of the sensitivity coefficient as a function of dimensionless time for three dimensionless locations relative to U = 145
is studied. Figure 4 shows the variation of the sensitivity coefficient as a function of dimensionless time for three dimensionless locations relative to U = 145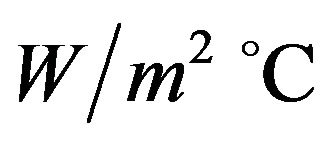 . According to this figure, the magnitude of the sensitivity coefficient with respect to
. According to this figure, the magnitude of the sensitivity coefficient with respect to  attains large values, especially in the
attains large values, especially in the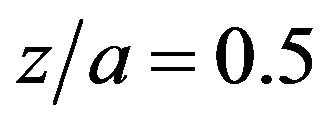 . Therefore, the estimation of
. Therefore, the estimation of  is not difficult in the given situation. Also, it reveals that the magnitude of sensitivity coefficient decreases as the sensor is located either close to the surface of phantom, i.e.:
is not difficult in the given situation. Also, it reveals that the magnitude of sensitivity coefficient decreases as the sensor is located either close to the surface of phantom, i.e.: , or far from it i.e.:
, or far from it i.e.: .
.
Table 2 lists the summary of the results obtained for the estimation of OHTC. The Iteration row represents the number of iterations required to converge to the solution. As expected, with increasing the standard deviation, less accurate results are obtained, so that accurate estimates cannot be achieved with a standard deviation of equal to
t/tf
Figure 4. Sensitivity coefficient in three different dimensionless sensor locations.
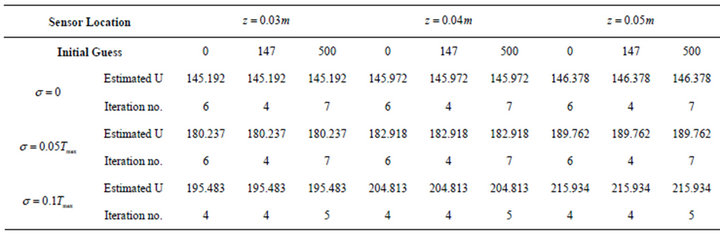
Table 2. Results of estimation of OHTC.
or more than 5% of . It is remarkable that the initial guess did not affect the estimation. This table also shows that the sensor position nearly has no effect on the final estimation of OHTC. However, results of the effect of sensor positions used in the simulation reveal that for position close to the surface of the phantom, the estimation is worse than for two other cases of sensor positions. Therefore, in accordance with Figure 4, it is possible to attain good results with a sensor located 0.03 m below the surface of the phantom.
. It is remarkable that the initial guess did not affect the estimation. This table also shows that the sensor position nearly has no effect on the final estimation of OHTC. However, results of the effect of sensor positions used in the simulation reveal that for position close to the surface of the phantom, the estimation is worse than for two other cases of sensor positions. Therefore, in accordance with Figure 4, it is possible to attain good results with a sensor located 0.03 m below the surface of the phantom.
Due to the symmetry consideration of the model, only one half of the temperature distribution inside the phantom is presented in the following figures. A comparison between spatial temperature distribution inside the phantom computed from the exact and estimated OHTC for different measured error levels for a sensor located at  is presented in Figure 5. Although, reasonably precise results can be achieved with smaller standard deviation of measurements, but in accordance with Table 2, the estimation of OHTC becomes less accurate when utilized standard deviation in the analysis is increased and as expected, it is especially remarkable near the surface of the phantom. Furthermore, due to the small difference between the exact and estimated OHTC with
is presented in Figure 5. Although, reasonably precise results can be achieved with smaller standard deviation of measurements, but in accordance with Table 2, the estimation of OHTC becomes less accurate when utilized standard deviation in the analysis is increased and as expected, it is especially remarkable near the surface of the phantom. Furthermore, due to the small difference between the exact and estimated OHTC with , the relevant curves are very similar to each other.
, the relevant curves are very similar to each other.
3.2. Results of Phantom Experiment
Assuming the thickness and the thermal conductivity of the casing layer are constant, the value of OHTC can be affected only through the heat transfer coefficient of water. This is done by means of controlling the flow conditions of the cooling water. The spatial and temporal temperature distributions are shown in the following figures, when these conditions have been changed. If the water flows with the rate of 0.18 , the relevant Nusselt (Nu) number and heat transfer coefficient become 354 and 212
, the relevant Nusselt (Nu) number and heat transfer coefficient become 354 and 212 , respectively, Which is corresponds to
, respectively, Which is corresponds to . In Figures 6 and 7, the computed temperature distributions are compared with the experimental ones inside the phantom. The computed temperature is obtained by using the errorless measured temperatures
. In Figures 6 and 7, the computed temperature distributions are compared with the experimental ones inside the phantom. The computed temperature is obtained by using the errorless measured temperatures
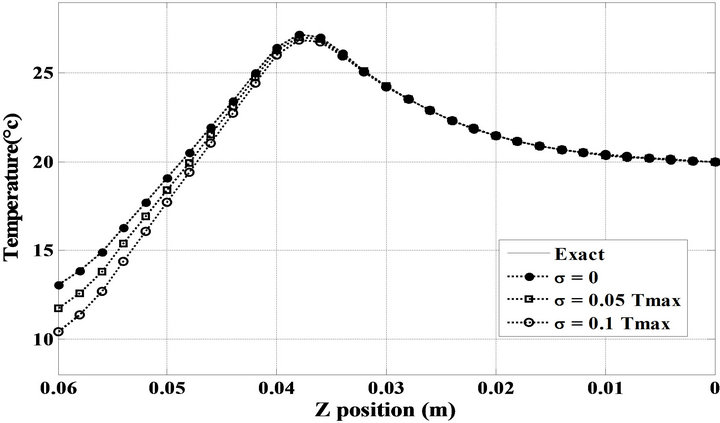
Figure 5. Comparison of spatial temperature distribution inside the phantom with exact and estimated OHTC at t = 200 s.

Figure 6. Comparison between computed temperatures and experimental ones inside the phantom at t = 200 s.
(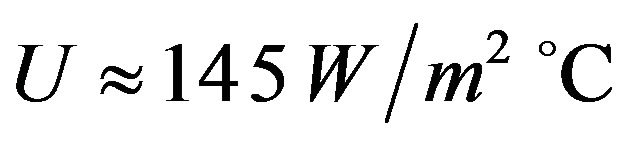 —see Table 2) when the minimum of the objective functional is satisfied. It is observed that the experimental temperatures and the computed ones are slightly different. Similarly, Figure 7 presents the temperature distributions result from the solution of the transient thermal problem during the total heating process. The temperature readings inside the phantom at the final time of the process are also given in this figure. In addition, it is clear to be sufficient to obtain the steady state temperature inside the phantom in approximately 20 minutes, while the temperature of the surface remains approximately constant in this time period.
—see Table 2) when the minimum of the objective functional is satisfied. It is observed that the experimental temperatures and the computed ones are slightly different. Similarly, Figure 7 presents the temperature distributions result from the solution of the transient thermal problem during the total heating process. The temperature readings inside the phantom at the final time of the process are also given in this figure. In addition, it is clear to be sufficient to obtain the steady state temperature inside the phantom in approximately 20 minutes, while the temperature of the surface remains approximately constant in this time period.
The validation of the presented inverse method is also depicted in Figure 8. As mentioned in Table 2, by prescribing 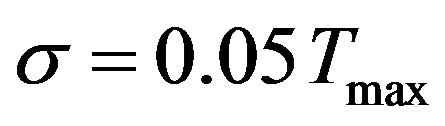 and
and  in the analysis, the OHTC for a sensor located at
in the analysis, the OHTC for a sensor located at  is obtained 180.2 and 195.5
is obtained 180.2 and 195.5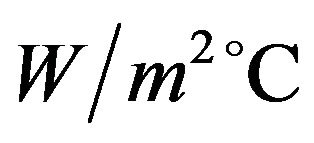 , respectively. If we increase the mass flow rate from 0.36
, respectively. If we increase the mass flow rate from 0.36  to 0.49
to 0.49 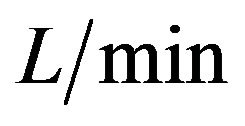 in the experimental setup, the relevant Nu number increases from 475 to 580, then the heat transfer coefficient of water is from 285 to 347
in the experimental setup, the relevant Nu number increases from 475 to 580, then the heat transfer coefficient of water is from 285 to 347 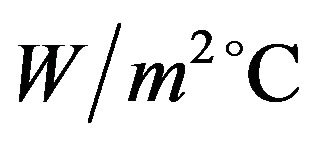 which are corresponddent to
which are corresponddent to 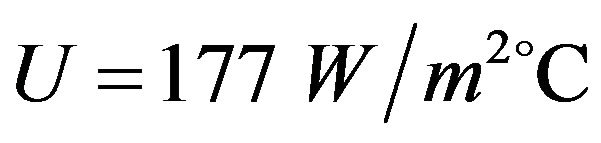 and
and , respectively. The observed slight difference between experimental and theoretical values in Figures 6-8 may be due to the some factors including the existing mismatch between the corresponding OHTCs, the geometry of the cooling system as well as the experimental conditions. Although, the foregoing factors independently could cause negligible effects on temperature distribution, but collectively, they are impressive and cause the difference between experimental and theoretical values of temperatures.
, respectively. The observed slight difference between experimental and theoretical values in Figures 6-8 may be due to the some factors including the existing mismatch between the corresponding OHTCs, the geometry of the cooling system as well as the experimental conditions. Although, the foregoing factors independently could cause negligible effects on temperature distribution, but collectively, they are impressive and cause the difference between experimental and theoretical values of temperatures.
Up to our knowledge, none of the previous studies concerns with the estimation of the cooling system properties by means of CGM and its experimental validation, and in this respect, the present study is a novel one. In comparison with the other common techniques for solving the estimation problems, our proposed method have some advantages such as its insensitivity to the initial
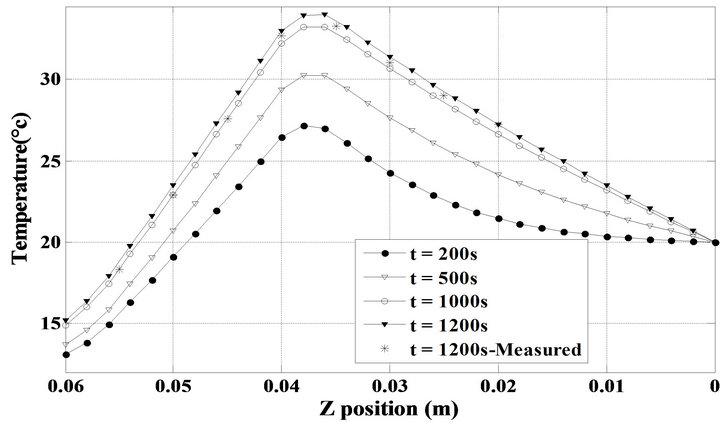
Figure 7. Transient computed temperature field using the errorless measured temperatures along with the experimental temperatures at t = 1200 s.

Figure 8. The measured temperatures with two different OHTC and the computed ones using two relevant measured errors at t = 200 s.
choice of unknown parameters and that it does not require a priori information about the unknowns. In the perspective of the present study, we believe that the proposed algorithm developed here has the potential to provide a more complete understanding of the cooling system ability for RF beam-forming role to control the temperature profile in tissue. This purpose is attainable through using proper shape of fluid or solid patches with appropriate heat convection or thermal conduction coefficient inside the cooling system. In other words, the configuration of the inserted patches into the cooling system, should resemble to the tumor shape so that we should be capable of conforming heat to any shaped target tumor with limiting the heating to the surrounding normal tissue to an acceptable level.
4. CONCLUSION
The conjugate gradient method with adjoint equation was successfully applied to the solution of the inverse problem to determine the OHTC. The presented results also show that the accuracy of the estimation decreases when the sensor is located closer to the surface as well as the noise of simulated data increases. Results obtained from the experimental setup are found to be nearly in agreement with the theory and we can thus confirm the ability and robustness of the proposed method. We believe that our study is very useful in a large variety of hyperthermia treatments. However, the effective performance of this method under clinical conditions needs to be further investigated.
REFERENCES
- Wust, P., et al. (2002) Hyperthermia in combined treatment of cancer. The LANCET Oncology, 3, 487-497. doi:10.1016/S1470-2045(02)00818-5
- Lee, E.R., Kapp, D.S., Lohrbach, A.W. and Sokol, J.L. (1994) Influence of water bolus temperature on measured skin surface and intra thermal temperatures. International Journal of Hyperthermia, 10, 59-72. doi:10.3109/02656739409009332
- De Bruijne, M., Samras, T., Bakker, J.F. and Rhoon, G.C. (2006) Effects of water bolus size, shape and configuration on the SAR distribution pattern of the Lucite cone applicator. International Journal of Hyperthermia, 22, 15- 28. doi:10.1080/02656730500384297
- Griffithsh, H., Ahmed, A. and Smith, C.W. (1984) Power loss in skin cooling pillows during RF hyperthermia. British Journal of Radiology, 57, 254-256. doi:10.1259/0007-1285-57-675-254
- Reddy, N.M.S., Balakrishnan, I.S., Bhaskar, B.K., Krishnamurthi, S. and Shanta, V. (1986) Optimization of power deposition and the rate of heating of tissue during RF capacitive hyperthermia. International Journal of Hyperthermia, 2, 321-323. doi:10.3109/02656738609016489
- Reddy, N.M.S., Shanta, V. and Krishnamurthi, S. (1986) On minimization of toxicity to skin during capacitive radiofrequency hyperthermia. British Journal of Radiology, 9, 1129-1131. doi:10.1259/0007-1285-59-707-1129
- Neuman, D.G., Stauffer, P.R., Jacobsen, S. and Rossetto, F. (2002) SAR pattern perturbations from resonance effects in water bolus layers used with superficial microwave hyperthermia applicators. International Journal of Hyperthermia, 18, 180-193. doi:10.1080/02656730110119198
- Sherar, M.D., et al. (1993) Beam shaping for microwave waveguide hyperthermia applicators. International Journal of Radiation Oncology Biology Physics, 25, 849-857. doi:10.1016/0360-3016(93)90315-M
- Kumaradas, J.C. and Sherar, M.D. (2003) Optimization of a beam shaping bolus for superficial microwave hyperthermia waveguide applicators using a finite element method. Physics in Medicine and Biology, 48, 1-18. doi:10.1088/0031-9155/48/1/301
- Ebrahimi-Ganjeh, M.A. and Attari, A.R. (2008) Study of water bolus effect on SAR penetration depth and effective field size for local hyperthermia. Progress in Electromagnetic Research B, 4, 273-283. doi:10.2528/PIERB08011403
- Huang, C.H. and Wang, S.P. (1999) A three dimensional inverse heat conduction problem in estimating surface heat flux by conjugate gradient method. International Journal of Heat and Mass Transfer, 42, 3387-3403. doi:10.1016/S0017-9310(99)00020-4
- Dhar, P.K. and Sinha, D.K. (1988) Temperature control of tissue by transient-induced microwave. International Journal of Systems Science, 19, 2051-2055. doi:10.1080/00207728808964097
- Loulou, T. and Scott, E.P. (2002) Thermal dose optimization in hyperthermia treatments by using the conjugate gradient method. Numerical Heat Transfer, Part A: Applications, 42, 661-683. doi:10.1080/10407780290059756
- Loulou, T. and Scott, E.P. (2006) An inverse heat conduction problem with heat flux measurements. International Journal for Numerical Methods in Engineering, 67, 1587-1616. doi:10.1002/nme.1674
- Pennes, H.H. (1948) Analysis of tissue and arterial blood temperatures in the resting human forearm. Journal of Applied Physiology, 1, 93-122.
- Holman, J. P. (2002) Heat transfer. 9th Edition, McGraw Hill, New York.
- Ozisik, M.N. and Orlande, H.R.B. (2000) Inverse heat transfer fundamentals and applications. Taylor & Francis, New York.
- Kato, H. and Ishida, T. (1987) Development of agar phantom adaptable for simulation of various tissues in the range 5 - 40 MHz (Hyperthermia treatment of cancer). Physics in Medicine and Biology, 72, 221-226. doi:10.1088/0031-9155/32/2/006



