Intelligent Information Management
Vol.07 No.04(2015), Article ID:57863,13 pages
10.4236/iim.2015.7474015
A Time-Dependent Vehicle Routing Problem with Time Windows for E-Commerce Supplier Site Pickups Using Genetic Algorithm
Suresh Nanda Kumar1, Ramasamy Panneerselvam2
1Doctoral Candidate, School of Management, Pondicherry University, Pondicherry, India
2Professor, School of Management, Pondicherry University, Pondicherry, India
Email: snkumar27@gmail.com, panneer_dms@yahoo.co.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2015; accepted 7 July 2015; published 10 July 2015
ABSTRACT
The VRP is classified as an NP-hard problem. Hence exact optimization methods may be difficult to solve these problems in acceptable CPU times, when the problem involves real-world data sets that are very large. To get solutions in determining routes which are realistic and very close to the actual solution, we use heuristics and metaheuristics which are of the combinatorial optimization type. A literature review of VRPTW, TDVRP, and a metaheuristic such as the genetic algorithm was conducted. In this paper, the implementation of the VRPTW and its extension, the time-dependent VRPTW (TDVRPTW) has been carried out using the model as well as metaheuristics such as the genetic algorithm (GA). The algorithms were implemented, using Matlab and HeuristicLab optimization software. A plug-in was developed using Visual C# and DOT NET framework 4.5. Results were tested using Solomon’s 56 benchmark instances classified into groups such as C1, C2, R1, R2, RC1, RC2, with 100 customer nodes, 25 vehicles and each vehicle capacity of 200. The results were comparable to the earlier algorithms developed and in some cases the current algorithm yielded better results in terms of total distance travelled and the average number of vehicles used.
Keywords:
Vehicle Routing Problem, Exact Methods, Heuristics, Metaheuristics, VRPTW, TDVRPTW, Optimization, Genetic Algorithms, Matlab, HeuristicLab, C#, DOT NET

1. Introduction
Vehicle Routing Problem (VRP) is one of the most important topics in operations research. It deals with determining least cost routes from a depot to a set of scattered customers. The routes have to satisfy the following set of constraints:
・ Each customer is visited exactly once
・ All routes start and end at the depot
・ Sum of all demands on a route must not exceed the capacity of a vehicle
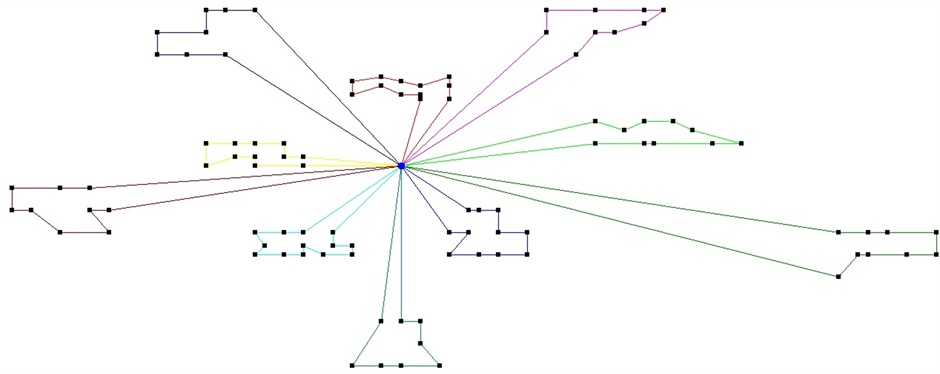
The vehicle routing problem is depicted in Figure 1. As we can see the vehicles originate at the depot, visit all the nodes once, fulfill their demands at the nodes and then return to the depot once again.
VRP is closely related to TSP, and according to Bullheimer et al. [1] , as soon as the customers of the VRP are assigned to vehicles, the problem is reduced to several or multiple TSPs.
The Vehicle Routing Problem (VRP) is used to design an optimal route for a fleet of vehicles, to service a set of customers given a set of constraints. The VRP is used in supply chain management in the physical delivery of goods and services. There are several variants to the VRP. These are formulated based on the nature of the transported goods, the quality of service required and the characteristics of the customers and the vehicles. The VRP is of the NP-hard type.
The vehicle routing problem (VRP) has been very extensively studied in the optimization literature. It started with the seminal papers of Dantzig and Ramser [2] and Clarke and Wright [3] . Now, VRP offers a wealth of heuristic and metaheuristic approaches, which are surveyed in the papers of Laporte [4] Gendreau et al. [5] and Cordeau et al. [6] . The VRP is so widely studied because of its wide applicability and its importance in determining efficient strategies for reducing operational costs in distribution networks. Today, exact VRP methods have a size limit of 50 - 100 orders depending on the VRP variant and the time-response requirements. To overcome this limitation, the research on VRP currently concentrates on approximate algorithms and metaheuristics that are capable of finding high quality solutions in limited time, in order to be applicable to real-life problem instances that are characterized by large vehicle fleets and affect significantly logistics and distribution strategies.
The VRP was first stated by Dantzig and Remser [2] that was about the routing of a fleet of gasoline delivery trucks between a bulk terminal and a number of service stations supplied by the terminal. The distance between any two locations is given and a demand for a given product is specified for the service stations.
The Time-Dependent Vehicle Routing Problem is a class of vehicle routing problems where the time to serve the customers vary and have to take into consideration the traffic conditions in the route. In order to collect the items from the various suppliers, the 3PL logistics transportation service provider must visit all scheduled suppliers during different opening hours. Some suppliers may further request visits within certain time windows. It is not always easy to meet the time window delivery requirement because the delivery processes are usually affected by traffic flow conditions. The traffic congestion during the rush hours might cause severe delays and
Figure 1. An example solution to a vehicle routing problem.
could make the buyers’ carriers fail the suppliers’ pickup requirement. Hence in order to pick-up items from the suppliers more efficiently, this study seeks to solve several challenging missions simultaneously among customers and suppliers, in a 3PL kind of arrangement, whereby the buyer’s vehicle visits the suppliers’ sites to pickup the items ordered, in an e-commerce setup, including: 1) to satisfy suppliers’ specific time windows; 2) to approximate travel time affected by urban traffic.
The basic vehicle routing problem with time windows (VRPTW) is further extended and the time dependent vehicle routing problem with time windows is studied and the efficiency of implementation using genetic algorithm and tabu search metaheuristics techniques is carried out and is compared. Every vehicle starts from the depot of the customer, visits all suppliers within the requested time windows, and then returns to the depot. Most suppliers’ time windows correspond to their business hours, which means vehicles cannot arrive early or late based on the time window. In order to reflect effect of traffic flow on vehicle travel time, a time-dependent constraint is added.
The VRPTW has been extensively examined and classified as a NP-hard problem (e.g. Fu, [7] ; Meng et al., [8] ). Solomon [9] first presented a mix integer programming (MIP) for the VRPTW and introduced a set of well-known benchmark problems now known as “Solomon Instances.” He subsequently designed and analysed algorithms for the VRPTW (Solomon, [9] ). To consider traffic congestion, the time-dependent traveling time is added into the VRPTW as the time-dependent vehicle routing problem with time windows (TDVRPTW). Malandraki & Daskin [10] discussed diversified traffic conditions at different times of the day; the time horizon is divided into M slices and then a constant travel time is assigned to each arc in every interval. The idea is sound; however, the discontinuous travel time settings may violate the first in, first out (FIFO) property. Hill & Benton [11] also considered TDVRP without time windows but based on time-dependent travel speed. Ichoua et al. [12] assigned a speed distribution to each arc during the time horizon and then obtained the travel time distribution by integration.
2. Literature Review
Many of the most successful meta-heuristics for the large VRPTW instances are based on some form of parallel computation. During the past few years, numerous papers have been written on generating good solutions for VRPTW with GAs. Genetic Algorithms (GA for short) are a class of adaptive heuristics based on the Darwinian concept of evolution survival of the fittest. A brief review of the relevant literature is given below.
2.1. Metaheuristics
Le Bouthiller and Crainic [13] have proposed a cooperative parallel meta-heuristic for the VRPTW, based on the solution warehouse strategy. Here several search threads cooperate asynchronously, exchanging information on the best solutions identified. The exchanges are performed through a mechanism called solution warehouse, which holds and manages a pool of solutions.
Blanton and Wainwright [14] were the first to apply a genetic algorithm to VRPTW. They hybridized a genetic algorithm with a greedy heuristic. Under this scheme, the genetic algorithm searches for a good ordering of customers while the construction of the feasible solution is handled by the greedy heuristic. Several papers present hybridizations of a GA with different construction heuristics Berger et al. [15] , local searches (Thangiah et al. [16] ; Potvin and Bengio, [17] ; Zhu [18] ) and other metaheuristics such as tabu search (Wee Kit [19] ) and ant colony system (Berger et al. [15] ).
Homberger and Gehring [20] propose a two-phase hybrid meta-heuristic for the VRPTW. The objectivefunction of the VRPTW considered here combines the minimization of the number of vehicles (primary criterion) and the total travel distance (secondary criterion). The aim of the first phase is the minimization of the number of vehicles by means of a (l; k)-evolution strategy, whereas in the second phase the total distance is minimized using a tabu search algorithm. Mester and Bräysy [21] present a new and effective metaheuristic algorithm, active guided evolution strategies, for the vehicle VRPTW. The algorithm combines the strengths of the guided local search and evolution strategies belonging to metaheuristics into an iterative two-stage procedure. Guided local search is used to regulate a composite local search in the first stage and the neighbourhood of the evolution strategies algorithm in the second stage.
Russel and Chiang [22] have used a scatter search metaheuristics to solve the VRPTW. Both a common arc method and an optimization-based set covering model are used to combine vehicle routing solutions. A reactive tabu search metaheuristic and a tabu search with an advanced recovery feature, together with a set covering procedure are used for solution improvement.
Alba and Dorronsoro [23] propose a cellular Genetic Algorithm (cGA) which is a kind of decentralized population based heuristic, which is used for solving CVRP, improving several of the best existing results so far in the literature. Our study shows a high performance in terms of the quality of the solutions found and the number of function evaluations (effort).
2.2. Genetic Algorithm
Genetic Algorithm was first developed by J. Holland at the University of Michigan in 1975. Solutions to a combinatorial problem are encoded as chromosomes. The chromosomes are evaluated for their fitness by an evaluation function, and good properties of a generation of solutions are propagated to a next generation.
Genetic algorithms typically have the following structure:
initialize timer generate a random population evaluate fitness
while not terminated do
{
increment timer
select the fittest parents
recombine genes of selected parents
introduce mutations
evaluate fitness
select survivors that will become the next generation
}
A typical genetic algorithm (GA) will start with a set of chromosomes called the initial population. Each chromosome represents a solution to the problem. The initial population is either randomly generated (in which case it would take longer time for the algorithm to converge to the solution) or generated using some form of heuristics (in which case the population is already closer to the solution, and would hence take less time to converge).
The next step in the GA method is the selection mechanism where the selection of the prospective parents based on their fitness is carried out and which is computed by the evaluation function. Their offspring will constitute the next generation. The selected parent chromosomes will then be recombined via the crossover operator to create a potential new population.
After the crossover process the next step will be to mutate a small number of the newly obtained chromosomes, in order to introduce a level of randomness that will preserve the GA from converging to a local optimum. A mutation is typically a random swap in the gene sequence, or a random negation of a bit if the chromosome was bit-encoded. Finally, new population will then be selected based on the fitness of the candidate chromosomes.
The genetic algorithm will continue through this process until a stopping criterion was met, which can be one of the following:
・ predefined number of generations has been produced
・ there was no improvement in the population, which would mean that the GA has found an optimal solution
・ a predefined level of fitness has been reached.
2.3. Time-Dependent Vehicle Routing Problem with Time Windows
Time dependent vehicle routing problems have received considerably little attention among researchers. The time dependent VRP was first formulated by Malandraki [24] and Malandraki and Daskin [10] using a mixed integer linear programming formulation. They proposed a greedy nearest-neighbor heuristic based on travel time between customers, as well as a branch and cut algorithm to solve TDVRP without time windows. Next Hill and Benton [11] considered a node-based time dependent vehicle routing problem (without time windows). Computational results for one vehicle and five customers were reported. Ahn and Shin [25] introduced certain modifications to the savings, insertion, and local improvement algorithms to better deal with TDVRP. In randomly generated instances, they reported reductions in computation time as a percentage of the “unmodified” savings, insertion, and local improvement algorithms. Malandraki and Dial [26] proposed a dynamic programming algorithm for the time-dependent traveling salesman problem, i.e. for a fleet of just one vehicle. A nearest-neighbor type heuristic was used to solve randomly generated problems.
An important property for time dependent problems is the First In-First Out (FIFO) property proposed by Ahn and Shin, [25] and Ichoua et al. [12] . A model which has a FIFO property guarantees that if a vehicle leaves customer i to go to customer j at any time t, any identical vehicle with the same destination leaving customer i at a time t + e, where e > 0, will always arrive later. This is an intuitive and desirable property though it is not present in all models. Earlier formulations and solutions methods, Malandraki [24] , Malandraki and Daskin [10] , Hill and Benton [11] , and Malandraki and Dial [26] , do not guarantee the FIFO property as reported by Ichoua et al. [12] . Later research efforts have modeled travel time variability using “constant speed” time periods which guarantees the FIFO property, as shown by Ichoua et al. [12] . Ichoua et al. [12] proposed a tabu search solution method, based on the work of Taillard et al. [27] , in order to solve time dependent vehicle routing problems with soft time windows. Fleischmann et al. [28] utilized a route construction method of savings and insertion, to solve uncapacitated time dependent VRP with and without time windows. They tested their algorithms in instances created from Berlin travel time data. Jung and Haghani [29] proposed a genetic algorithm to solve time dependent problems. Using randomly generated test problems, the performance of the genetic algorithm was evaluated by comparing its results with exact solutions (up to 9 customers and 15 time periods) and a lower bound (up to 25 customers and 10 time periods).
Donati et al. [30] proposed a solution that adapted the ant colony optimization metaheuristic and a local search improvement method which stores and updates the slack times or feasible delays. They used Solomon’s benchmark instances as the test data. More recently, Soler et al. [31] proposed a method to solve, optimally, TDVRP instances that are too small for practical purposes and was likely to experience exponential growth of computational time as a function of problem size. Dabia et al. [32] deals with a one-vehicle vehicle routing problem (TSP) using a dynamic programming approach. Kok [33] deals with the TDVRP with a focus on departure time optimization and driver break scheduling. The study by Kok uses a modification of the set of benchmark instances for the VRP with time dependent travel speeds proposed by an early working paper by Figliozzi [34] . Ichoua et al. [12] used the well-known Solomon’s 56 benchmark problems for the VRP with time windows. However, capacity constraints were not considered, optimal fleet size was given. An important real- life property found in transportation problems in the retail industry are time-dependent travel times, also known as dynamic travel times, where travel time depends on the time of departure, modeling traffic conditions such as rush hours.
The VRP with dynamic travel times is described by van Woensel et al. [35] , using queueing theory to obtain travel times, Kok et al. [36] proposing a post-processor to determine optimal departure times for the vehicle routes, and Kuo et al. [37] introduces a separate calculation model to calculate the total operation time of all vehicles, and uses a modified Tabu Search to optimize the sequence of customers visited in the routes. Bettinelli et al. [38] describes a version where multiple warehouses are considered, using a branch-and-cut-and-price algorithm. As the problem we study is NP-hard, the computation time to solve an instance to optimality increases exponentially with the size of the instance. Because of this we will use metaheuristics rather than exact algorithms. Rodger [39] developed a Bayesian Probabilistic Technique to determine the backorder levels and using a fuzzy clustering technique. The model developed was called the Fuzzy Feasibility Bayesian Probabilistic Estimation Model.To show the importance of considering both dimensions of uncertainty in system modeling (i.e., stochastic variability and imprecision), Tuysuz and Kahraman [40] used stochastic Petrinets together with fuzzy sets to model and analyze time-critical, dynamic, and complex systems. Toktas-Palut and Ulengin [41] coordinated the inventory policies in a decentralized supply chain with stochastic demand by means of contracts and modeled a queuing system in which centralized and decentralized models were developed. Their comparison of the optimal solutions to these models revealed that the supply chain needs coordination. This method by Rodger can be used to solve the TDVRPTW as well since the Fuzzy Bayesian Probabilistic technique can be used to solve dynamic vehicle routing, since there is uncertainty due to traffic conditions, time window constraints at the suppliers’ sites and changing peak traffic hours. Hence we can use this to solve the TDVRP variant as well.
3. Problem Formulation and Problem Definition
Using a traditional flow-arc formulation (Desrochers et al. [42] ), the time dependent vehicle routing problem with time windows can be described as follows. Let G = (V, A) be a graph where A = {(vi, vj): i ≠ j ˄ i, j Î V} is an arc set and the vertex set is V = (v0, 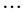 , vn+1). Vertices v0 and vn+1 denote the depot at which vehicles of capacity qmax are based. Each vertex in V has an associated demand qi ≥ 0, a service time gi ≥ 0, and a service time window [ei, li]; in particular the depot has g0 = 0 and q0 = 0. The set of vertices C = {v1,
, vn+1). Vertices v0 and vn+1 denote the depot at which vehicles of capacity qmax are based. Each vertex in V has an associated demand qi ≥ 0, a service time gi ≥ 0, and a service time window [ei, li]; in particular the depot has g0 = 0 and q0 = 0. The set of vertices C = {v1, 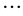 , vn} specifies a set of n customers. The arrival time of a vehicle at customer i, i.e. C is denoted ai and its departure time bi. Each arc (vi, vj) has an associated constant distance dij ≥ 0 and a travel time tij (bi) ≥ 0 which is a function of the departure time from customer i. The set of available vehicles is denoted K.
, vn} specifies a set of n customers. The arrival time of a vehicle at customer i, i.e. C is denoted ai and its departure time bi. Each arc (vi, vj) has an associated constant distance dij ≥ 0 and a travel time tij (bi) ≥ 0 which is a function of the departure time from customer i. The set of available vehicles is denoted K.
The cost per unit of route duration is denoted ct; the cost per unit distance traveled is denoted cd. It is assumed that the problem is feasible, i.e. it is always possible to feasibly serve any individual customer starting from the depot. The primary objective function for the TDVRP is the minimization of the number of routes or the number of vehicles utilized; the optimal number of routes is unknown. A secondary objective is the minimization of total time or distance travelled. There are two decision variables in this formulation;  is a binary decision variable that indicates whether vehicle k travels between customers i and j. The real number decision variable
is a binary decision variable that indicates whether vehicle k travels between customers i and j. The real number decision variable  indicates service start time for customer i served by vehicle k. The TDVRP is formulated as follows:
indicates service start time for customer i served by vehicle k. The TDVRP is formulated as follows:
Mathematical Model for Time Dependent VRPTW
The mathematical model of TDVRPTW is given as below.
Primary objective:
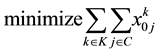 (1)
(1)
Secondary objective:
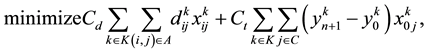 (2)
(2)
Subject to:
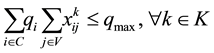 (3)
(3)
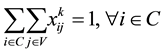 (4)
(4)
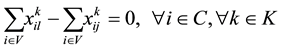 (5)
(5)
 (6)
(6)
 (7)
(7)
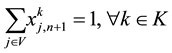 (8)
(8)
 (9)
(9)
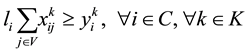 (10)
(10)
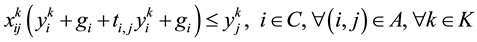 (11)
(11)


The primary and secondary objectives of the TDVRPTW are defined by (1) and (2) respectively. The constraints are defined as follows: the vehicle capacity should not be exceeded (3); all the customer must be served and exactly once (4); if a vehicle arrives at a customer it must also depart from that customer (5); routes must start and end at the depot (6); each vehicle leaves from and returns to the depot exactly once, (7) and (8) respectively; service times must satisfy time window start (9) and ending (10) times; and service start time must allow for travel time between customers (11). Decision variables type and domain are indicated in (12) and (13).
4. Methodology of Genetic Algorithm
In this section the methodology used to develop the genetic algorithm-based solution for the time-dependent VRP is given. A new crossover technique called the random insertion-based crossover (RIX) is described in detail and the pseudocode is also given for the algorithm.
4.1. Methodology Summary for Genetic Algorithm in Solving Time-Dependent Vehicle Routing Problem
Given in this section is the methodology of developing the algorithm using genetic algorithm with a new crossover technique. The GA and the crossover technique are explained below. The pseudo-code of the algorithm is also given.
4.2. Chromosome Representation
The representation of the chromosome as a set of genes representing the nodes in a route is shown below in Figure 2.
1) Assume that there are 7 elements in each array, where n = 7.
2) Arrays are of fixed length.
3) Each array represents a chromosome.
4) The elements of the array represent the genes in the chromosome.
5) c1, c2, 
6) Every customer is identified by a Customer ID/Node.
7) A road chromosome contains a list of elements or genes
8) Each element or gene contains a Customer ID/Node.
9) Genes whose value is −1 is considered not used, does not have a Customer ID.
10) E.g. c1, c2, c3 only used 3 genes in the array of 1 elements, rest of elements or genes in the array is placed with null value, −1.
11) The element of chromosome will be filled up with road id or customer id/node that forms a solution path.
12) From the chromosome, a three-element random segment is generated by a random probability process by generating a random number between 1 and 5 (1 ≤ n ≤ 5) This is because 3 genes are chosen and the last three genes will be the elements 5, 6 and 7 in a seven-element chromosome.
13) Element of chromosome will be placed a null value when the customer id of an element in this segment is found duplicate with other customer id contained in other elements.
14) The crossover operation is depicted in this crossover process.
Crossover operator is a major process of producing children solutions from current population. There are many methods for crossover operation according to different problems. An easy crossover operator named Random.
Insertion-based Crossover (RIX) is introduced below to fulfill the task. The crossover operation for a simple example with 7 demand points is shown in Figure 3.
The process is described as:
Step 1: Two chromosomes are randomly chosen as parents, then crossover chromosome segments are generated randomly.
Generation of two random integers is carried out, one is for crossover point, the other is for segment length, as Figure 3 (a);
Step 2: Swap the crossover genes segment, as Figure 3 (b);
Step 3: Validity checking carried out for the constraints of VRP, each demand point (customer node) can only be visited once, crossover gene segment kept intact, delete the same number in their parent, such as Figure 3 (c);
Step 4: Obtain two new chromosomes with crossover gene segment and saved to next generation, as shown in Figure 3 (d).
Figure 2. Chromosome sample 1.
Figure 3. Crossover operation.
15) The child chromosomes are tested for fitness values
16) Every road chromosome has its own fitness value, defined as fitness value, where
a) fitness value = The sum of Road Cost for every road in a route chromosome + Road_Not_Connected_Weight + PNCW
b) Road_Not_Connected_Weight is added to the fitness value when the path represented by the specified route chromosome is not connecting the source and destination location.
c) PNCW (Path_Not_Connected_Weight) is a weight that will add to the fitness value when an adjacent road is not connected. Otherwise, a weight will be deducted from the fitness value
d) The smaller the “fitness value” value, the stronger road chromosome is obtained.
The cost of using a road is defined as Route Cost, where
e) Every chromosome is initialized as the route which contains the source location and the destination location is fixed at the start and end of the array.
Each chromosome is a solution path.
4.3. Genetic Algorithm Used
The pseudo code for the genetic algorithm used for the TDVRPTW is depicted below.
Pseudo Code
1) Initialize populations
2) Set g = 0 where g = number of population.
a) While (g still less than proposed generation)
i) Select C1 chromosome using Tournament Selection Algorithm
ii) Select C2 chromosome using Tournament Selection Algorithm
iii) Select a segment of the 2 chromosomes for performing the crossover.
iv) Perform two-point random Cross-Over using the random insertion-based crossover (RIX) over the segments of the selected chromosomes C1 and C2
1) Let us assume I is the size of the chromosome.
2) Compute two random variables e1, e2 where 1 ≤ e1, e2 ≤ I
3) mi = 0 for all I = 1, 
4) For each i = e1, 
5) Refer to mask vector m, swap chromosome value at index i where mi = 1.
v) Sort the population chromosome based on fitness value before Mutation
vi) For population index which more than (Overlapping Value/100)*Population, perform Random Mutate operation.
6) For each i = 1, 
a) Compute a random value, e, where 0 < e < 1
b) If e ≤ mutation rate then replace the old element value at index i with a new generate value.
vii) Increase generation counter, g.
viii) Sort the chromosome set based on their fitness value.
ix) Repeat step (a).
4.4. Flow Chart Depicting the Genetic Algorithm Process
The flowchart in Figure 4, depicting the genetic algorithm process showing the various steps like the selection, crossover, mutation, etc. are shown below.
5. Results
The mathematical model for VRPTW is solved using MATLAB optimization software. The results obtained are shown. The graph of the VRPTW by using the mathematical model and giving the various input parameters such as problem size 100 nodes (customers), vehicle capacity (200), time window constraint, number of vehicles are given in the MATLAB implementation. The Solomon’s benchmark instance of C101 is taken as the test data input for the program. The results obtained from the mathematical model are shown in the Table 1 for the Solomon’s benchmark problem instance C101.
The input parameters are given as below:
Figure 4. Flowchart depicting the GA process.
1) Number of nodes (customer locations) = 100
2) Vehicle capacity = C1 = 200, C2 = 700, R1 = 200, R2 = 1000, RC1 = 200, RC2 = 1000
3) Number of Vehicles = 25
4) The demand at each customer location is given
5) Distance of the customer location from the depot and from each other is given in the distance matrix
The Genetic Algorithm metaheuristic for the time dependent vehicle routing problem with time windows wasimplemented using Visual C# as plugin and then it is added as a plugin in the HeuristicLab optimization software. The standard test data used as input for the solving the TDVRPTW using genetic algorithm is the Solomon’s 56 benchmark instances.
HeuristicLab is used to solve the TDVRPTW. The results are got by running the time-dependent VRPTW in the HeuristicLab using Genetic Algorithm for allthe 56 benchmark instances. The experiments were run on a computer with Windows 8.1 OS and an Intel Core i3, 1.70 GHz Processor (CPU). The installed memory (RAM) being 4 GB. The 56 benchmark instances are divided into 6 groups or classes C1, C2, R1, R2, RC1, RC2. The average number of vehicles utilized (number of routes), average distance travelled for each problem class and the average total travel time for each class is computed and compared with previous studies.
In this section the computational results on the problem with 100 nodes and constant travel speeds are presented, i.e., the original Solomon’s benchmark problem. The computational results on the problems with 100 nodes and constant travel speeds are presented in Table 2. Notice that for the best ever solution the primary objective is to minimise the number of vehicles and the secondary objective is to minimise the total distance travelled, which is the same objective of the study of Figliozzi [43] which uses constant speed problems. Referring to the Table 2 and Table 3, we can see that the results obtained in our study with respect to the average number of vehicles used and average distance travelled are very near the values obtained in the study by Figliozzi [43] . The cumulative values show the total average number of vehicles utilized for all the problem classes and the total average distance travelled for all the problem classes. The results of the current study are tabulated in Table 2 below:
CNV is the cumulative number of vehicles and CDT is the cumulative total distance travelled.
Further, the results obtained from this study are compared with the solutions from earlier studies on TDVRPTW for the problem instance R103, shown in Table 4. From the study of Figliozzi [43] , we can see that the number of vehicles utilized is 12.58, for the problem instance R103. This value is better than the current study. The total distance travelled is comparable with Figliozzi’s [43] study (1248 km). For the problem instance R103, the best known solution in terms of number of vehicles and travelled distances is presented order to order by Gambardella [38] . The Best ever results (Gamberdella [44] ) have a vehicle utilization of nearly 12 (two less than the present study), while the total distance travelled is 1210 km (53 km less than the present study). The total
Table 1. Results of the TDVRPTW using the mathematical model.
Table 2. Results of the TDVRPTW for 56 solomon’s benchmark instances using genetic algorithm.
Table 3. Figliozzi’s results of TDVRP for average number of vehicles and average distance travelled.
hours travelled is 47.9 in the present study which is slightly higher than that of the best ever of 45.49.
The Figure 6 represents the best solution for the TDVRPTW for the total distance travelled by all the vehicles for the problem instance R103.
The distance travelled graph is shown in Figure 5. The distance travelled has a best value of 1263 km in this study. The TDVRP solutions of this study are compared with the results obtained in previous studies for problem class R103 of Solomon’s benchmark instances and shown in Table 4. The different routes taken by all the vehicles to visit all the 100 nodes are shown in Figure 6.
Comparison with Best Result in Literature
Two independent samples t-test was conducted to compare the means of the distances travelled for the Solomon’s 56 benchmark instances between the best known solution (SINTEF [46] ) and the results of this study. From the t-test results in Table 5, it can be inferred that there is no significant difference in the mean distance travelled between the two groups.
Table 4. Comparison of the different solution algorithms for TDVRP problem class R103.
Table 5. T-test group statistics for comparing mean distance travelled between the best results and current study.
Figure 5. Distance travelled for Problem Instance R103.
Figure 6. Routes taken by the 14 Vehicles of the R103, 100 nodes problem instance.
6. Conclusion and Suggestions for Future Research
In this paper the time-dependent vehicle routing problem has been studied and a suitable metaheuristic, the genetic algorithm has been used to solve the TDVRPTW. A new crossover technique called the Random Insertion-based Crossover (RIX) has been developed. This crossover technique has been used to implement the TDVRP. A plug-in was developed using C# and Dot Net 4.5 framework. This plug-in was added to the HeuristicLab optimization software and experiments for the 56 Solomon’s benchmark instances for 100 customer nodes, 25 vehicles and each with a capacity of 200 were conducted. The results obtained were compared with the results of previous studies. While the number of vehicles utilized is slightly higher in this study using our GA method, the distance travelled is less than those reported in previous study. The mathematical model was also solved using MATLAB and the results have been tabulated. This study can be useful for planning the supplier site pickups by e-commerce companies, taking into consideration the traffic conditions during different periods of the day, where there will be peak traffic hours and off-peak traffic hours and they should also consider the time window requirements of the suppliers. Future researchers can implement the TDVRP using other metaheuristics and compare the efficiencies of the various metaheuristics.
Acknowledgements
This research was made possible due to the most invaluable contributions of researchers Mr. Andreas Scheibenpflug and Mr. Philipp Fleck of FH Hagenberg, Austria. The authors wish to express their deepest gratitude to the researchers for their help. The authors also wish to thank the reviewers of the paper for their very constructive and objective feedback and suggestions, which have been incorporated in this paper.
Cite this paper
Suresh NandaKumar,RamasamyPanneerselvam, (2015) A Time-Dependent Vehicle Routing Problem with Time Windows for E-Commerce Supplier Site Pickups Using Genetic Algorithm. Intelligent Information Management,07,181-194. doi: 10.4236/iim.2015.7474015
References
- 1. Solomon, M. (1987) Algorithms for the Vehicle Routing and Scheduling Problem with time Window Constraints. Operations Research, 35, 254-265. http://dx.doi.org/10.1287/opre.35.2.254
- 2. Malandraki, C. and Daskin, M.S. (1992) Time-Dependent Vehicle-Routing Problems—Formulations, Properties and Heuristic Algorithms. Transportation Science, 26, 185-200.
http://dx.doi.org/10.1287/trsc.26.3.185 - 3. Hill, A.V. and Benton, W.C. (1992) Modeling Intra-City Time-Dependent Travel Speeds for Vehicle Scheduling Problems. Journal of the Operational Research Society, 43, 343-351.
http://dx.doi.org/10.1057/jors.1992.49 - 4. Ichoua, S., Gendreau, M. and Potvin, J.Y. (2003) Vehicle Dispatching with Time-Dependent Travel Times. European Journal of Operational Research, 144, 379-396.http://dx.doi.org/10.1016/S0377-2217(02)00147-9
- 5. Le Bouthillier, A. and Crainic, T.G. (2005) A Cooperative Parallel Meta-Heuristic for the Vehicle Routing Problem with Time Windows. Computers & Operations Research, 32, 1685-1708.
http://dx.doi.org/10.1016/j.cor.2003.11.023 - 6. Blanton, J.L. and Wainwright, R.L. (1993) Multiple Vehicle Routing with Time and Capacity Constraints Using Genetic Algorithms. In: Forrest, S., Ed., Proceedings of the 5th International Conference on Genetic Algorithms, Morgan Kaufmann Publishing, San Francisco, 452-459.
- 7. Berger, J., Salois, M. and Begin, R.A. (1998) Hybrid Genetic Algorithm for the Vehicle Routing Problem with Time Windows. Lecture Notes in Artificial Intelligence, 1418, 114-127.
- 8. Thangiah, S.R., Osman, I.H. and Sun, T. (1995) Hybrid Genetic Algorithms, Simulated Annealing and Tabu Search Methods for Vehicle Routing Problems with Time Windows. Technical Report UKC/OR94/4, Institute of Mathematics and Statistics, University of Kent, Canterbury.
- 9. Potvin, J.-Y. and Bengio, S. (1996) The Vehicle Routing Problem with Time Windows—Part II: Genetic Search. INFORMS Journal on Computing, 8, 165-172. http://dx.doi.org/10.1287/ijoc.8.2.165
- 10. Zhu, K.Q.L. (2000) A New Genetic Algorithm for VRPTW. National University of Singapore.
- 11. Wee Kit, H., Chin, J. and Lim, A. (2001) A Hybrid Search Algorithm for the Vehicle Routing Problem with Time Windows. International Journal on Artificial Intelligence Tools, 10, 431-449.
http://dx.doi.org/10.1142/S021821300100060X - 12. Homberger, J. and Gehring, H. (2005) A Two-Phase Hybrid Meta-Heuristic for the Vehicle Routing Problem with Time Windows. European Journal of Operational Research, 162, 220-238.
http://dx.doi.org/10.1016/j.ejor.2004.01.027 - 13. Mester, D. and Brãysy, O. (2005) Active Guided Evolution Strategies for Large-Scale Vehicle Routing Problems with Time Windows. Computers & Operations Research, 32, 1593-1614.
http://dx.doi.org/10.1016/j.cor.2003.11.017 - 14. Russell, R.A. and Chiang W.-C. (2006) Scatter Search for the Vehicle Routing Problem with Time Windows. European Journal of Operational Research, 169, 606-622.
http://dx.doi.org/10.1016/j.ejor.2004.08.018 - 15. Alba, E. and Dorronsoro B. (2005) The Exploration/Exploitation Tradeoff in Dynamic Cellular Genetic Algorithms. IEEE Transactions on Evolutionary Computation, 9, 126-142.
http://dx.doi.org/10.1109/TEVC.2005.843751 - 16. Malandraki, C. (1989) Time Dependent Vehicle Routing Problems: Formulations, Solution Algorithms and Computational Experiments. PhD Dissertation, Northwestern University, Evanston.
- 17. Shin Ahn, B.-H. and Shin, J.Y. (1991) Vehicle-Routing with Time Windows and Time-Varying Congestion. Journal of the Operational Research Society, 42, 393-400.
http://dx.doi.org/10.1057/jors.1991.81 - 18. Desrochers, M., Lenstra, J.K., Savelsbergh, M.W.P. and Soumis, F. (1988) Vehicle Routing with Time Windows: Optimization and Approximation. Vehicle Routing: Methods and Studies, 16, 65-84.
- 19. Figliozzi, M.A. (2012) The Time Dependent Vehicle Routing Problem with Time Windows: Benchmark Problems, an Efficient Solution Algorithm, and Solution Characteristics. Transportation Research Part E, 48, 616-636. http://dx.doi.org/10.1016/j.tre.2011.11.006
- 20. Gambardella, L.M. (1999) MACS-VRPTW: A Multiple Ant Colony System for Vehicle Routing Problems with Time Windows. McGraw-Hill, London, 63-76.
- 21. Stegers, E. (2009) A Solution Method for Vehicle Routing Problems with Time-Dependent Travel Times. Masters Thesis, Delft University of Technology, Delft.
- 22. SINTEF. Solomon’s Benchmark Instances.
https://www.sintef.no/projectweb/top/vrptw/solomon-benchmark/ - 23. Toktas-Palut, P. and Ulengin, F. (2011) Coordination in a Two-Stage Capacitated Supply Chain with Multiple Suppliers. European Journal of Operational Research, 212, 43-53.
http://dx.doi.org/10.1016/j.ejor.2011.01.018 - 24. Tuysuz, F. and Kahraman, C. (2010) Modeling a Flexible Manufacturing Cell Using Stochastic Petri Nets with Fuzzy Parameters. Expert Systems with Applications, 37, 3910-3920.
http://dx.doi.org/10.1016/j.eswa.2009.11.026 - 25. Rodger J.A. (2014) Application of a Fuzzy Feasibility Bayesian Probabilistic Estimation of Supply Chain Backorder Aging, Unfilled Backorders, and Customer Wait Time Using Stochastic Simulation with Markov Blankets. Expert Systems with Applications, 41, 7005-7022.
http://dx.doi.org/10.1016/j.eswa.2014.05.012 - 26. Bettinelli, A., Ceselli, A. and Righini, G. (2011) A Branch-and-Cut-and-Price Algorithm for the Multi-Depot Heterogeneous Vehicle Routing Problem with Time Windows. Transportation Research Part C, 19, 723-740. http://dx.doi.org/10.1016/j.trc.2010.07.008
- 27. Kuo, Y., Wang, C.-C. and Chuang, P.-Y. (2009) Optimizing Goods Assignment and the Vehicle Routing Problem with Time-Dependent Travel Speeds. Computers and Industrial Engineering, 57, 1385-1392.
http://dx.doi.org/10.1016/j.cie.2009.07.006 - 28. Kok, A.L., Hans, E.W. and Schutten, J.M.J. (2011) Optimizing Departure Times in Vehicle Routes. European Journal of Operational Research, 210, 579-587.
http://dx.doi.org/10.1016/j.ejor.2010.10.017 - 29. van Woensel, T., Kerbache, L., Peremans, H. and Vandaele, N. (2008) Vehicle Routing with Dynamic Travel Times: A Queueing Approach. European Journal of Operational Research, 186, 990-1007.
http://dx.doi.org/10.1016/j.ejor.2007.03.012 - 30. Figliozzi, M.A. (2009) A Route Improvement Algorithm for the Vehicle Routing Problem with Time Dependent Travel Times. Proceedings of the 88th Transportation Research Board Annual Meeting, Washington DC, 11-15 January, 616-636.
- 31. Kok, A.L. (2010) Congestion Avoidance and Break Scheduling within Vehicle Routing. PhD Thesis, University of Twente, Enschede.
- 32. Dabia, S., Van Woensel, T. and De Kok, A.G. (2010) A Dynamic Programming Approach to Multi-Objective Time-Dependent Capacitated Single Vehicle Routing Problems with Time Windows. Working Paper 313, Eindhoven University of Technology, School of Industrial Engineering, Netherl-ands.
- 33. Soler, D., Albiach, J. and Martínez, E. (2009) A Way to Optimally Solve a Time-Dependent Vehicle Routing Problem with Time Windows. Operations Research Letters, 37, 37-42.
http://dx.doi.org/10.1016/j.orl.2008.07.007 - 34. Donati, A.V., Montemanni, R., Casagrande, N., Rizzoli, A.E. and Gambardella, L.M. (2008) Time Dependent Vehicle Routing Problem with a Multi Ant Colony System. European Journal of Operational Research, 185, 1174-1191. http://dx.doi.org/10.1016/j.ejor.2006.06.047
- 35. Jung, S. and Haghani, A. (2001) Genetic Algorithm for the Time-Dependent Vehicle Routing Problem. Transportation Research Record, 1771, 164-171. http://dx.doi.org/10.3141/1771-21
- 36. Fleischmann, B., Gietz, M. and Gnutzmann, S. (2004) Time-Varying Travel Times in Vehicle Routing. Transportation Science, 38, 160-173. http://dx.doi.org/10.1287/trsc.1030.0062
- 37. Taillard, E., Badeau, P., Gendreau, M., Guertin, F. and Potvin, J.-Y. (1997) A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows. Transportation Science, 31, 170-186.
http://dx.doi.org/10.1287/trsc.31.2.170 - 38. Malandraki, C. and Dial, R.B. (1996) A Restricted Dynamic Programming Heuristic Algorithm for the Time Dependent Traveling Salesman Problem. European Journal of Operational Research, 90, 45-55.
http://dx.doi.org/10.1016/0377-2217(94)00299-1 - 39. Meng, Q., Lee, D.H. and Cheu, R.L. (2005) Multiobjective Vehicle Routing and Scheduling Problem with Time Window Constraints in Hazardous Material Transportation. Transportation Engineering, 131, 699-707. http://dx.doi.org/10.1061/(ASCE)0733-947X(2005)131:9(699)
- 40. Fu, L. (2002) Scheduling Dial-A-Ride Paratransit under Time-Varying, Stochastic Congestion. Transportation Research Part B, 36, 485-506. http://dx.doi.org/10.1016/S0191-2615(01)00014-5
- 41. Cordeau, J.-F., Gendreau, M., Hertz, A., Laporte, G. and Sormany, J.S. (2005) New Heuristics for the Vehicle Routing Problem. In: Langevin, A. and Riopel, D., Eds., Logistics Systems: Design and Optimization, Springer, New York, 279-297. http://dx.doi.org/10.1007/0-387-24977-x_9
- 42. Gendreau, M., Laporte, G. and Potvin, J.-Y. (2002) Metaheuristics for the VRP. In: Toth, P. and Vigo, D., Eds., The Vehicle Routing Problem, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, 129-154. http://dx.doi.org/10.1137/1.9780898718515.ch6
- 43. Laporte, G. (1992) The Vehicle Routing Problem: An Overview of Exact and Approximate Algorithms. European Journal of Operational Research, 59, 345-358.
http://dx.doi.org/10.1016/0377-2217(92)90192-C - 44. Clarke, G. and Wright, J.R. (1964) Scheduling of Vehicle Routing Problem from a Central Depot to a Number of Delivery Points. Operations Research, 12, 568-581.
http://dx.doi.org/10.1287/opre.12.4.568 - 45. Dantzig, G. and Ramser, J. (1959) The Truck Dispatching Problem. Management Science, 6, 80-91.
http://dx.doi.org/10.1287/mnsc.6.1.80 - 46. Bullnheimer, B., Hartl, R.F. and Strauss, C. (1997) Applying the Ant System to the Vehicle Routing Problem. Department of Management Science, University of Vienna.