Intelligent Information Management
Vol.06 No.06(2014), Article ID:51228,22 pages
10.4236/iim.2014.66025
An Integrated Multi-Echelon Model for a Sustainable Closed Loop Supply Chain Network Design
Muthusamy Aravendan1, Ramasamy Panneerselvam2
1Department of Leather Design (Footwear & Products), National Institute of Fashion Technology, Chennai, India
2Department of Management Studies, School of Management, Pondicherry University, Pondicherry, India
Email: aravendan@yahoo.com, panneer_dms@yahoo.co.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2014; revised 2 October 2014; accepted 31 October 2014
ABSTRACT
The integration of entire supply and value chain into a closed loop network is gaining more importance in recent times in order to ensure a business to be economically and environmentally sustainable with the changing trends in business and social environments, growing environmental consciousness in the society and government legislations to protect the environment as well as the business. In this context, this paper considers a multi-echelon closed loop supply chain network design with forward and reverse logistics components. An attempt has been made to develop a mixed integer non-linear programming model for this problem with different costs so that the sum of the total cost is minimized subject to different constraints pertaining to capacities of the entities of the system, demands of first customers and second customers. A generalized model is presented and then its application is illustrated using an example problem by solving the model using LINGO14. This model forms as a tool to compare future meta-heuristics to check the closeness of their solutions with corresponding optimal solutions.
Keywords:
Closed Loop, Forward, Integrated Model, Multi-Echelon, MINLP, Network Design, Responsiveness, Reverse, Sustainable

1. Introduction
A supply chain network design is the most important strategic decision of supply chain management for any business firm where the network is designed sequentially to link supplier, manufacturer, distributors/wholesalers, retailers and customers, and organization of flow in the channels between them to acquire raw materials, pro- cessing and converting them into finished goods or products, and distribute them through an efficient channel to the end customers. Supply chain network design decisions include the assignment of facility role, location of manufacturing, storage or transportation-related facilities and the allocation of capacity and markets to each facility.
The role played and the processes performed at the facility are significant because they determine the amount of flexibility the supply chain has in changing the way it meets demand. Location of facility has a long-term impact on a supply chain’s performance because it is very expensive to close down a facility or move it to a different location. A good location decision can help a supply chain to be responsive, while keeping it cost low. In contrast, a poorly located facility makes it very difficult for a supply chain to perform close to the efficient frontier. Capacity allocation to each facility also has a significant impact on supply chain performance as it impacts the responsiveness and the cost of the supply chain. Market and supply resources to facilities have a significant impact on the supply chain performance because they affect the total production, inventory and transportation costs incurred by the supply chain to satisfy customer demands. This decision should be reconsidered on a regular basis so that the allocation can be changed as market conditions or plant capacities change. Of course, the allocation of markets and supply resources can only be changed if the facilities are flexible enough to serve different markets and receive supply from different sources. These network design decisions determine the supply chain configuration and set of constraints within which the other supply chain drivers can be used to decrease supply chain cost and to increase responsiveness. All the network design decisions affect each other and hence this must be taken into consideration while designing the network.
There is a change in the trends of designing and establishing the supply chain network due to the changing business and social environments, growing environmental consciousness in the society and government legislations to protect the environment and also due to uncertainty of likes, interests and demands of the customers in recent years. Many big companies dealing with industrial machinery, consumer electronics, computers & peripherals, automobiles, home appliances, fashion apparels, luxury lifestyle products, fast moving consumer goods, etc. have started focusing on product recovery activities by collecting the product returns from the customers. The recoverable products and parts of the returned products are repaired, remanufactured, refurbished, recycled and redistributed back to the first and second customers in the market. The business factors are related to the economic benefits of using returned products and liberal return policies for gaining customer satisfaction and attracting more customers. Therefore, a proper and systematic reverse logistics network integrated with the forward logistics network becomes very essential and inevitable in the present economic, social and business environments.
In this paper, we propose an integrated forward-reverse logistics model for a closed loop network design which addresses the problem of escalating costs in establishing and implementing an effective supply chain network. Concepts of hybrid processing facilities are incorporated in the network to reduce the fixed costs of the facilities. Minimization of un-utilized capacity cost is also considered as the elimination of inventory cost and avoidance of penalty cost due to the fulfillment of the customers’ known demands, for minimizing the overall cost of the proposed network model. The model also increases the responsiveness and quality service to the customers by meeting the complete demand through prompt supply of products in both forward and reverse chains and also by providing the efficient service through the repair/service center.
The structure of the paper is framed as follows. The related literature is reviewed in Section 2. The concerned problem is defined in Section 3. The model description, assumptions & limitations and model formulation of the proposed integrated multi-echelon model for the closed loop network design are presented in Section 4, Section 5 and Section 6 respectively. The demonstration of the model is presented in Section 7. The discussion on results and directions for future research are covered in Section 8 and finally the concluding remarks are given in Section 9.
2. Literature Review
The concept of closed loop supply chains is now widely gaining importance as a result of the recognition that both the forward and reverse supply chains need to be managed jointly. The configuration of both forward and reverse supply chain networks has a strong influence on the performance of each other. Therefore to avoid the sub-optimality resulting from the separated design, the design of the forward and reverse supply chain networks should be integrated. In this section, we reviewed, analyzed and presented the literature of the previous researchers on the closed loop and reverse supply chain network models.
Krikke et al. [1] developed a quantitative model for concurrent product design considering the modularity, reparability and recyclability, and closed loop supply chain design with an application to refrigerators. They executed the model for different scenarios using different parameters settings like centralized versus decentralized processing, alternative product designs, varying quality and quantity, and potential environmental legislation based on producer responsibility. Schultmann et al. [2] presented modeling of reverse logistics tasks within closed loop supply chains based on an example considering the end of life vehicle (ELV) treatment practiced in the automobile industry of Germany. They proposed different design options for a closed loop supply chain concentrating on the handling of the reverse material flows to reintegrate them into their genuine supply chains. They modeled the reverse logistics aspects with vehicle routing planning and developed a problem-tailored algorithm.
Salema et al. [3] proposed an optimization model for the design of a capacitated multi-product reverse network with uncertainty. They considered capacity limits, multi-product management and uncertainty on product demands in order to contemplate the generic network design for reverse logistics. The model is solved by developing a mixed integer formulation and solved using B&B techniques. Staikos and Rahimifard [4] presented a decision-making model for waste management in the footwear industry through reverse logistics model which investigated into the steps required to consider the end-of-life implication of shoes and promote post-consumer recycling practices in the industry. In the product recovery process, they included the recycle, repair/reuse, land- filling and incineration operations to minimize the cost and EOL wastage for an environmentally sustainable network model. Ko and Evans [5] developed an optimization model and associated algorithm to design an integrated logistics network for 3PL providers. They considered the simultaneous flow of forward and reverse logistics network and presented a mixed integer nonlinear programming model which is a multi-period, two-echelon, multi-commodity, capacitated network design problem. They proposed a method which includes GA-based heuristic with genetic operations and transshipment algorithm to solve the problem. Lu and Bostel [6] presented a two level location model with three types of facility in a specific reverse logistics system named Remanufacturing Network (RMN) in which the forward and reverse flows are simultaneously considered. An algorithm based on the Lagrangian heuristic approach was proposed to solve the problem.
Du and Evans [7] designed a bi-objective logistics network for post-sale service to address the minimization of the overall costs and minimization of the total tardiness of cycle time. They adopted a solution approach consists of three algorithms: scatter search, the dual simplex method and the constraint method for solving this bi- objective model. Both installation costs and transportation costs in the first objective function involve in the trade-off relationship with the second objective. The optimization for the first objective function leads to a centralized network structure and that of the second objective function leads to a decentralized network structure. Lee and Dong [8] adopted a heuristic approach to logistics network design for end of lease computer products recovery. They first developed a mathematical model for the integration of forward and reverse distribution network design and the locations of facilities jointly used by forward and reverse logistics operations. Then they developed a two-stage heuristic algorithm as the first attempt in solving the integrated forward and reverse logistics network design problem using meta-heuristics. A tabu search is also applied to obtain the improved solution of shipping the returned products.
Lee and Dong [9] explored a stochastic approach for the dynamic reverse logistics network design under uncertainty. They developed a two stage stochastic programming model which integrates the SAA method with a SA based heuristic algorithm. It provides an efficient framework for identifying and statistically solving the large scale dynamic network problems. Lin et al. [10] formulated an integrated multi-stage logistics network model by considering the direct shipment and direct delivery of logistics and inventory. A mixed integer programming model is formulated with an objective function to minimize the sum of transportation cost, inventor holding cost, fixed ordering cost and open cost of facilities. They addressed the problem as location-allocation problem combined with lot sizing problem which is NP hard in nature. An effective hybrid evolutionary algorithm is proposed to solve this much larger and more complex problem. Mutha and Pokharel [11] presented a model for strategic network design of reverse logistics and remanufacturing using new and old product modules. They assumed that the returned products are consolidated in the warehouse before they are sent to reprocessing centers for inspection and dismantling. Dismantled parts are sent for remanufacturing or to the secondary market as spare parts. On simulating the model with different quantities of returned products, it is concluded that it might be beneficial to locate processing centers at location where resources viz., labour, energy and land are cheaper and to locate remanufacturing centers at places where new modules of the remanufactured products are available at cheaper rate. Salema et al. [12] presented a strategic and tactical model for closed loop supply chain. They integrated the strategic network design decisions with the tactical decisions like production, storage and distribution planning and achieved the integration by considering the micro and macro time scales. They also formulated a mixed integer linear programming and solved the model using standard branch & bound techniques.
Dahel [13] considered the design of a multi-echelon, closed loop supply chain network and the planning of product recovery for remanufacturing under uncertainty. In the network, the author included a number of plants and disassembly centers of unknown location and a number of customer zones and disposal sites at fixed locations. The author modeled it as a multi-period cost minimizing stochastic programming problem to determine the location of plants and disassembly centers and to specify the optimal remanufacturing/production quantities as well as the number of used products to be collected and disassembled for recovering adequate cores to maintain product flows between the various facilities in the supply chain. Salema et al. [14] proposed a multi-period and multi-product network model for designing and planning the supply chains with reverse flows simultaneously. They employed a graph approach. They strategically designed the supply chain to deal simultaneously the tactical planning of its operations which include supply, production, storage and distribution.
El-Sayed et al. [15] developed a multi-period, multi-echelon forward-reverse logistics network design under risk. The network structure includes three echelons in the forward direction (suppliers, facilities and distribution centers) and two echelons in the reverse direction (disassembly and redistribution centers), first customer zones in which the demands are stochastic and second customer zones in which the demand is assumed to be deterministic. They formulated the problem in a stochastic mixed integer linear programming (SMILP) decision making form as a multi-stage stochastic program to maximize the total expected profit. Pishvaee et al. [16] proposed a model for integrated logistic network design to address the issues due to increasing network costs and network responsiveness in supply chain and reverse logistics. They presented a bi-objective mixed integer non-linear programming (MINLP) model for the integrated forward and reverse logistics network design. The researchers designed a multi-objective memetic algorithm with dynamic local search mechanism (MOMA) to solve the model with non-dominated set of solutions. The proposed model outperformed the multi objective genetic algorithm (MOGA) of Altiparmark et al. (2006) in terms of average ratio of Pareto-optimal solutions obtained. On comparison with LINGO, MOMA obtained a reasonable quality of solutions on the multiple capacity test problems. Wang and Hsu [17] proposed a closed loop model for the logistics planning by formulating a cyclic logistics network problem into an integer linear programming model. As the model is NP hard in nature and complicated to solve, an efficient algorithm was proposed based on a determinant encoding approach, to revise the existing spanning- tree based genetic algorithm. The researchers evaluated the algorithm, compared with LINGO and CPLEX for its accuracy and reported the results.
Khajavi et al. [18] presented an integrated forward/reverse logistics network optimization model for multi- stage capacited supply chain network. The model is proposed by formulating the generalized logistics network problem into a bi-objective mixed-integer programming model to minimize the total costs and maximize the responsiveness of the CLSC network simultaneously. The proposed model was able to integrate the forward and reverse logistics network design decisions to avoid the sub-optimality resulted from separated and sequential designs. Liao and Rachmat [19] proposed a mathematical model for a multi-product reverse logistics for third party logistics (3PLs) by considering uncertain conditions in a multi-echelon network to minimize the total cost of the reverse logistics. The model is solved with LINGO. The model decreases the total cost of the reverse logistics managed by a 3PL by 13.8%. Pishvaee et al. [20] proposed a robust optimization model to closed-loop supply chain network design under uncertainty. They developed a deterministic mixed-integer linear programming model for designing the network and presented its robust counterpart using the recent extensions in robust optimization theory. The solutions of the robust optimization model were compared with that of the deterministic MILP model under different test problems. They found that the robust model is superior in both handling the uncertain data and the robustness of the solutions than the deterministic MILP model. Nandita [21] proposed a reverse logistics model for the apparel product acquisition via two channels viz., used garment collectors and used garment importers in the Indian apparel market. The author also presented the recovery process of the used garments as per their value potential and level of reconditioning required, and examined the reconditioning, reconstruction and recycling processes in the reverse logistics chain for the redistribution and sales in the apparel aftermarket in India.
Nenes and Nikolaidis [22] presented a MILP model for optimizing the decisions of a remanufacturing company carrying out procurement, remanufacturing, salvaging and stocking of used products for multiple periods of time. The result indicates that the potential profitability of using the proposed model over the simple alternative of using multiple times for a single period model may be substantial. Ozkir and Basligil [23] proposedmodeling of product recovery processes in closed loop supply chain network design, where a mixed integer linear programming model was applied to obtain CLSC network design in which the recovery process occurs as material recovery, component recovery and product recovery. Piplani and Saraswat [24] adapted robust optimization approach to design service networks for reverse logistics. They proposed a mixed-integer linear programming (MILP) model to minimize the total cost subject to flow balance and logical constraints. They first determine the kind of facilities to be used in the network model and associated flows. Then they developed a min-max robust optimization model to address the uncertainties like number of product returns, percent of faulty products and warranty fraction of modules. Vahdani et al. [25] presented a reliable design of a forward-reverse logistics network under uncertainty. They developed a bi-objective mathematical programming formulation that reduces the total costs and the expected transportation costs after failures of facilities of a logistic network. They introduced a hybrid solution methodology by combining robust optimization approach, queuing theory and fuzzy multi-objective programming.
Ramezani et al. [26] presented a new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level. They included three echelons in forward flow viz. suppliers, plants and distribution centers and two echelons in the backward flow viz. collection centers and disposal centers. They evaluated the systematic supply chain configuration maximizing the profit, customer responsiveness and quality to achieve the objectives of the network. Rosa et al. [27] presented a robust sustainable bi-directional logistics network design under uncertainty which handles a network of multiple supply stages, including production allocations, uncertain data development, facility locations and flexible capacity adjustments. They first introduced a detailed deterministic model assessing the impact of incorporating reverse logistics into a forward-oriented supply chain then extended it to a robust capacitated facility location model, which minimizes the expectations of relative regrets for a set of scenarios over a multi-period planning horizon, by considering uncertainty in supplying and collecting goods.
Subramanian et al. [28] considered a closed loop supply chain and addressed the issues of designing the network and of optimizing the distribution. They considered four variants of the problems and modeled it as an integer linear programming. They developed a constructive heuristic based on Vogel’s approximation method-total opportunity cost method to provide good initial solutions to a priority based simulated annealing heuristic to accelerate its convergence. Mahmoudi et al. [29] proposed mathematical modeling for minimizing costs in a multi- layer, multi-product reverse supply chain. They presented an integer linear programming model for multi-layer, multi product reverse supply chain that minimizes the products and parts transportation costs among centers and also sites launch, operation parts, maintenance and remanufacturing costs at the same time. The model was solved and validated using LINGO 9 software. Eskandarpur et al. [30] proposed a multi objective post sales network design model to minimize total fixed and variable costs, total tardiness and environmental pollution. They developed a parallel multi-objective heuristic based on variable neighbourhood search (VNS) to tackle the model and to find Pareto-optimal solutions. They compared the efficiency of the proposed method with an available efficient multi-objective memetic algorithm (MOMA) and compared the results with those of branch and bound methods of two commercial optimization packages for small and medium sized instances.
Hafeti and Jolai [31] proposed a robust and reliable network design for forward-reverse logistics design which simultaneously takes care of uncertain parameters and facility disruptions in the network. They proposed a mixed integer linear programming model with augmented p-robust constraints considered to control the reliability of the network during disruptions thereby reducing the nominal cost and disruptions risks. They compared the performance of the augmented p-robust criterion with that of the other conventional robust criteria. Keyvanshokooh et al. [32] developed a dynamic pricing approach for returned products in an integrated forward/reverse logistics network design in order to determine the acquisition price of the used products to find out the percentage of returned products collected from customer zones. They developed a mixed integer linear programming to consider the dynamic pricing for used products, supply chain network configuration and inventory decisions. They solved the model using CPLEX for few test problems and showed that the effect of a dynamic pricing of used products versus the static pricing and also showed that the linearization of pricing concept for this model have the acceptable solution. Diabat et al. [33] developed a multi-echelon reverse logistics network for product returns to minimize the total reverse logistics cost, which includes the costs of renting, carrying inventory, handling materials, set up and shipping. They developed a mixed integer non-linear programming (MINLP) model to arrive at the number and location of initial collection points and centralized return centers required for an effective return and collection system, and also the maximum holding time (collection frequency) for aggregation of small volumes of returned products into large shipments. They implemented and compared the genetic algorithm and artificial immune system for solving the model.
Amin and Zhang [34] presented a multi-objective facility location model for closed-loop supply chain network under uncertain demand and return. They investigated the CLSC network which includes multiple plants, collection centers, demand markets and products. They proposed a mixed integer linear programming model that minimizes the total cost. Cardoso et al. [35] developed a mixed integer linear programming for the design and planning of supply chains with reverse flows by simultaneously considering the production, distribution and reverse logistics activities for which the product demand is uncertain. The model defines the maximization of the expected net present value and provides details on sizing and location of plants, warehouses and retailers, definition of processes to install, establishment of forward and reverse flows and inventory levels to achieve. Devika et al. [36] presented the design of a sustainable closed loop supply chain network to cover the gap in the quantitative modeling by considering the social impacts, environmental impacts and economic impacts in the network design problem. They developed three new hybrid meta-heuristic methods based on adapted imperialist competitive algorithms and variable neighbourhood research, to solve this NP hard problem. They compared the algorithms with each other and also with other strong algorithms to assess the efficiency and effectiveness of the proposed algorithms.
3. Problem Definition
The closed loop supply chain network model proposed in this paper is a multi-echelon and multi stage network which includes manufacturers, wholesalers, retailers and first customers in the forward chain and service/repair centers, collector/dismantler/re-furbisher(CDR), remanufacturers, recyclers, disposal centers/land-fillers, resellers and second customers in the reverse chain. The network deals with the two types of product returns i.e. product returns due to repair and product returns due to end of use or life, in its reverse chain. The repair products are sent directly to the repair/service centre by the first customer for getting them repaired and the end of life products are returned either directly or through the retailer to the collector/dismantler/re-furbisher by the first customer for re-processing. The returned products thus collected in the CDR locations are sorted; parts are dismantled and segregated into recoverable and non-recoverable or waste items. The recoverable items are again segregated into re-furbishable, remanufacturable, recyclable items and shipped to the respective facilities or locations for recovery process. The non-recoverable or the waste items are shipped to the disposal centers/Land- fillers and disposed through land filling or incineration. The recovered products through the process of refurbishing and remanufacturing are shipped to the second customers via resellers. The items recovered through recycling process are shipped to the raw material suppliers market by the recycler. Based on these discussions, it is clear that the returned products due to EOL are shipped from the first customers to the recovery facilities through a push mechanism and recovered products are shipped from the recovery facilities to the second customers through a pull logistics mechanism. In this context, the objective of the proposed model is to minimize the total cost which is the sum of the costs of both forward and reverse supply chains there by increasing the total profit of the closed loop network.
4. Model Description
The proposed model is the formulation for the closed loop network design problem which integrates both forward and reverse logistics in the supply chain. The closed loop network presented in this paper is a single product, single period and multi-echelon supply chain which channelizes manufacturers, wholesalers, retailers and first customers in the forward chain and channelizes repair/service centers, collectors/dismantlers/re-furbishers, remanufacturers, recyclers, land fillers, resellers and second customers in the reverse chain as shown in Figure 1.
Figure 1. Integrated framework of forward and reverse supply chain network.
The variables of the entities in Figure 1 are presented below:
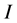 is the number of manufacturers/remanufacturers;
is the number of manufacturers/remanufacturers;
 is the number of wholesalers;
is the number of wholesalers;
 is the number of retailers;
is the number of retailers;
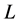 is the number of first customers;
is the number of first customers;
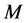 is the number of repair/service centers;
is the number of repair/service centers;
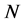 is the number of collectors/dismantlers/re-furbishers;
is the number of collectors/dismantlers/re-furbishers;
 is the number of land-fillers;
is the number of land-fillers;
 is the number of recyclers;
is the number of recyclers;
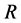 is the number of resellers;
is the number of resellers;
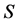 is the number of second customers.
is the number of second customers.
As shown in the closed loop network design model, in the forward supply chain, the manufacturers are responsible for manufacturing new or virgin products and supplying them to the wholesalers for distribution. The wholesalers are responsible for the distribution of new products to the retailers in their region. The retailers are responsible for selling the new products to the first customers as per their demands and also responsible for facilitating the after sales service. The customers’ nodes represent one or more customers or a group of customers. The first customers are responsible to return the products supplied to them as per the demand, either during the usage or after the usage of the products as either repair product returns or end of life product returns (EOL) respectively.
In the reverse supply chain, the first customers return the repair products to the service/repair centre for getting them repaired and to reuse. The repair/service centers are responsible for providing the quality service to the customers and to ensure the prompt delivery of the repaired products to the first customers for reuse. The end of life products are returned to the collector/dismantler/re-furbisher (CDR) either directly or via retailers by the first customers. These CDR locations are responsible for collecting, dismantling and sorting the returned products and dismantled parts for refurbishing, remanufacturing, recycling and disposing via landfill or incineration. They are also responsible for supplying the remanufacturable to the manufacturers, recyclable to the recyclers, disposables to the land-fillers/incinerators. The CDR locations recondition the refurbishable products and distributing them directly to the resellers. The resellers also receive the remanufactured products from the remanufacturers and they sell both remanufactured and refurbished products to the second customers as per their demands. The recyclers are responsible for recycling the recyclable items received from CDR locations. The disposal centers/land-fillers are responsible for the safe disposal of the unusable wastes received from CDR locations either by landfilling or incinerations.
The various costs incurred at different nodes of the closed loop supply chain network are explained below:
1) Manufacturers
The different costs associated at manufacturers are investment fixed cost due to the opening of each manufacturing plant, operation cost, un-utilized capacity cost and transportation cost.
2) Wholesalers
The different costs associated at wholesalers are investment fixed cost due to the opening of each wholesaler, operation cost, and transportation cost.
3) Retailers
The different costs associated at retailers are investment fixed cost due to the opening of each retailer, operation cost, and transportation cost.
4) Repair/Service Centers
The different costs associated at repair/service centers are investment fixed cost due to the opening of each repair/service center, repairing cost/operation cost, and transportation cost.
5) Collectors/Dismantlers/Re-furbishers
The different costs associated at collectors/dismantlers/re-furbishers are investment fixed cost due to the opening of each Collector/Dismantler/Refurbisher, operation cost (collection, dismantling and refurbishing costs) and transportation cost.
6) Remanufacturers
The different costs associated at remanufacturers are investment fixed cost due to the opening of each remanufacturing plant, remanufacturing cost/operation cost, un-utilized capacity cost and transportation cost.
7) Resellers
The different costs associated at resellers are investment fixed cost due to the opening of each reseller location, operation cost, and transportation cost.
8) Recyclers
The different costs associated at recyclers are investment fixed cost due to the opening of each recycling center, recycling costs/operation cost and transportation cost.
9) Land fillers
The different costs associated at land fillers are investment fixed cost due to the opening of each disposal center, disposal cost/operation cost and transportation cost.
5. Model Assumptions and Limitations
The assumptions and limitations of the proposed model are considered as follows:
1) The model is for a single product and single period network design;
2) The locations of the first customers and second customers are known and are with certain demands;
3) The quantities of products returned are certain and all the products supplied are returned as EOL products and repair product;
4) 60% of the products supplied are returned as EOL products and 40% are returned as repair product;
5) 50% of the EOL products are returned via retailers and remaining 50% of the EOL products are returned directly, to the Collectors/Dismantlers/Re-furbishers (CDR);
6) Out of the total returned EOL products, 30% are refurbishable items, 45% are remanufacturable items, 20% are recyclable items and 5% are non-recoverable and disposed by land-filler;
7) The quality of the remanufactured, refurbished and repaired products is different from that of the new product;
8) The potential locations of manufacturers, wholesalers, retailers, collectors/dismantlers/re-furbishers, repair/service centers, recyclers, land fillers and resellers are assumed;
9) The capacity of each location is known;
10) The costs parameters considered (viz., opening costs, operating costs, un-utilized capacity costs and transportation costs) are known for all the facilities and node;
11) The measure of quantity of products transported per trip is defined in the form of number of units per trip;
12) There is no shipment happening between the nodes in the same stage.
6. Model Formulation
This section gives a mathematical formulation for minimizing the total cost of the proposed multi-echelon model for a sustainable closed loop supply chain network design problem.
The maximum count of each facility/node in the supply chain network is presented below:
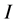 is the number of manufacturers and remanufacturers;
is the number of manufacturers and remanufacturers;
 is the number of wholesalers;
is the number of wholesalers;
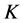 is the number of retailers;
is the number of retailers;
 is the number of first customers;
is the number of first customers;
 is the number of repair/service centers;
is the number of repair/service centers;





The indices of the each facility/node in the supply chain network are presented below:

































Capacity of facilities






























Demand of customers






Unit price of products






Distance between different pairs of facilities/nodes






































































Transportation cost
TC is the transportation cost per unit per kilometer.
Fraction of returns from first customer demand
FCDFRR is the repair products return fraction of the first customer demand shipped from




FCDFEOLR is the EOL products return fraction of the first customer demand shipped from




EOLFRT is the EOL products return fraction shipped from




EOLFCDR is the EOL products return fraction shipped directly from




Fraction of recovery from CDR
CDRF1 is the CDR fraction supplied from




CDRF2 is the CDR fraction supplied from




CDRF3 is the CDR fraction supplied from




CDRF4 is the CDR fraction supplied from




Decision variables
The decision variables of the model are defined as follows:
Integer variables with respect to the quantity of shipments









































































Binary variables with respect to the opening and non-opening of facilities/nodes


=0, otherwise, where





=0, otherwise, where


=0, otherwise, where


=0, otherwise, where


=0, otherwise, where


=0, otherwise, where


=0, otherwise, where
Note: There is some discontinuity in numbering variables like


Objective function
The proposed model has the objective of minimizing the total cost i.e. the cost of both forward and reverses supply chains for which the objective function is defined as follows:
The formula for the total cost is given as:
The components of objective function
The costs involved in the total cost of CLND are formulated as follows:
Opening costs of facilities/nodes
where,


















Operation cost of facilities/nodes









where,


















Un-utilized capacity cost
where








Transportation cost
Mathematical model
A complete model of the proposed MINLP model for the closed loop supply chain network design problem is presented below.
Subject to
Demand Constraints (DC)


Capacity Constraints (CC)












Balance Constraints (BC)














where,




























































Constraints (1) and (2) correspond to the demands of the first customers and second customers respectively. Constraint (3) makes sure that the sum of the outflows from each manufacturer to all the wholesalers does not exceed the capacity of the manufacturers. Constraint (4) makes sure that the sum of the outflows from each manufacturer to all the wholesalers plus sum of the outflows from the each manufacturer to all the resellers minus sum of the outflows from each CDR to all the manufacturers for remanufacturing does not exceed the capacity of the manufacturers. Constraint (5) makes sure that the sum of the outflows from each wholesaler to all the retailers does not exceed the capacity of the wholesalers. Constraint (6) makes sure that the sum of the outflows from each retailer to all the first customers and CDRs does not exceed the capacity of the retailers. Constraint (7) makes sure that the sum of the outflows from each repair center to all the first customers does not exceed the capacity of the repair centers. Constraint (8) makes sure that the sum of the outflows from each CDR to all the remanufacturers, resellers, recyclers and land fillers does not exceed the capacity of the CDRs. Constraint (9) makes sure that the sum of the inflows to land fillers from all CDRs does not exceed the capacity of the land fillers. Constraint (10) makes sure that the sum of the inflows to recyclers from all CDRs does not exceed the capacity of the recyclers. Constraint (11) makes sure that the sum of the outflows from each re-furbisher under CDRs to all the resellers does not exceed the refurbishing capacity of CDRs. Constraint (12) makes sure that the sum of the outflows from each remanufacturer to all the resellers does not exceed the capacity of the remanufacturers. Constraint (13) makes sure that the sum of the inflows to resellers from all the CDRs (refurbished items) and from all the remanufacturers does not exceed the capacity of the resellers. Constraint (14) makes sure that the sum of the outflows from each reseller to all the second customers does not exceed the capacity of the resellers. Constraint (15) makes sure that the sum of the quantities produced by the manufacturers is equal to the sum of the demands of the first customers. Constraint (16) makes sure that the sum of the quantities produced by the manufacturers is equal to the sum of the outflows from the manufacturers. Constraint (17) makes sure that the sum of the inflows to the wholesalers from each manufacturer is equal to the sum of outflows from the wholesalers to the retailers. Constraint (18) makes sure that the sum of the inflows to the retailers from each wholesaler is equal to the sum of the outflows from the retailers to first customers. Constraint (19) makes sure that the sum of the inflows to each first customer from retailer is greater than or equal to the sum of the outflows from each first customers to repair centers and CDRs. Constraint (20) makes sure that the sum of the outflows from each first customer to the repair center is less than or equal to the demand fraction for repair returns of the sum of the demands of the first customers. Constraint (21) makes sure that the sum of the inflows to each repair center from all the first customers is equal to the sum of the outflows from each repair center to all the first customers. Constraint (22) makes sure that the sum of the outflows from each first customer as EOL via retailer or directly to the CDRs is less than or equal to the demand fraction for EOL returns of the sum of the demands of the first customers. Constraint (23) makes sure that the sum of the outflows from each first customer as EOL via retailer to the CDRs is less than or equal to its return fraction of the sum of the EOL returns. Constraint (24) makes sure that the sum of the outflows from each first customer as EOL directly to the CDRs is less than or equal to its return fraction of the sum of the EOL returns. Constraint (25) makes sure that the sum of the EOL returns inflows to each CDR from first customer via retailer and directly is equal to the sum of the flow of CDR fractions exiting from each CDR to all the land fillers, recyclers, resellers and remanufacturers. Constraint (26) makes sure that the sum of the inflows to all the remanufacturers from each CDR is less than or equal to the sum of the outflows from the remanufacturers to resellers. Constraint (27) makes sure that the sum of the inflows to all the resellers from each CDR and each remanufacturer is equal to the sum of the outflows from the resellers to the second customers. Constraint (28) makes sure that the sum of the outflows from each reseller to all the second customers is equal to the sum of the demands of all the second customers.
7. Demonstration of the Model
A closed loop supply chain model with maximal number of facilitates at different stages and with a given number of first customers as well as that of second customers is shown in Figure 2 by assuming hypothetical data. The model is proposed for a single period and single product and multi-echelon closed loop supply chain network. It has 4 echelons in the forward chain and 4 echelons in the reverse chain. The number of facilities and nodes in the entire network is given in Table 1.
The maximum count of the facilities and the nodes as per Table 1 with the entire forward and reverse flows between the pair of facilities and nodes are illustrated in Figure 2.
Table 1. Facilities and nodes in the network model.
Figure 2. Network design showing all the forward and reverse flows in the Closed Loop Supply chain.
Table 2. Hypothetical values for model parameters and variables.
Figure 3. Network design showing the optimized forward and reverse flows in the Closed Loop Supply chain.
Based on the assumptions and limitations presented in the Section 5, the hypothetical values for different data are assumed and presented in Table 2.
The distances between different pairs of facilities/nodes and those between different pairs of facilities and customers (first customer and second customer) are given in Appendix 1.
Based on the assumed data in Table 1, Table 2 and Appendix 1, a mixed integer non-linear programming (MINLP) model for the closed loop supply chain network design problem has been formulated and solved using LINGO14 software and the optimal design of the closed loop supply chain network is shown in Figure 3.
The Lingo software was run on MS Windows 7 Professional platform in a 64-bit operating system of Hewlett- Packard Lap Top Computer with a processor: Intel(R) Core(TM) i5-2430 CPU@2.40 GHz 2.40 GHz. with 4.00 GB installed memory (RAM) capacity.
8. Discussion on Results and Directions for Future Research
From the formulation and demonstration of the forward and reverse supply chain network design problem, it is clear that the number of constraints as well as the number of variables will grow exponentially. Though LINGO14 gives the optimum result in a reasonable time for assumed problem, for very large size problems, it may take hours together to solve them optimally, because of the combinatorial nature of the problem. Hence, there is a need for developing meta-heuristic to solve this large size problem and to obtain very near optimal solution for very large size problems. In future, researchers may concentrate in developing genetic algorithm, ant colony optimization algorithm, greedy random adaptive search procedure (GRASP), hybrid algorithms which are some combination of meta-heuristics, etc. for solving this closed loop network design problem.
9. Conclusions
The design of closed loop supply chain network is an important problem in supply chain management. In this paper, foreword supply chain and reverse supply chain are considered simultaneously with the objective of minimizing the total costs of the entire network. A mixed integer non-linear programming model (MINLP) is presented for the proposed problem and it is demonstrated using a sample set of data. LINGO14 software is used to solve the model and the solution for the design of the closed loop supply chain is presented at the end.
For the size of the problem considered in this paper, the CPU time to solve the problem is 32 minutes. If the problem size is increased, the CPU time will grow in an exponential order. So, an efficient meta-heuristic may be developed to solve large size problems. The mathematical model presented in this paper will be a handy tool to compare the performance of heuristics/meta-heuristics that will be developed by future researchers.
Acknowledgements
The authors profusely thank M/S. Lindo Systems Inc., Chicago for their technical support by providing the license for the extended version of LINGO 14 optimization software package. The authors also thank the anonymous referees for their constructive feedback and useful comments, which have been addressed in this research paper.
References
- Krikke, H., Ruwaardz, J.B. and Van Wassenhove, L.N. (2003) Concurrent Product and Closed-Loop Supply Chain Design with an Application to Refrigerators. International Journal of Production Research, 41, 3689-3719. http://dx.doi.org/10.1080/0020754031000120087
- Schultmann, F., Zumkeller, M. and Rentz, O. (2006) Modeling Reverse Logistic Tasks within Closed-Loop Supply Chains: An Example from the Automotive Industry. European Journal of Operational Research, 171, 1033-1050. http://dx.doi.org/10.1016/j.ejor.2005.01.016
- Salema, M.I.G., Povoa, A.P.B. and Novais, A.Q. (2007) An Optimization Model for the Design of a Capacitated Multi- Product Reverse Logistics Network with Uncertainty. European Journal of Operational Research, 179, 1063-1077. http://dx.doi.org/10.1016/j.ejor.2005.05.032
- Staikos, T. and Rahimifard, S. (2007) A Decision-Making Model for Waste Management in the Footwear Industry. International Journal of Production Research, 45, 4403-4422. http://dx.doi.org/10.1080/00207540701450187
- Ko, H.J. and Evans, G.W. (2007) A Genetic Algorithm-Based Heuristic for the Dynamic Integrated Forward/Reverse Logistics Network for 3PLs. Computers & Operations Research, 34, 346-366. http://dx.doi.org/10.1016/j.cor.2005.03.004
- Lu, Z. and Bostel, N. (2007) A Facility Location Model for Logistics Systems Including Reverse Flows: The Case of Remanufacturing Activities. Computers & Operations Research, 34, 299-323. http://dx.doi.org/10.1016/j.cor.2005.03.002
- Du, F. and Evans, G.W. (2008) A Bi-Objective Reverse Logistics Network Analysis for Post-Sale Service. Computers & Operations Research, 35, 2617-2634. http://dx.doi.org/10.1016/j.cor.2006.12.020
- Lee, D.H. and Dong, M. (2008) A Heuristic Approach to Logistics Network Design for End-of-Lease Computer Products Recovery. Transportation Research Part E, 44, 455-474. http://dx.doi.org/10.1016/j.tre.2006.11.003
- Lee, D.H. and Dong, M. (2009) Dynamic Network Design for Reverse Logistics Operations under Uncertainty. Transportation Research Part E, 45, 61-71. http://dx.doi.org/10.1016/j.tre.2008.08.002
- Lin, L., Gen, M. and Wang, X. (2009) Integrated Multistage Logistics Network Design by Using Hybrid Evolutionary Algorithm. Computers & Industrial Engineering, 56, 854-873. http://dx.doi.org/10.1016/j.cie.2008.09.037
- Mutha, A. and Pokharel, S. (2009) Strategic Network Design for Reverse Logistics and Remanufacturing Using New and Old Product Modules. Computers & Industrial Engineering, 56, 334-346. http://dx.doi.org/10.1016/j.cie.2008.06.006
- Salema, M.I.G., Povoa, A.P.B. and Novais, A.Q. (2009) A Strategic and Tactical Model for Closed-Loop Supply Chains. OR Spectrum, 31, 573-599. http://dx.doi.org/10.1007/s00291-008-0160-5
- Dahel, N.E. (2010) Modeling Supply Chain Network Design and Product Recovery Planning under Uncertainty. Northeast Decision Sciences Institute Proceedings, Virginia, 26-28 March 2010, 714-719.
- Salema, M.I.G., Povoa, A.P.B. and Novais, A.Q. (2010) Simultaneous Design and Planning of Supply Chains with Reverse Flows: A Generic Modeling Framework. European Journal of Operational Research, 203, 336-349. http://dx.doi.org/10.1016/j.ejor.2009.08.002
- El-Sayed, M., Afia, N. and El-Kharbotly, A. (2010) A Stochastic Model for Forward-Reverse Logistics Network Design under Risk. Computers & Industrial Engineering, 58, 423-431. http://dx.doi.org/10.1016/j.cie.2008.09.040
- Pishvaee, M.S., Farahani, R.Z. and Dullaert, W. (2010) A Memetic Algorithm for Bi-Objective Integrated Forward/ Reverse Logistics Network Design. Computers & Operations Research, 37, 1100-1112. http://dx.doi.org/10.1016/j.cor.2009.09.018
- Wang, H.F. and Hsu, H.W. (2010) A Closed-Loop Logistic Model with a Spanning-Tree Based Genetic Algorithm. Computers & Operations Research, 37, 376-389. http://dx.doi.org/10.1016/j.cor.2009.06.001
- Khajavi, L.T., Seyed-Hosseini, S.M. and Makui, A. (2011) An Integrated Forward/Reverse Logistics Network Optimization Model for Multi-Stage Capacitated Supply Chain. iBusiness, 3, 229-235. http://dx.doi.org/10.4236/ib.2011.32030
- Liao, T.Y. and Rachmat, A. (2011) A Multi-Product Reverse Logistics Model for Third Party Logistics. International Conference on Modeling, Simulation and Control, IPCSIT, IACSIT Press, Singapore, 48-52.
- Pishvaee, M.S., Rabbani, M. and Torabi, S.A. (2011) A Robust Optimization Approach to Closed-Loop Supply Chain Network Design under Uncertainty. Applied Mathematical Modelling, 35, 637-649. http://dx.doi.org/10.1016/j.apm.2010.07.013
- Nandita, A. (2011) The Apparel Aftermarket in India—A Case Study Focusing on Reverse Logistics. Journal of Fashion Marketing and Management, 15, 211-227. http://dx.doi.org/10.1108/13612021111132645
- Nenes, G. and Nikolaidis, Y. (2012) A Multi-Period Model for Managing Used Product Returns. International Journal of Production Research, 50, 1360-1376. http://dx.doi.org/10.1080/00207543.2011.609650
- Ozkir, V. and Basligil, H. (2012) Modeling Product-Recovery Processes in Closed-Loop Supply-Chain Network Design. International Journal of Production Research, 50, 2218-2233. http://dx.doi.org/10.1080/00207543.2011.575092
- Piplani, R. and Saraswat, A. (2012) Robust Optimization Approach to the Design of Service Networks for Reverse Logistics. International Journal of Production Research, 50, 1424-1437. http://dx.doi.org/10.1080/00207543.2011.571942
- Vahdani, B., Mogaddham, R.T., Modarres, M. and Baboli, A. (2012) Reliable Design of a Forward/Reverse Logistics Network under Uncertainty: A Robust M/M/c Queuing Model. Transportation Research Part E, 48, 1152-1168. http://dx.doi.org/10.1016/j.tre.2012.06.002
- Ramezani, M., Bashiri, M. and Moghaddam, R.T. (2013) A New Multi-Objective Stochastic Model for a Forward/ Reverse Logistic Network Design with Responsiveness and Quality Level. Applied Mathematical Modelling, 37, 328- 344. http://dx.doi.org/10.1016/j.apm.2012.02.032
- Rosa, V.D., Gebhard, M., Hartmann, E. and Wollenweber, J. (2013) Robust Sustainable Bi-Directional Logistics Network Design under Uncertainty. International Journal of Production Economics, 145, 184-198. http://dx.doi.org/10.1016/j.ijpe.2013.04.033
- Subramanian, P., Ramkumar, N., Narendran, T.T. and Ganesh, K. (2013) PRISM: Priority Based Simulated Annealing for a Closed Loop Supply Chain Network Design Problem. Applied Soft Computing, 13, 1121-1135. http://dx.doi.org/10.1016/j.asoc.2012.10.004
- Mahmoudi, H., Fazlollahtabar, H. and Mahdavi, I. (2013) Mathematical Modeling for Minimizing Costs in a Multilayer Multi-Product Reverse Supply Chain. Industrial Engineering & Management, 2, 1-6.
- Eskandarpur, M., Zegordi, S.H. and Nikbakhsh, E. (2013) A Parallel Variable Neighborhood Search for the Multi- Objective Sustainable Post Sales Network Design Problem. International Journal of Production Economics, 145, 117- 131. http://dx.doi.org/10.1016/j.ijpe.2012.10.013
- Hafeti, S.M. and Jolai, F. (2013) Robust and Reliable Forward-Reverse Logistics Network Design under Demand Uncertainty and Facility Disruptions. Applied Mathematical Modelling, 38, 2630-2647.
- Keyvanshokooh, E., Fattahi, M., Hosseini, S.M.S. and Moghaddam, R.T. (2013) A Dynamic Pricing Approach for Returned Products in Integrated Forward/Reverse Logistics Network Design. Applied Mathematical Modelling, 37, 10182-10202. http://dx.doi.org/10.1016/j.apm.2013.05.042
- Diabat, A., Kannan, D., Kaliyan, M. and Svetinovic, D. (2013) An Optimization Model for Product Returns Using Genetic Algorithms and Artificial Immune System. Resources, Conservation and Recycling, 74, 156-169. http://dx.doi.org/10.1016/j.resconrec.2012.12.010
- Amin, S.H. and Zhang, G. (2013) A Multi-Objective Facility Location Model for Closed Loop Supply Chain Network under Uncertain Demand and Return. Applied Mathematical Modelling, 37, 4165-4176. http://dx.doi.org/10.1016/j.apm.2012.09.039
- Cardoso, S.R., Paula, F.D.A., Povoa, B. and Relvas, S. (2013) Design and Planning of Supply Chains with Integration of Reverse Logistics Activities under Demand Uncertainty. European Journal of Operational Research, 226, 436-451. http://dx.doi.org/10.1016/j.ejor.2012.11.035
- Devika, K., Jafarian, A. and Nourbakhash, V. (2014) Designing a Sustainable Closed-Loop Supply Chain Network Based on Triple Bottom Line Approach: A Comparison of Metaheuristics Hybridization Techniques. European Journal of Operational Research, 235, 594-615. http://dx.doi.org/10.1016/j.ejor.2013.12.032
Appendix 1
Tables of Distance between the pair of Facilities/Nodes and Customers in kilometers.
Table A1. Distance between Manufacturers (I) and Wholesalers (J) D1.
Table A2. Distance between Wholesalers (J) and Retailers (K) D2.
Table A3. Distance between Retailers (K) and First Customers FC (L) D3.
Table A4. Distance between First Customers FC (L) and Repair Centers (M) D4 = D5.
Table A5. Distance between First Customers FC (L) and Collectors/Disman- tlers/Re-furbishers CDR (N) D6.
Table A6. Distance between First Customers FC (L) and Retailers (K) D7.
Table A7. Distance between Retailers (K) and Collectors/Dismantlers/Re- furbishers CDR (N) D8.
Table A8. Distance between Collectors/Dismantlers/Re-furbishers CDR (N) and Land Fillers (O) D9.
Table A9. Distance between Collectors/Dismantlers/Re-furbishers CDR (N) and Recycler (P) D10.
Table A10. Distance between Collectors/Dismantlers/Re-furbishers CDR (N) and Resellers (R) D11.
Table A11. Distance between Collectors/Dismantlers/Re-furbishers CDR (N) and Remanufacturers (I) D12.
Table A12. Distance between Remanufacturers (I) and Resellers(R) D13.
Table A13. Distance between Resellers (R) and Second Customers SC (S) D14.











