Intelligent Information Management
Vol.5 No.4(2013), Article ID:33850,14 pages DOI:10.4236/iim.2013.54011
A Video Game Based on Optimal Control and Elementary Statistics
1Dipartimento di Scienze Sociali “D. Serrani”, Università Politecnica delle Marche, Ancona, Italy
2CERI-Centro di Ricerca Previsione Prevenzione e Controllo dei Rischi Geologici, Università di Roma “La Sapienza”, Roma, Italy
Email: m.giacinti@univpm.it, fra_mariani@libero.it, m.c.recchioni@univpm.it, zirilli@mat.uniroma1.it
Copyright © 2013 Marco Giacinti et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 15, 2013; revised May 16, 2013; accepted June 10, 2013
Keywords: Video Game; Differential Games; Mechanical Dynamical System; Closed Loop Optimal Control
ABSTRACT
The video game presented in this paper is a prey-predator game where two preys (human players) must avoid three predators (automated players) and must reach a location in the game field (the computer screen) called preys’ home. The game is a sequence of matches and the human players (preys) must cooperate in order to achieve the best performance against their opponents (predators). The goal of the predators is to capture the preys, which are the predators try to have a “rendez vous” with the preys, using a small amount of the “resources” available to them. The score of the game is assigned following a set of rules to the prey team, not to the individual prey. In some situations the rules imply that to achieve the best score it is convenient for the prey team to sacrifice one of his components. The video game pursues two main purposes. The first one is to show how the closed loop solution of an optimal control problem and elementary statistics can be used to generate (game) actors whose movements satisfy the laws of classical mechanics and whose behaviour simulates a simple form of intelligence. The second one is “educational”, in fact the human players in order to be successful in the game must understand the restrictions to their movements posed by the laws of classical mechanics and must cooperate between themselves. The video game has been developed having in mind as players for children aged between five and thirteen years. These children playing the video game acquire an intuitive understanding of the basic laws of classical mechanics (Newton’s dynamical principle) and enjoy cooperating with their teammate. The video game has been experimented on a sample of a few dozen children. The children aged between five and eight years find the game amusing and after playing a few matches develop an intuitive understanding of the laws of classical mechanics. They are able to cooperate in making fruitful decisions based on the positions of the preys (themselves), of the predators (their opponents) and on the physical limitations to the movements of the game actors. The interest in the game decreases when the age of the players increases. The game is too simple to interest a teenager. The game engine consists in the solution of an assignment problem, in the closed loop solution of an optimal control problem and in the adaptive choice of some parameters. At the beginning of each match, and when necessary during a match, an assignment problem is solved, that is the game engine chooses how to assign to the predators the preys to chase. The resulting assignment implies some cooperation among the predators and defines the optimal control problem used to compute the strategies of the predators during the match that follows. These strategies are determined as the closed loop solution of the optimal control problem considered and can be thought as a (first) form of artificial intelligence (AI) of the predators. In the optimal control problem the preys and the predators are represented as point masses moving according to Newton’s dynamical principle under the action of friction forces and of active forces. The equations of motion of these point masses are the constraints of the control problem and are expressed through differential equations. The formulation of the decision process through optimal control and Newton’s dynamical principle allows us to develop a game where the effectiveness and the goals of the automated players can be changed during the game in an intuitive way simply modifying the values of some parameters (i.e. mass, friction coefficient, ···). In a sequence of game matches the predators (automated players) have “personalities” that try to simulate human behaviour. The predator personalities are determined making an elementary statistical analysis of the points scored by the preys in the game matches played and consist in the adaptive choice of the value of a parameter (the mass) that appears in the differential equations that define the movements of the predators. The values taken by this parameter determine the behaviour of the predators and their effectiveness in chasing the preys. The predators personalities are a (second) form of AI based on elementary statistics that goes beyond the intelligence used to chase the preys in a match. In a sequence of matches the predators using this second form of AI adapt their behaviour to the preys’ behaviour. The video game can be downloaded from the website: http://www.ceri.uniroma1.it/ceri/zirilli/w10/.
1. Introduction
This paper shows how optimal control models and elementary statistics can be used to simulate intelligent behaviour in a video game involving two teams of actors. The movements of the actors are restricted by the physical laws of classical mechanics. The video game is a prey-predator game where two human players (preys) face the opposition of three automated players (predators). The preys pursue the goal of avoiding the predators and of reaching a location on the game field called preys’ home. The predators pursue the goal of capturing the preys (i.e. of having a “rendez vous” with the preys) using a small amount of the “resources” available to them.
The game is a sequence of matches and the human players (preys) must cooperate in order to achieve the best score against their opponents (predators). The score of the game is the sum of the scores of the matches. The score of a match is assigned following a set of rules described in Subsection 4.3 to the prey team, not to the individual players. The situation where, at the end of a match, a prey is captured and the other one has reached the preys’ home generates a score higher than the score generated by the situation where, at the end of the match, the two preys have avoided the rendez vous with the predators but neither of them has reached the preys’ home. This fact implies that in some circumstances to achieve the best score for the prey team it is convenient to sacrifice one of the preys. This is an incentive to cooperate for the human players. It is believed that this kind of cooperation has several positive effects on the psychological attitude of the players especially if they are aggressive young children [1].
The video game is addressed to human players aged between five and thirteen years and can be used to stimulate children to develop an intuitive understanding of the physical laws involved in the game. The children aged between five and thirteen years are usually not aware of the relations among mass, friction forces, active forces and trajectories implied by Newton’s dynamical principle. Playing with the video game and observing the behaviour of its actors these children develop an intuitive understanding of the dynamical laws. This understanding allows them to make effective decisions about the strategy to implement to reach the goals of the game. During a game match some simple forms of cooperation, communication and strategic reasoning are employed by the preys and by the predators. These features make the video game amusing.
The video game can be downloaded from the website: http://www.ceri.uniroma1.it/ceri/zirilli/w10/.
1.1. The Advantages of Using Optimal Control and Elementary Statistics to Develop a Video Game
The main advantage of using optimal control in the development of a video game is that allows to manage the personalities (i.e. the behaviours) of the automated players (sometimes called “autonomous synthetic characters”) in a simple way and allows to define trajectories satisfying physical laws. The effectiveness of the predators in chasing the preys depends on the choice of the utility functional of the optimal control problem considered in the video game (see Formula (7)) and on the equations of motion that are the constraints of the control problem. In particular it depends on the choice of the parameters that appear in the utility functional and in the equations of motion. The equations of motion express the physical laws involved in the game. That is modeling the video game via an optimal control problem generates predators that are able to chase the preys and whose movements depend on their physical properties (i.e. mass, friction coefficient, ···) and on the trajectories of the preys. Note that there is no preassigned scheme for the movement of the predators.
The automated players (autonomous synthetic characters) developed in this video game have two forms of artificial intelligence (AI). The first one is used to chase the preys during a game match. The second one is used when a sequence of matches is played to simulate in the autonomous characters the behaviour in similar circumstances of human players. This second AI form is articulated in three different levels. The first one guarantees that the predators behave in a slightly different way in each match that is they behave depending on the humor of the moment. The second level consists in the dynamic change of the game difficulty to avoid that the players are discouraged or bored as a consequence of the fact that the game is too difficult or too easy. The last level simulates the emotional reaction of the predators corresponding to the human satisfaction or anger for a sequence of victories or of defeats (see Subsection 4.8 for technical details).
The mathematical model that determines the movement of the predators during a match, that is that determines the first form of AI, is the optimal control problem. In the optimal control problem the game actors are represented as point masses. The action of the actors (preys and predators) during a game match can be seen as an attempt to solve a “rendez vous” problem for a set of point masses that satisfy Newton’s dynamical principle. These point masses are subject to external forces and to friction forces. The movements of the preys and of the predators are obtained as solution of differential equations that depend on the external forces. These differential equations express Newton’s dynamical principle. The external forces acting on the preys are chosen by the human players using joypads and those acting on the predators are computed by the game engine as the closed loop solution of the optimal control problem considered. The utility functional of the control problem depends on the prey positions and its minimization corresponds to pursuing the goal of chasing the preys using a small quantity of the resources available to the predators, which are using a small quantity of the external forces acting on the predators. The utility functional chosen determines a form of cooperation among the predators. In a sequence of matches the autonomous characters of the video game (predators) modify their behaviour depending on the behaviour of the human players (preys) that confront them, which is depending on the points scored by the human players in the matches played. This second form of AI is built using elementary statistics and exploiting the properties of the control problem employed in the video game. In fact the statistical analysis of the points scored by the human players in a sequence of matches is used to adapt the game in relation to the human players actually playing. This approach has something in common with the idea introduced in [2] of defining a difficulty evaluation function for a video game. In the video game presented in this paper thank to the mathematical model (i.e. the optimal control problem) used it is easy to establish a relation between the ability of the human players and the values of the parameters of the model. That is, it is easy to modify dynamically the game difficulty level.
1.2. Research Background
In recent years the interest in autonomous synthetic characters has been constantly growing due to the increased importance of computer animation and of interactive media. In the technical literature several approaches have been suggested to build this kind of characters see, for example, Prada and Paiva [3] and Millington [4].
In video games these characters are associated to automated players. In [4] the behaviour of the automated players is based on pathfinding algorithms (Section 4.2 of [4]), and the decision making capability of these players is based on the analysis of random trees. Moreover in [4] Chapter 7 the question of how to manage learning experiences of human and automated players based on AI and on elementary statistics is discussed (see Section 7.3.2 of [4]).
Indeed one of the most relevant challenges in video game AI is to create automated players having an appropriate level of effectiveness in pursuing their goals. This is often done implementing a finite state machine (see Section 5.3 of [4]), that is presenting the game at several “levels” of difficulty. This approach suffers from some drawbacks, such as the fact that it is not possible to adjust strategies or difficulty dynamically during the game. Recently an alternative approach to the finite state machine has been introduced (see [5] and the references therein). This approach is called Dynamic Difficulty Adjustment (DDA) and consists in changing automatically in real time parameters, scenarios or behaviours in the video game based on player’s ability and performance. In [5] in a simple prey-predator game the DDA approach is implemented through a Monte-Carlo tree search.
However the problem of defining a measure of the game difficulty is in general an open question and several approaches have been suggested. One of them consists in introducing a difficulty evaluation function defined as a conditional probability (see [2] and the reference therein) on the “lose” or “win” events. In [2] the authors underline that, once established a measure of the game difficulty, in general it is not easy to change the game difficulty dynamically using simple mathematical expressions of the game parameters. The use of optimal control and of elementary statistics to drive the difficulty adjustment algorithm proposed in this paper is an example of a practical tool to handle this issue. In fact using these mathematical models we are able to generate video games with a level of difficulty calibrated on the individual players. In the following Sections and in [6] it is explained why modeling a video game through an optimal control problem or a differential game is a way to parameterize the difficulty of the video game in an intuitive way.
Another important issue when a multitude of automated players is considered is the simulation of group behaviour. The simulation of group behaviour of a multitude of characters is inspired by the study of human behaviour in the social sciences and usually involves some elementary mathematical models limited to path-finding algorithms and to some elementary formulae that define the movements of the synthetic characters in the game scene (see [3,7-10]). The problem of building mathematical models to describe the behaviour of a multitude of autonomous characters interacting as a group has also been studied outside the context of AI and of social sciences. For example it has been studied in natural sciences, in fact in 1987 Reynolds [11] developed a mathematical model of the flocking behaviour of a group of flying creatures (birds or insects). Since then several mathematical models of the social behaviour of several species of animals, such as birds, fishes, insects, have been studied. These models are based on dynamical systems and usually do not involve optimal control or differential games. The three automated players of the video game presented here have some cooperative behaviour (see Section 1.3) but are not a multitude and do not exhibit a group behaviour.
The movements of the actors in prey-predator video games are realized most of the times using mathematical approaches simpler than the optimal control approach used here (see [9,10,12]). For example in [9,10] the movements of automated players are based on ordinary differential equations and on several heuristic rules that define the movements of articulated bodies consisting of rigid links connected by joints. In absence of joints each link has six degrees of freedom, three translational and three rotational. In [9,10] the authors model the movements of these bodies, but do not deal with the problem of generating players able to make decisions and to cooperate to pursue a goal. In [12] the problems of modeling movements and of simulating a decision making process are dealt together and the results presented have some similarities to the ones presented in this paper. In fact in [12] each actor of the game is characterized by its position vector and by a unit vector called “heading direction”. The heading directions are not necessarily the velocities of the actors in the game scene and their dynamics is described by a system of ordinary differential equations that depends on the interactions among actors. These interactions are modeled through a function inspired by an analogy with potential theory (see [12] for further details). Similarly in [13] the authors deal with the problem of modeling prey-predator interactions using mathematical models that go beyond simple attraction/ repulsion models. In fact in [13] a mathematical model obtained modifying the Lotka-Volterra two species equations [14] is proposed. The Lotka-Volterra two species equations describe the interaction between two species in an ecosystem, a predator and a prey species, and consists in two ordinary differential equations, the first one describes how the prey population changes and the second one describes how the predator population changes. In [13] the authors propose an algorithm to reproduce collective crowd behaviour based on a Lotka-Volterra two species model and on some steering rules that try to simulate realistic crowd behaviours. Recall that being a member of a crowd changes the behaviour of the individual. The models used in [12,13] suffer from the drawback of not being able to change the game difficulty dynamically.
Finally video games where basic physics principles hold are presented in [15,16]. In [15,16] the authors are motivated by robotics. Their work is based on the ALERT (Active Learning Environments with Robotic Tangibles) systems. The ALERT systems have been developed for e-learning purposes and recently have been used to develop educational video games [16]. However these are special cases and the majority of the commercial games violate basic physics principles and give to the players the feeling that physics principles can be disregarded. For example often in video games movement is considered only from the kinematic point of view and dynamic principles are neglected. Note that the models proposed in [12,13,15,16] do not involve optimal control problems or differential games.
The video game proposed in this paper is an extension of the video game presented in [6]. In fact both these games are based on mathematical models involving differential equations and define actors whose movements satisfy Newton’s dynamical principle. In [6] the strategies implemented by the predators are suboptimal solutions of the control problem that models the prey-predator dynamics. Moreover in [6] the video game does not adapt the predators effectiveness to their human opponents. The video game presented in [6] is implemented at three different levels of difficulty. The levels of difficulty considered are given. The predators of [6] have only the intelligence needed to chase the prey in a game match complying with Newton’s dynamical principle. The video game presented in this paper uses optimal solutions of the control problem and has a mechanism to adjust its difficulty to the ability of the human players.
Let us conclude this subsection noting that in mathematics rendez vous problems involving two actors or two sets of actors whose dynamics is defined by systems of differential equations have been widely studied. The most common mathematical models used to study these problems are optimal control models or differential games (see, for example, Athans [17], Isaacs [18]). Differential games are the natural model to describe situations where two sets of actors having conflicting goals moving on trajectories implicitly defined by differential equations must choose their strategies respectively to maximize or to minimize a cost functional. The game developed here is an attempt to investigate the potentiality of these mathematical models in context of video games.
1.3. Interactive and Cooperative Behaviours in the Video Game
Let us summarize the prey-predator interaction and cooperation that will be explained in detail in Section 4. Let us group the game actors in two teams, which are the team 1 actors, the preys, and the team 2 actors, the predators.
Let us explain more in detail of the interaction and cooperation among the game actors. We have already mentioned that the cooperation between the human players is induced by the rules used to assign the game score (see Subsection 4.3 for further details) and in particular by the fact that the score is given to the human team not to the individual players.
At the beginning of the first match played the video game engine opens a window on the computer screen for each human player (see Figure 1). During the game execution each prey is always at the center of its own window. Each window shows a neighborhood of the prey at its center. Moreover in each window there is a second view of the game scene that shows the game scene on a global scale, which is on a scale that shows the location of all the actors of the game and the location of the preys’ home (see Figure 1). Also this global view of the game scene has the prey in its center and in the sequel is attributed to the “radar” of the player.
Each human player before beginning to play a match observes the initial scene of the game on his radar and chooses a strategy to play the match that follows cooperating with the other human player. For example, observing the predators’ positions each human player decides if it is convenient for his survival and for the score of the human team in the following match to move towards or outwards the preys’ home.
When the game match starts each human player watches the time evolution of the game scene in his window and uses a joypad to implement the strategy chosen. In each match the human players (preys) and the automated players (predators) have a finite amount of time to achieve their goals. After the expiration of this time the match ends. At the end of each match depending on the outcome of the match the human players score some points (see Subsection 4.3). Under some conditions a new match can be played, that is the game can be resumed from a new initial scene. During the match the interaction between preys and predators takes place.
In the actual implementation of the game the rendez vous of a predator with a prey during a game match corresponds to the fact that the distance between the prey and the predator becomes smaller than a given tolerance. Similarly during the game match a prey reaches its home when the distance of the prey from its home becomes smaller than a given tolerance. The preys’ home is represented as a brown disk in the game field (see Figure 1). A prey after having a rendez vous with a predator or after reaching the preys home is removed from the game scene for the remaining part of the match.
During the execution of a game match the data generated by the human players using the joypads are transferred continuously in time to the game engine. The game engine processes these data in real time, that is in real time computes the new positions and velocities of the preys, and computes the closed loop solution of the optimal control problem considered to determine the new
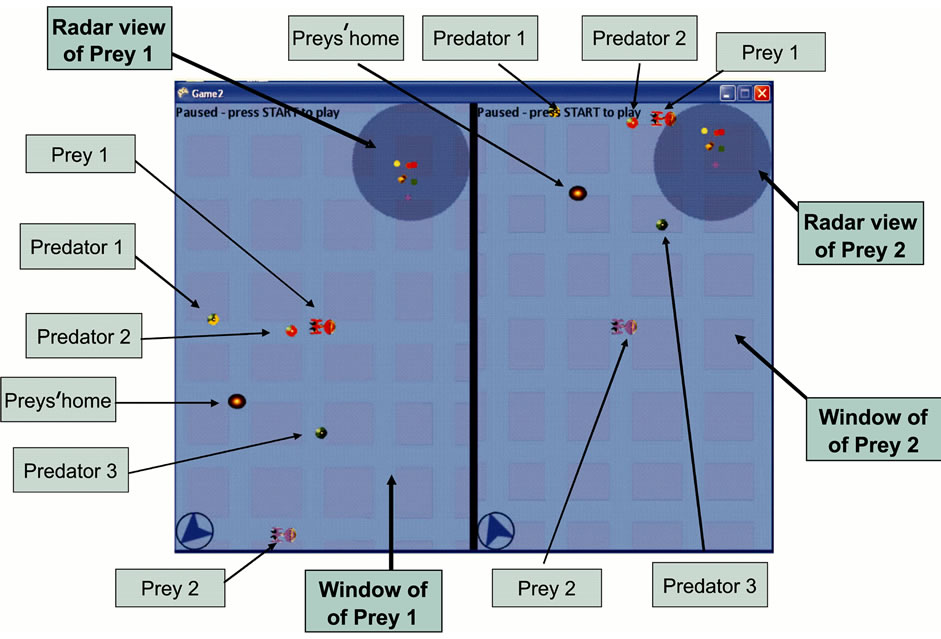
Figure 1. An initial scene of the game.
positions and velocities of the predators. Finally the game engine redraws preys and predators positions in the windows of the players and updates the global views of the game scene shown by the radars of the players. Moreover at the beginning of each match and when necessary during a match the game engine solves the assignment problem.
During a sequence of matches, depending on the statistical analysis of the points scored by the human players in the matches played, some parameters that define the behaviour of the predators are changed. In the implementation of the video game presented in Section 4 the parameters changed are the masses of the predators, however it is possible to change several other parameters appearing in the model defining predators with more sophisticated behavioural patterns than those implemented in Section 4. This mechanism makes the game difficulty adaptive and simulate an elementary form of personality in the predators.
1.4. Outline of the Paper
In Section 2 we discuss the “rendez vous” problem and its formulation as an optimal control problem. In Section 3 we present the closed loop solution of the optimal control problem formulated in Section 2. In Section 4 we explain the video game, in particular we explain the cooperative behaviour of the preys and of the predators and we show how the personalities of the predators are generated and adaptively changed during a sequence of matches (see Section 4.8). Moreover we present some technical and practical details of the implementation of the video game. In Section 5 we summarize the experience of a few dozen of children that have played with the video game and we draw some conclusions.
2. The Mathematical Model Used in the Game Engine
Let us formulate the optimal control problem whose solution is implemented in the engine of the video game. The position of the five actors of the video game (two preys and three predators) is given by five two-dimensional vectors in the Euclidean plane. These vectors and all the other vectors appearing in this paper are column vectors. The preys and the predators are point masses moving in the Euclidean plane. We use the vectors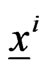 ,
,  to denote the prey positions and the vectors
to denote the prey positions and the vectors ,
, 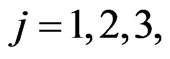 to denote the predator positions. Let
to denote the predator positions. Let 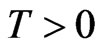 be a constant, we assume that the game matches begin at time
be a constant, we assume that the game matches begin at time  and end at time
and end at time . That is the game matches take place for
. That is the game matches take place for 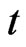 such that
such that . The vectors
. The vectors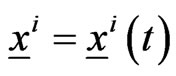 ,
, 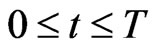 ,
, 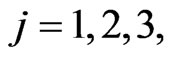
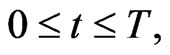
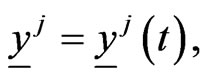
 describe the movements of the game actors in the Euclidean plane during a match, that is they describe the action going on in the game scene during a match.
describe the movements of the game actors in the Euclidean plane during a match, that is they describe the action going on in the game scene during a match.
The human players animate the preys located in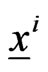 ,
, 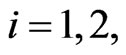 and in the time interval
and in the time interval 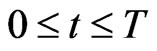 pursue the goals of avoiding the rendez vous with the predators located in
pursue the goals of avoiding the rendez vous with the predators located in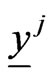 ,
, 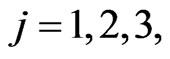 and of reaching as soon as possible the preys home (that is a fixed location in the plane). These goals are pursued acting on two joypads. The action on the joypads of the human players defines two vector functions
and of reaching as soon as possible the preys home (that is a fixed location in the plane). These goals are pursued acting on two joypads. The action on the joypads of the human players defines two vector functions 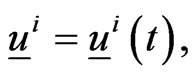
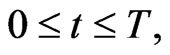
 taking values in the Euclidean plane. For
taking values in the Euclidean plane. For 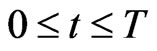 the vector
the vector 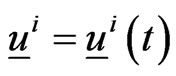 is the active force acting on the point mass representing the prey
is the active force acting on the point mass representing the prey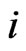 ,
,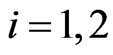 .
.
Let 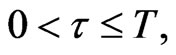 given the forces
given the forces 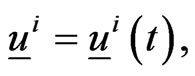
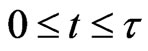 ,
, 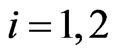 , the game engine computes the corresponding movements of the preys
, the game engine computes the corresponding movements of the preys ,
, 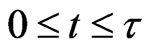 ,
,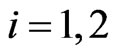 . In the video game for every
. In the video game for every 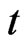 such that
such that , at time
, at time 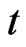 the positions of the preys up to time
the positions of the preys up to time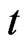 , that is
, that is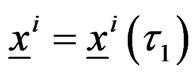 ,
,  ,
,  are known to the automated players. The preys have a similar knowledge of the preys and predators positions.
are known to the automated players. The preys have a similar knowledge of the preys and predators positions.
The automated players (predators) located in 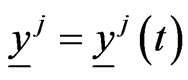 ,
,  ,
, 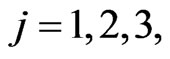 in the time interval
in the time interval 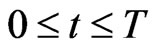 pursue the goals of having a rendez vous with the preys located in
pursue the goals of having a rendez vous with the preys located in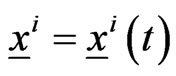 ,
,  ,
,  using a “small quantity” of the active forces at their disposal. These active forces are denoted with
using a “small quantity” of the active forces at their disposal. These active forces are denoted with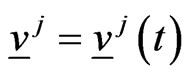 ,
, 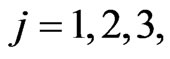
 and are functions of
and are functions of 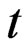 taking values in the Euclidean plane. The force
taking values in the Euclidean plane. The force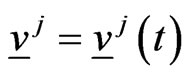 ,
, 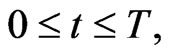 acts on the point mass representing the predator
acts on the point mass representing the predator 
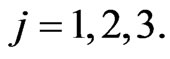
2.1. Newton’s Dynamical Principle Applied to Preys and Predators Movement
The functions ,
,  ,
,  are solutions of the following differential equations:
are solutions of the following differential equations:
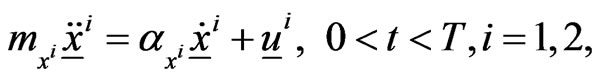 (1)
(1)
with the initial conditions:
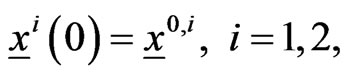 (2)
(2)
 (3)
(3)
where ,
,  denote respectively the first and second order derivatives with respect to
denote respectively the first and second order derivatives with respect to 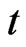 of
of  and
and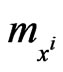 ,
, 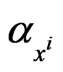 ,
, 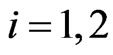 , are real constants. The constants
, are real constants. The constants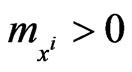 ,
, 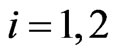 , are the masses of the preys. The constants
, are the masses of the preys. The constants 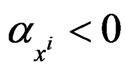 ,
, 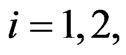 are the coefficients of the friction forces acting on the preys. The vectors
are the coefficients of the friction forces acting on the preys. The vectors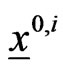 ,
, 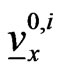 are given and represent respectively the initial position and the initial velocity of the prey
are given and represent respectively the initial position and the initial velocity of the prey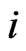 ,
, . Note that the forces
. Note that the forces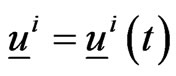 ,
, 
 , appear in (1) as forcing terms.
, appear in (1) as forcing terms.
The predators functions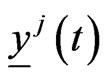 ,
,  ,
, 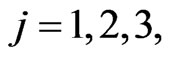 are solutions of the following differential equations:
are solutions of the following differential equations:
 (4)
(4)
with the initial conditions:
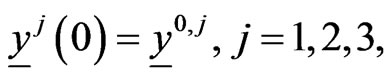 (5)
(5)
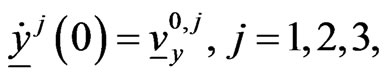 (6)
(6)
where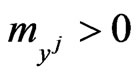 ,
, 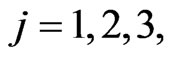 are the masses of the predators and
are the masses of the predators and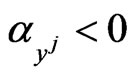 ,
,  are the coefficients of the friction forces acting on the predators. The vectors
are the coefficients of the friction forces acting on the predators. The vectors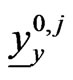 ,
, 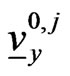 are given and represent respectively the initial position and the initial velocity of the predator
are given and represent respectively the initial position and the initial velocity of the predator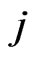 ,
, 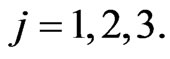 Note that the forces
Note that the forces ,
, 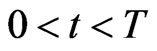 ,
,  appear in (4) as forcing terms and that they are determined as solution of the optimal control problem formulated below.
appear in (4) as forcing terms and that they are determined as solution of the optimal control problem formulated below.
The differential Equations (1) and (4) are interpreted as Newton’s dynamical principle 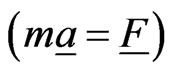 for two sets of point masses representing respectively the preys and the predators. In this sense they are inspired by classical mechanics and the movements implicitly defined by them, that is the trajectories of the preys and of the predators, satisfy basic physics laws. Let us point out that for every
for two sets of point masses representing respectively the preys and the predators. In this sense they are inspired by classical mechanics and the movements implicitly defined by them, that is the trajectories of the preys and of the predators, satisfy basic physics laws. Let us point out that for every  such that
such that 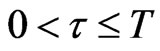 once known the data
once known the data ,
, 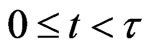 ,
, 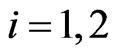 , it is possible to derive an explicit formula that gives the corresponding trajectories of the preys
, it is possible to derive an explicit formula that gives the corresponding trajectories of the preys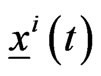 ,
, 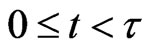 ,
, 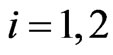 , up to time
, up to time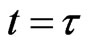 . This formula reduces the solution of the initial value problem (1), (2), (3), that defines
. This formula reduces the solution of the initial value problem (1), (2), (3), that defines 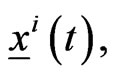
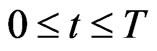 , to the evaluation of an integral that contains the control function
, to the evaluation of an integral that contains the control function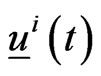 ,
,  ,
, . A similar statement holds for the initial value problems (4)-(6).
. A similar statement holds for the initial value problems (4)-(6).
2.2. The Optimal Control Problem and the Dynamics of the Game Actors
Given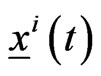 ,
, 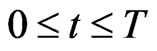 ,
,  we determine
we determine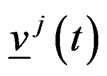 ,
, 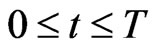 ,
,  as solution of the optimal control problem:
as solution of the optimal control problem:
 (7)
(7)
subject to the constraints (4), (5), (6). In (7)  denotes the scalar product in the Euclidean plane. Later
denotes the scalar product in the Euclidean plane. Later  will denote the scalar product in a generic Euclidean space not necessarily two dimensional. The quantities
will denote the scalar product in a generic Euclidean space not necessarily two dimensional. The quantities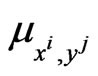 ,
, 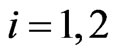 ,
, 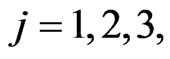 and
and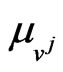 ,
, 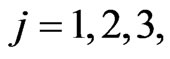 that appear in (7) are nonnegative constants satisfying some conditions that will be specified later. Note that in order to be usable in the video game engine the solution of the control problem (7), (4), (5), (6) must be in closed loop form. That is for any
that appear in (7) are nonnegative constants satisfying some conditions that will be specified later. Note that in order to be usable in the video game engine the solution of the control problem (7), (4), (5), (6) must be in closed loop form. That is for any 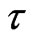 such that
such that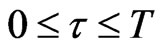 , from the knowledge of
, from the knowledge of ,
,  ,
, 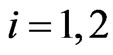 , we must determine
, we must determine ,
,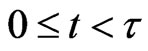 .
.
Let us explain why the initial value problem (1), (2), (3) and the control problem (7), (4), (5), (6) are a legitimate mathematical model of the game described in the Introduction. In fact the control functions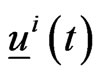 ,
,
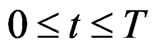 ,
,  are chosen by the human players acting on the joypads based on the observation of the scene on the computer screen and are interpreted as forces acting on the preys. These forces define implicitly (through the initial value problems (1), (2), (3)) the strategy followed by the human players to achieve their goals. The choice of the control functions
are chosen by the human players acting on the joypads based on the observation of the scene on the computer screen and are interpreted as forces acting on the preys. These forces define implicitly (through the initial value problems (1), (2), (3)) the strategy followed by the human players to achieve their goals. The choice of the control functions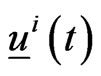 ,
, 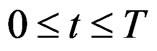 ,
, 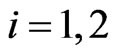 , is reflected in the control problem (7), (4), (5), (6) through the presence in (7) of the functions
, is reflected in the control problem (7), (4), (5), (6) through the presence in (7) of the functions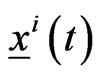 ,
,  ,
, 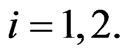 This implies that the choice of the control functions made by the human players determines the behaviour of the automated players obtained solving the control problem (7), (4), (5), (6). The control functions
This implies that the choice of the control functions made by the human players determines the behaviour of the automated players obtained solving the control problem (7), (4), (5), (6). The control functions ,
, 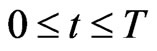 ,
, 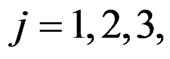 solution of (7), (4), (5), (6) define implicitly through the initial value problems (4), (5), (6) the movements of the predators. Let us explain more in detail the cost functional (7). For
solution of (7), (4), (5), (6) define implicitly through the initial value problems (4), (5), (6) the movements of the predators. Let us explain more in detail the cost functional (7). For ,
, 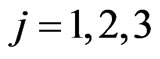 when the nonnegative constant
when the nonnegative constant 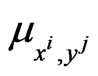 is greater than zero making small the term
is greater than zero making small the term
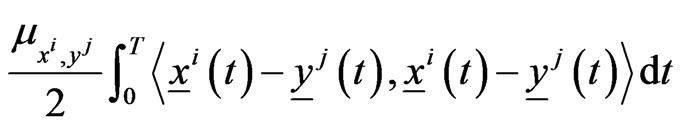 of (7) corresponds to trying to realize the rendez vous between the predator
of (7) corresponds to trying to realize the rendez vous between the predator 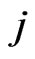 and the prey
and the prey  and similarly when the nonnegative constant
and similarly when the nonnegative constant 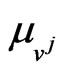 is greater than zero making small the term
is greater than zero making small the term  of (7) corresponds to the attempt of using a “small quantity” of the control function
of (7) corresponds to the attempt of using a “small quantity” of the control function 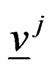 (i.e. the available resource) during the rendez vous. In the game implementation we choose
(i.e. the available resource) during the rendez vous. In the game implementation we choose ,
,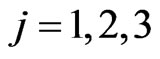 . The choice of the constants
. The choice of the constants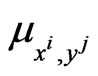 ,
, 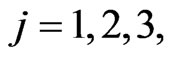
 corresponds to the solution of the assignment problem mentioned previously, that is corresponds to the assignment of the preys to the predators. In fact for
corresponds to the solution of the assignment problem mentioned previously, that is corresponds to the assignment of the preys to the predators. In fact for 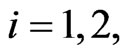
 when
when 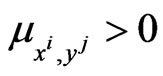 the prey
the prey 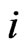 is assigned to the predator
is assigned to the predator  (that is the predator
(that is the predator 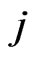 chases the prey
chases the prey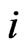 ), when
), when 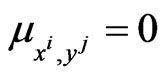 the prey
the prey  is not assigned to the predator
is not assigned to the predator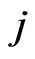 . The value of the constant
. The value of the constant 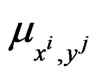 is a measure of the “attraction” of the predator
is a measure of the “attraction” of the predator  towards the prey
towards the prey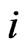 ,
, 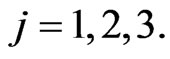
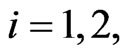 That is for
That is for 
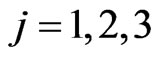 increasing the value of the constant
increasing the value of the constant 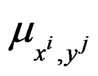 increases the attraction of the predator
increases the attraction of the predator 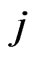 toward the prey
toward the prey . In the implementation of the game when
. In the implementation of the game when 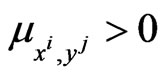 we choose
we choose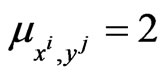 ,
, 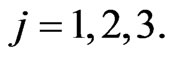
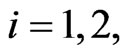 The assignment of the preys to the predators done by the game engine at the beginning of each match satisfies the following rules: 1) each predator must chase only one prey, 2) each prey must be chased by at least one predator. These rules imply a kind of cooperation between the predators. The assignment of the preys to the predators is redone during a match when a prey is captured by a predator (i.e. there is a rendez vous) or when a prey reaches the preys’ home. In these cases only one prey remains active in the game scene and all the predators chase it. Note that when a rendez vous takes place or a prey reaches the prey home the differential models (1), (2), (3) and (7), (4), (5), (6) are reformulated in an obvious way to take care of the situation determined by these events.
The assignment of the preys to the predators done by the game engine at the beginning of each match satisfies the following rules: 1) each predator must chase only one prey, 2) each prey must be chased by at least one predator. These rules imply a kind of cooperation between the predators. The assignment of the preys to the predators is redone during a match when a prey is captured by a predator (i.e. there is a rendez vous) or when a prey reaches the preys’ home. In these cases only one prey remains active in the game scene and all the predators chase it. Note that when a rendez vous takes place or a prey reaches the prey home the differential models (1), (2), (3) and (7), (4), (5), (6) are reformulated in an obvious way to take care of the situation determined by these events.
The match begins at time 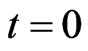 and ends at time
and ends at time 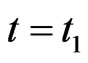 ,
, 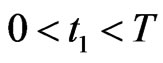 , where
, where  is the smallest time value such that for
is the smallest time value such that for  two preys have reached the preys’ home or one prey has been captured and the other one has reached the prey home or two preys have been captured. In all the remaining cases the match ends when the time assigned to the match is expired, that is when
two preys have reached the preys’ home or one prey has been captured and the other one has reached the prey home or two preys have been captured. In all the remaining cases the match ends when the time assigned to the match is expired, that is when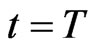 . At the beginning of each match when a new (initial) scene is proposed the game engine does the assignment of the preys to the predators (i.e. chooses the constants
. At the beginning of each match when a new (initial) scene is proposed the game engine does the assignment of the preys to the predators (i.e. chooses the constants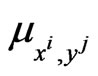 ,
,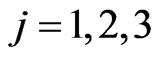
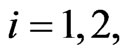 ) simply associating to each prey the nearest predator. Moreover the engine verifies that the assignment obtained in this way satisfies the rules stated above. For example when using the “nearest predator rule” two preys are assigned to the same predator the engine changes this assignment, assigning to this predator only the nearest prey and giving the other prey to the nearest predator among the remaining ones. In the assignment problem when necessary some simple choices are done. For example, degenerate cases such as the case when there are two preys at the same distance from the nearest predator are solved making random choices. The assignment chosen by the game engine satisfies always the rules stated above.
) simply associating to each prey the nearest predator. Moreover the engine verifies that the assignment obtained in this way satisfies the rules stated above. For example when using the “nearest predator rule” two preys are assigned to the same predator the engine changes this assignment, assigning to this predator only the nearest prey and giving the other prey to the nearest predator among the remaining ones. In the assignment problem when necessary some simple choices are done. For example, degenerate cases such as the case when there are two preys at the same distance from the nearest predator are solved making random choices. The assignment chosen by the game engine satisfies always the rules stated above.
3. The “Closed Loop” Solution of the Optimal Control Problem Used in the Game Engine
Let 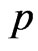 be a positive integer,
be a positive integer, 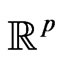 be the
be the 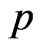 dimensional real Euclidean space and
dimensional real Euclidean space and 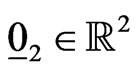 be the two dimensional null vector. Let us solve in closed loop form the optimal control problem (7), (4), (5), (6). We define the vector of the state variables of problem (7), (4), (5), (6) at time
be the two dimensional null vector. Let us solve in closed loop form the optimal control problem (7), (4), (5), (6). We define the vector of the state variables of problem (7), (4), (5), (6) at time ,
, 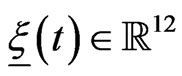 ,
,  , and the vector
, and the vector ,
,  , that contains the position of the prey
, that contains the position of the prey  at time
at time ,
,  , that is:
, that is:
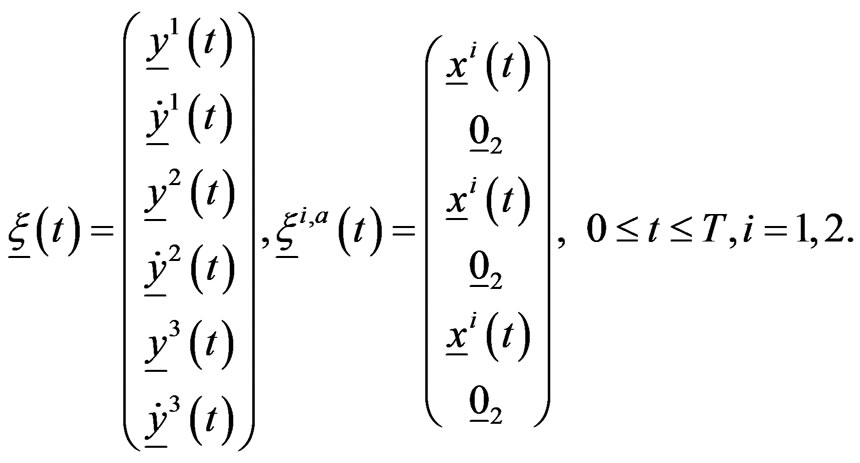 (8)
(8)
Moreover let us introduce the vector of the control functions at time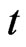 ,
,  ,
, 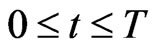 , that is:
, that is:
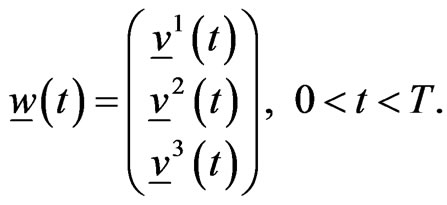 (9)
(9)
Recall that the vectors defined in (8), (9) are column vectors. For later convenience we define 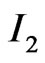 to be the
to be the 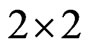 identity matrix and
identity matrix and 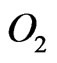 to be the
to be the 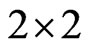 null matrix. The optimal control problem (7), (4), (5), (6) can be rewritten as follows:
null matrix. The optimal control problem (7), (4), (5), (6) can be rewritten as follows:
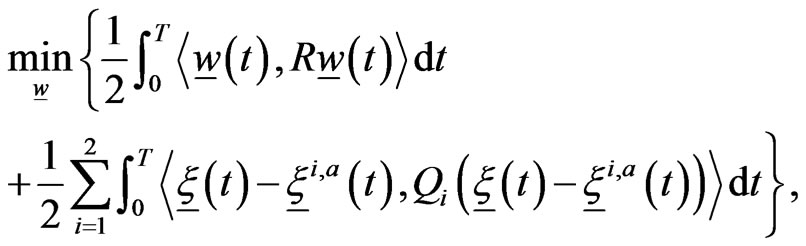 (10)
(10)
subject to the constraints:
 (11)
(11)
with the initial condition:
 (12)
(12)
where 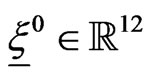 is a column vector. The matrices
is a column vector. The matrices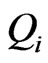 ,
, 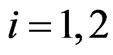 , and
, and  are
are 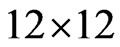 real matrices,
real matrices, 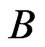 is a
is a 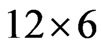 real matrix and
real matrix and 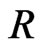 is a
is a 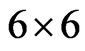 real matrix. These matrices are given by:
real matrix. These matrices are given by:
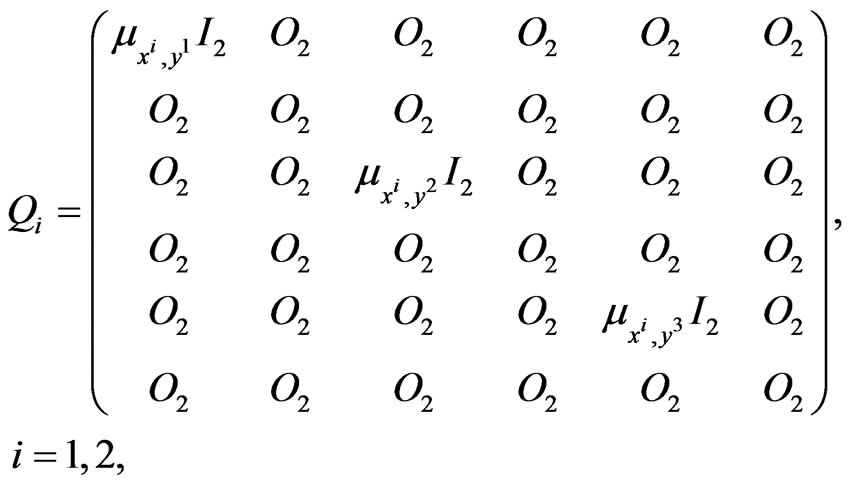 (13)
(13)
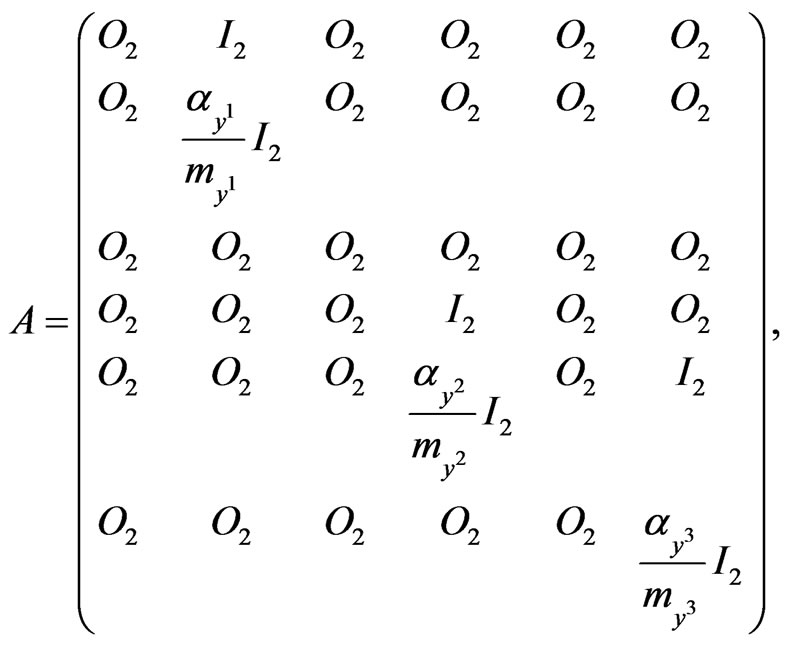 (14)
(14)
 (15)
(15)
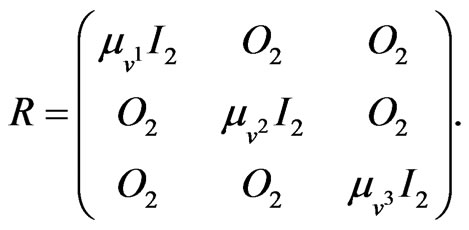 (16)
(16)
The matrix vector products appearing in (10), (11) are the usual rows by columns matrix, vector products.
Note that for 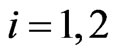 the matrix
the matrix  defines the assignment of the prey
defines the assignment of the prey  to the predators, and that the functions
to the predators, and that the functions ,
, 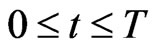 ,
, 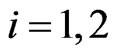 , are data in the optimal control problem (10), (11), (12).
, are data in the optimal control problem (10), (11), (12).
It is easy to see that the first and the second term of the cost functional (10) correspond respectively to the first and the second term of the cost functional (7).
The special form of the optimal control problem (10), (11), (12) (i.e.: quadratic cost functional and linear constraints) guarantees that the Hamilton Jacobi equation associated to it can be reduced to a system of ordinary differential equations that can be integrated numerically (see [19] pp. 138-142) to obtain an approximate closed loop solution of the optimal control problem (10), (11), (12) or equivalently of the problem (7), (4), (5), (6). Proceeding in this way we approximate the strategy of the predators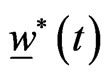 ,
,  , solution of problem (10), (11), (12), as follows:
, solution of problem (10), (11), (12), as follows:
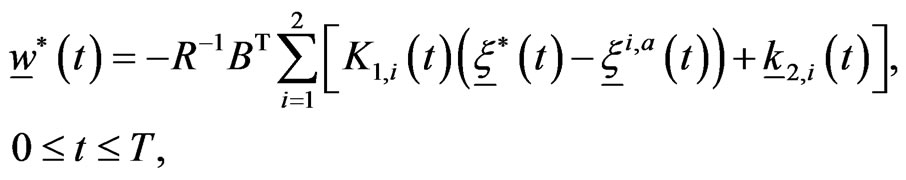 (17)
(17)
where the optimal trajectory of the state variables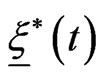 ,
, 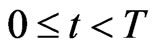 , is the solution of the following system of differential equations:
, is the solution of the following system of differential equations:
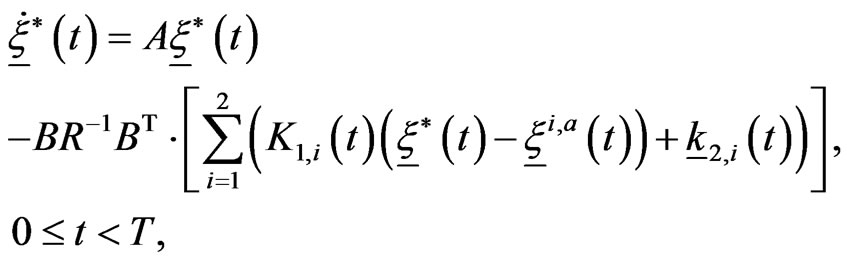 (18)
(18)
with the initial condition:
 (19)
(19)
and 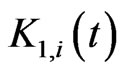 is a
is a 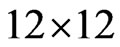 real matrix,
real matrix,  is a vector,
is a vector, 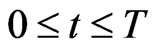 ,
,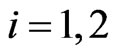 . The quantities
. The quantities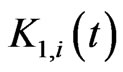 ,
,  ,
, 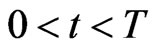 ,
, 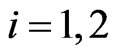 , that appear in (17), (18) are solutions of the following systems of differential equations:
, that appear in (17), (18) are solutions of the following systems of differential equations:
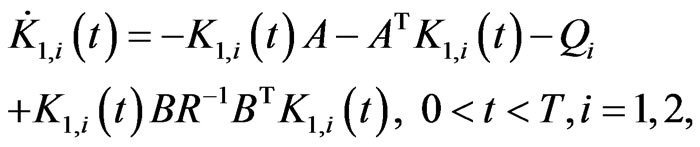 (20)
(20)
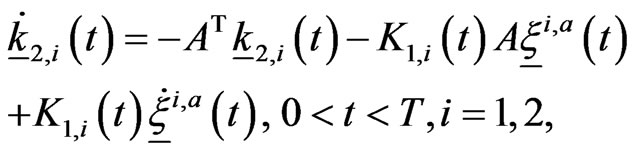 (21)
(21)
with the final conditions:
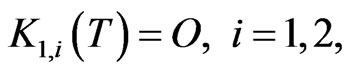 (22)
(22)
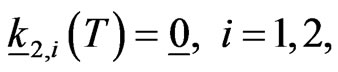 (23)
(23)
where in (22), (23) 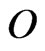 and
and 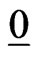 are respectively the
are respectively the  null matrix and the 12 dimensional null vector. The system of ordinary differential Equations (20) is Riccati system of differential equations. Note that the matrices
null matrix and the 12 dimensional null vector. The system of ordinary differential Equations (20) is Riccati system of differential equations. Note that the matrices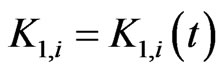 ,
, 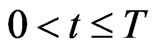 ,
, 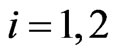 , solutions of (20), (22), can be computed (numerically) at time
, solutions of (20), (22), can be computed (numerically) at time 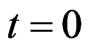 integrating backward in time (20) starting from the final condition (22). This can be done, for example, using Euler method. This is possible since Equations (20), (22) do not depend on the trajectories
integrating backward in time (20) starting from the final condition (22). This can be done, for example, using Euler method. This is possible since Equations (20), (22) do not depend on the trajectories ,
, 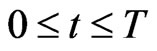 ,
,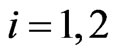 .
.
The vectors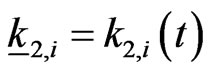 ,
, 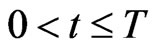 ,
, 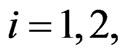 solutions of (21), (23) cannot be computed at time
solutions of (21), (23) cannot be computed at time 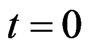 in the same way since to do that we should know at time
in the same way since to do that we should know at time 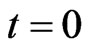 the functions
the functions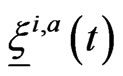 ,
,  in the interval
in the interval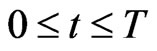 . However it is not possible to assume that at time
. However it is not possible to assume that at time 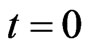 the prey trajectories contained in the functions
the prey trajectories contained in the functions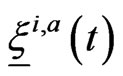 ,
, 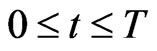 ,
, 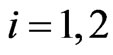 , are known in the time interval
, are known in the time interval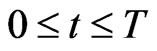 .
.
Hence in order to compute the solution of the optimal control problem (10), (11), (12) we proceed as follows:
Step 0. Decompose the interval  in
in 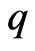
subintervals, that is let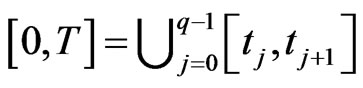 , where
, where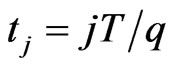 ,
, 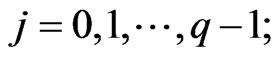 For
For  do the following steps:
do the following steps:
Step 1. Solve numerically using Euler method backward in time the system of ordinary differential Equations
(20) in the interval  with the null condition at
with the null condition at  and store the approximation
and store the approximation 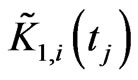 of
of ,
, 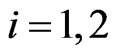 , obtained in this way.
, obtained in this way.
Step 2. From the knowledge of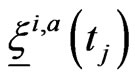 ,
,  ,
, 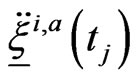 approximate
approximate 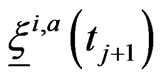 and
and  respectively with
respectively with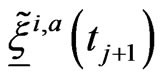 ,
, 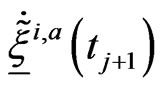 given by the following formulae:
given by the following formulae:
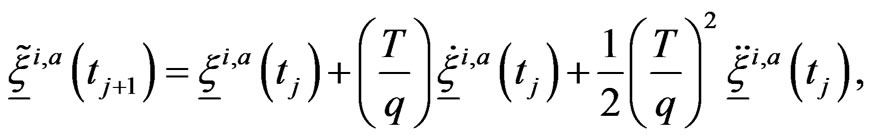 (24)
(24)
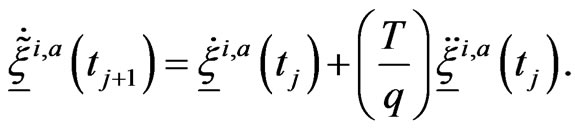
 (25)
(25)
Solve numerically using Euler method backward in time the system of differential Equations (21) in the interval , with the null condition at
, with the null condition at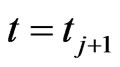 , that is compute:
, that is compute:
 (26)
(26)
with the final conditions:
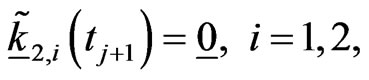 (27)
(27)
where 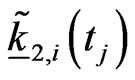 is the quantity that approximates
is the quantity that approximates 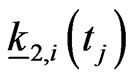 ,
,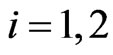 .
.
Step 3. From the knowledge of an approximation
 of
of  compute numerically an approximation
compute numerically an approximation 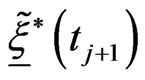 of
of 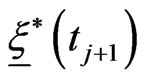 at time
at time  solving
solving
(18), (19) using Euler method forward in time, which is compute:
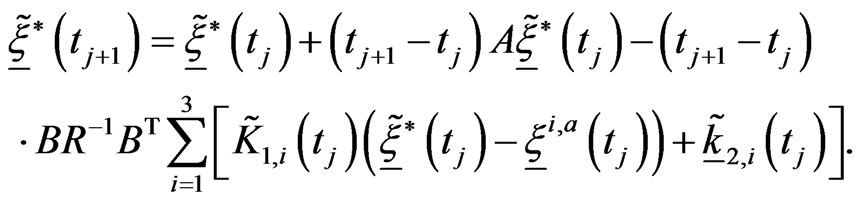 (28)
(28)
Recall that the initial condition at 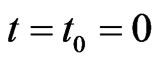 of
of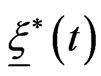 ,
, 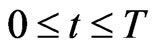 , is given by:
, is given by:
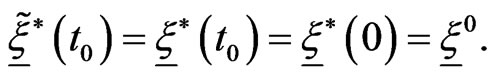 (29)
(29)
Finally compute the approximation 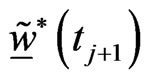 of the optimal control
of the optimal control  at time
at time  using formula (17).
using formula (17).
Note that using the Steps 0-3 in order to approximate the optimal strategy 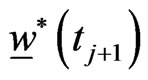 and the optimal trajectory
and the optimal trajectory 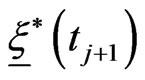 at time
at time 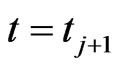 it is necessary to know only
it is necessary to know only 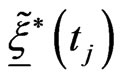 and
and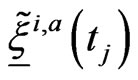 ,
, 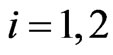 ,
,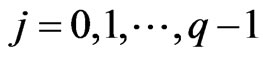 .
.
In the implementation of the video game described in Section 4 Steps 0-3 are used with 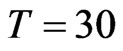 seconds and
seconds and .
.
4. The Video Game Implementation and the Personalities of the Predators
The video game described in the previous Sections and further specified in this Section has been implemented in C# (C sharp) language and can be downloaded from the website: http://www.ceri.uniroma1.it/ceri/zirilli/w10/. The website contains also some auxiliary material that helps the understanding of this paper.
4.1. System Requirements
The video game works under Windows XP, Vista and Windows 7 both on 32-bit and on 64 bit thank to a setup that recognizes the hardware configuration (32 or 64 bit). To play it is necessary to use the joypad Xbox 360 controller for Windows (see Figure 2). Each human player must have a joypad.
4.2. Game Setting
The human players must avoid the rendez vous with the three automated players (the predators) and must reach a given location in the plane called preys’ home. The preys’ home is represented by a brown disk with a yellow center on the computer screen. The game field is the entire plane and each prey has at its disposal a window on the computer screen (see Figure 1). During the game each prey is always at the center of its window. That is the window scrolls up, down, left and right according to the movement of the prey. In every window in the right top corner there is a global view of the game scene provided by the “radar” of the prey. This global view of the scene has the prey at its center and shows all the actors of the game and the preys’ home. Finally in the left bottom corner of every window there is an arrow that indicates

Figure 2. The joypad Xbox 360.
the direction (within the window) of the vector that joins the center of the window with the preys’ home. This arrow is particularly useful when the preys’ home does not appear in the local view of the game scene shown in the window to indicate to the prey the direction where to go to find its home. Figure 1 shows the two windows of the preys as they appear on the computer screen.
The possible outcomes of a game match are: 1) two preys reach the preys’ home, 2) one prey reaches the preys’ home and the other prey has not been captured at time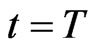 , 3) one prey reaches the preys’ home and the other prey has been captured, 4) two preys have not reached the preys’ home and have not been captured at time
, 3) one prey reaches the preys’ home and the other prey has been captured, 4) two preys have not reached the preys’ home and have not been captured at time , v) one prey has not reached the preys’ home and has not been captured at time
, v) one prey has not reached the preys’ home and has not been captured at time 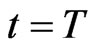 and the other prey has been captured, 6) both preys have been captured. To these different outcomes are attributed points following the rules specified in Section 4.3.
and the other prey has been captured, 6) both preys have been captured. To these different outcomes are attributed points following the rules specified in Section 4.3.
The game consists in a sequence of matches, each match has a duration of thirty seconds, that is 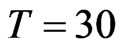 seconds. Each match starts from its own initial scene. An initial scene is made of the location of the preys’ home and of the preys and predators positions at time
seconds. Each match starts from its own initial scene. An initial scene is made of the location of the preys’ home and of the preys and predators positions at time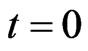 . The velocities of the preys and of the predators at time
. The velocities of the preys and of the predators at time  are chosen to be zero. The initial scenes of the matches are generated randomly. The way of specifying the personalities of the predators in a sequence of matches is discussed in Section 4.8. At the beginning of each match the human players observe the initial scene of the game looking at their windows on the screen, in particular looking at the image of the game scene shown by their radars. Before the beginning or during a pause of a match the game action is stopped and the human players can agree on an eventually cooperative strategy to play the match. The choice of the strategy is dictated by the desire of making in the match the best point score that is compatible with the game scene and with the game rules. The strategy chosen must be implemented by the human players using the joypads in the action that takes place after starting or resuming the match.
are chosen to be zero. The initial scenes of the matches are generated randomly. The way of specifying the personalities of the predators in a sequence of matches is discussed in Section 4.8. At the beginning of each match the human players observe the initial scene of the game looking at their windows on the screen, in particular looking at the image of the game scene shown by their radars. Before the beginning or during a pause of a match the game action is stopped and the human players can agree on an eventually cooperative strategy to play the match. The choice of the strategy is dictated by the desire of making in the match the best point score that is compatible with the game scene and with the game rules. The strategy chosen must be implemented by the human players using the joypads in the action that takes place after starting or resuming the match.
As already said the match is over when 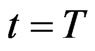 or before
or before  when one of the following conditions are satisfied: the two preys have been captured, the two preys have reached their home, one prey has been captured and the other has reached the preys’ home. The game ends when one of the human players presses the BACK button of the joypad or when the maximum number of matches allowed has been played. In the downloadable version of the game the maximum number of matches allowed is 100.
when one of the following conditions are satisfied: the two preys have been captured, the two preys have reached their home, one prey has been captured and the other has reached the preys’ home. The game ends when one of the human players presses the BACK button of the joypad or when the maximum number of matches allowed has been played. In the downloadable version of the game the maximum number of matches allowed is 100.
4.3. Score Rules
The score of the game is computed summing the scores made in the matches. The score of a match is computed using the following rules:
1) One point for each prey that has not reached the preys’ home and has not been captured at the end of the match, that is at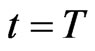 2) Three points for each prey that has reached the preys’ home during the match.
2) Three points for each prey that has reached the preys’ home during the match.
The points scored are attributed to the team of the human players not to the players individually.
Note that the score rules, the initial scene of the match, the rules used in the assignment of the preys to the predators and the personalities of the predators (see Section 4.8) determine the strategy that the human players must choose at the beginning of each match.
4.4. Radar View of the Game
The global view of the game scene shown by the radar is a disk on the right top corner of the window associated to each prey (Figure 1). In this view the game scene is shown completely, that is in this view of the scene the preys’ home (brown disk with a yellow center), the predators (green, orange and yellow disks) and the preys (red and violet disks) are shown. Each prey is at the center of the scene shown by its radar. The view of the scene shown by the radar can be removed from the window pressing the GREEN button of the joypad.
4.5. Preys’ Home
The preys’ home is a location in the plane denoted with a brown disk with a yellow center (Figure 1). This location is generated randomly at the beginning of each match and remains unchanged during the match. The preys’ home is always visible in the global view of the game scene shown by the radars and the arrow in the left bottom corner of the window of each prey indicates the direction within the window where to go to find the preys’ home (Figure 1).
4.6. Preys Movements and Cooperation
The preys are point masses represented as colored disks (red or violet) in the global views of the scene shown on the computer screen and their movements are implicitly defined by the equations of motion (1) with the initial conditions (2), (3). In its own window the prey is the colored (red, violet) guy at the center of the window (see Figure 1). The masses and the friction coefficients of the preys are assigned at the beginning of the game by the game engine and they remain unchanged until the end of the game.
Five buttons of the joypad are used by the human players during the game, that is: START button, BACK button, GREEN button, top left washer and bottom right washer (see Figure 2).
The forces ,
, 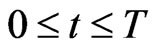 ,
, 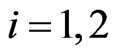 , appearing in Equation (1) are chosen by the human players acting on the joypads as follows. The movement of the top left washer to the right provides a force that pushes the prey to the right of the computer screen, the movement of the top left washer up provides a force that pushes the prey upwards on the computer screen and so on. The force magnitude is directly proportional to the washer slope. That is the signals transmitted by the top left washers of the joypads to the game engine are interpreted as two pairs of real numbers
, appearing in Equation (1) are chosen by the human players acting on the joypads as follows. The movement of the top left washer to the right provides a force that pushes the prey to the right of the computer screen, the movement of the top left washer up provides a force that pushes the prey upwards on the computer screen and so on. The force magnitude is directly proportional to the washer slope. That is the signals transmitted by the top left washers of the joypads to the game engine are interpreted as two pairs of real numbers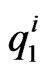 ,
, 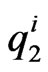 belonging to the range
belonging to the range  that can be identified respectively with the Cartesian components (in the “natural” frame of reference) of the vectors
that can be identified respectively with the Cartesian components (in the “natural” frame of reference) of the vectors  appearing in Equation (1),
appearing in Equation (1),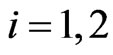 . These pairs of numbers are functions of time. The movements impressed on the top left washers as a function of time define the forces that the human players provide to the corresponding preys as a function of time.
. These pairs of numbers are functions of time. The movements impressed on the top left washers as a function of time define the forces that the human players provide to the corresponding preys as a function of time.
Before starting a match (or before resuming a paused match) the human players must observe the game scene on their radar views and depending on the scene observed they must choose a strategy to play the match that follows. For example, if one prey is close to the preys’ home but has two predators in its immediate vicinity, these predators are presumably assigned to its capture. In this case it could be convenient in order to maximize the score made in the match to move this prey far from the preys’ home forcing the two predators assigned to its capture to follow it and as a consequence to move far from the preys’ home. This makes easier for the other prey to reach home. The choice of the previous strategy is motivated by the fact that the score made when one prey reaches home and the other is captured or remains alive until the end of the match is higher than the score obtained when the two preys remain alive until the end of the match but neither of them reaches the preys’ home. Note that in the choice of their strategy the human players must keep in mind that at the beginning of the match one of the preys will be chased by one predator and the other one will be chased by two predators. Moreover the strategy chosen must consider the assignment rule, that is must consider the fact that basically the predators are assigned to chase the prey nearest to them in the initial scene. Hence at the beginning of a match looking at the initial scene shown by the radars the human players can image which one of the preys will be chased by two predators. Moreover the human players must consider the fact that in the initial scene of a match the velocities of the preys and of the predators are zero and that this is not true in general in the scene of a paused match. After a few matches, the human players should be able to evaluate the differences between the predators. This information is relevant in the choice of the prey strategies in particular it is relevant when the predators are located near the preys’ home. However as will be seen in Section 4.8 the personalities of the predators change during a sequence of matches and as a consequence the human players in the choice of their strategy must adapt their criteria to the changes of the predator personalities.
4.7. Predators Movements and Cooperation
The predators are point masses represented as colored disks (green, orange and red) on the computer screen and their movements are implicitly defined by the equations of motion (4) with the initial conditions (5), (6). Each predator pursues the goal of chasing the prey assigned to it by the game engine using a “small quantity” of the resources available to it (i.e. of its control function). The predators are different one from the others. That is the parameters that appear in the predator equations are different for the red, orange and green predator. As explained in Section 4.8 in the game actually implemented during a sequence of matches the masses of the predators change depending on the behaviour of the preys while the values of the other parameters have a standard value that remains unchanged.
4.8. The Predator Personalities
When a sequence of matches is played in order to simulate a predators behaviour similar to the (supposed) human behaviour in the similar circumstances an elementary statistical analysis of the points scored by the human players in the matches played is used. This mechanism provides a form of artificial intelligence to the predators that goes beyond the artificial intelligence used to chase the preys in a match. In particular out of this mechanism three specific forms of artificial intelligence (in short AI forms) are implemented. The first AI form consists in having the predators to behave in a slightly different way in each match. This corresponds to the fact that the human behaviour in similar circumstances is not always the same but, for example, depends on the humor of the moment. The second AI form consists in calibrating the effectiveness of the predators in chasing the preys according to the ability of the preys. This is done to avoid to discourage or to bore the human players as a consequence of the fact that the predators are too effective or too ineffective in chasing the preys. The third AI form wants to simulate in the predator behaviour the emotional reaction of a human player to a sequence of defeats or of victories.
Let us go into the details of how these three AI forms are implemented.
For 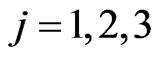 we begin assigning to the mass
we begin assigning to the mass  of the predator
of the predator 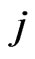 three possible values
three possible values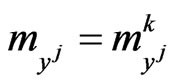 ,
, 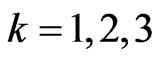 , such that
, such that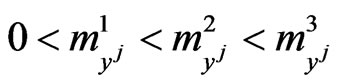 . The parameters
. The parameters ,
, 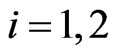 ,
, 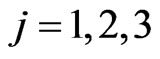 , are chosen solving the assignment problem and take the values zero or two. The parameters
, are chosen solving the assignment problem and take the values zero or two. The parameters ,
,  ,
,  , are assigned at the beginning of the game and kept constant during the matches. We have
, are assigned at the beginning of the game and kept constant during the matches. We have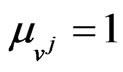 ,
, 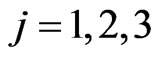 , and
, and  (pink predator),
(pink predator), 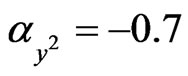 (yellow predator) and
(yellow predator) and  (green predator).
(green predator).
To implement the first AI form we do the following: at the beginning of each match a random variable  is sampled,
is sampled,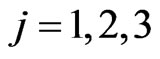 . The random variable
. The random variable 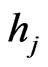 assigns to the mass of the predator
assigns to the mass of the predator  the values
the values ,
, 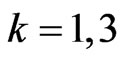 , with probability
, with probability 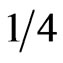 and the value
and the value  with probability
with probability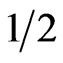 ,
, .
.
To implement the second AI form, once every ten matches, the game engine checks the score made by the human players in the last ten matches and compares it with the maximum score attainable in the matches. If the score made is smaller than 20% of the maximum score attainable the masses of the predators are increased of 20%, that is ,
, 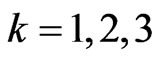 ,
, 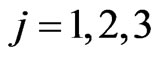 , if the score made is greater than 70% of the maximum score attainable the masses of the predators are decreased of 20%, that is
, if the score made is greater than 70% of the maximum score attainable the masses of the predators are decreased of 20%, that is ,
, 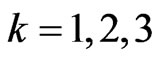 ,
, 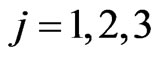 . Let us point out that increasing the mass of a predator makes it slower in its movement and, as a consequence, makes easier for the preys to avoid the “rendez vous” with this predator. Similarly decreasing the mass of a predator makes it faster in its movement and, as a consequence, makes more difficult for the preys to avoid the “rendez vous” with this predator. That is increasing the masses of the predators makes the game easier for the human players and decreasing the masses of the predators makes the game more difficult for the human players. In this way the difficulty of the game increases or decreases depending on the ability of the human players. Moreover the random behaviour of the masses of the predators that vary between the values
. Let us point out that increasing the mass of a predator makes it slower in its movement and, as a consequence, makes easier for the preys to avoid the “rendez vous” with this predator. Similarly decreasing the mass of a predator makes it faster in its movement and, as a consequence, makes more difficult for the preys to avoid the “rendez vous” with this predator. That is increasing the masses of the predators makes the game easier for the human players and decreasing the masses of the predators makes the game more difficult for the human players. In this way the difficulty of the game increases or decreases depending on the ability of the human players. Moreover the random behaviour of the masses of the predators that vary between the values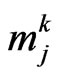 ,
, 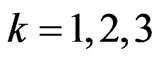 , depending on the value sampled from the random variable
, depending on the value sampled from the random variable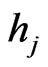 ,
, 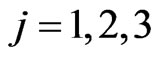 , makes impossible to know precisely the ability of the predators when planning a strategy at the beginning of a match.
, makes impossible to know precisely the ability of the predators when planning a strategy at the beginning of a match.
Let us call defeat a match where two preys have been captured and victory a match where both preys have reached the preys’ home. To realize the third AI form we check the number 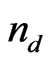 of consecutive defeats and the number
of consecutive defeats and the number 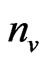 of consecutive victories of the human players. When
of consecutive victories of the human players. When 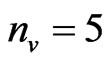 the masses of the predators are decreased of 30%. This simulates the fact that the predators are “hungry” due to the repeated victories of the human players and become aggressive. When
the masses of the predators are decreased of 30%. This simulates the fact that the predators are “hungry” due to the repeated victories of the human players and become aggressive. When  the masses of all predators are increased of 30%. This simulates the fact that the predators are satisfied due to the repeated defeats of the human players and become relaxed.
the masses of all predators are increased of 30%. This simulates the fact that the predators are satisfied due to the repeated defeats of the human players and become relaxed.
5. Experimental Results and Conclusions
We have done an experiment on a sample of a few dozens of young players aged between five and thirteen years to see the reaction of these players to the exposure to the video game. The previous experiences with video games of these children were very different. The children were divided in three groups. The first group was made of children who had never played video games, the second one was made of children having a little experience with video games and the third one was made of children used to play video games. The players of the first group were five-six years old, the age of the players of the remaining groups was between five and thirteen years old. The experiment has shown that children aged between five and eight years belonging to the first two groups enjoy playing the video game and in the first matches played find difficult to cooperate. However, after some matches, these young players understand the presence of restrictions to their movements and to the movements of their opponents coming from Newton’s dynamical principle and develop strategies coherent with these restrictions. An interesting finding is that even the youngest players (five-six years old) after playing a few matches develop an intuitive understanding of Newton’s dynamical principle and consequently are able to improve their ability to escape from the pursuit with the predators and to cooperate with their teammate. Playing the video game is an enjoyable experience for the first two groups of children. In fact the simplicity and the dynamic change of the level of difficulty of the game encourage the players of the first group and the cooperation amuses the players of the second group. The players of the third group, in particular the teenager players, after a while get bored by the video game. In fact these players are already acquainted with the richness of commercial video games and are disappointed by the simplicity of the video game presented here.
Concluding the video game at least for the younger and inexperienced players is a practical tool to understand intuitively some basic physical laws and to develop a cooperative attitude with their teammate.
Moreover the video game is an example of how mathematical models taken from optimal control and elementary statistics can be used to develop prey-predator games where the actors’ movements satisfy Newton’s dynamical principle and the automated actors simulate a form of intelligent behaviour that changes dynamically depending on the behaviour of the human players during the game. No “a priori” schemes are used to determine the automated players’ behaviour.
REFERENCES
- A. K. Bay-Hinitz, R. F. Peterson and H. R. Quilitch, “Cooperative Games: A Way to Modify Aggressive and Cooperative Behaviours in Young Children,” Journal of Applied Behavior Analysis, Vol. 27, No. 3, 1994, pp. 435- 446. doi:10.1901/jaba.1994.27-435
- M. V. Aponte, G. Levieux and S. Natkin, “Scaling the Level of Difficulty in Single Player Video Games,” Proceedings of the 8th International Conference on Entertainment Computing, Paris, 3-5 September 2009, S. Natkin and J. Dupire, Eds., ICEC 5709, 2009, pp. 24-35.
- R. Prada and A. Paiva, “Teaming up Humans with Autonomous Synthetic Characters,” Artificial Intelligence, Vol. 173, No. 1, 2009, pp. 80-103. doi:10.1016/j.artint.2008.08.006
- I. Millington, “Artificial Intelligence for Games,” Elsevier, Morgan Kaufmann Publications, 2006.
- L. Sha, S. He, J. Wang, J. Yang, Y. Gao, Y. Zhang and X. Yu, “Creating Appropriate Challenge Level Game Opponent by the Use of Dynamic Difficulty Adjustment,” 2010 6th International Conference on Natural Computation (ICNC 2010), IEEE Circuits and Systems Society, 2010, pp. 3897-3901.
- M. Giacinti, F. Mariani, M. C. Recchioni and F. Zirilli, “A Video Game Based on Elementary Equations,” Annals of Mathematics and Artificial Intelligence, 2012.
- N. Beume, H. Danielsiek, T. Hein, B. Naujoks, N. Piatkowski, R. Stüer, A. Thom and S. Wessing, “Towards Intelligent Team Composition and Maneuvering in RealTime Strategy Games,” IEEE Transactions on Computational Intelligence and AI in Games, Vol. 2, No. 2, 2010, pp. 82-98. doi:10.1109/TCIAIG.2010.2047645
- D. B. Fogel, T. J. Haysa and D. R. Johnson, “A Platform for Evolving Intelligently Interactive Adversaries,” Biosystems, Vol. 85, No. 1, 2006, pp. 72-83. doi:10.1016/j.biosystems.2006.02.010
- V. Kokkevis, “Practical Physics for Articulated Characters,” Game Developers Conference 2004, San Jose, 2004, pp. 1-16. http://www.red3d.com/cwr/games/#ai-papers
- I. Millington, “Game Physics Engine Developments,” Elsevier Inc., San Francisco, 2007.
- C. W. Reynolds, “Flocks, Herds, and Schools: A Distributed Behavioral Model,” Computer Graphics, Vol. 21, No. 4, 1987, pp. 25-34. doi:10.1145/37402.37406
- S. I. Nishimura and T. Ikegami, “Emergence of Collective Strategies in a Prey-Predator Game Model,” Artificial Life, Vol. 3, No. 4, 1997, pp. 243-260. doi:10.1162/artl.1997.3.4.243
- S. Kim, C. Hoffman and J. M. Lee, “An Experimental in Rule-Based Crowd Behaviour for Intelligent Games,” ICCIT, 2009 IEEE Fourth International Conference on Computer Sciences and Convergence Information Technologies, Seoul, 24-26 November 2009, pp. 410-415. doi:10.1109/ICCIT.2009.239
- K. Gopalsamy, “Exchange of Equilibria in Two Species Lotka-Volterra Competition Models,” The Journal of the Australian Mathematical Society (Series B), Vol. 24, No. 2, 1982, pp. 160-170. doi:10.1017/S0334270000003659
- B. Lahey, W. Burleson, C. N. Jensen, N. Freed, P. Lu and K. Muldner, “Integrating Video Games and Robotic Play in Physical Environments,” Proceedings of the 2008 ACM SIGGRAPH Symposium on Video Games, Los Angeles, ACM Publishing, New York, 2008, Vol. 1, pp. 153-170.
- B. Lahey, N. Freed, P. Lu, C. N. Jensen, K. Muldner and W. Burleson, “Human-Robot Interactions to Promote Play and Learning,” Proceedings of the 8th International Conference on Interaction Design and Children (IDC 2009), Como, ACM Publishing, New York, 2009, pp. 280-281.
- M. Athans, “On Optimal Allocation and Guidance Laws for Linear Interception and Rendez Vous Problems,” IEEE Transactions on Aerospace and Electronics Systems, Vol. AES7, No. 5, 1971, pp. 843-853. doi:10.1109/TAES.1971.310324
- R. Isaacs, “Differential Games,” Dover Publication, New York, 1999.
- T. L. Friesz, “Dynamic Optimization and Differential Games,” International Series in Operations Research & Management Science, Vol. 135, Springer, New York, 2010, pp. 138-142.

