Intelligent Information Management
Vol.3 No.6(2011), Article ID:8235,4 pages DOI:10.4236/iim.2011.36026
Research on Reliability of Knowledge-Updating in a Kind of Network Knowledge System
1Mathematics Department, Yanbian University, Jilin, China
2Department of Information Management, Peking University, Beijing, China
E-mail: yinzhe@ybu.edu.cn
Received June 11, 2011; revised September 14, 2011; accepted September 22, 2011
Keywords: Reliability, Redundant, Knowledge Resource Management, Joint Reserve
Abstract
The definition of reliability of knowledge-updating in network knowledge resource management system (NKRM system for brief) has been given in this paper, which has important reference value to the evaluation of NKRM system. Besides, two kinds of models in NKRM system have been introduced. And one of the most common methods to improve reliability is the redundant technique. However, reliability and efficiency are inconsistent each other. By treating each knowledge as one part of the system, this paper proposes method of joint reserve of knowledge that may resolve this problem.
1. Introduction
Moore [1] did the classification according the functions of spare parts. Because of the influence of spare parts to manufacture and economy, many scholars have studied the amounts of the spare parts needed. P. Flint [2] provided the advice that we should develop the fellowship and the resource sharing to reduce the cycle time. Besides, Foote [3] studied stocks prediction, and Luxhoj and Rizzo [4] obtained the method of amounts of spare parts needed of the same set based on the set model. Kamath [5] used the Bayesian method to predict the amounts of spare parts needed. NKRM system has been introduced in this paper, which is shown as follows: (Figure 1).
Method of joint reserve of knowledge in NKRM system has been proposed to improve the reliability and efficiency.

Figure 1. Knowledge resource management system.
2. Self-Updated Model and Calculation of Its Demand of Knowledge
2.1. Reliability of Knowledge-Updating
Probability that the percentage of amounts of knowledge-updating are more than a certain value, that is: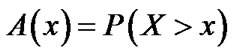 , where x denotes the percentage of amounts of knowledge-updating.
, where x denotes the percentage of amounts of knowledge-updating.
Assume that reserve of knowledge of a certain new NKRM system starts from the zero moment, assessment will be done every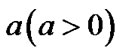 . If the management system is normal(that is, all the knowledge are the newest), we will continue use these knowledge; otherwise, we will do self-updating to the knowledge, that is, after the temporary self-updating which cost time
. If the management system is normal(that is, all the knowledge are the newest), we will continue use these knowledge; otherwise, we will do self-updating to the knowledge, that is, after the temporary self-updating which cost time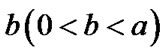 , management system recovers “normal” and proceeds reserve of knowledge, and this kind of model is called selfupdated model, which is as follows: (Figure 2)
, management system recovers “normal” and proceeds reserve of knowledge, and this kind of model is called selfupdated model, which is as follows: (Figure 2)
For briefly expressing, state random variable 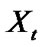 is introduced.
is introduced.

Let 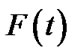 be the distribution function of random variable Z which is the first failure time of NKRM system. From the assumption of the model we can know, when
be the distribution function of random variable Z which is the first failure time of NKRM system. From the assumption of the model we can know, when , availability of system at time t (probability
, availability of system at time t (probability
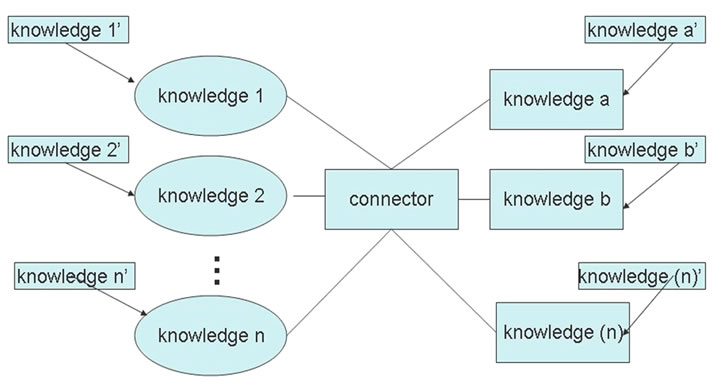
Figure 2. Self-updated model.
of system is in the normal state at time t)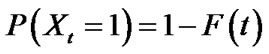
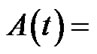 ; when
; when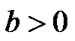 , note
, note 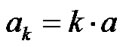
 ,
, 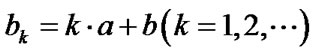 ,
, 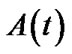 satisfies these formulas according to the model assumption:
satisfies these formulas according to the model assumption:
when
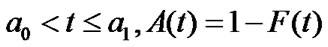 (1)
(1)
when 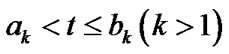
 (2)
(2)
when 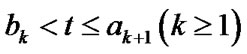
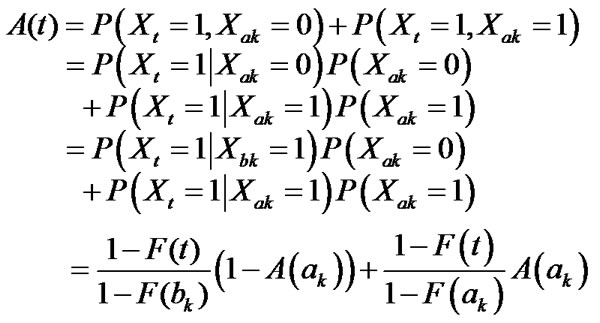 (3)
(3)
From (2) and (3) we can see that 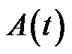 can be obtained once we calculate all the
can be obtained once we calculate all the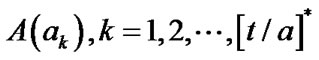 . Let
. Let 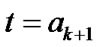 in (3), when
in (3), when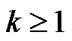 , we have:
, we have:

According to the formula above and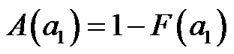 , we can calculate
, we can calculate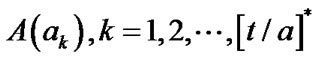 , and then
, and then  can be obtained.
can be obtained.
2.2. Calculation of Demand of Knowledge
Suppose there are N systems starting the reserve of knowledge from time 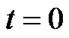 at the same time on the same condition, besides, the state of these N systems is independent each other. Then minimum of probability that there are at least N normal regional sub-systems at the given moment during the reserve period is not less than
at the same time on the same condition, besides, the state of these N systems is independent each other. Then minimum of probability that there are at least N normal regional sub-systems at the given moment during the reserve period is not less than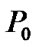 is:
is:
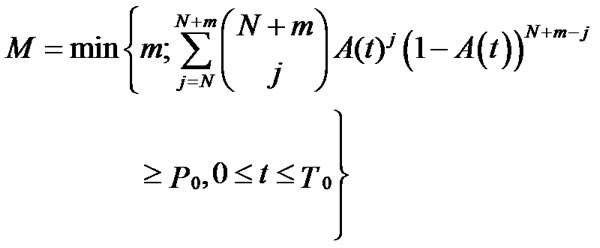 (4)
(4)
M is just the amount of the reserve of knowledge we needed.
3. Knowledge-Introduced Model
The basic assumption is similar with the self-updated model, the difference is that the updating process will be finished by the introducing other knowledge from elsewhere when the knowledge should be updated, which is shown as follows: (Figure 3).
4. Calculation of Amounts of Joint Reserve of Knowledge Needed
Generally, a knowledge updating of NKRM system in different regions is carried out independently. However, considering the problem of reducing the costs as possible as we can on the condition that the joint reserve of knowledge model is satisfied, we propose a new reserve way—joint reserve of knowledge, that is the method that amounts of joint reserve of knowledge needed are calculated uniformly after determining sum of NKRM system in each region. Assume that there are n systems which belongs to similar areas, and once there is a new knowledge such as knowledge 1’, knowledge 2’, …, knowledge n’, these similar systems can update the new knowledge at the same time, that is, the new knowledge can beshared in these similar systems, which is as show as Figure 4:

Figure 3. Knowledge-introduced model.

Figure4 . Joint reserve of self-updated model.
In the “self-updated” model, suppose there are N1 systems in region A, starting the reserve of self-updating from time 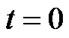 at the same time on the same condition, besides, the state of these N1 systems is independent each other. Then minimum of probability that there are at least N1 normal systems during the reserve period isn’t less than
at the same time on the same condition, besides, the state of these N1 systems is independent each other. Then minimum of probability that there are at least N1 normal systems during the reserve period isn’t less than 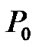 is:
is:
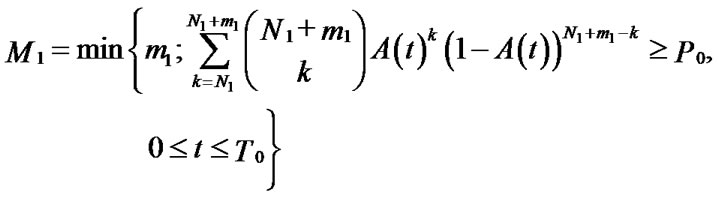
At the same time, there are N2 systems meeting “self-updated” model,the conditions are the same as region A, then amounts of reserve of knowledge needed—M2 is:
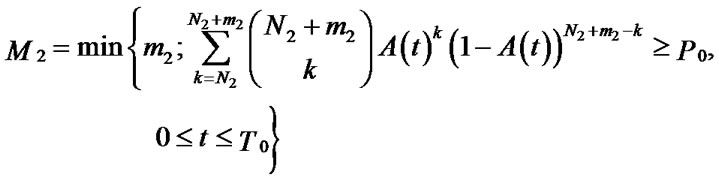
According the idea of joint reserve of knowledge, sum of these N1 + N2 systems can be treated as N joint reserve of NKRM systems, then amounts of knowledge needed—M is:
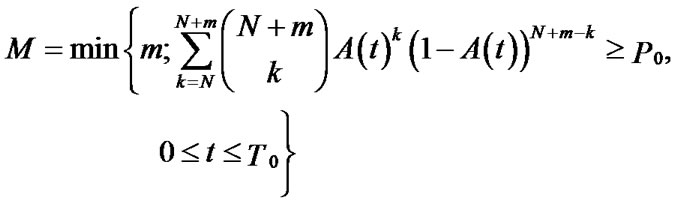
5. Calculation Instances
1) Suppose there are 10 (N = 10) same NKRM systems, which obey Weibull distribution- , where
, where

Table 1. Simulation result of “self-updated” model.
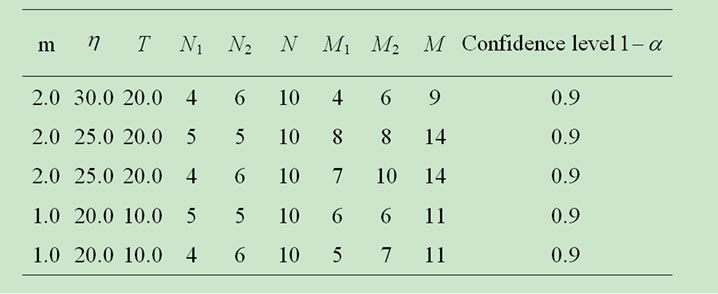
Table 2. Simulation result of “knowledge-introduced” model.
examination time interval a = 1.0, training time b = 0.2, repair rate 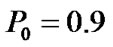 and predetermined period of reserve of knowledge
and predetermined period of reserve of knowledge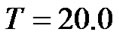 . In the “self-updated” model, taking some groups of parameter to simulate, results are shown as Table 1:
. In the “self-updated” model, taking some groups of parameter to simulate, results are shown as Table 1:
From Table 1 above, we can see .
.
2) Next, simulation of “knowledge-introduced” model is also carried out on the same condition, whose results are show as Table 2 below:
From Table 2 we can also obtain that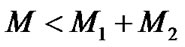 .
.
6. Conclusions
Through treating each knowledge as one part of the system, this paper proposes method of joint reserve of knowledge that can improve reliability and efficiency. Besides, we can get the conclusion that amounts of knowledge needed of joint model are less than those of model in which knowledge are updated or introduced separately, which shows the importance of the knowledge-sharing.
7. References
[1] R. Moore, “Establishing an Inventory Management Program,” Plant Engineering, Vol. 50, No. 3, 1996, pp. 113-116.
[2] P. Flint, “Too Much of a Good Thing: Better Inventory Management Could Save the Industry Millions While Improving Reliability,” Air Transport World, Vol. 32, No. 9, 1995, pp. 103-106.
[3] B. Foote, “On the Implementation of a Control-Based Forecasting System for Air-Craft Spare Parts Procurement,” IIE Transactions, Vol. 27, No. 2, 1995, pp. 210-216. doi:10.1080/07408179508936733
[4] J. T. Luxhoj and T. P. Rizzo, “Probabilistic Spaces Provisioning for Repairable Population Models,” Journal of Business Logistics, Vol. 9, No. 1, 1988, pp. 95-117.
[5] K. R. Kamath and T. P. M. Pakkala, “A Bayesian Approach to a Dynamic Inventory Model Under an Unknown Demand Distribution,” Computers and Operations Research, Vol. 29, No. 4, pp. 403-422. doi:10.1016/S0305-0548(00)00075-7

