Intelligent Information Management
Vol.3 No.5(2011), Article ID:7186,8 pages DOI:10.4236/iim.2011.35020
Pricing Models in Marketing Research
GfK Custom Research North America, Minneapolis, USA
E-mail: {stan.lipovetsky, shon.magnan}@gfk.com, andrea.zanettipolzi@gfk.com
Received March 27, 2011; revised July 27, 2011; accepted August 5, 2011
Keywords: market research, price, revenue, Gabor-Granger technique, van Westendorp price sensitivity, discrete choice modeling
Abstract
Pricing a product is one of the most important decisions an organization can make. Marketing research has developed several different approaches to price optimization. They include direct methods such as estimation of willingness to pay, indirect methods such as Gabor-Granger and van Westendorp techniques, and product/price mix methods such as various discrete choice models. All of them are widely used in practical marketing research for evaluation of optimal prices for different products and product innovations. This work describes and compares several main of these approaches.
1. Introduction
One of the hardest decisions an organization has to make is how to price its products. Price a product too low and you may not cover your costs or generate profits. Price the product too high and potential customers never turn into paying customers. Pricing strategies help a manager to answer such questions as:
• How should I price my product?
• How much will sales fall if I increase my price?
• To whom would your product lose market share to if price changes appeared?
• Are there price thresholds?
• Should I price products differently to achieve maximum sales of the entire line?
Marketing research has long recognized the importance of price optimization. Survey research can help explore those pricing questions. Survey pricing evaluation can be thought of as a continuum that moves from quick and easy but less precise to complicated but more accurate methods. Among these methods are:
• Direct methods, including willingness to pay (WTP), or what price would you pay eliciting, and incentive-aligned WTP techniques
• Indirect methods, such as Gabor-Granger, traditional and extended van Westendorp models
• Product/Price Mix methods, such as Discrete Choice, and Advanced Choice Models.
In fact, some of the best known econometricians have developed techniques to address these problems. For instance, Clive W. J. Granger, Nobel Prize winner in economics in 2003, is best known for his numerous papers and books on econometrics and time-series analysis. An area of his research that is less known was done in collaboration with André Gabor on a pricing model project for the Nottingham University Consumer Study Group in the 1960’s. Granger recalled in [1]: “During this period I was also involved with André Gabor on some practical price research. To get data to test our theories and estimate models, we arranged with local supermarkets to conduct experiments in which we altered prices of popular products and recorded the change in sales. I believe that more economic micro-theory could be better tested by doing real world experiments rather than believing such an approach is impossible”. Indeed, their collaboration had been prolific and together they created the method now known as Gabor-Granger (or GG-models) price modeling [2-15]. Most of their work has also been presented in a special issue [16], and incorporated into the monograph [17] where Granger wrote the mathematical appendix. As noted in [17], the authors’ approach can be traced back to earlier work by Scitovsky [18], and even more to the French school’s development on the so called “psychological price” presented by Stoetzel [19], Adam [20], and Fouilhé [21] (republished also in [22]). These works probably were inspired by the ideas of measuring subjective probability of a “would-be bought” product, developed at that time in game and utility theories [23]. The Nottingham group’s GG-models [2-15] subsequently have been applied in numerous marketing research projects in different companies and countries. The GG-models have been used by other researchers as the foundation for other pricing optimization approaches. A popular technique based on GG-models (a development of approaches [2,8]) was created by Dutch economist Peter H. van Westendorp (VW-model) and called price sensitivity meter [24].
GG-models are based on data elicited from respondents on their willingness to pay for a product innovation, a service, or concept at various price points. The approach is somewhat limited as price is not always a conscious variable, competitive price awareness isn’t always high, and pricing often varies across distributors. In spite of these limitations, GG and VW techniques are popular due to the nature of their convenient descriptive data analysis and visualization especially when compared to numerous other more theoretically based price and cost models (see, for instance, [25-30]). These models serve as “workhorse” instruments in marketing research for empirical pricing of concepts and products (for instance, [31-35]).
In this work we consider some main features of the direct, indirect, and discrete choice models for finding optimal prices. The paper is organized as follows. Section 2 describes the direct price techniques, Sections 3 and 4 concern the indirect methods of Gabor-Granger and van Westendorp, respectively. Section 5 considers discrete choice models, and Section 6 summarizes.
2. Direct Price Techniques
Direct methods are based on willingness to pay (WTP) estimation. A simplest approach to pricing research consists in asking the consumers to directly state their WTP for a specific product through an open-ended question format. The respondents answer to the question: What is the highest price you would be willing to pay for product X? An example of the elicited results is presented in Figure 1.
A modified version of WTP is called incentive-aligned WTP in which participants are obligated to purchase a product if the price drawn from a lottery is less than or

Figure 1. Percent of respondents profiled by the price of a product.
equal to his/her stated WTP [36]. Since real money is on the line, respondents have incentive to give realistic stated WTP. Obviously, this approach only works in special circumstances.
Among the advantages of the direct methods are their suitability for new products, easy to collect, and little prior knowledge required from the respondents. But these methods suffer serious disadvantages. Particularly, it was observed that respondents often overstate their price sensitivity. Also, though a little prior knowledge is typically required, if the new product concept is very unusual, respondents may not have any notion what price range is appropriate.
3. Gabor-Granger Indirect Price Models
Indirect methods are generally more accurate than direct methods as respondents are faced with more realistic scenarios. These methods are quick and simple to administer and also derive information on why respondents chose not to buy a product.
One such method that is widely recognized and used in the marketing science industry is the Gabor-Granger approach. It is a convenient and practical pricing technique to determine the highest price a respondent is willing to pay for a given product. In this approach, a set of price levels to test are first determined. Then a sample of respondents is gathered and the product is described to each respondent with a randomly chosen price from the predetermined list attached. The respondent is asked her willingness to purchase the product at that given price (for instance in a 5-point scale ranging from definitely would purchase to definitely would not purchase). If the respondent is willing to purchase the product at that price, the product is shown again but this time with a randomly chosen higher price from the predetermined price list and her willingness to purchase asked. If the respondent is not willing to purchase the product at the first price shown, the product is again shown to her but with a randomly chosen lower price from the predetermined list and her willingness to purchase elicited. This pattern is repeated several times with lower and higher prices taken from the predetermined price point list until the highest price point a respondent is willing to pay is determined.
GG-model is suitable for a new product development. It aims to establish maximum price each respondent is willing to pay for a given product using a series of predetermined price points, usually 5 or 7 of them. For example, a scheme of data eliciting can be presented by th graph shown in Figure 2, where a set of prices $3, $4, $4.5, $5, $6 is used.
A demand curve can be generated by calculating the cumulative frequency distribution of the highest prices
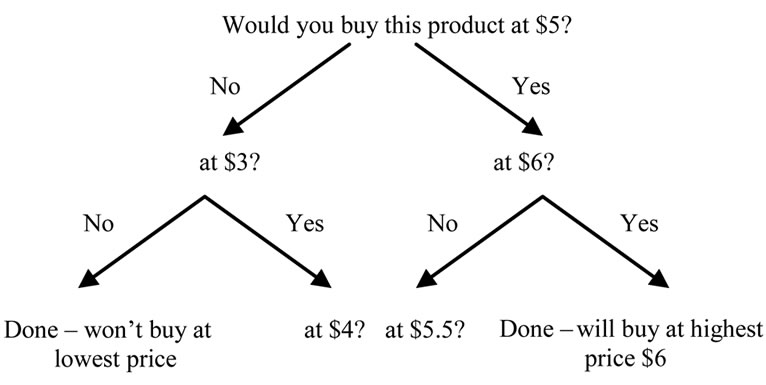
Figure 2. Gabor-Granger scheme of price eliciting.
respondents are willing to pay for a given product. An example with a real data from a marketing research project is presented in Figure 3.
By multiplying each price point by its corresponding demand it is possible to consider the corresponding revenue curve―an example is given in Figure 4. The revenue curve can be used to determine an acceptable price which maximizes a projected revenue value. Additional curve of a possible loss from optimal revenue is presented in Figure 5.
The results of GG-modeling can be summarized in the numerical Table 1.
The method described above corresponds to just one of several different GG models which are applied when pricing established products ([17], ch. 14). Another variation of the GG model is to simply ask respondents the highest price they would agree to pay and the lowest price they would find acceptable before suspecting a poor quality product. This approach does not assume a respondent buys at a single given price, but that lower

Figure 3. Gabor-Granger price model―the demand curve.
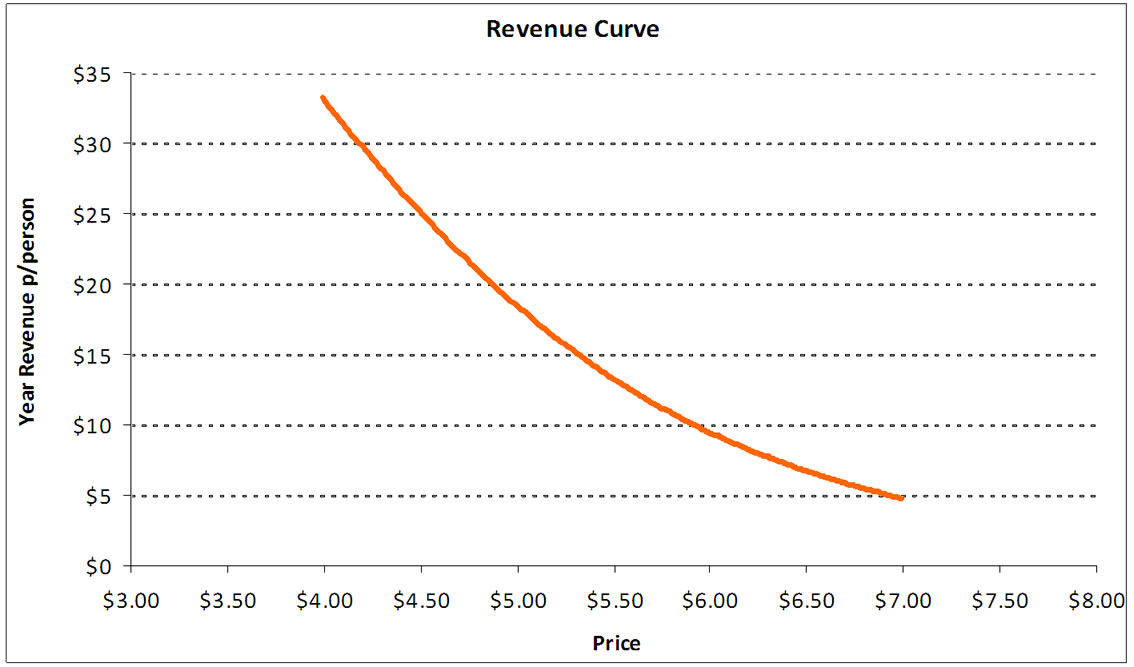
Figure 4. Gabor-Granger price model―the revenue curve.

Figure 5. Gabor-Granger price model―the loss from optimal revenue curve.

Table 1. The results of Gabor-Granger price modeling.
prices are also acceptable (which can correspond to the case of the so called Giffen goods [37]). To analyze such data, a frequency distribution of the willingness-to-buy is constructed―a concave curve of reach percentage of the respondents agreeing to buy the product at that price [17] (ch. 12). Among the advantages of the GG-models, we can mention that it is simple and easy to complete the data eliciting and analysis, and the checked prices are clearly isolated. So it best suited for pricing situations that are later in the product development cycle and the clients have a clear idea of range of prices they want to use. Among the weaknesses of this approach are some bias towards overstating price and lack of context.
4. Van Westedorp Price Sensitivity Models
An extension of the above described techniques is the van Westendorp (VW) “psychological price” modeling specifically focused on finding an acceptable price as a quality indicator. The VW approach takes into account concerns about low prices possibly indicating low quality as well as too high pricing. It is suitable for new product development, and it aims to establish limits of price elasticity, or price thresholds. The VW approach is based on the assumption that reasonable prices exist for consumers in every category and for each perceived level of quality within a category. Consumer price decisions are made by balancing value against price; and there is an upper and lower bound to the price a consumer will pay for a product or service. Data elicited in the VW process consists in the answers to four indirect questions to calibrate price from different perspectives: Cheap―at what price does this product start to seem cheap to you, that is, when does it start to seem like a bargain? Expensive―at what price does this product start to seem expensive to you? Too Cheap―at what price does this product become too cheap, that is, so cheap that you would question its quality and not buy it? Too Expensive―at what price does this product become too expensive, that you would not consider buying it? For each of the four price questions the cumulative frequencies are plotted against the current price on the same graph (but the Too Cheap and Expensive curves are displayed in the reversed direction)―see Figure 6.
The intersection of the reversed Too Cheap curve with Cheap curve according to VW is called the point of “marginal cheapness”. The intersection point of the reversed Expensive curve with Too Expensive curve is called “marginal expensiveness”. The range between these two points shows the area of the price acceptable for most consumers. The intersection of the Cheap and the reversed Expensive curves also correspond to the “indifference price” point, where there are an equal number of respondents for both these questions. The intersection of the reversed Too Cheap and Too Expensive curves defines the point of “optimal pricing”. Among the advantages of this traditional approach—it permits to avoid imposing price points on respondents, it best suited for pricing situations that are very early in the product development cycle and the client doesn’t really have a clear idea of the price range to play in, it also is simple and easy to complete. On the other hand, respondents often overstate their price sensitivity, results can be unstable as even small changes in the sample can results in large changes in the price curves, and the range of acceptable prices can be quite large.
To overcome these problems, the extended VW approach (EVW) had been elaborated where the VW data can be considered in statistical regression modeling via a set of ordinal logistic regressions [35]. If to use only two questions on lower and higher prices, VW model reduces to GG model of price as quality indicator ([17], ch. 12 and analytical appendices). Statistical modeling suggested in [35] can be seen as a developed approach described in [17]. In EVW we get much more exact acceptable price estimates (the max reach of the OK curve), estimate confidence intervals for significance testing, and considering the OK price perception probability along with the probabilities of the other shares we can estimate acceptable prices for a variety of scenarios. The pricing analysis provides estimates of both share of consumers and revenue. The EVW can be adjusted to a broad span of products. First, researchers can set the range of prices acceptable. This approach is most relevant when the target price is known in advance. A second approach is to let respondents set the price range: it enables consumers to fully express their price expectations, without any direction, resulting in a wider range of prices. Finally, respondents can evaluate manufacturer-chosen price points: the concept shown to respondents is priced; then they are asked the price sensitivity questions. The first two alternatives are usually preferred in practice.
An example of the probabilities profiled by prices is shown in Figure 7 and in Table 2.

Figure 6. Traditional van Westendorp cumulative frequencies.
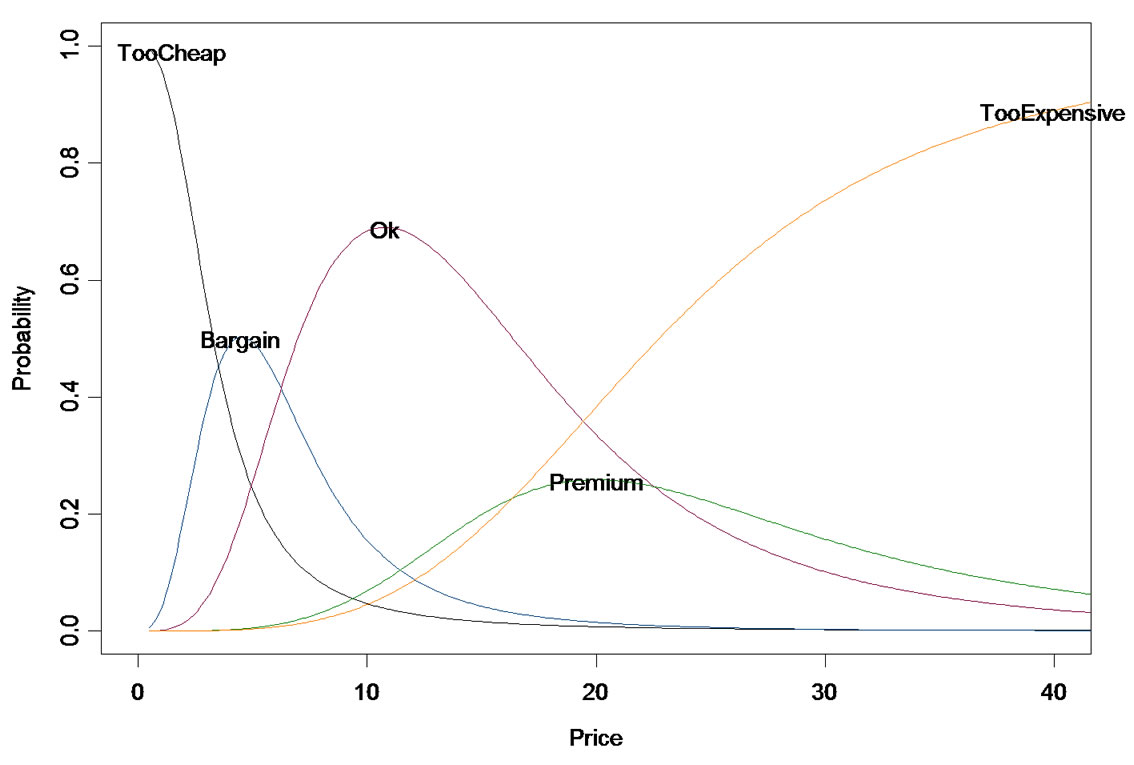
Figure 7. Extended van Westendorp price probabilities.
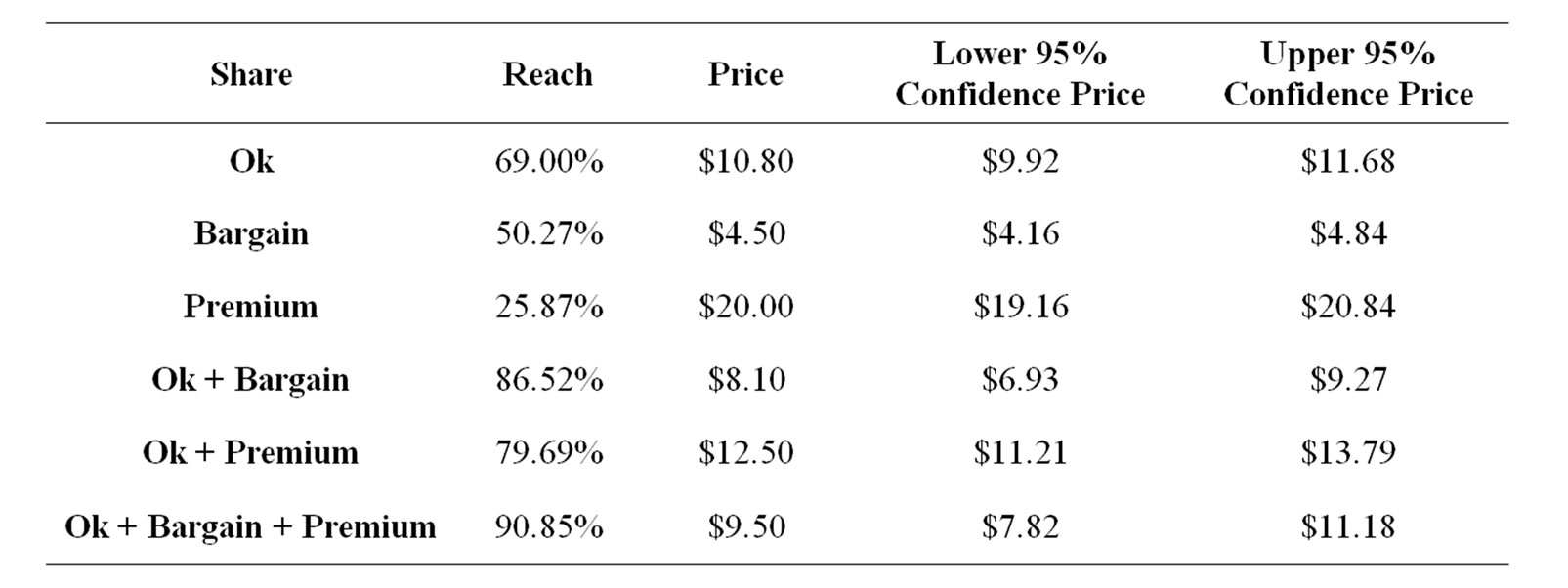
Table 2. The results of extended van Westendorp price modeling.
5. Product/Price Mix Models
The next step for finding optimal prices is presented by various pricing techniques used in conjoint and discrete choice models (DCM) [38-43]. A simple DCM with price the sole variable, the so-called price challenger, is described in [34]. General conjoint and DCM methods typically include additional variables taking into account covariates of brands, size, demographics, etc. DCM is best in the situations when simulating immediate response to competitive offerings, especially brand and price studies, decisions are made on the basis of relatively few, well-known, concrete attributes, consumers make these decisions on the basis of competitive differences among attributes given, and we want to account for possible interactions between levels of different attributes. This is a realistic approach mimicking actual choices people are faced with in the store.
DCM studies for pricing can be performed as follows: Ask a person to choose among competing products at different prices. Change the prices and/or product attributes and ask the respondent to choose again, etc. With such a data we build a model to predict the likelihood that a person will choose a specific product given the relative prices of the products in the test. Respondents are shown multiple scenarios at a time (task) and asked to pick the one they would choose/purchase. Through experimental design, balanced (orthogonal) sets of choice tasks are produced. Typically, 12 - 15 tasks are evaluated by each respondent. The advantages of this approach: it is reflective of “real world” marketplaces with competing products; it can accommodate conditional variables; brands can be customized to match market reality; it avoids impossible combinations and is easy to administer; it can capture interactions more efficiently than a fullprofile design. Among the limitations, we can mention that it is impossible to handle too many attributes (8-ish at a max), to truly predict preference share (not market share), this approach assumes same awareness and distribution, and the results are based on calibration which uses several assumptions that may not be realistic. Advances in DCM for pricing utilize only price changes have been shown to accurately reflect actual price elasticities in the market. Choice models with thresholds accurately predict in-market price elasticities and in fact seem to always increase model accuracy. Modern noncompensatory models started to make headway. Noncompensatory decision making is driven by a rule by which positive evaluation of an attribute does not compensate for a negative evaluation of the same object on some other attribute. Some non-compensatory models include lexicographic and disjunctive/conjunctive cut off models.
6. Summary
Pricing research is one of the core methodologies in custom research. There are a multitude of approaches one can take and the exact method we recommend depends on the particular circumstances of the request. We described main features of Gabor-Granger, van Westedorp, and product/price mix models, their specifics and areas of the application in practical marketing research for evaluation of optimal prices for different products and concepts. Direct/indirect methods are not the most accurate pricing techniques; they cannot really factor in competitive effects but only consider each product in isolation. The discrete choice techniques are much more flexible and accurate because they try to replicate real market conditions as close as possible, but on the other hand―they are complicated and require nearly always a separate study because of the data setting and the needed intensive design support. The GG and VW models can also be used for each set of fixed covariates and produce an optimal price which then can be compared across all these combinations. It is the reason that the GaborGranger and van Westedorp models are widely used in practical marketing research for express analysis of optimal prices for different products and concepts.
7. References
[1] C. W. J. Granger, “Autobiography,” 2003. http://nobelprize.org/nobel_prizes/economics/laureates/2003/granger-autobio.html
[2] A Gabor and C. W. J. Granger, “On the Price Consciousness of Consumers,” Applied Statistics, Vol. 10, No. 3, 1961, pp. 170-188. doi:10.2307/2985208
[3] A. Gabor and C. W. J. Granger, “Price sensitivity of the consumer,” Journal of Advertising Research, Vol. 4, No. 4, 1964, pp. 40-44.
[4] A. Gabor and C. W. J. Granger, “The pricing of new products,” Scientific Business, Vol. 3, August 1965, pp. 3-12.
[5] A. Gabor and C. W. J. Granger, “Price as an indicator of quality: Report on an enquiry,” Economica, Vol. 33, No. 129, 1966, pp. 43-70. doi:10.2307/2552272
[6] A. Gabor and C. W. J. Granger, “Price sensitivity of the consumer,” In: K. Cox, Ed., Readings in the Marketing Research, Appleton-Century Crofts, New York, 1967.
[7] A. Gabor and C. W. J. Granger, “The attitude of the consumer to prices,” In: B. Taylor and G. Wills, Eds., Pricing Strategy, Staples Press, London, 1969, pp. 132- 151.
[8] A. P. Sowter, A. Gabor and C. W. J. Granger, “The influence of price differences on brand shares and switching,” European Journal of Marketing, Vol. 3, No. 4, 1969, pp. 223-230.
[9] A. Gabor, C. W. J. Granger and A. P. Sowter, “Real and hypothetical shop situations in market research,” Journal of Marketing Research, Vol. 7, No. 3, 1970, pp. 355-359. doi:10.2307/3150294
[10] A. P. Sowter, A. Gabor and C. W. J. Granger, “The effect of price on choice: a theoretical and empirical investigation,” Applied Economics, Vol. 3, No. 3, 1971, pp. 167-181. doi:10.1080/00036847100000002
[11] A. Gabor, C. W. J. Granger and A. P. Sowter, “Comments on ‘Psychophysics of Prices’,” Journal of Marketing Research, Vol. 8, No. 2, 1971, pp. 251-252. doi:10.2307/3149773
[12] C. W. J. Granger and A. Billson, “Consumer’ attitudes toward package size and price,” Journal of Marketing Research, Vol. 9, No. 3, 1972, pp. 239-248. doi:10.2307/3149533
[13] A. Billson, A. Gabor, C. W. J. Granger and A. P. Sowter, “Decimalisation and the Consumer,” Consumer Study Group, University of Nottingham, October 1972.
[14] A. Gabor and C. W. J. Granger, “Ownership and acquisition of consumer durables,” European Journal of Marketing Vol. 6, No. 4, 1972, pp. 234-248.
[15] A. Gabor and C. W. J. Granger, “A systematic approach to effective pricing,” In: L. W. Rodger, Ed., Marketing Concepts and Strategies in the Next Decade, Cassell/ Associated Business Programmes, London, 1973, pp. 171-194.
[16] A. Gabor and C. W. J. Granger, Selected papers in: Management Decision (Archive), Vol. 17, No. 8, 1979, pp. 528-812. http://www.emeraldinsight.com/journals.htm?issn=0025-1747&volume=17&issue=8
[17] A. Gabor and C. W. J. Granger, “Pricing: Principles and Practices,” Heinemann Educational, London, 1977.
[18] T. Scitovsky, “Some consequences of the habit of judging quality by the price,” Review of Economic Studies, Vol. 12, No. 2, 1944, pp. 100-105. doi:10.2307/2296093
[19] J. Stoetzel, “La prix comme limité,” In: P. L. Reynaud, Ed., La Psychologie économique, Librairie Marcel Riviere et Cie, Paris, 1954, pp. 183-188.
[20] D. Adam, “Les Réactions du Consommateur devant le Prix,” Société d’Études pour le Développement Économique et Social (SEDES), Paris, 1958.
[21] P. Fouilhé, “Evaluation subjective des prix,” Revue Francais de Sociologie, Vol. 1, No. 1-2, 1960, pp. 163-172.
[22] B. Taylor and G. Wills, “Pricing Strategy,” Staples Press, London, 1969.
[23] R. D. Luce and H. Raiffa, “Games and Decisions,” Wiley, New York, 1958.
[24] P. H van Westendorp, “NSS Price Sensitivity Meter (PSM)—A New Approach to study Consumer-Perception of Prices,” Proceedings of the 29th ESOMAR Congress, Venice, 5-9 September 1976, pp. 139-167.
[25] A. R. Rao and M. E. Bergen, “Price Premium Variations as a Consequence of Buyers’ Lack of Information,” Journal of Consumer Research, Vol. 19, No. 3, 1992, pp. 412-423. doi:10.1086/209311
[26] T. T. Nagle and R. K. Holden, “The Strategy and Tactics of Pricing: A Guide of Profitable Decision Making,” 2nd Edition, Prentice-Hall, Englewood Cliffs, 1995.
[27] G. W. Cermak, “Budget Allocation as a Measure of Potential Demand,” Journal of Economic Psychology, Vol. 17, No. 5, 1996, pp. 591-613. doi:10.1016/S0167-4870(96)00026-8
[28] A. Tishler and S. Lipovetsky, “The flexible CES-GBC family of cost functions: derivation and application,” The Review of Economics and Statistics, Vol. 79, No. 4, 1997, pp. 638-646. doi:10.1162/003465397557042
[29] A. Tishler and S. Lipovetsky, “A Globally Concave, Monotone and Flexible Cost Function: Derivation and Application,” Applied Stochastic Models in Business and Industry, Vol. 16, No. 4, 2000, pp. 279-296. doi:10.1002/1526-4025(200010/12)16:4<279::AID-ASMB419>3.0.CO;2-0
[30] R. Wildner and M. Conklin, “Price thresholds and prospect theory,” The 12th Annual Advanced Research Techniques Forum of the American Marketing Association, Monterey, 3 June 2003, pp. 55-60.
[31] C. Blamires, “Pricing research techniques: A review and a new approach,” Journal of the Market Research Society, Vol. 23, No. 3, 1981, pp. 103-126.
[32] C. Greenhalgh, “Research for New Product Development,” In: R. M. Worcester and J. Downham, Eds., Consumer Market Research Handbook, 3rd Edition, McGraw-Hill, London, 1986, pp. 426-469.
[33] P. Comley, “What do We Know about Pricing Research,” World Advertising Research Center (WARC), January 1997, pp. 11-13.
[34] R. Wildner, “Price is a hot issue,” GfK Insite Magazine, No. 3, 2003, pp. 30-33.
[35] S. Lipovetsky, “Van Westendrop Price Sensitivity in Statistical Modeling,” International Journal of Operations and Quantitative Management, Vol. 12, No. 2, 2006, pp. 141-156.
[36] K. M. Miller, R. Hofstetter, H. Krohmer and Z. J. Zhang, “How Should Consumers’ Willingness to Pay Be Measured? An Empirical Comparison of State-of-the-Art Approaches,” Journal of Marketing Research, Vol. 48, No. 1, 2011, pp. 172-184.
[37] J. M. Henderson and R. E. Quandt, “Microeconomic Theory: A Mathematical Approach,” McGraw-Hill, Auckland, 1980.
[38] M. Ben-Akiva and S. R. Lerman, “Discrete Choice Analysis,” MIT Press, Cambridge, 1985.
[39] M. Wedel and W. Kamakura, “Market Segmentation: Conceptual and Methodological Foundations,” Kluwer Academic Publishers, Dordrecht, 1999.
[40] J. J. Louviere, D. A. Hensher and J. Swait, “Stated Choice Methods: Analysis and Applications,” Cambridge University Press, Cambridge, 2000.
[41] K. Train, “Discrete Choice Methods with Simulation,” Cambridge University Press, New York, 2003. doi:10.1017/CBO9780511753930
[42] D. McFadden, “Economic Choices,” Nobel lecture on the microeconometric analysis of choice behavior of consumers who face discrete economic alternatives, 2000. http://emlab.berkeley.edu/pub/users/mcfadden/nobel/final-nobel.pdf
[43] S. Lipovetsky, “Conditional and multinomial logits as binary logit regressions,” Advances in Adaptive Data Analysis, Vol. 3, No. 1, 2011, pp. 1-16.

