Intelligent Information Management
Vol.2 No.7(2010), Article ID:2213,7 pages DOI:10.4236/iim.2010.27048
Assessment of a Proposed Software Design for the Solution of Multi-Phase Mechanics Problems on Networked Laptops
Department of Mechanical Engineering, College of Engineering, San Diego State University, San Diego, USA
E-mail: tom.impelluso@sdsu.edu
Received October 19, 2009; revised April 2, 2010; accepted May 18, 2010
Keywords: Software Design, Multi-Phase Mechanics Problems, Networked Laptops
Abstract
This paper presents the design of a computational software system that enables solutions of multi-phase and multi-scale problems in mechanics. It demonstrated how mechanicians can design “process-driven” software systems directly, and that such efforts are more suitable in solving multi-phase or multi-scale problems, rather than utilizing the “data-driven” approaches of legacy network systems. Specifically, this paper demonstrates how this approach can be used to solve problems in flexible dynamics. Then it suggests a view of mechanics algorithms as ‘state equilibrium’ enforcers residing as servers, rather than as computer programs that solve field equations. It puts forth the need for identical input/output files to ensure widespread deployment on laptops. Then it presents an assessment of the laptop platform. A software system such as the one presented here can also be used to supply virtual environments, animations and entertainment/education software with physics.
1. Introduction
The finite element (FE) method is used in computational mechanics to analyze the deformation of materials. In the FE method, the field differential equations are first converted into integral equations; then, the domain is discretized with interpolation functions (meshed). Algebraic algorithms (such as conjugate gradient methods or direct solvers) are used to solve the resulting system for the displacement variables, forces and other internal phenomena. While the method can be extrapolated to account for the motion of objects and their contact with each other, the fundamental algorithm―as deployed in solid mechanics―is to solve for the deformation of objects subjected to loads and sufficient boundary conditions which ensure a non-singular system of algebraic equations.
The multi-body dynamics method is the method used in computational mechanics to analyze the motion of rigid objects (as opposed to the FE method which is focused on the deformation of stationary objects). The motions of objects are constrained by formulating various types of joints―e.g.: revolute, ball, translational―as geometric constraints on the equations, and then using these constraint equations to reduce the degrees of freedom of the system. Algorithms such as Runge-Kutta are used to update the system configuration (position, velocity, acceleration and forces), incrementally as a timestepping solver.
The term ‘multi-phase’ is a generalization of the techniques used to solve coupled problems in mechanics such as solid/fluid interaction or flexible linkages.
In January of 2003, the U.S. National Science Foundation Advisory Committee on Environmental Research and Education published a report [1] that identified cyber-infrastructure (CI) as a suite of tools and research essential to the study of engineering systems. The CI describes research environments supporting advanced data acquisition, data storage, data management, mining, visualization and other computing and information processing services. In scientific usage, the CI and its ancillary technologies enable solution to the problem of efficiently connecting data, computers, and people with the goal of enabling derivation of novel scientific theories and knowledge. This, then, enables researchers and developers to port data between various large-scale software systems. In general, the CI encompasses the lowlevel inter-process communication facilities that are bundled with operating systems, and the higher-level applications which extend them and build upon them.
Currently, some use these higher-level applications, such as Globus, to automate the transfer of data from one mechanics algorithm (say, finite element) to another (multibody dynamics) to solve for coupled problems. All such methods adhere to a sense of ‘data’ as driving the solution; and this research demonstrates that there is a better approach.
Continuing, the term ‘inter-process communication’ encompasses the fundamental technologies of the CI. These include techniques to enable codes to replicate themselves, instantiate themselves on other computers, enable processes to communicate with one another and to control each other. This paper will step through the design of a software system built upon fundamental technologies of the CI (the low-level―but not in the pejorative sense―tools upon which higher order applications are built) to solve problems in flexible dynamics. This research advocates that such an approach can and should be taken in the solution of multi-phase and multiscale problems by computational mechanicians.
2. Distributed Computing and Multi-Phase Mechanics
2.1. Distributed Computing
Distributed computing began in the early 1970’s with the arrival of minicomputers and ubiquitous networks. While the smaller computers were less powerful than their larger mainframe cousins they were also much cheaper. An easy way of scaling a computation was to buy more of such machines and distribute the problem over the multiple CPUs. Distributed computing differs from other parallel computation models in that the CPU nodes are autonomous and that all connections and procedure calls are accomplished by message passing or socket communication.
Software for managing memory communication and process management can either be “homemade”, commercially purchased or found within the open source community. Typical applications include: “smart instruments”, teraflop desktops, collaborative engineering, and distributed supercomputing. The system consists of packages such as: resource allocation managers, authentication services, network analysis monitoring systems, and secondary storage systems. Globus, an open source grid computing library, enables researchers to share large scale software systems across a “global” network. Such large-scale software systems include heart models, physiology models, manufacturing models and many others.
2.2. Multi-Phase Mechanics
Three groups developed the analysis of multi-phase mechanical systems in the 1970s: Northwestern University, California Institute of Technology, and Lockheed Palo Alto Research Labs (by J. A. DeRuntz, C. A. Felippa, T. L. Geers and K. C. Park). This initial work focused on different applications and evolved into different problem-decomposition techniques. For example, Belytchko and Mullen at Northwestern considered node-by-node partitions whereas Hughes and Liu at Cal Tech developed what eventually became known as element-byelement methods. The Lockheed group began its investigation in the underwater-shock problem for the Office of Naval Research (ONR) in 1973. In this work an FE computational model of the submarine structure was coupled to Geers’ “doubly asymptotic” boundary-element model of the exterior acoustic fluid, which functions as a silent boundary. In 1976 Park developed a staggered solution procedure to treat this coupling. Belytchko and Mullen give a more detailed historical overview as well as a summary of the methodology in the aforementioned work.
The formulation of the equations of motion for a flexible multi-body system invites coupling in many ways. Geradin and Cardona [2] formulated an approach in which the inertial frame becomes the reference frame. Coupling of FE and MD has also been done with linear [3] and non-linear [4] FE methods. Contact has also been introduced using unilateral constraints [5] or continuous contact forces [6]. The availability of state variables in multibodies allows for different control paradigms in the framework of vehicle dynamics, biomechanics or robots [7]. The coupling of fluid and structural dynamics allows for solid fluid interactions in which there are large rotations of system components [8].
2.3. Distributed Computing for Multi-Phase Mechanics
The previous methods used to solve multi-phase problems do not deploy existing distribution methodologies. These methods do solve certain coupled problems: solid/ fluid or flexible multi-bodies, however, they do not exploit the technologies of the CI. They are not scaleable and lack the ability to be readily extended to encompass new physics modules. Once they are running, new physics modules cannot join process groups, nor can modules leave groups once they are no longer needed. The systems are not fault tolerant: certain physics algorithms cannot be restarted with new parameters without having to restart the entire system. Computational modules cannot be easily targeted for the most efficient platforms. The results cannot be easily delivered to clients that might need them, including, for example, near-real time, fault tolerant, immersive visualization environments. It is still difficult to port data from one physics process group to another and when this does happen, it relies on largescale network packages.
To begin to address these issues, it is first necessary to categorize computations. Computational software can be broken down into two categories: process driven vs. data driven. Software packages for seismology or bioinformatics must manipulate data (object oriented coding: C++, Ada). Software packages for physics simulations should manipulate processing (processing oriented coding: FORTRAN, C).
3. Background and Proof-of-Concepts
As segue to the effort reported here, two prototypes are first discussed.
3.1. Phase 1
The preliminary platform reproduced a real stress-testing machine as a 3D model in a simulated computational environment. And then it created an interface to drive both the real stress testing machine and the virtual stresstesting machine simultaneously [9]. The functionality of the system is described herein.
First, in the client/server paradigm of inter-process communication, a server is simply a code that waits for remote communication. A client is a process that requests help from a server.
In this test-bed, then, a client requests a FE analysis of an object. The client connects to a server. As indicated in Figure 1, the server parses the control client request and fork()/execs() a process manager (PM). (In the parlance of inter-process communication, when a process forks() itself, it basically spawns a duplicate copy of itself― much like the replication of a strand of DNA. Such a dual process has access to the same memory, files and peripheral devices s the parent.) The child (or fork’d) process then execs() another process. (Exec() is a method in which a process replaces itself with a second process such that this new child process retains access to external sources and devices.) This exec’d child process will be called a process manager (PM).
The PM extracts all pertinent field information received from the remote client process. It then creates the shared memory in which to store the geometry of the specimen under deformation, and then creates the semaphores to ensure process regulation (see traffic lights in Figure 2). The PM then fork/execs two processes: the finite element process (FE) to perform the analysis of the deformation and a reader process (RD) whose role is to

Figure 1. Network schematic for virtual stress testing machine.
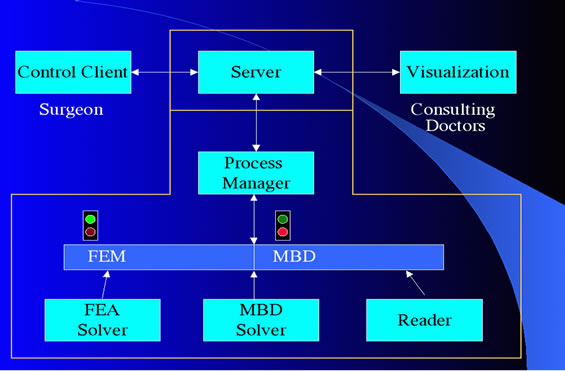
Figure 2. Network schematic for phase 1 design.
relay data back to any client that wishes to view the results. The semaphores (semaphores are simply integer flags that facilitate control and access to data when two competing codes are both trying to modify the data) control access to the shared memory ensuring that all clients view the same updated configuration of the specimen. In this scenario an unlimited number of clients can request visualization of the physical phenomenon and the reader process manages this.
Some preliminary data is needed to set up the “virtual” experiment: material properties, geometric properties, numerical mesh data, location of boundary conditions. This process will first read the initial input data to describe the nature of the virtual experiment, and then continuously read the secondary input data to drive the virtual experiment. As the experiment runs, data is used to drive it: in this case, the value of the applied forces or displacements. The analysis produces several output parameters―such as stress or strain―which are then visualized. Thus, there will be a visualization client (computer program to view the scene), a control client (to interact with the scene), a general server that will orchestrate network connections, and, finally, a physics server to run the virtual experiment. This approach, using shared memory was the first step taken in the next phase.
3.2. Phase 2
The goal of this platform was to expand the aforementioned test-bed to solve for two coupled phenomena: (multi-body dynamics) MD and (finite element) FE (labeled, respectively, as MBD and FEA in Figure 2.
Consider the solution scenario as indicated in Figure 2. A control client creates a data set to describe the parameters of a multi-phase problem. Then it connects to a server capable of moderating a solution. The server receives the request from the control client. The server forks() and execs() a process manager (PM). The PM creates a shared memory arena for processing the geometry and physics data, and deposits descriptive geometries pertinent to the FE and MD methods, in appropriate segments of the shared memory. The PM also creates the semaphores that regulate access to the shared memory. The PM then forks() and execs() the FE and MD processes to analyze the coupled problem of 2D flexible linkages. The PM now orchestrates the solution using the FE and MD methods, incrementally―first Newton-Raphson and then Runge-Kutta. At each time step, one method produces a result that is passed to the next method. Iteration between the two methods brokered by the PM provides the final solution.
This project had its deficiencies. First, while the use of shared memory proved fast and efficient, it did require all processes to reside on the same computer. Each process―MD and FE―has its own implementation issues (convergence, stability, etc.) and if more processes were to be added (each with their own issues), there would still only be one CPU to handle all numerical methods. Further, if the server node faulted, the entire system would fault. Finally, this approach is not easily distributed and does not readily allow for worldwide remote participation, which is the objective of this research.
4. Current Prototype
The operation of the current system is presented in Figure 3 (with the addition of a macroscopic fluids mechanics process to demonstrate an extended vision of the system).
First, a user creates (using a text editor) a data frame, which defines the problem: mesh data, material properties, and so on. The frame is delivered to a server (connection 1 in the Figure 3) from a client control process.
Upon receipt of “the problem description”, the server “fork/execs” a process manager to broker the solution (connection 2).
The PM reads the data frame (to extract what mechanics processes are requested for the coupled problem) and then instantiates the appropriate processes (finite
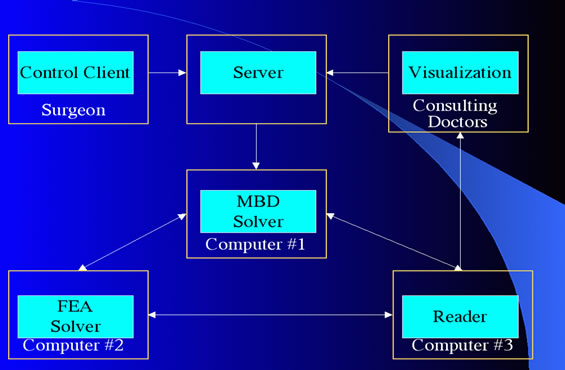
Figure 3. Revised network schematic for multi-phase mechanics.
element and multi-body dynamics, in this case) on targeted hardware (a dual CPU for the FE’s solver and a single CPU machine for the dynamics solver) (connection 3). Those processes then each become a server (inverting the client/server paradigm), and the PM then connects as a client to each of these physics servers: its role now is to broker the solution and relay data between various modules.
The PM delivers the results to a visualization workstation for viewing (connection 4). Once the paradigm is inverted, the visualization process is a client of the PM and the PM is a client of the server.
More specifically, the user requests a multi-body dynamics analysis of the deformable linkage system. The FE process conducts an analysis at a given time step, producing displacement, stresses, strains and other data that is delivered to the PM. The PM extracts the data requested by the visualization client. It also extracts and parses the data that is needed for the MD process to function. The MD code updates the time step and conducts the Runge-Kutta method to find the next configuration of the links: position, velocities, accelerations and forces. Upon completion it delivers the data to the PM and then halts. The PM delivers the data that is requested by the analyst and then it delivers the data requested by the FE coded. At this point the FE code commences again and the system continues.
While the system is running, the user can request a deformation analysis to be added. For example, the PM can instantiate an FE code on a new target (one target for each mesh) and set up the network communication to allow the FE and MD codes to communicate. At any point, the user can decide that an FE analysis of any link is no longer necessary. At any point, other processes can join the group.
5. Assessment
The system was assessed and verified using two numerical process multi-body dynamics and finite element analysis; both codes were two-dimensional systems. The data set was a model of a human lower leg consisting of, femur, tibia, fibia, and homogenized foot (in which there was, in this case, one deformable body for the foot to avoid complexity at this stage). The multi-body dynamics system consisted of three linkages; femur, tibia-fibia, foot and three revolute joints; hip, knee, ankle. In the initial configuration, the femur was horizontal to the ground plane and the tibia-fibia perpendicular to the femur, the leg was then allowed to free swing under gravity.
There were three data sets for the finite element code― femur, tibia-fibia, foot―each consisting of approximately 1000 nodes and 1000 elements. The intent of these models was not to examine the intricate working of human motion and the resulting forces; rather, it was to demonstrate the feasibility of a distributed system. Qualitative evidence of the analysis is offered in Figures 4-6 along with analyses obtained using large scale finite element package: MSC Marc/Mentat and Adams.
The PM accepted data from the user interface started the selected numerical processes on the targeted machines and successfully passed the necessary data between numerical processes and the user display. Initial experimentation was completed in a UNIX environment using the IRIX operating system.
This system was expanded to function on Linux operating systems. Linux test beds were HP Compaq nx9420 laptops. The transition from UNIX to Linux operating systems including a transition from wired LAN to a WiFi network.
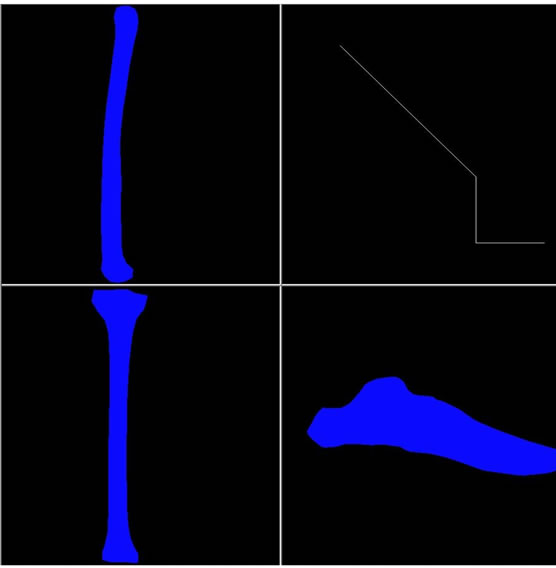
Figure 4. Visualization of three FE, and one MBD process at time 0.
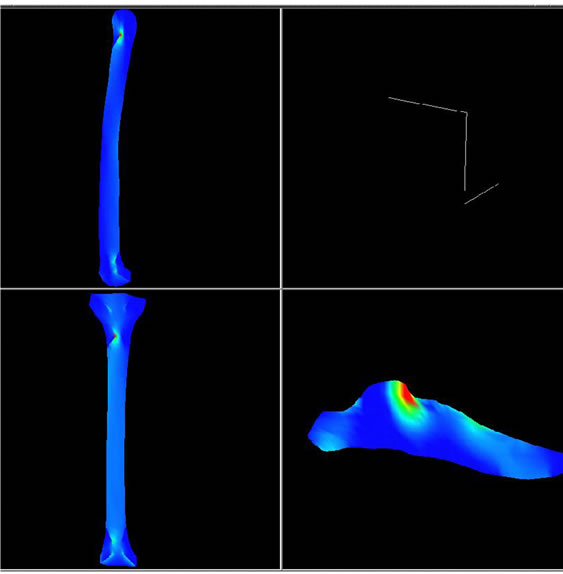
Figure 5. Visualization of three FE, and one MBD process at time 5.0.
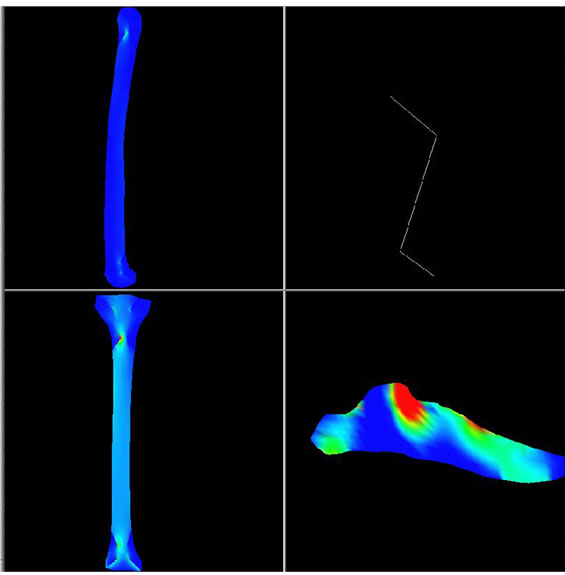
Figure 6. Visualization of three FE, and one MBD process at time 10.0.
Quantitative system analysis was performed by timing the period the PM was brokering data. In the coupled MD FE system the MD process provides the initial data as such the PM will start the MD code first. The PM was timed from the point the MD process was instantiated to the point the process was terminated.
Sixty simulations were performed using three HP nx9420 laptops running; Fedora Core III, Ubuntu, and Debian flavors of the Linux operating system. One machine served as the PM, GUI, and Visualization client, the other two machines performed the numerical analysis. Each machine served as the GUI, Visualization, and PM for twenty simulations. The PM randomly selected which remaining machines for each numerical process. The fastest and slowest recorded processing period was removed from the dataset. When the computers were networked on a wired LAN the remaining fifty-eight data points were averaged, yielding 15.182 seconds with a standard deviation of 0.023 seconds. When the same experiment was performed on an 802.1 G wireless network the average time was 15.201 with a standard deviation of 0.019 seconds.
This minor difference in processing time can be attributed to the relatively small amount of data that was passed from each of the finite element processes to the PM. Datasets were on the order of 30 Kbytes, further experimentation with larger datasets should be completed to determine where the time discrepancy originates, and if the relationship between transmission time and data size were linear as it would be expected.
The use of LINUX platform demonstrated that an open source operating system was robust and compliant to POSIX procedures to allow a system that was developed on a UNIX platform to be easily ported to less expensive machines. The low cost and abundance of hardware options makes PC’s the ideal machines to operate a distributed numerical network.
6. Future Plan
During the past two decades, advances in modeling (FE, MD, and CFD) were made through the use of sophisticated graphical user interfaces. These interfaces allowed for rapid model creation, mesh generation, and installation of boundary and initial conditions. However, these same interfaces now pose a problem in an era evolving research needs. The use of such legacy software results in the creation of lock files, history files, trace files, and all sorts of other peripheral data files that are required to run certain codes. As a result, it is cumbersome to re-run a large analysis a year later, let alone feed the data from an FE code into an MD code or into a CF code. It is exceedingly difficult to use these large-scale codes for multi phase problems such as the analysis of flexible linkages. Just as difficult, also, is the use of such codes to model effects across length scale gaps, e.g., combined use of molecular dynamics and continuum mechanics. An alternative must be sought―and Globus attempts to address these needs by being a platform to facilitate inter-process communication at a very high level, and, generally, for legacy packages. While it can also be used to integrate lower, level, simpler codes, such a legacy system might be inimical to the needs of computational mechanicians; further, there might simply be too much overhead with such a system.
Consider the spirit of the open source operating system, wherein an operating system command is a data converter e.g., an operating system command can covert a *.doc file into a *.pdf file. A physics command should operate on a data set the same way. The only command line options for a physics code hold be the names of the input and output files. The input.dat and output.dat file formats should be conceptually identical, while all fields need not be filled in; the format should be identical, enabling an FE code to read both input and output files. As a result of adhering to strict formatting rules the FE code can also be viewed as a data converter: it should be able to read a file and ensure it represents the equilibrium state. A user, for example, should be able to edit an output file (modify a stress), and feed it back into the same FE code.
In fact, as FE solvers have now moved toward iterative methods for solutions, abandoning direct solvers, this makes much more sense. In such solvers a ‘state’ can be read, concomitant with all field variables: stress, strain, displacements, forces, velocities and so on. The FE solver then simply inspects the data set, modifies it to ensure equilibrium, and then writes it out again for the next physics server to read.
This coding philosophy now promotes a new view of physics coding wherein an iterative FE code is not just a large-scale analytical tool, but a simple equilibrium enforcer on a data set. In such cases, one should consider the physics processes (FE, MD and others) to be processes that descend upon a data set, inspect it to see if the process has rights to act on the data, and then modify the data to ensure physical equilibrium.
The same philosophy then also holds for multi-body dynamics wherein such a code should be viewed as not just solving the entire motion path, but ensuring that at each times step, equilibrium is assured; i.e.: that the Newton-Raphson implementation has converged for a time-step of Runge-Kutta.
This view quickly enables computational mechanics algorithms to be deployed as simple computational blocks from which a multi-phase and multi-scale server can be assembled―worldwide researchers, without access to legacy hardware or software, can contribute to domain knowledge readily.
While contact processing (CX) has not yet been implemented, it remains a critical issue which will make the described software system more compelling.
Contact between finite element meshes has historically been resolved by calling a subroutine within an FE code. In the spirit of the physics coding described in Section 4.1, a new approach is advocated to solve for contact between deformable objects. Rather than relegating contact analyses to a subroutine within a, contact (CX) should be elevated to become a process of its own, enabling those in the field of geometric visualization to work with those in mechanics computation.
Suppose one mesh in a process group has millions of elastic finite elements, while another mesh has several thousand inelastic elements. Each FE mesh can be analyzed on optimal hardware for that algorithm, while the CX algorithm runs on yet another. This can enhance optimization and load balancing as meshes with specific properties can be targeted for certain architectures. Functionally, after an equilibrium update, data from each FE process is delivered to CX process by the PM. The CX process will inspect the data and provide contact forces to the PM. The PM then delivers the appropriate contact force that each mesh (FE process) needs to prevent penetration.
7. Summary
While the interfaces provided by commercial software have facilitated analysis of specific single-phase or single-scale problems, they are not open to the lightweight, distributed, fault-tolerant needs that the CI can enable. Further, the emerging systems to allow for software integration seems predicated on the continuing value of largescale legacy systems: they are data-driven. As the appendix shows, the low level techniques of the CI are not that complicated. This paper advocates a return to simplicity in mechanics software design for multi-phase problems. This simplicity is finally realized with the suggested software design.
Many researchers are conducting analyses of multiphase and multi-scale problems. Packages such as Globus enable this research by enabling existing largescale legacy systems to be stitched together. This proposed effort builds the system from the bottom. This system is topologically flat and scaleable with the potential for high fault tolerance. It resists legacy in one software “house” and enables a distributed contribution to the solution of such problems for once the interfaces are defined, any one module can be written by any researcher and a server can be notified that a given machine, anywhere in the world, can contribute to an analysis. If, however, the climate moves toward the use of Globus, the results of this work will enable computational scientists to quickly assimilate the technologies of CI and contribute to a new dialogue.
Once again, one day, a package such as Globus might evolve to satisfy such needs. But this author advocates that it is in the interest of computational mechanicians to take the time to understand the intricacies of software needed to integrate the modules of mechanics.
8. References
[1] Atkins, NSF Report. http://www.communitytechnology.org/ nsf_ci_report/
[2] M. Geradi and A. Cardona, “Flexible Multibody Dynamics: A Finite Element Approach,” John Wiley and Sons, England, 2001.
[3] J. Goncalves and J. Ambrósio, “Complex Flexible Multibody Systems with Application to Vehicle Dynamics,” Multibody System Dynamics, Vol. 6, No. 2, 2001, pp. 163-182.
[4] J. Ambrósio and P. Nikravesh, “Elastic-Plastic Deformation in Multibody Dynamics,” Nonlinear Dynamics, Vol. 3, No. 2, 1992, pp. 85-104.
[5] F. Pfeiffer and C. Glocker, “Multibody Dynamics with Unilateral Contacts,” John Wiley and Sons, New York, 1996.
[6] H. M. Lankarani and P. E. Nikravesh, “Continous Contact Force Models for Impact Analysis in Multibody Systems,” Nonlinear Dynamics, Vol. 5, No. 2, 1994, pp. 193-207.
[7] M. Z. Valesek and Z. Sika, “Evaluation of Dynamic Capabilities of Machines and Robots,” Multibody System Dynamics, Vol. 6, No. 2, 2001, pp. 183-202.
[8] H. Moller and E. Lund, “Shape Sensitivity Analysis of Strongly Coupled Fluid-Structure Interaction Problems,” Proceedings of the 8th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, 2000, pp. 4823-4833.
[9] R. Harris and T. Impelluso, “Virtual Stress Testing Machine and the Cyber-Infrastructure,” Engineering with Computers, Vol. 24, No. 2, 2008, pp. 107-117.

