Positioning
Vol.07 No.03(2016), Article ID:70586,10 pages
10.4236/pos.2016.73009
Stochastic Analysis of Low-Cost Single-Frequency GPS Receivers
Mohamed Elsayed Elsobeiey
Department of Hydrographic Surveying, Faculty of Maritime Studies, King Abdulaziz University, Jeddah, Kingdom of Saudi Arabia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 16, 2016; Accepted: August 28, 2016; Published: August 31, 2016
ABSTRACT
Typically, dual-frequency geodetic grade GNSS receivers are utilized for positioning applications that require high accuracy. Single-frequency high grade receivers can be used to minimize the expenses of such dual-frequency receivers. However, user has to consider the resultant positioning accuracy. Since the evolution of low-cost single-frequency (LCSF) receivers is typically cheaper than single-frequency high grade receivers, it is possible to obtain comparable positioning accuracy if the corresponding observables are accurately modelled. In this paper, two LCSF GPS receivers are used to form short baseline. Raw GPS measurements are recorded for several consecutive days. The collected data are used to develop the stochastic model of GPS observables from such receivers. Different functions are tested to determine the best fitting model which is found to be 3 parameters exponential decay function. The new developed model is used to process different data sets and the results are compared against the traditional model. Both results from the newly developed and the traditional models are compared with the reference solution obtained from dual-fre- quency receiver. It is shown that the newly developed model improves the root- mean-square of the estimated horizontal coordinates by about 10% and improves the root-mean-square of the up component by about 39%.
Keywords:
Single-Frequency Receiver, Stochastic Analysis, Precise Point Positioning

1. Introduction
Typically, differential GPS based on carrier phase observables is the first alternative for users seeking centimeter level accuracy [1] . However, a major disadvantage of such technique is its dependency on corrections or data from a reference receiver, i.e. at least two dual-frequency receivers are required [2] [3] . Commercial GPS receivers vary according to their receiving capabilities. With availability of precise ephemerides and termination of Aelective Availability (SA), it becomes possible to obtain position accuracy comparable to that which can be obtained from differential techniques using single receiver. This technique is well known as “Precise Point Positioning” (PPP). In PPP, the undifferenced carrier phase and pseudoranges on both frequencies are utilized to form the first-order ionosphere-free linear combination to eliminate the first-order ionosphere-delay effect. PPP was first introduced by researchers at the Jet Propulsion Laboratory [4] . However, to achieve such accuracy all errors and biases must be rigorously modelled [5] . Few millimeters accuracy is achievable if precise orbit and clock corrections are applied [6] . For more details about the PPP technique and the corresponding error modelling one can refer to [4] [7] [8] .
Unlike dual-frequency receivers, however, ionosphere delay represents a major challenge for single-frequency receivers. There are two main techniques to account for ionosphere delay in case of single-frequency receivers [9] . The first technique is to use ionosphere models to correct for the ionosphere delay. These models may be empirical models such as Klobuchar model, which can account for up to 60% of the delay at mid- latitudes [3] . Klobuchar model coefficients are transmitted in the navigation message and can be improved by extending the eight parameters original Klobuchar model to ten-parameters to account for the ionosphere variation during the night time [10] . Corrections from regional or global network may be estimated and then applied to single-frequency receivers [11] . An example for the global ionosphere corrections, which is used in this paper, is the Global Ionosphere Maps (GIMs) produced by the International GNSS service (IGS). Another option for real-time ionosphere delay correction is to broadcast ionosphere corrections from Space Based Augmentation Systems (SBAS) [12] and [13] .
The second technique to account for ionosphere delay is to form ionosphere-free linear combination using both code and carrier phase observations on L1 from the single-frequency receiver. This technique is based on the Group and Phase Ionosphere Calibration (GRAPHIC) [9] [14] - [16] .
In addition to the low-cost, high sensitivity single-frequency receiver are able to acquire signals with low decibel watt (dBW) [17] . Standalone relative localization system can be established using low-cost receivers to monitor the relative motion of the neighboring notes rather than the absolute position of each node [18] . Ambiguity resolution, on the other hand, can be achieved for single-frequency data [19] . Sub-cm and few centimeters accuracy levels can be achieved for horizontal and vertical directions, respectively, if 10 minutes of accumulated data are used [20] . Moreover, geodetic grade antenna can be used with LCSF receivers to improve its performance [21] .
In this paper, performance of LCSF receivers is improved by developing its unique stochastic model that fits its observables. Two u-blox NEO-7P LCSF GPS receivers are used to form short baseline. Both pseudorange and carrier phase measurements are recorded at sampling rate of 1 Hz. The collected data are used to determine the stochastic characteristics hence improving the positioning performance of such receivers.
2. Mathematical Model
The mathematical models for undifferenced pseudorange and carrier phase measurements can be written as follows [22] [23] :
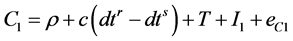 (1)
(1)
 (2)
(2)
where, 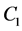 is the pseudorange (code) measurements on L1;
is the pseudorange (code) measurements on L1;  is the carrier phase measurements on L1 scaled to distance (m);
is the carrier phase measurements on L1 scaled to distance (m);  are the satellite and receiver clock errors, respectively;
are the satellite and receiver clock errors, respectively;  is the L1 carrier phase wavelength;
is the L1 carrier phase wavelength;  is the L1 integer ambiguity; c is the speed of light in vacuum (m/sec);
is the L1 integer ambiguity; c is the speed of light in vacuum (m/sec); 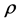 is the true geometric distance between satellite antenna phase center and receiver antenna phase center at reception time (m);
is the true geometric distance between satellite antenna phase center and receiver antenna phase center at reception time (m); 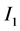 is the L1 ionosphere delay (m); T is the slant tropospheric delay (m); and
is the L1 ionosphere delay (m); T is the slant tropospheric delay (m); and  are the unmodeled errors including residual orbital error, hardware delay, noise and multipath effect.
are the unmodeled errors including residual orbital error, hardware delay, noise and multipath effect.
3. Stochastic Model
The final solution of least-squares of positioning model (Equations (1) and (2)) does not depend only on the mathematical formulation of the unknowns, but also depend on the statistical representation of the observations and unknowns. The observations stochastic properties are reflected in the weight matrix of observations, which includes the corresponding relative and absolute accuracies. The GPS signal’s power can be used as a measure of the signal quality. For example, the signal-to-noise ratio and carrier-to- noise power density ratio can be used as a measure of the GPS signal power and used to weight different signals [24] . Elevation angle, on the other hand, can be used to differentiate between the data quality from each satellite. The relationship between the precision of observations and the corresponding satellite elevation can be expressed in sine or cosine function as seen in Equation (3).
 (3)
(3)
Stochastic properties of GPS receiver’s signals can be determined through the calibration process. Typically, receiver noise can be examined using zero baseline [25] . However, short baseline test can be used to evaluate the full system noise (GPS antenna and receiver) by collecting data over two consecutive days. In this case, the combination of the double-differenced residuals of one day will contain both effects of multipath (if it exists) and system noise. Because every sidereal day the multipath effect is repeated, differencing the double-differenced combination over two consecutive days cancels out the multipath effect and leaves the system noise only [3] . By differencing the double-differenced combination between two consecutive days the system noise is doubled. To obtain the standard deviation of the double-differenced system noise, the system noise should be divided by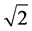 .
.
Alternatively, the GPS system noise can be tested by differencing pseudorange and the carrier phase measurements [5] . The noise level of the carrier phase measurements is approximately 1% of that of the pseudorange measurements. Hence, the carrier phase noise and multipath can be neglected in comparison with those of pseudorange measurements. The C/A-code pseudorange noise can be computed as follows:
 (4)
(4)
Equation (4) can be differenced between the two receivers forming between receiver single difference, which sufficiently cancels out the ionosphere delay. The remaining terms include the integer ambiguity, hardware delay, system noise and multipath effect. Since the multipath effect is repeated each sidereal day, it can be sufficiently removed by differencing over two consecutive days. The integer ambiguity number is constant as long as the receiver tracks the satellite and hardware delay is stable over several days. As such, both can be removed from the combination by subtracting the first value of the time series. At this stage, we have only the differenced system noise in the time series. The differenced combination can be divided into bins based on the satellite elevation angle, and the best fitted mathematical function for observations standard deviation can be determined.
4. Field Test
To investigate the stochastic properties of LCSF receiver, two u-box New-7P GPS receivers are used to form short baseline. The short baseline is fixed on the roof top of Faculty of Maritime Studies (FMS) building beside a base station established using Topcon GR3 GNSS receiver (used as a reference). GPS data are collected at sampling frequency of 1 Hz from both single-frequency and dual-frequency receiver. The collected data are used to examine the noise level of single-frequency receivers. The developed model is used to process new session of GPS data collected using the same single-frequency receivers.
5. Results and Discussion
The single frequency data collected for two consecutive days is used to compute code- carrier observable (Equation (4)) for both receivers. The new observable from the two receivers is used to form between-receiver single-difference combination to remove the ionosphere delay. However, the resultant combination is affected by the multipath effect. Since the multipath effect is repeatable every sidereal day, subtracting such combination from two consecutive days will successfully remove the multipath effect. It should be noted here that the sidereal day is 23 hours 56 minutes and 4 seconds which is less than the solar day by 3 minutes and 56 seconds (i.e., 256 Seconds). Hence, to remove the multipath effect, the second day series should be shifted by 236 seconds. Figure 1 shows noise and multipath effect for PRN06, as an example, for DOY047 and DOY048 before applying the time shift while Figure 2 shows noise and multipath effect after applying time shift of 236 seconds.
It is clear from Figure 1 and Figure 2 that there is multipath effect on the location where the data was collected. That is the main reason to use two consecutive days and
Figure 1. Multipath and Noise for PRN06 During DOY047 and DOY048, 2016.
Figure 2. Multipath and noise for PRN06 during DOY047 and DOY048, 2016. After applying 236 seconds time shift to DOY048.
apply the time shift for the second day then subtract the two days to eliminate the multipath effect. The next step is to classify the resultant noise for each satellite according to elevation angle. The elevation angles are divided into bins of 5 degrees each. The mean value of the noise and the corresponding standard deviation is then calculated. The last step to develop the stochastic model is to perform fitting to determine the best mathematical function that fits the data. Different techniques are applied to determine the best model that fits the data including 2 parameters exponential decay function, 3 parameters exponential decay function, 4 parameters exponential decay function, 3 parameters rational equation, 2 parameters rational equation, 2 parameters hyperbolic decay function, and 3 parameters hyperbolic decay function. Table 1 summarizes the fitting parameters for all tested models.
Figure 3 shows that the standard deviation of C/A code is about 0.5 m and 1.5 m at 90° and 05° elevation angles, respectively. These results makes sense for single-frequency receiver if Trimble R7 GNSS receiver’s model has corresponding values of 0.2 m and 0.7 m at elevation angles of 90° and 05°, respectively [5] . To test the developed model, new raw data are collected using the same single-frequency receivers in addition to dual-frequency data of the base station which is used as a reference. The mathematical model used as in Equations (1) and (2). The ionosphere delay is modelled using the IGS GIMs. Satellite orbit and clock corrections are accounted for using the corresponding IGS final products. Tropospheric delay is modelled using the Global Pressure and Temperature 2 (GPT2) model [26] . ECMWF’s “European Centre for Medium-Range Weather Forecasts” Vienna mapping function 1 (VMF1) is used for mapping tropospheric delays to the elevation angle of each satellite [27] [28] . All remaining errors, in-
Table 1. Summary of fitted models parameters.
Where, el is the satellite elevation angle, and  is the noise standard deviation. It is clear from Table 1 that the best model that fit the relationship between elevation angle and noise standard deviation is the 3 parameters exponential decay function. Figure 3 shows the relationship between the elevation angle and the noise standard deviation for C/A code of NEW-7P u-blox single-frequency low-cost receiver.
is the noise standard deviation. It is clear from Table 1 that the best model that fit the relationship between elevation angle and noise standard deviation is the 3 parameters exponential decay function. Figure 3 shows the relationship between the elevation angle and the noise standard deviation for C/A code of NEW-7P u-blox single-frequency low-cost receiver.
Figure 3. The best fitted model for the relationship between elevation angle and standard deviation.
cluding ocean loading, Earth tides, carrier phase windup, relativity, and sagnac effect are accounted for using existing models [29] . The processing is performed using two different models for observations weights. The first model is the traditional model (Equation (3)), which is used for most GNSS processing software by default. The second model is the developed model (3 parameters exponential decay function), which developed based on our experiment. Our results showed that the developed model improves the solution of Easting, Northing, and Up components. Moreover, using the dual-fre- quency solution as a reference, the uncertainty of the estimated coordinates using both (traditional and developed) models are at 39% confidence level then transformed to 95% confidence level as follows [30] :




where 







Table 2 shows that the total horizontal error is 5.410 m and 4.880 m for the traditional and the developed models at 95% confidence level, respectively. This means that an improvement by about 10% in the horizontal component can be achieved by the developed model. The vertical component, on the other hand, shows that the total vertical error is 1.960 m for traditional model compared with 1.203 m for the developed model which means an improvement of 39% in the vertical component.
6. Conclusion
In this paper, we investigated the stochastic properties of low-cost-single-frequency receivers. The main objective is to develop stochastic model to improve the positioning performance of such receivers. Raw GPS measurements are collected using two low-cost single-frequency GPS receivers fixed to form short baseline. A third dual-frequency receiver is used as a reference to evaluate the performance of low-cost single-frequency receivers. Between receivers, single difference is formed using the code-carrier combination from both receivers and the ambiguity term and hardware delay constants are removed from each satellite pass. The resultant combination is differenced over two consecutive days to eliminate the multipath effect. The final noise is used to develop the relationship between the satellite elevation angle and signal standard deviation. Different functions are tested to determine the best model that fits such relationship. It is found that the 3 parameters exponential decay function is the best fit model. The developed model is used to process different data sets. Both solutions from the traditional (sine function) and the developed models are compared with the reference solution. It is shown that the developed model can improve the accuracy of the estimated coordinates by about 10% and 39% for the horizontal and up components,
Table 2. Summary statistics of the developed model compared with the traditional model.
respectively. These results can be considered significant to improve the performance of low-cost single-frequency receivers.
Cite this paper
Elsobeiey, M.E. (2016) Stochastic Analysis of Low-Cost Single- Frequency GPS Receivers. Positioning, 7, 91- 100. http://dx.doi.org/10.4236/pos.2016.73009
References
- 1. Grewal, M.S., Weill, L.R. and Andrews, A.P. (2007) Global Positioning Systems, Inertial Navigation, and Integration. 2nd Edition, Wiley-Interscience, Hoboken.
http://dx.doi.org/10.1002/0470099720 - 2. El-Rabbany, A. (2006) An Autonomous GPS Carrier-Phased-Based System for Precision Navigation. Intelligent Transportation Systems Conference, 2006. ITSC’06, 17-20 September 2006.
http://dx.doi.org/10.1109/itsc.2006.1706837 - 3. El-Rabbany, A. (2006) Introduction to GPS: The Global Positioning System. 2nd Edition, Artech House Mobile Communications Series, Artech House, Boston, xiv, 210 p.
- 4. Zumberge, J.F., Heflin, M.B., Jefferson, D.C., Watkins, M.M. and Webb, F.H. (1997) Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. Journal of Geophysical Research: Solid Earth, 102, 5005-5017.
http://dx.doi.org/10.1029/96JB03860 - 5. Elsobeiey, M. and El-Rabbany, A. (2010) On Stochastic Modeling of the Modernized Global Positioning System (GPS) L2C Signal. Measurement Science and Technology, 21, 055105.
http://dx.doi.org/10.1088/0957-0233/21/5/055105 - 6. Kouba, J. and Héroux, P. (2001) Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solutions, 5, 12-28.
http://dx.doi.org/10.1007/PL00012883 - 7. Witchayangkoon, B. (2000) Elements of Gps Precise Point Positioning, in Department of Spatial Information Science and Engineering. The University of Maine, Orono.
- 8. Bisnath, S. and Gao, Y. (2009) Precise Point Positioning: A Powerful Technique with a Promising Future. GPS World, 20, 43-50.
- 9. Cai, C., Liu, Z. and Luo, X. (2013) Single-Frequency Ionosphere-Free Precise Point Positioning Using Combined GPS and GLONASS Observations. The Journal of Navigation, 66, 417-434.
http://dx.doi.org/10.1017/S0373463313000039 - 10. Wang, N., Yuan, Y., Li, Z. and Huo, X. (2016) Improvement of Klobuchar Model for GNSS Single-Frequency Ionospheric Delay Corrections. Advances in Space Research, 57, 1555-1569.
http://dx.doi.org/10.1016/j.asr.2016.01.010 - 11. Wübbena, G., Schmitz, M. and Bagge, A. (2005) PPP-RTK: Precise Point Positioning Using State-Space Representation in RTK Networks. Proceedings of ION GNSS, Long Beach, 13-16 September 2005, 2584-2594.
- 12. Hofmann-Wellenhof, B., Lichtenegger, H. and Wasle, E. (2008) GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More. Springer, Wien, New York, xxix, 516 p.
- 13. Arbesser-Rastburg, B. (2002) Ionospheric Corrections for Satellite Navigation Using EGNOS. Proceedings of 27th URSI General Assembly, Maastricht, 17-24 August 2002.
- 14. Shi, C., Gu, S., Lou, Y. and Ge, M. (2012) An Improved Approach to Model Ionospheric Delays for Single-Frequency Precise Point Positioning. Advances in Space Research, 49, 1698-1708.
http://dx.doi.org/10.1016/j.asr.2012.03.016 - 15. Sterle, O., Stopar, B. and Pavlovcic Preseren, P. (2015) Single-Frequency Precise Point Positioning: An Analytical Approach. Journal of Geodesy, 89, 793-810.
http://dx.doi.org/10.1007/s00190-015-0816-2 - 16. Schüler, T., Diessongo, H. and Poku-Gyamfi, Y. (2011) Precise Ionosphere-Free Single-Frequency GNSS Positioning. GPS Solutions, 15, 139-147.
http://dx.doi.org/10.1007/s10291-010-0177-5 - 17. Schwieger, V. (2007) High-Sensitivity GPS—The Low Cost Future of GNSS. FIG Working Week, Hong Kong, 13-17 May 2007, 1-16.
- 18. Hedgecock, W., Maroti, M., Sallai, J., Volgyesi, P. and Ledeczi, A. (2013) High-Accuracy Differential Tracking of Low-Cost GPS Receivers. Proceeding of the 11th Annual International Conference on Mobile Systems, Applications, and Services, Taipei, 25-28 June 2013, 221-234.
http://dx.doi.org/10.1145/2462456.2464456 - 19. Odijk, D., Teunissen, P. and Zhang, B. (2012) Single-Frequency Integer Ambiguity Resolution Enabled GPS Precise Point Positioning. Journal of Surveying Engineering, 138, 193-202.
http://dx.doi.org/10.1061/(ASCE)SU.1943-5428.0000085 - 20. Odijk, D., Teunissen, P.G. and Khodabandeh, A. (2014) Single-Frequency PPP-RTK: Theory and Experimental Results. In: Rizos, C. and Willis, P., Eds., Earth on the Edge: Science for a Sustainable Planet, Springer, Berlin, 571-578.
http://dx.doi.org/10.1007/978-3-642-37222-3_75 - 21. Takasu, T. and Yasuda, A. (2008) Evaluation of RTK-GPS Performance with Low-Cost Single-Frequency GPS Receivers. Proceedings of International Symposium on GPS/GNSS, Tokyo, 11-14 November 2008, 852-861.
- 22. Kleusberg, A. and Teunissen, P.J.G. (1998) GPS for Geodesy. 2nd Edition, Vol. 14, Springer, Berlin, 650 p.
- 23. Leick, A. (2004) GPS Satellite Surveying. 3rd Edition, Vol. 24, John Wiley, Hoboken, 435 p.
- 24. Ozlüdemir, M.T. (2004) The Stochastic Modeling of GPS Observations. Turkish Journal of Engineering and Environmental Sciences, 28, 223-232.
- 25. Nolan, J., Gourevitch, S. and Ladd, J. (1992) Geodetic Processing Using Full Dual Band Observables. Proceedings of the 5th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1992), Albuquerque, 16-18 September 1992, 1033-1041.
- 26. Lagler, K., Schindelegger, M., Bohm, J., Krásná, H. and Nilsson, T. (2013) GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques. Geophysical Research Letters, 40, 1069-1073.
http://dx.doi.org/10.1002/grl.50288 - 27. Boehm, J., Niell, A., Tregoning, P. and Schuh, H. (2006) Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data. Geophysical Research Letters, 33, Article ID: L07304.
http://dx.doi.org/10.1029/2005gl025546 - 28. Boehm, J., Werl, B. and Schuh, H. (2006) Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data. Journal of Geophysical Research: Solid Earth, 111, Article ID: B02406.
http://dx.doi.org/10.1029/2005jb003629 - 29. Kouba, J. (2009) A Guide to Using International GNSS Service (IGS) Products.
http://igscb.jpl.nasa.gov/igscb/resource/pubs/GuidetoUsingIGSProducts.pdf - 30. El-Diasty, M. and Elsobeiey, M. (2015) Precise Point Positioning Technique with IGS Real-Time Service (RTS) for Maritime Applications. Positioning, 6, 71-80.
http://dx.doi.org/10.4236/pos.2015.64008





