Positioning
Vol.05 No.04(2014), Article ID:51260,11 pages
10.4236/pos.2014.54011
Using Multiple GNSS Constellations with Strict Quality Constraints for More Accurate Positioning in Urban Environments
Hiroko Tokura1, Hideki Yamada2, Nobuaki Kubo1, Sam Pullen3
1Tokyo University of Marine Science and Technology, Tokyo, Japan
2Hitachi Zosen Corporation, Tokyo, Japan
3Stanford University, Stanford, US
Email: lacto.h@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 August 2014; revised 17 September 2014; accepted 17 October 2014
ABSTRACT
Combined multi-global navigation satellite system (GNSS) signals are capable of improving satellite availability for both standalone and differential positioning. Currently, the potential for high- accuracy automobile navigation using GNSS is constrained by severe multipath and poor satellite geometry, especially in “urban canyons” in large cities. With differential GNSS (D-GNSS) positioning, inconvenient system time differences can be removed by reference-station processing, allowing a user’s receiver position to be accurately calculated using four or more visible satellite signals. Therefore, in the future, we can filter numerous multi-GNSS measurements based on their quality in order to enhance the positioning performance in urban environments. In this paper, we present several methods that use multi-GNSS to filter signals from satellites containing severe multipath errors. In addition, we select single-frequency code-based D-GNSS because it has significant potential due to its low cost and robustness. The first method uses the measured carrier-to-noise ratio (C/N0). When only reflected signals are received in dense urban areas, the C/N0 will decrease by more than 6 dB-Hz, with the exception of high-elevation satellites. Thus, by comparing the measured and expected C/N0 at various elevation angles, we may be able to detect the presence of severe multipath signals. The second method involves using the error residual from the Receiver Au- tonomous Integrity Monitoring (RAIM), which is a well-known technique for checking the quality of measurements. Signals having severe multipath effects result in significant deterioration of measurements. In addition to the above methods, we introduce several points that should be noted in order to improve D-GNSS. To evaluate our proposed method, we perform positioning tests using a car in an urban environment. Differential positioning was used for multi-GNSS with GPS, QZSS, BeiDou, and GLONASS. We present an evaluation of each technique that is used to mitigate multipath errors. The results show that our proposed techniques effectively improved the horizontal accuracy. In addition, the accuracy of the horizontal errors was improved by more than 50% in two different environments.
Keywords:
GNSS, GPS, QZSS, BeiDou, GLONASS, Multipath, Satellite Selection

1. Introduction
The availability of global navigation satellite system (GNSS) applications is expected to improve over the next few years because of the introduction of new positioning satellites. In particular, Asia will be able to benefit from “multi-GNSS” using the U.S. global positioning system (GPS), the Russian GLONASS, the European Galileo, the Chinese navigation satellite system (BeiDou), and the Japanese Quasi-Zenith satellite system (QZSS). BeiDou has already been officially commissioned, and is expected to eventually provide operational services for the whole Asia-Pacific region with a constellation of over 10 satellites [1] . QZSS is the Japanese regional navigation satellite system, and uses inclined geosynchronous orbits to continuously provide at least one satellite at high elevation over Japan and neighboring countries.
At present, the potential for high-accuracy automobile navigation using GNSSs is constrained by severe multipath and poor satellite geometry, especially in “urban canyons” in large cities. Strong multipath reflections from multiple obstacles degrade both pseudo-range and carrier-phase measurements, causing large measurement errors and incorrect fixes on carrier-phase integer ambiguities. For this reason, various techniques that attempt to mitigate multipath have been developed, but they are still far from perfect [2] [3] .
In the era of multi-GNSS with many more visible satellites, it should be possible to select a subset of the visible satellites that have high-quality measurements, enabling the elimination of satellites affected by multipath. When we use differential positioning with multiple GNSS constellations, the system time differences between different satellite systems are removed by the application of differential corrections by users. Differential-GNSS (D-GNSS) thus allows a user’s receiver position to be accurately calculated using four or more visible satellite signals, although many more satellites are usually visible. Therefore, in the future, we can filter the numerous multi-GNSS measurements according to their quality in order to enhance the positioning performance in urban environments, enabling us to more easily detect and exclude satellites that show signs of significant multipath errors.
In this paper, we aim to evaluate satellite selection methods for multi-constellation GNSS in urban environments that are challenging for moving vehicles. Based on our previous research, when a direct line-of-sight signal is blocked and the signal is received only via reflections, the carrier-power-to-noise-density ratio (C/N0) decreases by more than 6 dB-Hz, except in cases involving very high elevation satellites [4] - [6] . Previously, the C/N0, which depends on the elevation angle, would be determined for each satellite system and orbit [7] . The threshold line was set at about 7 - 8 dB-Hz below the C/N0. When the C/N0 of each satellite is lower than the threshold line, the satellite is removed from the positioning. The second method is based on the receiver autonomous integrity monitoring (RAIM) method, which is a well-known technique that is used to detect satellites provided that there are over-determined pseudo-range measurements [8] [9] . RAIM uses these error residuals. When a large residual error is detected, the satellite is then removed from the positioning. In addition to the previous two methods, other significant points are introduced. For example, difficulties are experienced when using even very high-elevation satellites in dense urban areas. We show one good example where even a high-eleva- tion satellite over 80˚ sometimes has large multipath errors in dense urban areas.
To examine the effectiveness of our proposed techniques, we performed positioning tests using a car in an urban environment in Tokyo, Japan. First, we checked the multi-GNSS performance using normal D-GNSS. Then, we evaluated the proposed methods to determine their effectiveness. The results confirmed that our proposed methods were effective in significantly reducing the horizontal positioning errors. Furthermore, we discuss the multipath error obtained for satellites with very high elevations. Even when we used a satellite with an elevation that is over 80 degrees, we found that the satellite signal occasionally encountered multipath errors.
2. Differential GNSS Positioning
D-GNSS enables the determination of GNSS positions using corrections determined and broadcast from a receiver that is fixed at an accurately surveyed position, which is known as a reference station. This method takes advantage of the slow variation of errors with time and user position due to ephemeris, satellite clock, and ionospheric and tropospheric delays. Pseudo-range measurements including these errors at the reference station are given by Equation (1), while at the rover position, it is given by Equation (2).
 (1)
(1)
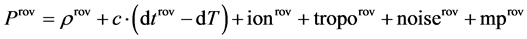 (2)
(2)
The superscript refers to each of the receivers (reference station and rover), where 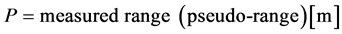 ,
,  ,
,  ,
,  ,
, 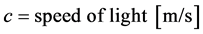 ,
,  ,
, 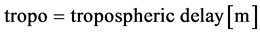 ,
,  , and
, and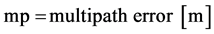 . The errors that are due to satellite clock error, ionospheric delay, and tropospheric delay are of the order of several meters, whereas the errors that are due to the noise at each receiver and multipath error at the reference station are of the order of several centimeters. In addition, there is a satellite orbit error, which has an error of the order of several tens of centimeters and characteristics of bias.
. The errors that are due to satellite clock error, ionospheric delay, and tropospheric delay are of the order of several meters, whereas the errors that are due to the noise at each receiver and multipath error at the reference station are of the order of several centimeters. In addition, there is a satellite orbit error, which has an error of the order of several tens of centimeters and characteristics of bias.
When calculating the position, the receiver clock error is estimated by the least-square method. Some receivers estimate the receiver clock error and mitigate this error prior to outputting the pseudo-range measurement. The satellite clock error is calculated using the satellite clock correction factor given by the ephemeris [10] . The ionospheric delay is estimated by Klobuchar model and tropospheric delay is estimated by Saastamoinen model. Usually, for single-point positioning, the ionospheric delay, tropospheric delay, and satellite clock errors are used to estimate the value. However, these corrections do not entirely eliminate the errors, and there some errors that are of the order of several meters are caused by errors associated with single-point positioning. When the differential positioning for the distance between the reference and rover station is within 300 - 1000 km, the ionospheric delay, tropospheric delay, satellite clock error, and satellite orbit error have high correlation that can be removed. These errors are calculated more precisely by the reference station than that which is estimated by each model. At the reference station, the true ranges between the reference station and satellites are calculated using the satellites’ positions and post-processed precise reference positions. To apply this correction data to the rover receiver, the correction data should have a smaller capacity for ease of transmission. Therefore, the correction data generated at the reference station reduces the estimated satellite clock error. The system computes the correction using Equation (3) as follows:
 (3)
(3)
Note that the receiver clock error and the satellite clock error are estimated by the reference station. Therefore, the errors in Equation (4) are not precise. In order to apply these corrections, we have to ensure that the two receivers have a line-of-sight to the same set of GNSS satellites.
When we combine different satellite systems for positioning, we have to factor the different system times in the different systems. When the receiver uses the basis of the master clock satellite for GPS, Equations (4) and (5) are extensions of Equations (1) and (2) where GLONASS and GPS are combined for differential positioning, Moreover, Equations (6) and (7) are extensions of Equations (1) and (2), where BeiDou and GPS are combined for differential positioning.
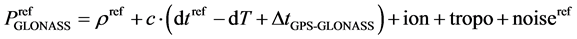 (4)
(4)
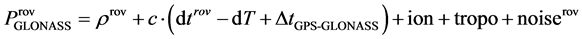 (5)
(5)
 (6)
(6)
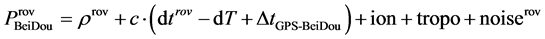 (7)
(7)
where 


The satellite system time difference values in both the reference and rover station are the same. Therefore, the system time differences are canceled. Differential positioning is therefore used to easily correct the system time difference when combining multiple satellite systems.
Uncorrelated errors that exist between the reference station and the user, such as multipath and noise errors, cannot be corrected by the differential technique. In the following section, we introduce our proposed methods that can mitigate mainly the multipath errors.
3. Satellite Selection Method
As discussed earlier, multipath errors are usually dominant sources of DGNSS errors in urban areas. In this paper, we propose two combinations of satellite selection methods to mitigate the large multipath errors. These are proposed below.
3.1. The Use of C/N0 Measurements
The first method uses the received signal strength as measured by the estimated C/N0 at the user receiver. This method is based on the characteristics of the measured C/N0 depending on the elevation angle. The C/N0 of the satellite signal reflected by a building usually fluctuates if a direct signal is received. Without the direct signal, the C/N0 of the satellite must be lower than the expected signal strength based on the elevation-dependent C/N0. Figure 1 shows the typical case of multipath error without a direct signal. In this case, the signal strength occasionally falls by about 6 dB-Hz [4] .
To detect and remove the satellites containing severe multipath errors, we carefully check the C/N0 measurements. The expected plots for elevation-dependent C/N0 were created for each of the satellite systems, i.e., GPS, QZSS, BeiDou, and GLONASS. Note that BeiDou satellites are placed into three orbits. The expected plots for GEO (BeiDou PRN 01 to 05) are 2 - 3 dB-Hz lower than satellites in other orbits [7] . If the measured C/N0 of the satellite is below the threshold, depending on the elevation angle, the satellite is not used for positioning. The threshold of the elevation-dependent C/N0 is set using statistical data acquired over a 24-h period obtained under open-sky conditions. In fact, the threshold is set to be approximately −7 to −8 dB-Hz from the elevation-dependent C/N0, as shown in Figure 2. To determine the optimal value of the threshold, the balance between availability and accuracy is very important. Further, the characteristics of the commercial receiver should be considered when deciding the threshold value.
3.2. RAIM (Receiver Autonomous Integrity Monitoring)
The second proposed method for improving the quality is the pseudo-range error residual approach based on Receiver Autonomous Integrity Monitoring (RAIM), which is a well-known technique for checking the quality of ranging measurements [8] [9] .
When five or more satellite pseudo-range measurements are available (one more than the minimum of four required for 3-D positioning), the extra pseudo-ranges should all be consistent with the computed position. In simple terms, positioning with over-determined pseudo-range measurements provides both an expected position and residuals that represent the difference between the full set of measurements and a subset of these measurements. Positioning using pseudo-range measurements that have small multipath errors causes these error residuals to remain small. However, the addition of poor-quality pseudo-range measurements, such as those with severe multipath errors, creates relatively large error residuals. As a result, large residual errors are correlated with incorrect positions. In this paper, current residual measurements are used as a self-consistency check.
After determining the user position, residual errors are computed for each individual satellite used in the position calculation. If the absolute values of one or more residual errors are higher than the threshold value, we search for the satellite that has the maximum residual error. If this satellite’s maximum residual is higher than the threshold, it is regarded as having severe multipath errors, and is removed and not used for positioning.
Using the fault-detection and exclusion capabilities of RAIM, satellites containing severe multipath errors can be removed automatically, allowing the receiver position to be calculated more accurately and reliably using the
Figure 1. Example of decreased C/N0 levels.
Figure 2. Elevation-dependent C/N0.
remaining satellite measurements. Note that, unlike the use of RAIM for detecting rare system failures, the thresholds for error residuals are set relatively stringently to detect significant multipath errors, which are much more frequent in urban environments than are system failures.
To determine the threshold values for RAIM, the residual error value was calculated under open-sky conditions using multi-GNSS (a combination of GPS, BeiDou, and GLONASS) during a 6-h period on June 3, 2014 using a Trimble NetR9 multi-constellation GNSS receiver. Table 1 shows the resulting residual errors for 3 h at 1 Hz. The first row is the average of all residual errors for each satellite system, the second row is the standard deviation of all residual errors, while the third row is the maximum residual error of each satellite system. Table 2 shows the residual error for another 3-h period at 1 Hz. For the condition involving little multipath influence, 21 of 416,628 epochs are more than 3 m of the absolute value. Based on these results, the threshold value was set to be within an absolute value of 3 m.
4. Testing and Results
To examine the effects of the proposed techniques, two positioning car tests were performed in a sub-urban area and a dense urban environment in Tokyo, Japan. Course 1 was tested in the sub-urban area for 85 min, while Course 2 was tested in the dense-urban area for 60 min. The driving courses used in this experiment are shown in Figure 3 and Figure 4, respectively. We set up a GNSS receiver antenna on the roof of a car and moved around in the urban-canyon environment. The reference station was set within 5 km of the vehicle path using the same receiver as that which was used in the automobile. Kinematic raw data were obtained with an update rate of 10 Hz under urban conditions using a Trimble NetR9 multi-constellation GNSS receiver on October 1, 2013. The satellite constellations used for the test were GPS, QZSS, BeiDou, and GLONASS. Figure 5 and Figure 6 show sky plots obtained during the car test.
A reference or “truth” position was established using a position and orientation system for land vehicles (POS LV). POS LV is a compact, fully integrated, turnkey position and orientation system that utilizes integrated inertial technology to generate stable, reliable, and repeatable positioning solutions for land-based vehicular applications. According to the specifications, a horizontal accuracy of 10 cm is guaranteed for 60 s without GNSS. A differential GNSS position error was calculated by differencing the POS LV “truth” position from that provided by DGNSS.
Table 1. Result of residual error (first 3-h period).
Table 2. Result of residual error (second 3-h period).
Figure 3. Tukishima (sub-urban area in Tokyo).
Figure 4. Marunouchi (dense-urban area in Tokyo).
The positioning conditions were as follows. The horizontal-dilution of precision (HDOP) was over 10 in order to detect poor satellite geometries that may lead to large position errors, while the C/N0 of L1, B1, and G1 were below 20 dB-Hz and the elevation angle was below 15˚.
Figure 5. Sky plot at Tukishima.
Figure 6. Sky plot at Marunouchi.
4.1. The Effect of Multi-GNSS
Before applying the two proposed methods, we performed a simple evaluation of the effect of multi-GNSS. Table 3 shows the results of each multi-GNSS combination of satellite constellations in Course 1, while Table 4 shows the differential results in Course 2.
We observed that generally, there were improvements in the availability results, especially in the dense urban areas. Compared with GPS + QZSS, the availability was increased by over 20% by including BeiDou and GLONASS. On the other hand, the availability in the sub-urban areas was not improved as much because the constellation of GPS + QZSS already provided about 95% availability. The same tendency was observed for the accuracy, although the percentage of absolute horizontal errors within 5 m did not change as much. We observed that all of the results for the horizontal accuracy appeared to have very large errors because the best accuracy was still approximately 9 m, even when there were absolute horizontal errors in the sub-urban areas.
4.2. Validation of Proposed Method
Our proposed methods were validated using the same test data. The other analysis conditions were the same as those described in Section 4.1.
Table 3. Multi-GNSS results in Tukishima.
Table 4. Multi-GNSS results in Marunouchi.
The threshold values for the two methods are as follows:
Method 1: C/N0 measurement quality test
For GPS-L1 C/A, QZS L1-C/A, BeiDou B1, and GLONASS G1-C/A, satellites whose C/N0 measurements are 8 dB-Hz lower than the expected value (elevation-dependent) are not used for the positioning process.
Method 2: RAIM
We search for the satellite that has the maximum residual error. If the absolute value of the maximum residual error is higher than 3 m, the satellite is not used for positioning.
First, we test the C/N0 measurements described in Section 3.1. The remaining satellites are used to calculate the position and generate residual errors. At the same time, we check the HDOP value to determine if it is lower than the threshold. Then, we detect and remove satellites using the RAIM-based residual method described in Section 3.2. If any satellites are removed by RAIM, we again calculate and check the HDOP value using the new, smaller set of satellites.
Table 5 summarizes the results for Course 1. The third row shows the D-GNSS results, the fourth row shows the results obtained using method 1, and the fifth row shows the results obtained using both methods 1 and 2. Figure 7 shows the temporal results of the horizontal errors. After applying both methods 1 and 2, the horizontal accuracy had more than doubled compared with the normal D-GNSS, and the availability was still about 98%. The percentage of satellites having errors within 5 m was improved from approximately 87% to 97%. According to Figure 7, many large errors over 20 m were corrected by using these methods. This indicates that our proposed method was effective when using multi-GNSS. However, while there remained large errors, the number of epochs with large errors was few. Additionally, if GLONASS satellites are not used in the Tsukishima test, the horizontal accuracy was improved from about 3 m (as shown in the fifth row of Table 5) to below 2 m, while the availability remained above 97%.
Table 6 summarizes the results for Course 2. The third row shows the D-GNSS results, the fourth row shows the results obtained using method 1, and the fifth row shows the results obtained when using both methods 1 and 2. Figure 8 shows the temporal results of horizontal errors. After applying both methods 1 and 2, the horizontal accuracy also more than doubled compared with the normal D-GNSS, and the availability decreased from 94% to 86%. The percentage of satellites having errors within 5 m was improved from approximately 60% to 73%. According to Figure 8, many large errors over 100 m were corrected by using these methods. This indicates that our proposed method was also effective when using multi-GNSS. Unfortunately, several large errors remained even when the proposed methods were applied, as shown by the large horizontal accuracy in the fifth row of Table 6. In fact, horizontal errors of over 200 m can be seen in Figure 8 for both methods 1 and 2. Based on these results, we investigated the causes of these large errors, and in Sections 4.3 and 4.4, we made a suggestion for the improvement of the performance.
Table 5. Validation of proposed method in Tukishima.
Figure 7. Comparison of horizontal error when methods 1 and 2 were applied in Tukishima.
Table 6. Validation of proposed method in Marunouchi.
Figure 8. Comparison of horizontal error when method 1 is applied in Marunouchi.
4.3. Multipath Error Caused by High-Elevation Satellite
In this section, we considered the case of large multipath errors caused by the use of high-elevation satellites. Generally, signals from high-elevation satellites do not deteriorate as much due to multipath, and they are useful for high-accuracy positioning. However, very high-elevation satellites were observed to affect the positioning performance for the dense-urban areas included in this test. Analysis of the C/N0 values of all satellites in the Marunouchi test showed that the signal strength of the BeiDou 08 satellite was approximately 5 - 6 dB-Hz lower than the elevation-dependent signal strength, even when the elevation angle was over 80˚ throughout most of the test period.
Table 7 compares the average horizontal errors of the GPS/QZSS/BeiDou constellation and the constellation without BeiDou 08. As observed in Table 7, the average horizontal errors were significantly improved from over 3 m to below 1 m in the latitudinal direction. Figure 9 shows the temporal horizontal errors for the GPS/QZSS/BeiDou constellation and the constellation without BeiDou 08. The figure clearly shows that there is significant improvement in terms of the bias in the latitudinal direction. Furthermore, the relationship between the C/N0 of BeiDou 08 and the temporal latitudinal errors is shown in Figure 10. As observed in Figure 8, even
Table 7. Average horizontal errors in Marunouchi.
Figure 9. Latitude error with GPS/QZSS and BeiDou/true heading by POSLV at Marunouchi.
Figure 10. Evaluation of BeiDou PRN 08 C/N0 with latitude error (GPSTIME 195900 - 196500).
if we use the proposed method mentioned in section 3.1, BeiDou 08 was not removed from positioning because the degradation of the C/N0 was sometimes below 5 - 6 dB-Hz. Because the threshold in this paper was set to 8 dB-Hz, BeiDou 08 was considered in the positioning even though its signal was actually contaminated by either diffraction or reflection. Figure 11 shows the satellite geometry and actual horizontal position results for true positions, which were obtained using about data acquired over a 10-min period. During this period, latitudinal direction errors were around −20 m from the true position. Table 8 compares the results obtained for the GPS/QZSS/BeiDou constellation and the constellation without BeiDou 08. Although the availability of the positioning decreased by 10%, the percentage of horizontal errors that were within 5 m increased by about 16%.
5. Conclusions
In this paper, we evaluated single-frequency code-based D-GNSS using our proposed methods to filter out satellites whose signals are contaminated by multipath effects. It is commonly accepted that as the number of satellites that are employed increases, the overall availability also increases. However, with respect to the accuracy, it is not easy to improve the performance using multi-GNSS satellites because GPS is still the leading GNSS in use globally.
Based on our test results, the use of our proposed methods in sub-urban areas improved the horizontal accuracy from 9.8 m to 4.1 m. In addition, the availability was decreased by only about 1%. In the dense urban areas, the horizontal accuracy was improved from 37.5 m to 16.9 m using our proposed method although the availability decreased by 8%. In fact, if we use only GPS/QZSS for positioning in these two tests, the obtained accuracy was the highest although the availability decreased significantly.
The results also show that the addition of GLONASS sometimes led to large errors in urban areas. For example, if we do not use GLONASS satellites in the Tsukishima test sub-urban areas, the horizontal accuracy improved from 4.1 m to 2.3 m, while the availability remained over 97%. We aim to perform additional data analysis to verify the ideal combinations of multi-GNSS satellites. Finally, we showed only the case for which even high-elevation satellites sometimes cause large multipath errors. One of the main reasons for this is that the C/N0 of high-elevation satellite does not decrease significantly compared with medium- or low-elevation satellites.
Figure 11. Illustration of satellite geometry for large latitude error (GPSTIME = 196280).
Table 8. Results obtained for Marunouchi.
Acknowledgements
The authors would like to thank the Advanced Telecommunications Research Institute International (ATR) for providing POS/LV data of the automobile tests. Financial support was provided by “Strategic Information and Communications R&D Promotion Programme (SCOPE)” of Ministry of Internal Affairs and Communications.
References
- China Satellite Navigation Office (2013) BeiDou Navigation Satellite System Signal in Space Interface Control Document. http://www.beidou.gov.cn/attach/2013/12/26/20131226b8a6182fa73a4ab3a5f107f762283712.pdf
- Groves, P.D., Jiang, Z., Rudi, M. and Strode, P. (2013) A Portfolio Approach to NLOS and Multipath Mitigation in Dense Urban Areas. ION GNSS 2013, Manassas, US, 3231-3247.
- Lee, Y.-W. and Shibasaki, R. (2010) Development of Spatial Method for GNSS Accuracy Improvement. Theory and d Applications or GIS, 18, 73-84.
- Suzuki, T., Kubo, N. and Yasuda, A. (2004) The Possibility of the Precise Positioning and Multipath Error Mitigation. International Symposium on GPS/GNSS, Sydney, Australia, 6-8 December 2004.
- Kubo, N. (2010) Analyzing the Multipath Errors for the Vehicle in the Dense Urban Areas. ENC-GNSS 2010, Germany, 19-21 October 2010.
- Kubo, N. and Yasuda, A. (2003) Reduction of Code Multipath Error in Static Positioning. The IEICE Transactions, J86-B, 104-112.
- Montenbruck, O., Hauschild, A., Steigenberger, P., Hugentobler, U., Teunissen, P. and Nakamura, S. (2013) Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System. GPS Solutions, 17, 211-222. http://dx.doi.org/10.1007/s10291-012-0272-x
- Axelrad, P. and Parkinson, B.W. (1988) Autonomous GPS Integrity Monitoring Using the Pseudorange Residual. Navigation, 35, 255-274.
- Feng, S., Ochieng, W.Y., Walsh, D. and Ioannides, R. (2006) A Measurement Domain Receiver Autonomous Integrity Monitoring Algorithm. GPS Solutions, 10, 85-96. http://dx.doi.org/10.1007/s10291-005-0010-8
- (2013) IS-GPS-200, Navstar GPS Space Segment/Navigation User Interfaces. http://www.gps.gov/technical/icwg/IS-GPS-200H.pdf













