Positioning
Vol.05 No.02(2014), Article ID:46149,8 pages
10.4236/pos.2014.52005
A New Independent GPS-Free System for Geo-Referencing from Space
P. Kaufmann1,2, P. L. Kaufmann3, S. V. D. Pamboukian1,4, R. Vilhena de Moraes5
1Escola de Engenharia, CRAAM, Universidade Presbiteriana Mackenzie, São Paulo, Brasil
2Centro de Componentes Semicondutores, Universidade Estadual de Campinas, Campinas, Brasil
3Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, Brasil
4Escola de Engenharia, Laboratório de Geotecnologias, Universidade Presbiteriana Mackenzie, São Paulo, Brasil
5Dinâmica Orbital e Planetologia, Universidade Federal do Estado de São Paulo, São José dos Campos, Brasil
Email: pierrekau@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 February 2014; revised 21 March 2014; accepted 20 April 2014
ABSTRACT
A new system’s geo-referencing from space is entirely free from any GNSS (GPS or equivalent) systems. The system addresses to various strategic and economic applications such as in remote clock synchronism, aircraft and balloon navigation, missile and smart bombs tracking, satellite orbital determination and remote target geo-positioning. The new geometry concept corresponds to an “inverted GPS” configuration, utilizing four ground-based reference stations, synchronized in time, installed at well known geodesic coordinates and a repeater in space, carried by an aircraft, balloon, satellite, etc. Signal transmitted by one of the reference bases is retransmitted by the transponder, received back by the four bases, producing four ranging measurements which are corrected for the time delays undergone in every retransmission. A minimization function was derived to compare the repeater’s positions referred to at least two groups of three reference bases, to correct for the signal transit time at the repeater and propagation delays, and consequently to provide the accurate repeater position for each time interaction. Once the repeater’s coordinates are known, the other determinations and applications become straightforward. The system solving algorithm and process performance has been demonstrated by simulations adopting a practical example with the transponder carried by an aircraft moving over bases and a target on the ground. Effects produced by reference clock synchronism uncertainties at the four bases on the measurements are reviewed.
Keywords:
Geo-Referencing from Space, GPS-Free Time Synchronization, Navigation and Positioning, Space Geodesy, Remote Ranging Transponder Transit Times, Propagation Path Delays

1. Introduction
A very well known principle to determine indirectly the distance of a remote object utilizes the echo of a transmitted signal, which propagation speed is known. A remote repeater with three dimensional positions can be geometrically determined in relation to at least three transmitters at known position coordinates. This principle led to the concept of a geo-referencing system [1] which may be visualized as “inverted GPS” geometry in space. However in practical applications, when applied to time reference marks transported by electromagnetic waves, the feasibility of the concept becomes critically dependent on the knowledge of temporal effects due to four principal causes: (a) the signal speed propagation the medium causing path length variations; (b) propagation time at instruments, cables and connectors at the transmission module; (c) propagation time at instruments, cables and connectors at the final reception modules; and (d) time of signal transit at the remote transponder, which distance is to be determined.
The cause (a) is generally sufficiently well predicted by models for propagation in various media (ionosphere, troposphere) as well as in space (see for example Refs. [2] -[7] and references therein). The path length variations, however, depend on the elevation angle the object (carrying a repeater) that is seen from the bases, which need to be determined.
Causes (b) and (c) can be measured directly, with sufficiently high accuracy, depending on the quality of the instruments that are utilized. The cause (d) however is undetermined since the remote object, carrying the transponder, is inaccessible for direct measurements. There are various long distance wireless transmission options using electromagnetic waves, such as the radio waves. The signals are sent to great distances using retransmission repeating links represented by a transponder or repeater. At the transponders that the signals are received, they may or may not be stored or processed, be amplified, and then retransmitted at a frequency which may be the same, or different from the incoming frequency. The signal transit time at the transponder is affected by several sources. It undergoes changes in its internal signal propagation thermal dependent physical characteristics, which can change with time, changes in internal digital processing time which may be different for distinct coded time messages, when it is the case, or for each sequence of signals used to determine its distance of the repeater.
Other known time changes need to be considered on fast moving transponders carried by satellites for example. Doppler path change caused by frequency shifts in the direction of the repeater [8] [9] and of relativistic effects relative to the reference system containing the sites to which the distances are to be determined, which become further accentuated when the satellites move over distinct gravity potentials relative to the geoid [10] . They may be neglected for velocities the speed of light, because they produce effects much smaller in comparison to propagation and delays at the repeater.
On the other hand, passive transponders, such as the signal scattered reflection by meteor trails in the upper terrestrial atmosphere in the VHF frequency band [11] , may undergo significant phase delays which need to be taken into account for distance measurements.
Therefore for accurate ranging measurements, it becomes essential requirements to know the precise knowledge of the path length changes due to propagation as well as time changes for each coded time signal interaction at the transponder, for applications in time synchronization, navigation and remote positioning.
2. The System and Method
The new system consists in four reference bases on the ground at known geodesic position coordinates, synchronized among themselves, and a repeater in space. The method to determine delays compares the positions of the repeater referred to at least two distinct sets of three of the four reference bases on the ground [11] [12] (see Figure 1). A set of tentative possible delay values within a certain time interval is established in advance. For a given single time-coded transmitted signal, the calculations of the repeater’s position coordinates are performed for different values assigned to the delays for each set of three reference bases on the ground (ABC, ACD and ABD). Calculations are done using a known algorithm [13] for every set of three reference bases on the ground.
With a time signals transmitting site located at base A, the other reference bases B, C, D and a target in P, the segments measurements obtained are [12] :
Figure 1. The four ground based geodetic reference bases, A, B, C and D, the repeater in the sky R, and a remote site P. Time signals are emitted by one reference base A, retransmitted by R and received by all ground bases and the target where time differences are measured [11] [12] .
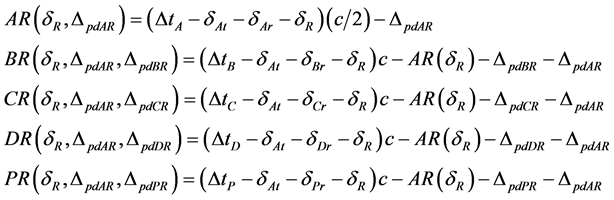 (1)
(1)
where the parameters to be determined are the coded time signal transit time at the repeater dR and the propagation path delays, DpdAR, DpdBR, DpdCR, DpdDR.
AR, BR, CR, DR and PR are the distances of bases A, B, C, D and of the target P to the repeater R, respectively, expressed as a function of time variations caused by the signal transit at the repeater dR, to be determined, and corrected for the respective propagation path delays DpdAR, DpdBR, DpdCR, DpdDR and DpdPR; DtA, DtB, DtC , DtD and DtP are the time differences effectively measured at bases A, B, C and D, as well as at the target P, respectively, with respect to their clocks; dAt is the time variation due to signal transit in circuits and cables when transmitted from base A, previously measured and known; dAr, dBr, dCr, dDr and dPr are the time variations due to the coded time signal transits on circuits and cables when received at bases A, B, C, D and P, respectively, previously measured and known; and c is the speed in free space of the electromagnetic waves that transport the coded time signal.
Since the repeater’s position in the sky is not known a priori, the time variations dR at the repeater and the path delays can, in practice, be determined simultaneously. As we determine dR, the approximate repeater’s position is determined, and consequently the elevation angles it is seen from each one of the four bases are defined. The propagation path delays for each distances AR, BR, CR and DR are found utilizing the repeater’s elevation angles as seen from the bases applied to a selected propagation model to derive the fully corrected repeater’s position. Therefore the values for path delays DpdAR, DpdBR, DpdCR, and DpdDR are added to the system of Equations (1), which become a function of dR only. The value of DpdPR will be found similarly but afterwards, when the target position is determined.
The coordinates of the repeater platform R in relation to the x, y and x coordinate axis to be found using the known algorithm [13] . With measurements obtained at bases A, B, and C, as function of the transit time at the repeater dR we obtain xR(dR), yR(dR) and zR(dR). On the other hand, adding the measurements obtained with bases A, B and D, we get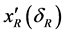 ,
,  and
and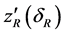 .
.
The pair of systems of equations to obtain the repeaters’ coordinates in relation to bases A, B, C and A, B, D (2) allow us to formulate the discrepancy between the repeater’s positions caused by the transit time dR value given by the following expression [11] [12] :
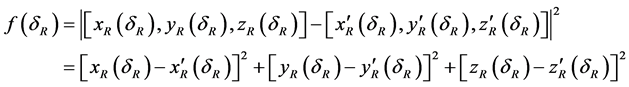 (2)
(2)
The closest value found for dR for every time signal interaction at the repeater corresponds to the minimum value obtained for f(dR) with varying values of dR. This can be found by a number of well known numerical calculation methods, such as by iterative procedures or by successive approximations, as it will be shown in the simulations later in this paper. The accuracy of dR determinations will be in the limit of the instrumental accuracies utilized for the coordinate’s determination. The same procedure may be repeated simultaneously, using measurements at bases A, C, and D, improving the accuracy by averaging the two independent estimates for dR.
The path delays for each distance AR, BR, CR and DR, caused by propagation in the medium, DpdAR, DpdBR, DpdCR, and DpdDR, are derived at the same time calculations are performed to determine dR, adopting the respective elevation angles the repeater is seen from each one of the four bases, which were determined during calculations. For the path delay derivation, an adequate propagation model must be adopted, depending on the frequency band used for the coded time signals transmissions. At higher SHF and EHF radio bands, for example, the corrections are due to propagation in the lower atmosphere [7] . The path delay corrections can be approximated using a plane parallel model for the atmosphere
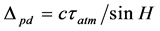 (3)
(3)
where c is the speed of light, tatm the atmosphere zenith delay, and H the object elevation angle with respect to the horizon. At low frequency bands, at VHF and UHF and to a certain extent at L-band, the path delay corrections are mostly caused by propagation in the upper atmosphere, ionosphere and plasmasphere [5] .
3. Applications
3.1. Synchronism of a Remote Clock
Every transmitted coded time signal will be also received at other targets, as the example P given in Figure 1. Assuming that the position coordinates of P is known, once the coordinates of the repeater R is determined, the segment PR becomes known in advance. Therefore the discrepancy between the local clock at P and the time received from the clock at the transmitter A can be written as:
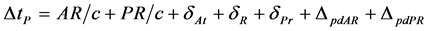 (4)
(4)
where the segments AR and PR are measured by ranging, dAt and dPr are experimentally determined and known, and dR, DpdAR and DpdPR are determined by the method described here. The clock time correction at P, needed for synchronization will be Dtp – Dp, where Dp is the theoretical correct time expected for the clock at position P.
This application can be extended to synchronize clocks at various actuators simultaneously. These may be telecommunications re-transmitters which essential requirement is to operate synchronized to prevent cross-talks and mutual message garbling interferences. The precision of clock corrections can be close to the accuracy attained in the synchronization of reference bases A, B, C and D.
3.2. Repeater’s Position and Navigation
The values of dR and of DpdAR, DpdBR, DpdCR, and DpdDR found with this method are introduced in the system of equations [13] to obtain the repeater’s actual coordinates, for each coded time interaction. The navigation of the platform is straightforward. It is immediately derived from successive repeater’s positions determinations.
3.3. Remote Target Location
The remote target coordinates corrected for time delays at the repeater and due to propagation are readily calculated using the known algorithm [13] . The distance from the repeater R, PR, can be determined by a single time interaction, provided that (a) the clock at P is sufficiently well synchronized with respect to the reference bases A, B, C and D and (b) the temporal change of the coded time signal at the repeater dR and the propagation path delays are determined accordingly to the method demonstrated here. The coordinates of P can be determined univocally by obtaining four different measurements of its distance to the repeater R, at four distinct instants, provided that the respective repeaters’ positions are not part of a straight line. The calculations are applied here referring to one set of three reference bases, including A where the time code transmitter is located (i.e., A, B, C or A, B, D or A, C, D). We obtain the equations for four spheres which intersections give the coordinates of the target P. The fourth position might not be needed when the surface of the Earth is taken as the fourth sphere of reference.
4. Simulations
4.1. The Algorithm Demonstration and the System Performance
A new software has been specifically developed [14] to demonstrate the algorithm [13] for the geo-referencing applications and to perform simulations using the minimization function (2) for multiple three bases sets shown here. Details on the software description, using MATLAB, version R2010a [15] has been given elsewhere [12] [14] .
An updated practical application is shown in Figure 2, exhibiting a realistic representation of the selected ground-based reference base locations at four cities in São Paulo State, Brazil: São Paulo, Itú, Campinas and Bragança Paulista, with known geodesic coordinates. The city of Atibaia, in the same State, has been selected to simulate the target P. It has been conceived a transponder carried by an aircraft flying at an altitude of about 6 km above the city of Jundiaí.
The minimization of the repeater position discrepancy process, i.e., the iterative minimization of function (2) performed by the new software, has been done adopting an initial value for transit time and setting an upper and lower range for its variation. The correct time delay at the repeater is found at the end of the minimization process. To proceed with simulations the bases and target position coordinates were converted into the ECEF (Earth-Centered, Earth-Fixed) coordinates system, using datum WGS84 [16] -[18] for the reference ellipsoid. The location of a point in this system can be done in coordinates (x, y, z). The origin of axes (0, 0, 0) is the cen-
Figure 2. Realistic simulation scenario with ground-based reference bases at four cities in São Paulo state, Brazil with known geodesic coordinates. Another city in the same state has been selected to represent the target. It has been conceived that a transponder is carried by an aircraft flying at an altitude of about 6 km at above the city of Jundiaí, being seen by all four bases and the target.
ter of the Earth, the axis Z points to the North, axis X points to Greenwich meridian (where latitude = 0 degrees). The altitude is taken as the distance perpendicular and above the surface of the ellipsoid [16] -[18] . The iterative process has been repeated for three more positions of the transponder, to allow the target position determination.
To demonstrate initially the functionality of the algorithm and of the software application we have assumed that the exact coordinates for the bases are previously known, as well as for the target, and for the respective assumed positions for the aircraft carrying the repeater. The time delays due to the signal propagation in the medium were introduced in the following step, assuming a propagation model. The calculations of delays at the repeater, of the repeater’s position, and propagation path delays relative to each base were obtained by simultaneous iterations since these variables are interdependent. To obtain a new position for the repeater the path delay lengths were then added, after the model expressed by equation (3), for the approximate calculated elevation angle the repeater as observed from the reference bases and target at every iteration. The process has been repeated until obtaining the convergence of values. The results obtained with the simulation software assuming known positions and synchronized clocks, demonstrate the full algorithm functionality, exhibiting discrepancies in the repeater’s position and in the target position less than 0.001 mm . This value, of course, is just for the algorithm test demonstration. In practice the discrepancies are larger, depending primarily on reference and target clocks synchronization uncertainties, as it will be shown in the following section.
The results obtained from the above simulations demonstrate the algorithm applicability. For previously assumed known base’s and target coordinates, the clocks of the system perfectly synchronized, the ideal error at the receiving location is practically zero.
4.2. The Effect of Gaussian Distributed Uncertainties
The major source of uncertainties in the determinations is related to errors between clocks and/or in delays miscalculations. The two sources can be added together within a certain approximation. To perform simulations of the clocks (and/or delays) uncertainties on the determinations of dR and of path delays we have introduced here a realistic Gaussian distribution of errors generating random values for clock/delay uncertainties at the four reference bases and at the target, within a plausible time interval.
We adopted here clock accuracies consistent with realistic compact simple and compact rubidium clocks available in the marked, exhibiting short term stability (typically one month) of the order of 10−11 s, and long term stability (one year) of few nanoseconds (see for example Refs. [19] -[21] ). To calculate the system errors on the remote clock synchronism, on the repeater’s position and on the target location caused by propagation, we adopted a Gaussian distribution of uncertainties set in the r.m.s. range of ±0.5 ns, which is attainable when the bases and target clocks are periodically synchronized, as for example every month.
The resulting system error distributions are shown in Figure 3. The plots correspond to 1000 randomly generated delay values within the Gaussian distribution, for four repeater’s positions. For each delay it was determined the scattering (or errors) in remote clock synchronization accuracy, in the repeater’s position, and the the target position. It can be seen that the typical errors on remote clock synchronization are comparable to the transmitted setting uncertainties. For reference bases and target clock uncertainties of ±0.5 ns, r.m.s, the errors become smaller than few tenths of a ns; less than 0.4 meters in the repeater’s position, and less than few meters for the target location.
5. Concluding Remarks
We have presented the functionality, tested the algorithm and simulated the performance of a new independent and GPS-free space’s geo-referencing system. This is a powerful space’s geo-referencing system and method to be used for remote clock synchronization, the navigation of various types of platforms carrying at repeater, and remote target positioning and with very high accuracy.
The system concept may roughly be seen as an “inverted GPS geometry”, using at least four reference bases at known locations on the ground and a remote transponder in space. With this configuration, it is possible to eliminate the most critical errors caused by time delays of signals transiting by the repeater, and others caused by the signal propagation in the medium. Special software has been developed to demonstrate the new system’s functionality and performance. It has demonstrated the accuracy of the analytical algorithm solutions for practical application.
Although the new system is not intended to be regarded as a replacement of the well settled and commercially
Figure 3. Example of errors caused by clock synchronism uncertainties at reference bases and at target, which may include the path delays errors. The scatter plots assume a Gaussian distribution of errors in a range of ±0.5 ns, r.m.s, for 1000 randomly generated delay values. In (a) the error in a remote clock synchronization; (b) the error in the repeater’s position; and (c) the error on the target location.
successful space geo-referencing based on GNSS, specially GPS (and equivalent systems such as GLONASS, COMPASS, Galileo), it may bring profound impact on a number of commercial and strategic applications, for its competitive simpler implementation; for its independence from complex and expensive permanent geo-ref- erence’s satellite orbital ephemeris updating needed because of irregular earth rotation, such as the regular support from geodetic very long baseline interferometry (VLBI) monitoring. It can also be used as a back-up replacement of existing systems on critical disturbance situations (environmental or operational). It is able to be used independently from any other space-based positioning systems for certain strategic uses such as aircraft and balloon navigation, missile and smart bombs tracking.
In sum, the new system provides means, with certain advantages over existing space based systems, to synchronize accurately remote clock at locations where the coordinates are known. The accuracies might be better than those obtained by the new generation of GPS timing receivers (of tens of ns) [22] . This is a known requirement for remote actuators which must operate in synchronism, such as in a number of telecommunication repeaters’ networks in extended areas, assuring their regular operation without depending on GPS-dependent clocks. The system can be readily used to obtain the transponder platform’s actual coordinates, for each coded time interaction. Thus the platform navigation is readily derived from successive repeater’s positions determinations. Immediate foreseen applications are for the navigation of aircrafts, balloons and drones. For a repeater placed in an artificial satellite, its position can be determined for every-time mark interaction with the same errors or uncertainties found for repeaters at lower altitudes, shown here. A study is currently being developed on a new method to determine satellite orbital parameters using the new system.
This system can also be used to determine the coordinates of an unknown remote target. This requires measurements of its distance to the repeater at four distinct instants, provided that the respective repeater’s positions are not part of a straight line. Or alternatively, at the same instant, if four repeaters are simultaneously available on the target’s field of view. This possibility might be particularly relevant as a back-up to other space-based GNSS geo-referencing or for independent applications of strategic interest.
Acknowledgements
This research was partially supported by Brazil agencies CNPq, CAPES and FAPESP (grant No. 2012/21023-6).
References
- Kaufmann, P. (1997) Sistema e processo de posicionamento geográfico e navegação. Patent of Invention No. PI- 9101270-8.
- Marini, J.W. (1974) Correction of Satellite Tracking Data for an Arbitrary Tropospheric Profile. Radio Science, 7, 223-231. http://dx.doi.org/10.1029/RS007i002p00223
- Anderson, A. J. (1979) Path Length Variations Due to Changes in Tropospheric Refraction. In: Tengstrom, E., Teleki, G., Ohlsson, I. and Reidel, D., Eds., Proceedings of IAU Symposium nr. 89—Refractional Influences in Astrometry and Geodesy, Dordrecht, 157-162.
- Klobuchar, J.A. (1986) Design and Characteristics of the GPS Ionospheric Time Delay Algorithm for Single Frequency Users, in PLANS’86. Position Location and Navigation Symposium, Las Vegas, 4-7 November 1986, 280-286.
- Hunt, S.M., Close, S., Coster, A.J., Stevens, E., Schuett, L.M. and Vardaro, A. (2000) Equatorial Atmospheric and Ionospheric Modeling at Kwajalein Missile Range. Lincoln Laboratory Journal, 12, 45-64.
- Radovanovic, T.S. (2002) Adjustment of Satellite-Based Ranging Observations and Deformation Monitoring. Ph.D., Dissertation, University of Calgary, Calgary.
- Honma, M., Tamura, Y. and Reid, M.J. (2008) Tropospheric Delay Calibrations for VERA. Publications of the Astronomical Society of Japan, 60, 951-960. http://dx.doi.org/10.1093/pasj/60.5.951
- Skolnick, M.I. (1962) Introduction to Radar Systems. McGraw-Hill, New York.
- Larson, K.M. (2007) An Assessment of Relativistic Effects for Low Earth Orbiters: The GRACE Satellites. Metrologia, 44, 484-490. http://dx.doi.org/10.1088/0026-1394/44/6/007
- Wislez, J.-M. (1996) Forward Scattering of Radio Waves in Meteor Trails. Proceedings of the International Meteor Conference, Brandenburg, 1995, 99-117.
- Kaufmann, P. and Levit Kaufmann, P. (2012) Process and System to Determine Temporal Changes in Retransmission and Propagation of Signals Used to Measure Distances, Synchronize Actuators and Georeference Applications. Patent of Invention PI03003968-4, Filed in Brazil on 19 March 2012, International PCT, Application Filed on 17 April 2012.
- Kaufmann, P., Kaufmann, P.L., Pamboukian, S.V.D. and Vilhena de Moraes., R. (2012) Signal Transreceiver Transit Times and Propagation Delay Corrections for Rangiung and Geo-Referencing Applications. Mathematical Problems in Engineering, 2012, 1-15. http://dx.doi.org/10.1155/2012/595823
- Kaufmann, P.L., Vilhena de Moraes, R., Kuga, H.K., Beraldo, L.A., Motta Marins, C.N. and Kaufmann, P. (2006) Nonrecursive Algorithm for Remote Geolocation Using Ranging Measurements. Mathematical Problems in Engineering, 2006, 1-9. http://dx.doi.org/10.1155/MPE/2006/79389
- Pamboukian, S.V.D. (2012) Novo processo de georeferenciamento: determinação de posição de transponder remoto e aplicações no posicionamento de alvos e disseminação de tempos. Software Registered in Brazil, Protocol 02012- 0032225.
- Matlab, M. (2012) The Language of Technical Computing. http://www.mathworks.com/products/matlab/.
- Dana, P.H. (1995) Geodetic Datum Overview. http://www.colorado.edu/geography/gcraft/notes/datum/datum.html.
- NIMA (National Imagery and Mapping Agency) (1997) Third Edition of “Department of Defense World Geodetic System 1984: Its Definition and Relationships with Local Geodetic Systems”. NIMA TR8350.2, National Imagery and Mapping Agency, Bethesda. http://earth-info.nga.mil/GandG/publications/tr8350.2/wgs84fin.pdf
- EUROCONTROL (European Organization for the Safety of Air Navigation) and IfEN (Institute of Geodesy and Na- vigation) (1998) WGS 84 Implementation Manual-Version 2.4. Brussels-Belgium, Munich. http://www2.icao.int/en/pbn/ICAO%20Documentation/GNSS%20and%20WGS%2084/Eurocontrol%20WGS%2084.pdf
- Knappe, S., Gerginov, V., Schwindt, P.D.D., Shah, V., Robinson, H.G., Hollberg, L. and Kitching, J. (2005) Atomic Vapor Cells for Chip-Scale Atomic Clocks with Improved Long-Term Frequency Stability. Optics Letters, 30, 2351- 2353. http://dx.doi.org/10.1364/OL.30.002351
- Affolderbach, C., Breschi, E., Schori, C. and Mileti, G. (2006) Gas-Cell Atomic Clocks for Space: New Results and Alternative Schemes. In: Wilson, A., Ed., 6th International Conference on Space Optics, Proceedings of ESA/CNES ICSO, Noordwijk, 27-30 June 2006.
- (2008) Ultra Low Cost Rubidium (LCR-900). http://www.spectratime.com/documents/lcr_spec1.pdf
- Clark, T.A. and Hambly, R.H. (2006) Improving the Performance of Low Cost GPS Timing Receivers. Proceedings of 38th Annual PTTI Meeting, Reston, 7-9 December 2006, 37.




