Positioning
Vol.4 No.2(2013), Article ID:31485,7 pages DOI:10.4236/pos.2013.42013
Frequency Structures Vibration Indentified by an Adaptative Filterging Techiques Applied on GPS L1 Signal
![]()
1Department of Transportation Engineering, Polytechnic School, University of Sao Paulo, São Paulo/SP, Brazil; 2Department of Transportation Engineering, São Carlos Engineering School, USP, São Carlos/SP, Brazil.
Email: larocca.ana@usp.br
Copyright © 2013 Ana Paula C. Larocca et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 14th, 2012; revised December 17th, 2012; accepted January 2nd, 2013
Keywords: L1 GPS Frequency Processing; Filtering Techniques; Millimetric Displacements; Single Frequency Receiver
ABSTRACT
This paper is part of a research under enhancement since 2001, in which the main objective is to measure small dynamic displacements by analysis of L1 GPS carrier frequency with 1575.42 MHz—wavelength 19.05 cm, under an adaptive method for collecting data and filtering techniques. This method, named Phase Residual Method (PRM) is based on the frequency domain analysis of the phase residuals resulted from the L1 double difference static data processing of two satellites in almost orthogonal elevation angle. In this work it is proposed to obtain the phase residuals directly from the raw phase observable collected in a short baseline during a limited time span, in lieu of obtaining the residual data file from regular GPS processing programs. In order to improve the ability to detect millimetric displacements, two filtering techniques are introduced. The first one is the autocorrelation that reduces the phase noise with random time behavior. The other one is the running mean to separate low frequency from the high frequency phase sources. Two trials are presented to verify the proposed method and filtering techniques applied. One simulates a 2.5 millimeter vertical GPS antenna displacement and the second using the data collected during a bridge dynamic load test. The results show a good consistency to detect millimetric oscillations from L1 frequency and filtering techniques.
1. Introduction
The approach of this paper is applied an update on the method based on interferometer idea for analyzing the Global Positioning Systems signals applying adaptive filtering techniques on the phase residuals computed though the double difference adjusted by the 3rd order polynomial. The method is based on the frequency domain analysis of the phase residuals resulted from the L1 double difference static data processing of only two satellites. This research improves the ability to characterize the dynamic behavior of large structures though the detection of millimeter-level data of structural amplitude oscillation response and its frequency value. The research aims to support Civil Engineering Community by collaborating on monitoring vibrations of spans and towers of medium and large bridges; determination of amplitude oscillations value and low-frequency modal values. The paper presents two trials to verify the proposed methodology for using GPS as a tool for monitoring large structures.
2. Enhancement of the Phase Residual Method (PRM)
The PRM [1-5] has been extensively applied on signal GPS filtering techniques for monitoring healthy structure. It is based on the analysis of the L1 double difference phase residuals (DDPR) of regular static observation over a short baseline and short time span. Most scenarios of displacement monitoring include a reference point in the neighborhood of a few hundredths meters, allowing the use of single frequency receivers. In most of cases, the vibration modes frequencies of the structures are excited in short time span under moving loads [6].
The DDPR is composed by atmosphere scintillation, satellite and receiver electronics noise, multipath, antennas phase center pattern, satellites orbital dynamics and any antenna movement ranging from millimeters to some centimeters. Fortunately, in this particular case, the double differenced time variations of each one of these effects are quite distinguishable, presenting a different frequency spectrum.
The electronics receiver and the atmosphere present a rapid random behavior as a function of the equivalent phase detector noise bandwidth; multipath in most scenarios is a slow time varying function; antennas phase center pattern and satellites dynamics can be neglected for a short time observations and, finally, the antenna movement contribution will depend on inner vector product between the movement direction and the unit vector to the satellite direction. The large structures vibrations are mostly a periodic time function and converting the residual data to the frequency domain using the Fast Fourier Transform and the different disturbing sources can be separated [7].
The dynamic behavior of structure can be described by periodical vertical, lateral and torsional oscillations. To detect a vertical oscillation for example, a reference satellite must be close to the horizon and the measuring satellite close to zenith. Ten degrees of tolerance will not compromise the results because angular corrections can be done mathematically.
3. Direct Phase Residual Method (DPRM)
The first task for obtaining the phase residuals from the raw data is to verify the data quality looking for phase jumps and missing epochs. This can be done looking the data continuity of the chosen satellites. The loose of some sporadic epoch and any small phase jump that stays within the noise level will not compromise the results. In case of a large phase jump the data must be disregarded and a proper window must be selected, as no phase jump correction is performed.
The L1 double difference phase observable is given by [8]:
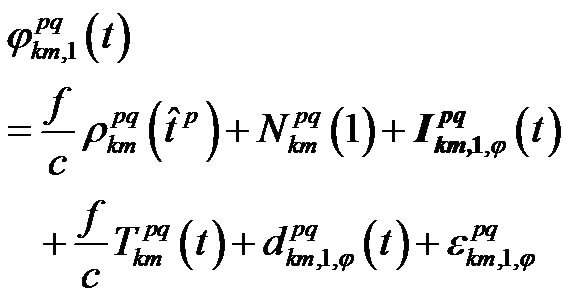 (1)
(1)
Multiplying both side of Equation (1) by L1 wavelength l1:
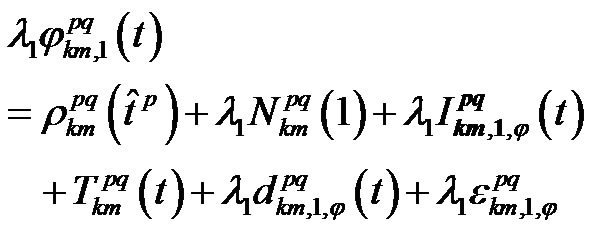 (2)
(2)
The first term of the right side of Equation (2) is the double difference of topocentric distances between p, q satellites and k, m receivers. The second term is the first epoch ambiguity and it has not time dependence. The time dependence of third and fourth terms, respectively related to the Ionosphere and Troposphere, can be separated in two behaviors. For a short baseline, one is almost a steady state and the second will depend on the non correlation among the Ionosphere and Troposphere scintillation with a random time behavior. The fifth term is any time dependent phase disturbance. Finally, the last term is related to receivers phase noise with a random behavior.
Rearranging the Equation (2) joining terms with similar time behavior:
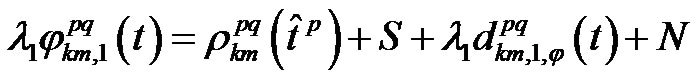 (3)
(3)
The term S comprises the stationeries components and N the random phase noise. The topocentric distance, as a function of time, between satellite p and receiver k is given by the equation:
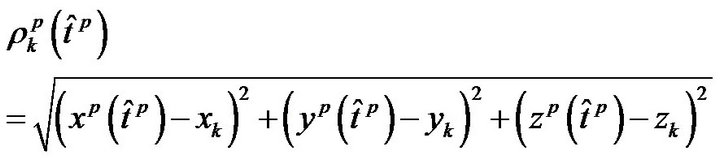 (4)
(4)
Same equations are for the other three distances. The double difference among topocentric distances in a short baseline as a function of time can be represented by a polynomial function:
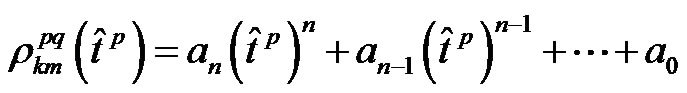 (5)
(5)
Substituting Equation (5) in (3):
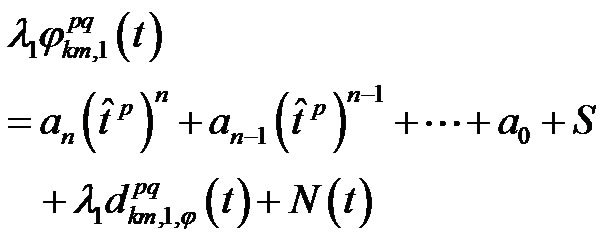 (6)
(6)
In the Equation (6) the coefficient a0 can be added to the steady sate components S and, the time behavior of observed double difference can be fitted to the polynomial function witch residuals contain the time dependent phase disturbances and random phase noise. Equation (7) gives the phase residuals, 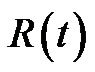 , in meters:
, in meters:
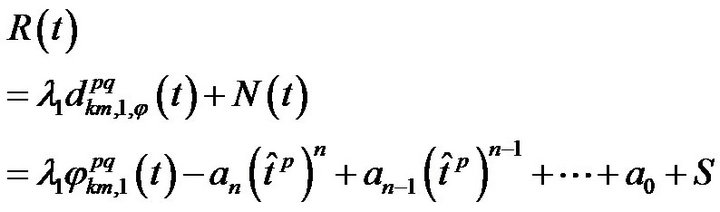 (7)
(7)
The polynomial fit can be done by parametric minimum least square method [4]. With this approximation it is possible to obtain directly the phase residual from the raw data, independent of a regular data processing program, to be analyzed in the frequency domain by the FFT.
Millimeter or unstable periodic oscillations caused by movements of a large structure are difficult to separate from the random noise, degrading the precision of the measurement. One way to improve the signal to noise ratio is the auto-correlation technique. Autocorrelation enhances periodic functions and lessen random values. In the autocorrelation a data of n samples is converted to a half time sample because the delay can only be shifted half the original sample. Equation (8) presents the applied autocorrelation function with the delay  ranging from 0 to
ranging from 0 to 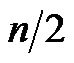 [9].
[9].
 (8)
(8)
4. Method Tests and Results
In order to test the proposed method a simulation trial was conducted under a controlled condition. The trial was carried out 24th of August, 2005 at the Department of Transportation of the Sao Carlos Engineering School (EESC) of the University of São Paulo (USP) using a pair of Leica GX1230 receivers equipped with Leica AX1202 geodetic antenna collecting 20 Hz data. To ensure a known phase periodic source on the data, a forced vertical sine-wave movement was applied to the rover antenna installed over an electro-mechanical oscillator (EMO) as shown in Figure 1.
The baseline is approximately 2 meters and an observing time session of 8 minutes was made. The oscillation amplitude span applied on the rover antenna was 2.5 millimeters and the frequency close to 1 Hz. The EMO frequency is dependent of voltage applied to a DC driver motor which is not stabilized, but can be considered constant during the trial.
The period of observation session was selected to ensure a high elevation satellite, which phase data would be directly affected by the antenna movement (G30 at 85 degrees of elevation). As phase reference satellite, any other low elevation satellite can be chosen because its phase data will almost not affected by the movement

Figure 1. The antennas at the EESC - USP Campus and the rover antenna is mounted over the EMO.
(G25 at 8 degrees of elevation)
The first step of the DPRM is to compute the raw phase double difference from the RINEX observation data. Careful is taken to time synchronization and avoid phase jumps. Figure 2 presents the double difference, in meters. In order to obtain the phase residuals, a 3rd degree polynomial was adjusted to period of 2048 epochs, of the Raw Phase Double Difference which is about 100 seconds of observation. This time is short enough to disregard higher order terms. The resulting residuals are shown in Figure 3. The amplitude of the random noise is in the order of 10 millimeters, masking the 2.5 millimeter imposed to the antenna. Figure 4 presents the residuals after applying auto-correlation filtering.
The relation between the periodic signal and the noise remarkable increased presenting a clear detection of the antenna oscillation. Autocorrelation enhances all other frequencies present in the residuals, mostly generates by the multipath.
One method to separate these low frequencies from the higher frequencies in the time domain is to subtract a running mean computed with number of samples larger than the number of epochs that define the period of the higher frequency. In this trial, period of the EMO takes about 20 epochs, so a 30 samples mean was chosen. Figure 5 shows the resulted difference. As the third step, the FFT was applied on values from the difference between autocorrelation and running mean for identifying the peak due to the frequency of EMO what was done with successful as shows the Figure 6.
To show how the filtering technique improves the detection of the higher frequencies oscillation, the FFT was computed directly on the residuals as shown in the Figure 7.
The spectrum below 0.2 Hz is generated by the low frequency phase sources, witch are not under analyses in this article. As this technique gave so promising results it was decided to apply on previous trial conducted on the 30th of October, 2003 at the Hawkshaw Cable-stayed Bridge, in New Brunswick, Canada [2-4,10]. Its deck is composed by one north span of 54.44 m; one south span of 29.44 m and the center span with 217.32 m of length. Two towers with 36 m of height support the deck by a harp-type arrangement with six steel cables. During this trial the rover antenna at the bridge was also installed on the same EMO device with 12 mm displacement, to provide a phase reference to all bridge vertical measurements.
The data analyzed and presented were collected with a pair of TRIMBLE 5700 receivers with one Trimble ZephyrTM Geodetic antenna (on reference station) and one Trimble StealthTM Ground Plane (as a rover antenna on the middle of the deck) under 10 Hz data rate. During the selected observation period, the highest satellite (G25)
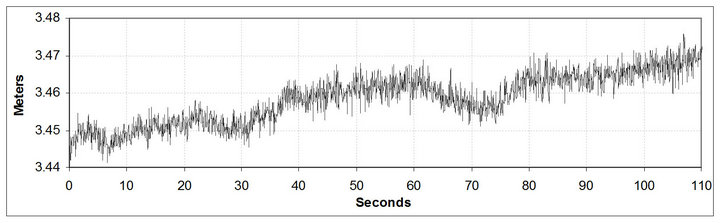
Figure 2. Raw Phase Double Difference (G30 signal at 85˚ of elevation and G25 signal at 08˚) in a 2 m baseline.
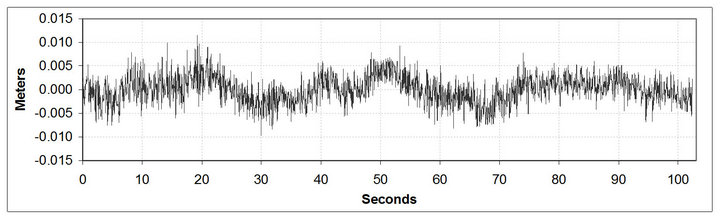
Figure 3. L1 Phase residuals obtained from a 3rd order polynomial.
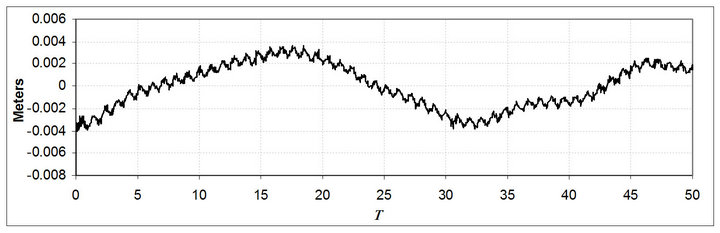
Figure 4. Autocorrelation of the phase residuals.
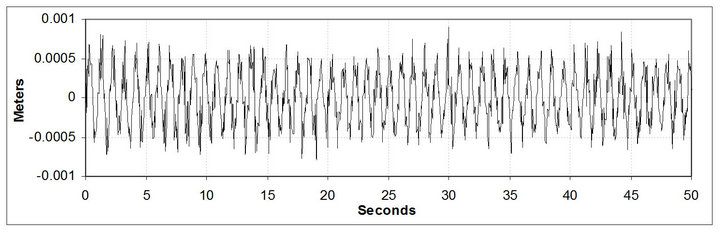
Figure 5. Difference values from autocorrelation and running mean.
was at 80˚ degrees of elevation and the lowest (G13) at 09˚ degrees of elevation, providing a good geometry to measure vertical displacements. The baseline is 284 meters and two observing time sub-session of 8 minutes were analyzed.
The computed raw phase Double Difference from the RINEX observation data is presented in Figure 8. After that it was computed the phase residuals from the Double Difference adjusted by the 3rd order polynomial fit as shown in Figure 9. Figure 10 presents the residuals after applying autocorrelation.
It is possible to observe well defined periodical during the initial 40 seconds. This is related due to design trucks that were crossing the deck and their position on it [1,10].
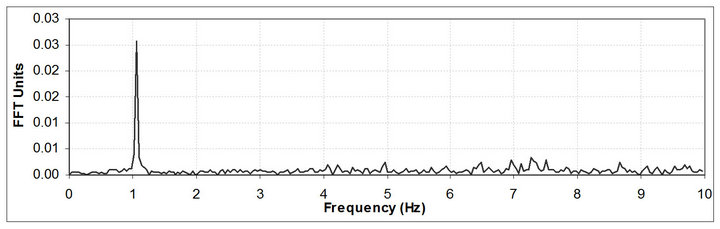
Figure 6. Frequency spectrum of the values from the difference between autocorrelation and running mean.
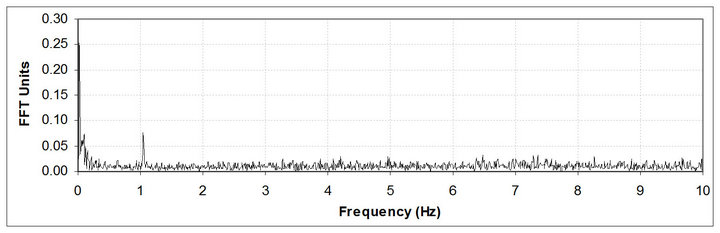
Figure 7. Frequency spectrum of the original phase residuals.
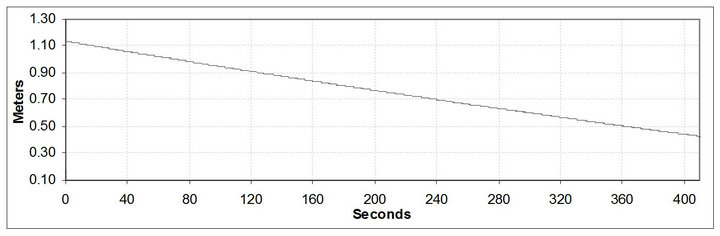
Figure 8. Raw Phase Double Difference (G25 signal at 80˚ of elevation and G13 at 09˚) in a 284 m baseline.
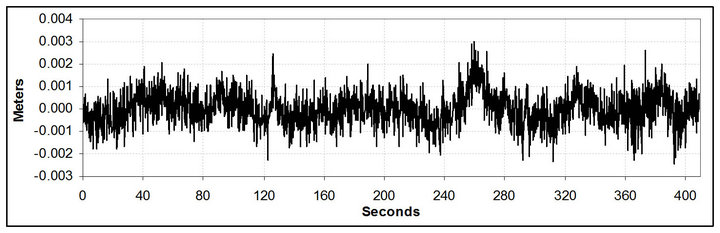
Figure 9. Hawkshaw Bridge L1 phase residuals obtained by the 3rd order polynomial.
After that it was computed the difference values between the autocorrelation values minus the running mean of 40 samples as shown for the first 50 seconds in Figure 11.
FFT was applied on values from the difference between autocorrelation and running mean for identify the peak due to the frequency expected caused by the moving load composed by four different trucks. The theoretical vertical frequency value expected, 0.57 Hz [11]. Figure 12 presents the spectrum obtained from the FFT where the moving load 0.57 Hz oscillation, the 1.0 Hz EMO is clearly and a 2.15 Hz oscillation with no well known source that is under study.
Figure 13 presents the spectrum of the phase residuals without applying autocorrelation and any other filtering

Figure 10. Hawkshaw Bridge auto-correlated residuals.

Figure 11. Autocorrelation of the phase residuals.
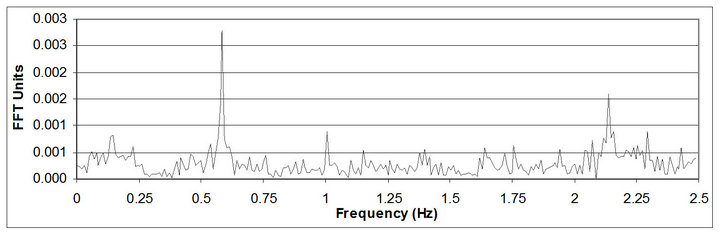
Figure 12. Hawkshaw Bridge frequency spectrum of the values from the difference between autocorrelation and running mean.
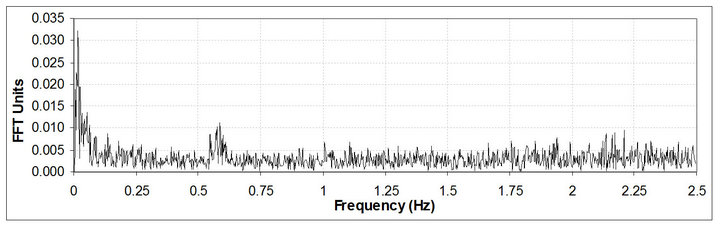
Figure 13. Hawkshaw Bridge frequency spectrum of the phase residual values.
technique. The oscillation caused by the moving load spreads around the nominal value. The EOM oscillation is masked by the noise and the unknown source oscillation is not clear.
5. Conclusion
Both, simulation and the bridge trials had presented consistent results with the proposed method. The proposed method to detect higher frequencies directly from raw phase data is very straightforward in monitoring large structures. Short baseline and short time session dispense the use of fancy position processing programs. The autocorrelation process is fundamental to signal demodulation of the GPS signal because is a function of a random binary code is similar to the pulse waveform and it is very handful to enhance the oscillations and the running mean is useful to clean up undesired lower frequentcies. The PRM and filtering techniques applied can be used as a robust quality assurance for monitoring structural dynamic oscillations.
6. Acknowledgements
The authors express their gratitude to Dr. Marcelo C. Santos and Dr. Richard B. Langley of the Department of Geodesy and Geomatics Engineering from the University of New Brunswick, Canada, for providing all the conditions to carry out the research and trials on Hawkshaw Cable-stayed Bridge. Also thanks to CNPq for the author’s productivity grants (PQ2).
REFERENCES
- A. P. C. Larocca and R. E. Schaal, “Millimeters in Motion Dynamic Response Precisely Measured,” GPS World, Vol. 16, No. 1, 2005, pp. 16-23.
- A. P. C. Larocca, R. E. Schaal and M. C. Santos, “Using GPS to Monitor Movement of a Cable-Stayed Bridge,” Professional Surveyor Magazine, Vol. 5, No. 3, 2005, pp 15-19.
- A. P. C. Larocca, R. E. Schaal and A. C. B. Barbosa, “A Low-Frequency Vibrations Detection with High-Rate Data and Filtering,” GPS World, Vol. 21, No. 4, 2010, pp. 28-35.
- A. P. C. Larocca, “Using High-Rate GPS Data to Monitor the Dynamic Behavior of a Cable-Stayed Bridge,” Proceedings of 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS ’04), Long Beach, 21-24 September 2004.
- A. P. C. Larocca, R. E. Schaal and G. N. Guimarães, “Use of a Single L1 GPS Receiver for Monitoring Structures: First Results of the Detection of Millimetric Dynamic Oscillations,” Journal of Surveying Engineering, Vol. 138, No. 2, 2012, pp. 92-95. doi:10.1061/(ASCE)SU.1943-5428.0000070
- T. Irvine, “The Tacoma Narrows Bridge Failure,” Revision A. Newsletter, 2001. http://www.vibrationdata.com/Newsletters/September2001_NL.pdf
- E. O. Brigham, “The Fast Fourier Transform and Its Applacations,” Prentice-Hall, Inc., New Jersey, 1974, pp. 1- 252.
- A. Leick, “GPS Satellite Surveying,” 3rd Edition, Wiley, New York, 2004. pp. 1-435.
- F. D. Patrick, “Measurement and Data Analysis for Engineering and Science,” McGraw-Hill, New York, 2005.
- A. P. C. Larocca, “Using High-Rate GPS Data to Monitor the Dynamic Behavior of a Cable-Stayed Bridge,” Proceedings of 17th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS ’04), Long Beach, 21-24 September 2004.
- G. Hirsh and H. Bachmann, “Vibration Problems in Structures and Suspension and Cable-Stayed Bridges,” In: Bulletin d’Information No. 209. Chapter 3.6, Comité EuroInternational du Béton (CEB), Lausanne, 1991, pp. 109- 144.

