Positioning
Vol.1 No.1(2010), Article ID:3158,7 pages DOI:10.4236/pos.2010.11001
Distribution of Electromagnetic Field Momentum in Dielectrics in Stipulation of Self-InducedTransparency
![]()
Department of Medical and Biological Physics, Samara State Medical University, Samara, Russia
Email: volobuev@samaramail.ru
Received December 29th, 2009; revised September 8th, 2010; accepted September 12th, 2010
Keywords: Electromagnetic Impulse, Self-Induced Transparency, Equations Maxwell-Bloch, Filling Number, Non-Linear SCHRÖDINGER Equation
ABSTRACT
The laws of formation of the impulse of electromagnetic radiation in dielectric environment for conditions self-induced transparency are considered. The insufficiency of the description of such impulse with the help of the equations Maxwell-Bloch is shown. The way of connection of an average number filling and energy of the impulse taking into account energy saturation of environment are offered. The calculation of an electrical component of the impulse is submitted.
1. Introduction
Distribution of electromagnetic field momentum in dielectrics is conditioned by the interaction of field’s content with atoms and molecules of substance. In [1] the forming of electric component of momentum in dielectrics at low intensity of electromagnetic field momentum is concerned. This research paper is devoted to the basic phenomenological laws, which characterize the forming of electric and magnetic components of high-intensity impulse.
The description of momentum distribution with the dissipation of power is an exceptionally complex problem. However, in the majority of practically important cases the loss of impulse power in the medium can be disregarded. From this point of view the most trivial is the description of momentum at self-induced transparency (SIT). The phenomenon of SIT can occur in the rarefied gas (n < 1018 atoms/cm3) for short laser impulses (t < 10-9 s) in the condition of momentum power sufficient for shift to the raised state of all atoms in the area of momentum influence [2]. In this case, the reversed dispersion of electromagnetic radiation is absent, the dissipation characteristics of system “impulse-medium” vanish and it turns into the conservative state. The electromagnetic momentum gains permanent, solitary state. The symmetry and stability of impulse can simplify its mathematical description.
Up to recent period the mathematical description of such electromagnetic solitary, on the basis of semi-classical system of Maxwell-Bloch equations [3], from our perspective, are in unsatisfactory condition. The Maxwell-Bloch equations were written in 1946, long before the laser creation and discovery of the SIT phenomenon in 1965.
The physical basis of these equations, except Maxwell’s equations are, firstly, the second law of Newton for the nuclear electron and secondly, proportionality of the average data N of atoms in the field of impulse influence to the volumetric density of electromagnetic wave power w, i.d. N ~ w. The value N provides with the measure of inversion in system of atom-radiators by raised atoms [2]. The procedure of electromagnetic momentum description, including wave equation, further frequently passes through the field exertion’s devision to the low envelope amplitude and the wave of filling. Such course is typical of processes, submitted to the Schrödinger’s nonlinear equations. However the description of envelope amplitude, described on the basis of the MaxwellBloch theory is based on the Sin-Gordon’s equation [3], which do not contains wave of filling in its solving. Such course is unlimited and internally contradicting. The reason of the limitation of the Maxwell-Bloch equation usage for the SIT description would be analyzed further.
We believe that the consideration of the SIT process should be done on the basis of consecutive procedure of the Schrödinger’s nonlinear equation. However, the prevalent Schrödinger's nonlinear equation with cube nonlinearity, which can produce the solitary wave with filling is inappropriate for the SIT description. The reason is that the solitary solving of Schrödinger’s nonlinear equation with cube nonlinearity is related to the momentum, in which the phase rate of wave of filling is less then the rate of the impulse itself [4]. For the SIT momentum the inversed correlation of rates is typical [5].
The aim of this research paper is to formulate the equation and its solution for the electric and magnetic consistent parts of impulse—the soliton in the case of self-induced transparency.
2. Coordination of the Electromagnetic Impulse with the Substance
Firstly, consider the one-dimensional task the electric part of electromagnetic field momentum with the dielectric substance, which posses a certain numerical concentration n of centrosymmetrical atoms-oscillators. For the certainty of the analysis we suggest the atom to be oneelectronic. It is also agreed, that no micro current or free charge are present in the medium. The peculiarities of interaction between magnetic aspect of momentum and the atoms will be considered later.
We accept that there takes place the interaction of quantum of electromagnetic radiation with nuclear electrons, thus quantum is absorbed by the electrons. By gaining the energy of quantum the electrons shift to the advanced power levels. Further, by means of resonate shift of electrons back, appears the quantum radiation forward. The considered medium lacks non-radiating shift of electrons, i.d. the power of quantum is not transfered to the atom.
Thus, the absorption of electromagnetic radiation in the case of its power dissipation in the substance, owing to SIT, is disregarded. There appears the atomic sypraradiation of quantum. Thus, the forefront of momentum passes the power on to the atomic electrons of the medium, forming its back front.
The probabilities of quantum’s absorption and radiation by the electrons in the unity of time, with a large quantity of quantum in the impulse, according to Einstein, can be referred to as the approximately identical [6]. For the separate interaction of the with the electron this very probability is the same and is proportional to the cube of the fine-structure constan t~(1/137)3 [7]. Consider a random quantity—the number of interactions of quantum with atomic electrons in the momentum. In accordance with the Poisson law of distribution, the probability of that will not be swallowed up any quantum atomic’s electrons (will not take place any interaction), at rather low probability of separate interaction, is equal an exponent from the mathematical expectation of a random variable—an average quantity of interactions l of quantums and electrons in impulse, taken with the minus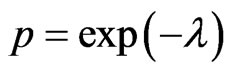 . Therefore, as it will be explained further, it is possible that the intensity of non-absorbed power of impulse by the atomic electrons of the medium in it forefront is determined by the exponential Bouguer law [3] (in German tradition—Beer law)
. Therefore, as it will be explained further, it is possible that the intensity of non-absorbed power of impulse by the atomic electrons of the medium in it forefront is determined by the exponential Bouguer law [3] (in German tradition—Beer law)
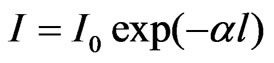 (1)
(1)
where a—index of electromagnetic wave and substance interaction, l—length of interaction layer, I0—intensity of incident wave. Thus, the intensity of atomic electron’s power recoil into impulse on its back front could be described with the help of the Bouguer law with the negative index of absorption [8].
The index of interaction is![]() , where a—effective section of atom-oscillator interaction with the wave. Hence,
, where a—effective section of atom-oscillator interaction with the wave. Hence,
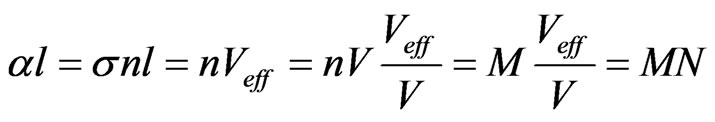 (2)
(2)
where Veff—the effective volume of interaction. In defying (2) the right part of the formula is multiplied and divided by the geometric volume V, in which there is M of particles interacting with the radiation. The ratio
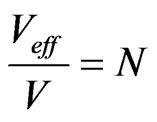 . The ratio of effective volume of interaction to the geometric volume characterizes the medium possibility of electromagnetic radiation’s interaction with the atom. Hence, by exponential function in the Bouguer law (1) the mathematical expectation of random variable is supposed, which subdues to the Poisson law distribution—average variable of atoms interacting with the electromagnetic radiation in the area of impulse influence
. The ratio of effective volume of interaction to the geometric volume characterizes the medium possibility of electromagnetic radiation’s interaction with the atom. Hence, by exponential function in the Bouguer law (1) the mathematical expectation of random variable is supposed, which subdues to the Poisson law distribution—average variable of atoms interacting with the electromagnetic radiation in the area of impulse influence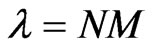 .
.
Taking into account that the wave intensity is 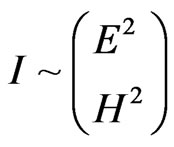 we shall have
we shall have
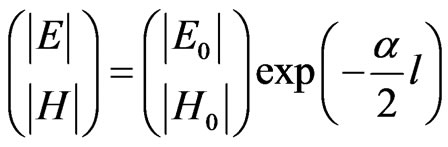 (3)
(3)
where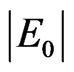 ,
,![]() —the amplitudes of electric and magnetic fields’ strength of the impulse on longitudinal coordinate X = 0.
—the amplitudes of electric and magnetic fields’ strength of the impulse on longitudinal coordinate X = 0.
In the formula (3) and further the upper variables in parentheses are referred to electric field, and lower to the magnetic field of impulse.
By the ratio (2) it is possible to find
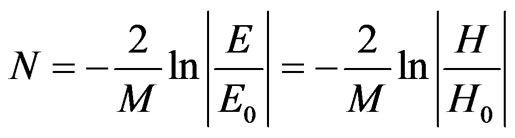 (4)
(4)
The formula (4) demands some further consideration. If E < E0, that reflects the process of wave absorption by atomic electrons N > 0 and classical consideration of electromagnetic wave interaction with the atom is quite admissible. The case when E > E0 reflects the process of wave over-radiation. Thus, N < 0 and variable N can not be considered as the probability of electromagnetic wave interaction with the atom. In this case we speak about the quantum-mechanical character of the process of interaction between the quantum and the bi-level power system of the atom, provided that the power transition’s radiation is reversed. Variable N in this case possess the notion of united average of filling by atom (–1 < N < 1). Due to the use of the average of filling to raise the atom and bend of its magnetic moment in the magnetic field of the impulse, the existence of bi-level quantum system by magnetic quantum numbers. Thus, the variable N provides with the measure of inversion of the system of atom-radiators by the raised atoms [2] as well as the measure of inversion of the magnetic moment of the atom’s system by magnetic quantum numbers. If N = –1 all the atoms occur in the basic condition [3].
We consider the dependence of the average of filling on the time N(t). If to accept the proportion of polarization of separate bi-level atom to the intensity of electric field in the impulse, then, in accordance with the Maxwell-Bloch equations, the average by atoms of considered volume, the filling number is proportional to the volumetric density of electromagnetic wave power N~w [3]. However such a monotonous dependence between these variables can not remain on the whole extent of the impulse. Firstly, by the high volumetric density of impulse power w, typical of SIT, when the central part of impulse power is higher than any variable w, there exists energetic saturation of the medium. The average filling number thus N = 1, all the atoms are raised, Figure 1 (curve 1—the dependence w of time, thicker curve 2 —the considered dependence N of time). The violation of proportion N~w in the central part of impulse is the basic drawback of frequently used system of Maxwell-Bloch equations for the SIT description.
Secondly, the period of variable N relaxation is not less than 1 ns [2] that is why the dependence N(t) can not repeat high-frequently oscillations on both frontsof the impulse. The dependence N~w could characterize the proportion of average filling number and envelope w
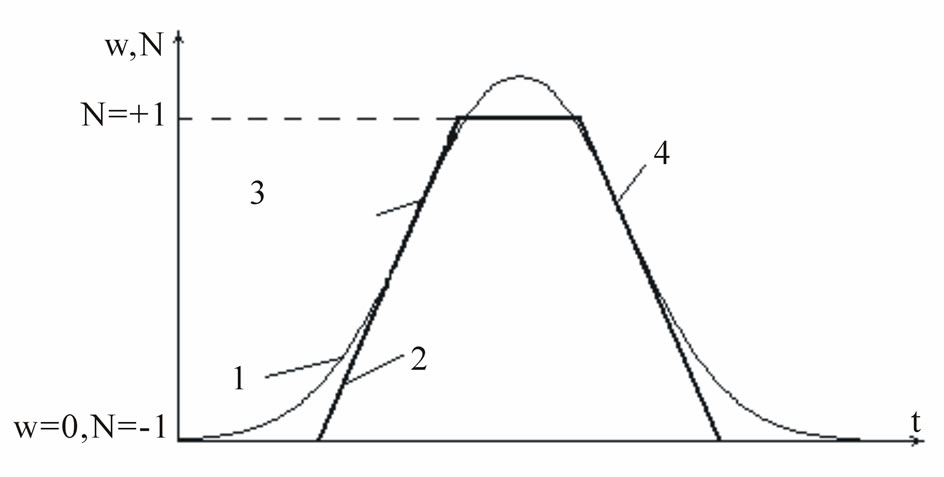
Figure 1. Dependence of volumetric density of energy of electromagnetic radiation impulse w (curve 1) and average on atoms of number of filling N (curve 2) from time; 3 and 4 —points of an excess of function w(t).
(curve 1) in the impulse. However, in two points of the fold (3 and 4 in Figure 1) on the sites of increase and decrease if the envelope w the variable  hence, also
hence, also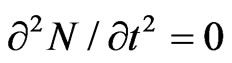 . Besides, the dependence N(t) has the symmetrical character as at the SIT impulse becomes the conservative system (there is no reverse dispersion and dissipation of power) [2]. Therefore, it could be thoroughly concerned that on the whole extent of impulse, except the points of curve’s N(t) fold, the condition remains
. Besides, the dependence N(t) has the symmetrical character as at the SIT impulse becomes the conservative system (there is no reverse dispersion and dissipation of power) [2]. Therefore, it could be thoroughly concerned that on the whole extent of impulse, except the points of curve’s N(t) fold, the condition remains
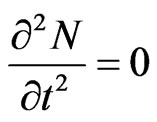 (5)
(5)
while the dependence N(t) has the character as shown on the Figure 1, curve 2. It could be also highlighted the high generality of formula (5), which is possible for any piecewise linear function N(t). Thus, the points of function break are excluded, as the derivates undergo the break.
3. Non-Linear Schrödinger Equation
One-dimensional wave equation for electric and magnetic aspects of electromagnetic field for the considered problem is [2].
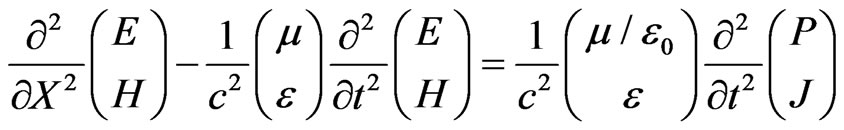 (6)
(6)
where ,
,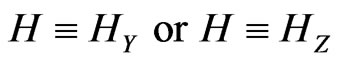 , X and t—accordingly the coordinate alongside of which the impulse and the time are distributed, P—polarization of substance, J—its magnetization,
, X and t—accordingly the coordinate alongside of which the impulse and the time are distributed, P—polarization of substance, J—its magnetization,  and
and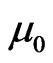 —electrical and magnetic constant, e—relative static permittivity of substance, m—relative magnetic permittivity,
—electrical and magnetic constant, e—relative static permittivity of substance, m—relative magnetic permittivity,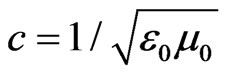 —speed of light in vacuum.
—speed of light in vacuum.
We introduce the transformation of electric field intensity be formula
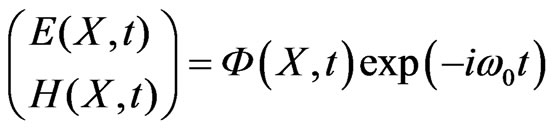 (7)
(7)
The function Ф(X, t) is less rapidly changing one in time then E(X, t) or H(X, t), w0—aspect of cyclic frequency of high-frequent oscillations of the field.
By substituting (7) and (6) we get (8).
We estimate the relative variable of first and second items in the parenthesis of the left side (8). For this purpose we would introduce the scales of variables time t and Ф
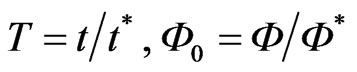
where the asterisk designates dimensionless parameters. For the time scale the duration (period) of impulse T should be logically chosen. The scale Ф0 is chosen from a condition that dimensionless second derivative 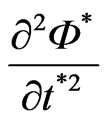
and the dimensionless function Ф* are in the same order. Hence, the first item in round brackets (8) is
 , and the last one
, and the last one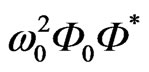 . Instead of impulse T period we introduce cyclic frequency of impulse
. Instead of impulse T period we introduce cyclic frequency of impulse
 . By comparing these items, it is realized, that
. By comparing these items, it is realized, that
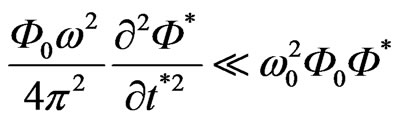 as the cyclic frequency of impulse is far less than infrequences of field’s oscillations, especially when
as the cyclic frequency of impulse is far less than infrequences of field’s oscillations, especially when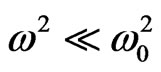 . Similarly, it can be presented that the second item in the round brackets (8) is far more that the first one.
. Similarly, it can be presented that the second item in the round brackets (8) is far more that the first one.
Hence, by disregarding the small item in (8), we observe (9).
By accepting vector of polarization P or magnetizing J to be directly proportional, accordingly, to the electric and magnetic fields strength, we could derive the wave equation from (6), which is possible to any form of the wave. However, there exists a physical mechanism, which restricts the wave form. This mechanism is connected with the way of over-radiating of electromagnetic impulse with the atomic electrons. This process is precisely considered further.
We consider the strength of electric and magnetic fields of impulse as
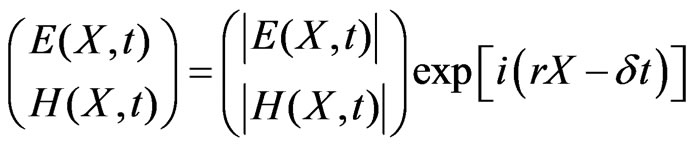 (10)
(10)
where r and d are constants, |E(X, t)| and |H(X, t)| are the modules of functions E(X, t) and H(X, t).
Formulas (4) and (5) reflect the offered physical model of electric and magnetic field of impulse interaction with atoms in SIT.
Hence, taking into account (4) and (5) there is
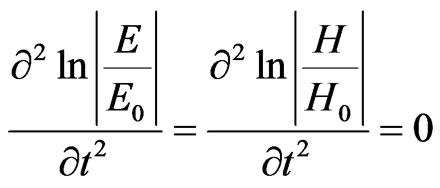 (11)
(11)
By transforming (11) we have
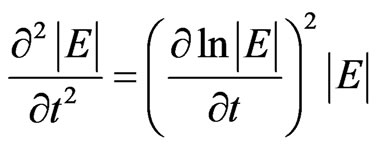 (12)
(12)
The similar ratio can be also referred to the function |H|. These ratios should not be regarded as the equations to define the module of electric and magnetic aspect of impulse. It is the approximate expression of the second derivative 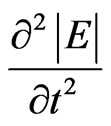 or
or 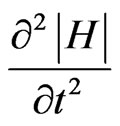 for the considered physical model and reflects several non-linear effects of interaction between electromagnetic radiation and substance. The approximate ratio (12) defines the connection of medium polarization P with the strength of impulse electric field (similarly to the magnetization J with the magnetic field strength), that would be considered further. The electromagnetic field impulse strengths should be estimated from the Equation (6) taking into account the ratio (12).
for the considered physical model and reflects several non-linear effects of interaction between electromagnetic radiation and substance. The approximate ratio (12) defines the connection of medium polarization P with the strength of impulse electric field (similarly to the magnetization J with the magnetic field strength), that would be considered further. The electromagnetic field impulse strengths should be estimated from the Equation (6) taking into account the ratio (12).
In accordance with (10),
 , hence, from (12) we estimate equation for the electromagnetic field impulse
, hence, from (12) we estimate equation for the electromagnetic field impulse
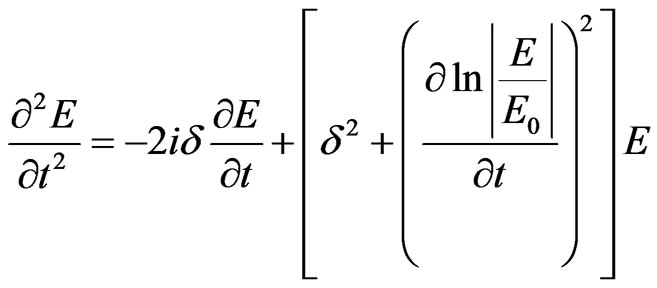 (13)
(13)
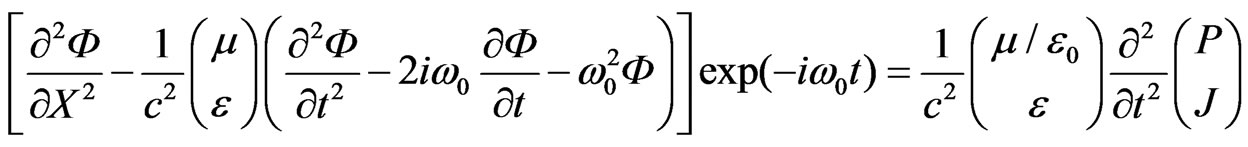 (8)
(8)
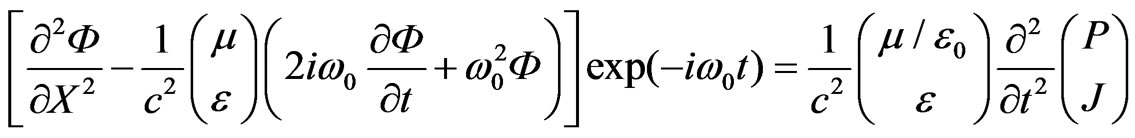 (9)
(9)
The same ratio exists for the magnetic field also. Passing over to (13) to the function Ф(X,t) by formula (7) and by concerning , where c–relative dielectric permittivity of substance, we have (14).
, where c–relative dielectric permittivity of substance, we have (14).
For the variable 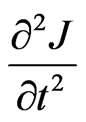 by using
by using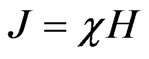 , where c—relative magnetic permittivity of substance, we get the ratio, similar to (14), except that the right part lacks e0.
, where c—relative magnetic permittivity of substance, we get the ratio, similar to (14), except that the right part lacks e0.
The variables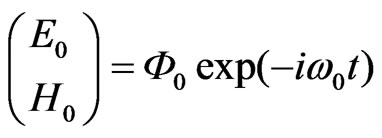 . By comparing (7) and (10) we state
. By comparing (7) and (10) we state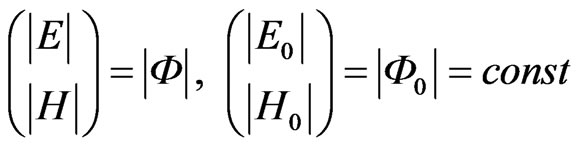 .
.
By substituting (14) into (9).
In the Equation (15) the variable c is meaningful to dielectric permittivity for electric and magnetic permittivity for the magnetic aspects of electromagnetic field.
The non-linear Schrödinger equation with complicated type of linearity is received. We introduce the signs:
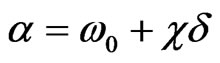 ,
,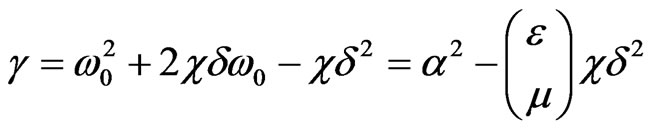 ,
,
where 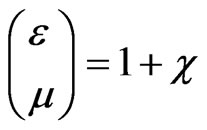 –relative permittivities of the substance. Hence, the Equation (15) will be
–relative permittivities of the substance. Hence, the Equation (15) will be
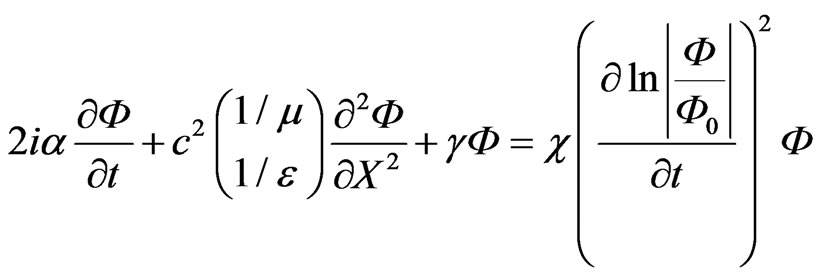 (15)
(15)
We shall find the solution to the non-linear Schrödinger Equation (16) as in [9]
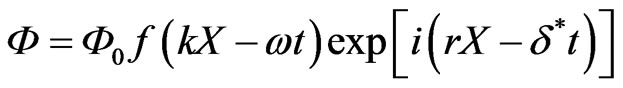 (17)
(17)
where the type of the function  is still unknown. The variables k, w and d*—constants. By marking
is still unknown. The variables k, w and d*—constants. By marking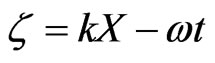 , and substituting (17) in (16) and concerning
, and substituting (17) in (16) and concerning 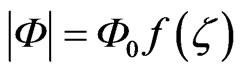 we get (18).
we get (18).
If to permit that 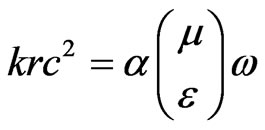 as there should not be any imaginary items in (18), this equation is transformed to (19).
as there should not be any imaginary items in (18), this equation is transformed to (19).
We consider the solution of the Equation (19) by
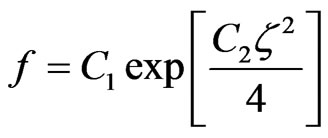 (20)
(20)
where C1 and C2—constants. By substituting (20) into (19) we get that the constant C1 could be the arbitrary variable, .
.
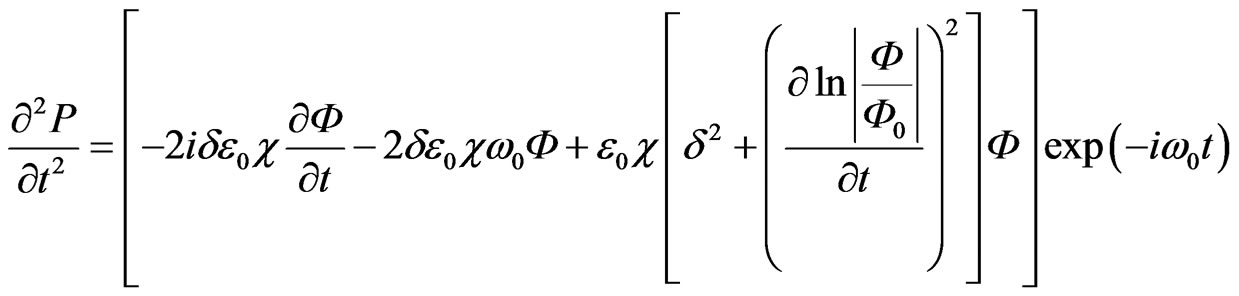 (14)
(14)
 (15)
(15)
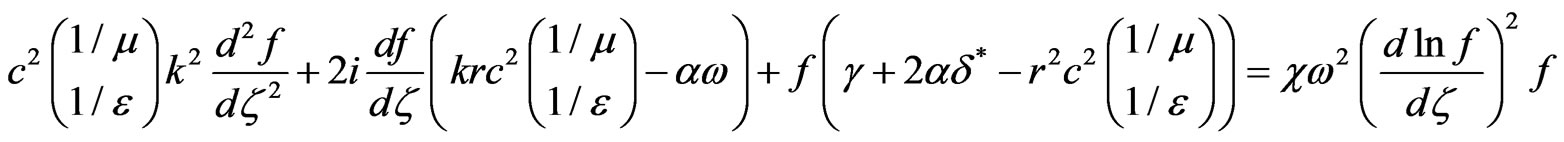 (18)
(18)
The constant C2 could not depend upon the parameters of equation. It is accepted that C2 = –1. Then the frequency and the wave number in (17), accordingly, are
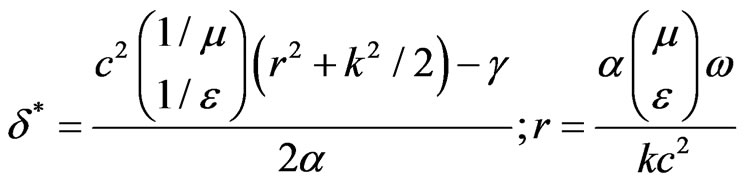 (21)
(21)
The formulas (21) associate the frequency and the wave number of oscillations of function Ф(X,t) with the parameters of substance and electromagnetic field impulse.
The simplest ratios between the parameters are gained, when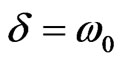 . In this case
. In this case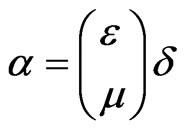 ,
,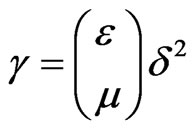 . From the equations in (21), and concerning
. From the equations in (21), and concerning 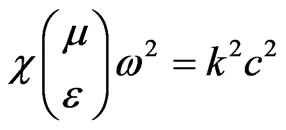 there is
there is
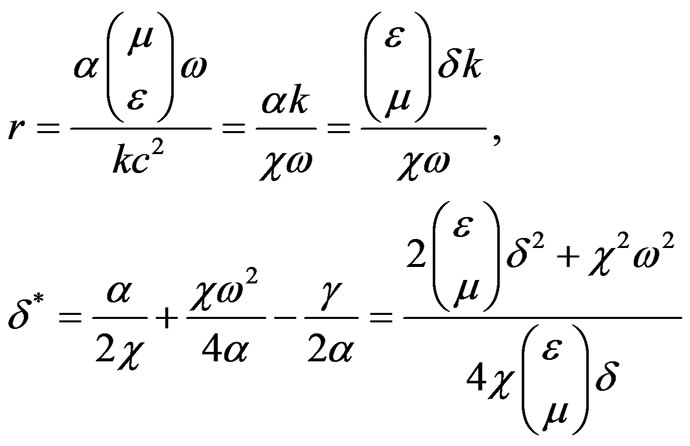 (22)
(22)
By concerning that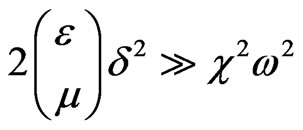 , we have
, we have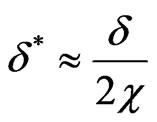 . This inequality is true, as for the rarefied gas (n < 1018 atoms/cm3)
. This inequality is true, as for the rarefied gas (n < 1018 atoms/cm3) ![]()
![]() c and the frequency of wave filling of impulse d is far more than frequency of impulse envelope w.
c and the frequency of wave filling of impulse d is far more than frequency of impulse envelope w.
Taking into account (10), (20) and the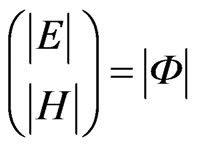 we can find the laws of electromagnetic field strengths shifting by
we can find the laws of electromagnetic field strengths shifting by
 (23)
(23)
It should be stressed, that though, the ratios for the electric aspect of impulse in [1] and (23) are similar to each other and feature the same phases of oscillations, that is possible on some distance from the over-radiating atom, the non-linear Schrödinger equations are differ in type of non-linearity. The reason of this lies in the fact that in [1] the impulse was considered with regard to low intensity, the one that does not lead to the energetic saturation of medium, in which it is disseminated.
For the estimation, like in [1] we have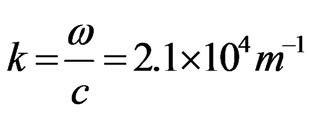 ,
, 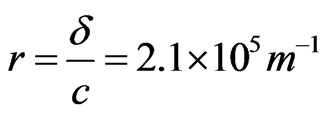 ,
,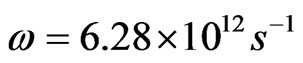 ,.
,.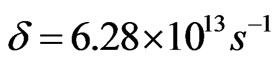 .
.
For instance, the result of strength estimation of the electric filed impulse by the coordinate X, calculated with the MathCAD system by formula (23), is shown in Figure 2.
Taking in to account the reciprocal orthogonality of planes of vectors’ envelopes of electric and magnetic fields impulse, we could gain the type of electromagnetic soliton, Figure 3.
Figure 4 shows the envelopes of electric field impulse in the SIT, based on formula (23), curve 1, and by formula (24), being the consequence of Maxwell-Bloch theory, curve 2. The impulse envelope of electric field strength in this theory is expressed as the first derivative of the Sin-Gordon equation solving and is (24).
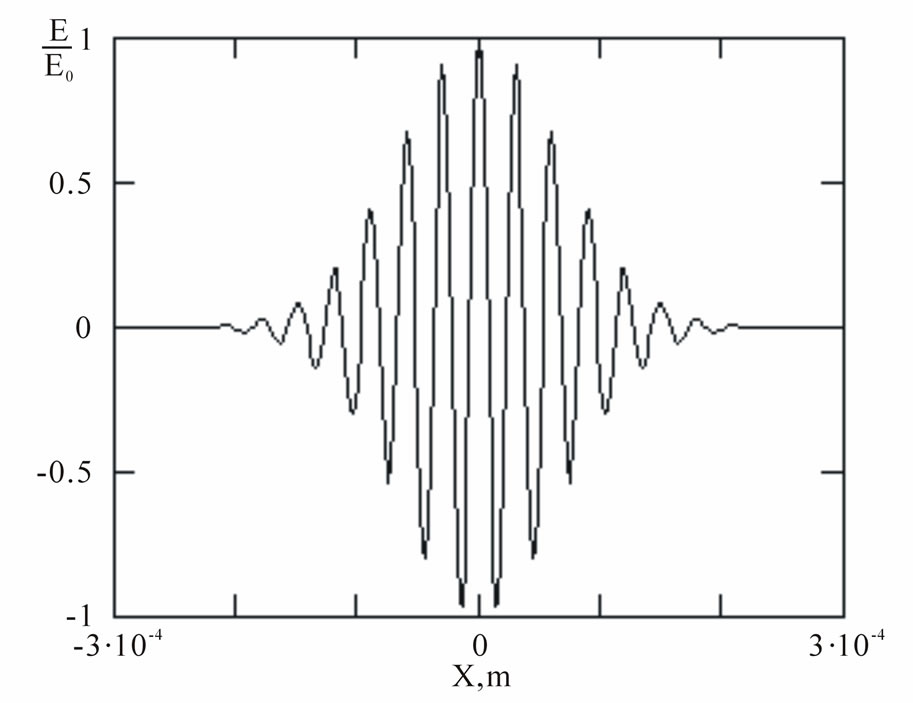
Figure 2. Calculation of the electric component of electromagnetic radiation impulse in dielectric.
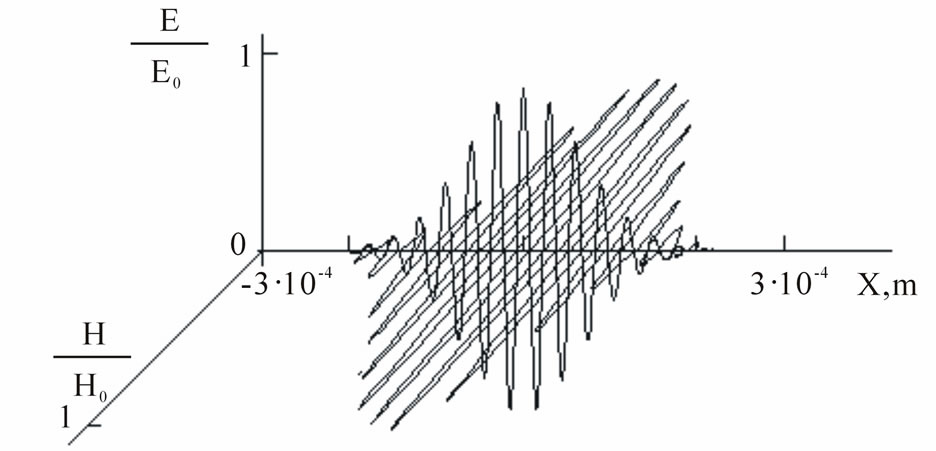
Figure 3. Intensity of electric and magnetic fields electromagnetic solitone in dielectric in conditions of the self-induced transparency.
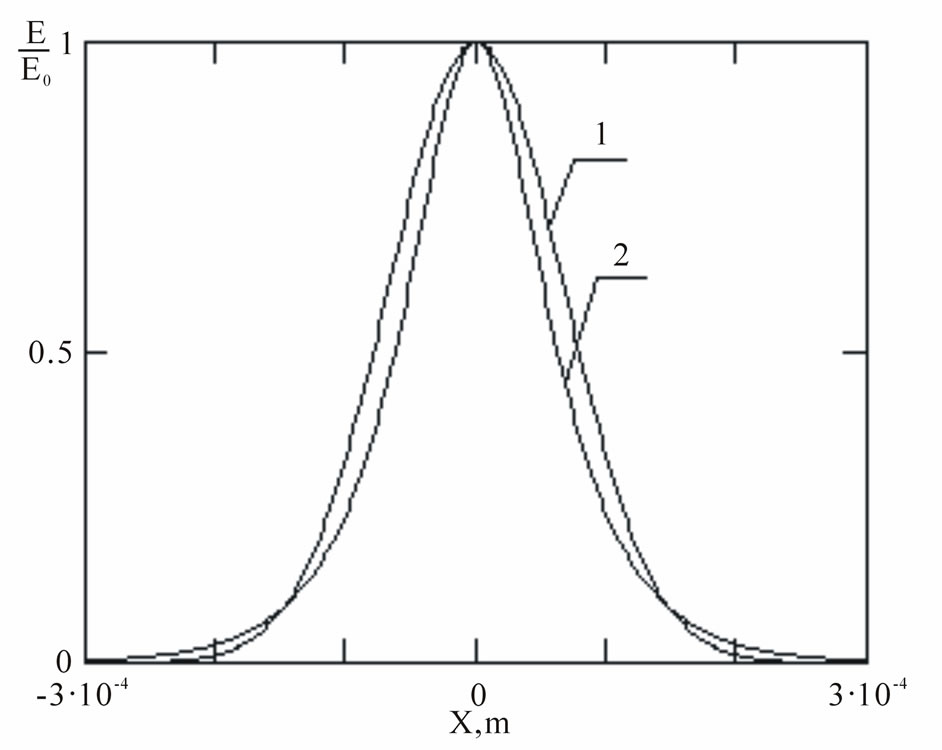
Figure 4. Comparison bending around of the electromagnetic field impulse, received on the basis of the offered theory, a curve 1, and the equations the Maxwell-Bloch, curve 2.
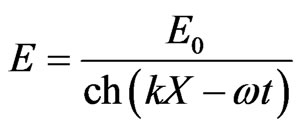 (24)
(24)
Evidently, the first derivative of Sin-Gordon equation solving is similar to the soliton envelope in the non-linear Schrödinger equation with cube non-linearity solving (27). Curves 1 and 2 in Figure 4 are designed for the same parameters as the function in Figure 2. We can infer from Figure 4 that impulse, referred to formula (23), curve 1, is broader in its central part, but asymptotically shorter than impulse, inferred by the Maxwell-Bloch theory, curve 2. Evidently, it is bound with the energetic permittivity of medium in the central part of impulse.
REFERENCES
- A. N. Volobuev and V. A.Neganov, “The Electromagnetic Envelope Soliton Propagating in Dielectric,” Technical Physics Letters, Vol. 28, No. 2, 2002, pp. 15-20.
- R. K. Dodd, J. C. Eilbeck, J. D. Gibbon and H. C. Morris, “Solitons and Nonlinear Wave Equation,”. Harcourt Brace Jovanovich, London, 1982.
- M. J. Ablowitz and H. Segur, “Solitons and the Inverse Scattering Transform,” Society for Industrial and Applied Mathematics, Philadelphia, 1981, pp. 374-378.
- A. N. Volobuev, “Modeling of Physical Processes, to Describe by Nonlinear Schrodinger Equation,” Mathematical Modelling, Vol. 17, No. 2, 2005, pp. 103-108.
- G. L. Lamb and D. W. McLaughlin, “Aspects of Solitons Physics,” In: R. K. Bulllough and P. J. Caudrey, Ed., Solitones, Springer-Verlag, Berlin, 1980, pp. 59-102.
- V. B. Berestetskij, E. M. Lifshits and L. P. Pitaevskij, “Quantum Electrodynamics,” Science, Moscow, 1989, p. 192.
- A. S. Davidov, “Quantum Mechanics,” Physmatlit, Moscow, 1963, p. 335.
- J. P. Birnbaum, “Optical Quantum Generators,” Soviet Radio, Moscow, 1967, pp. 49-50.
- G. B. Whitham F. R. S, “Linear and Nonlinear Waves,” John Wiley & Sons, New York, 1974.

