Journal of Geographic Information System
Vol.07 No.02(2015), Article ID:54379,13 pages
10.4236/jgis.2015.72007
Detection and Mapping of Water Quality Variation in the Godavari River Using Water Quality Index, Clustering and GIS Techniques
Indrani Gupta1, Awkash Kumar2*, Chandrakant Singh1, Rakesh Kumar1
1CSIR-NEERI, Mumbai Zonal Laboratory, Worli, Mumbai, India
2Centre for Environmental Science and Engineering, IIT Bombay, Mumbai, India
Email: *awkash.narayan@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2015; accepted 27 February 2015; published 3 March 2015
ABSTRACT
The objective of this research is to develop a tool for planning and managing the water quality of River Godavari. This is achieved by classifying the pollution levels of Godavari River into several categories using water quality index and a clustering approach that ensure simple but accurate information about the pollution levels and water characteristics at any point in Godavari River in Maharashtra. The derived water quality indices and clusters were then visualized by using a Geographical Information System to draw thematic maps of Godavari River, thus making GIS as a deci- sion support system. The obtained maps may assist the decision makers in managing and controlling pollution in the Godavari River. This also provides an effective overview of those spots in the Godavari River where intensified monitoring activities are required. Consequently, the obtained results make a major contribution to the assessment of the State’s water quality monitoring network. Three significant groups (less polluted, moderately and highly polluted sites) were detected by Cluster Analysis method. The results of Discriminant Analysis revealed that five parameters i.e. pH, Dissolved Oxygen (DO), Faecal Coliform (FC), Total Coliform (TC) and Ammonical Nitrogen (NH3-N) were necessary for analysis in spatial variation. Using discriminant function developed in the analysis, 100% of the original sites were correctly classified.
Keywords:
GIS, Water Quality Index, Cluster Analysis, Discriminant Analysis

1. Introduction
Water Pollution is a major environmental issue in India. The largest source of water pollution in India is untreated sewage [1] . Other sources of pollution include agricultural runoff and unregulated small scale industry. Most rivers, lakes and surface water in India are polluted [2] . The Godavari is the second longest river in India after the river Ganges. It starts in Maharashtra and flows for 1465 kilometers into the Bay of Bengal. It forms one of the largest river basins in India. The catchment area of the river is 312,812 sq∙km and is spread in the states of Maharashtra (48.6%), Andhra Pradesh (23.4%), Madhya Pradesh (10.0%), Chattisgarh (10.9%), Orissa (5.7%) and Karnataka (1.4%) [3] . In this study, the large database comprising of 34 monitoring stations of the Godavari River obtained during 5 years (2007-2011) was analyzed. water quality index was calculated based on four parameters viz. pH, DO, BOD and FC. The derived Water quality indices were then visualized by using Geographical Information System (GIS) to draw thematic maps. The data was also subjected to cluster analysis (CA) and discriminant analysis (DA) based on seven water quality parameters, with a view to extract information about the similarities or dissimilarities among the sampling sites. Cluster and discriminant analysis have been successfully applied in a number of studies, till date [3] -[12] . The clusters were then visualized by using GIS to draw thematic map of Godavari River in Maharashtra State.
2. Methodology
The data sets of the 30 water quality monitoring stations, which comprised of 7 water quality parameters monitored monthly over 5 years (2007-2011), were obtained from the Maharashtra Pollution Control Board. The selected water quality parameters included pH, dissolved oxygen (DO), Biochemical oxygen demand (BOD), Ammonical Nitrogen (NH3-N), Nitrate (NO3), Faecal Coliform (FC) and Total Coliform (TC).
2.1. Cluster Analysis (CA)
CA is an exploratory data analysis tool for solving classification problems. Its objective is to sort cases (monitoring points) into groups, or clusters, so that the degree of association is strong between members of the same cluster and weak between members of different clusters. Each cluster thus describes, in terms of the data collected, the class to which its members belong; and this description may be abstracted through use from the particular to the general class or type. Different types of cluster analysis have been applied to view water quality data for both surface and ground waters.
2.2. Discriminant Analysis (DA)
DA is a method to classify cases into categories by one or more continuous or binary independent variables. DA is performed with prior knowledge of membership of objects to a particular group or cluster. This is in contrast to CA where there is no prior knowledge of the group membership. It operates on raw data. The DA technique builds up a discriminant function by creating one or more linear combinations of independent variables. The total number of discriminant functions is either Ng − 1 where Ng = number of groups, or p (the number of independent variables), whichever is smaller. The first function maximizes the differences between groups on that function. The second function maximizes differences, but also must not be correlated with the previous function. The percentage of correct classification given in classification table, or prediction matrix, measures the performance of DA. DA is useful in determining whether all independent variables are necessary for predicting category membership and also whether the variables being monitored are sufficient for predicting group membership.
2.3. Water Qualiy Index (WQI)
An index is a mean device to reduce a large quantity of data down to a simplest form. The water quality indices help to evaluate the water quality profile of a river in its entire stretch as well as to identify the reaches where the gap between the desired and the existing water quality is significant enough to warrant urgent pollution control measures. In India the National Sanitation Foundation WQI (NSFWQI) is being used by Central Pollution Control Board, with a slight modification in weights [14] . The NSF WQI is expressed mathematically as:
 (1)
(1)
where, Ii = sub index for ith water quality parameter, Wi = weight (in terms of importance) associated with water quality parameter, and p = number of water quality parameters.
The modified weights (Wi) and the equation for the sub-indices (Ii) as per CPCB, are given in Table 1 and Table 2 respectively. The range of the NSF WQI corresponding to various designated best use classification is given in Table 3.
Table 1. Original and modified weights for the computation of NSF WQI (CPCB 2001).
Table 2. Sub-index equations for water quality parameters (NSF WQI)*.
*Abbasi 2002.
Table 3. NSF WQI for various designated best use*.
*CPCB 2001, Abbasi 2002.
2.4. GIS Application
GIS are well-established software tools that combine cartographic and database technologies [15] [16] . These information systems capture, store, manage, and present various data sets such as maps of cities and rivers that are linked to location. Users can create interactive queries, analyze spatial information, and thus better understand relationship and interactions between human activities and their surroundings. The results are viewed on maps, and this visualization which is advantageous over traditional records and tables used in spreadsheets and databases. The GIS data mapping used in this study were on the software package ArcGIS 9.1 Desktop.
3. Results and Discussion
Figure 1 gives the box plots of pH, DO, BOD, FC, TC, NH3-N and Nitrate. A box plot or a box-and whisker diagram or plot is a convenient way of graphically depicting groups of numerical data through their five-number summaries: the minimum, lower quartile, median, upper quartile, and sample maximum. A box plot may also indicate which observations, if any, might be considered outliers. The ends of the whiskers represent the minimum and maximum of all the data. The bottom and top of the box are the 25th and 75th percentiles. The center represents the 50th percentile. Any data not included between the whiskers is plotted as an outlier with a small circle, or star. If the data are normally distributed, the locations of the five marks on the box plot will be equally spaced.
3.1. Percent Exceedances
Percent exceedances of water quality parameters viz. pH, DO, BOD, TC, NH3-N and Nitrate with respect to MPCB A-II standard are given in Table 4. DO, BOD, NH3-N and pH are not meeting the MPCB A-II standards at 27, 43, 30 and 63% of the locations. At all locations, Nitrate concentrations are within the standard. At Tapovan, Nashik BOD and DO levels do not meet the standard 93 and 23% of the time. Similarly, at Kapila Nashik, BOD and DO levels do not meet the standard 90 and 26% of the time. At Pathegaon, NH3-N do not meet the standard 47% of the time. TC also do not meet the standard at 1 location viz, Kopargaon and percent exceedance is 50% at this station.
3.2. Water Quality Index
Yearly and average WQI of five years is given in Table 5. However, there were number of missing values and WQI could not be calculated for these years. In many cases, data was available for few months of the year and the yearly WQI have been calculated based on the available data. Average Water Quality Indices of 30 sitesvaried between Good to Excellent, Medium to Good and Bad. The average WQI was “good” at 27 sites, “medium to good” at 2 sites and “bad” at 1 site. Straight line fit was carried out on these 5 years data and slopes were calculated. Positive values imply an increasing trend and negative values imply a decreasing trend. At 11 locations
Figure 1. Boxplots of water quality parameters.
Table 4. Percent exceedance of water quality parameters.
Table 5. Water quality indices of Godavari River during 2007-2011.
slopes are negative implying a deterioration of water quality. At 19 locations slopes are positive implying improvement of water quality. Yearly WQI are shown in Figure 2 to Figure 6.
3.3. Cluster Analysis
Spatial cluster analysis was carried out with average concentrations for five years. Spatial cluster analysis produced a dendrogram with three groups (Figure 7). Dendrogram gives an idea of how great the distance was between cases or groups that are clustered in aparticular step, using a 0 to 25 scale along the top of the chart. The bigger the distances before two clusters are joined, the bigger the differences in these clusters. The branching- type nature of the dendrogram allows one to trace backward or forward to any individual case or cluster at any level.
Group 1 consists of 20 sites which were less polluted. Group 2 comprised of 9 sites which were moderately polluted. Group 3 comprised of 1 monitoring location which was bad. Table 6 presents the means and standard deviations for the clusters for the examined parameters. The clusters were well separated by the water quality
Figure 2. WQ classification of Godavari River in 2007.
Figure 3. Water quality classification of Godavari River in 2008.
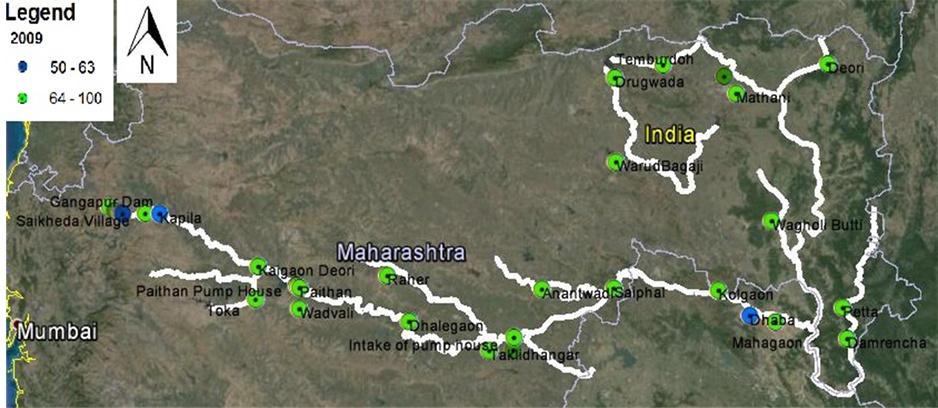
Figure 4. Water quality classification of Godavari River in 2009.
Figure 5. Water quality classification of Godavari River in 2010.
Figure 6. Water quality classification of Godavari River in 2011.
Figure 7. Dendrogram of 30 monitoring locations using ward method.
Table 6. Mean and standard deviations for water quality parameters of 3 clusters in Godavari River.
parameters. Highest DO, lowest BOD and lowest TC were observed in cluster 1. However, moderate FC and Nitrate were observed in cluster 1. In cluster 2 moderate BOD and TC were observed. In cluster 3, highest BOD, FC and TC were observed. However, moderate DO and Nitrate were observed in cluster 3. The results were also viewed in a GIS layer (Figure 8).
The results of water quality index and those of cluster analysis more or less match since water quality index considers only 4 parameters, viz. pH, BOD, DO and FC while cluster analysis was performed using 7 parameters, viz. pH, BOD, DO, FC and TC, NH3-Nand Nitrate. The results of water quality index and those of cluster analysis match at 23 locations.
3.4. Discriminant Analysis
Discriminant analysis is carried after standardizing the independent variables. Table 7 presents the Tests of Equality of Group Means. It indicates whether there is a statistically significant difference among the dependent variable means for each independent variable. The smaller the Wilks’ Lambda, the more important is the independent variable. Here only Nitrate is not statistically significant and hence we drop the Zscore (Nitrate). Table 8 gives the results of Box’s Test of Equality of Covariance Matrices. The Box’s M test tests the homogeneity of covariance assumption. This test is also sensitive to meeting the assumption of multivariate normality. Table 10 shows that the test is significant so we conclude the groups have equal covariance matrices. Table 9 gives the summary of Canonical Discriminant Functions. The larger the eigen value the more of the variance in the dependent variable is explained by that function. The magnitudes of the eigen values are indicative of the functions’ discriminating abilities. Since there are three categories or groups there are two discriminant functions in the descending order of importance. Percent of variance is the proportion of discriminating ability of the continuous variables found in a given function. The squared canonical correlation is the percent of variation in the dependent discriminated by the independents in DA. In this analysis, the first function accounts for 100% of the discriminating ability of the discriminating variables. Table 10 gives the Wilks’ lambda which tests the significance of the eigen value for each discriminant function. In this case both are significant. Standardized discriminant function coefficients in Table 11 indicate the relative importance of the independent variables in predicting the dependent. Table 12 provides an indication of the success rate for prediction of membership of the grouping variable’s categories using the discriminant function developed from the analysis. Percentage of correct classification for original cases was observed to be 100%. Percentage of correct classification for cross-validated grouped cases was observed to be 90%.
4. Conclusion
Average water quality index for five years i.e. for 2007 to 2011 was calculated with four parameters viz. DO, BOD, FC and pH. The results show that out of 30 locations on Godavari River in Maharashtra, 27 have “good to excellent” water quality, 2 have “medium to good” water quality and 1 has “bad” water quality. The slope of the
Figure 8. Water quality classification of Godavari River based on cluster analysis.
Table 7. Tests of equality of group means.
Table 8. Box’s test of equality of covariance matricesa.
aSome covariance matrices are singular and the usual procedure will not work. The non-singular groups will be tested against their own pooled within-groups covariance matrix. The log of its determinant is −20.306.
Table 9. Summary of canonical discriminant functions.
aFirst 2 canonical discriminant functions were used in the analysis.
Table 10. Wilks’ Lambda.
Table 11. Standardized canonical discriminant function coefficients.
Table 12. Classification resultsbc.
aCross validation is done only for those cases in the analysis. In cross validation, each case is classified by the functions derived from all cases other than that case; b100% of original grouped cases correctly classified; c90% of cross-validated grouped cases correctly classified.
*Corresponding author.
Acknowledgements
The authors are thankful to the Director of NEERI for his encouragement.
References
- Central Pollution Control Board, Evaluation of Operation and Maintenance of Sewage Treatment Plants in India (2007). http://www.cpcb.nic.in
- Central Pollution Control Board, Annual Report (2008-2009). http://cpcb.nic.in/upload/AnnualReports//AnnualReport_37_ANNUAL_REPORT-08-09.pdf
- Central Pollution Control Board, Environmental Atlas of India (2001) New Delhi.
- Bierman, P., Lewis, M., Ostendorf, B. and Tanner, J. (2011) A Review of Methods for Analyzing Spatial and Temporal Patterns in Coastal Water Quality. Ecological Indicators, 11, 103-114. http://dx.doi.org/10.1016/j.ecolind.2009.11.001
- Einax, J.W., Truckenbrodt, D. and Kampe, O. (1998) River Pollution Data Interpreted by Means of Chemometric Methods. Microchemical Journal, 58, 315-324. http://dx.doi.org/10.1006/mchj.1997.1560
- Gazzaz, N.M., Yusoff, M.K., Ramli, M.F., Aris, A.Z. and Juahir, H. (2012) Characterization of Spatial Patterns in River Water Quality Using Chemometric Pattern Recognition Techniques. Marine Pollution Bulletin, 64, 688-698. http://dx.doi.org/10.1016/j.marpolbul.2012.01.032
- Guler, C., Thyne, G.D., McCray, J.E. and Turner, K.A. (2002) Evaluation of Graphical and Multivariate Statistical Methods for Classification of Water Chemistry Data. Hydrogeology Journal, 10, 455-474. http://dx.doi.org/10.1007/s10040-002-0196-6
- Gupta, I., Dhage, S., and Kumar, R. (2009) Study of Variations in Water Quality of Mumbai Coast through Multivariate Analysis Techniques. Indian Journal of Marine Sciences, 38, 170-177.
- Gupta, I., Salunkhe, A., Rohra, N. and Kumar, R. (2013) Chemometrics Data Analysis of Marine Water Quality of Maharashtra, West Coast of India. Indian Journal of Geo Marine Sciences, 42, 97-105.
- Kovacs, J., Kovacs, S., Magyar, N., Tanos, P., Hatvani, I.G. and Anda, A. (2014) Classification into Homogeneous Groups Using Combined Cluster and Discriminant Analysis. Environmental Modeling & Software, 57, 52-59. http://dx.doi.org/10.1016/j.envsoft.2014.01.010
- Santos-Roman, M.D., Warner, S.G. and Scatena, F. (2003) Multivariate Analysis of Water Quality and Physical Characteristics of Selected Watershed in Puerto Rico. Journal of the American Water Resources Association, 829-839. http://dx.doi.org/10.1111/j.1752-1688.2003.tb04408.x
- Xu, H.S., Xu, Z.X., Wu, W. and Tang, F.F. (2012) Assessment and Spatiotemporal Variation Analysis of Water Quality in the Zhangweinan River Basin, China. Procedia Environmental Sciences, 13, 1641-1652. http://dx.doi.org/10.1016/j.proenv.2012.01.157
- Zeng, X. and Rasmussen, T.C. (2005) Multivariate Statistical Characterization of Water Quality in Lake Lanier, Georgia, USA. Journal of Environmental Quality, 34, 1980-1991. http://dx.doi.org/10.2134/jeq2004.0337
- Abbasi, S.A. (2002) Water Quality Indices State-of-the-Art, Pondicherry University, Centre for Pollution Control & Energy Technology, Pondicherry.
- Nemeth, T., Szabo, J., Pasztor, L. and Bakacsi, Z. (2002) Elaboration of a Complex GIS Application in a Catchment Area. Water Science and Technology, 45, 133-140.
- Shaban, M., Urban, B., El-Saadi, A. and Faisal, M. (2010) Detection and Mapping of Water Pollution Variation in the Nile Delta Using Multivariate Clustering and GIS Techniques. Journal of Environmental Management, 91, 1785-1793. http://dx.doi.org/10.1016/j.jenvman.2010.03.020
NOTES
*Corresponding author.