Journal of Geographic Information System
Vol.06 No.05(2014), Article ID:50288,7 pages
10.4236/jgis.2014.65036
Comparison of Digital Maps: Recognition and Quantitative Measure of Changes
Lev Spivak1, Ivan Spivak2, Alexey Sokolov1, Sergey Voinov3
1Dubna International University, Moscow Region, Russia
2Real Geo Project, Moscow Region, Russia
3University of Applied Sciences, Stuttgart, Germany
Email: levspivak@mail.ru, spivak@neolant.ru, asokolov.dubna@gmail.com, sergey.voinov@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 July 2014; revised 18 August 2014; accepted 12 September 2014
ABSTRACT
A new methodology of comparing digital raster maps was proposed which allows not only detecting changes in the maps, but also obtaining quantitative measures of the importance of selected differences. Procedure of object interpretation of satellite images and forming of OMT (Object Map of Territory) is described. A list of allowable differences between two OMTs is defined. Two steps technique of quantitative measuring is proposed. At the first stage functions are constructed for calculating local measures of differences in the amount, areas and locations of objects on the map, as well as relations between the objects. In the second stage local measures are used to calculate the integral measure in order to get generalized assessment of difference between maps. The methods for constructing functions which calculate local and integral measures of differences are described. Examples of comparing and measuring the differences between OMTs are provided. Obtained results by utilizing this technique can be used to analyze trends, forecast of development and might be helpful for choosing most efficient scenarios for sustainable spatial planning and land management.
Keywords:
Maps Comparison, Object Map of Territory, Change Detection, Local Measure of Difference, Integral Measure of Difference, Sustainable Spatial Planning and Land Management

1. Introduction
One of the key functions for sustainable spatial and environmental planning, land management as well as policy is detection and analysis of changes of territory conditions [1] -[3] . Obviously, the most common way to solve this task is to compare descriptions of the same territory for different points of time. Maps are traditionally used as territory descriptions for different scales. Nowadays, the most effective solutions for storing, processing and visualizing maps are based on Geographical Informational Systems (GIS). All popular GIS like ArcGIS, qGIS, MapInfo, AutoDesketc, are able to solve very wide range of tasks, but in matter of map comparison they are very limited. Although “change detection” function, which is often included in image and remote sensing data processing software, is able to detect pixels which differ by spectral characteristics, it cannot provide the meaning of these changes. Therefore creation of appropriate methodology for map comparisons might be useful contribution in this field. Proposed in this paper methodology allows to detecting changes as well as quantitatively assessing the meaning of detected changes. Methodology based on ideas is presented in [3] [4] .
2. Comparison of Digital Maps
Comparing maps utilizing proposed in this paper approach must be formed appropriate way. Therefore a three- step methodology of creating OMTs is described besides comparing techniques itself. A general workflow of entire process illustrated in Figure 1.
Block of inputs consist of raster imagery, which used as a source for creation OMTs, and user defined data, such like object specifications and specific criteria’s for constructing measuring functions.
Processing block. Object interpretation section is responsible for creation of OMTs and described in the next subsection. Calculating of local and integral measures is the main part of this work, which presented in the second section of this chapter.
2.1. Methodology of Creating Maps of Territory Objects
As a source data for creating maps can be used contact as well as remotely sensed data. The procedure of creating maps based on remote sensing data called “thematic interpretation”. In the fact, it is necessary to distinguish object and parametric interpretations. Object interpretation means extraction of borders of objects that corresponds to a certain classes on the surface―classification by object types, when parametric interpretation means extracting quantitative values of object properties (land cover characteristics) based of EO data. Note, result of object interpretation is supported with scale of names, but result of parametric interpretation is supported with absolute scale [5] .
Generally, in the task of object interpretation it is contemplated to transit from digital image1 of observing territory T, which represented by matrix of pixels 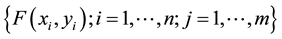 with size of
with size of 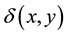 and
and
Figure 1. A general workflow of the proposed comparing procedure.
brightness/gray value , to its representation as a system of spatial objects
, to its representation as a system of spatial objects 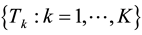 belonging to different classes with sizes of
belonging to different classes with sizes of 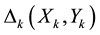 and relations of R. Note,
and relations of R. Note, 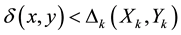 ,
,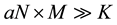 .
.
The result of object interpretation is digital raster map, which we will call in further steps “Object Map of Territory” (OMT). Objects in OMT should meet following conditions:
1) Every object Tk is a set of connected pixels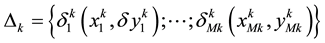 ;
;
2) All pixels of object Tk are belong to the same land cover class, i.e. 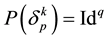 for all
for all . The value of predicate P is ID number of class taken from the list defined by object classifier
. The value of predicate P is ID number of class taken from the list defined by object classifier ;
;
3) , i.e. set of all objects covers entire territory T;
, i.e. set of all objects covers entire territory T;
4)  for all
for all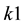 ,
,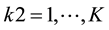 ;
;
Before doing object interpretation it is necessary to build object classifier and spectral signatures, which will define criteria for classifying pixels (e.g. Land cover classification system (LCCS)). The object classifier used as a legend for OMT.
The task of object interpretation is similar to image segmentation [6] and as a matter of fact adds up to zoning of territory [3] . In the fact, any result of zoning of territory is OMT.
In the common case, object interpretation task and creating OMT includes three main steps.
At the first step a classical pixel-based pattern recognition problem has to be solved, where every pixel assigned to the name of corresponding class. This procedure is similar to the coloring the cell sheet from a notebook. Each object class is painted a special color. Result of this operation is base matrix of OMT (see Figure 2(a)).
In the second step, the boundaries and contours of objects are allocated. As a result, the elements of base matrix acquired unique compound names
In the last step, the contours of objects specified with additional conditions and limitations, in particular to the spatial dimensions of the objects. The output is a final product OMT (see Figure 2(c)).
OMT formed for a certain point of time and allows formulizing following facts and statements:
1) Within the territory T there are K objects of different classes

2) Single objects 


3) Spatial allocation of object Тk defined by set of connected pixels.

4) Area of single object 



5) Objects Тk1 and Тk2 has relation R. Generally, binary relation R defined by pairs of objects, i.e. 

Set of relations R often plays important role in describing the current status of territory T. Special importance

Figure 2. Steps of creating OMT: (a) forming of base matric OMT; (b) allocating of object contours; (c) specifying additional conditions: area of objects from class А should not be less than 2 pixels.
takes relation of type “neighbor”, which defines set of object pairs having common border. In particular, relation of type “neighbor” from OMT, shown in Figure 2(c), has six pairs of objects: {(А1, В1); (А1, С1); (А1, С2); (А2, В1); (А2, С2); (В1, С2)}. Corresponding adjacency matrix illustrated below.
Note, adjacency matrices of binary relations are always symmetrical. This can be used in order to reduce amount of memory for their storage.
2.2. Comparison of OMTs and Quantitative Assessment of Changes
To detect changes it is necessary to compare OMTs corresponding to sequence of times. OMT of territory T for the point of time t we will call
The comparison is based on the following scheme:

Of course, in order to detect changes correctly, comparing OMTs must have the same pixel size and spatial extend. If these conditions are met, two comparing OMTs will have a finite number of valid types differences as listed in Table 1.
Detection of changes is only half the story. Practically, the most important thing is to differentiate detected changes between important ones and not important ones. For quantitative assessment and ranking changes it is necessary to have some special criteria and functions which allow calculating the measure of differences.
Note, it is not possible to construct one universal function to compare maps with different content. Furthermore, for every special situation it might be necessary to construct specific measuring functions which are depends on specifics of observing area and task.
When comparing maps it is necessary to distinguish integrated and local measuring functions [4] . Local functions allows to measure some specific changes (shown in Table 1), when integral ones can measure general difference of maps.
In order to measure local differences it is necessary to construct local measuring functions for the following measures:
λ1―measure, for changes in number of classes;
Table 1. List of possible changes when compared two OMTs.
λ2―measure, for changes in number of objects of different classes;
λ3―measure, for changes in areas of objects of different classes;
λ4―measure, for changes in spatial allocation of objects;
λ5―measure, for changes in relations between objects.
Measurement of λ1, λ2 and λ3 presents no special difficulties, corresponding procedures are described in [4] . To measure λ4 it is possible to use operational approach proposed in [3] . It involves determining the number and “cost” of operations required to convert the situation “was” to “became”. Every operation allows you to convert class of a single pixel. “Cost” of operations can be specified using the corresponding adjacency matrix of object classes. In particular, such matrix for OMT from Figure 2(c) will have following form:
In the common case “cost” matrix is not symmetrical. For example, transformation of forest into the field will have higher cost than another way around, therefore
If all pixels of OMT have the same “cost”, measure of difference between two lines (of images) can be calculated using following formulation:

where:


The final (total) local measure l4 (OMT1, OMT2) calculated by summing of measures of individual lines.
Additional difficulties when calculating λ4 may arise due to dependency of operation cost from pixel position in the base matrix. For example, conversion of the central pixels might cost more than peripheral ones. Furthermore, each pixel may have its own weight, defined by its location on the map. In such case it is necessary to define a weight matrix of conversion for all pixels in the source map for every operation.
2.2.1. Measurement of Relation Changes between Objects
When measuring relation changes it is necessary to consider differences in number of relations as well as its consistency. This means:

where:
λ51―measure of number of changes;
λ52―measure of consistence of changes.
Strictly speaking, the whole list of relations (classifier) as well as classifier of objects should be defined on the phase of forming of OMT (3 stages) and should not be changed further. In case of changes in forming OMT phase, corresponding changes in measuring functions should be applied as well.
Changes in component consistency are based on changes in spatial allocation and quantity of objects. If consistence of relations defined by list of object pairs, then as changes would be considered adding or deleting such pairs. For every relation the “cost” of adding or deleting of objects pairs might be different. In case if the “cost” is always the same or constant, then total “cost” can be calculated using following formulation:

where:




In case of non-constant “cost” of adding/deleting of object pairs provided formulation should be modified correspondingly.
2.2.2. Integral Measure
Local measure used to construct integral measure. In simple case, integral measure can be formulated by linear combination of local measures

where,
Maps with small integral measures of differences should be considered as similar.
If local and integral measures are above defined thresholds, then detected changes recognized as “significant” and considered for further analysis. Calculated quantitative measures can be further used to analyze trends, forecast of development and might be helpful for choosing most efficient scenarios for sustainable spatial planning and management.
When comparing maps, which are sequential in time, the cumulative effect of small changes should be considered. In particular, the differences between two maps―the previous and current can be low (below the threshold), but if we compare maps corresponding to the beginning and to the end of a large time interval, the differences may be significant.
3. Example of OMT Comparison
As an example we will compare three OMT which illustrated in Figure 3.
Given that the number of classes does not vary, as an integral measuring function we take
Let’s assume that adding/deleting of object pairs has a constant “cost”. In this case local measure of differences for number of objects would have following formulation:
where:


In our case, measuring function λ2 can have following formulation:
Here we can calculate:
Figure 3. Example of OMT for comparison.
To calculate λ4 we will use operational approach, allowing us indirectly assess changes in object areas. In order to simplify our task we will assume that “cost” of transformation is the same for all pixels and adjacency matrix is similar and looks like shown below.
As a result we will get following measures:
・
・
・
To calculate λ5, we have to form lists of relations “neighbor”:
・
・
・
We already agreed that “cost” of adding/deleting of object pairs is constant. If we take as a “cost” value of 5, we can calculate following measures:
・
・
・
Finally, we can calculate integral measures of differences:
It is clear that difference between OMT2 and OMT3 is significantly lower than difference between OMT1 and OMT3. Particularly, if OMT3 is desirable substance and OMT1 and OMT2 are alternative scenarios, then we can select OMT2 because it is closer to our goal.
4. Conclusions and Recommendations
1) Developed methodology allows obtaining quantitative measures of differences between pairs of Object Maps of Territory based on five different measures of changes:
λ1―number of classes;
λ2―number of objects of different classes;
λ3―areas of objects of different classes;
λ4―spatial allocation of objects;
λ5―relations between objects.
The task of comparing these maps reduced to the choice of measuring functions and weights that reflect the importance (“cost”) of the detected differences (changes).
2) Approaches to calculating local and integral measures of differences are proposed. In the simplest case, the integral measure of changes can be formulated as linear combination of local measures.
3) One of the most important problems in calculating of integral measures is to define appropriate weights. There is no common rule for solving this problem. It always depends on task and maps content.
Based on provided methodology, it is planned to develop GIS techniques for analysis of time series maps. Furthermore, a handbook describing ways to apply approach for decision makers in accordance with the workflow
Cite this paper
LevSpivak,IvanSpivak,AlexeySokolov,SergeyVoinov, (2014) Comparison of Digital Maps: Recognition and Quantitative Measure of Changes. Journal of Geographic Information System,06,415-422. doi: 10.4236/jgis.2014.65036
References
- 1. Cheremisina, E.N., Spivak, L.F. and Spivak, I.L. (2013) Information and Analytical Tools of Situational Center of Territory Control. Geoinformatica, 3, 1-7. [Черемисина, Е.Н., Спивак, Л.Ф., Спивак, И.Л. (2013) Информационно-аналитическое обеспечение ситуационного центра управления территорией. Геоинформатика, 3, 1-7.]
- 2. Cheremisina, E.N. and Spivak, I.L. (2011) Conceptual Bases of Development of the Automated Management Systems for Territories. Geoinformatica, 4, 14-17. [Черемисина, Е.Н., Спивак, И.Л. (2011) Концептуальные основы построения автоматизированных систем управления территориями.Геоинформатика, 4, 14-17.]
- 3. Voronin, Yu.A. and Spivak, L.F. (2004) Theory of Zoning and Management of Territories. SO RAN, Novosibirsk, 230 p. [ВоронинЮ.А., СпивакЛ.Ф. (2004) Теория районирования и управление территориями.Новосибирск: Изд-во СО РАН, 230с.]
- 4. Spivak, L.F. and Spivak, I.L. (2010) Method of Quantitative Evaluation of Mapschanges. Geoinformatica, 2, 41-46. [Спивак, Л.Ф., Спивак, И.Л. (2010) Методика количественной оценки изменений картографических результатов мониторинга. Геоинформатика, 2, 41-46.]
- 5. Spivak, I.L. (2010) Thematic Interpretation Tasks in Space Monitoring Systems. Geoinformatica, 4, 61-65. [Спивак, И.Л. (2010) Задачи тематического дешифрирования в системах космического мониторинга. Геоинформатика, 4, 61-65.]
- 6. Gonzales, R.S. and Woods R.E. (2002) Digital Image Processing. Prentice Hall, Upper Saddle River, 567 p.
Nomenclature
OMT Object Map of Territory
GIS Geographical Informational Systems
EO Earth Observation
LCCS Land Cover Classification Systems
λ1 measure of changes in number of classes
λ2 measure of changes in number of objects of different classes
λ3 measure of changes in areas of objects of different classes
λ4 measure of changes in spatial allocation of objects
λ5 measure of changes in relations between objects
Λ Integral measure of changes
NOTES
1In the common case there could be several images with different time of acquisition, spatial resolution and spectral ranges. Important is that based on the result of their interpretation will be formed a single map.



























