Journal of Geographic Information System
Vol. 4 No. 2 (2012) , Article ID: 18745 , 9 pages DOI:10.4236/jgis.2012.42011
Mineral Prospectivity Mapping Method Integrating Multi-Sources Geology Spatial Data Sets and Case-Based Reasoning
1School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, China
2College of Geophysics, Chengdu University of Technology, Chengdu, China
3College of Geosciences, Chengdu University of Technology, Chengdu, China
Email: binbinhe@uestc.edu.cn, {chjh3, chencuihua}@163.com
Received October 26, 2011; revised December 20, 2011; accepted January 4, 2012
Keywords: Mineral Prospectivity Mapping; Case-Based Reasoning; Metallogenic Case Representation; Metallogenic Case Retrieval; Eastern Kunlun Mountains
ABSTRACT
Extracting and synthesizing information from existing and massive amounts of geology spatial data sets is of great scientific significance and has considerable value in its applications. To make mineral exploration less expensive, more efficient, and more accurate, it is important to move beyond traditional concepts and establish a rapid, efficient, and intelligent method of predicting the existence and location of minerals. This paper describes a case-based reasoning (CBR) method for mineral prospectivity mapping that takes spatial features of geology data into account and offers an intelligent approach. This method include a metallogenic case representation that combines spatial and attribute features, metallogenic case-based storage organization, and a metallogenic case similarity retrieval model. The experiments were performed in the eastern Kunlun Mountains, China using CBR and weights-of-evidence (WOE), respectively. The results show that the prediction accuracy of the CBR is higher than that of the WOE.
1. Introduction
Mineral prospectivity analysis and quantitative resource estimation have been recognized as important when integrating multi-source geology spatial data in recent years [1]. The statistical and mathematical approaches developed recently for multi-resources geological spatial data integration include weights-of-evidence (WOE) [2-8], and the logistic regression [9,10]. The fuzzy logic [11, 12], artificial neural networks [13,14] and the Fractal method [15] have been applied in the assessment of mineral resources potential. Although these methods promote the efficiency and effectiveness of mineral resource prospecting, their algorithms are unable to accumulate knowledge, and lack intelligent reasoning. Meanwhile, similar deposit types occur in similar geological conditions and spatial distributions. The metallogenic geological conditions and spatial distribution of discovered and typical deposits can be used to construct a historical case-base for mineral prospectivity analysis. Traditional analysis methods cannot mine the depth of information or make intelligent inferences. In recent years, some researchers have begun applying case-based reasoning (CBR) to the environment, urban planning, and land use.
Lekkas et al. [16] suggested using CBR to predict air pollution levels; Holt and Benwell [17] tried using CBR to classify soil; Ye et al. [18] integrated CBR and GIS for urban planning approval; and Du et al. [19] applied CBR for land use change prediction. CBR is a branch of artificial intelligence that began in the research of Schank and Abelson [20]. CBR does not require a precise domain model, and it solves new cases by using historical knowledge. Its application is based on two assumptions about the objective world: 1) similar problems have similar solutions; and 2) similar problems may recur. CBR uses the principle of similarity to find strategies for new cases; it also offers a method that resembles the human problem-solving approach of extracting and storing expertise. From a methodological point of view, CBR proposes a comprehensive, problem-oriented approach to analysis that is more adaptable than rule-based and model-based reasoning. CBR is particularly suitable for areas in which it is difficult to summarize, abstract, and express expertise; this makes CBR useful for solving ambiguous problems. CBR can do quantitative analysis and prediction without a careful mechanism study, and it has advantages in the simplification of knowledge acquisition, the improvement of efficiency and quality, and the accumulation of knowledge. Additionally, CBR and the identification process are highly automated and reusable. CBR is an effective method in cases in which prior knowledge is lacking or for constructing complex issues in quantitative models.
In this paper, a method for mineral prospectivity mapping was proposed integrating multi-sources geology spatial data sets and case-based reasoning, including a metallogenic case representation model that combines spatial and attribute features, the metallogenic case-feature weights-determining model, metallogenic case-based storage organisation, and a metallogenic case-similarity retrieval model. The experiment was performed in the eastern Kunlun Mountains, China to predict the existence of potential iron deposits using case-based reasoning and weights-of-evidence, respectively.
2. Methodology
The mineral prospectivity mapping method using casebased reasoning include three main components: a metallogenic case representation model, metallogenic case storage, and a metallogenic case retrieval model. Figure 1 describes the flow of mineral prospectivity mapping method using CBR.
2.1. Metallogenic Case Representation Model
Generally, a case in a traditional CBR model is composed of both attribute and goal features. Because of the spatial distribution and regional laws of geological entities, the case representation is different from a traditional one. The features of a metallogenic case include both spatial and attribute features, which are selected or extracted from metallogenic entities.
During the construction of a metallogenic case representation model, each grid of a certain size is taken as a representative object. First, typical feature attributes related to ore control that are contained in vector grids of existing mineral points are extracted. Then, the corresponding names of mines in vector grids and relevant result values are determined. The extracted-features attribute, the corresponding names, and the relevant results are all described by the rules of case expression. To extract spatial features, the orientation relations, the metric relations, and the topology relations related to ore control in each vector grid are extracted, and spatial relations are transformed to attribute mode. Therefore, a metallogenic case consists of general attributes and spatial-relation property items. The basic expression is as follows:
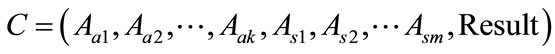 (1)
(1)
where Aai is the general feature property item, Asj is the spatial-relation feature property item, and Result represents the result of the case. To solve a new case, existing cases can be extracted by spatial relations under certain rules (e.g., spatial coding). After that, candidates for a historical case set are obtained.
2.2. Metallogenic Case Storage
After a typical metallogenic case is constructed, it is stored in a spatial database in database tables or into document systems in a text file. The stored cases are then indexed to improve the efficiency of the metallogenic case-similarity retrieval model.
2.3. Metallogenic Case Retrieval Model
Because a metallogenic case has spatial features, it is different than a traditional CBR model. First, during the construction of a metallogenic case retrieval model, all vector grids are set as unsolved cases under the metallogenic case representation model. In other words, each case describes typical attribute and spatial features, and the results description (i.e., the case-determining attribute) is set to blank. Second, a similarity-measure threshold is set, and each unsolved case is retrieved for similarity. After a similar case is found, its result is assigned to the unsolved case according to the threshold and the strategy given. If the case obtained is unsatisfactory, it can be modified by expertise. Its result can then be assigned to the unsolved case. The retrieval unsolved cases in all
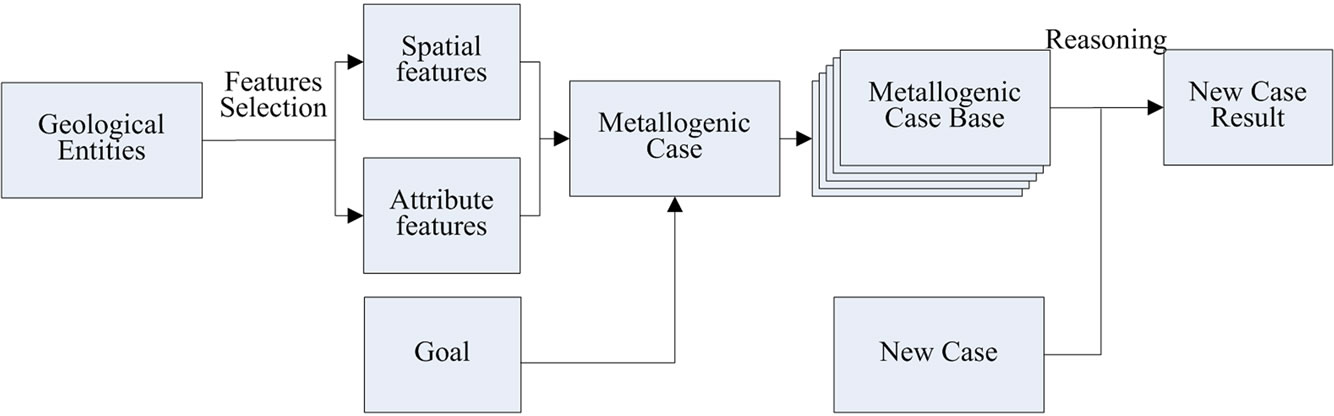
Figure 1. The flow of mineral prospectivity mapping method using CBR.
vector grids are then completed. Third, the typical cases obtained or modified can be stored into the case base for expansion and update.
After a metallogenic case base is constructed, the metallogenic case retrieval model (Figure 2) can use it to compare existing metallogenic cases with new ones. The similarity measurement formulas for existing and new cases are as follows:
 (2)
(2)
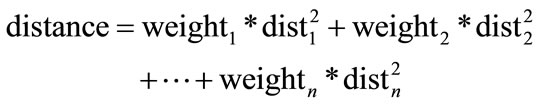 (3)
(3)
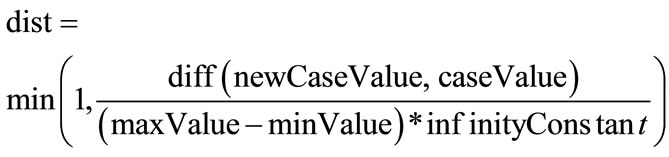 (4)
(4)
where “S%” is similarity ranged between 0% and 100%; “distance” is the weighted sum of the squares of “disti” ranged between 0 and 1; “searchedWeightsSum” is the sum of the weights, with the new case feature and the actual case feature both being non-empty; “totalWeightsSum” is the sum of the weights of all case features; “disti” is the distance between the new case feature and the actual case feature, in which the value is the smaller of either 1 or the Euclid distance between the new case feature and the actual case feature; “newCaseValue” is the new case feature value; “caseValue” is the actual case feature value; “maxValue” and “minValue” are the case corresponding feature’s maximum and minimum values; and “infinityConstant” is a large constant.
To measure similarity, each new case is compared with all cases in the case base. The return value is based on the selection strategies of the maximum, threshold, or K nearest neighbors. If the value is unsatisfactory, it can be modified by the return value and relevant expertise. The typical cases obtained and the cases modified can be stored into the case base for expansion.
3. Experiments
To verify the effectiveness of the proposed method, the experiments of mineral potential prediction for iron deposits were performed in the eastern Kunlun Mountains, using the metallogenic CBR model and the weights-ofevidence model, respectively. All of the data sets used in this paper were derived from our established multisource geology spatial database, which contains geological, geophysical, geochemical, and remote-sensing data. The metallogenic CBR model was implemented with C# based on ArcEngine GIS components. The weights-of-evidence model was performed with Arc-SDM [21].
3.1. Geological Setting of Study Area
The eastern Kunlun Mountains are within Qinghai Province, China, and are shown as an insertion from left to right to the provincial map (Figure 3). The Mountains are within latitudes 34˚57′ and 37˚56′N, and longitudes 90˚31′ and 100˚04′E. Of the study area, the eastern Kunlun orogenic belt is attached to the southern margin of the Qaidam Basin.
The area consists of three major deep crustal-scale faults that divide the area roughly from north to south into subtectonic belts (Figure 4). Kunbei (“Kun” is short for Kunlun. “bei” means north in Chinese) belt is in the north. It belongs to the Kunbei Caledonian back-arc basin situated mainly in the northwestern part of the Kunlun Mountains. The belt is made of early Palaeozoic folding belts dominated by the Ordovician marine sediments
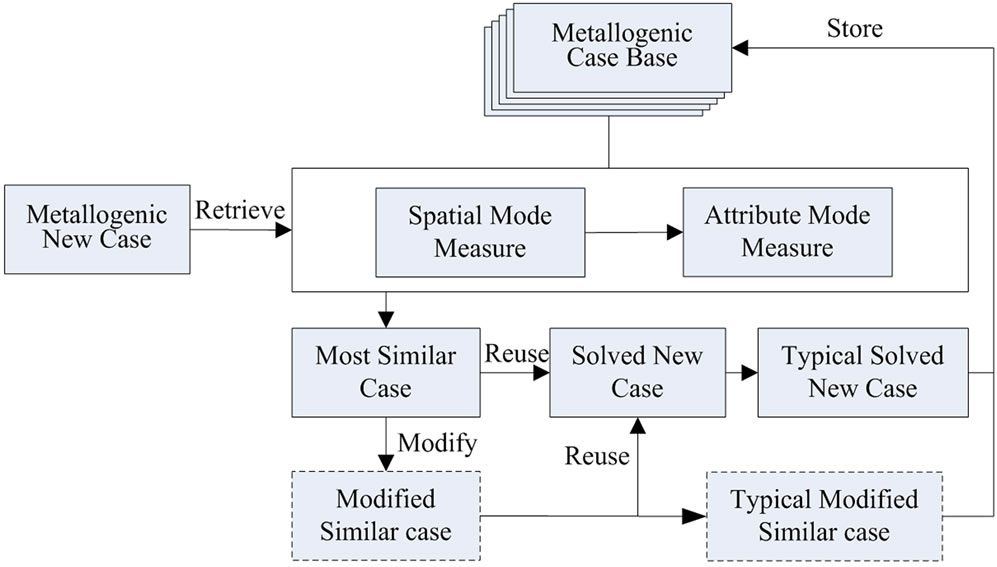
Figure 2. Metallogenic case similarity retrieval model.
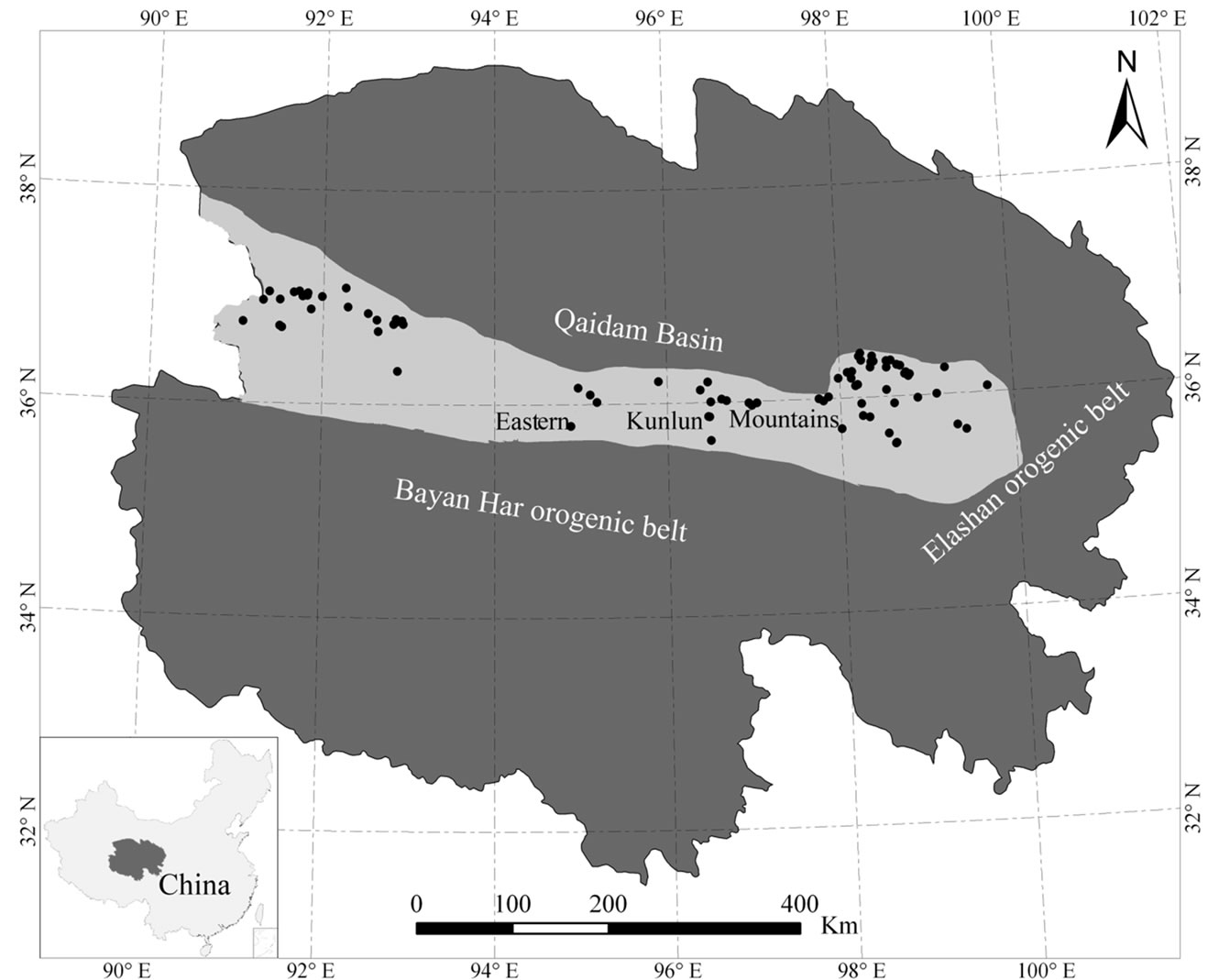
Figure 3. Eastern Kunlun Mountains within Qinghai Province, China.
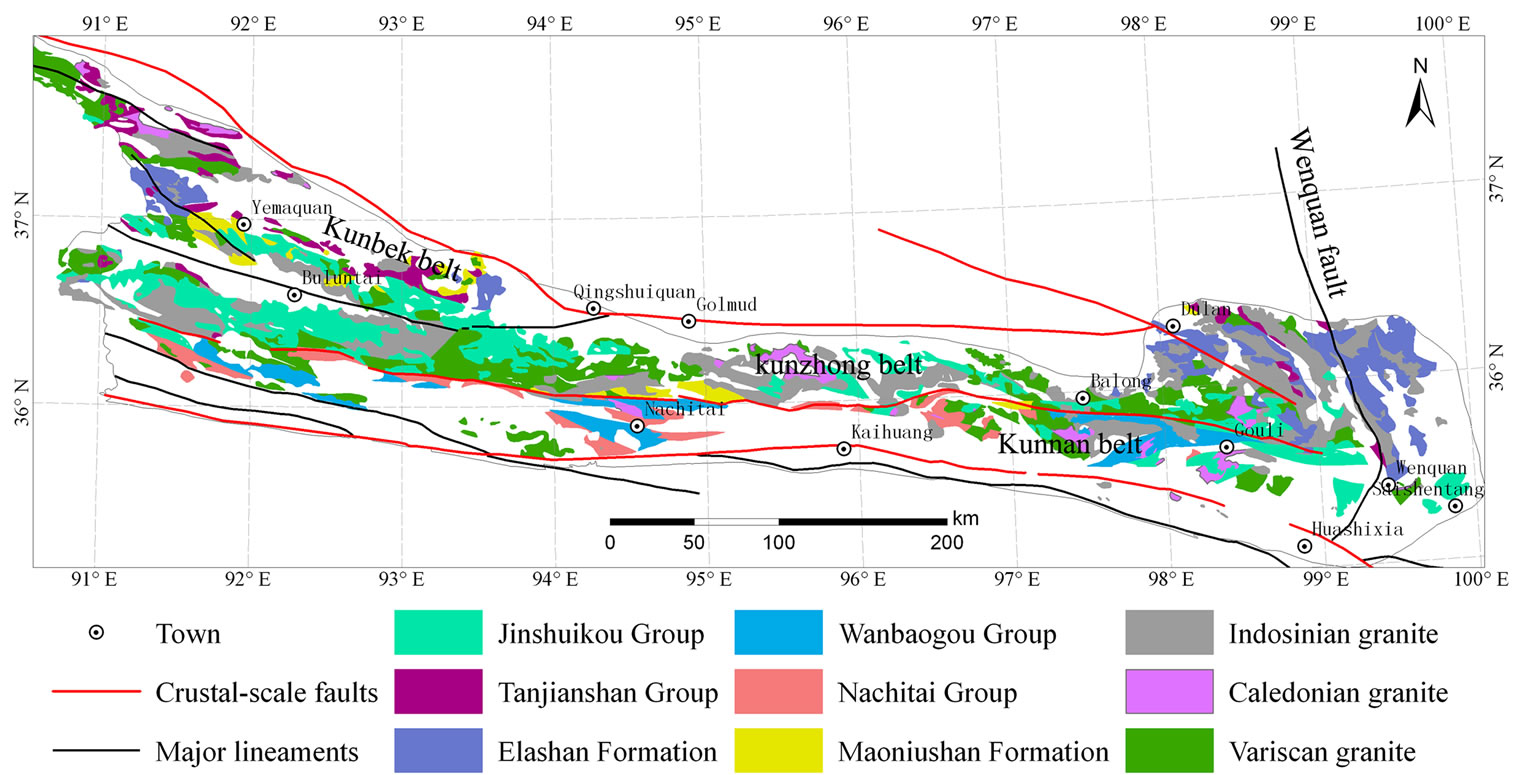
Figure 4. A simplified geological map of the eastern Kunlun Mountains, China.
Note: Showing major lithologic units, stratigraphic units, and crustal-scale faults. The east Kunlun orogenic belt is subdivided into the Kunbei belt, and the Kunnan belt.
and low-grade metamorphic rock. Kunzhong (“zhong” is middle in Chinese) belt is the basement of an uplift belt and a granitic belt. It is made predominantly of the middle to late Proterozoic metamorphic sequences, and Palaeozoic and Mesozoic granitic rock. The Devonian continental sandstones, conglomerate, and volcanic rock, and Carboniferous marine limestone and sedimentary rock lie over the metamorphic and plutonic basement. The composition of Kunnan (“nan” means south in Chinese) belt is geologically similar to that of the Kunzhong belt, but it consists of numerous Triassic successions. As of today, there are 81 known sites of iron formation within the area. Their locations are shown as black dots in Figure 3.
Within the study area, regions exposed mainly by lithologic and stratigraphic units are displayed in Figure 4. The Jinshuikou Group is the oldest crystalline basement that comprises gneiss, amphibolite rock, migmatite, and marble. It belongs to a suite of middle-to-high grade of metamorphic rock [22]. The Tanjianshan Group of the Ordovician-Cambrian period is composed of intermediate-mafic volcanic rock, and phyllite crystalline limestone and sandstone. The Elashan Formation of the Triassic time consists basically of volcanic rock that is intermediate-acid. The rock is with sandstone intercalation. The Wanbaogou Group of the New Mesoproterozoic period is subdivided into an upper unit and a lower one, comprising mainly carbonate rock and intermediate-mafic volcanic rock. Both types of rock belong to the pre-Cambrian folding basement with a low-grade of metamorphism [23]. The volcanic rock and carbonaceous slate of the Wanbaogou Group serve as important ore beds of precious metal (e.g., gold) and non-ferrous metals (copper, cobalt, and nickel) in the Kunnan belt [24]. The Nachitai Group of the Ordovician period consists largely of schist, mafic volcanic rock, chert, and crystalline limestone. The Maoniushan Formation of the Devonian time is composed of an intermediate-acid volcanic rock underlain by clastic rock. The Variscan-Indosinian granite is closely associated with the metalliferous mineralization in the region when the granite occurs extensively, diversely and permanently [25]. Known iron mineralization occurred mainly in the Yemaquan metallogenic belt located in the western part of the Mountains, whereas the Dulan-Elashan metallogenic belt lies in the east.
3.2. Data Preprocessing and Metallogenic Case Construction
The best ore-controlling variable and threshold were determined using proximity analysis of the weights-ofevidence model. On the basis of a correlation analysis among evidence variables, the authors selected vector ore-controlling data of stratum, unconformity, fault, regional geochemical data, remote-sensing mineralization information, Bouguer gravity data, aeromagnetic dataand mineral occurrence for this experiment. Before constructing the specific metallogenic case, the region was partitioned into 96,576 grids, each one being 1 km by 1 km. All of the evidence-variable data were spatially joined to a grid polygon, and each grid had corresponding feature-attribute values. The unconformity, fault, and mineral occurrences were buffered by with distances of 3000 m, 300 m, and 1000 m, respectively.
To extract the spatial features of the metallogenic case, the fault’s direction (orientation relationship), the shortest distance between mineral occurrence and faults (metric relationship), the disjoint relationship between mineral occurrence and faults, and the unconformities (topology relationship) were computed and extracted in each grid polygon. The spatial relationships were then transformed into attributes and stored in the attribute tables of each grid polygon. This process paved the way for metallogenic case retrieval. In this way, the metallogenic representation model combined with spatial and attribute features was constructed. Each grid polygon became a case representation object. By analyzing each grid layer’s attribute table in tandem with ore-controlling factors, the authors established the metallogenic case’s attribute features by using lithological characters, chronostratigraphy, unconformity, fault, regional chemical anomaly, remote-sensing mineralisation anomaly, Bouguer gravity anomaly, and aeromagnetic anomaly. In this way, specific genetic types became object attributes. The metallogenic case representation model in this research is as follows:
C = (unconformity, regional geochemical anomaly, Bouguer gravity anomaly, aeromagnetic anomaly, chronostratigraphy, lithological characters, remote-sensing mineralisation anomaly, fault characters, fault directions, short distance to fault, distance to unconformity, disjoint fault, disjoint unconformity, genetic type).
Prior to analysis, the attribute and spatial features of the above case are set corresponding weights, which are determined and assigned based on the Analytic Hierarchy Process (AHP) [26]. On the basis of expert knowledge, the importance of AHP case features is as follows: regional geochemical anomaly > fault directions > short distance to fault = disjoint fault > fault characters = remote-sensing mineralisation anomaly > chronostratigraphy = lithological characters > distance to unconformity = disjoint unconformity > unconformity characters = Bouguer gravity anomaly = aeromagnetic anomaly. Table 1 shows the comparison matrix of metallogenic CBR features by AHP. The matrix is equalised and simplified to seven features. After calculating, uniformity has been passed and each feature weight determined; identical, important features have the same weights (Table 2).
To grid the polygonal layers that are overlapped by attribute and spatial features, the authors analysed each grid

Table 1. The CBR features comparison matrix by AHP.
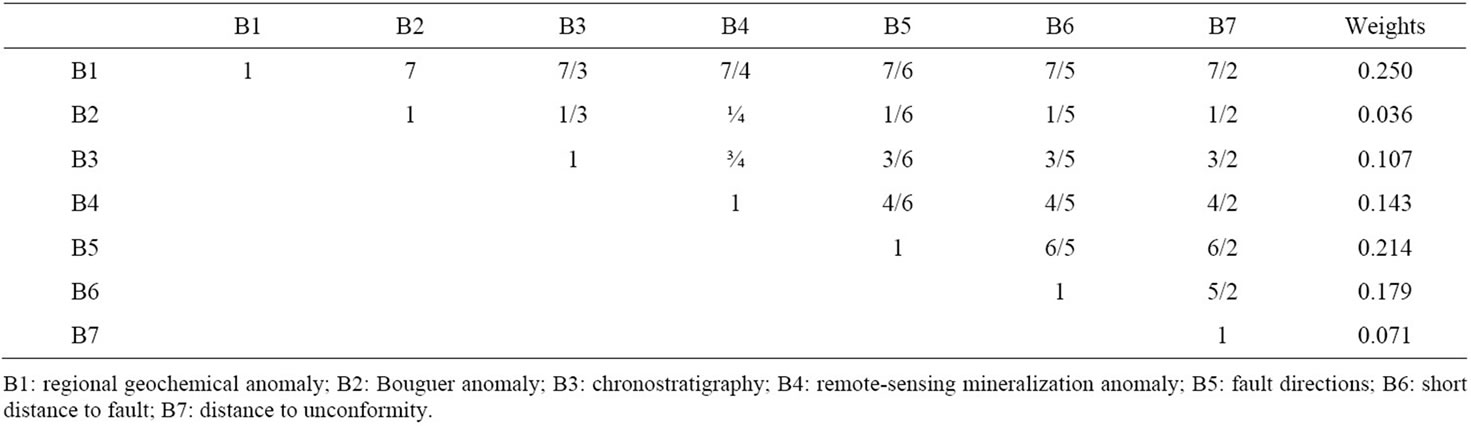
Table 2. The CBR equivalent property features comparison matrix and weights determined by AHP.
layer’s attribute table, selected all the records in which the field showing the genetic type of mineral occurrence was non-empty, and exported those records for further analysis. The final records were stored in a text file in which all attribute values were separated by tabs. The corresponding genetic type case base was then constructed. The attribute tables of relevant grid polygon layers were exported and stored in a text file, and each unsolved case set was constructed (each grid represents an unsolved case object). Each grid in the polygon layers corresponds to an unsolved metallogenic case. After a similarity measurement, each grid was assigned a genetic type, and the similarities were assigned values between 0 and 100%. In this way, the classification strategy automatically outlined a regional metallogenic prediction map showing high, medium, and low potentials.
3.3. Mineral Potential Prediction Results and Analysis
Based on the data-processing and metallogenic CBR model described above, an experiment regarding mineral potential prediction for iron deposits was performed in the eastern Kunlun Mountains, China. Figure 5 reports, respectively, the curves representing the relationships between 1) posterior probability based on the WOE and cumulative mineral occurrence; and 2) posterior probability and cumulative areas. Table 3 and Figure 6 show the favorable metallogenic potential regions (i.e., areas of high and medium potential) extracted using weights-ofevidence model. Highand medium-potential areas occupy 21% of the study area and contain 62 points of 81 known deposit points (i.e., 77% of known deposit points). High-potential areas occupy 11% of the total area and include 45 known deposit points (i.e., 56% of known deposit points). Medium-potential areas occupy 10% of the total area and include 17 known deposit points (i.e., 21% of known deposit points).
Table 3 and Figure 7 present the potential prediction results for iron deposits using the proposed metallogenic CBR method. Favorable metallogenic regions (i.e., highand medium-potential areas) account for 21% of the

Table 3. The contrast of prediction results using CBR and WOE.
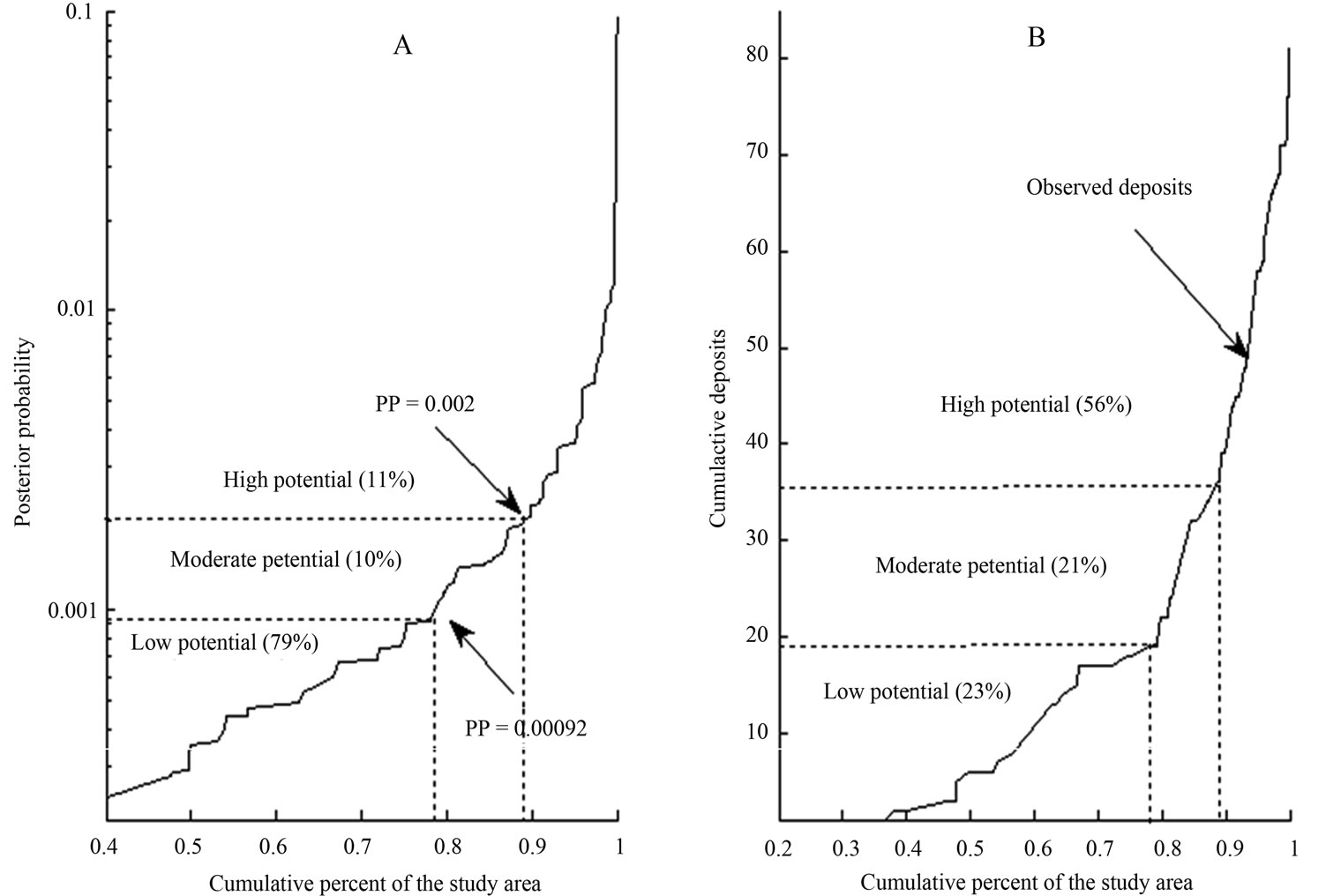
Figure 5. Variation of cumulative area with sum of weights and cumulative deposits using WOE.
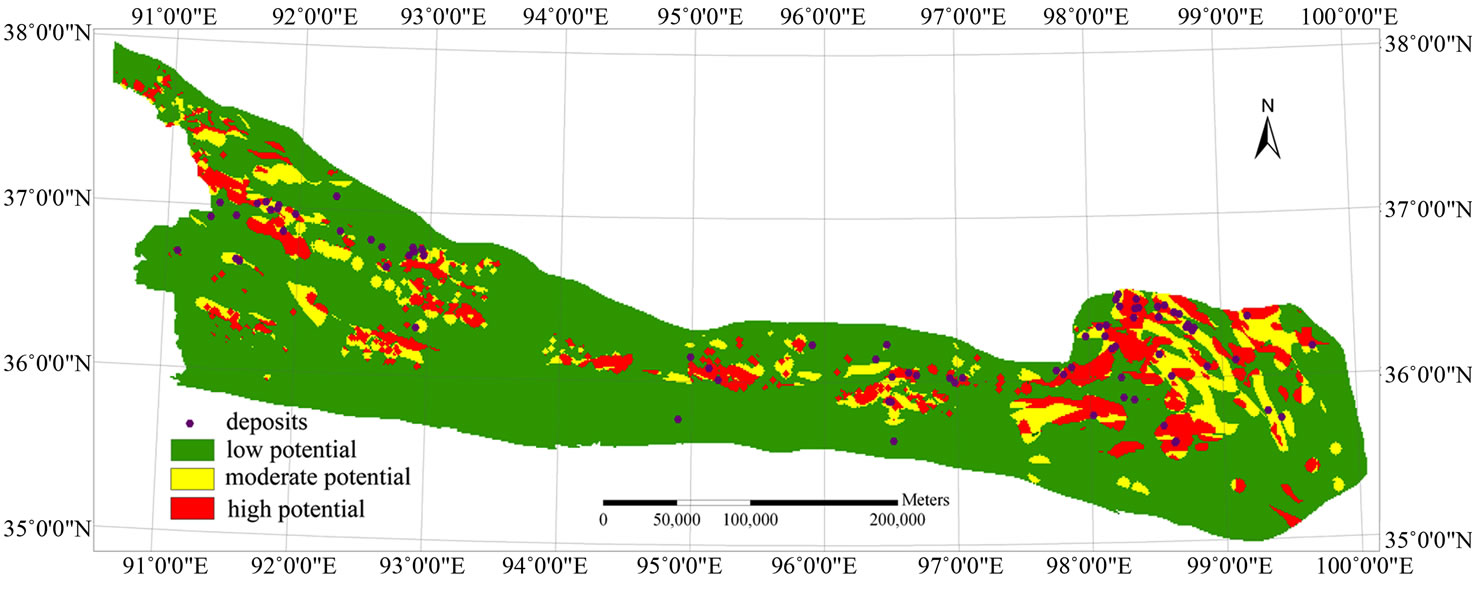
Figure 6. Potential prediction map for iron deposits using WOE in eastern Kunlun Moutains, China.
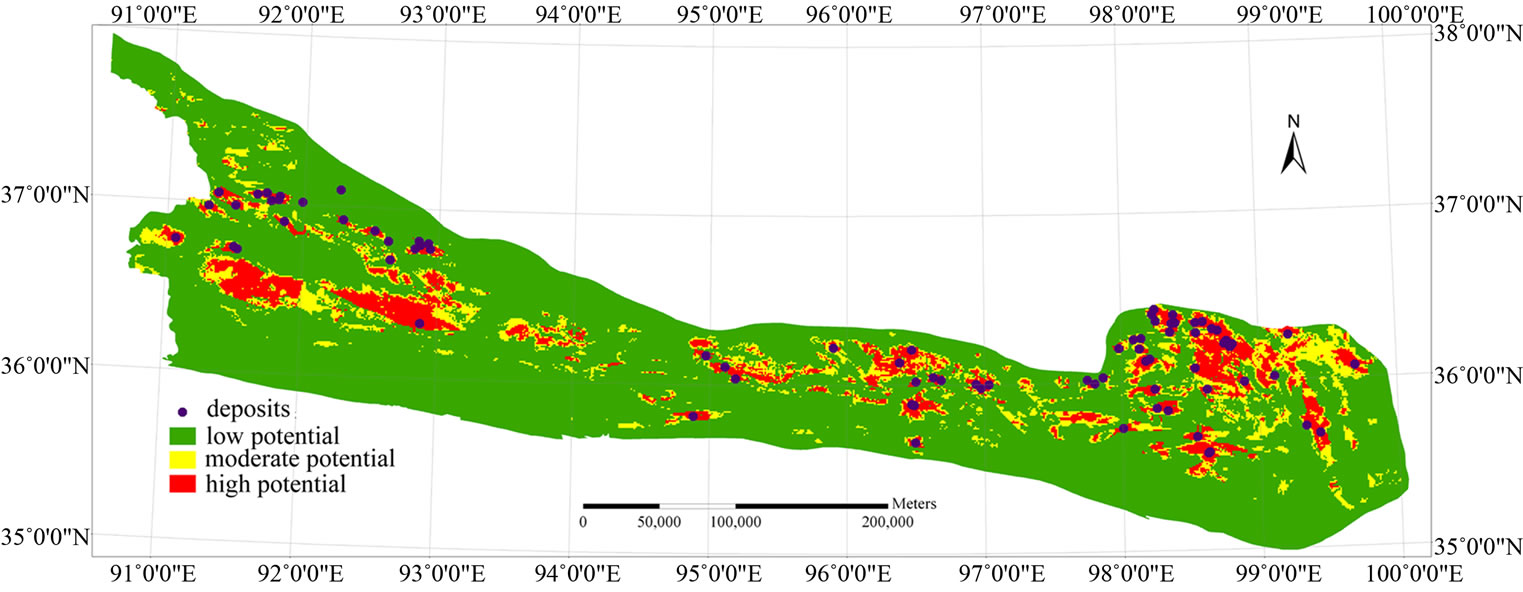
Figure 7. Potential prediction map for iron deposits using CBR in eastern Kunlun Mountains, China.
study area, with high-potential areas accounting for 10% of the total area and the medium-potential areas accounting for 11% of the total area. The prediction results show that known mineral occurrence is highly consistent with the high-potential areas, as analysis predicts that 68 of 81 known mineral occurrences fall into the high-potential areas (84%), 5 fall into the medium-potential areas (6%), and 8 fall into the low-potential areas (10%). Overall prediction accuracy (highand medium-potential areas account for 90%) is significantly higher than the accuracy of the traditional weights-of-evidence model (i.e., 77%).
4. Conclusion
The metallogenic CBR method for regional mineral prospectivity mapping is a new and intelligent prediction method. It makes full use of multisource massive geology spatial data. It also surpasses traditional mineralprediction approaches to improve the intelligence, efficiency, and accuracy of mineral prediction. This paper takes spatial features of geology data into account and proposes an integral metallogenic CBR method, which includes the metallogenic case representation model, metallogenic case storage, and the metallogenic case similarity retrieval model. Finally, an application of mineral potential prediction for iron deposits was performed in the eastern Kunlun Mountains, China, using a metallogenic CBR and WOE, respectively. The results indicated that the prediction accuracy of the metallogenic CBR is significantly higher than the accuracy of the traditional weights-of-evidence model.
5. Acknowledgements
This study was supported by the National Natural Science Foundation of China (Grant No. 41171302 & 40701146) and the National High-Tech R&D Program of China (Grant No. 2007AA12Z227). We express our gratitude to Zhuang Yongcheng from the Qinghai Institute of Geology Survey for his directions.
REFERENCES
- A. K. Porwal and O. P. Kreuzer, “Introduction to the Special Issue: Mineral Prospectivity Analysis and Quantitative Resource Estimation,” Ore Geology Reviews, Vol. 38, No. 3, 2010, pp. 121-127. doi:10.1016/j.oregeorev.2010.06.002
- G. F. Bonham-Carter, F. P. Agterberg and D. F. Wright, “Weights of Evidence Modeling: A New Approach to Mapping Mineral Potential,” In: F. P. Agterberg, et al., Eds., Statistical Applications in the Earth Sciences, Canadian Government Publishing Centre, Ottawa, 1989, pp. 171-183.
- F. P. Agterberg, “Combining Indicator Patterns in Weights of Evidence Modeling for Resource Evaluation,” Natural Resources Research, Vol. 1, No. 1, 1992, pp. 39-50. doi:10.1007/BF01782111
- J. R. Harris, L. Wilkinson and E. C. Grunsky, “Effective Use and Interpretation of Lithogeochemical Data in Regional Mineral Exploration Programs: Application of Geographic Information Systems (GIS) Technology,” Ore Geology Reviews, Vol. 16, No. 3-4, 2000, pp. 107-143. doi:10.1016/S0169-1368(99)00027-X
- E. J. M. Carranza, “Weights of Evidence Model of Mineral Potential: A Case Study Using Small Number of Prospects, Abra, Philippines,” Natural Resources Research, Vol. 13, No. 3, 2004, pp. 173-187. doi:10.1023/B:NARR.0000046919.87758.f5
- B. Daneshfar, A. Desrochers and P. Budkewitsch, “Mineral-Potential Mapping for MVT Deposits with Limited Data Sets Using Landsat Data and Geological Evidence in the Borden Basin, Northern Baffin Island, Nunavut, Canada,” Natural Resources Research, Vol. 15, No. 3, 2006, pp. 129-149. doi:10.1007/s11053-006-9020-7
- A. Porwal, I. González-Álvarez, V. Markwitz, T. C. McCuaig and A. Mamuse, “Weights-of-Evidence and Logistic Regression Modeling of Magmatic Nickel Sulfide Prospectivity in the Yilgarn Craton, Western Australia,” Ore Geology Reviews, Vol. 38, No. 3, 2010, pp. 184-196. doi:10.1016/j.oregeorev.2010.04.002
- B. B. He, C. H. Chen and Y. Liu, “Gold Resources Potential Assessment in Eastern Kunlun Mountains of China Combining Weights-of-Evidence Model with GIS Spatial Analysis Technique,” Chinese Geographical Science, Vol. 20, No. 5, 2010, pp. 461-470. doi:10.1007/s11769-010-0420-6
- F. P. Agterberg, G. F. Bonham-Carter, Q. M. Cheng and D. F. Wright, “Weights of Evidence Model and Weighted Logistic Regression in Mineral Potential Mapping,” In: J. C. Davis, et al., Eds., Computers in Geology, Oxford University Press, New York, 1993, pp. 13-32.
- E. J. M. Carranza and M. Hale, “Logistic Regression for Geologically Constrained Mapping of Gold Potential, Baguio District, Philippines,” Exploration and Mining Geology, Vol. 10, No. 3, 2001, pp. 165-175. doi:10.2113/0100165
- F. Aminzadeh, “Applications of Fuzzy Expert Systems in Integrated Oil Exploration,” Computers & Electrical Engineering, Vol. 20, No. 2, 1994, pp. 89-97. doi:10.1016/0045-7906(94)90023-X
- X. Luo and R. Dimitrakopoulos, “Data-Driven Fuzzy Analysis in Quantitative Mineral Resource Assessment,” Computers & Geosciences, Vol. 29, No. 1, 2003, pp. 3-13. doi:10.1016/S0098-3004(02)00078-X
- K. Koike, S. Matsuda, T. Suzuki and M. Ohmi, “Neural Network-Based Estimation of Principal Metal Contents in the Hokuroku District, Northern Japan, for Exploring Kuroko-Type Deposits,” Natural Resources Research, Vol. 11, No. 2, 2002, pp. 135-156. doi:10.1023/A:1015520204066
- J. P. Rigol-Sanchez, M. Chica-Olmo and F. Abarca-Hernandez, “Artificial Neural Networks as a Tool for Mineral Potential Mapping with GIS,” International Journal of Remote Sensing, Vol. 24, No. 5, 2003, pp. 1151-1156. doi:10.1080/0143116021000031791
- P. Gumiel, D. J. Sanderson, M. Arias, S. Roberts and A. Martín-Izard, “Analysis of the Fractal Clustering of Ore Deposits in the Spanish Iberian Pyrite Belt,” Ore Geology Reviews, Vol. 38, No. 4, 2010, pp. 307-318. doi:10.1016/j.oregeorev.2010.08.001
- G. P. Lekkas, N. M. Avouris and L. G. Viras, “CaseBased Reasoning in Environmental Monitoring Applications,” Applied Artificial Intelligence, Vol. 8, No. 3, 1994, pp. 359-376. doi:10.1080/08839519408945448
- A. Holt and G. L. Benwell, “Applying Case-Based Reasoning Techniques in GIS,” International Journal of Geographical Information Science, Vol. 13, No. 1, 1999, pp. 9-25. doi:10.1080/136588199241436
- J. A. Ye and X. Shi, “Integrating Case-Based Reasoning and GIS for Handling Planning Applications,” Journal of Urban Planning Department, No. 3, 2001, pp. 34-40.
- Y. Y. Du, W. Wen, F. Cao and J. Min, “A Case-Based Reasoning Approach for Land Use Change Prediction,” Expert Systems with Applications, Vol. 37, 2010, pp. 5745-5750. doi:10.1016/j.eswa.2010.02.035
- R. C. Schank and P. A. Robert, “Scripts, Plans, Goals, and Understanding: An Inquiry into Human Knowledge Structures,” Lawrence Erlbaum, Hillsdale, 1977.
- L. D. Kemp, G. F. Bonham-Carter and G. L. Raines, “ArcWofE: ArcView Extension for Weights of Evidence Mapping [EB/OL],” 1999. http://gis.nrcan.gc.ca/software/arcview/wofe
- G. C. Wang, Q. H. Wang, P. Jian and Y. H. Zhu, “Zircon SHRIMP Ages of Precambrian Metamorphic Basement Rocks and Their Tectonic Significance in the Eastern Kunlun Mountains, Qinghai province, China,” Earth Science Frontiers , Vol. 11, No. 4, 2004, pp. 481-490 .
- Y. S. Pan, W. M. Zhou and R. H. Xu, “The Early Palaozoic Geological Features and Evolutions of the Kunlun Mountain,” Science in China (Series D), Vol. 26, No. 4, 1996, pp. 302-307.
- X. D. Guo, Y. J. Zhang, G. G. Liu, A. J. Pan and F. Zhang, “Metallogenic Regularities and Prospecting Direction of Gold and Copper in Eastern Kunlun,” Gold Geology, Vol. 10, No. 4, 2004, pp. 16-22.
- Z. Z. Qian, Z. G. Hu, J. Q. Liu and H. M. Li, “Active Continental Margin and Regional Metallogenesis of the Palaeo-Tethys in the East Kunlun Mountains,” Geotectonica et Metallogenia, Vol. 24, No. 2, 2000, pp. 134-139.
- T. L. Saaty and L. G. Vargas, “Uncertainty and Rank Order in the Analytic Hierarchy Process,” European Journal of Operational Research, Vol. 32, No. 1, 1987, pp. 107- 117. doi:10.1016/0377-2217(87)90275-X

