Natural Science
Vol.08 No.12(2016), Article ID:72355,12 pages
10.4236/ns.2016.812051
Molecular Dynamics Simulation of Interaction of Short Lysine Brush and Oppositely Charged Semax Peptides
Elena Popova1, Boris Okrugin2, Igor Neelov3,4
1Research Institute of Hygiene, Occupational Pathology and Human Ecology, St. Petersburg, Russia
2St. Petersburg State University, St. Petersburg, Russia
3ITMO University, St. Petersburg, Russia
4Institute of Macromolecular Compounds, Russian Academy of Sciences, St. Petersburg, Russia

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 27, 2016; Accepted: November 26, 2016; Published: November 29, 2016
ABSTRACT
The possibility of complex formation by short lysine brush and therapeutic Semax peptides was investigated using molecular dynamics method. Lysine dendrimers and polymer brushes are used for drug and other (e.g., DNA, peptides, and polysaccha- rides) molecules delivery to different target cells. It is known that they could penetrate blood brain barrier. Since short lysine brush is nontoxic, a system containing of such brush and 8 oppositely charged Semax peptides was studied. It was obtained that stable complexes consisting of brush and peptides formed and structures of these complexes were investigated. Such complex can be used in future for delivery of Semax peptides to brain since these peptides have significant antioxidant, antihypoxic and neuroprotective effects.
Keywords:
Lysine Brush, Semax Peptides, Computer Simulation, Method of Molecular Dynamics

1. Introduction
Interest to macromolecules with regular branched structure grows every year [1] . Beside well known dendrimers and in particular lysine dendrimers [2] and dendritic brushes [3] recently the new dendritic structure: dendrigraft was synthesized [4] . Dendrigrafts could be described from one hand as dendrimers with short linear chain in their core or from another hand as dendritic brush with short main chain and long side chains. Lysine dendrigrafts consist entirely of lysine aminoacid residues [4] [5] . At the same time their terminal groups could be functionalized by other aminoacids or by other active groups or molecules [6] . Lysine dendrigrafts are polymers that are rich with amines. Due to this reason they could be used as antibacterial [7] or antiviral agents [8] . It also makes possible the creation of biocompatible and biodegradable complexes with different drugs and other biological or bioactive molecules. In particular they could make complexes with oppositely charged peptides due to strong electrostatic interaction between their positively charged groups ( ) and negatively charged amino acid side groups (COO−) of peptides. Hydrogen bonds between dendrigraft and peptide and hydrophobic interactions between their nonpolar groups are also important for creation of such complexes. Due to this ability to make complexes the dendrigrafts like other dendritic molecules could be used as multifunctional nanocarriers for delivery of drug or/and other molecules [9] for treatment of various disease.
) and negatively charged amino acid side groups (COO−) of peptides. Hydrogen bonds between dendrigraft and peptide and hydrophobic interactions between their nonpolar groups are also important for creation of such complexes. Due to this ability to make complexes the dendrigrafts like other dendritic molecules could be used as multifunctional nanocarriers for delivery of drug or/and other molecules [9] for treatment of various disease.
Therapeutic Semax peptide [10] was selected for our study as a model peptide because it belongs to a class of regulatory peptides and has an antioxidant, antihypoxic and neuroprotective properties. Semax peptide is used for acute ischemic stroke prevention, during traumatic brain injury treatment, recovery of a patient after a stroke, in the case of optic nerve disease and glaucoma optic neuropathy. The drug is used in the form of solution for injection and as a spray. This peptide has molecular weight 863 Da and isoelectric point (pI) 5,13. Amino acid sequence of the peptide is shown on Figure 1.
In our previous paper we studied complexes of Semax peptides with lysine dendrimer [11] . The goal of this paper is to study the interaction between lysine dendrigraft of second generation and therapeutic peptide Semax using molecular dynamics method to determine whether the dendrigraft could adsorb peptide molecules and thus could be used for delivery of these peptides into cells.
2. Methods and Materials
2.1. Molecular Dynamics Method
Molecular dynamics (MD) method is currently the main method for simulation of

Figure 1. Amino acid sequence of Semax peptide.
polymer and biopolymer systems. The method consists in numerical solution of the classical Newton equations of motion for all atoms of the all molecules in the system. It was used first in the mid-fifties of the last century [12] for two-dimensional modeling of hard disks system (2D-model of a monoatomic gas), and then was used to simulate a variety of liquids, including water [13] [14] . In 1972 this method was first applied to the simulation of a simple model of a linear polymer chain consisting of atoms connected by rigid bonds [15] . In 1975 the dynamics of short n-alkanes was studied [16] . In subsequent years MD was used for study of many specific molecules using both coarse- grained and detailed full-atomic models. The potential energy of these models usually include valence bonds, valence angles and dihedral angle energies as well as van der Waals and electrostatic energies. The definition of parameters set adequately describing the test molecule properties (force-field) is challenging and requires the experimental data for these molecules, quantum chemical calculations as well as iterative procedures and a very large amount of machine time. Due to this reason several packages of standard computer programs, in which these parameters are defined for a fairly wide range of molecules become widely used in recent years. Currently the most popular molecular modeling packages are GROMACS, AMBER, CHARMM, and some others. Our simulation was performed by molecular dynamics method using the GROMACS 4.5.6 software package [17] and one of the most modern AMBER_99SB-ildn force fields [18] .
2.2. Model and Calculation Method
Modeling was performed using the molecular dynamics method for systems consisting of one lysine dendrigraft of second generation containing 8 lysine residues in main chain, 48 positively charged 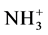 groups in 8 side chains, 8 Semax peptides (with charge −1 each), water molecules and 40 chlorine counterions in a cubic cell (the edge of the cube equal to 9 nanometers) with periodic boundary conditions. The initial conformations for dendrigraft and peptides with internal rotation angles of j = −135˚, y = 135˚, q = 180˚ was constructed using molecular editor Avogadro. The structures were optimized in vacuum using molecular mechanics of AMBER force field. Further energy minimizations and simulations were performed using the GROMACS 4.5.6 software package and AMBER_99SB-ildn force fields. The potential energy of this force field consists of valence bonds and angles deformation energy, internal rotation angles, van der Waals and electrostatic interactions. The procedure of molecular dynamics simulation used for lysine dendrigraft and peptides has been described earlier (for dendrimers and linear polyelectrlytes) in [19] - [31] . In all calculations the normal conditions (temperature 300 K, pressure 1 ATM) were used. Computing resources on supercomputers “Lomonosov” were provided by supercomputer center of Moscow State University [32] .
groups in 8 side chains, 8 Semax peptides (with charge −1 each), water molecules and 40 chlorine counterions in a cubic cell (the edge of the cube equal to 9 nanometers) with periodic boundary conditions. The initial conformations for dendrigraft and peptides with internal rotation angles of j = −135˚, y = 135˚, q = 180˚ was constructed using molecular editor Avogadro. The structures were optimized in vacuum using molecular mechanics of AMBER force field. Further energy minimizations and simulations were performed using the GROMACS 4.5.6 software package and AMBER_99SB-ildn force fields. The potential energy of this force field consists of valence bonds and angles deformation energy, internal rotation angles, van der Waals and electrostatic interactions. The procedure of molecular dynamics simulation used for lysine dendrigraft and peptides has been described earlier (for dendrimers and linear polyelectrlytes) in [19] - [31] . In all calculations the normal conditions (temperature 300 K, pressure 1 ATM) were used. Computing resources on supercomputers “Lomonosov” were provided by supercomputer center of Moscow State University [32] .
3. Results and Discussion
Snapshots of a system consisting of dendrigraft of second generation, peptides, ions and water during simulation are shown on Figure 2 (water molecules are not shown Fclarity). It is clearly seen that at the beginning of process (Figure 2(a)) peptide molecules

Figure 2. Stages of the dendrimer and Semax peptides complex formation (initial, intermediate and final): system of dendrimer and 8 peptides: t = 0 (a); t = 30 ns (b); t = 200 ns (c). Atoms of dendrigraft molecule is shown as beads with diameter equal to their van der Waals radii. Valence bonds of various peptides are shown with lines of different colors (backbone of each peptide is shown by thick line of the same color as valence bonds).
are far from dendrigraft. After 30 ns (Figure 2(b)) most of peptide molecules are already adsorbed on the surface of dendrigraft, and in the end (Figure 2(c)) all peptide molecules in both systems are on its surface.
To characterize the size of the subsystem containing dendrigraft and peptides during the equilibration the square of instant gyration radius 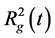 was used. It was calculated using (1):
was used. It was calculated using (1):
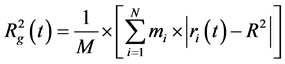 (1)
(1)
where R―is the center mass of dendrigraft, ri и mi―coordinates and masses of i atom correspondingly, N―is the total number of atoms in dendrigraft, M is the total mass of dendrigraft. This function was calculated using g_gyrate function of GROMACS software [17] .
3.1. Modeling of Equilibrium Process Establishment
The time dependence of radius of gyration Rg of dendrigraft and peptides at the beginning of calculation describes the kinetics of process of complex formation (Figure 3). From Figure 3 it can be seen that dendrigraft complex with 8 peptides forms within first 20 ns. After that the complex size Rg fluctuate slightly, but its average value practically does not change with time. Therefore, we can assume that the system is in equilibrium state.
The time dependence function of distances between dendrigraft and peptides also demonstrates the formation of complex within first 20 - 30 ns of simulation. Plateau on curves of Figure 3(b) (at times greater than 20 - 30 ns) means that system is in equilibrium state and all peptides are already adsorbed on surface of dendrigraft molecule. This function was calculated using g_bond function of GROMACS software [17] . Thus the dendrigraft makes complex with 8 peptides within first 20 - 30 ns of simulation.
Another quantity that can characterize the rate of complex formation is the total number of hydrogen bonds (N) between dendrigraft and peptides. The dependence of this value on time is shows on Figure 4 and demonstrates how the number of specific contacts between them increases during complex formation. This function was calculated using g_hbonds package of GROMACS.
From Figure 4 it can be concluded that the system reaches equilibrium (plateau) for the first time after 20 - 30 ns. It correlates with the results for the radius of gyration obtained in Figure 3.

Figure 3. System of dendrigraft DG2 and 8 Semax peptides: (a) time dependence of radius of gyration, (b) time dependence of distance between dendrigraft and peptides.
Figure 4. Time dependence of hydrogen bonds number (N) during the complex formation: DG2 and 8 Semax.
3.2. Modeling of the Equilibrium State
The size of complex in equilibrium state is evaluated by mean square of radius of gyration averaged through the time after equilibration (2):
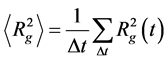 (2)
(2)
where Dt = tmax − teq , tmax―full time of calculation and and teq―time of equilibration and < > means averaging the through equilibrium part of MD trajectory.
In equilibrium state the size of the complex (DG2 and 8 Semax peptides) is larger than the size of dendrigraft (see Table 1). It is quite natural, since it correlates with the increase of molecular weight of the complexes compared to the molecular weight of the individual dendrigraft.
The shape of complex can be characterized by its tensor of inertia main component ratio (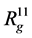 ,
, 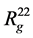 ,
,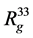 ), that are in Table 1. For example, in the simplest case, anisotropy can be characterized by
), that are in Table 1. For example, in the simplest case, anisotropy can be characterized by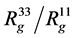 .
.
The shape of complex could be roughly characterised by ratio of largest and smallest eigenvalues of inertia tensor describing our system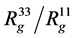 . Calculated values of these anisotropy for our systems are presented in Table 2. Thus the anisotropy of complex in water is slightly less than anisotropy of single dendigraft in water itself.
. Calculated values of these anisotropy for our systems are presented in Table 2. Thus the anisotropy of complex in water is slightly less than anisotropy of single dendigraft in water itself.
Information about the internal structure of the equilibrium complex could be obtained using radial density distribution (3) of different groups of atoms relatively center of inertia of system.
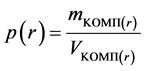 (3)
(3)
where mcomp―mass of all atoms in complex; Vкомп―volume of complex.
The radial distribution functions (not normalized) calculated using g_rdf function of GROMACS are shown on Figure 5. Figure 5 demonstrates that dendrigraft (curve 2,
Table 1. Eigenvalues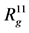 ,
, 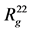 ,
, 
Table 2. The values of anisotropy of shape 
Figure 5. Radial distribution p(r) curves: dendrigraft DG2 and 8 Semax. Distribution curves: peptide atoms (1); dendrigraft atoms (2); all atoms of complex (3).
Figure 5) is located mainly in the center of the complexes and peptides (curve 1, Figure 5) mainly on the surface of complex. At the same time some fraction of peptides could slightly penetrate into outer part of dendrigraft but not to its inner part (see Figure 5).
The number of hydrogen bonds between peptides and dendrigraft shows how tightly peptides associate with dendrigraft. From equilibrium part of Figure 4 (at times greater 20 - 30 ns) it follows that average hydrogen bonds number in equilibrium state between dendrigraft DG2 and 8 Semax peptides is equal to 25.
The distribution function of hydrogen bonds number (Figure 6) shows how the number of hydrogen bonds in the equilibrium state can deviate relative to the average value. We obtained that the resulting function for complex has a peak of numbers of bonds equal 25 which coincide with average number of hydgrogen bonds between dendrimer and peptides. Thus this function is quite symmetrical. Fluctuations in hydrogen bonds number for our system are in the range of 15 - 40.
The other characteristic of interaction between dendrigraft and peptides in complex is the distribution of ion pairs number between their charged groups. Figure 7 shows the dependence of probability (not normalized) of different distances between positive groups of dendrimer and negative groups of peptides. It is seen that there is a sharp first peak, corresponding to the direct contact between positively charged groups (
Figure 6. The distribution function P(N) of hydrogen bonds number N of complex: complex DG2 and 8 Semax.
Figure 7. Radial distribution function of ion pairs:complex of DG2 and 8 Semax molecules, 

To evaluate the translational mobility of our systems, the time dependence of the mean square displacements (4) of the centers of inertia (MSD), were calculated (Figure 8). MSD was calculated using g_msd function of GROMACS [17] .
We have found that dependence of MSD function on time is almost linear in some interval of time t in double logarithm coordinates (not shown). It means that in this interval the motion of complex is the diffusion-like motion (see Figure 8). Coefficient of translational diffusion of the complex was determined from the slope of the obtained time dependence of MSD for system and was equal D = 0.18 ± 0.01 sm2/s.
4. Conclusion
The system consisting of second generation dendrigraft and 8 Semax molecules in water with counterions has been studied. The process of complex formation by lysine dendrigraft of second generation and therapeutic Semax peptides and the equilibrium structure of the complex was investigated for the first time by the method of molecular dynamics simulation. It was shown that dendrigraft-peptide complex formation occurs rather quickly (in first 20 - 30 ns). After this time the complex is stable and the dendrigraft atoms are mainly inside the complex, while the peptide atoms are mainly on the surface of dendrigraft. In future it is necessary to study process of complexes formation and stability of similar complexes with greater number of peptides to define maximum capacity of this particular dendrigraft for delivery of Semax peptide.
Acknowledgements
This work was partly supported by grant 074-U01 of Government of RF and RFBR
Figure 8. Mean square displacements of the centers of inertia: complex of DG2 and 8 Semax.
grants 16-03-00775 and 15-33-20693mol_a_ved. Computing resources on supercomputers “Lomonosov” were provided by supercomputer center of Moscow State University [32] .
Cite this paper
Popova, E., Okrugin, B. and Neelov, I. (2016) Molecular Dynamics Simulation of Interaction of Short Lysine Brush and Oppositely Charged Semax Peptides. Natural Science, 8, 499-510. http://dx.doi.org/10.4236/ns.2016.812051
References
- 1. Frechet, J.M.J. and Tomalia, D.A. (2001) Dendrimers and Other Dendriric Polymers. John Wiley & Sons Ltd., West Sussex.
https://doi.org/10.1002/0470845821 - 2. Denkewalter, R.G., Kolc, J. and Lukasavage, W.J. (1983) Macromolecular Highly Branched Homogeneous Compound. US Patent No. 4410688.
- 3. Lee, C.C. and Fréchet, J.M.J. (2006) Synthesis and Conformations of Dendronized Poly-L-Lysine. Macromolecules, 39, 476-481.
https://doi.org/10.1021/ma052078b - 4. Cottet, H., Martin, M., Papillaud, A., Souaid, E., Collet, H. and Commeyras, A. (2007) Determination of Dendrigraft Poly-L-Lysine Diffusion Coefficients by Taylor Dispersion Analysis. Biomacromolecules, 8, 3235-3243.
https://doi.org/10.1021/bm070268j - 5. Collet, H., Souaid, E., Cottet, H., Dératani, A., Boiteau, L., Dessalces, G., Rossi, J.-C., Commeyras, A. and Pascal, R. (2010) Expeditious, Multigram Scale Synthesis of Lysine Dendrigraft (DGL) Polymers by Aqueous N-Carboxyanhydride Polycondensation. Chemistry: A European Journal, 16, 2309-2316.
https://doi.org/10.1002/chem.200901734 - 6. Rossi, J.-C., Boiteau, L., Collet, H., Tsamba, B.M., Larcher, N. and Pascal, R. (2012) Functionalisation of Free Amino Groups of Lysine Dendrigraft (DGL) Polymers. Tetrahedron Letters, 53, 2976-2979.
https://doi.org/10.1016/j.tetlet.2012.03.082 - 7. Oukacine, F., Romestand, B., Goodall, D.M., Massiera, G., Garrelly, L. and Cottet, H. (2012) Study of Antibacterial Activity by Capillary Electrophoresis Using Multiple UV Detection Points. Analytical Chemistry, 84, 3302-3310.
https://doi.org/10.1021/ac300004t - 8. Cadiere, A., Couturaud, B., Boismard, J., Le Cann, P., Gerard, A., Mas, A., Faye, C., Garrelly, L. and Roig B. (2013) Assessment of Poly-L-Lysine Dendrigrafts for Virus Concentration in Water: Use of MS2 Bacteriophage as Proof of Concept. Journal of Applied Microbiology, 115, 290-297.
https://doi.org/10.1111/jam.12209 - 9. Li, J., Guo, Y., Kuang, Y., An, S., Ma, H. and Jiang, C. (2013) Choline Transporter-Targeting and Co-Delivery System for Glioma Therapy. Biomaterials, 34, 9142-9148.
https://doi.org/10.1016/j.biomaterials.2013.08.030 - 10. Shypshyna, M.S., Veselovsky, N.S., Myasoedov, N.F., Shram, S.I. and Fedulova, S.A. (2015) Effect of Peptide Semax on Synaptic Activity and Short-Term Plasticity of Glutamatergic Synapses of Co-Cultured Dorsal Root Ganglion and Dorsal Horn Neurons. Fiziologicheskiî Zhurnal, 61, 48-55.
- 11. Popova, E.V., Shavykin, O.V., Neelov, I.M. and Leermakers, F. (2016) Molecular Dynamics Simulation of Lysine Dendrimer and Semax Peptides Interaction. Scientific and Technical Journal of Information Technologies, Mechanics and Optics, 16, 716-724.
https://doi.org/10.17586/2226-1494-2016-16-4-716-724 - 12. Alder, B.J. and Wainwright, T.E. (1957) Molecular Dynamics by Electronic Computers. In: Prigogine, I., Ed., International Symposium on Transport Processes in Statistical Mechanics, John Wiley Int., New York, 97-131.
- 13. Verlet, L. (1967) Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Physical Review, 159, 98-103.
https://doi.org/10.1103/PhysRev.159.98 - 14. Rahman, A. and Stillinger, F.H. (1972) Mollecular Dynamics Study of Temperature Effects on Water Structure and Kinetics. Journal of Chemical Physics, 57, 1281-1292.
https://doi.org/10.1063/1.1678388 - 15. Balabaev, M.N.K., Grivtsov, A.G. and Shnol, E.E. (1972) Numerical Modeling of Motion of Molecules. Motion of Isolated Polymer Chain. Institute of Applied Mathematics, 4, 38.
- 16. Ryckaert, J.P., Ciccotti, G. and Berendsen, H.V.C. (1977) Numerical Integration of Cartesian Equations of Motion of Systems with Constraints-Molecular Dynamics of N-Alkanes. Journal of Computational Physics, 23, 327-341.
https://doi.org/10.1016/0021-9991(77)90098-5 - 17. Hess, B., Kutzner, C., Spoel, D. and Lindahl, E. (2008) GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. Journal of Chemical Theory and Computation, 4, 435-447.
https://doi.org/10.1021/ct700301q - 18. Hornak, V., Abel, R., Okur, A., Strockbine, D., Roitberg, A. and Simmerling, C. (2006) Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins: Structure Function and Genetics, 65, 712-725.
https://doi.org/10.1002/prot.21123 - 19. Neelov, I.M., Markelov, D.A., Falkovich, S.G., Ilyash, M.Y., Okrugin, B.M. and Darinskii, A.A. (2013) Mathematical Simulation of Lysine Dendrimers: Temperatiure Dependences. Polymer Science, 55, 154-161.
https://doi.org/10.1134/s1811238213050032 - 20. Falkovich, S., Markelov, D., Neelov, I. and Darinskii, A. (2013) Are Structural Properties of Dendrimers Sensitive to the Symmetry of Branching? Computer Simulation of Lysine Dendrimers. Journal of Chemical Physics, 139, Article ID: 064903.
https://doi.org/10.1063/1.4817337 - 21. Neelov, I., Falkovich, S., Markelov, D., Paci, E., Darinskii, A. and Tenhu, H. (2013) Molecular Dynamics of Lysine Dendrimers. Computer Simulation and NMR. In: Klajnert, B., Peng, L. and Cena, V., Eds., Dendrimers in Biomedical Applications, RSC Publishing, London, 99-114.
https://doi.org/10.1039/9781849737296-00099 - 22. Neelov, I.M., Janaszewska, A., Klajnert, B., Bryszewska, M., Makova, N., Hicks, D., Pearson, N., Vlasov, G.P., Ilyash, M.Y., Vasilev, D.S., Dubrovskaya, N.L., Zhuravin, I.A., Turner, A.J. and Nalivaeva, N.N. (2013) Molecular Properties of Lysine Dendrimers and Their Interactions with Ab-Peptides and Neuronal Cells. Current Medical Chemistry, 20, 134-143.
https://doi.org/10.2174/0929867311302010013 - 23. Neelov, I.M., Mistonova, A.A., Khvatov, A.Y. and Bezrodnij, V.V. (2014) Molecular Dynamic Simulation of Peptide Polyelectrolytes. Scientific and Technical Journal of Information Technologies, Mechanics and Optics, 169-175.
- 24. Popova, E.V., Shavykin, O.V., Neelov, I.M. and Leemakers, F. (2016) Molecular Dynamics Simulation of Lysine Dendrimer and Semax Peptides Interaction. Scientific and Technical Journal of Information Technologies, Mechanics and Optics, 16, 716-724.
https://doi.org/10.17586/2226-1494-2016-16-4-716-724 - 25. Markelov, D.A., Falkovich, S.G., Neelov, I.M., Ilyash, M.Y., Matveev, V.V., Lahderanta, E., Ingman, P. and Darinskii, A.A. (2015) Molecular Dynamics Simulation of Spin-Lattice NMR Relaxation in Poly-L-Lysine Dendrimers. Manifestation of the Semiflexibility Effect. Physical Chemistry and Chemical Physics, 17, 3214-3226.
https://doi.org/10.1039/C4CP04825C - 26. Ennari, J., Elomaa, M., Neelov, I. and Sundholm, F. (2000) Modelling of Water Free and Water Containing Solid Polyelectrolytes. Polymer, 41, 985-990.
https://doi.org/10.1016/S0032-3861(99)00235-9 - 27. Ennari, J., Neelov, I. and Sundholm, F. (2000) Comparison of Cell Multipole and Ewald Summation Methods for Solid Polyelectrolyte. Polymer, 41, 2149-2155.
https://doi.org/10.1016/S0032-3861(99)00382-1 - 28. Ennari, J., Neelov, I. and Sundholm, F. (2000) Molecular Dynamics Simulation of the PEO Sulfonic Acid Anion in Water. Computational and Theoretical Polymer Science, 10, 403-410.
https://doi.org/10.1016/S1089-3156(00)00006-4 - 29. Ennari, J., Neelov, I. and Sundholm, F. (2000) Molecular Dynamics Simulation of the Structure of PEO Based Solid Polymer Electrolytes. Polymer, 41, 4057-4063.
https://doi.org/10.1016/S0032-3861(99)00642-4 - 30. Ennari, J., Neelov, I. and Sundholm, F. (2001) Estimation of the Ion Conductivity of a PEO-Based Polyelectrolyte System by Molecular Modeling. Polymer, 42, 8043-8050.
https://doi.org/10.1016/S0032-3861(01)00311-1 - 31. Ennari, J., Neelov, I. and Sundholm, F. (2004) Modellling of Gas Transport Properties of Polymer Electrolytes Containing Various Amount of Water. Polymer, 45, 4171-4179.
https://doi.org/10.1016/j.polymer.2004.03.096 - 32. Sadovnichy, V., Tikhonravov, A., Voevodin, V. and Opanasenko, V. (2013) Contemporary High Performance Computing: From Petascale toward Exascale, CRC Press, Boca Raton, 283-307.







